Binary Classifier Calibration Using a Bayesian Non-Parametric Approach

Abstract

Learning probabilistic predictive models that are well calibrated is critical for many prediction and decision-making tasks in Data mining. This paper presents two new non-parametric methods for calibrating outputs of binary classification models: a method based on the Bayes optimal selection and a method based on the Bayesian model averaging. The advantage of these methods is that they are independent of the algorithm used to learn a predictive model, and they can be applied in a post-processing step, after the model is learned. This makes them applicable to a wide variety of machine learning models and methods. These calibration methods, as well as other methods, are tested on a variety of datasets in terms of both discrimination and calibration performance. The results show the methods either outperform or are comparable in performance to the state-of-the-art calibration methods.

1 Introduction

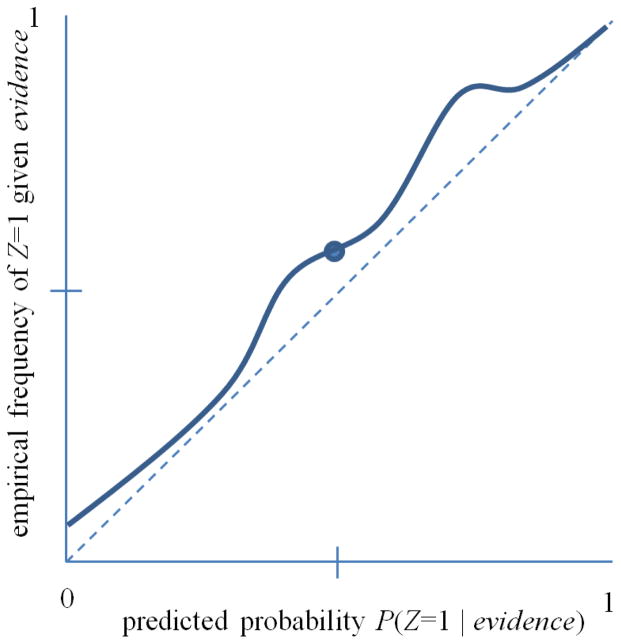
A rational problem solving agent aims to maximize its utility subject to the existing constraints [11]. To be able to maximize the utility function for many practical prediction and decision-making tasks, it is crucial to develop an accurate probabilistic prediction model from data. Unfortunately, the majority of existing data mining models and algorithms are not optimized for obtaining accurate probabilities and the predictions they produce may be miscalibrated. Generally, a set of predictions of a binary outcome is well calibrated if the outcomes predicted to occur with probability p do occur about p fraction of the time, for each probability p that is predicted. This concept can be readily generalized to outcomes with more than two values. Figure 1 shows a hypothetical example of a reliability curve [3, 9], which displays the calibration performance of a prediction method. The curve shows, for example, that when the method predicts Z = 1 to have probability 0.5, the outcome Z = 1 occurs in about 0.57 fraction of the instances (cases). The curve indicates that the method is fairly well calibrated, but it tends to assign probabilities that are too low. In general, perfect calibration corresponds to a straight line from (0,0) to (1,1). The closer a calibration curve is to this line, the better calibrated is the associated prediction method.

Figure 1.

The solid line shows a calibration (reliability) curve for predicting Z = 1. The dotted line is the ideal calibration curve.

Producing well-calibrated probabilistic predictions is critical in many areas of science (e.g., determining which experiments to perform), medicine (e.g., deciding which therapy to give a patient), business (e.g., making investment decisions), and others. However, model calibration and the learning of well-calibrated probabilistic models has not been studied in literature as extensively as for example discriminative machine learning models that are built to achieve the best possible discrimination among classes of objects. One way to achieve a high level of model calibration is to develop methods for learning probabilistic models that are well-calibrated, ab initio. However, this approach would require one to modify the objective function used for learning the model and it may increase the cost of the associated optimization task. An alternative approach is to construct well-calibrated models by relying on the existing machine learning methods and by modifying their outputs in a post-processing step to obtain the desired model. This approach is often preferred because of its generality, flexibility, and the fact that it frees the designer of the machine learning model from the need to add additional calibration measures into the objective function used to learn the model. The existing approaches developed for this purpose include histogram binning, Platt scaling, or isotonic regression. In all these the postprocessing step can be seen as a function that maps output of a prediction model to probabilities that are intended to be well-calibrated. Figure 1 shows an example of such a mapping.

Existing calibration methods can be divided into parametric and non-parametric methods. An example of a parametric method is Platt’s method that applies a sigmoidal transformation that maps the output of a model (e.g., a posterior probability) [10] to a new probability that is intended to be better calibrated. The parameters of the sigmoidal transformation function are learned using the maximum likelihood estimation framework. A limitation of the sigmoidal function is that it is symmetric and does not work well for highly biased distributions [6]. The most common non-parametric methods are based either on binning [13] or isotonic regression [1].

In the histogram binning approach, also known as quantile binning, the raw predictions of a binary classifier are sorted first, and then they are partitioned into B subsets of equal size, called bins. Given a (uncalibrated) classifier prediction p_in, the method finds the bin containing that prediction and returns as p_out the fraction of positive outcomes (Z = 1) in the bin. Histogram binning has several limitations, including the need to define the number of bins and the fact that the bins and their associated boundaries remain fixed over all predictions [14]. The isotonic regression algorithm can be viewed as a special adaptive binning approach that assures the isotonicity (monotonicity) of the probability estimates. Although isotonic regression based calibration yields a good performance in many real data applications [9, 2, 14], the violation of isotonicity assumption in practice is quite frequent secondary to the choice of the learning models and algorithms. This could specifically happen in learning data mining models in large scale problems in which we have to make simplifying assumption in building computationally tractable models. So, the relaxation of the isotonicity constraints may be appropriate.

A new non-parametric calibration method called adaptive calibration of predictions (ACP) was recently introduced [6]. ACP requires a 95% confidence interval (CI) around a particular prediction p_in to define a bin. It sets p_out to be the fraction of positive outcomes (Z = 1) among all the predictions that fall within the bin.

In this paper we introduce two new Bayesian non-parametric calibration methods. The first one, the Selection over Bayesian Binnings (SBB), uses dynamic programming to efficiently search over all possible binnings of the posterior probabilities within a training set in order to select the Bayes optimal binning according to a scoring measure. The second method, Averaging over Bayesian Binnings (ABB), generalizes SBB by performing model averaging over all possible binnings. The advantage of these Bayesian methods over existing calibration methods is that they have more stable, well-performing behavior under a variety of conditions.

Our probabilistic calibration methods can be applied in two prediction settings. First, they can be used to convert the outputs of discriminative classification models, which have no apparent probabilistic interpretation, into posterior class probabilities. An example is an SVM that learns a discriminative model, which does not have a direct probabilistic interpretation. Second, the calibration methods can be applied to improve the calibration of predictions of a probabilistic model that is miscalibrated. For example, a Naïve Bayes (NB) model is a probabilistic model, but its class posteriors are often miscalibrated due to unrealistic independence assumptions [9]. The methods we describe are shown empirically to improve the calibration of NB models without reducing its discrimination. The methods can also work well on calibrating models that are less egregiously miscalibrated than are NB models.

The remainder of this paper is organized as follows. Section 2 describes the methods that we applied to perform post-processing calibration. Section 3 describes the experimental setup that we used in evaluating the calibration methods. The results of the experiments are presented in Section 4. Section 5 discusses the results and describes the advantages and disadvantages of proposed methods in comparison to other calibration methods. Finally, Section 6 states conclusions, and describes several areas for future work.

2 Methods

In this section we present two new Bayesian non-parametric methods for binary classifier calibration that generalize the histogram-binning calibration method [13] by considering all possible binnings of the training data. The first proposed method, which is based on Bayesian Model selection, is called Selection over Bayesian Binnings (SBB). We also generalize SBB by model averaging over all possible binnings; it is called Averaging over Bayesian Binnings (ABB). There are two main challenges here. One is how to score a binning model, and we use a Bayesian score. The other is how to efficiently search over such a large space of binnings, and we use dynamic programming to address this issue.

2.1 Bayesian Calibration Score

Let $p_{in}^i$ and Z_i define respectively an uncalibrated classifier prediction and the true class of the i’th instance. Also, let D define the set of all training instances ( $p_{in}^i$, Z_i). In addition, let S be the sorted set of all uncalibrated classifier predictions { $p_{in}^1,p_{in}^2,\dots ,p_{in}^N$} and S_l,u be a list of the first elements of S, starting at l’th index and ending at u’th index, and let Pa denote a partitioning of S into a fixed number of bins. A binning model M induced by the training set is defined as:

$$M\equiv \{B,S,Pa,\mathrm{\Theta }\},$$ (2.1)

where, B is the number of bins used to define Pa, and Θ is the set of all the calibration model parameters Θ = { θ₁, …, θ_B}, which are defined as follows. For a bin b, which is determined by S_lb,ub, the distribution of the class variable P(Z = 1|B = b) is modeled as a binomial distribution with parameter θ_b. Thus, Θ specifies all the binomial distributions for all the existing bins in Pa. We note that our binning model is motivated by the model introduced in [7] for variable discretization, which is here customized to perform classifier calibration. We score a binning model M as follows:

$$\mathit{Score}(M)=P(M)·P(D\mid M)$$ (2.2)

The marginal likelihood P(D|M) in Equation 2.2 is derived using the marginalization of the joint probability of P(D, Θ) over all parameter space according to the following equation:

$$P(D\mid M)={\int }_{\mathrm{\Theta }}P(D\mid M,\mathrm{\Theta })P(\mathrm{\Theta }\mid M)d_{\mathrm{\Theta }}$$ (2.3)

Equation 2.3 has a closed form solution under the following assumptions: (1) All samples are i.i.d and the class distribution P(Z|B = b),which is the class distribution for instances located in bin number b, is modeled using a binomial distribution with parameter θ_b, (2) the distribution of class variables over two different bins are independent of each other, and (3) the prior distribution over binning model parameters θs are modeled using a Beta distribution. We also assume that the parameters of the Beta distribution α and β are both equal to one, which corresponds to having a uniform distribution over each θ_b. The closed form solution to the marginal likelihood given the above assumptions is as follows [5]:

$$P(D\mid M)=\prod _{b=1}^B\frac{n_{b0}!n_{b1}!}{(n_b+1)!},$$ (2.4)

where n_b is the total number of training instances located in bin b. Also, n_b0 and n_b1 are respectively the number of class zero and class one instances among all n_b training instances in bin b.

The term P(M) in Equation 2.2 specifies the prior probability of a binning of calibration model M. It can be interpreted as a structure prior, which we define as follows. Let Prior(k) be the prior probability of there being a bin boundary between $p_{in}^k$ and $p_{in}^{k+1}$ in the binning given by model M, and model it using a Poisson distribution with the mean parameter λ. For k from 1 to N − 1, we define the prior(k) function as:

$$\mathit{Prior}(k)=1-e^{-\lambda \frac{d(k,k+1)}{d(1,n)}}$$ (2.5)

where, $d(i,j)=p_{in}^j-p_{in}^i$ represents the distance between the two (uncalibrated) classifier output $p_{in}^j$ and $p_{in}^i$, and $p_{in}^j$ is greater than $p_{in}^i$. For the boundary cases where k = 0 and k = N, we define Prior(0) = 1 and Prior(N) = 1 which correspond to have a bin boundary at the lowest and the highest possible uncalibrated probabilities in S.

Consider the prior probability for the presence of bin b, which contains the sequence of training instances S_lb,ub according to model M. Assuming independence of the appearance of partitioning boundaries, we can calculate the prior of the boundaries defining bin b by using the Prior function as follows:

$$\mathit{Prior}(u_b)\left(\prod _{k=l_b}^{u_b-1}(1-\mathit{Prior}(k))\right)$$ (2.6)

where the product is over all training instances from S_lb to S_ub−1, inclusive. Expression 2.6 gives the prior probability that no bin boundary is presented between any consecutive pairs of values $p_{in}^k$ in the sequence S_lb,ub and at least one bining boundary between the values $p_{in}^{u_b}$ and $p_{in}^{u_{b+1}}$. Combining Equations 2.6 and 2.4 into Equation 2.2, we obtain the following Bayesian score for calibration model M:

$$\mathit{Score}(M)=\prod _{b=1}^B\left[\mathit{Prior}(u_b)\left(\prod _{k=l_b}^{u_b-1}(1-\mathit{Prior}(k))\right)\frac{n_{b0}!n_{b1}!}{(n_b+1)!}\right]$$ (2.7)

2.2 The SBB and ABB models

We can use the above Bayesian score to perform model selection or model averaging. Selection involves choosing the best partitioning model M_opt and calibrating a prediction x as P(x) = P(x|M_opt). As mentioned, we call this approach Selection over Bayesian Binnings (SBB). Model averaging involves calibrating predictions over all possible binnings. We call this approach Averaging over Bayesian Binnings (ABB) model. A calibrated prediction in ABB is derived as follows:

$$\begin{array}{l}P(x)=\sum _{i=1}^{2^{N-1}}P(M_i\mid D)P(x\mid M_i)\\ \propto \sum _{i=1}^{2^{N-1}}\mathit{Score}(M_i)P(x\mid M_i),\end{array}$$ (2.8)

where N is the total number of predictions in D (i.e., training instances).

Both (SBB) and (ABB) consider all possible binnings of the N predictions in D, which is exponential in N. Thus, in general, a brute-force approach is not computationally tractable. Therefore, we apply dynamic programming, as described in the next two sections.

2.3 Dynamic Programming Search of SBB

This section summarizes the dynamic programming method used in SBB. Recall that S is the sorted set of all un-calibrated classifier’s outputs { $p_{in}^1,p_{in}^2,\dots ,p_{in}^N$} in the training data set. Let S_1,u define the prefix of set S including the set of the first u uncalibrated estimates { $p_{in}^1,p_{in}^2,\dots ,p_{in}^u$}. Consider finding the optimal binning models M_1,u corresponding to the subsequence S_1,u for u ∈ 1, 2, …, N of the set S. Assume we have already found the highest score binning of these models M_1,1, M_1,2, …, M_1,u−1, corresponding to each of the subsequences S_1,1, S_1,2, …, S_1,u−1. Let $V_1^f,V_2^f,\dots ,V_{u-1}^f$ denote the respective scores of the optimal binnings of these models. Let Score_i,u be the score of subsequence { $p_{in}^1,p_{in}^2,\dots ,p_{in}^u$} when it is considered as a single bin in the calibration model M_1,u. For all l from u to 1, SBB computes $V_{l-1}^f\times {\mathit{Score}}_{l,u}$, which is the score for the highest scoring binning M_1,u of set S_1,u for which subsequence S_l,u is considered as a single bin. Since this binning score is derived from two other scores, we call it a composite score of the binning model M_1,u. The fact that this composite score is a product of two scores follows from the decomposition of Bayesian scoring measure we are using, as given by Equation 2.7. In particular, both the prior and marginal likelihood terms on the score are decomposable.

In finding the best binning model M_1,u, SBB chooses the maximum composite score over all l, which corresponds to the optimal binning for the training data subset S_1,u; this score is stored in $V_u^f$. By repeating this process from 1 to N, SBB derives the optimal binning of set S_1,N, which is the best binning over all possible binnings. The computational time complexity of the above dynamic programming procedure is O(N²).

2.4 Dynamic Programming Search of ABB

The dynamic programming approach used in ABB is based on the above dynamic programming approach in SBB. It focuses on calibrating a particular instance P(x). The ABB algorithm uses the decomposability property of the Bayesian binning score in Equation 2.7. Assume we have already found in one forward run of the SBB method the highest score binning of the models M_1,1, M_1,2, …, M_1,N, which correspond to each of the subsequences S_1,1, S_1,2, …, S_1,N, respectively; let the values $V_1^f,V_2^f,\dots ,V_N^f$ denote the respective scores of the optimal binning for these models, which we cache. We perform an analogous dynamic programming procedure in SBB in a backward manner (from highest to lowest prediction) and compute the highest score binning of these models M_N,N, M_{N−1, N}, …, M_1,N, which correspond to each of the subsequences S_N,N, S_N−1,N, …, S_1,N, respectively; let the values $V_N^b,V_{N-1}^b,\dots ,V_1^b$ denote the respective scores of the optimal binning for these models, which also cache. Using the decomposability property of the binning score given by 2.7, we can write the Bayesian model averaging estimate given by Equation 2.8 as follows:

$$P(x)\propto \sum _{1\le l\le u\le N}\left(V_{l-1}^f\times {\mathit{Score}}_{l,u}\times V_{u+1}^b\times {\widehat{p}}_{l,u}(x)\right)$$ (2.9)

where p̂_l,u(x) is obtained using the frequency¹ of the training instances in the bin containing the predictions S_l,u. Remarkably, the dynamic programming implementation of ABB is also O(N²). However, since it is instance specific, this time complexity holds for each prediction that is to be calibrated (e.g., each prediction in a test set). To address this problem, we can partition the interval [0, 1] into R equally spaced bins and stored the ABB output for each of those bins. The training time is therefore O(RN²). During testing, a given p_in is mapped to one of the R bins and the stored calibrated probability is retrieved, which can all be done in O(1) time.

3 Experimental Setup

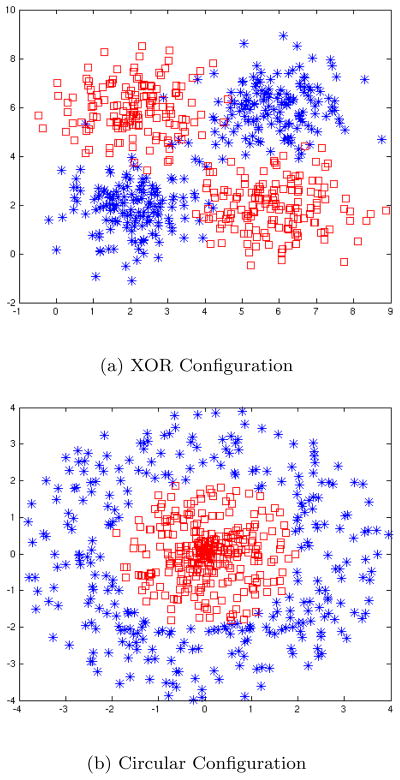
This section describes the set of experiments that we performed to evaluate the calibration methods described above. To evaluate the calibration performance of each method, we ran experiments using both simulated data and real data. In our experiments on simulated data, we used logistic regression (LR) as the base classifier, whose predictions are to be calibrated. The choice of logistic regression was made to let us compare our results with the state-of-the-art method ACP, which as published is tailored for LR. For the simulated data, we used two synthetic datasets in which the outcomes were not linearly separable. The scatter plots of the two simulated datasets are shown in Figure 2. These extreme choices allow us to see how well the calibration methods perform when the classification model makes over simplifying (linear) assumptions in learning nonlinear concepts. Also, in the simulation data we used 600 randomly generated instances for training the LR model, 600 random instances for learning calibration-models, and 600 random instances for testing the models ²

Figure 2.

Scatter plots of the simulated data

We also performed experiments on three different sets of real binary classification data. The first set is the UCI Adult dataset. The prediction task is a binary classification problem to predict whether a person makes over $50K a year using his or her demographic information. From the original Adult dataset, which includes 48842 total instances with 14 real and categorical features, after removing the instances with missing values, we used randomly 2000 instances for training classifiers, 600 for calibration-model learning, and 600 instances for testing.

We also used the UCI SPECT dataset, which is a small biomedical binary classification dataset. SPECT allows us to examine how well each calibration method performs when the calibration dataset is small in a real application. The dataset involves the diagnosis of cardiac Single Proton Emission Computed Tomography (SPECT) images. Each of the patients is classified into two categories: normal or abnormal. This dataset consists of 80 training instances, with an equal number of positive and negative instances, and 187 test instances with only 15 positive instances. The SPECT dataset includes 22 binary features. Due to the small number of instances, we used the original training data as both our training and calibration datasets, and we used the original test data as our test dataset.

For the experiments on the Adult and SPECT datasets, we used three different classifiers: LR, naïve Bayes, and SVM with polynomial kernels. The choice of the LR model allows us to include the ACP method in the comparison, because as mentioned it is tailored to LR. Naïve Bayes is a well-known, simple, and practical classifier that often achieves good discrimination performance, although it is usually not well calibrated. We included SVM because it is a relatively modern classifier that is being frequently applied ³.

The other real dataset that we used for evaluation contains clinical findings (e.g., symptoms, signs, laboratory results) and outcomes for patients with community acquired pneumonia (CAP) [4]. The classification task we examined involves using patient findings to predict dire patient outcomes, such as mortality or serious medical complications. The CAP dataset includes a total of 2287 patient cases (instances) that we divided into 1087 instances for training of classifiers, 600 instances for learning calibration models, and 600 instances for testing the calibration models. The data includes 172 discrete and 43 continuous features. For our experiments on the naïve Bayes model, we just used the discrete features of data, and for the experiments on SVM we used all 215 discrete and continuous features. Also, for applying the LR model to this dataset, we first used the PCA feature transformation because of the high dimensionality of data and the existing correlations among some features, which produced unstable results due to singularity issues.

4 Experimental Results

This section presents experimental results of the calibration methods when applied to the datasets described in the previous section. We show the performance of the methods in terms of both calibration and discrimination, since in general both are important.

For the evaluation of the calibration methods, we used 5 different measures. The first two measures are Accuracy (Acc) and the Area Under the ROC Curve (AUC), which measure discrimination. The three other measures are the Root Mean Square Error (RMSE), Expected Calibration Error (ECE), and Maximum Calibration Error (MCE). These measures evaluate calibration performance. The ECE and MCE are simple statistics that measure calibration relative to the ideal reliability diagram [3, 9] (Figure 1 shows an example of a reliability diagram). In computing these measures, the predictions are sorted and partitioned into K fixed number of bins(K = 10 in our experiments). The predicted value of each test instance falls into one of the bins. The ECE calculates Expected Calibration Error over the bins, and MCE calculates the Maximum Calibration Error among the bins, using empirical estimates as follows:

$$\begin{array}{ll}\hfill \mathit{ECE}& =\sum _{i=1}^{10}P(i)·\mid o_i-e_i\mid \\ \hfill \mathit{MCE}& =max(\mid o_i-e_i\mid )\end{array}$$

where o_i is the true fraction of positive instances in bin i, e_i is the mean of the post-calibrated probabilities for the instances in bin i, and P(i) is the empirical probability (fraction) of all instances that fall into bin i. The lower the values of ECE and MCE, the better is the calibration of a model.

The Tables [1a, 1b, …, 1k] show the comparisons of different methods with respect to evaluation measures on the simulated and real datasets. In these tables in each row we show in bold the two methods that achieved the best performance with respect to a specified measure.

As can be seen, there is no superior method that outperforms all the others in all data sets on all measures. However, SBB and ABB are superior to Platt and isotonic regression in all the simulation datasets. We discuss the reason why in Section 5. Also, SBB and ABB perform as well or better than isotonic regression and the Platt method on the real data sets.

In all of the experiments, both on simulated datasets and real data sets, both SBB and ABB generally retain or improve the discrimination performance of the base classifier, as measured by Acc and AUC. In addition, they often improve the calibration performance of the base classifier in terms of the RMSE, ECE and MCE measures.

5 Discussion

Having a well-calibrated classifier can be important in practical machine learning problems. There are different calibration methods in the literature and each one has its own pros and cons. The Platt method uses a sigmoid as a mapping function. The parameters of the sigmoidal transformation function are learned using a maximum likelihood estimation framework. The main advantage of the Platt scaling method is its fast recall time. However, the shape of the sigmoid function can be restrictive, and it often cannot produce well calibrated probabilities when the instances are distributed in feature space in a biased fashion (e.g. at the extremes, or all near separating hyper plane) [6].

Histogram binning is a non-parametric method which makes no special assumptions about the shape of mapping function. However, it has several limitations, including the need to define the number of bins and the fact that the bins remain fixed over all predictions [14]. ABB alleviates these problems by performing Bayesian averaging over all set of possible binning models on the training data.

Isotonic regression-based calibration is another non-parametric calibration method, which requires that the mapping (from pre-calibrated predictions to post-calibrated ones) is chosen from the class of all isotonic (i.e., monotonicity increasing) functions [9, 14]. Thus, it is less restrictive than the Platt calibration method. The pair adjacent violators (PAV) algorithm is one instance of an isotonic regression algorithm [1]. The PAV algorithm can be considered as a binning algorithm in which the boundaries of the bins are chosen according to how well the classifier ranks the examples[14]. It has been shown that Isotonic regression performs very well in comparison to other calibration methods in real datasets [9, 2, 14]. However, isotonic regression has some weaknesses. The most significant limitation of the isotonic regression is its isotonicity (monotonicity) assumption. As seen in Tables [1a, 1b] in the simulation data, when the isotonicity assumption is violated through the choice of classifier and the nonlinearity of data, isotonic regression performs relatively poorly, in terms of improving the discrimination and calibration capability of a base classifier. The violation of this assumption can happen in real data secondary to the choice of learning models and algorithms, specifically when we encounter large scale classification problems in which we have to make simplifying assumptions to build the learning models. In order to mitigate this pitfall, Menon et. al [8] proposed a new isotonic based calibration method using a combination of optimizing AUC as a ranking loss measure, plus isotonic regression for building an accurate ranking model. However, this is counter to our goal of developing post-processing methods that can be used with any existing classification models. There is also another interesting extension of isotonic regression for calibrating the output of multiple classifiers [15], but it is not included in our experiments, since we focus on calibrating the output of a single binary classifier in this paper.

A classifier calibration method called adaptive calibration of predictions (ACP) was recently introduced [6]. A given application of ACP is tied to a particular model M, such as a logistic regression model, that predicts a binary outcome Z. ACP requires a 95% confidence interval (CI) around a particular prediction p_in of M. ACP adjusts the CI and uses it to define a bin. It sets p_out to be the fraction of positive outcomes (Z = 1) among all the predictions that fall within the bin. On both real and synthetic datasets, ACP achieved better calibration performance than a variety of other calibration methods, including simple histogram binning, Platt scaling, and isotonic regression [6]. The ACP post-calibration probabilities also achieved among the best levels of discrimination, according to the AUC. ACP has several limitations, however. First, it requires not only probabilistic predictions, but also a statistical confidence interval (CI) around each of those predictions, which makes it tailored to specific classifiers, such as logistic regression [6]. Second, based on a CI around a given prediction p_in, it commits to a single binning of the data around that prediction; it does not consider alternative binnings that might yield a better calibrated p_out. Third, the bin it selects is symmetric around p_in by construction, which may not optimize calibration. Finally, it does not use all of the training data, but rather only uses those predictions within the confidence interval around p_in. The proposed ABB method mitigates these problems by performing a Bayesian averaging over all set of possible binning models on the training data. As one can see from the tables, ACP performed well when logistic regression is the base classifier, both in simulated and real datasets. Also, SBB and ABB performed as well or better than ACP in both simulation and real data sets.

In general, the SBB and ABB algorithms appear promising, especially ABB, which overall outperformed SBB. Neither algorithm makes restrictive (and potentially unrealistic) assumptions, as does Platt scaling and isotonic regression. They also are not restricted in the type of classifier with which they can apply, unlike ACP.

The main disadvantage of SBB and ABB is their running time. If N is the number of training instances, then SBB has a training time of O(N²), due to its dynamic programming algorithm that searches over every possible binning, whereas the time complexity of ACP and histogram binning is O(NlogN), and it is O(N) for isotonic regression [6]. Also, the cached version of ABB has a training time of O(RN²), where R reflects the number of bins being used. Nonetheless, it remains practical to use these algorithms to perform calibration on a desktop computer when using training datasets that contain thousands of instances. Note that, the amount of data that is needed to calibrate classification models is much less than the amount needed to train them, because the calibration feature space has only one single dimension ⁴. In addition, the testing time is only O(b) for SBB where b is the number of binnings found by the algorithm and O(1) for the cached version of ABB. Table 2 shows the time complexity of different methods in learning for N training instances and recall for only one instance.

Table 2.

Time complexity of calibration methods in learning and recall

	Platt	Hist	IsoReg	ACP	SBB	ABB
Time Complexity (Learning/Recall)	O(NT)=O(1)	O(NlogN)=O(b)	O(N)=O(b)	O(NlogN)=O(N)	O(N2)=O(b)	O(RN2)=O(1)

Note that N and b are the size of training sets and the number of bins found by the method respectively. T is the number of iteration required for convergence in Platt method and R reflects the number of bins being used by cached ABB.

6 Conclusion

In this paper we introduced two new Bayesian, non-parametric methods for calibrating binary classifiers, which are called SBB and ABB. The proposed methods post process the output of a binary classification algorithm; thus, it can be readily combined with many existing classification algorithms. The approach can be viewed as a refinement of the histogram-binning calibration method in that it considers all possible binnings of the training data and their combination to yield more robust calibrated predictions. Neither algorithm makes restrictive assumptions, as does Platt scaling and isotonic regression. They also are not restricted in the type of classifier with which they can apply, unlike ACP. Experimental results on simulated and real data support that these methods perform as well or better than the other calibration methods that we evaluated.

In future work, we plan to explore how the two new methods perform when using Bayesian model averaging over the hyper parameter λ. We also will extend them to perform multi-class calibration. Finally, we plan to investigate the use of calibration methods on posterior probabilities that are inferred from models that represent joint probability distributions, such as maximum-margin Markov-network models [12, 17, 16].

Table 1.

Experimental Results on Simulated and Real datasets

(a) Non-Linear XOR configuration results
	LR	ACP	IsoReg	Platt	Hist	SBB	ABB
AUC	0.497	0.950	0.704	0.497	0.931	0.914	0.941
Acc	0.510	0.887	0.690	0.510	0.855	0.887	0.888
RMSE	0.500	0.286	0.447	0.500	0.307	0.307	0.295
MCE	0.521	0.090	0.642	0.521	0.152	0.268	0.083
ECE	0.190	0.056	0.173	0.190	0.072	0.104	0.062

(b) Non-Linear Circular configuration results
	LR	ACP	IsoReg	Platt	Hist	SBB	ABB
AUC	0.489	0.852	0.635	0.489	0.827	0.816	0.838
Acc	0.500	0.780	0.655	0.500	0.795	0.790	0.773
RMSE	0.501	0.387	0.459	0.501	0.394	0.393	0.390
MCE	0.540	0.172	0.608	0.539	0.121	0.790	0.146
ECE	0.171	0.098	0.186	0.171	0.074	0.138	0.091

(c) Adult Naïve Bayes
	NB	IsoReg	Platt	Hist	SBB	ABB
AUC	0.879	0.876	0.879	0.877	0.849	0.879
Acc	0.803	0.822	0.840	0.818	0.838	0.835
RMSE	0.352	0.343	0.343	0.341	0.345	0.343
MCE	0.223	0.302	0.092	0.236	0.373	0.136
ECE	0.081	0.075	0.071	0.078	0.114	0.062

(d) Adult Linear SVM
	SVM	IsoReg	Platt	Hist	SBB	ABB
AUC	0.864	0.856	0.864	0.864	0.821	0.864
Acc	0.248	0.805	0.748	0.815	0.803	0.805
RMSE	0.587	0.360	0.434	0.355	0.362	0.357
MCE	0.644	0.194	0.506	0.144	0.396	0.110
ECE	0.205	0.085	0.150	0.077	0.108	0.061

(e) Adult Logistic Regression
	LR	ACP	IsoReg	Platt	Hist	SBB	ABB
AUC	0.730	0.727	0.732	0.730	0.743	0.699	0.731
Acc	0.755	0.783	0.753	0.755	0.753	0.762	0.762
RMSE	0.403	0.402	0.403	0.405	0.400	0.401	0.401
MCE	0.126	0.182	0.491	0.127	0.274	0.649	0.126
ECE	0.075	0.071	0.118	0.079	0.092	0.169	0.076

(f) SPECT Naïve Bayes
	NB	IsoReg	Platt	Hist	SBB	ABB
AUC	0.836	0.815	0.836	0.832	0.733	0.835
Acc	0.759	0.845	0.770	0.824	0.845	0.845
RMSE	0.435	0.366	0.378	0.379	0.368	0.374
MCE	0.719	0.608	0.563	0.712	0.347	0.557
ECE	0.150	0.141	0.148	0.145	0.149	0.157

(g) SPECT SVM Quadratic kernel
	SVM	IsoReg	Platt	Hist	SBB	ABB
AUC	0.816	0.786	0.816	0.766	0.746	0.810
Acc	0.257	0.834	0.684	0.845	0.813	0.813
RMSE	0.617	0.442	0.460	0.463	0.398	0.386
MCE	0.705	0.647	0.754	0.934	0.907	0.769
ECE	0.235	0.148	0.162	0.180	0.128	0.131

(h) SPECT Logistic Regression
	LR	ACP	IsoReg	Platt	Hist	SBB	ABB
AUC	0.744	0.742	0.733	0.744	0.738	0.733	0.741
Acc	0.658	0.561	0.626	0.668	0.620	0.620	0.626
RMSE	0.546	0.562	0.558	0.524	0.565	0.507	0.496
MCE	0.947	1.000	1.000	0.884	0.997	0.813	0.812
ECE	0.181	0.187	0.177	0.180	0.183	0.171	0.173

(i) CAP Naïve Bayes
	NB	IsoReg	Platt	Hist	SBB	ABB
AUC	0.848	0.845	0.848	0.831	0.775	0.838
Acc	0.730	0.865	0.847	0.853	0.832	0.865
RMSE	0.504	0.292	0.324	0.307	0.315	0.304
MCE	0.798	0.188	0.303	0.087	0.150	0.128
ECE	0.161	0.071	0.097	0.056	0.067	0.067

(j) CAP Linear SVM
	SVM	IsoReg	Platt	Hist	SBB	ABB
AUC	0.858	0.858	0.858	0.847	0.813	0.863
Acc	0.907	0.900	0.882	0.887	0.902	0.908
RMSE	0.329	0.277	0.294	0.287	0.285	0.274
MCE	0.273	0.114	0.206	0.110	0.240	0.121
ECE	0.132	0.058	0.093	0.057	0.083	0.050

(k) CAP Logistic Regression
	LR	ACP	IsoReg	Platt	Hist	SBB	ABB
AUC	0.920	0.910	0.917	0.920	0.901	0.856	0.921
Acc	0.925	0.932	0.935	0.928	0.897	0.935	0.932
RMSE	0.240	0.240	0.234	0.242	0.259	0.240	0.240
MCE	0.199	0.122	0.286	0.154	0.279	0.391	0.168
ECE	0.066	0.062	0.078	0.082	0.079	0.103	0.069