A Residue-Specific Force Field (RSFF2) Improves the Modeling of Conformational Behavior of Peptides and Proteins

Abstract

A recent report of ³J_HNHα scalar coupling constants for hundreds of two-residue peptides has provided an important opportunity to test simulation force fields for proteins. Here we compare the abilities of three derivatives of the Amber ff99SB force field to reproduce these data. We report molecular dynamics (MD) simulations of 256 two-residue peptides and show that the recently developed residue-specific force field (RSFF2) produces a dramatic improvement in the agreement with experimental ³J_HNHα coupling constants. We further show that RSFF2 also appears to produce a modest improvement in reproducing the ³J_HNHα coupling constants of five model proteins. Perhaps surprisingly, an analysis of neighboring residue effects (NREs) on the ³J_HNHα coupling constants of the two-residue peptides indicates little difference between the force fields’ abilities to reproduce experimental NREs. We speculate that this might indicate limitations in the force fields’ descriptions of nonbonded interactions between adjacent sidechains or with terminal capping groups.

In recent years, molecular dynamics (MD) simulations have emerged as an important complement to experimental approaches for investigating the conformational dynamics of biological macromolecules.¹ While a significant advantage of using MD is that it provides a truly atomic-level view of biomolecular dynamics, the predictive utility of the method relies heavily on the accuracy of the force fields.² In recent years, owing in part to the realization that force fields for proteins can show biased secondary structure preferences,^3–5 considerable effort has been focused on improving the backbone and sidechain dihedral angle potential functions of a number of force fields.^6–9 While continuing improvements mean that current force fields are generally adequate for modeling globular proteins in their native states, there remain questions about their ability to accurately reproduce the thermodynamics of protein folding,¹⁰ and both the conformational propensities⁶ and scalar coupling constants of peptide systems.^11–12

One very useful experimental measure of the conformational behavior of protein and peptide systems is the ³J_HNHα scalar coupling constant: this provides a relatively direct measure of the backbone dihedral angle, ϕ.¹² In important recent work, the Cho group has reported ³J_HNHα coupling constants for each residue in a complete set of 361 two-residue peptides;¹³ the availability of this experimental dataset provides an excellent chance to test the abilities of current simulation force fields to describe the conformational properties of model peptide systems. In a preliminary step in this direction, we recently reported MD simulations of the 441 possible two-residue peptides that can be formed from the twenty common amino acids when histidine is modeled in both its neutral and protonated states.¹¹ Using a force field combination that had previously been shown by the Pande group to be among the best at reproducing ³J coupling constants and chemical shifts in other peptide systems,¹⁴ we obtained a reasonable, but far from perfect agreement between the MD-predicted ³J_HNHα coupling constants and the experimental values reported by the Cho group.¹³

Here, we extend that work and explicitly test the abilities of three recent iterations of the AMBER protein force field to reproduce the ³J_HNHα coupling constants of a large number of two-residue peptides. The basis of all three force fields tested here is the influential ff99SB force field developed by the Simmerling group in order to improve the description of ϕ/ψ torsions in peptide and protein simulations.¹⁵ The first force field that we test, ff99SB-ILDN,⁷ adds to the original ff99SB parameterization a set of modified dihedral functions developed by the Shaw group to improve modeling of Ile, Leu, Asp and Asn sidechains. The second, ff99SB-ILDN-NMR,⁸ adds to this the modified backbone dihedral functions parameterized by the Brüschweiler group to improve reproduction of chemical shifts in protein simulations. The final force field that we test, RSFF2,¹⁶ represents a quite different extension of ff99SB that includes additional 1–4, 1–5 and 1–6 nonbonded potential functions designed to reproduce the conformational distributions of the twenty common amino acids observed in a protein coil library.

Using all three force fields in combination with the TIP3P water model,¹⁷ we have performed 1 μs-long MD simulations of 256 two-residue peptides with the same capping groups used as in the experimental studies¹³ (see Computational Methods for details of the simulations). All peptides were of the form Ace-X-Y-NH², where X and Y represent any of the standard amino acids excluding Pro, Asp, Glu and His: Pro was omitted as it was not included in the experimental studies;¹³ Asp and Glu were omitted (as outlined in our previous work¹¹) because they are likely to be in a mixture of protonation states at the pH studied experimentally; finally, His was omitted because its protonated form (appropriate to the experimental pH) has not yet been explicitly parameterized in RSFF2. Snapshots taken at 0.6 ps intervals from each of the simulations were used to compute ³J_HNHα coupling constants via an empirical Karplus relationship¹⁸ parameterized by the Bax group against experimental data on the small protein GB3;¹⁹ for purposes of comparison, calculations of the ³J_HNHα coupling constants were repeated using an earlier parameterization reported by the same group based on data for ubiquitin.²⁰

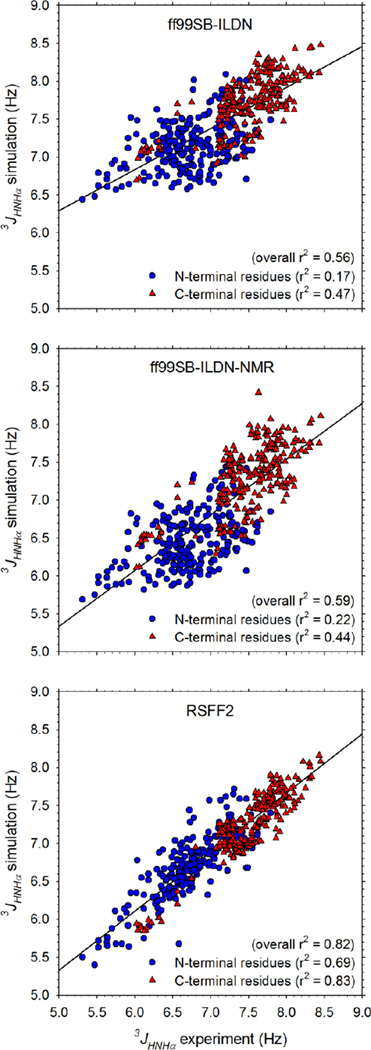
Figure 1 compares the MD-computed ³J_HNHα coupling constants with the corresponding experimental measurements¹³ for all non-Gly residues for each of the force fields tested. All three force fields produce a reasonable correspondence with the experimental data, with the ³J_HNHα coupling constants of C-terminal residues being consistently better reproduced than those of N-terminal residues (see r² values for linear regressions listed in Figure 1). Similarly, all three force fields reproduce the observation that the ³J_HNHα coupling constants of C-terminal residues (red triangles) are generally significantly higher than those of N-terminal residues (blue circles) in two-residue peptides. In terms of their overall agreement with experiment, ff99SB-ILDN-NMR (r² = 0.59) performs slightly better than ff99SB-ILDN (r² = 0.56), but the two force fields’ predicted ³J_HNHα coupling constants are highly correlated with each other (r² = 0.96; Figure S1); the close correspondence between these independent predictions suggests that the simulations are sufficiently converged to give statistically reliable results. Compared to the two ILDN-based force fields, RSFF2 performs much better and produces an overall level of agreement with experiment that is very high (r² = 0.82). It is also apparent that RSFF2 improves results significantly both at the N-terminal and the C-terminal positions, with the r² for the N-terminal residues, in particular, improving dramatically from 0.17 and 0.22 with ff99SB-ILDN and ff99SB-ILDN-NMR, respectively, to 0.69 with RSFF2; the corresponding r² values for the C-terminal residues are 0.47, 0.44, and 0.83, respectively. Effectively identical sets of r² values are obtained when the ³J_HNHα coupling constants are instead calculated using the earlier Karplus parameterization due to Hu & Bax²⁰ (Figure S2); it is not surprising to find, therefore, that the ³J_HNHα coupling constants calculated with the two sets of Karplus parameters are highly correlated with each other (Figure S3). Interestingly, however, the root mean square (RMS) errors in the computed ³J_HNHα coupling constants are generally lower with the more recent Vögeli et al. parameter set¹⁹ (Figure S4); in what follows, therefore, we present the results using this parameter set in the main text and, where relevant, provide the corresponding results obtained with the older Hu & Bax parameter set²⁰ in the Supporting Information.

Figure 1. Comparison of computed ³J_HNHα coupling constants with experimentally measured values for 256 two-residue peptides.

Panels show the results for: ff99SB-ILDN (top), ff99SB-ILDN-NMR (middle), and RSFF2 (bottom). ³J_HNHα coupling constants calculated using the Karplus parameterization due to Vögeli et al.¹⁹

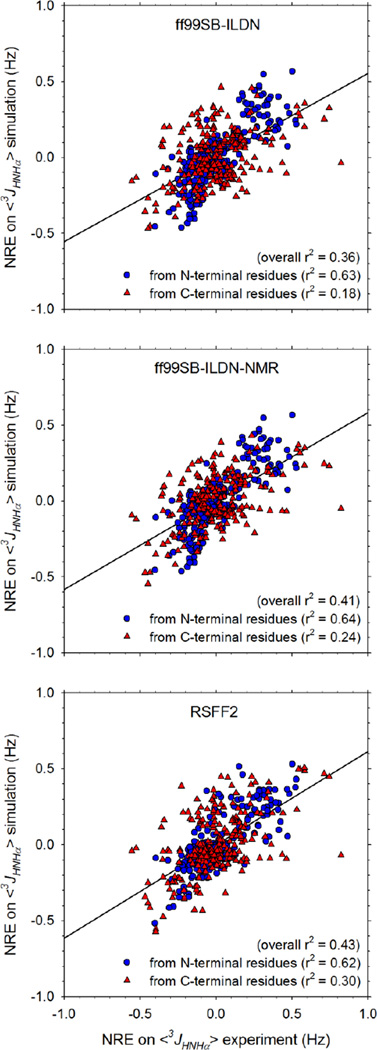
As we reported previously,¹¹ it is also possible to compare the neighboring residue effect (NRE) that each residue exerts on the ³J_HNHα coupling constant of an adjacent residue with corresponding experimental data (see Computational Methods for a description of how NREs are calculated). Figure 2 compares the MD-computed NREs on ³J_HNHα coupling constants with the corresponding experimental measurements¹³ for all three force fields. Here, the level of agreement with experiment is consistently lower, but with all three force fields the NREs exerted by N-terminal residues on neighboring C-terminal residues are significantly better reproduced than those exerted by C-terminal residues on N-terminal neighbors (see r² values for linear regressions listed in Figure 2). Given that the ³J_HNHα coupling constants of the C-terminal residues are consistently better predicted than those of the N-terminal residues (Figure 1; see above), it is possible that this indicates that a prerequisite for successful reproduction of the NRE exerted at a given residue is that the ³J_HNHα coupling constant of that residue, and by implication its backbone conformational preferences, be accurately reproduced.

Figure 2. Comparison of computed neighboring residue effects (NREs) on ³J_HNHα coupling constants with experimentally measured values for 256 two-residue peptides.

Panels show the results for: ff99SB-ILDN (top), ff99SB-ILDN-NMR (middle), and RSFF2 (bottom). ³J_HNHα coupling constants calculated using the Karplus parameterization due to Vögeli et al.¹⁹

In terms of the relative abilities of the force fields to reproduce the NREs it is interesting to note that while there is an apparent increase in the overall r² in passing from ff99SB-ILDN to ff99SB-ILDN-NMR to RSFF2 (Figure 2), it only appears significant for the NREs exerted by C-terminal residues. The NRE data, grouped and averaged according to residue type, are shown in bar-graph form in Figures S5 and S6. All three force fields successfully reproduce the principal experimental finding that aromatic amino acids such as Phe and Tyr tend to increase the ³J_HNHα coupling constants of adjacent residues, while basic amino acids Arg and Lys at the C-terminal position tend to decrease the ³J_HNHα coupling constants of N-terminal residues (Figure S6). Other results, however, are not reproduced by any of the force fields: e.g. the negative NRE exerted by a C-terminal Gly is not predicted, positive NREs exerted by C-terminal β-branched residues are not predicted, and an erroneously large positive NRE is predicted to be caused by a C-terminal Trp by all three force fields (Figure S6). Interestingly, RSFF2 significantly improves predictions of the NREs caused by Asn, regardless of position, but worsens predictions of the NREs caused by Arg and Lys at the N-terminal position (Figure S5).

A visual summary of the r² values for all of the data shown in Figures 1 and 2 is provided in Figure 3A. From this it is clear that RSFF2 results in a dramatic improvement in the reproduction of ³J_HNHα coupling constants but a much smaller, and perhaps insignificant, improvement in the overall reproduction of NREs. To explore whether the former results carry over to proteins we carried out MD simulations, in explicit TIP3P water, of five model proteins ranging in size from 67 to 149 residues (Figure S7), for which structures and experimental ³J_HNHα coupling constants have been reported in the literature. We simulated each protein for 1 μs, using each of the three force fields, and performed linear regressions of the computed ³J_HNHα coupling constants with the corresponding experimental measurements (see Computational Methods); in the special case of the largest protein studied, staphylococcal nuclease (SNase), we performed three independent replicate 1 μs simulations in order to determine the extent to which the results might be sensitive to the initial velocities assigned in the simulations. A complete set of scatter plots comparing the computed ³J_HNHα coupling constants with experimental values for all of these simulations can be found in Figure S8. A visual comparison of the r² values for all linear regressions of simulation with experiment is shown in Figure 3B, and a plot of the RMS errors in the predicted ³J_HNHα coupling constants is shown in Figure 3C; corresponding plots obtained when the calculations are repeated using the Hu & Bax parameters are provided in Figure S9.

Figure 3. Comparisons of computed and experimental ³J_HNHα coupling constants for peptide and protein systems.

A. Summary of linear regression r² values obtained from analysis of two-residue peptide simulations. Each column represents the result of a different linear regression involving the data points shown in Figures 1 and 2. The column marked ‘3J@N’, for example, shows r² values obtained from linear regression of computed and experimental ³J_HNHα coupling constants for residues at the N-terminal position only; these data points are the blue circles in Figure 1. B. Summary of linear regression r² values obtained from analysis of simulations of model proteins; error bars represent the standard deviations of the r² values obtained when each 1 μs trajectory is analyzed in 3 contiguous 333 ns segments. NLTP is the nonspecific lipid transfer protein from rice, PPIase is the peptidylprolylisomerase domain of trigger factor from M. genitalium, SNase is staphylococcal nuclease. Note that for SNase, results are shown for three independent replicate 1 μs simulations. C. Same as B but showing the RMS errors of the computed ³J_HNHα coupling constants. All ³J_HNHα coupling constants were calculated using the Karplus parameterization due to Vögeli et al.¹⁹

The regression results for the protein simulations generally confirm the trends established above by the two-residue peptide simulations: Figures 3B and S9A show that the r² values obtained with RSFF2 always exceed those obtained with either of the two other (earlier) force fields, while those obtained with ff99SB-ILDN-NMR generally exceed those obtained with ff99SB-ILDN. Averaged over the 7 simulations performed with each force field, the increase in r² due to changing from ff99SB-ILDN to RSFF2 is 0.075 ± 0.040; the increase in r² due to changing from ff99SB-ILDN-NMR to RSFF2 is 0.054 ± 0.041 (for this latter calculation we omitted villin, for which the ff99SB-ILDN-NMR results appear anomalously poor; see Figure 3B).

When the RMS errors in the predicted ³J_HNHα coupling constants are examined, however, the trends are more equivocal (Figure 3C): while in 4 out of 7 cases, the errors are lowest with RSFF2 (including in all 3 replicates of the SNase simulation), in other cases, notably NLTP, the errors associated with RSFF2 are no better, or are somewhat worse, than those obtained with the other force fields (see Figure 3C and Figure S9B). Two further surprises are encountered when we examine the RMS deviations (RMSDs) of the proteins from their initial structures over the course of the simulations: Figure S10 shows the RMSDs of the backbone heavy atoms as a function of time for all simulations, while Figure S11 presents the same results in averaged form. The first surprise is that, with all three force fields, the average backbone RMSDs for NLTP are lower than those of any of the other proteins (Figure S11), despite the fact that we obtain the worst reproduction of ³J_HNHα coupling constants for this protein (Figures 3B and 3C). The second, more minor surprise is that the average backbone RMSDs of simulations performed with the RSFF2 force field are not significantly different from those obtained with the earlier force fields. Both of these results indicate that, at least on a timescale of 1 μs, there is no simple relationship between the average RMSDs sampled during the simulations and the abilities of the simulations to reproduce experimental ³J_HNHα coupling constants.

In recent years, NMR scalar coupling data have been used repeatedly to effectively diagnose the strengths and weaknesses of force fields for proteins.^{5, 14, 21} The work reported here continues this trend and demonstrates that the very recently developed RSFF2 force field yields dramatically improved predictions of ³J_HNHα coupling constants in two-residue peptides, and a more equivocal improvement for proteins. The clear improvement with the two-residue peptides is encouraging given that both of the force fields to which we compare RSFF2 have already been shown to perform among the best in a recent NMR-based benchmark study of peptide and protein force fields.¹⁴ It also provides strong support for the philosophy, advocated by the Wu group, that underlies their parameterization of RSFF2¹⁶ and the related OPLS-based RSFF1 force field;²² in particular, it is to be noted that reproduction of ³J_HNHα coupling constants was not a specific goal of the RSFF parameterization schemes, even though good results for single amino acids were reported.^{16, 22}

On the other hand, the observation that predictions of NREs on the ³J_HNHα coupling constants of two-residue peptides are not hugely improved by the use of RSFF2 suggests that factors not adjusted in the RSFF2 parameterization scheme are likely to be responsible for the remaining discrepancies with experiment. Foremost among these factors for the two-residue peptides may be the description of nonbonded interactions – either those operating between sidechain atoms and the capping groups of the peptides, or those operating between sidechain atoms on adjacent residues. Issues with describing interactions with the acetyl capping groups, for example, might explain why predictions of the ³J_HNHα coupling constants for N-terminal residues are worse than those for C-terminal residues with all three force fields (Figure 1). Possible deficiencies in the description of nonbonded interactions of adjacent sidechains, on the other hand, might be responsible for difficulties in reproducing the NREs: recent work by the Zagrovic group, for example, has suggested that excessively favorable nonbonded residue-residue interactions might be a general feature of current pairwise protein force fields.²³ Regardless of their precise origins, however, it is likely that targeting errors in the computed ³J_HNHα coupling constants of small peptide systems might be a fruitful way to carry out further refinements of the force fields studied here.

The results we obtain for the proteins are more difficult to summarize neatly. Of the five protein structures used to perform simulations here, two – ubiquitin and SNase – are crystal structures while the remaining three are solution NMR structures. It is interesting to note, therefore, that the simulation results are consistently good for the two crystal structure proteins (Figures 3B and 3C) and that, for SNase in particular, RSFF2 leads to clear improvements in both the r² values and the RMS errors in all three replicate simulations (see also Figures S9A and S9B). It is also worth noting – as pointed out to us by a reviewer of this manuscript – that the lowest RMS errors obtained from any of the comparisons with experiment are for ubiquitin using the ubiquitin-optimized Karplus parameters derived by Hu and Bax²⁰ (Figure S9B). Although ubiquitin’s results remain the best when the Karplus parameters of Vögeli et al.¹⁹ are used instead (Figure 3C), this does suggest that RMS errors of ~0.8 Hz might be approaching the limit of what can currently be achieved from simulations of proteins, at least when simulations are performed on a timescale of 1 μs. The comparatively poor results obtained for NLTP, on the other hand, are harder to understand, especially since its backbone RMSD is the lowest of any of the proteins simulated (Figure S11). Interestingly, however, for this protein (and others) there are certain residues whose ³J_HNHα coupling constants appear to be poorly reproduced by all three force fields (Figure S7). It seems likely, therefore, that a detailed analysis of such outliers in a wider selection of proteins might help to identify further possible directions for force field refinement.

Computational Methods

In this work, 256 blocked two-residue peptides of the form Ace-X-Y-NH₂ were constructed in fully extended conformations, where X and Y represent any of the standard amino acids, excluding Pro, Asp, Glu and His (see main text); the acetylated N-terminus and amidated C-terminus correspond to the capping groups used in the Cho group’s recent NMR studies.¹³ In addition to these peptide systems, five different proteins were each simulated; these are listed, together with their corresponding PDB codes, residue counts, and technical origins as follows: the villin headpiece domain (1QQV; 67 residues; NMR structure), ubiquitin (1UBQ; 76 residues; crystal structure), Nonspecific Lipid Transfer Protein (NLTP) (1BV2; 91 residues; NMR structure), the PPIase domain of the chaperone trigger factor (1HXV; 113 residues; NMR structure), and Staphylococcal nuclease (SNase) (1SNC; 149 residues; crystal structure). All protein simulations were started from the native state structure. In the exceptional case of the PPIase domain, 30 amino acids at the N-terminus are missing from the structure: these residues – for which ³J_HNHα coupling constants were not reported – were built in a random coil configuration so that the construct used in the simulation was identical, chemically, to that used in the experiments.

All simulations were performed using the molecular dynamics software package GROMACS version 4.6.5.^24–25 Simulations were performed with each of the following force fields: Amber ff99SB-ILDN,⁷ Amber ff99SB-ILDN-NMR,⁸ and RSFF2,¹⁶ all in combination with the TIP3P water model.¹⁷ The first two of these force fields are already implemented in GROMACS; RSFF2 was implemented using Python scripts kindly provided to us by the developers of that force field. For the 256 two-residue peptide simulations, each peptide was immersed in a 30 Å octahedral box containing explicit solvent. For proteins, each protein was immersed in a cubic box large enough so that every atom of the protein was at least 1.0 nm from the box edge. All systems were first energy minimized using steepest descent minimization for 1000 steps, gradually heated to the target temperature over the course of 420 ps, and then equilibrated for a period of 1 ns. The target temperatures were chosen to match the conditions in the corresponding NMR experiments: two-residue peptides were simulated at 298 K, villin at 293 K,²⁶ ubiquitin at 303 K,²⁷ NLTP at 298 K,²⁸ PPIase at 298 K,²⁹ and SNase at 308 K.³⁰ All production simulations were carried out in the NPT ensemble for 1 μs with the coordinates of the solutes saved every 0.6 ps. Following the protocol used in the original development of RSFF2, a cutoff of 9 Å was applied to short-range nonbonded interactions, the PME method³¹ was used to calculate all long-range electrostatic interactions, covalent bonds were constrained to their equilibrium lengths using the LINCS algorithm³² and a 3 fs time step was employed throughout.

The ϕ backbone dihedral angle of each residue of interest was computed for every snapshot from the MD simulations and converted into a ³J_HNHα coupling constant using an empirical Karplus relation:¹² J(ϕ) = A cos²(ϕ + θ) + B cos(ϕ + θ) + C, where A, B, C represent parameters, and θ denotes a phase shift value. Here we have used two Karplus parameter sets: the more recent set, due to Vögeli et al.,¹⁹ has the following parameters (expressed in Hz): A = 8.40, B = −1.36, C = 0.33, θ = −60°; the older set, used in our recent work¹¹ and due to Hu and Bax,²⁰ has the parameters: A = 7.09, B = −1.42, C = 1.55, θ = −60°. Others have shown, and the results presented here confirm this, that the extent of correlation between simulation and experiment is largely independent of the exact set of parameters used in the Karplus equation.²² With the exception of the Gly residues of two-residue peptides, all calculated ³J_HNHα coupling constants were compared with corresponding experimental data; Gly residues of two-residue peptides were omitted, as in our previous work, owing to uncertainties in assignment of the two Hα atoms.¹³

Neighboring residue effects (NREs), which quantify the extent to which a residue type causes a neighboring residue type’s ³J_HNHα coupling constant to deviate from its mean value, were computed as described in our earlier work.¹¹ For example, the NRE exerted by a C-terminal Phe on the ³J_HNHα coupling constant of an N-terminal Ala, is calculated as the difference between: (a) the ³J_HNHα coupling constant of the N-terminal Ala in Ala-Phe, and (b) the mean ³J_HNHα coupling constant of the N-terminal Ala in all possible peptides Ala-Ala, Ala-Cys, Ala-Gln … Ala-Val. Individual NREs computed in this way are plotted in Figure 2. To obtain the average NRE caused by a C-terminal Phe, we carry out similar calculations for the Cys in Cys-Phe, the Gln in Gln-Phe etc and average the results; these average NREs are plotted in Figures S5 and S6. In order to allow an unambiguous comparison with the experimental data reported by the Cho group, experimental NREs were recomputed here using the original data for only those peptides that were simulated.

We note that the simulations we report here for ff99SB-ILDN-NMR differ from those we reported recently using the same force field¹¹ in the following ways: (1) the present simulation times are considerably longer (1 μs versus 300 ns), (2) the water model used here is TIP3P versus TIP4P-Ew in the earlier work, and (3) the peptides are simulated here using the same capping groups used in the experimental studies. Despite these differences, the results we obtained here are very similar to those we reported previously when we use the same Karplus parameterization²⁰ (r² = 0.92; Figure S12); the principal differences involve large C-terminal sidechains for which differences in the extent of sampling issues and in the identity of the C-terminal capping group may be significant.