Abstract
Cells are complex viscoelastic materials that are frequently in deformed morphological states, particularly during the cancer invasion process. The ability to study cell mechanical deformability in an accessible way can be enabling in many areas of research where biomechanics is important, from cancer metastasis to immune response to stem cell differentiation. Furthermore, phenomena in biology are frequently exhibited in high multiplicity. For instance, during metastasis, cells undergoing non-proteolytic invasion squeeze through a multitude of physiological barriers, including many small pores in the dense extracellular matrix (ECM) of the tumor stroma. Therefore, it is important to perform multiple measurements of the same property even for the same cell in order to fully appreciate its dynamics and variability, especially in the high recurrence regime. We have created a simple and minimalistic micropipette system with automated operational procedures that can sample the deformation and relaxation dynamics of single-cells serially and in a parallel manner. We demonstrated its ability to elucidate the impact of an initial cell deformation event on subsequent deformations for untreated and paclitaxel treated MDA-MB-231 metastatic breast cancer cells, and we examined contributions from the cell nucleus during whole-cell micropipette experiments. Finally we developed an empirical model that characterizes the serial factor, which describes the reduction in cost for cell deformations across sequential constrictions. We performed experiments using spatial, temporal, and force scales that match physiological and biomechanical processes, thus potentially enabling a qualitatively more pertinent representation of the functional attributes of cell deformability.
1. Introduction
Cell mechanics is an emerging field that is becoming more relevant in many different areas in biology, from cancer to hematology to stem cell biology. Many specialized techniques, including atomic force microscopy (AFM), micropipette aspiration (MPA), optical tweezers, and magnetic twisting cytometry, have been developed or tailored to enable researchers to study the mechanical properties of cells.1 One particular property – deformability – has become increasingly popular, as cell deformations have important functional roles in a broad spectrum of biological phenomena. As an important example, cancer metastasis involves a series of mechanical events at the single-cell level. In order to invade to distal sites, aggressive cells must be able to squeeze across small spaces in the extracellular matrix (ECM) of the tumor stroma and endothelial barrier and circulate and traffic through microvessels smaller than the size of the cell.2–4 Under such confined microenvironments, these cells must acquire deformed morphologies. There have been many studies on cell deformability, with techniques ranging from more conventional AFM5,6 and MPA7 to more recent microfluidic systems with active (optical forces, hydro-dynamic inertial focusing)8–10 and passive (microconstrictions)11–13 deformation actuators. In particular, we are interested in deformations in the most extreme form observed in physiological systems – deformations at the subnucleus scale. This is important because such large deformations with strained and elongated nuclei, which are not fully understood from current approaches, are often observed in cell invasion through the ECM, across endothelial junctions, and in microcirculation from various cell-in-gel and animal metastasis models as well as in histological slides of tumor slices.4,14–18 These events in the metastatic process suggest that cell deformability is an important property in the context of cancer.
Recent work using microfluidic techniques has shown that deformability may be correlated with disease states in cells, metastatic potential, and stem cell differentiation.8,10,13 Deformability in these cases is often measured by the aspect ratio of a cell under a fixed stress, such that more deformable cells exhibit a higher aspect ratio. Another common metric is the amount of time it takes a cell to flow through a micro-constriction under pressure. While these metrics are simple in nature, they nonetheless are proving to have clinical implications.10 Additionally, these assays are typically high throughput and automated, requiring minimal manual operations, during measurements, which offer appeal towards clinical applications.
A key disadvantage of these high throughput microfluidic assays is that the information content is typically simplistic and does not fully appreciate the complexity of a biological phenomenon. In particular, the mechanical properties of cells are intrinsically complex in nature and heterogeneous. Not only does heterogeneity exist between different components of the cell, such as the cytoplasm, cytoskeleton, and nucleus, but heterogeneity exists even within the cytoskeletal and nucleo-skeletal networks. Additionally, the cytoskeleton and nucleo-skeleton are viscoelastic and their response under stress is dynamic.7,19 These dynamics have rich mathematical representations,7,20 and the structural subcellular components, such as actin and intermediate filament networks, also have complex and dynamic behaviors when perturbed.21,22 As a result, a simple one-shot measurement of each cell (i.e. aspect ratio under asymmetric stress or average transit time across a barrier), while offering an appealing and simple assay, is a reductionist characterization of biological cells. Fundamental properties, such as creep strain dynamics, that are pertinent to the deformability of viscoelastic materials are difficult to measure with such techniques. As such, conventional, high resolution and more comprehensive measurements from traditional techniques such as AFM and MPA offer more detailed information about the state and fundamental properties of individual cells.
Micropipette aspiration and atomic force microscopy have been used to elucidate more complex phenomena associated with the mechanical properties of cells and nuclei. For instance, micropipette studies were able to produce high resolution data that revealed and enabled the development of mathematical models of the viscoelasticity of different cell types, which as an example characterized the distinction between solid like cells (endothelial cells) and liquid like cells (neutrophils).7 Additionally, MPA of isolated cell nuclei identified the contributions of different subnucleus structures on force bearing properties under different conditions (swollen and unswollen nuclei) and further revealed that the creep compliance of the nucleus follows a power-law temporal dependence over time scales from 0.1 to 1000 seconds.19 AFM studies have also been critical in revealing local cell stiffness as well as cell forces and stress under compression and extension.6,23
In these existing methods, there is a tradeoff between (1) experimental simplicity and automation and (2) the complexity of the measurable properties. More complex material properties such as cell strain dynamics during deformation and relaxation require more complicated procedures that are practicable typically only in labor intensive and bulky apparatuses (MPA and AFM),5–7 while more automated systems such as microfluidic constriction assays, optical stretchers, and inertial focusing methods8–12 produce static and reductionist measurements and are currently limited to simple experimental procedures. The incorporation of more functionality in microfluidic assays often requires more manual labor or additional components such as robotic actuators for image-assisted flow modulation, thus reducing their automation or adding to their already bulky systems that require external pressure pumps and optical components (e.g. high power lasers). These tradeoffs limit the adoptability of the mentioned techniques and thus the practicability of the field of cell biomechanics to select experts in select settings. Mechanical properties such as cell deformability and viscoelasticity, however, are critical and complementary to many areas in cell biology, with implications in cancer metastasis, immune cell responses, tissue homeostasis, blood diseases, and stem cell differentiation.23–31 Therefore there is a need for multifunctional, procedurally adept, and automated systems that require minimal labor and components in order to promote accessibility and technology adoption.
To address this need, to eliminate the tradeoff, and to simplify labor for complex experimental procedures – we considered several factors. In order to fully appreciate the biomechanical properties of cells but in a high throughput and automated manner, it is necessary to develop a scalable microfluidic design that incorporates scale matching in important experimental parameters, such as spatial, temporal, and force properties. Not only is it important for feature sizes of the device to be on the order of the cell and nucleus size, but the time scale of measurements should match biomechanical time scales as in strain and relaxation events. It may also be important for externally applied forces onto cells to be comparable in magnitude to those present in biological systems in order to appreciate physiological responses, as in migration and invasion driven by cell generated forces. For instance, if the flow rate used in microfluidic techniques is too high, which is typically the case in previous studies aimed at high throughput operations, relaxation dynamics cannot be studied and appreciated since they are slower. If the flow rate is too low, experiments would be impractical as cells would not deform sufficiently. Additionally, in vivo flow velocities are on the order of 0.5 μm s−1 and tumor interstitial pressures are around 1000 Pa.32,33 By performing time-scale matching, we can appreciate the properties conferred upon the cell by the coupling of relaxation and deformation dynamics. This is particularly interesting in the context of cancer metastasis, in which cells undergo frequent squeezing and recovery events during and after invasion across highly confined physiological spaces (e.g. constricted gaps in the ECM, endothelial junctions, microvessels).4,14,34-36 Furthermore, while typical experiments especially in microfluidics can sample many cells, individual cells are usually sampled only once. Because each cell is a highly complex system, a single sample per cell may not provide details about the diversity of and dynamics associated with the responses of a single cell. Thus, such data, while high throughput, are limited by their inability to distinguish the variability between different cells in a population and the variability of a property within an individual cell.
The device we present here is a parallel array of serial micropipettes capable of performing both deformation and relaxation measurements of individual cancer cells. Each cell is sampled multiple times for the assessment of consequential effects, which enables us to answer questions such as (1) how does one deformation event impact subsequent deformation events and (2) what are the key dynamics that govern serial deformations? Addressing these questions is important because it offers a more comprehensive assessment of a complex cell mechanical property (deformability) over a one-shot measurement (e.g. the aspect ratio of a cell under a fixed stress). This is also important for physiological relevance because, for instance, during the metastatic cascade, cells typically undergo a multitude of deformation events, from active invasion across confined spaces of the ECM in the tumor stroma to circulation across small blood and lymphatic vessels. Cancer cells therefore undergo constant deformations. Because cells are viscoelastic, their deformability is impacted by their conformational states conferred from their previous deformation events. However, the dynamics of serial deformations are unclear, and our device enables these dynamics to be elucidated. By understanding if and how a cell is conditioned by deformations in subsequent events, we can begin to gain potential insights toward the mechanical elements that govern cancer metastasis.
For our experiments, we used the MDA-MB-231 cell line, which model highly metastatic breast adenocarcinoma. Their metastatic nature and previous studies8,37,38 indicate that their deformation dynamics are of particular interest. Our results demonstrate several key findings. An initial deformation event facilitates subsequent serial deformations of the same cell, and this mechanical conditioning is dependent on the initial and remaining strain on the cell. The strain dynamics during deformation are dependent on both the viscoelastic cell body and nucleus. These experiments were performed in a simple microfluidic design with an automated experimentation scheme, which increases the capacity of practicable experiments and provides an instantly enabling technology to any basic biology lab setting in a small self-reliant form factor requiring no external equipment or micromanagement.
2. Results and discussion
2.1 Device design and operations
The device consists of parallel microchannels. Each channel contains a series of microconstrictions to serve as a serial micropipette capable of deforming objects multiple times via pressure driven flow. The larger region of the channel has a width of 15 μm, which is on the order of the size of a cell. The smaller constriction region is 3.3 μm, which is smaller than the cell nucleus, thus ensuring that the cell undergoes a substantial deformation that samples a key organelle in the cell that often limits cell squeezing in physiological landscapes due to its size and stiffness. Additionally, two different lengths of the constriction region are incorporated, one that is 10 μm-long (shorter than a typical cell) and one that is 60 mm-long (longer than a typical cell), mimicking short physiological barriers such as ECM-pores and long physiological barriers such as microvessels, respectively (Fig. 1a inset). A pressure gradient is induced on-chip across each channel by applying a difference in liquid height between the inlet and the outlet of the device. This enables device operation without external pressure sources. For the experiments here, we applied a pressure gradient of around 400 Pa, which is comparable to interstitial pressures in tumors.33 Our device design and operations facilitate more conventional micropipette studies than existing microfluidic constriction or deformation schemes, enabling multifaceted studies in an automated manner as shown in Fig. 1 and described in the following.
Fig. 1.
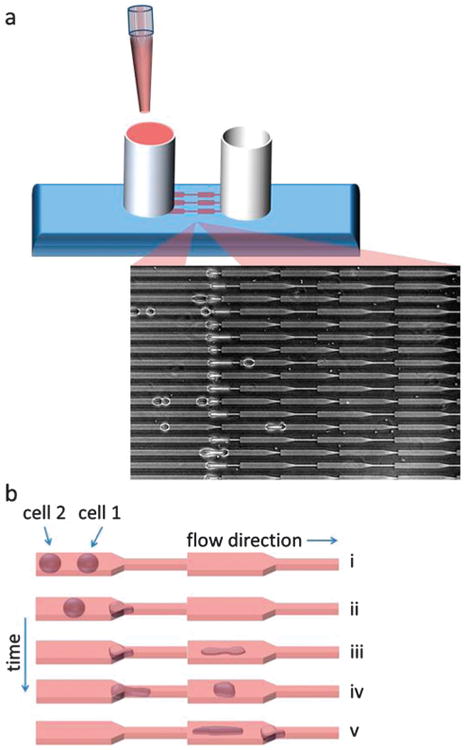
Schematic of device and operations. (a) The user simply pipettes the sample of interest into the inlet reservoir (left) and gravity drives the flow, enabling the device to operate without any external pressure actuators. Cells are automatically driven to the micropipette constrictions (inset). (b) After sample loading, the multi-step serial cell deformation experiments are performed automatically with no manual input required. 5 main steps are performed in an automated manner: (i) multiple cells flow through the channels and into the constriction region, (ii) cell 1 enters the constriction and clogs the flow as it undergoes deformation under a fixed pressure gradient, (iii) cell 1 fully transits across the barrier and cell 2 subsequently clogs the flow, enabling (iv) cell 1 to relax towards equilibrium at a fixed position, (v) cell 2 fully transits across the barrier and cell 1 clogs the flow at the next constriction, allowing cell 2 to relax at a fixed position while cell 1 undergoes a secondary deformation. The width of the larger channel region is 15 μm, the width of the smaller channel (constriction) region is 3.3 μm, and two different lengths are incorporated at the constrictions (10 μm and 60 μm), as shown in Fig. 1a inset. The height of the channels is a constant 10 μm.
Strain rate at fixed pressure
Cells that enter the constriction region essentially clog the flow, inducing in that channel zero volumetric flow rate and infinite hydrodynamic resistance,39 so the pressure drop (400 Pa) across the channel is entirely across the cell. In considering the cross-sectional area of the channel and thus the area of the cell that the pressure is acting on, this translates into an applied force across the cell of around 60 nN, which is on the scale of the forces that an individual cell generates.40–42 Timelapse microscopy enables the tracking of the cell strain over time under this fixed pressure. In our experiments, since each cell flows in one direction (longitudinal) and is stretched along that direction, the strain J that we measure is defined to be the length that the cell is stretched from its equilibrium ΔL divided by its equilibrium length L0 as measured by the cell length in the larger channel before reaching the constriction. This is the definition used throughout this paper and is consistent with conventional micropipette studies.7,19
Release and relaxation after an initial strain
After an initial strain is applied to the cell during constriction transit, cell relaxation dynamics can be assessed. This is accomplished in an automated manner in this device as subsequent cells will plug the constrictions as they undergo transits, stopping the flow, and enabling the previously deformed cell to relax at a fixed position for tracking.
Tracking serial cell deformations
Every micropipette channel is designed with multiple constrictions in series to enable the multiple sampling of each transiting cell. This is important because each cell is dynamic and heterogeneous, and a static measurement of a cell property does not provide insights into its full capacity. The serial design induces cells to necessarily transit across multiple barriers to probe dynamic effects. However, even at relatively low pressures, subsequent transit times can be fast due to a mismatch in the relaxation rates and flow speeds (the cell is still in a highly deformed state in subsequent transits), thus masking the dynamic regime in the behavior of serial deformations. With our device, because each serial micropipette consists of a single channel, intermittent flow pauses are automatically generated as multiple cells are transiting across the same micropipette channel, as shown in Fig. 1 and ESI,† Video S1, thus enabling cells to relax back towards its initial conformation before the next deformation event. This enables us to probe into the dynamics that govern multiple cell deformations and cell mechanical properties that result from the coupling between relaxation and deformation.
2.2 Repeated cell transits and taxol treatment
Using the procedure demonstrated previously, we measured the transit times of the same cell across 5 sequential constrictions. Here, we considered situations in which only one cell was present in the serial micropipette channel, so cell 2 from Fig. 1 was not present, and we examined experiments from the 10 μm-long constriction design. Because cell 2 was not present, cell relaxation between constrictions is typically less than 1 second. We investigated the serial deformations of both untreated cells and cells treated with 10 μM paclitaxel (taxol), a chemotherapeutic drug that stabilizes microtubules and inhibits cell division,43–45 for 1 day. As shown in Fig. 2a, the transit times across constrictions decrease after the first transit. The transit time across the first constriction is larger for taxol treated cells, which we may expect as the size of these cells is significantly larger than untreated cells (Fig. 2a inset) due to mitotic inhibition. Here, the size is defined by the length of the cells in the microchannel, since the cell width generally fills the channel width. As the cells transit across subsequent barriers, however, the transit times collapse between the two cell groups, demonstrating that once the cells are under sufficient deformation, cell size becomes less important in determining transit times. Interestingly, we also found that cell permeation across constrictions is further facilitated after the second transit, as illustrated in Fig. 2b. For each cell, we normalized the transit times across the third, fourth, and fifth constrictions to the transit time across the second constriction of the same cell, and our results show that cells can transit across the later constrictions more quickly.
Fig. 2.
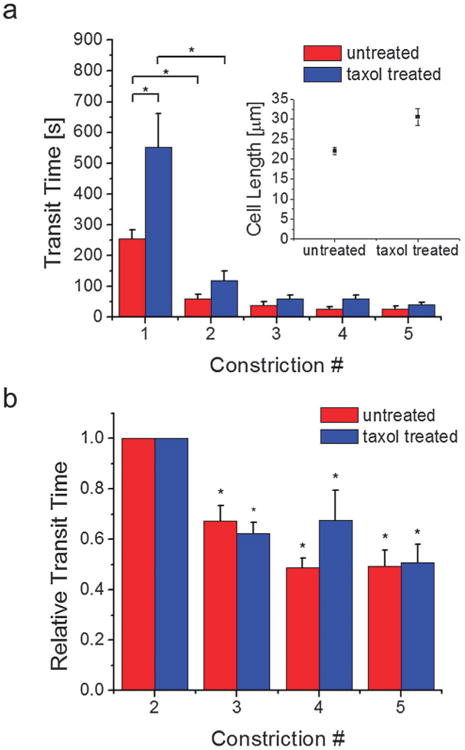
Cell permeation across sequential micropipette constrictions and the effects of taxol treatment. (a) Individual untreated and taxol treated cells were driven via pressure driven flow to permeate across sequential subnucleus-scaled constrictions. Taxol treated cells are larger (length = 31 ± 2 μm, n = 26) (inset) and require a longer transit time across the first constriction (550 ± 109 s, n = 26) than untreated cells (length = 22 ± 0.9 μm, n = 36; transit time 1 = 254 ± 59 s, n = 34). For both cell groups, the initial transit requires the longest time. Subsequent transits are faster and the difference between the two cell groups is reduced. The number of cells n examined in subsequent transit events ranged from 20 to 40. * denotes p < 0.01. (b) The transit times across the third, fourth, and fifth constrictions are normalized by the transit time across the second constriction of the same cell. Transit times are further reduced at subsequent constrictions after the second permeation. * denotes p < 0.01 when compared to unity. Error bars are s.e.m.
These findings suggest that cells that undergo perpetual deformations exhibit less difficulty in permeating across highly confining subnucleus-scaled mechanical barriers. Since aggressive cancer cells are constantly undergoing deformations, particularly across dense ECM networks with subnucleus-scaled pore sizes, it may be easier for them to invade than more static cells. In nutrient-deprived regions, as in locations where large tumors are forming, energetic efficiency may be important in tumor activity, and invasion becomes more efficient for more aggressively invasive cells. Additionally, we showed that taxol treatment, which is a common therapeutic for metastatic breast cancer, increases the size of the cell and the initial transit time. Once the cell is conditioned after the initial deformation event, the relative difference in cell transit times becomes less distinguishable, suggesting that for aggressive cells, size may not be critical in the cost of invasion. Taxol, however, also reduces directionally polarized migratory behavior,46,47 which makes persistent invasion across confined barriers more difficult. This suggests that anti-invasion properties of taxol46,48 may result from a synergy of cell size increase and decreased directional persistence in migration, which would decrease the probability of occurrence of the initial deformation event and thus inhibit subsequent easier invasions. Taxol treatment for 1 day also has the impact of increasing the size of cell nuclei (ESI,† Fig. S2), as cells fail to divide during cytokinesis. Since the nucleus, due to its size and stiffness, is mechanically the most obstructive intracellular component during invasion,4 its size increase likely also plays an important role in impeding the initial deformation event. Finally, since microtubule disruption and taxol are known not to have a significant impact on the rigidity of cells,49–52 our results show that passive anti-invasive effects of taxol are most likely caused by the increase in cell and nucleus size.
2.3 The strain dynamics of serial deformations
Next we examined the serial deformation dynamics of cells in which cell 2 in the configuration in Fig. 1 was present. This allowed for more substantial cell relaxation over longer durations, on average over 3 minutes as shown in ESI,† Fig. S2, between subsequent deformations. The results for the remainder of this paper will be based on this coupled-cell configuration in order to better appreciate both deformation and relaxation dynamics. In the previous section we considered short recovery times during which cells remained in highly deformed states after the first transit and here we considered substantially longer recovery times during which many cells recovered their equilibrium shapes. Thus our study covers a large range in the spectrum of recovery times and relaxation states that may occur in vivo.
Our experiments show that even after prolonged relaxation, an initial deformation event facilitates subsequent deformations, as demonstrated in Fig. 3a. The initial deformation requires the longest time, and the strain vs. time curve displays several phases. Here, strain refers exclusively to the strain of each cell along the long axis of the channel, i.e. the length that the cell is stretched from equilibrium divided by the cell's equilibrium length. With respect to the strain rate of the cell, the three main phases identifiable are (1) the initial shortest and fastest phase followed by (2) a longer, stagnant phase then followed by (3) a moderately fast phase. Deformations across subsequent barriers have reduced or eliminated phases 2 and 3, enabling the cell to deform and transit across the barrier more easily.
Fig. 3.
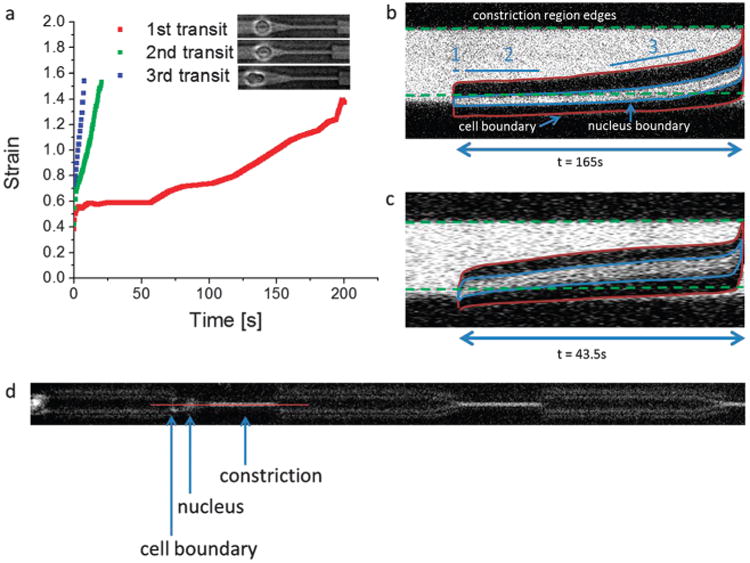
Serial deformation dynamics. (a) The same MDA-MB-231 cell is deformed across multiple microconstrictions (3.3 μm × 10 μm × 60 μm) in series in the serial micropipette device. Subsequent transits are faster and display altered strain dynamics. The cell is allowed to relax before subsequent deformations, as described in the text, and the extent of their relaxed state right before the next deformation event is displayed in the corresponding pictures (on the label). In the first transit, multiple phases are exhibited in the strain dynamics – an initial rapid phase, followed by a stagnant phase, and a moderate rate final phase. (b) More details about the strain dynamics of the first transit are elucidated when considering the transit dynamics of the cell nucleus, as shown here with a live nucleus stain. The image is a kymograph along the center of the micropipette constriction (longitudinal axis vs. time). Simultaneous phase contrast and fluorescence imaging help display the cell boundaries, the nucleus, and the constriction. This enables a more comprehensive consideration of the contributing elements in the phases of cell deformation dynamics. As shown, phase 1 is the initial cell response to a fixed stress from the external pressure, phase 2 is when the stiff cell nucleus is obstructed at the entry of the constriction due to insufficient pressure but viscoelastic creep enables slow permeation, and during phase 3 the nucleus has sufficiently deformed (partially) into the constriction leading to an increase in subsequent strain rate. (c) The subsequent transit for the same cell as in (b) displays a faster strain rate without prolonged nucleus obstruction at the constriction interface. Both the cell boundaries and the nucleus deform into the constriction more quickly. (d) A representative image illustrating the slice, indicated by the red line, where the kymographs were taken. For scale reference, the length of the constriction is 60 μm.
To better gauge the nature of these phases, we stained the nuclei of live cells and performed simultaneous phase contrast and fluorescence imaging to distinguish relative contributions from the cell body (i.e. primarily the cytoskeleton) and the largest and stiffest organelle, the cell nucleus. Fig. 3b and ESI,† Video S2 show the kymograph and video, respectively, of a typical cell transit event, and the transit phases are now more apparent. The first phase is when part of the cell can easily deform into the constriction, likely due to a simple force balance between the applied pressure and the initial elastic response of the cell.53,54 This can be seen from the rapid increase in the longitudinal boundaries of the cell, outlined in red in the kymograph, at the very beginning under the label “1.” Phase 2 is when the nucleus is obstructed and its stiffness is too high to transit further into the constriction, as demonstrated by the nucleus being stuck at the constriction interface. However, a slow creep from its viscoelastic nature enables gradual permeation. This creep deformation can be interpreted from the increase in the length of the boundaries of the nucleus, represented by the blue outline, in the kymograph. Phase 3 is when the nucleus has deformed entirely into the constriction, leaving the remaining (less obstructive) portion of the cell to deform more quickly into the constriction. The cell body and nucleus are now highly deformed and the longitudinal boundaries are substantially longer than initially. We note here that phase 3 in the initial transit is much longer than the entirety of the transit period of the subsequent transits shown in Fig. 3a. This shows that while the nucleus appears to be the most obstructive element in cell transit, the serial deformation effect is a reflection of the conditioning of both the nucleus and the cytoskeleton. Once the cell is conditioned, its subsequent transit dynamics have an altered behavior that is faster than both phase 2 and phase 3. Fig. 3c shows the kymograph of the same cell as in Fig. 3b deforming across a second barrier. The strain dynamics of the whole cell as well as that of the nucleus are altered; there is no nucleus obstruction phase and the cell transits through the entire constriction much more quickly. Fig. 3d shows a representative spatial slice from which the kymographs were taken.
It is noteworthy here that under a fixed cell-scaled force of 60 nN (via 400 Pa of applied pressure completely dropped across the cell at the constriction), the cells examined in our experiments deformed and transited completely across the constriction within a matter of minutes (4.2 ± 0.5 and 7.3 ± 2 minutes for the first and thus longest deformation event through 10 μm-long and 60 μm-long constrictions, respectively). The times were even shorter for subsequent transits. This translates into comparable cell migration velocities in 3D gel studies,55,56 suggesting that simple creep strain dynamics under consistent force loads could play a basic role in cell invasion across subcellular-scaled confinements. For instance, even if an applied force from the cell is not sufficient to enable it to squeeze across a constriction instantaneously, the cell simply needs to wait while consistently applying a forward force, e.g. through actin polymerization, and viscoelastic creep will confer the cell a sufficiently deformed state to pass through the constriction. Thus, cell invasion may characteristically exhibit the coupling between both active (force generation) and passive (creep strain) processes. It is also notable that the phases observed here in the strain dynamics of flowing cells have qualitative similarities to the phases observed when cells are actively migrating across subnucleus-scaled barriers.4,37,46
2.4 The serial factor
To assess and appreciate the impact of repeated deformations on cells, we need a way to measure a factor, which we will now call the “serial factor” SF, that quantifies the relative degree of difficulty for a cell to transit across constrictions after it squeezes across an initial constriction. A good candidate for SF is the ratio of the transit times SF = ts/ti, where ti is transit time across the first constriction and ts is the transit time across a subsequent constriction.
First, our results show in Fig. 4 that the average SF is larger for serial transits across shorter constrictions. The average SF is 0.40 ± 0.04 (n = 20) and 0.20 ± 0.05 (n = 13) for 10 μm-long serial constrictions and 60 μm-long serial constrictions, respectively, where n is the number of single-cell serial transit events. We note here that in this data, the strains on the cells before subsequent transits for the 10 μm-long and 60 μm-long serial micropipette experiments are 0.24 ± 0.03 (n = 20) and 0.25 ± 0.05 (n = 13), respectively, and they are not statistically different. This indicates that longer constrictions, which induce larger overall deformations on the cell, facilitate subsequent deformations to a larger degree, even after the cell is allowed to relax back towards equilibrium.
Fig. 4.
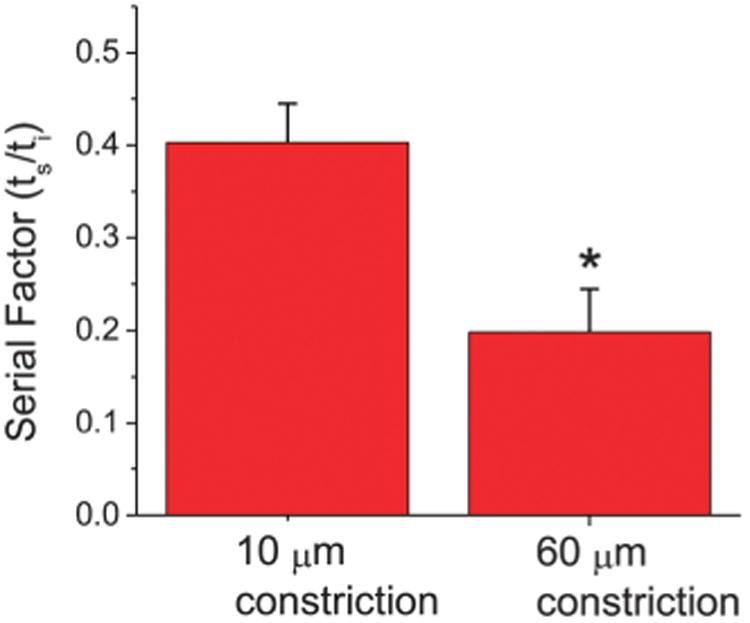
The serial factor vs. constriction length. Shorter constrictions (10 μm) that only span a fraction of the total cell length exhibit a longer normalized transit time in subsequent constrictions (ts/ti = 0.40 ± 0.04, n = 20) than longer constrictions (60 μm) that span most if not the entire deformed cell length (ts/ti = 0.20 ± 0.05, n = 13). The serial factor is thus larger for cells experiencing larger initial strains. Error bars represent standard error of the mean, and * indicates p < 0.01.
Next, we were interested in measuring SF as a function of the conformation of the cell after deformation in order to gauge how the shape or morphology of a previously deformed cell translates into its ability to deform across a subsequent constriction. Therefore, since we were conducting deformation and relaxation experiments on these cells, we were interested in the function SF(Jr), where Jr is the remaining strain on an initially deformed cell after it is given time to relax towards equilibrium. To derive this function, we considered previous micropipette studies that empirically characterized cells to exhibit a power-law creep under a fixed applied pressure, such that the creep strain is J(t) = Atα, where A is a constant scaling prefactor, t is the time the cell is under the applied pressure, and α is the power-law scaling exponent. We note that this simple power-law relation does break down over the entirety of the cell and may be impacted by our simultaneous sampling of the nucleus and the cytoskeleton with subnucleus-scaled constrictions.19,53 However, for simplicity and in order to derive an empirical effective model, here we adopted the power-law approximation. Next we also assumed that A remains constant for the same cell under serial deformations such that all changes in cell strain behavior are then attributed to α, which helps simplify our effective model. For our experiments, since most of the time the cell spends transiting across the barrier is time spent for the strain to increase until the cell reaches a conformation (i.e. when the cell is thin enough) that enables the cell to flow easily and rapidly through the constriction, we approximated ti and ts to be effectively the time when the cell strain is increasing under a constant applied pressure gradient. From this we derived SF as follows:
Since serial deformations are easier, the power-law scaling factor α is altered in subsequent deformations in comparison to the initial, such that there are two different strain dynamics relations:
| (1a) |
| (1b) |
where the indices 1 and 2 correspond to initial and subsequent strains, respectively. From this, we obtain:
| (2a) |
| (2b) |
| (2c) |
where Ji is the total strain from the initial deformation (1st transit), Js is the total strain in a subsequent deformation (the following serial transits), Jr is the remaining strain on the cell after relaxation and before the next deformation event, and tr is the virtual time that it would require the cell to strain from 0 to Jr. The total strains on the cells are the same for each transit since they are deforming across identical subsequent constrictions so Ji equals Js and it follows that:
| (3a) |
| (3b) |
which gives an analytical form of SF. Next, we impose the condition that as the cell is allowed to relax completely to its equilibrium state after deformation, α2 would recover to α1:
| (4) |
where C is a scaling coefficient and F is the normalized relaxation function that decays from 1 to 0 when the cell fully recovers (when Jr/Ji = 0). From the data, SF decays sharply initially and then plateaus near 0, so therefore we choose a simple function that displays that form:
| (5) |
where k × Ji is the characteristic decay length of F.
Fig. 5 shows the SF vs. Jr/Ji plot for the micropipette experiments with 60 μm-long constrictions. Only experiments from 60 μm-long constrictions were analyzed here because for 10 μm-long constrictions, since the constriction is shorter than the cell, there is non-uniform relaxation after cell transit (parts of the cell starts relaxing earlier than others), which complicates any analytical comparisons, particularly with our simple model. As shown in Fig. 5 by the blue fitted curve, the experimental data fits to our model for SF (R2 = 0.92). Previous studies focusing on the low strain regime have shown that the strain dynamics exhibit a weak power-law dependence with α < 1.19,53,57 We calculated and plotted the red curve in Fig. 5 that assumes a constant α = 0.25, a typical value in the low strain regime. As demonstrated, the curvatures of the two calculated curves are different with one that is concave and one that is convex. The actual SF data is concave, illustrating that in the serial deformation scenario, it is applicable to consider an evolving α that becomes larger than 1. Without considering the serial effect, it would be difficult to fully appreciate the details and degree to which subsequent deformations are facilitated, which are especially relevant to physiological phenomena that require cells to deform repeatedly such as in migration and invasion. Using our model for an evolving α that is dependent on the remaining strain before subsequent cell deformations, we can recover the typical characteristics of J(t) for differentially relaxed cell states, as shown in Fig. 6.
Fig. 5.
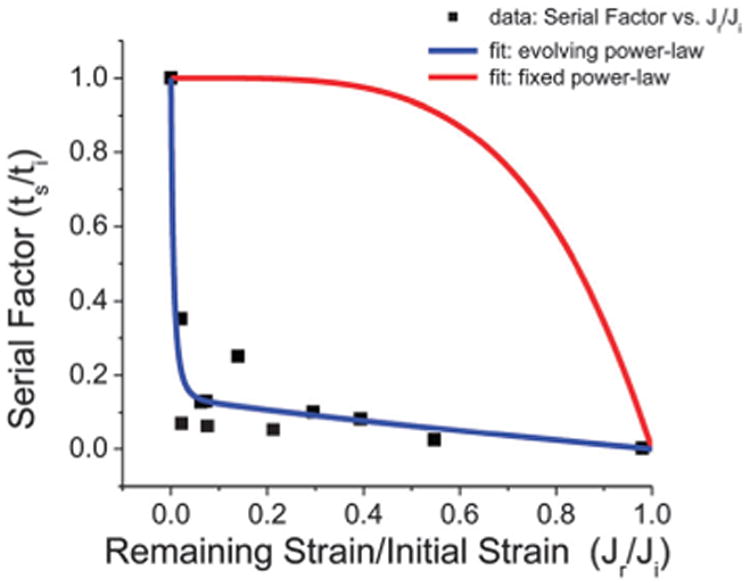
The serial factor vs. normalized remaining cell strain. After an initial cell deformation across a 60 μm long subnucleus-scaled (3.3 μm × 10 μm cross-sectional area) constriction, it becomes easier for cells to deform across subsequent (identical) constrictions. The relative degree of difficulty between subsequent and initial deformation processes can be interpreted from the relative transit times across the constrictions (ts/ti), i.e. the serial factor SF. As the remaining strain Jr is increased (relative to the total initial strain Ji) signifying less relaxation before the subsequent deformation, the transit process becomes faster. Moreover, SF exhibits a sharp initial decay, which our modified power-law based model for SF captures (blue fitted curve, R2 = 0.92). The conventional low strain, weak power-law model (α = 0.25) exhibits a different behavior (red curve).
Fig. 6.
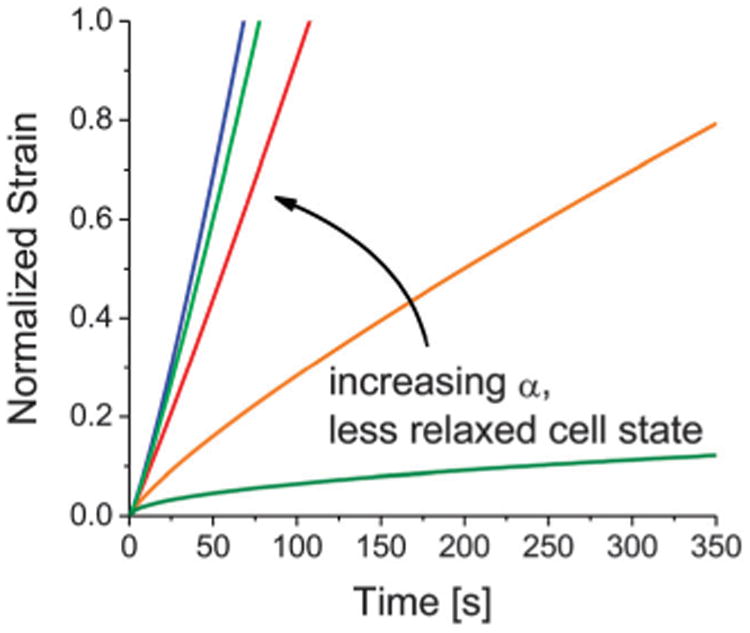
Strain dynamics under fixed pressure from the evolving power-law model. By assuming that the power-law scaling exponent α evolves based on the degree of relaxation of the cell state after an initial deformation, we plotted the normalized strain for different α's and recovered the typical behavior in serial strain dynamics under fixed pressure.
The results here show that unless a cell is allowed to relax completely back to its equilibrium state after a deformation event, any remaining strain indicates that the cell is in an enhanced “serial mode” that enables it to deform across subsequent constrictions more easily, in accordance to the serial factor. As illustrated in Fig. 7, this could have implications in the metastatic process in cancer, as non-proteolytic invasion induces cells to squeeze across narrow gaps that are often smaller than the cell nucleus, i.e. through constriction rings in the ECM.4,34 An initial invasion event would thus confer upon the cell faster strain dynamics that facilitate subsequent invasion through confining physiological barriers.
Fig. 7.
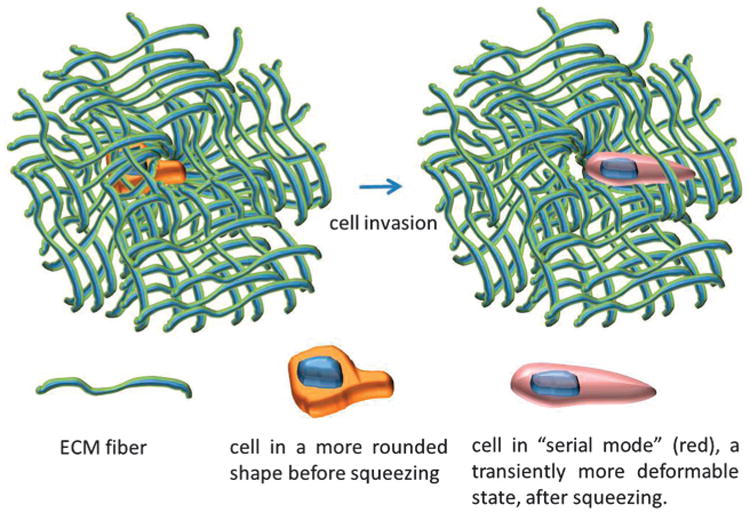
Illustration of the serial effect during cancer invasion. When a cell is in a more relaxed state and invades (non-proteolytically) across a constriction ring in the ECM, the cell is deformed and transiently enters a “serial mode” that exhibits a higher power-law scaling exponent in its strain dynamics, making the subsequent invasion events easier in accordance to the serial factor.
3. Conclusion
We developed a simple self-reliant system with no external parts or sources (syringe pumps, pressure manifolds, or other bulky connections that drive microfluidic devices) that requires only the loading of the cell samples of choice and performs multifaceted experiments in an automated manner without robotic assistance from programmable microscope stages, motorized parts, or other robotic actuators. We have demonstrated using this device that an initial cell deformation event, via a fixed cell-scaled force, conditions the cell for easier subsequent deformations, as the strain dynamics are altered. This conditioning is a function of the initial and remaining strain on the cell and may have physical implications for biological phenomena that require a multitude of deformation events, such as cancer invasion or immune cell diapedesis. We also gauged the contribution to the deformation strain dynamics from both the whole-cell body and the nucleus, which complements previous work that primarily considered only whole-cell boundaries or isolated nuclei or other intra-cellular components. Finally, we believe that the simplicity, form factor, automation, and multiple capabilities of this device can facilitate in a highly adoptable manner a broad array of cell mechanobiology studies, from measuring cell viscoelastic properties to disease diagnostics.
4. Experimental section
4.1 Cell culture
MDA-MB-231 cells were obtained from the NCI Physical-Sciences and Oncology Center. They were cultured in Leibovitz L-15 media (Life Technologies) with 10% fetal bovine serum (Atlanta Biologicals) and 1% penicillin–streptavidin (Life Technologies) at 37 °C without CO2.
4.2 Device fabrication
Device masters were fabricated at the Cornell NanoScale Facility (CNF). Standard photo- and soft-lithography techniques were used to create devices. Briefly, SU8 was spun onto a silicon wafer and exposed under a photomask with the micropipette patterns in a stepper. The patterned wafer was then developed to create a negative image of the device. PDMS was cast onto the master and crosslinked to create the micropipette channels. The channels were then bonded to glass slides to create the finished microfluidic device.
4.3 Experiments and analysis
Devices were treated with 1% bovine serum albumin (BSA) (Sigma-Aldrich) in serum-free media (L-15) for several hours before experiments in order to prevent stiction. Additionally, cells used in experiments were resuspended in serum-free media, as serum is a major contributor to cell adhesion.58 Cells were loaded into the inlet reservoir of the device and experiments were automatically conducted as described in the design and operations section of this paper. Gravity drives the flow with an applied pressure gradient equal to ρgΔh, where ρ is liquid density, g is the coefficient of gravity, and Δh is the difference in liquid height between the inlet and outlet. A fixed volume difference, which is directly proportional to a fixed liquid height difference, was set between the inlet and outlet reservoirs via pipetting. The volume difference for these experiments was 1.4 mL with a pipette resolution of 0.02 mL. The device was placed and kept on a heating plate set at 37 °C. Videos were recorded at 500 ms per frame under a microscope, which produced the data of the experiments. Experiments typically lasted 1–2 hours, after which the device inlet is usually clogged by excessive cells. Next generation designs that incorporate larger channels between the inlet and outlet to allow excessive cells to flow through instead of clog the device would likely extend the operational lifetime. Experimental analysis and cell tracking were performed using ImageJ and custom MATLAB programs. For statistical analysis, one-way ANOVA was used to determine statistical significance. Error bars on data represent standard error of the mean (s.e.m.). For taxol experiments, cells were incubated in 10 μM taxol (Cytoskeleton, Inc.) for 1 day prior to experiments. For fluorescence experiments, NucBlue (a live nucleus counterstain that is formulated from Hoechst 33342) (Life Technologies) was used and cells were incubated in the dye in complete growth media for 15 minutes.
Supplementary Material
Insight, innovation, integration.
We developed a highly adoptable, automated, serial micropipette device and assay usable in any existing cell biology lab without additional infrastructure. This platform minimizes the manual labor cost and peripheral instrumentation necessary in traditional cell deformability-related techniques, such as micropipette aspiration and atomic force microscopy. We applied our device and method to study multiple sequential deformations of individual cells at the subnucleus scale in a parallel manner, which offer insights beyond the more typical studies that sample cells at low strains and only once. This is especially relevant in phenomena such as cancer metastasis, which involves not simply a single deformation event but rather a multitude of deformations often at the subnucleus scale.
Acknowledgments
The work described was supported by the Cornell Center on the Microenvironment and Metastasis through Award Number U54CA143876 from the National Cancer Institute. This work was performed in part at the Cornell NanoScale Facility, a member of the National Nanotechnology Network, which is supported by the National Science Foundation (Grant ECS-0335765). Michael Mak is a NSF Graduate Research Fellow.
Footnotes
Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ib40128f
References
- 1.Bao G, Suresh S. Cell and molecular mechanics of biological materials. Nat Mater. 2003;2:715–725. doi: 10.1038/nmat1001. [DOI] [PubMed] [Google Scholar]
- 2.Chambers AF, Groom AC, MacDonald IC. Dissemination and growth of cancer cells in metastatic sites. Nat Rev Cancer. 2002;2:563–572. doi: 10.1038/nrc865. [DOI] [PubMed] [Google Scholar]
- 3.Friedl P, Wolf K. Tumour-Cell Invasion and Migration: Diversity and Escape Mechanisms. Nat Rev Cancer. 2003;3:363–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- 4.Friedl P, Wolf K, Lammerding J. Nuclear mechanics during cell migration. Curr Opin Cell Biol. 2011;23:55–64. doi: 10.1016/j.ceb.2010.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rosenbluth MJ, Lam WA, Fletcher DA. Force Microscopy of Nonadherent Cells: A Comparison of Leukemia Cell Deformability. Biophys J. 2006;90:2994–3003. doi: 10.1529/biophysj.105.067496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stewart MP, Toyoda Y, Hyman AA, Muller DJ. Tracking mechanics and volume of globular cells with atomic force microscopy using a constant-height clamp. Nat Protocols. 2012;7:143–154. doi: 10.1038/nprot.2011.434. [DOI] [PubMed] [Google Scholar]
- 7.Hochmuth RM. Micropipette aspiration of living cells. J Biomech. 2000;33:15–22. doi: 10.1016/s0021-9290(99)00175-x. [DOI] [PubMed] [Google Scholar]
- 8.Guck J, Schinkinger S, Lincoln B, Wottawah F, Ebert S, Romeyke M, Lenz D, Erickson HM, Ananthakrishnan R, Mitchell D, Kas J, Ulvick S, Bilby C. Optical Deform-ability as an Inherent Cell Marker for Testing Malignant Transformation and Metastatic Competence. Biophys J. 2005;88:3689–3698. doi: 10.1529/biophysj.104.045476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sraj I, Eggleton CD, Jimenez R, Hoover E, Squier J, Chichester J, Marr DWM. Cell deformation cytometry using diode-bar optical stretchers. J Biomed Opt. 2010;15:047010. doi: 10.1117/1.3470124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gossett DR, Tse HTK, Lee SA, Ying Y, Lindgren AG, Yang OO, Rao J, Clark AT, Carlo DD. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc Natl Acad Sci U S A. 2012;109:7630–7635. doi: 10.1073/pnas.1200107109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gabriele S, Benoliel AM, Bongrand P, Théodoly O. Microfluidic Investigation Reveals Distinct Roles for Actin Cytoskeleton and Myosin II Activity in Capillary Leukocyte Trafficking. Biophys J. 2009;96:4308–4318. doi: 10.1016/j.bpj.2009.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Adamo A, Sharei A, Adamo L, Lee B, Mao S, Jensen KF. Microfluidics-Based Assessment of Cell Deformability. Anal Chem. 2012;84:6438–6443. doi: 10.1021/ac300264v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang W, Kai K, Choi DS, Iwamoto T, Nguyen YH, Wong H, Landis MD, Ueno NT, Chang J, Qin L. Microfluidics separation reveals the stem-cell–like deform-ability of tumor-initiating cells. Proc Natl Acad Sci U S A. 2012;109:18707–18712. doi: 10.1073/pnas.1209893109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yamauchi K, Yang M, Jiang P, Yamamoto N, Xu M, Amoh Y, Tsuji K, Bouvet M, Tsuchiya H, Tomita K, Moossa AR, Hoffman RM. Real-time In vivo Dual-color Imaging of Intracapillary Cancer Cell and Nucleus Deformation and Migration. Cancer Res. 2005;65:4246–4252. doi: 10.1158/0008-5472.CAN-05-0069. [DOI] [PubMed] [Google Scholar]
- 15.Friedl P, Sahai E, Weiss S, Yamada KM. New dimensions in cell migration. Nat Rev Mol Cell Biol. 2012;13:743–747. doi: 10.1038/nrm3459. [DOI] [PubMed] [Google Scholar]
- 16.Pathak A, Kumar S. Biophysical regulation of tumor cell invasion: moving beyond matrix stiffness. Integr Biol. 2011;3:267–278. doi: 10.1039/c0ib00095g. [DOI] [PubMed] [Google Scholar]
- 17.Petushi S, Garcia FU, Haber MM, Katsinis C, Tozeren A. Large-scale computations on histology images reveal grade-differentiating parameters for breast cancer. BMC Med Imaging. 2006;6:14. doi: 10.1186/1471-2342-6-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jiang P, Yamauchi K, Yang M, Tsuji K, Xu M, Maitra A, Bouvet M, Hoffman RM. Tumor cells genetically labeled with GFP in the nucleus and RFP in the cytoplasm for imaging cellular dynamics. Cell Cycle. 2006;5:1198–1201. doi: 10.4161/cc.5.11.2795. [DOI] [PubMed] [Google Scholar]
- 19.Dahl KN, Engler AJ, Pajerowski JD, Discher DE. Power-Law Rheology of Isolated Nuclei with Deformation Mapping of Nuclear Substructures. Biophys J. 2005;89:2855–2864. doi: 10.1529/biophysj.105.062554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Vaziri A, Mofrad MRK. Mechanics and deformation of the nucleus in micropipette aspiration experiment. J Biomech. 2007;40:2053–2062. doi: 10.1016/j.jbiomech.2006.09.023. [DOI] [PubMed] [Google Scholar]
- 21.Yamada S, Wirtz D, Kuo SC. Mechanics of living cells measured by laser tracking microrheology. Biophys J. 2000;78:1736–1747. doi: 10.1016/S0006-3495(00)76725-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Crocker JC, Valentine MT, Weeks ER, Gisler T, Kaplan PD, Yodh AG, Weitz DA. Two-point microrheology of inhomogeneous soft materials. Phys Rev Lett. 2000;85:888–891. doi: 10.1103/PhysRevLett.85.888. [DOI] [PubMed] [Google Scholar]
- 23.Fletcher DA, Mullins RD. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–492. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Discher D, Dong C, Fredberg JJ, Guilak F, Ingber D, Janmey P, Kamm RD, Schmid-Schönbein GW, Weinbaum S. Biomechanics: cell research and applications for the next decade. Ann Biomed Eng. 2009;37:847–859. doi: 10.1007/s10439-009-9661-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lautenschläger F, Paschke S, Schinkinger S, Bruel A, Beil M, Guck J. The regulatory role of cell mechanics for migration of differentiating myeloid cells. Proc Natl Acad Sci U S A. 2009;106:15696–15701. doi: 10.1073/pnas.0811261106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kumar S, Weaver VM. Mechanics malignancy, and metastasis: the force journey of a tumor cell. Cancer Metastasis Rev. 2009;28:113–127. doi: 10.1007/s10555-008-9173-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Paszek MJ, Zahir N, Johnson KR, Lakins JN, Rozenberg GI, Gefen A, Reinhart-king CA, Margulies SS, Dembo M, Boettiger D, Hammer DA, Weaver VM. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 28.Park Y, Best CA, Badizadegan K, Dasari RR, Feld MS, Kuriabova T, Henle ML, Levine AJ, Popescu G. Measurement of red blood cell mechanics during morphological changes. Proc Natl Acad Sci U S A. 2010;107:6731–6736. doi: 10.1073/pnas.0909533107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fedosov DA, Caswell B, Suresh S, Karniadakis GE. Quantifying the biophysical characteristics of Plasmodium-falciparum-parasitized red blood cells in microcirculation. Proc Natl Acad Sci U S A. 2011;108:35–39. doi: 10.1073/pnas.1009492108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Grover WH, Bryan AK, Diez-Silva M, Suresh S, Higgins JM, Manalis SR. Measuring single-cell density. Proc Natl Acad Sci U S A. 2011;108:10992–10996. doi: 10.1073/pnas.1104651108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shelby JP, White J, Ganesan K, Rathod PK, Chiu DT. A microfluidic model for single-cell capillary obstruction by Plasmodium falciparum-infected erythrocytes. Proc Natl Acad Sci U S A. 2003;100:14618–14622. doi: 10.1073/pnas.2433968100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shields JD, Fleury ME, Yong C, Tomei AA, Randolph GJ, Swartz MA. Autologous Chemotaxis as a Mechanism of Tumor Cell Homing to Lymphatics via Interstitial Flow and Autocrine CCR7 Signaling. Cancer Cell. 2007;11:526–538. doi: 10.1016/j.ccr.2007.04.020. [DOI] [PubMed] [Google Scholar]
- 33.Boucher Y, Baxter LT, Jain RK. Interstitial Pressure Gradients in Tissue-isolated and Subcutaneous Tumors: Implications for Therapy. Cancer Res. 1990;50:4478–4484. [PubMed] [Google Scholar]
- 34.Wolf K, Mazo I, Leung H, Engelke K, Andrian UHv, Deryugina EI, Strongin AY, Bröcker EB, Friedl P. Compensation mechanism in tumor cell migration: mesenchymal–amoeboid transition after blocking of pericellular proteolysis. J Cell Biol. 2003;160:267–277. doi: 10.1083/jcb.200209006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wirtz D, Konstantopoulos K, Searson PC. The physics of cancer: the role of physical interactions and mechanical forces in metastasis. Nat Rev Cancer. 2011;11:512–522. doi: 10.1038/nrc3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kienast Y, Baumgarten Lv, Fuhrmann M, Klinkert WEF, Goldbrunner R, Herms J, Winkler F. Realtime imaging reveals the single steps of brain metastasis formation. Nat Med. 2010;16:116–122. doi: 10.1038/nm.2072. [DOI] [PubMed] [Google Scholar]
- 37.Mak M, Reinhart-King CA, Erickson D. Microfabricated Physical Spatial Gradients for Investigating Cell Migration and Invasion Dynamics. PLoS One. 2011;6:e20825. doi: 10.1371/journal.pone.0020825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Liu L, Duclos G, Sun B, Lee J, Wu A, Kam Y, Sontag ED, Stone HA, Sturm JC, Gatenby RA, Austin RH. Minimization of thermodynamic costs in cancer cell invasion. Proc Natl Acad Sci U S A. 2013;110:1686–1691. doi: 10.1073/pnas.1221147110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Stone HA, Stroock AD, Ajdari A. Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu Rev Fluid Mech. 2004;36:381–411. [Google Scholar]
- 40.Prass M, Jacobson K, Mogilner A, Radmacher M. Direct measurement of the lamellipodial protrusive force in a migrating cell. J Cell Biol. 2006;174:767–772. doi: 10.1083/jcb.200601159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kraning-Rush CM, Califano JP, Reinhart-King CA. Cellular Traction Stresses Increase with Increasing Meta-static Potential. PLoS One. 2012;7:e32572. doi: 10.1371/journal.pone.0032572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lemmon CA, Chen CS, Romer LH. Cell Traction Forces Direct Fibronectin Matrix Assembly. Biophys J. 2009;96:729–738. doi: 10.1016/j.bpj.2008.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schiff PB, Horwitz SB. Taxol stabilizes microtubules in mouse fibroblast cells. Proc Natl Acad Sci U S A. 1980;77:1561–1565. doi: 10.1073/pnas.77.3.1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jordan MA, Wilson L. Microtubules as Target for Anticancer Drugs. Nat Rev Cancer. 2004;4:253–265. doi: 10.1038/nrc1317. [DOI] [PubMed] [Google Scholar]
- 45.Gascoigne KE, Taylor SS. How do anti-mitotic drugs kill cancer cells? J Cell Sci. 2009;122:2579–2585. doi: 10.1242/jcs.039719. [DOI] [PubMed] [Google Scholar]
- 46.Mak M, Reinhart-King CA, Erickson D. Elucidating mechanical transition effects of invading cancer cells with a subnucleus-scaled microfluidic serial dimensional modulation device. Lab Chip. 2013;13:340–348. doi: 10.1039/c2lc41117b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Takesono A, Heasman SJ, Wojciak-Stothard B, Garg R, Ridley AJ. Microtubules Regulate Migratory Polarity through Rho/ROCK Signaling in T Cells. PLoS One. 2010;5:e8774. doi: 10.1371/journal.pone.0008774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Stearns ME, Wang M. Taxol Blocks Processes Essential for Prostate Tumor Cell (PC-3 ML) Invasion and Metastasis. Cancer Res. 1992;52:3776–3781. [PubMed] [Google Scholar]
- 49.Janmey PA, Euteneuer U, Traub P, Schliwa M. Viscoelastic properties of vimentin compared with other filamentous biopolymer networks. J Cell Biol. 1991;113:155–160. doi: 10.1083/jcb.113.1.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rotsch C, Radmacher M. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study. Biophys J. 2000;78:520–535. doi: 10.1016/S0006-3495(00)76614-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sato M, Schwartz WH, Selden SC, Pollard TD. Mechanical properties of brain tubulin and microtubules. J Cell Biol. 1988;106:1205–1211. doi: 10.1083/jcb.106.4.1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tsai MA, Waugh RE, Keng PC. Passive mechanical behavior of human neutrophils: effects of colchicine and paclitaxel. Biophys J. 1998;74:3282–3291. doi: 10.1016/S0006-3495(98)78035-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Desprat N, Richert A, Simeon J, Asnacios A. Creep Function of a Single Living Cell. Biophys J. 2005;88:2224–2233. doi: 10.1529/biophysj.104.050278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Thoumine O, Ott A. Time scale dependent viscoelastic and contractile regimes in fibroblasts probed by microplate manipulation. J Cell Sci. 1997;110:2109–2116. doi: 10.1242/jcs.110.17.2109. [DOI] [PubMed] [Google Scholar]
- 55.Fraley SI, Feng Y, Krishnamurthy R, Kim DH, Celedon A, Longmore GD, Wirtz D. A distinctive role for focal adhesion proteins in three-dimensional cell motility. Nat Cell Biol. 2010;12:598–604. doi: 10.1038/ncb2062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kraning-Rush CM, Carey SP, Lampi MC, Reinhart-King CA. Microfabricated collagen tracks facilitate single cell metastatic invasion in 3D. Integr Biol. 2013;5:606–616. doi: 10.1039/c3ib20196a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lenormand G, Millet E, Fabry B, Butler JP, Fredberg JJ. Linearity and time-scale invariance of the creep function in living cells. J R Soc, Interface. 2004;1:91–97. doi: 10.1098/rsif.2004.0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sagvolden G, Giaever I, Pettersen E, Feder J. Cell adhesion force microscopy. Proc Natl Acad Sci U S A. 1999;96:471–476. doi: 10.1073/pnas.96.2.471. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


