Abstract
Disease spreads as a result of people moving and coming in contact with each other. Thus the mobility patterns of individuals are crucial in understanding disease dynamics. Here we study the impact of human mobility on HIV transmission in different parts of Kenya. We build an SIR metapopulation model that incorporates the different regions within the country. We parameterise the model using census data, HIV data and mobile phone data adopted to track human mobility. We found that movement between different regions appears to have a relatively small overall effect on the total increase in HIV cases in Kenya. However, the most important consequence of movement patterns was transmission of the disease from high infection to low prevalence areas. Mobility slightly increases HIV incidence rates in regions with initially low HIV prevalences and slightly decreases incidences in regions with initially high HIV prevalence. We discuss how regional HIV models could be used in public-health planning. This paper is a first attempt to model spread of HIV using mobile phone data, and we also discuss limitations to the approach.
Introduction
Since the emergence of HIV/AIDS, modelling its dynamics has been dealt with extensively by many researchers. The basic approach is to describe the population in terms of three states: those who have not contracted HIV, susceptible, those who have HIV and remain sexually active, infectious and those individuals who are no longer engaged in spreading the disease, removed. This style of SIR model has been widely used to capture the dynamics of diseases, by for example [1–5] and in many other articles. For HIV, the SIR model is also applied, but with the assumption that infected individuals do not recover from the disease but rather stop being infectious [6–10]. SIR models consider the dynamics of diseases to depend only on the individual status like susceptible, infected or removed.
Under the standard SIR model, the transmission rates, infection periods, contact patterns and removed rates do not account for the spatial spread of the diseases. In this standard version, they ignore variations in demographic, social, cultural, economic and geographic factors [4, 11]. In reality, however, the spread of HIV is highly associated with geographic factors, such as population mobility, as well as the accessibility of and the proximity between infected areas [12]. Human mobility can be seasonal, short term and long term [13, 14]. Several studies have shown that migrant workers in urban areas can spread HIV to rural areas [15, 16]. For example, in South Africa, men who had moved away from a rural area to an urban area were twice as likely to have HIV than those still living in the rural area [12]. These migrant workers would regularly return to the rural area, potentially spreading the virus. Likewise, areas associated with high human mobility such as commercial farms and agricultural estates, mining areas, business centres and residential areas along busy roads have been connected to an increase in HIV infections [17–21]. Not all migrations appear to increase HIV transmission, and other studies have reported that the rural-urban migrations have little or no link to HIV risk [22, 23]. Overall, however, it appears that short-term human mobility, for example return visits from work to home town, are associated with high-risk behaviour. The migration to urban areas leads to an increased chance of interacting with individuals who are at higher-risk of being HIV infected, like sex workers [13, 14, 24]. Return visits to a home town then provide further spread of the disease.
Mathematical models that capture spatial scale for the spread of diseases dynamics are usually referred to as metapopulation models. In metapopulation models, the area under study is divided into different regions according to geographic positions. The distinct regions could be cities, towns or villages. The regions are connected by people travelling between them. Various studies have incorporated metapopulations in disease dynamics [25–30]. For example, Sattenspiel and Dietz [31], used a metapopulation model to show that increase in human mobility was associated with an increase of the spread of measles in the West Indian island of Dominica. Travel networks have very complex influence on disease dynamics, since they may fuel or may help disease extinction [29]. For example, Arino et al [32] used a two-region metapopulation model to study the influence of travel rates with respect to the stability of influenza. They observed that, for isolated regions, the disease in one of the regions approached the disease-free equilibrium while in the other region it approached the endemic. Introducing very small movements between the regions, the disease in all regions approached the endemic state. On increasing the movements rates, influenza died out in all the regions.
There have been a few earlier metapopulation models of the impact of human mobility on spread of HIV/AIDS. In one example, Coffee et al [13] looked at the impact of migration on the HIV epidemic in South Africa. They reported that, migrations when coupled to increased risk behaviour, have a causal effect on the increase of HIV. In a modelling study, Smith? et al [33] reported that, in order to globally eradicate HIV/AIDS, the money spent and other resources must aim at eradicating HIV/AIDS in all regions, since human mobility has an effect of sustaining the infections. However, the extent to which human mobility impacts the transmission of HIV infections still needs to be studied further. For example, one counterintuitive finding by Xiao et al [34], is that an increase in mobility rates among HIV/AIDS-infected individuals on mainland China decreased HIV infections in the country. Once again, it appears that there is a need to develop metapopulation models that are well-designed in order to clearly explain the impact of human mobility.
The purpose of this work is to develop a metapopulation model of the impact of human mobility to the transmission of HIV/AIDS. We modify the metapopulation model of Keeling and Rohani [35]. This model does not include a removed class, as is typical in HIV models. We thus introduce the removed class, which incorporates individuals who are in AIDS status and are no longer transmitting the disease. The model is parametrised using demographic data from Kenya at the time of the 2009 census [36] and the world bank data [37]. The rates of moving between regions is estimated from mobile phone data collected by Wesolowski et al [38]. Infection rate is estimated from Kenya HIV data KAIS 2007 [39] and the disease progression rate is adopted from the work of Baryama et al [9]. These data allow us to set up a full metapopulation HIV model for Kenya.
Our study builds on the work of Wesolowski et al [38], in analysing the impact of human mobility on malaria in Kenya. They used mobile phone data to track the regional travel of people between June 2008 and June 2009. Every call or message made by each user was mapped to one of 11,920 cell towers located in different regions in the country. From the call, an individual was assigned a primary settlement where they spent the majority of their night time. Using the primary settlements, they estimated the average monthly regional travel. We use their monthly mobility rate to study the impact of human mobility on HIV infections in Kenya.
Methods
We now present a SIR metapopulation model for the dynamics of HIV/AIDS, following closely a model presented by Keeling and Rohani [35]. The adult population in region i is divided into susceptible S i, Infectious I i and Removed R i, so that the total adult population in the region i is N i = S i + I i + R i. The exposed period from time of HIV infection to a stage when infected individual becomes infectious is very short, so that when an individual acquires infections, immediately becomes infectious [40–43]. For this reason, we use the SIR model. The dynamics of each sub-population includes only individuals aged 15–64 years only, because this is the group of individuals who are sexually active, hence susceptible to HIV infections.
To include different regions in our model, we define S ij, I ij, R ij and N ij to be respectively the number of Susceptible, Infectious, Removed and total adult individuals currently visiting region i but who live in region j. For example, infected individuals working and spending most of their time in region j and going back to visit their family in region i are denoted I ij. We assume a homogeneous mixing of individuals within the regions, meaning that any infectious individual has the same probability of transmitting the disease to any susceptible individual in the population. We define l ji to be the per individual rate per year of moving from region i to region j. We assume that r is the rate of return from visits to another region, which is assumed to be independent of the regions travelled between. We define to be the total adult population who are currently in region i.
We assume that the basic parameters governing the effects of the disease and population demographics are the same in all regions. We further assume that individuals return to their home region before departing for another region and there is no permanent migration and emigration between the sub-populations, so that individuals travel to other sub-population occasionally. In addition, we assume that the recruitment into classes occurs within home regions; i.e., S ii is the only term that increases through population growth.
The susceptible class in region i are those newly-recruited into the sexually active cohort at the rate ν i = ν × p i individuals per year and the total susceptible individuals returning in region i from region j at the rate individuals per year, where ν is the countrywide population growth rate and p i is the proportion of the total adult population living in region i. Susceptibles are lost by becoming HIV infected at the rate , by dying of natural causes at the rate μS ii and the total Susceptible individuals moving from region i to region j at a rate individuals per year respectively. Here β i is the HIV transmission parameter or transmission probability for region i.
The equation describing the dynamics of the susceptible individuals S ii in region i is given by
| (1) |
Susceptible individuals from region j who are current in region i are recruited by the rate which is governed by the number of people who move out from region j, at the rate l ij S jj and those returning to regional j at the rate rS ij individuals per year respectively. The susceptible are lost by natural death at the rate μS ij and those acquiring HIV infections at the rate individuals per year respectively. Similarly, the equation describing the dynamics of the susceptible individuals S ij in region i is given by
| (2) |
The infectious population I ii is recruited at a rate and those returning at a rate individuals per year respectively. Infectious are respectively reduced by those who die naturally at the rate μI ii, those who die due to the disease at the rate δ ii I ii, those who progress to the removed class at the rate γ ii I ii and those travelling out the region at the rate individuals per year. Together this gives
| (3) |
The infectious population I ij is recruited by those acquiring HIV infections in region i at the rate and from those coming for a visit at the rate l ij I jj individuals per year respectively. They are lost due to those who progress to the removed class at a rate γI ij, return to region i at a rate rI ij, die naturally at the rate μI ij and die due to the disease at the rate δI ij individuals per year respectively. The non-linear ordinary differential equation describing the dynamics of the infectious individuals I ij in region i is given by
| (4) |
The removed individuals R ii are respectively recruited by infectious individuals I ii who progress to the removed class at a rate γI ii and those returning from visits from different regions a the rate r∑j R ji individuals per year. They are decreased due to those who visit other regions at the rate l ji R ii, die due to the disease at the rate δR i and die naturally at a rate μR i individuals per year respectively. The non-linear ordinary differential equation describing the dynamics of the removed individuals R i in region i is given by
| (5) |
The removed individuals R ij are respectively recruited by infectious individuals I ij who progress to the removed class at the rate γI ij and those coming for a visit at the rate l ij R jj individuals per year. They are decreased due to those who return to region j at a rate rR ij, die due to the disease at the rate δ ii R ij and die naturally at a rate μR ij individuals per year respectively. The non-linear ordinary differential equation describing the dynamics of the infectious individuals R ij in region i is given by
| (6) |
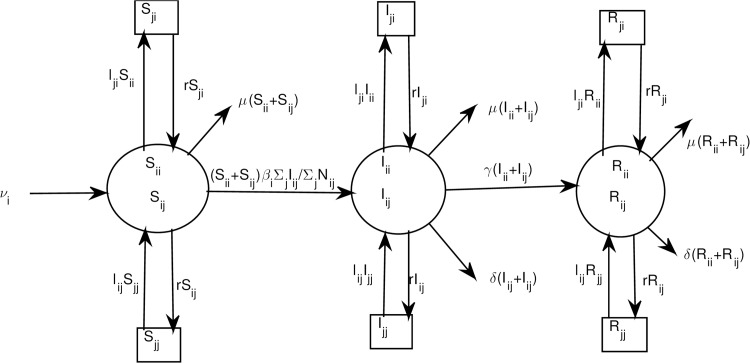
The model is summarised in Fig 1.
Fig 1. Flow diagram between regions for the SIR model with n-patches.
For clarity, we consider individuals travelling to another region after returning home first.
To compute the basic reproduction number R 0 of the system of equations from Eqs (1)–(6), we only consider equations of the states that include the infected individuals. These equations are referred to as the infected system [44]. In our model, we have assumed that the susceptible and the removed classes do not contribute to the transmission of HIV. The only class involved in the disease transmission is the infectious class. We therefore write the the system that represents the infectious individuals in a given region and those commuting between these regions as follows:
| (7) |
The computation of R 0 by the next-generation operator begins with equations of the system that involve the transmission part describing the production of new infections and then with those involve transition part, describing changes in state among the infected individuals [45].
The transmission part is represented by
Here S* represents the susceptible population at a disease free equilibrium point. Therefore F = F 1 ⊕ F 2 ⊕ … ⊕ F n.
The transition part, describing changes in state, is obtained from
Here κ ii = γ ii + μ ii + δ ii, κ ij = γ ij + μ ij + δ ij, κ in = γ in + μ in + δ in, κ ji = γ ji + μ ji + δ ji, κ jn = γ jn + μ jn + δ jn, and κ jj = γ jj + μ jj + δ jj.
Theorem 1: Let have a ij ≤ 0 for i ≠ j. If the sum of the entries in each column is positive, then A is non-singular m-matrix [46, 47].
By Theorem 1, it can be observed that the matrix V is a non-singular m-matrix; hence V −1 exists.
The basic reproduction number R 0 as proposed by van den Driesche and Whatmough [45], is the the spectral radius of the matrix G = FV −1 = (F 1⊕…⊕F n)V −1. So that R 0 = max{|λ 1, λ 2, …λ k|, λ 1, λ 2, …λ k ∈ σ(G)} = σ(G).
In this case, the basic reproduction numbers can not be written explicitly. However, it can be observed that the basic reproduction number depends on the travel rates, demographic and the epidemic parameters. Therefore, given the set of parameter values and the travel rates, R 0 can be computed numerically.
Note that, in the absence of mobility and regions (with β i = β, l ij = 0 and r = 0), the model is reduced to the standard SIR model
| (8) |
which has as the basic reproduction number.
Model Parameters
We start with the disease-related parameters, which are assumed to be the same for all regions. The progression rate from HIV to AIDS denoted by γ is 0.06897 < γ < 0.3846; this is because the HIV incubation period is between 2.6 to 14.5 years; [48]. The life expectancy in the AIDS class is about 8 years, so the HIV/AIDS-induced death rate δ is ≈0.125 [9]. The average life expectancy at birth of Kenya from 1960 to 2011 is about 57.9 years (see S1 Table), so the natural death rate μ is approximated to be 0.01727 per year and the average growth rate ν of Kenya from 1960 to 2011 is estimated to be 0.031648 [37].
We then look at the population and movement parameters. S2 Table gives the adult population for 2009 [36] and the estimate of people infected with HIV in 20 regions of Kenya for 2007 [39]. The rate at which individuals from region j visit region i, denoted by l ij individuals per year, is estimated from the monthly average number of trips per 1000 individuals over the course of the year (see S3 Table). The data is then divided by 1000 to get the average number of trips for an individual per year. We assume that visits last on average one week, so r = 52. Mobile phone data does not allow us to estimate this parameter more accurately, so we take this estimate as a starting point.
A challenge is to estimate the spread of the infection in various regions. In the absence of regional variation, this can be estimated from the basic reproduction number R 0. Specifically, if we assume that Eqs (1)–(6) have no regions and movement terms (i.e. l ij = r = 0) we then have β i = β and
The estimates of the HIV basic reproduction number R 0 worldwide is not clearly set. However, the available estimates varies much from country to country. In some countries, their estimates are very small and are even below one. For example, the HIV basic reproduction number for men having sex with men in Denmark is reported to be between 0.44 and 0.6, in Norway it is between 0.57 and 1.27, and in Sweden it is between 0.36 and 0.95 [49]. But in other countries, the estimates are above one. For example, in West Germany, the HIV R 0 is reported to lie between 3.43 and 4.08, in France it is between 3.38 and 3.381, and in the UK it is between 3.38 and 3.96 [50]. At the moment, we do not have good estimates of the basic reproduction number of HIV in Kenya. However, a study by Williams and Gouws [51] has reported that the R 0 for HIV for some African countries ranges between 1.94 and 8.93, and Kenya having 6.3 as an estimate of the HIV R 0 and the median value being 4.6 for sub-Saharan African countries. This shows that much work is needed to decrease the basic reproduction number below one.
The absence of good estimates for R 0 for both regions and Kenya as a whole limits the analysis we can do. However, we are interested in the role of space in determining the spread of the disease and to account for differences between regions (i.e. β i ≠ β). We therefore investigate two different scenarios, one in which R 0 for Kenya as a whole is slightly below one, and the other where R 0 is slightly greater than one. The aim of looking at these two scenarios is to get an overall understanding of the role of how regional (HIV/AIDS) differences influence the spread of disease under these scenarios, rather than to give exact predictions of how many people will have HIV in the future.
With this background, we set a parameter R B that gives the baseline R 0 for Kenya. We then set the β i for the individual regions to be
where I i(0) is the initial infectious individuals in region i and H is chosen to be the population mean of the most populated region, and in this case Nairobi is the most populated region as shown in S4 Table. The idea here is that those regions that currently have higher levels of infection have a higher value of disease transmission β i. The choice of H as a rate conversion constant is arbitrary, but it ensures that the β i’s do not become too large.
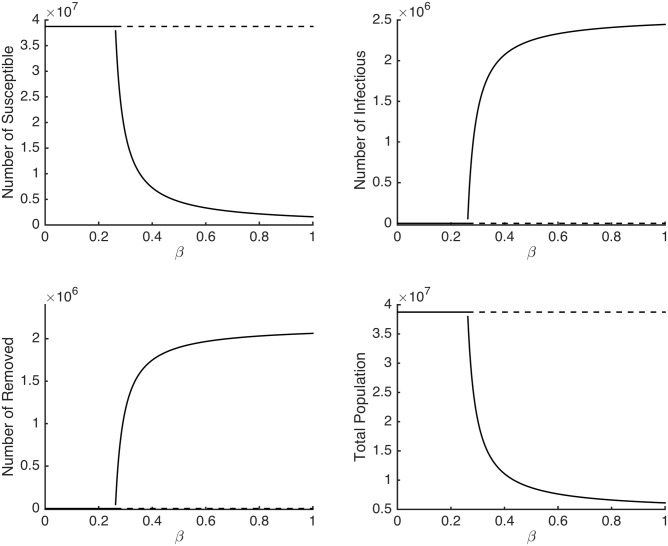
In order to set the baseline R B for Kenya from the metapopulation model, we plot the bifurcation diagram for the SIR model in the absence of movements (i.e., Eq (8)). From Fig 2, we remark that β ≈ 0.2623 is the threshold value for the existence or nonexistence of the disease for all regions. Choosing β = 0.22 gives R 0 = 0.8388 and choosing β = 0.42 gives R 0 = 1.6014. We therefore set the R B = 0.8388 for R 0 < 1 and R B = 1.6014 for R 0 > 1.
Fig 2. Bifurcation diagram of the of the system in Eq (8).
The solid and dotted lines show the values at which the disease-free equilibrium point is stable and unstable respectively. The solid curves show the values at which the endemic equilibrium point is stable.
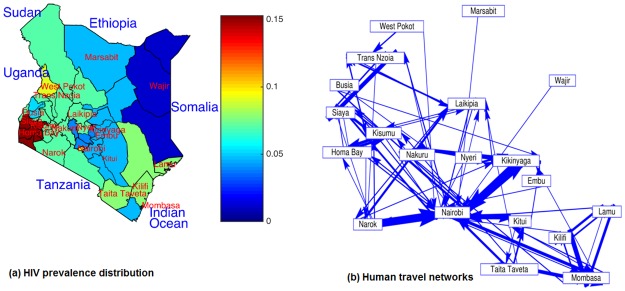
The prevalence of HIV infections in Kenya is distributed as shown in Fig 3a. Nyanza region, which includes Homa Bay, Kisumu and Siaya, has the highest percentage (15.5%); followed by Nairobi with 9.0%; coast region, which includes Lamu, Mombasa, Taita Taveta and Kilifi with 7.9%; rift valley, which includes West Pokot, Laikipia, Trans Nzoia, Narok and Nakuru with 7.0%; western region, which includes Kakamega, Busia with 5.1%; eastern region, which includes Marsabit, Embu, and Kitui with 4.7%; central region, which includes Nyeri and Kilinyaga with 3.8%; and the north Eastern region, which includes Wajir with the lowest adult HIV prevalences of 1.0% (S4 Table).
Fig 3.
(a) Map of Kenya showing HIV prevalence distributions. The color bar from blue to red is in the order of increasing HIV prevalence. For clarity, the names of counties included are the only ones included in this study (Source of data:ArcGIS.com: shapefile-The 47 counties of Kenya (shapefile by dmuthami S5 Table) and HIV data from [39]. (b) Human travel networks (S6 Table) as estimated by [38]. Monthly average number of trips per 1000 individuals between all pairs of regions over the course of the year. For clarity, only trips made per 1000 individuals that are more than 60 trips per year are shown, with arrows indicating the direction of movements from home region to a visited region. The thickness of the arrow represents the number of trips made.
In Fig 3b, we see that Nairobi is the main hub of the movements of people from all regions in Kenya. We also observe that the regions that are less connected seem to have low HIV prevalence rates. For example, Wajir region has 1.0% of HIV prevalence and is the list-connected region.
Results
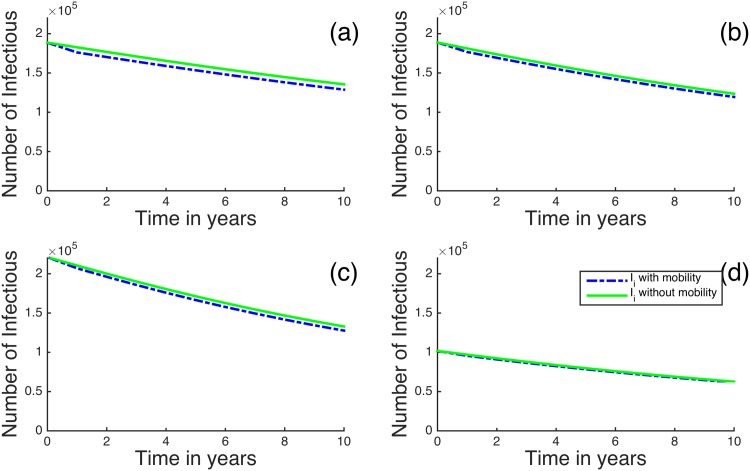
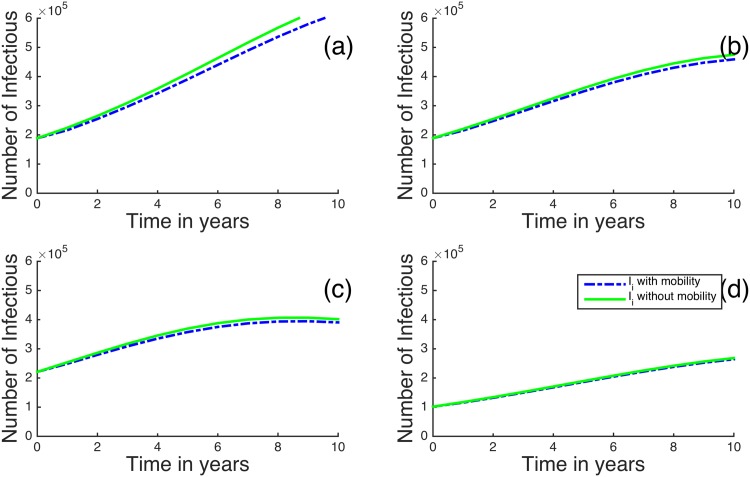
We first look at our model for the four regions in Kenya with the highest HIV/AIDS prevalences: Nairobi, Kisumu, Homa Bay and Siaya [39]. Fig 4 shows the case where R B < 1 so that the disease is decreasing overall. When human mobility is included, the infectious and the removed individuals decrease even more rapidly than in the case where no mobility is included in the model. Homa Bay has a higher percentage of infectious individuals compared to the other regions, followed by Nairobi and Kisumu. For regions with higher prevalence, the mobility has a observable but relatively small effect on the disease dynamics. For example, after 8 years if mobility is not included Siaya region has 68,910 infectious individuals, while including mobility it has 67,790 infectious individuals. This is approximately a 1.6% decrease.
Fig 4. Time evolution of the metapopulation model for (a) Nairobi, (b) Kisumu, (c) Homa Bay and (d) Siaya for R B < 1.
The dotted blue lines represent infectious individuals when there is human mobility and the solid green lines represent infectious individuals when there is no human mobility between the regions.
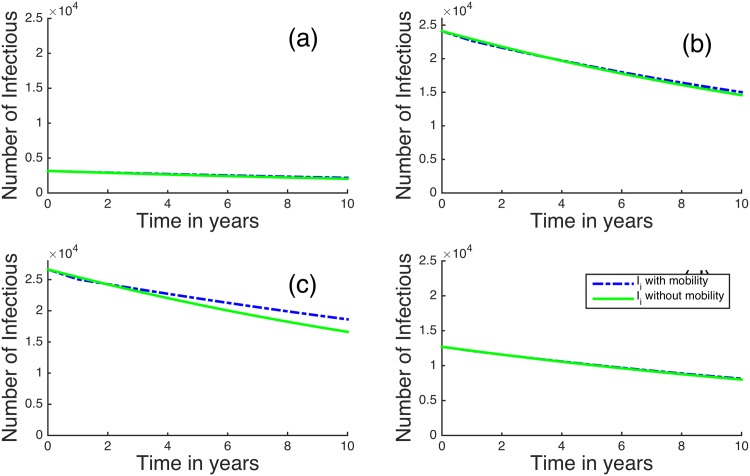
In Fig 5, we plot the results when R B < 1 for the four regions with the smallest initial HIV/AIDS prevalences: Wajir, Laikipia, Kirinyaga and Marsabit [39]. For these regions, including human mobility in the model dynamics slightly increases the number of infectious individuals in all the selected regions. For example, after 8 years without human mobility, Wajir region has 2,217 infectious individuals, while including human mobility gives 2,334 infectious individuals. This is approximately a 5% increase. It seems that human mobility tends to increase infectious individuals in regions with initially low HIV prevalences.
Fig 5. Time evolution of the metapopulation model for (a) Wajir, (b) Laikipia, (c) Kirinyaga, (d) Marsabit for R B < 1.
The dotted blue lines represent infectious individuals when there is human mobility and the solid green lines represent infectious individuals when there is no human mobility between the regions.
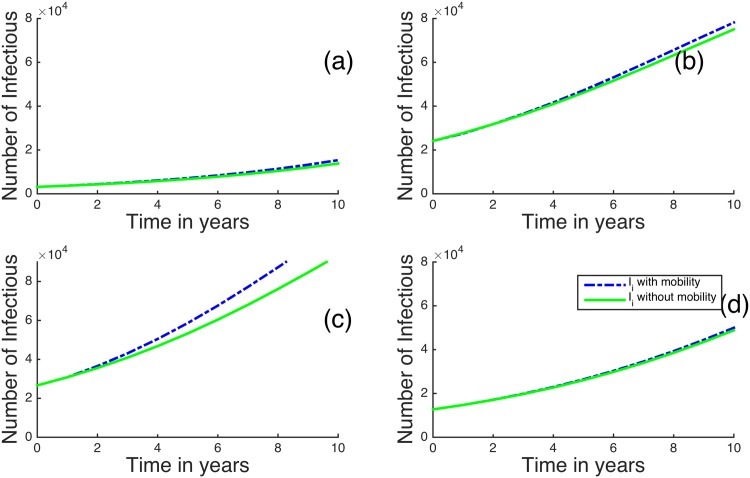
In Fig 6, we plot the results for the regions with the highest HIV prevalence when R B > 1. Once again, it seems that human mobility tends to slightly decrease the number of infectious individuals in these regions. For example, if the mobility is not included between the regions, after 8 years we see that Nairobi has an 567,500 infectious individuals, but if we introduce mobility in the model, it has an approximate of 536,300 infectious individuals; this is almost a 5.5% decrease. Fig 7 shows the dynamics of the four regions with the lowest initial HIV prevalences. It can also be observed that human mobility tends to increase the infectious individuals in regions with initially low HIV prevalences. For example, after 8 years without mobility, Marsabit region has 38,550 infectious individuals, while including human mobility gives 39,320 infectious individuals; this is approximately a 2% increase.
Fig 6. Time evolution of the metapopulation model for (a) Nairobi, (b) Kisumu, (c) Homa Bay and (d) Siaya for R B > 1.
The dotted blue represent infectious individuals when there is human mobility and the solid green lines represent Infectious individuals when there is no human mobility between the regions.
Fig 7. Time evolution of the metapopulation model for (a) Wajir, (b) Laikipia, (c) Kirinyaga, (d) Marsabit for R B > 1.
The dotted blue lines represent infectious individuals when there is human mobility and the solid green lines represent Infectious individuals when there is no human mobility between the regions.
Based on the results for the regions above, we see that human mobility decreases new HIV infections in the regions whose initial HIV prevalence is high and it increases new HIV infections in regions with low HIV prevalence. To summarise the effect of infections across regions, we look at the incidence rate. We define the incidence rate as estimated from the log of the gradient of the growth of the infectious class [52, 53]. First we find the increases of I i for each region. The solutions follow exponential growth, and we thus transform the solutions by taking the log. The region with the biggest positive slope corresponds to the region with highest increase in incidence rate of HIV infectious. The region with biggest negative slope corresponds to the one with the biggest decrease in incidence rate of the HIV infections.
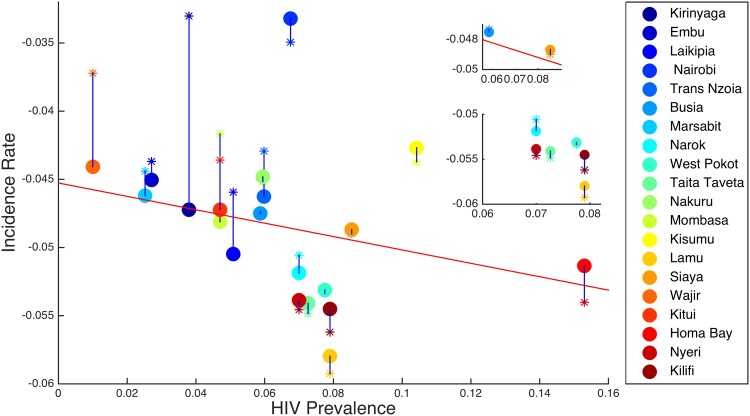
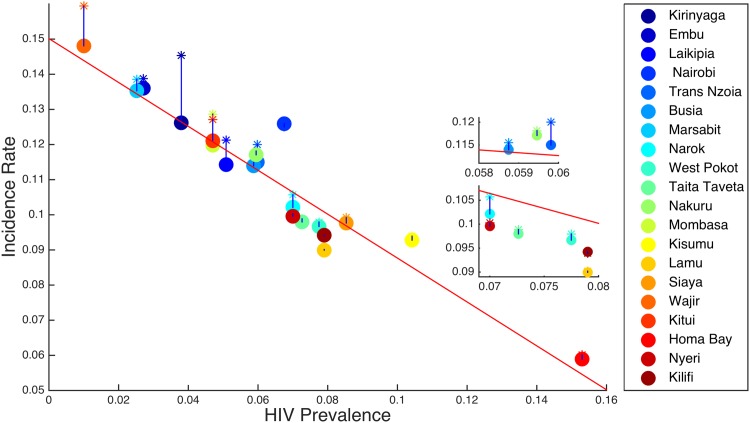
In Fig 8, we plot the incidence rate against the HIV prevalence rate, when there is no mobility and when there is mobility for R B < 1. It can be seen that human mobility tends to increase the HIV incidences for the regions with initially low HIV prevalence; at the same time it tends to decrease the incidence rate of most of the regions with initially high HIV prevalence. Specifically, with the exception of Narok and Nairobi, it can also be observed that 7% is a threshold value of initial HIV prevalence above which human mobility decreases the HIV infection rate; below this value, human mobility tend to increase the HIV infections rate in a region.
Fig 8. Incidence rate versus prevalence rate.
A dot represents the dynamics of HIV infections without human mobility between the regions and a star represents the dynamics of HIV infections when there is human mobility between the regions for R B < 1.
In Fig 9, we plot the incidence rate against the HIV prevalence rate for R B > 1. In this case, mobility increases the incidence rates in regions with low HIV prevalence and also slightly increases the incidence rates in the regions with high HIV prevalences, but the increase is very small compared to regions with low HIV prevalences.
Fig 9. Incidence rate versus prevalence rate.
A dot represents the dynamics of HIV infections without human mobility between the regions and a star represents the dynamics of HIV infections when there is human mobility between the regions for R B > 1.
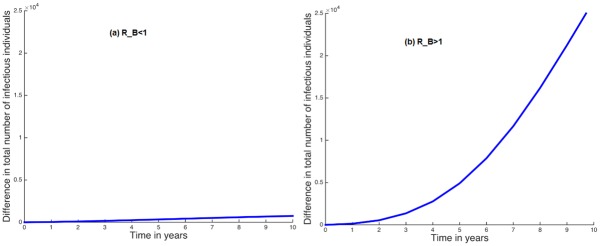
We also look at the country-wide impact of human mobility on HIV infections. In Fig 10a, we plot the difference of the total number of infectious in the country when R B < 1. Mobility slightly increases the number of infectious individuals in the country as a whole. For example, without including human mobility between the regions, after 8 years Kenya would have 902,300 infectious individuals, while including human mobility between its regions it has 600 additional infectious individuals. This is only a 0.07% increase. For R B > 1, we observe that human mobility increases the overall number of infectious individuals in the country (Fig 10b). We observe that, without human mobility in this case, Kenya would have 3,232,000 infectious individual compared to 3,248,000 infectious individuals with mobility. This gives a difference of 16,000 infectious individuals, an approximately 0.5% increase.
Fig 10.
(a) and (b) show the differences between the total number of infectious individuals when there is human mobility and when there is no human mobility within the regions in the country for R B < 1 and R B > 1 respectively.
Discussion
Our results show, using countrywide data, that human mobility can influence to the transmission of HIV. However, mobility plays a relatively small role. For example, we estimate that, over an eight year period in Kenya as a whole, it can contribute to about 0.5% additional cases of HIV. This contribution is even smaller if the disease decreases overall in the population. These results contrast with some other studies that report a positive correlations between mobility and the HIV prevalence [19, 54]. For example, a study of east and south Africa long-distance truck drivers found that mobility is the main contributing factor to the HIV transmission [55–58]. When a disease first spreads, we also expect mobility to play an important role. For example, air-transportation networks have been responsible for the global spread of severe acute respiratory syndrome (SARS) [59], and, because of the higher mobility in Europe, pandemic influenza could diffuse rapidly [60]. In our study, in which HIV is already endemic, overall mobility appears to make only a small difference to the total spread of the disease in Kenya.
Mobility does play an important role in local dynamics of HIV. Specifically, regions with initially low HIV prevalences experience an increase in the number of infectious individuals when mobility is accounted for, while regions with initially high HIV prevalences experience a slight decrease. Even when the overall trend is for the disease to decrease (i.e R B < 1) human mobility tends to delay eradication in low prevalence regions, and slightly speed up the eradication process in regions with high HIV prevalences. When the disease is in an endemic state, regions with initially low HIV prevalences tend to increase their HIV incidence rates more than the regions with initially high HIV prevalences. Here our results seem to be in agreement with other studies, which report that migrant workers in urban areas can spread HIV to rural areas on their trips back to their areas of origin [12, 15, 16]. For example, if we compare big cities, like Nairobi, and small cities, like Kirinyanga, mobility tends to slightly decrease the number of infectious individuals in the former and slightly increase infections in the latter. Infectious individuals travel from the most infected, typically urban areas, and infect susceptibles in the least infected, rural areas.
There are also differences between different high prevalence regions. For example, in Nairobi, initially infections grow faster than other regions, irrespective of mobility (Fig 6). When R B < 1, Nairobi converges very slowly to the disease-free equilibrium point compared to other regions (Fig 4). This can be attributed to the fact that Nairobi is the most populated region in the country and highly connected to other regions (Fig 3b). This result concurs with other studies, which associates high HIV infections with high human mobility in areas such as commercial farms and agricultural estates, mining areas, business centres and residential areas along busy roads [17–21]. It seems that more infectious individuals move from the most infected areas like Homa Bay, Siaya, Kisumu and other regions to Nairobi.
Our study suggests some policies for controlling HIV. For example, policies should concentrate on educating people working in urban areas to take care in their sexual relations while in the urban area by promoting safe sex, encouraging condom use, reducing the number of sex partners or reducing risky behaviours like having sex with sex workers [12, 15, 61]. Potentially, if migrants could travel with their partners to urban areas [14], then this would reduce the growth of the disease in rural areas. Proper education aimed at promoting behaviour changes and avoiding risk behaviours is crucial [61, 62].
Several improvements to our model are needed if we wanted to make quantitative predictions about HIV spread across regions. First, we did not account for state-dependent movements, where l ij differs for infectious and susceptibles. For example, there is stigmatization and discrimination of people living with HIV, so infected individuals tend to move away or hide their HIV status after being diagnosed [63, 64]. Secondly, we did not consider intervention in our model, through education strategies for example, which could lead to behaviour changes of susceptible and infectious individuals. Similarly, we do not model precautions taken by individuals who might avoid having sexual relationships with people coming from the highly infected areas [61, 62]. Including preventative measures would reduce the susceptible populations and hence decrease new infections. Finally, we treat those individuals who travel as being no more likely to engage in risky sexual behaviour than other people in the regions they live. Given that many of the visits from urban to rural areas are made by people who might exhibit more risky behaviour when living alone in the city [13, 14, 24], our original assumptions may not be justified.
The human mobility data we used were obtained from mobile phones. Such data can only be collected in areas where there are cell phone towers; as a result, cross-border migrants were not captured [38, 65]. Mobile phone data tends to under estimate the number of between-area visits and can lead to incorrect estimates in the number of clinical outcomes compared to official census data [66]. For example, in Kenya, in the urbanised area, malaria transmission estimated from mobile data were higher than the clinical cases, while in the peripheral areas, malaria clinical cases were higher than those estimated from mobile phone data [38]. Mobile phone data should be used as a substitute in the case of unavailability of higher-resolution data and as a useful starting point [66].
In our case, these data have helped us analyse the impact of human mobility on the transmission of HIV in Kenya. This provides a first metapopulation model of how human mobility can influence HIV/AIDS infections within a country based on the region’s initial HIV prevalence and can be improved on as data becomes available. Despite the minor impact of mobility observed in this study, mobility should not be underestimated and neglected. We suggest that the health practitioners and policy makers incorporate the impact of human mobility in the HIV/AIDS transmission-control programmes.
Supporting Information
It also provides the calculated average growth rate and the death rate of the country for 54 years.
(CSV)
(PDF)
(PDF)
(PDF)
(CSV)
(PDF)
(PDF)
Acknowledgments
We are grateful to the International Science Programme (ISP) in Sweden for the financial support. We also thank the PLOS One reviewers for their critical review and many useful suggestions on an earlier version of this Manuscript.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
The authors received no specific funding for this work. However, the International Science Programme (ISP) sponsored the corresponding author in his visits from Tanzania to Uppsala University, Sweden. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Lipsitch M, Cohen T, Cooper B, Robins JM, Ma S, James Lyn, et al. Transmission Dynamics and control of Severe Acute Respiratory Syndrome. Science. 2003;300(5627):1966–1970. 10.1126/science.1086616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Korobeinikov A. Lyapunov Functions and Global Stability for SIR and SIRS Epidemiological Models with Non-linear Transmission. Bulletin of Mathematical biology. 2006;68(3):615–626. 10.1007/s11538-005-9037-9 [DOI] [PubMed] [Google Scholar]
- 3. Makinde OD. Adomain decomposition approach to a SIR epidemic model model with constant vaccination strategy. Applied Mathematics and Computation. 2006;184(2):842–848. 10.1016/j.amc.2006.06.074 [DOI] [Google Scholar]
- 4. Hethcote HW. The mathematics of infectious diseases. SIAM review. 2000;42(4):599–653. 10.1137/S0036144500371907 [DOI] [Google Scholar]
- 5. Lu Z, Chi X, Chen L. The effect of constant and pulse vaccination of SIR epidemic model with horizontal and vertical transmission. Mathematical and Computer Modelling. 2002;36(9):1039–1057. 10.1016/S0895-7177(02)00257-1 [DOI] [Google Scholar]
- 6. Abdulkarim UM. Review of SIR Epidemic Model with Application To Transmission Dynamics of HIV/AIDS in a proportional mixing population. Research Journal of Applied Sciences. 2007;2(5):595–599. [Google Scholar]
- 7. Margevicius R and Joshi H. The influence of education in reducing the HIV epidemic. Involve, a Journal of Mathematics. 2013;6(2):127–135. 10.2140/involve.2013.6.127 [DOI] [Google Scholar]
- 8. Huang W, Cook KL, Castilo-Chavez C. Stability and Biurcation for multiple group model fro the dynamics of HIV/AIDS Transmission. Society for Industrial and Applied Mathematics. 1992;52(3):835–854. 10.1137/0152047 [DOI] [Google Scholar]
- 9. Baryarama F, Mugisha JYT, Luboobi LS. Mathematical model for HIV/AIDS with complacency in a population with declining prevalence. Computational and Mathematical Methods in Medicine. 2006;7(1):27–35. 10.1080/10273660600890057 [DOI] [PubMed] [Google Scholar]
- 10. Naresh R, Sharma D. An HIV/AIDS model with Vertical transmission and time delay. World Journal of Modelling and Simulations. 2011;7(3):230–240. [Google Scholar]
- 11. Keeling M, Danon L. Mathematical modelling of Infectious diseases. British Medical Bulletin. 2009;92(1):33–42. 10.1093/bmb/ldp038 [DOI] [PubMed] [Google Scholar]
- 12. Lurie MN, Williams BG, Zuma K, Makaya-Mwamburi D, Garnet GP, Sturn AW, et al. The impact of Migration on HIV-1 Transmission in South Africa: A study of Migrant and non migrant and their partners. Sexually transmitted diseases. 2002;30(2):149–156. 10.1097/00007435-200302000-00011 [DOI] [PubMed] [Google Scholar]
- 13. Coffee M, Lurie MN, Garnett GP. Modelling the impact of migration on the HIV epidemic in South Africa. Aids. 2007;21(3):343–350. 10.1097/QAD.0b013e328011dac9 [DOI] [PubMed] [Google Scholar]
- 14. Kishamawe C, Vissers DC, Urassa M, Isingo R, Mwaluko G, Borsboom GJJM, et al. Mobility ans HIV in Tanzania Couples: both mobile persons and their partners show increase risk. Aids. 2005;20(4):601–608. 10.1097/01.aids.0000210615.83330.b2 [DOI] [PubMed] [Google Scholar]
- 15. Lagarde E, van der Loeff MS, Enel C, Holmgren B, Dray-Spira R, Pison G, et al. Mobility and the spread of human immunodeficiency virus into rural areas of West Africa. International Journal of Epidemiology. 2003;32(5):744–752. 10.1093/ije/dyg111 [DOI] [PubMed] [Google Scholar]
- 16. Mmbaga EJ, Leyna GH, Hussain A, Mnyika KS, Sam NE, Klepp KI. The role of in-migrants in the increasing rural HIV-1 epidemic: results from a village population survey in the Kilimanjaro region of Tanzania. International Journal of Infectious Diseases. 2008;12(5):519–525. 10.1016/j.ijid.2008.02.007 [DOI] [PubMed] [Google Scholar]
- 17. Brewer TH, Hasbun J, Ryan CA, Hawes SE, Martines S, Sanchez J, et al. Migration, ethnicity and environment: HIV risk factors for women on the sugar cane plantations of the Dominican Republic. Aids. 1998;12(14): 1879–1887. 10.1097/00002030-199814000-00020 [DOI] [PubMed] [Google Scholar]
- 18. Barongo LR, Borgdorff MW, Mosha FF, Nicoll A, Grosskurth H, Senkolo KP, et al. The epidemiology of HIV-1 infection in urban areas, roadside settlements and rural villages in Mwanza Region Tanzania. Aids. 1992;6(12):1521–1528. 10.1097/00002030-199212000-00016 [DOI] [PubMed] [Google Scholar]
- 19. Zuma K, Lurie MN, Williams BG, Mkaya-Mwamburis D, Garnett GP, Sturm AW. Risk factors of sexually transmitted infections among migrant and non-migrant sexual partnerships from rural South Africa. Epidemiology and Infection. 2005;133(03):421–428. 10.1017/S0950268804003607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Hargrove J. Migration, mines and mores: the HIV epidemic in Southern Africa. South African Journal of Science. 2008;104(1-2):53–61. [Google Scholar]
- 21. Kamwanga J, Simbaya J, Luhana C. Corridors of Hope in Southern Africa: HIV prevention needs and opportunities in Four Border Towns. Family Health International. 2006. [Google Scholar]
- 22. Coffee MP, Garnett GP, Mlilo M, Voeten HACM, Chandiwana S, Gregson S. Patterns of Movement and Risk of HIV Infection in Rural Zimbabwe. Journal of Infectious Diseases. 2005;191(Suppl 1):S159–S167. 10.1086/425270 [DOI] [PubMed] [Google Scholar]
- 23. Coast E. Local understandings of, and responses to, HIV: Rural-urban migrants in Tanzania. Social science and medicine. 2006; 63(4):1000–1010. 10.1016/j.socscimed.2006.03.009 [DOI] [PubMed] [Google Scholar]
- 24. Dean KD, Parkhurst JO, Johnston D. Linking migration, mobility and HIV. Tropical Medicine and International Health. 2010;15(12):1458–1463. 10.1111/j.1365-3156.2010.02647.x [DOI] [PubMed] [Google Scholar]
- 25. Arino J, Jordan R, van den Driessche P. Quarantine in a multi-species epidemic model with spatial dynamics. Mathematical biosciences. 2005;206(1):46–60. 10.1016/j.mbs.2005.09.002 [DOI] [PubMed] [Google Scholar]
- 26. Hethcote HW, Van Ark JW. Epidemical models for Heterogeneous Populations:Proportionate Mixing, Parameters Estimation, and Immunization programs. Mathematical Biosciences. 1987;84(1):85–118. 10.1016/0025-5564(87)90044-7 [DOI] [Google Scholar]
- 27. Gualtieri AF, Hecht JP. Dynamics and control of infectious diseases in stochastic metapopulation models. Journal of Life Sciences. 2011;5(7):503–508. [Google Scholar]
- 28. Vergu E, Busson H, Ezanno P. Impact of the Infection Period Distribution on the Epidemic Spread in a Metapopulation Model. PLoS ONE. 2010;5(2):e9371 10.1371/journal.pone.0009371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Arino J, van den Driessche. Disease spread in metapopulations. Nonlinear dynamics and evolution equations. 2006;48:1–13. [Google Scholar]
- 30. Doungmo Goufo E, Oukouomi Noutchie S, Mugisha S. A Fractional SEIR Epidemic Model for Spatial and Temporal Spread of Measles in Metapopulations. Abstract and Applied Analysis. 2014;2014:1–6. 10.1155/2014/781028 [DOI] [Google Scholar]
- 31. Sattenspiel L and Dietz K. A structured Epidemic Model Incorporating Geographic Mobility Among Regions. Mathematical biosciences. 1995;128(1):71–91. 10.1016/0025-5564(94)00068-B [DOI] [PubMed] [Google Scholar]
- 32. Arino J, Davis JR, Hartley D, Jordan R, Miller JM, van den Driessche P. A multi-species epidemic model with spatial dynamics. Mathematical Medicine and Biology. 2005; 22(2):129–142. 10.1093/imammb/dqi003 [DOI] [PubMed] [Google Scholar]
- 33. Smith RJ, Li J, Gordon R, Hefferman JM. Can we spend our way of the AIDS epidemic? A world halting AIDS model. BMC Public Health. 2009;9(Suppl 1):S15 10.1186/1471-2458-9-S1-S15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Xiao Y, Tang S, Zhou Y, Smith? RJ, Wu J, Wang N. Predicting the HIV/AIDS epidemic and measuring the effect of mobility in mainland China. Journal of theoretical biology. 2013;317(2013):271–285. 10.1016/j.jtbi.2012.09.037 [DOI] [PubMed] [Google Scholar]
- 35. Keeling MJ and Rohani P. Modeling Infectious Dieseases in Human and Animals. Princeton University Press;2008. [Google Scholar]
- 36.Kenya S. Country-counties in Kenya;2013.
- 37.David Z, Claros E, Africa HDI, Stührenberg J, Market selection Ind, Julia S, Hiroko M, DataBank Home, and Corporate Procurement. Explore. Create. Share: Development Data;2015.
- 38. Wesolowski A, Eagle N, Tatem AJ, Smith DL, Noor AM, Snow RW, et al. Supplementary Material on the Quantifying the impact of human mobility on Malaria. Science. 2012;338(6104):267–270. 10.1126/science.1223467 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kenya, A.I.D.S. Indicator Survey 2007 Nairobi Kenya: National AIDS and STI Control Programme. Ministry of Health Kenya (NASCOP); 2008.
- 40. May RM, Anderson RM, Erwin ME. The transmission dynamics of human immunodeficiency virus. Philosophical Transactions of the Royal Society of London B: Biological Sciences. 1988;321(1207):565–607. 10.1098/rstb.1988.0108 [DOI] [PubMed] [Google Scholar]
- 41. Hollingsworth TD, Anderson RM, Fraser C. HIV-1 Transmission, by stage of Infection. Journal of Infectious Diseases. 2008;198(5):687–693. 10.1086/590501 [DOI] [PubMed] [Google Scholar]
- 42. Wawer MJ, Gray RH, Sewankambo NK, Serwadda D, Li X, Laeyendecker O, et al. Rates of HIV-1 Transmission per coital act, by stage of HIV-1 Infection, in Rakai, Uganda. Journal of Infectious Diseases. 2005;191(9):1403–1409. 10.1086/429411 [DOI] [PubMed] [Google Scholar]
- 43. Anderson RM. The Epidemiology of HIV Infections: Variable incubation plus Infectious periods and Heterogeneity in sexual Activity. Journal of the Royal Statistical Society. Series A (Statistics in Society);1988. 151(1):66–98. 10.2307/2982185 [DOI] [Google Scholar]
- 44. Diekmann O, Heesterbeek J, Roberts M. The construction of next-generation matrices for compartmental epidemic models. Journal of The Royal Society Interface. 2009;7(47):873–885. 10.1098/rsif.2009.0386 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. van den Driesche P. and Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences. 2002;180:29–48. 10.1016/S0025-5564(02)00108-6 [DOI] [PubMed] [Google Scholar]
- 46. Farina L, Rinaldi S. Positive linear systems. New York: Wiley; 2000. [Google Scholar]
- 47. Berman A, Plemmons R. Nonnegative matrices in the mathematical sciences. New York: Academic Press; 1979. [Google Scholar]
- 48. Lui KJ, Lawrence DN, Morgan WM, Peterman TA, Haverkos HW, Bregman DJ. A model-based approach for estimating the mean incubation period of transfusion associated acquired immunodeficiency syndrome. Proceedings of the National Academy of Sciences. 1986;83(10):3051–3055. 10.1073/pnas.83.10.3051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Amundsen EJ, Stigum H, Røttingen J, Aalen O. Definition and estimation of an actual reproduction number describing past infectious disease transmission: application to HIV epidemics among homosexual men in Denmark, Norway and Sweden. Epidemiol Infect. 1999;132(6):1139–1149. 10.1017/S0950268804002997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Nishiura H. Correcting the actual reproduction number: a simple method to estimate R 0 from early epidemic growth data. International journal of environmental research and public health. 2010;7(1):291–302. 10.3390/ijerph7010291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Williams B and Gouws E. R 0 and the elimination of HIV in Africa: will 90-90-90 be sufficient? arXiv preprint arXiv:1304.3720.
- 52. Flint JJ. Stream gradient as a function of order, Magnitude and Discharge. Water Resources Research. 1974;10(5):969–973. 10.1029/WR010i005p00969 [DOI] [Google Scholar]
- 53. Sternberg S. High- speed Scanning in Human Memory. Chicago: Science. 1966;153(3736): 652–654. [DOI] [PubMed] [Google Scholar]
- 54. Lurie M, Harrison A, Wilkinson D, Karim SA. Circular migration and sexual networking in Rural Kwazulu/Natal: Implication or the spread of HIV and other sexually transmitted diseases. Health Transition Review. 1997;7:17–27. [PubMed] [Google Scholar]
- 55. Wilson ME. Travel and the emergence of Infectious Diseases. Emerg Infect Dis. 1995;1(2):39–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Carswell JW, LIoyd G, Howells J. Short communications prevalence of HIV-1 in east African lorry drivers. AiDS. 1989;3(11):759–762. 10.1097/00002030-198911000-00013 [DOI] [PubMed] [Google Scholar]
- 57. Ramjee G, Gouws E. Prevalence of HIV Among Truck Drivers Visiting Sex Workers in KwaZulu Natal, South Africa. Sexually transmitted diseases. 200;29(1):44–49. 10.1097/00007435-200201000-00008 [DOI] [PubMed] [Google Scholar]
- 58. Bwayo J, Plummer F, Omari M, Mutere A, Moses S, Ndinya-Achola J, et al. Human immunodeficiency virus infection in long-distance truck drivers in east Africa. Archives of internal medicine. 1994;154(12):1391–1396. [PubMed] [Google Scholar]
- 59. Colizza V, Barrat A, Barthelemy N, Vespignani A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(7):2015–2020. 10.1073/pnas.0510525103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Merler S, Ajelli M. The role of population heterogeneity and human mobility in the spread of pandemic influenza. Proceedings of the Royal Society of London B: Biological Sciences. 2010;277(1681):557–565. 10.1098/rspb.2009.1605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Barnett T, Pakhurst J. HIV/AIDS:Sex, abstinence and behaviour change. The Lancet infectious diseases. 2005;5(9):590–593. 10.1016/S1473-3099(05)70219-X [DOI] [PubMed] [Google Scholar]
- 62. Singh S, Darroch JE, Bankole A. A, B and C in Uganda: The role of Abstinence Monogamy and Condom Use in HIV Decline. Reproductive Health Matters. 2004;12(23):129–135. 10.1016/S0968-8080(04)23118-4 [DOI] [PubMed] [Google Scholar]
- 63. Bygrave H, Kranzer K, Hilderbrand K, Whittall J, Jouquet G, Goemaere E, et al. Trends in Loss to Follow-Up among Migrant workers on Antiretraviral Therapy in a community Cohort in Lesotho. PLoS One. 2010;5(10):e13198 10.1371/journal.pone.0013198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Lima V, Fernandes K, Rachlis B, Druyts E, Montaner J, Hogg R. Migration adversely affects antiretroviral adherence in a population—based cohort of HIV/AIDS patients. Social science and medicine. 2009;68(6):1044–1049. 10.1016/j.socscimed.2008.12.043 [DOI] [PubMed] [Google Scholar]
- 65. Tatem A, Qiu Y, Smith D, Sabot O, Ali A, Moonen B. The use of mobile phone data for the estimation of the travel patterns and imported Plasmodium falciparum rates among Zanzibar residents. Malar J. 2009;8(1):10–1186. 10.1186/1475-2875-8-287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Tizzoni M, Bajard P, Decuyper A, Kikg GKK, Schneider CM, Blondel V, et al. On the use of Human Mobility Proxies for Modelling Epidemics. 20014; 10.1371/journal.pcbi.1003716 [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
It also provides the calculated average growth rate and the death rate of the country for 54 years.
(CSV)
(PDF)
(PDF)
(PDF)
(CSV)
(PDF)
(PDF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.