Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Dec 1.
Published in final edited form as: Exp Clin Psychopharmacol. 2015 Sep 21;23(6):422–427. doi: 10.1037/pha0000047

An application of analyzing the trajectories of two disorders: A parallel piecewise growth model of substance use and attention deficit/hyperactivity disorder

Mary Rose Mamey a,b, Celestina Barbosa-Leiker a,c,d,e, Sterling McPherson a,c,d,e, G Leonard Burns a, Craig Parks a, John Roll a,c,d,e
PMCID: PMC4658254  NIHMSID: NIHMS719150  PMID: 26389639

Abstract

Researchers often want to examine two comorbid conditions simultaneously. One strategy to do so is through the use of parallel latent growth curve modeling (LGCM). This statistical technique allows for the simultaneous evaluation of two disorders to determine the explanations and predictors of change over time. Additionally, a piecewise model can help identify whether there are more than two growth processes within each disorder (e.g., during a clinical trial). A parallel piecewise LGCM was applied to self-reported attention deficit/hyperactivity disorder (ADHD) and self-reported substance use symptoms in 303 adolescents enrolled in cognitive behavioral therapy treatment for a substance use disorder (SUD) and receiving either oral-methylphenidate or placebo for ADHD across 16 weeks. Assessing these two disorders concurrently allowed us to determine whether elevated levels of one disorder predicted elevated levels or increased risk of the other disorder. First, a piecewise growth model measured ADHD and SU separately. Next, a parallel piecewise LGCM was used to estimate the regressions across disorders to determine whether higher scores at baseline of the disorders (i.e., ADHD or SUD) predicted rates of change in the related disorder. Finally, treatment was added to the model to predict change. While the analyses revealed no significant relationships across disorders, this study explains and applies a parallel piecewise growth model to examine the developmental processes of comorbid conditions over the course of a clinical trial. Strengths of piecewise and parallel LGCMs for other addictions researchers interested in examining dual processes over time are discussed.

Keywords: Parallel LGCM, latent growth model, piecewise growth function, ADHD, substance use, comorbid disorders

Researchers have long been interested in understanding relationships among comorbid disorders, prompting the exploration of appropriate methods in which several questions between two or more disorders can be answered. Specifically, researchers have a growing interest in not only the relationship between two disorders at a certain time point, but also these relationships across time, and how treatment interventions can potentially influence both the targeted and comorbid disorders simultaneously. When working with clinical trials data, this type of information may prove itself useful in understanding treatment protocol in high-risk populations by understanding the dynamic association between two trajectories and their outcomes. Thus, a thorough investigation of how two related outcomes are associated over time and whether baseline characteristics and treatment effects can predict them can be examined through the use of unique methodological approaches, such as latent growth curve models.

A latent growth curve model (LGCM; Meredith & Tisak, 1990) allows for the modeling of the initial status or baseline values (i.e., intercept) and the rate(s) of change (i.e., slopes), as well as the modeling of the relationship between the two (i.e., Is the intercept and slope correlated, and if so, what is the direction and strength of the relationship? Kline, 2010). This approach can model specific types of change. The common linear growth function imposes a trajectory that steadily increases or decreases over time at a constant rate, and more advanced models such as quadratic or piecewise functions allow for the modeling of multiple types of change over time. These more advanced models are often used to describe data in randomized clinical trials, as different stages of the intervention may show different effects on the symptoms of the disorder. Latent growth curve models allow for this flexibility in growth processes. This technique also models the antecedents and consequences of change (i.e., the explanation of change) over time, and across treatment groups.

LGCMs can be a powerful analytic tool for researchers using clinical trials data. The use of an indicator to directly measure the latent growth factor allows for the researcher to plot latent means at each time point to understand the trend of participants over the course of the clinical trial (Geiser, 2013). Considering the feature of modeling the form of change in these growth models, researchers are also able to understand the pattern of the trajectory of the process, and whether change is linear or quadratic over the course of the clinical trial. However, randomized clinical trials may reveal two patterns of growth: an immediate decrease or increase in symptoms from the baseline to first assessment, followed by a consistent level of symptoms until the end of the trial. This pattern warrants recognition as a piecewise model, where two distinctive slopes for the same disorder are modeled (Hancock & Lawrence, 2006). A latent growth curve model with the addition of a piecewise function allows for the explanation of certain trends within the data over the course of treatment in order to better model the possible divergence in trends (e.g., Why do symptoms decrease at the start of the study and increase towards the end of the study?).

A parallel latent growth curve model allows the modeling of two growth trajectories simultaneously. These models allow the evaluation of the intercepts and slopes of two disorders in order to test a wide range of hypotheses about the relationships between them (Muthén, 2002). For example, the parallel LGCM can determine whether the initial status of one disorder differentially predicts the rate of change of the other disorder. This model adds the distinctive component of directional paths between growth factors, where the slope of one disorder can be regressed on the intercept of the other. A thorough investigation of how two developmental processes are related over time and whether they can be predicted by baseline characteristics can be examined.

In order to demonstrate this type of modeling, we applied parallel piecewise growth modeling to the comorbidty of ADHD and SUD. The comorbidity of ADHD and SUD (Frodl, 2010; Wilens, 2004: Wilens & Dodson, 2004; Wilens, Gignac, Swezey, Monuteaux, Biederman, 2006) suggests that combined treatment may prove to be the most effective and efficient mode of treatment delivery (Gray et al., 2011; Kalbag & Levin, 2005; Wilens & Dodson, 2004), though it is common to analyze the key treatment outcomes (i.e., ADHD and substance use symptoms) separately rather than simultaneously (Riggs et al., 1998; Riggs et al., 2011; Winhusen et al., 2010). Applying a parallel piecewise LGCM to these linked disorders will offer insight to better understand their dynamic relationship.

The purpose of this study was to illustrate the effectiveness of a parallel latent growth curve model to further understand the longitudinal relationships of two comorbid disorders. Specifically, this model was able to answer the following questions: (1) Does the initial SUD score predict the linear decrease in average levels of ADHD in adolescents between baseline and Week 4?; (2) Does the initial SUD score predict the linear decrease in average levels of ADHD in adolescents between Week 4 and Week 16?; (3) Does the initial ADHD score predict the linear decrease in average levels of SUD in adolescents between baseline and Week 4?; (4) Does the initial ADHD score predict the linear decrease in average levels of SUD in adolescents between Week 4 and Week 16?; (5) Does treatment have an impact on ADHD or SUD?

Method

Participants

This study contained a series of secondary analyses by using data from the National Drug Abuse Treatment Clinical Trials Network No. 0028 (http://www.ctndatashare.org/). A complete description of this study can be found in Riggs and colleagues (2011). Adolescents and their parents were recruited through referrals from primary care and mental health clinics, schools, and community-based substance use treatment programs. One thousand three hundred thirty-four individuals were originally screened, with 450 providing informed assent (if minors) and informed consent if 18 years of age. Parents provided informed consent for their participation as well as informed consent for the participation of minors. The adolescents had to meet the DSM-IV criteria for ADHD and at least one non-tobacco SUD. One hundred forty-seven were excluded (139 were not eligible, and 8 were excluded for other reasons). A list of exclusion criteria can be found in Riggs and colleagues (2011). A total of 303 adolescents (aged 13-18; 78.9% male) and their parents participated in the study.

Procedure

The adolescents were randomly assigned to either the experimental (n = 151) or control condition (n = 152). The experimental condition received both osmotic-release methylphenidate (OROS-MPH) with cognitive behavioral therapy (CBT), while the control condition received a matching placebo as well as CBT. The experimental group received a starting dosage of 18-mg at Week 0 (post-randomization), with a continued increase dosage until reaching the fixed dose of 72-mg after two weeks (Riggs et al., 2011). The experimental condition continued on the 72-mg dosage, while the control condition continued on the placebo over the course of the full 16 weeks of the clinical trial. CBT was administered for both groups over the full 16 weeks.

Intervention and Measures

Diagnostic Measures

The Schedule for Affective Disorders and Schizophrenia for School-Age Children – Epidemiologic Version (K-SADS-E) was used to establish DSM-IV diagnosis of ADHD (Orvaschel, 1994; Riggs et al., 2011). The Comprehensive International Diagnostic Interview (CIDI) was administered to participants to determine DSM-IV diagnosis of abuse or dependence in 11 drug classes (Riggs et al., 2011). Riggs and colleagues (2011) provides a list of the 11 drug classes.

Outcome Measures

ADHD was measured every week over the course of the 16-week clinical trial (16 time points) by using the DSM-IV ADHD Rating Scale. The ADHD rating scale contained 9 ADHD-inattention and 9 ADHD-hyperactivity/impulsivity symptoms (18 total symptoms) rated on a 4-point scale (0 = never/rarely; 1 = sometimes; 2 = often; and 3 = very often). This scale reflects ADHD symptoms on the day in which it is administered.

Substance use was measured by adolescent-reported past-28-day use of non-tobacco drug/alcohol using timeline follow-back (TLFB) procedures (Sobell & Sobell, 1992). At the beginning of the study, adolescents were asked for their past-28-day use of a substance (i.e., how many of the past 28 days did the adolescent use alcohol or drugs?). Values ranged from 0 – 28, with a report of 0 suggesting no drug or alcohol use in the past 28 days, and a score of 28 suggesting drug or alcohol use every day since the last assessment. The assessment was then taken every 28 days (four weeks) for a total of five assessments: Week 0 (post-randomization), Week 4, Week 8, Week 12, and Week 16 (trial completion). Because SUD was measured at five different time points, five time points were used for both ADHD and SUD in order to match time points for the trajectory and analysis.

Analysis

Preliminary analyses

Raw means were plotted in order to determine the trajectory of each disorder. Normality was checked to determine the type of estimation used. Linear, quadratic, and piecewise models were estimated in order to establish baseline models. Adjacent correlated residuals were added to each model (Kline, 2010). Each model consisted of five time points where both ADHD and substance use symptom outcomes of the adolescents were collected. The first series of models estimated ADHD and SUD symptom outcomes separately to build an accurate latent growth curve model for each disorder.

Piecewise Growth Model

The piecewise model was analyzed given the nature of the clinical data. The piecewise model estimated two separate linear slopes for each of the disorders separately: a slope estimated from Week 0 to Week 4 (due to the trend of the means between both time points), as well as from Week 4 to Week 16 (due to the trend of the means across Week 4, Week 8, Week 12, and Week 16). A separate analysis for ADHD and SU symptoms outcomes would ensure an accurate model before moving onto a tandem model.

Parallel Piecewise Growth Model

Once a good-fitting model was established for both ADHD and SU separately, a parallel piecewise growth curve model was estimated. This combined the two growth curve models to determine whether the two disorders were related over time. This model used regressions between the intercepts and slopes across disorders to determine whether intercepts predicted the different disorders' slopes in order to answer the previously stated questions. Specifically, we were interested in whether the initial score of SU predicted either decrease (i.e., between Week 0 and Week 4, or between Week 4 and Week 16) in average levels of ADHD over time, or whether initial levels of ADHD predicted either decrease in average levels of SU.

Parallel Piecewise Model Regressed on Treatment

This model included the time invariant covariate of the treatment group. Treatment group was considered to be time invariant because participants were assigned to only one condition and did not change throughout the course of the study. By regressing the intercepts and slopes of ADHD and SUD onto the treatment group, we were able to determine whether the two conditions changed at a statistically significant decrease over the course of the study. This answers the question: Does treatment status predict the variability in both intercept and slope of ADHD and SUD? More specifically, we were able to answer the following questions: (1) Does treatment influence the linear change for the first or second trajectory in ADHD symptoms?; (2) Does treatment influence the linear change for the first or second trajectory in SUD symptoms? Figure 1 is a schematic representation of this final model.

Figure 1.

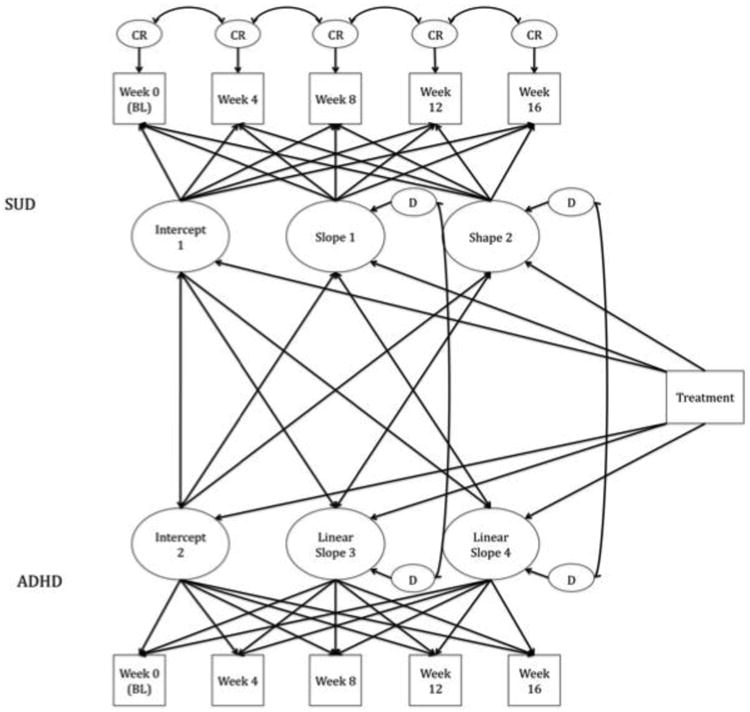
Figure 1

Open in a new tab

Schematic model of treatment regressed onto slopes of each disorder. Circles represent the latent variables; squares represent the manifest variables measured at each of the five time points. CR = adjacent correlated residuals. Single-headed arrows represent regressions; double-headed arrows represent correlations. Values are not depicted for readability.

Models were analyzed using Mplus 7.11 (Muthén & Muthén). Both ADHD and SUD were treated as continuous with nonnormality, thus a maximum likelihood (MLR) estimator was used for all models to account for the nonnormal data. The chi-square, comparative fit index (CFI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR), were used to determine adequate model fit, where benchmarks greater than 0.95 and less than .05, respectively, indicated good global fit (West et al., 2012). The BIC was also included, where lower values represented better fit.

Results

Preliminary Analyses Results

The raw means of both ADHD and SUD can be found in Table 1. ADHD and SUD were analyzed separately with a linear, quadratic, and piecewise model. The piecewise model was imposed to separate the first trajectory (from Week 0 to Week 4) from the second trajectory (from Week 4 to Week 16) based on these means.

Table 1. Means of ADHD and SU symptoms at 5 time points.

Model Week 0 Week 4 Week 8 Week 12 Week 16
ADHD 38.73 (8.87) 22.76 (11.65) 19.52 (11.23) 18.36 (11.64) 18.03 (11.81)
SU 14.58 (9.47) 10.40 (9.41) 9.83 (8.90) 9.27 (8.89) 8.71 (9.39)
Open in a new tab

ADHD Model Fit

The linear and quadratic models provided poor fit (see Table 2) for ADHD. The piecewise framework was imposed, though this did not provide adequate fit. Constraints on Week 8 and Week 12 were released in order for those paths in the second trajectory to be estimated as a “shape factor”. A shape factor allows for fixed first and last points (Week 4 and Week 16) for a growth trajectory, while estimating the middle points (Week 8 and Week 12). The fit for this new model (with an estimated slope from Week 0 and Week 4, and a shape factor from Week 4 to Week 16) was acceptable. This became our final ADHD growth model.

Table 2. Model Fit for ADHD and SU separately and together with five time points.
Model χ2 df CFI RMSEA (90% CI) SRMR BIC
ADHD
Linear 537* 14 .062 .351 (.326 -.377) .368 9236
Quadratic 166* 10 .721 .227 (.197 - .258) .165 8813
Piecewise 8 8 1.000 .000 (.000 - .067) .018 8627
SU
Linear 69* 10 .892 .140 (.109 - .172) .084 8337
Quadratic 17* 6 .981 .076 (.033 - .121) .044 8297
Piecewise 9 6 .994 .042 (.000 - .093) .021 8290
Open in a new tab

Note. CFI = comparative fit index; RMSEA = root mean square error of approximation; SRMR = standardized root mean square residual.

*

p < .05.

Each model of SU has adjacent correlated residuals, resulting in 4 less degrees of freedom than ADHD in linear and quadratic models. Final model of ADHD had shape model estimated for slope 2. This required 2 less degrees of freedom for the piecewise model.

SU Model Fit

The linear and quadratic model did not meet study criterion for fit (see Table 2) for SUD. Adjacent correlated residuals (e.g., correlating Week 0 with Week 4, correlating Week 4 with Week 8) were added to the model. The piecewise model was the only model that met study criterion. This became the final growth model for SU.

Piecewise Growth Models

ADHD Piecewise Growth Model

The means were estimated for ADHD across the five time points that were used for the analyses (Table 1). The average linear change between Week 0 and Week 4 (slope 3; M = -15.95) showed a large decline in these symptoms, while the change between Week 4 and Week 16 (slope 4; M = -1.57) showed little decline in symptoms. The intercept and slope 3 (r = -0.29, p = .000) had a moderate negative relationship, suggesting that those with higher scores on the ADHD rating scale had less of a linear decrease in average change in symptoms at the start of the study. There was no relationship between the intercept with slope 4 (r = -0.06, p =.527). There was a moderate negative relationship between slope 3 and slope 4 (r = -0.30, p = .000), suggesting that those with more change in the first part of the study had less change during the second part of the study, and vice versa.

SU Piecewise Growth Model

The means were estimated for SU at each of the five time points (Table 1). The average linear change between the first two time points for SUD (slope 1; M = -4.05) suggested a large decline in symptoms, while the average change for SUD between Week 4 and Week 16 (slope 2; M = -0.57) suggested a small decline in symptoms. There was a significant negative relationship between the intercept and slope 1 (r = -0.42, p = .000), as well as a weak (though significant) relationship between the intercept and slope 2 (r = -0.22, p = .007). Both of these suggest that higher initially reported SU resulted in less of a decrease in symptoms over both the first and second timeframes of the study.

Parallel Piecewise Regression Model on Treatment

The ADHD and SU growth models were combined into a parallel piecewise model (Figure 1). The fit of the model was very good (χ2 (30) = 39.70, p = .111; RMSEA = .033; CFI = .993; SRMR = .025). While the majority of the parameters had been estimated in the previous two models (ADHD and SU separately), estimating these two models simultaneously provided information on the relationships between intercepts of both disorders, slopes of both disorders, and intercept of one disorder on the slopes of the other disorder.

First we examined the correlations between disorders and then added the regression component to the model to determine whether intercepts predicted the different disorders' slopes (i.e., do baseline values of SUD predict change in ADHD throughout the course of the clinical trial?). Next, treatment was regressed onto the intercepts and slopes to determine whether there was a difference across the experimental and control conditions. The study underwent random assignment, so no significant relationship was found between treatment and initial status of either disorder. Finally, the model regressed treatment onto the trajectories of each disorder. As expected, treatment did not have an effect on the growth processes of either disorder, in line with the original study (Riggs et al., 2011). Interestingly, the two disorders were not correlated, nor did one disorder predict the other (Table 3).

Table 3. Regressions of slopes on different-disorder intercepts and regressions of treatment on slopes.

Treatment Interval β SE
1. Slope 1 regressed on ADHD -0.16 0.09
2. Slope 2 regressed on ADHD -0.21 0.14
3. Slope 3 regressed on SUD 0.10 0.08
4. Slope 4 regressed on SUD 0.13 0.09
5. Treatment on Slope 1 -0.03 0.07
6. Treatment on Slope 2 -0.07 0.11
7. Treatment on Slope 3 0.01 0.07
8. Treatment on Slope 4 0.06 0.08
Open in a new tab

Note. β = standardized regression coefficient, SE = standard error.

*

p < .05.

Slope 1 = SUD slope from Week 0 –Week 4; Slope 2 = SUD slope from Week 4 – Week 16; Slope 3 = ADHD slope from Week 0 – Week 4; Slope 4 = ADHD slope from Week 4 – Week 16.

Discussion

This study applied a parallel latent growth curve model to ADHD and SU symptom outcomes in a clinical trial in order to answer the following questions: (1) What are the mean starting points for both disorder symptoms (intercepts)?; (2) What is the linear change over time in the average levels of both disorders (slopes)?; (3) What are the trends of the growth trajectories of both disorders?; (4) What is the effect of one disorder on the other?; and finally, (5) Is there a treatment effect for either disorder?

A piecewise model was used to fit the data for the separate and synchronized analyses of both ADHD and SU. Considering the drastic drop over the course of the first four weeks of the study for both disorders (i.e., slope 1 and slope 3), a piecewise function was a reasonable addition to the model. The application of a piecewise model is a logical framework for longitudinal data; a single trajectory may not adequately account for several potential stages of the subject's development (Chou, Yang, Pentz, & Hser, 2004). Thus, a piecewise growth model can account for the discontinuity in paths during treatment programs, making this an advantage of LGCMs, as it allows the use of multiple time points to plot the shape of the trajectory in order to better understand the trend in the growth process. This type of model allows for such flexibility in order to estimate the best fitting model to the data. Specifically, the imposition of a treatment may reveal immediate signs of improvement; therefore such a planned analysis is important in capturing the most accurate growth trajectories. A piecewise framework has gained popularity in the assessment of longitudinal data in the substance use literature (Brown, Catalano, Fleming, Haggerty, & Abbott, 2005; Capaldi, Stoolmiller, Kim, & Yoerger, 2009).

The use of a parallel piecewise LGCM allowed for the simultaneous evaluation of two comorbid disorders in order to further understand the relationship between the two. This methodological approach examines the degree of association between two disorders' intercepts and slopes, such that the trajectory of one disorder can be regressed on the other in order to make conclusions about this link. This technique can provide substance use researchers with the tools necessary to understand how two disorders are related. Parallel piecewise LGCMs can also be useful in longitudinal clinical trials where treatment, among other covariates, can be added to the model in order to assess its effect on a dual diagnosis; this approach may reveal the differences in efficacy of treatment for those who are suffering from more than one disorder.

As expected, the findings replicated those of the original study (Riggs et al., 2011); the treatment group did not significantly improve in either ADHD or SU in comparison to those in the control condition. Furthermore, this study revealed no relationship between the two disorders being studied over the course of the clinical trial, such that the number of symptoms in one disorder did not predict the number of symptoms in the other disorder (i.e., initial levels of SUD and ADHD were unrelated). Additionally, the decrease of SUD symptoms did not predict a decrease in ADHD symptoms, and a decrease in ADHD symptoms did not predict a decrease in SUD symptoms. This indicates that the trajectory of one disorder did not influence the trajectory of the other disorder within this clinical trial. Further investigation of the comorbid relationship between ADHD and SUD should be examined.

One limitation of this study was that only five time points were used for ADHD, when a total of sixteen were collected over the course of the clinical trial. This was done in order to match the time points between both disorders with the purpose of determining whether the trajectories were similar. However, the use of all sixteen time points may have allowed for us to further understand the growth process of ADHD and whether a certain function may have then fit the data better (i.e., linear or quadratic). Future research in SUD and longitudinal clinical trials should make use of all available data.

The parallel piecewise LGCM is advantageous in this line of research because it can be used to understand the comorbidity of two disorders and to make conclusions about their relationship. By analyzing data with a parallel and piecewise component, researchers are not only able to determine how levels of one disorder may affect a persons' progress in the other disorder, but also distinguish between different timeframes of the study. The parallel piecewise LGCM can be used specifically in clinical trial research where the addition of treatment and other covariates can be analyzed in connection with two disorders.

Acknowledgments

This project was supported by grants from the Department of Justice, the Life Science Discovery Fund (Roll, PI) and a grant to the Clinical Trials network Pacific Northwest Node (award number 5 U10 DA013714-10) from the National Institute on Drug Abuse (NIDA; Donovan and Roll, Co-PIs). In addition, this project was supported by funds from the Pilot Study Support Program as part of the Center for Advancing Longitudinal Drug Abuse Research (CALDAR, award number P30DA016383; McPherson, PI) from the National Institute on Drug Abuse (NIDA). This project was also supported by the Alcohol and Drug Abuse Research Program (ADARP, award number 2474-1301; Mamey, PI) from Washington State University.

References

  1. American Psychiatric Association. Diagnostic and statistical manual of mental disorders (DSM-IV-TR) 4th. Washington, DC: Author; 2000. [Google Scholar]
  2. Brown EC, Catalano RF, Fleming CB, Haggerty KP, Abbott RD. Adolescent substance use outcomes in The Raising Healthy Children Project: A two-part latent growth curve analysis. Journal of Consulting and Clinical Psychology. 2005;73(4):699–710. doi: 10.1037/0022-006X.73.4.699. [DOI] [PubMed] [Google Scholar]
  3. Capaldi DM, Stoolmiller M, Kim HK, Yoerger K. Growth in alcohol use in at- risk adolescent boys: Two-part random effects prediction models. Drug and Alcohol Dependence. 2009;105:109–117. doi: 10.1016/j.drugalcdep.2009.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chou CP, Yang D, Pentz MA, Hser YI. Piecewise growth curve modeling approach for longitudinal prevention study. Computational Statistics & Data Analysis. 2004;46:213–225. [Google Scholar]
  5. Frodl T. Comorbidity of ADHD and Substance Use Disorder (SU): A neuroimaging perspective. Journal of Attention Disorder. 2010;14(2):109–120. doi: 10.1177/1087054710365054. [DOI] [PubMed] [Google Scholar]
  6. Geiser C. Data analysis with Mplus. New York: Guilford; 2013. [Google Scholar]
  7. Gray KM, Riggs PD, Min SJ, Mikulich-Gilbertson SK, Bandyopadhyay D, Winhusen T. Cigarette and cannabis use trajectories among adolescents in treatment for attention-deficit/hyperactivity disorder and substance use disorders. Drug and Alcohol Dependence. 2011;117(2-3):242–247. doi: 10.1016/j.drugalcdep.2011.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hancock GR, Lawrence FR. Using latent growth models to evaluate longitudinal change. In: Hancock GR, Mueller RO, editors. Structural Equation Modeling: A Second Course. Greenwood, CT: Information Age Publishing, Inc; 2006. [Google Scholar]
  9. Kalbag AS, Levin FR. Adult ADHD and substance abuse: Diagnostic and treatment issues. Substance Use & Misuse. 2005;40(13-14):1955–1981. 2043–1958. doi: 10.1080/10826080500294858. [DOI] [PubMed] [Google Scholar]
  10. Kline R. Principles and Practice of Structural Equation Modeling. 3rd. New York, NY: Guilford; 2010. [Google Scholar]
  11. Meredith W, Tisak J. Latent curve analysis. Psychometrika. 1990;55:107–122. [Google Scholar]
  12. Muthén BO. Beyond SEM: General latent variable modeling. Behaviormetrika. 2002;29(1):81–117. [Google Scholar]
  13. Orvaschel H. Schedule for Affective Disorder and Schizophrenia for School-Age Children Epidemiologic Version. Ft. Lauderdale, FL: Nova Southeastern University, Center for Psychological Studies; 1994. [Google Scholar]
  14. Riggs PD, Winhusen T, Davies RD, Leimberger JD, Mikulich-Gilbertson S, Klein C, et al. Liu D. Randomized controlled trial of osmotic-release methylphenidate with cognitive-behavioral therapy in adolescents with attention-deficit/hyperactivity disorder and substance use disorders. Journal of the American Academy of Child and Adolescent Psychiatry. 2011;50(9):903–914. doi: 10.1016/j.jaac.2011.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Riggs PD, Leon SL, Mikulich SK, Pottle LC. An open trial of bupropion for ADHD in adolescents with substance use disorders and conduct disorder. Journal of the American Academy of Child and Adolescent Psychiatry. 1998;37(12):1271–1278. doi: 10.1097/00004583-199812000-0001. [DOI] [PubMed] [Google Scholar]
  16. Sobell LC, Sobell MB. Timeline Follow-back: A technique for assessing self-reported alcohol consumption. In: Litten RZ, Allen JP, editors. Measuring Alcohol Consumption: Psychosocial and Biochemical Methods. Totoawa, NJ: Humana Press; 1992. pp. 41–72. [Google Scholar]
  17. West SG, et al. Model fit and model selection in structural equation modeling. In: Hoyle RH, editor. Handbook of Structural Equation Modeling. New York: Guilford; 2012. [Google Scholar]
  18. Wilens TE. Impact of ADHD and its treatment on substance abuse in adults. The Journal of Clinical Psychiatry. 2004;65 Suppl 3:38–45. [PubMed] [Google Scholar]
  19. Wilens TE, Dodson W. A clinical perspective of attention-deficit/hyperactivity disorder into adulthood. The Journal of Clinical Psychiatry. 2004;65(10):1301–1313. doi: 10.4088/jcp.v65n1003. [DOI] [PubMed] [Google Scholar]
  20. Wilens TE, Gignac M, Swezey A, Monuteaux MC, Biederman J. Characteristics of adolescents and young adults with ADHD who divert or misuse their prescribed medications. Journal of the American Academy of Child and Adolescent Psychiatry. 2006;45(4):408–414. doi: 10.1097/01.chi.0000199027.68828.b3. [DOI] [PubMed] [Google Scholar]
  21. Winhusen TM, Somoza EC, Brigham GS, Liu DS, Green CA, Covey LS, et al. Dorer EM. Impact of attention-deficit/hyperactivity disorder (ADHD) treatment on smoking cessation intervention in ADHD smokers: A randomized, double-blind, placebo-controlled trial. The Journal of Clinical Psychiatry. 2010;71(12):1680–1688. doi: 10.4088/JCP.09m05089gry. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Wu J, Witkiewitz K, McMahon RJ, Dodge KA. A parallel process growth mixture model of conduct problems and substance use with risky sexual behavior. Drug and Alcohol Dependence. 2010;111(3):207–214. doi: 10.1016/j.drugalcdep.2010.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES