Susceptibility and size quantification of small human veins from an MRI method

Abstract

Recently a method called CISSCO (Complex Image Summation around a Spherical or a Cylindrical Object) was introduced for accurately quantifying the susceptibility and the radius of any narrow cylindrical object at any orientation using a typical two-echo gradient echo sequence. This work further optimizes the method for quantifying oxygen saturation in small cerebral veins in the human brain. The revised method is first validated through numerical simulations and then applied to data from phantom and human brain. The effect of phase high pass filtering on the quantified parameters is studied and procedures for mitigating its adverse effects are suggested. Uncertainty of each measurement is estimated from the error propagation method. It is shown that the revised method allows for accurate quantification of both the vessel size and its oxygen saturation even in the case of a low SNR (signal to noise ratio) in the vein. The results are self consistent across different veins within a given subject with a variation of less than 6%. Finally, imaging parameters and some procedures are suggested for accurate susceptibility and radius quantifications of small human veins.

1. Introduction

Measuring oxygen saturation can provide an important clinical diagnostic tool. Susceptibility of the venous blood is directly related to the oxygenation level of the blood, (e.g., [1,2]). Several groups have developed methods to quantify the susceptibility of veins [3–14]. Some researchers have measured the susceptibility of veins using complex images from multi-echo gradient echo sequences [4,7], while others have estimated venous susceptibility values only from phase information [5,6,13,14]. Sedlacik et al. [7] has quantified the susceptibilities and sizes of veins by fitting the oscillating signals from 20-echo gradient echo images. The main disadavntage of their method is the long scan time. The susceptibilities of veins have also been quantified using quantitative susceptibility mapping (QSM) techniques [8–11,13]. However, the accuracy of quantified susceptibility of a cylindrical object decreases when the size of the object decreases [8,15], mainly due to partial-voluming. We have developed an alternate method (CISSCO) of quantifying magnetic moment, susceptibility, and the size of the narrow cylindrical object [15,16,17] even if they are partial volumed. The results from CISSCO can differ from the expected susceptibilities by 5% but other QSM methods can differ by 30% [16,15]. However, before CISSCO can be used practically, the problems connected with local phase induced from other tissues, low SNR of veins at long echo times, and little (or no) phase information outside veins at low orientations must be dealt with.

In this paper, we have improved our CISSCO method by using double echo gradient echo images for the quantifications of venous susceptibilities and sizes. Practically, as long as the ratio of the length to the diameter of a vein is at least 5:1, we can model the middle portion of the vein as an infinitely long cylinder. Finally, based on uncertainty analyses, we suggest imaging parameters and procedures for susceptibility and radius quantifications of veins at 3 T.

2. Methods and materials

2.1. Theory: susceptibility quantification of a cylindrical object with an MR signal

A more complete description of our original CISSCO method for susceptibility quantification of a cylindrical object with an MR signal has been presented in [15]. Here we summarize the major points and equations. Our method adds up complex MR signals around a cylindrical object of interest and equates that complex sum to equations containing the unknown susceptibility value and radius of the cylinder. We then systematically solve the unknowns.

If the radius of a cylindrical object is a, the overall MR complex signal S within a coaxial cylinder with radius R is

$$S=\pi \ell {\rho }_0\wp {\int }_{\wp /R^2}^{g\prime }\frac{dx}{x^2}{J}_0(x)+\pi \ell a^2{\rho }_{0,c}{e}^{i{\varphi }_{\mathit{\text{in}}}}$$ (1)

with

$${\varphi }_{\mathit{\text{in}}}\equiv -\gamma \frac{\mathrm{\Delta }\chi }{6}(3{\text{cos}}^2\theta -1)B_0{T}_E\equiv \frac{g}{3}(1-3{\text{cos}}^2\theta )$$ (2)

where ℓ is the slice thickness of the image or can be an arbitrary length of the cylindrical object, ρ₀ is the effective spin density of the tissue outside the object, ρ_0,c is the effective spin density inside the object, ℘ is the effective magnetic moment, which can be expressed by ℘ ≡ga² · sin²θ≡g′a², g′≡g · sin²θ is the extremum phase value at the surface of the object, θ is the orientation of the cylinder (see Fig. 1a) and can be estimated from images [15], g≡0.5γB₀ΔχT_E, γ is the proton gyromagnetic ratio (2π · 42.58 MHz/T), B₀ is the main magnetic field, Δχ is the susceptibility difference between the regions inside and outside the object (hereafter, Δχ refers to susceptibility), T_E is the echo time, and J₀ is the zeroth order Bessel function. The complex signal S can be directly calculated from images.

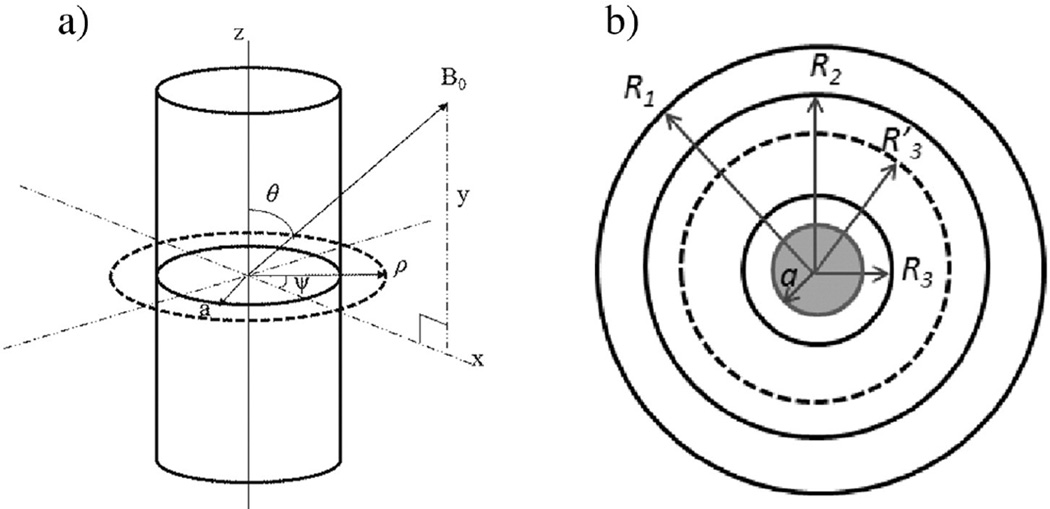
Fig. 1.

(a) A cylinder has an orientation θ away from the main field. (b) A schematic drawing shows the cross section of a cylindrical object with radius a, enclosed by four coaxial pseudo cylinders whose radii are R₃, $R_3^{\prime }$, R₂, and R₁. The MR signal within each pseudo cylinder is S₃, $S_3^{\prime }$, S₂, and S₁, respectively.

Note that our effective magnetic moment ℘ is linearly proportional to T_E and the word “effective” is dropped hereafter. Four unknowns in Eq. (1) are the radius, susceptibility, and two spin densities (ρ_0,c and ρ₀). The two effective spin densities depend on imaging parameters, actual spin densities, and relaxation times T₁ and T₂. Eq. (1) is valid only when the image slice is perpendicular to the axis of the cylindrical object. We have adopted SI units throughout this paper.

If we choose three coaxial cylinders with radii R₁ > R₂ > R₃ around the cylinder of interest in Fig. 1(b), with the use of Eq. (1), we can write down the following equation with ℘ being the only unknown and solve it

$$\mathit{\text{Re}}(S_1-S_2){\int }_{\wp /R_3^2}^{\wp /R_2^2}\frac{dx}{x^2}{J}_0(x)=\mathit{\text{Re}}(S_2-S_3){\int }_{\wp /R_2^2}^{\wp /R_1^2}\frac{dx}{x^2}{J}_0(x)$$ (3)

Then we can solve for ρ₀ from Re(S₁ − S₂) using Eq. (1).

After solving ℘ and ρ₀, by eliminating πℓa²ρ_0,c in Eq. (1), the complex signal S can be rewritten in terms of the susceptibility Δχ as

$$\mathit{\text{Re}}(S)\text{sin}{\varphi }_{\mathit{\text{in}}}-\mathit{\text{Im}}(S)\text{cos}{\varphi }_{\mathit{\text{in}}}+\pi \ell {\rho }_0\wp \text{sin}{\varphi }_{\mathit{\text{in}}}{\int }_{\wp /R^2}^{g\prime }dx{J}_0(x)/x^2$$ (4)

where Re(S) and Im(S) are the real part and the imaginary part of the complex signal S, respectively. Both values are directly calculated from images. After solving for Δχ, we can solve radius a from $\sqrt{\wp /g\prime }$ [15].

2.1.1. Solution of the measured susceptibility

In theory, Eq. (4) should lead to a solution of the measured susceptibility Δχ. However, due to the presence of noise in images, it is possible that we cannot obtain a solution from Eq. (4). In other words, h(Δχ) defined in the following equation rewritten from Eq. (4) is not zero.

$$h(\mathrm{\Delta }\chi )\equiv \mathit{\text{Re}}(S)\text{sin}{\varphi }_{\mathit{\text{in}}}-\mathit{\text{Im}}(S)\text{cos}{\varphi }_{\mathit{\text{in}}}-\pi \ell {\rho }_0\wp \text{sin}{\varphi }_{\mathit{\text{in}}}{\int }_{\wp /R^2}^{g\prime }dx{J}_0(x)/x^2$$ (5)

In this situation, we can derive the uncertainty of Eq. (5) (see Appendix A)

$$\delta h{(\mathrm{\Delta }\chi )}_{\mathit{\text{max}}}=\sqrt{{\left(\sigma \ell \sqrt{\mathrm{\Delta }x\mathrm{\Delta }y\pi R^2}\right)}^2+{(\delta \wp )}^2{\left(\pi \ell {\rho }_0\text{sin}{\varphi }_{\mathit{\text{in}}}\right(\frac{J_0(\wp /R^2)}{\wp /R^2}-{\int }_{\wp /R^2}^{g\prime }dx\frac{J_0(x)}{x^2}\left)\right)}^2}$$ (6)

where Δx and Δy are in-plane resolutions, σ is the standard deviation of the signal, and δ℘ is the uncertainty of the magnetic moment. The goal is to estimate Δχ, which is not known yet. If we plot h(Δχ) ±δh(Δχ) as a function of Δχ and search for the range of Δχ when h(Δχ) ± δh(Δχ) = 0, then the center of the Δχ range can be considered as the measured Δχ. In addition, half of the Δχ range can also be considered as the uncertainty of Δχ.

2.1.2. Improved procedures for susceptibility quantification of objects at large orientations

When a cylindrical object with a large orientation relative to the main field has sufficient phase values and SNRs both inside and outside, our above procedures can solve the susceptibility and radius of the object from a single echo gradient echo image [15]. However, for susceptibility quantifications of veins, SNRs inside veins (i.e., ρ_0,c/σ) can be low at long echo times. The lower the SNR is inside a vein, the larger the uncertainty of the measured susceptibility. For example, if the SNR inside a vein is lower than 3:1, the uncertainty of the susceptibility can be higher than 50%. Using gradient echo images from two echoes can reduce the uncertainty of the measured susceptibility. We can first quantify the magnetic moment ℘ of a given vein using Eq. (3) from the longer echo time, as the uncertainty of ℘ at the longer echo time is smaller [17]. Then we scale the magnetic moment to the shorter echo time and solve the susceptibility of the same vein using Eq. (4) at the shorter echo time. This is because at the shorter echo time, we have a higher SNR inside the vein for more accurate susceptibility quantification. However, this echo time cannot be too short, as we still need sufficient phase value and SNR inside the vein.

2.1.3. Solving susceptibilities of objects at small orientations

This scenario and its mathematical derivations have been described in [15]. Briefly, as little or no phase distributions are outside cylindrical objects at small orientations relative to the main field, it is very difficult to accurately quantify the magnetic moment. We can bypass this problem with the following approach. Consider the expansion of Eq. (4)

$$\mathit{\text{Re}}(S_n)\text{sin}{\varphi }_{\mathit{\text{in}},n}=\mathit{\text{Im}}(S_n)\text{cos}{\varphi }_{\mathit{\text{in}},n}+\pi \ell {\rho }_{0,n}\text{sin}{\varphi }_{\mathit{\text{in}},n}(R^2+\frac{g{\prime }_n^2{a}^4}{4R^2}-a^2-\frac{g{\prime }_n^2{a}^4}{4})$$ (7)

where the subscript n is referred to each variable obtained at the n^th echo time T_En. Applying two coaxial cylinders to images acquired at each echo time, we can first solve each ρ_0,n. Then using images from different echo times, we can solve the susceptibility and cross-sectional area of the object of interest from the following equation and Eq. (7) through an iterative procedure

$$({\rho }_{0,2}\mathit{\text{Re}}(S_1)-{\rho }_{0,1}\mathit{\text{Re}}(S_2))\text{sin}\left({\varphi }_{\mathit{\text{in}},1}\right)\text{sin}\left({\varphi }_{\mathit{\text{in}},2}\right)=\pi \ell {\rho }_{0,1}{\rho }_{0,2}\text{sin}\left({\varphi }_{\mathit{\text{in}},1}\right)\text{sin}\left({\varphi }_{\mathit{\text{in}},2}\right)\frac{a^2}{4}(1-\frac{a^2}{R^2})({g\prime }_2^2-{g\prime }_1^2)+{\rho }_{0,2}\mathit{\text{Im}}(S_1)\text{sin}\left({\varphi }_{\mathit{\text{in}},2}\right)\text{cos}\left({\varphi }_{\mathit{\text{in}},1}\right)-{\rho }_{0,1}\mathit{\text{Im}}(S_2)\text{sin}\left({\varphi }_{\mathit{\text{in}},1}\right)\text{cos}\left({\varphi }_{\mathit{\text{in}},2}\right)$$ (8)

Due to little phase outside the vein, we visually determined the center of the vein. The slightly inaccurate determination of the center would not alter our quantified results later. We selected two disk areas, A₁ > A₂, centering around the vein and we summed up the overall complex signals U₁ and U₂ within the areas. Note that for biological tissues, the susceptibility solved from Eq. (8) is unique [15]. After solving for Δχ and πa², ρ_0,c can be solved from the imaginary part Im(S) = πℓa²ρ_0,c sin ϕ_in of the image.

2.2. Revisions of our method due to the presence of a local uniform field

Even if we can precisely remove the background fields due to air/tissue interfaces, susceptibility differences between tissues will still produce fields around the vein of interest. Thus, we need to take this into account in our equations. As the phase induced by other tissues in the local area around the vein of interest perhaps varies slowly, we may approximate that phase to be a constant, ϕ_bkg. As a result, the complex signal S shown in Eq. (1) becomes U = Se^iϕ_bkg. This local background phase does not affect the quantification of magnetic moment. We will explain the reason in Section 2.2.3. However, the background field could affect the accuracy of searching the center of the object and will definitely affect the susceptibility quantification. The following three subsections describe the effects on the center determination and magnetic moment. We will also show how to estimate this local background phase.

2.2.1. Identification of the center of the object

In our procedures, we first need to determine the center of a given object. We can identify the center by minimizing the overall real part of the complex signal within a circle enclosing the object [17]. This circle has a radius R and is chosen by us. With the existence of ϕ_bkg, this procedure may fail. However, from Appendix B, we have proved that if |ϕ_bkg| is less than π/4 and if the maximal phase value at the boundary of the circle (|℘/R²|) is less than 2.63 radians, then our original procedure of finding the center of the object will still be valid.

2.2.2. Magnetic moment quantification

With the existence of ϕ_bkg, the overall signal in an annular region becomes

$$U_j-U_i=e^{i{\varphi }_{bkg}}\pi \ell {\rho }_0\wp {\int }_{\wp /R_j^2}^{\wp /R_i^2}\frac{dx}{x^2}{J}_0(x)$$ (9)

where the subscripts i and j refer to different coaxial cylinders or concentric circles. The magnetic moment can again be solved by using Eq. (3). It should be clear that ϕ_bkg cancels out in Eq. (3) and it does not change the solution of Eq. (3). Alternatively, we can also replace Re(U_j − U_i) in Eq. (3) by |U_j − U_i|.

2.2.3. Local background phase estimation

Since the imaginary part of the overall signal within a coaxial cylinder only comes from the object itself (see Eq. (1)), we can calculate ϕ_bkg from the annular region between R₂ and R₃. From Eq. (9),

$${\varphi }_{bkg}={\text{tan}}^{-1}\frac{\mathit{\text{Im}}(U_2-U_3)}{\mathit{\text{Re}}(U_2-U_3)}$$ (10)

After estimating ϕ_bkg, we subtract ϕ_bkg from the phase image, and then calculate the complex signal S. Next, we quantify the magnetic moment with Eq. (3) and other unknowns including the susceptibility.

If the orientation of an object is small, such that no sufficient phase distribution is outside the object, we can still consider an annular region around the object and use Eq. (10) to estimate ϕ_bkg. In this case, the signal symbol U represents the complex signal summed around the object. In fact, the area that leads to the signal U does not need to be a circular region. In addition, we do not need to identify the center of the object in this case.

2.3. Simulations

All of our following simulations, except for those in the high pass filter studies, assumed a main field of 3 T, Δχ of 0.4 ppm, and radius of the object a = 1 pixel. In those simulations, the orientation of the object was perpendicular to the main field, except for two cases where the objects had relatively small orientations (10° and 30°). We simulated each cylindrical object on a 4096 × 4096 matrix and converted the matrix to 256 × 256 through Fourier transformation. We also added the Gaussian noise in images such that ρ₀/σ is 10:1 at T_E = 0 ms, with an infinite T₂. Similarly, ρ_0,c/σ is 9:1 at T_E = 0 ms, with a $T_2^{*}$ of the object to be 24 ms. Detailed descriptions of these procedures can be found in [17,15]. From ρ_0,c at T_E = 0 ms and the $T_2^{*}$ value, with σ assigned to be unity, ρ_0,c were 4.4, 3.3, and 2.6 at T_E = 17 ms, 24 ms, and 30 ms, respectively. These were the echo times selectively used in the following scenarios, except for the high pass filter studies.

2.3.1. Presence of the local background field

In order to validate our ideas presented in Section 2.2, in this subsection we purposely added a local background phase of 0.1 radian into simulated images at T_E = 24 ms. We estimated the local background phase using Eq. (10). Then we quantified the magnetic moment from Eq. (3), susceptibility value from Eq. (4), and other unknowns, with and without the removal of the background phase.

2.3.2. Susceptibility quantification at large orientations

We simulated two sets of images at T_E = 17 ms and T_E = 30 ms for an object perpendicular to the main field. The magnetic moment ℘ at T_E = 30 ms was first quantified from Eq. (3). We then scaled ℘ to the value at T_E = 17 ms. From the images at T_E = 17 ms, we quantified the susceptibility.

2.3.3. Susceptibility quantification at low orientations

In this set of simulations, we simulated two objects. One object was simulated with an orientation of 10° at T_E = 17 ms and T_E = 24 ms. The other object had an orientation of 30° but was simulated at two different echo time combinations, T_E = 17 ms and T_E = 24 ms, and T_E = 17 ms and T_E = 30 ms. We quantified susceptibility, cross-sectional area, and two spin densities of these three cases with Eqs. (7) and (8).

2.3.4. Influence of the high pass filter

For this set of studies, we simulated cylindrical objects at B₀ = 3 T, Δχ = 0. ppm, a = 1 pixel and 3 pixels, and T_E = 10, 20, 30, 40, and 50 ms. Both perpendicular and parallel orientation were simulated on 1024 × 1024 matrices which were further converted to 64 × 64 matrices through Fourier transformations. No Gaussian noise or T₂ decay were included in any of these simulated images. We chose ρ₀ = ρ_0,c = 10.

We applied the homodyne high pass filter (16 × 16) to these simulated images. In order to study the high pass filter effect, we quantified and compared the magnetic moment of each object at perpendicular orientation with and without the application of the high pass filter. In addition, we also compared the phase value inside each object at both orientations with and without the high pass filter. If the magnetic moment and phase value inside each object do not change before and after the application of the high pass filter, then we know the high pass filter has no influence onto our quantifications of the magnetic moment and susceptibility. Given the convenient use of the high pass filter, we chose the high pass filter in this work over other background phase removal methods.

2.4. Re-examination of phantom images with an object at a low orientation

In our previous work [15], we applied the methods described in Section 2.1.3 to objects at the parallel orientation. Here, we want to show that those methods are also applicable to objects at low orientations. Thus, we re-examined phantom images in [15] with a straw oriented at 28.2° from the main field and filled by the Gadolinium solution with a theoretical Δχ = 0.58 ± 0.05 ppm. The diameter of the straw was 4.92 ± 0.02 mm, which led to a cross-sectional area of 19.0 ± 0.2 mm². The images were acquired from a single-echo 3D gradient echo sequence on 3 T, repeated three times with three different echo times: T_E = 11 ms, 17 ms, and 20 ms. The image resolution was 1 mm isotropic. We quantified susceptibilities and radii of the straw from two slices (number 12 and 16) for comparisons. For each slice, we obtained quantified values from two sets of echo time combinations. One set used T_E = 11 ms and 17 ms and the other set used T_E = 11 ms and 20 ms.

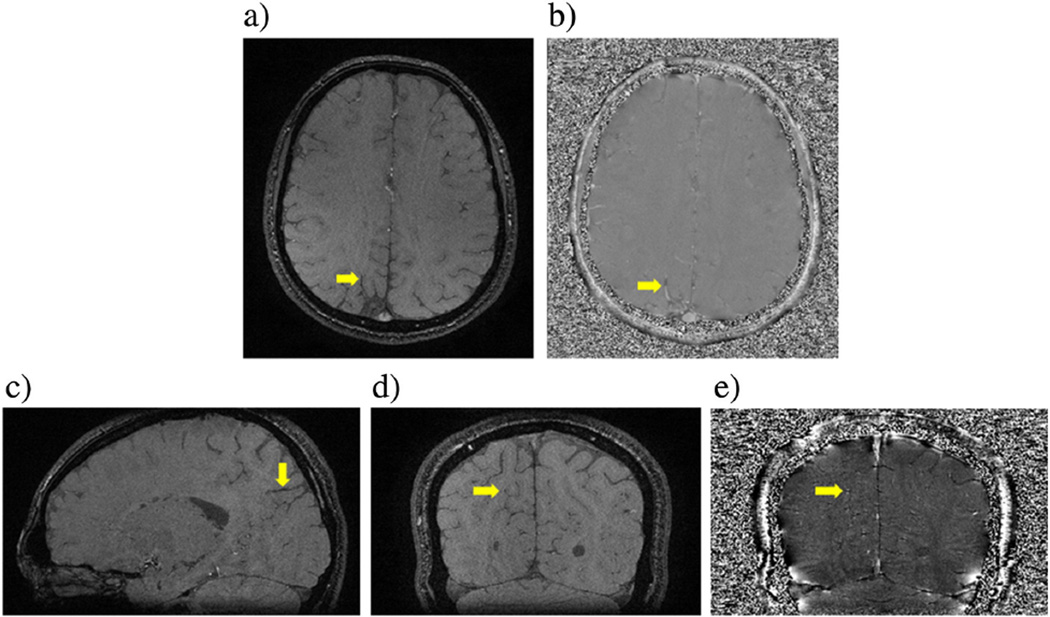
The background phase of those phantom images were already removed by a manual phase unwrapping method and a 2D quadratic fitting program. Thus, we did not apply the high pass filter to those images. An example of the magnitude and phase image of the Gd-DTPA doped straw are shown in Fig. 2a and b.

Fig. 2.

(a) The magnitude and (b) its associated filtered phase image at echo time 20 ms acquired from a 3 T machine. The straw filled with Gd-DTPA solution had a diameter of 4.92 ± 0.02 mm. The straw was immersed in a gel phantom and had an orientation of 28.2° to the main field.

2.5. Uncertainties of susceptibility and other unknowns

The two major independent noise sources contributing uncertainties in our quantified results are from the Gaussian noise and the systematic noise due to discrete pixels, partial volume effect, and Gibbs ringing in images. Uncertainties of quantified unknowns can be derived from the error propagation method [18]. These have been discussed in the past (e.g. [15]). However, if the choice of radius $R\equiv R_3^{\prime }$ used in Eq. (4) is larger than R₃ (see Fig. 1(b)), which is used to quantify the magnetic moment, then we need to rederive the uncertainties of the measured susceptibility value, the cross-sectional area of the object, and the spin density inside the object. In this scenario, as the annular region between $R_3^{\prime }$ and R₃ overlaps with the annular region between R₂ and R₃, we must rewrite δ(S₂–S₃) in terms of $\delta (S_3^{\prime }-S_3)$ and $\delta (S_2-S_3^{\prime })$, where the signal $S_3^{\prime }$ is the overall complex signal within $R_3^{\prime }$. In Appendix C, we show the uncertainties of quantified variables when $R_2>R_3^{\prime }>R_3$.

In this work, we use a two-echo approach to solve susceptibilities of cylindrical objects. As we quantify magnetic moment and susceptibility from two different images, no correlation is between measured results. We provide uncertainty formulas in Appendices D and E. For cylindrical objects at low orientations, we derive uncertainties of the susceptibility and the cross-sectional area (δΔχ/Δχ and δA₀/A₀) by varying susceptibility and area in Eq. (7). We treat δΔχ/Δχ and δA₀/A₀ as two unknowns in a new set of linear equations derived from the variations of Eq. (7). Then we solve δΔχ/Δχ and δA₀/A₀ simultaneously from this new set of linear equations. We evaluate these two uncertainties through the error propagation method.

2.6. In vivo MR data collection and processing

We applied our methods to several isolated veins (see Figs. 3 and 4) from branches of anterior, inferior, superior cerebral veins, and transverse sinus, which were from two sets of existing MR images [8,9]. A 3D gradient echo single-echo sequence with velocity compensation in all three directions was used for the acquisitions of both datasets. One set of the images was acquired from a female volunteer at a 3.96 T Bruker machine. A single channel birdcage head coil was used in this case. The imaging parameters were: isotropic resolution 0.5 mm, T_E = 11.6 ms and 19.2 ms, T_R = 26.0 ms, flip angle = 11°, read bandwidth = 120 Hz/pixel and field of view = 256 mm × 176 mm × 45 mm. The k-space data were used for analyses. The scan was performed twice, but individually for each echo time.

Fig. 3.

A set of 3D gradient echo images at T_E = 17.3 ms from 2.89 T shows a vein, whose susceptibility has been analyzed. (a) Magnitude and (b) its associated phase image from a volunteer. (c) Sagittal view of the same vein as shown in (a) and (b). The orientation of this vein is 80° ± 3° to the main field. The same vein is also displayed in the coronal (d) magnitude and (e) its associated phase image.

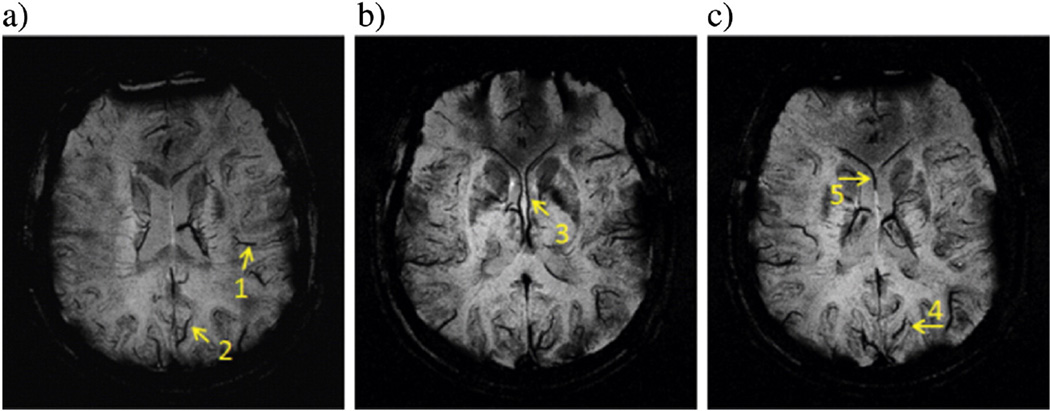
Fig. 4.

A set of SWI images having minimal intensity projections (mIP) over 8 slices at T_E = 19.2 ms from 3.96 T shows a total of five well-separated veins. Quantified results of those veins are listed in Table 6. The mIP images help to display the entire length of each vein, which is not necessarily lying on the original transverse plane. Results of these veins are given in the first 5 rows in Table 6.

The other set of images was acquired from a male volunteer at a 2.89 T Siemens VERIO machine. A 12-channel head coil was used in this case. The imaging parameters were: isotropic resolution 0.5 mm, T_E = 14.3 ms and 17.3 ms, T_R = 26 ms, flip angle = 15°, read bandwidth = 121 Hz/pixel, and field of view = 256 mm × 184 mm × 128 mm. Only combined magnitude and phase images were saved for this scan. The images were also acquired twice, one from each individual echo time.

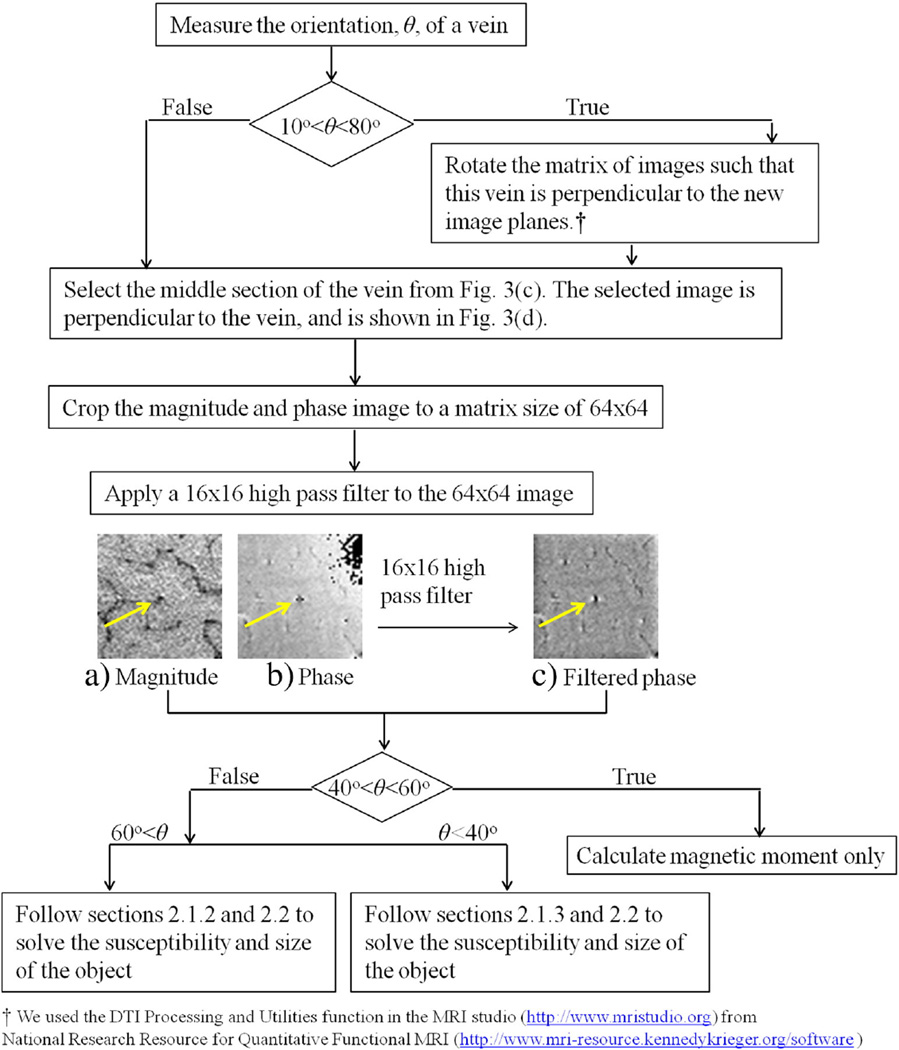
With these two sets of existing images, we first displayed each vein of interest from the transverse, coronal, and sagittal plane. Fig. 3 shows an example. Then we estimated the direction and orientation of the vein from those three imaging planes. The detailed procedure of estimating the orientation of a cylindrical object was given in [15]. We summarize other post-processing procedures in the flow chart in Fig. 5. For comparisons, we also solved for the susceptibility of the vein from Eq. (4) at the longer echo time. In some cases, $R_3^{\prime }$ was chosen between R₂ and R₃.

Fig. 5.

The flow chart of in-vivo MR data post-processing procedures. The vein is pointed by the yellow arrows at the center of (a), (b), and (c). The signals of this vein and of the surrounding area in magnitude (a) and filtered phase images (c) have been used for extracting the susceptibility and the cross-sectional area of the vein.

3. Results

In this section, we present results of quantified magnetic moments, susceptibility values, cross-sectional areas of cylindrical objects, and spin densities from simulations, previous phantom images, and existing human data.

3.1. Simulations

3.1.1. Presence of the local background field

With the assigned local background phase of 0.1 radian, we have estimated a local background phase of 0.10 radian using radii 1.5 pixels and 2.5 pixels in Eq. (10). The measured magnetic moments are the same with and without the correction of the local background phase. However, the quantified susceptibility value and other parameters are improved with the correction of the local background phase (see Table 1). This shows that it is necessary to correct a small local background phase.

Table 1.

Quantified results from simulated images at T_E = 24 ms and with an orientation of 90°.

unit	℘	Δχ	A	ρ0,c	ρ0
	rad · pixel2	ppm	pixel2
Before	3.82	0.44	2.84	5.54	9.91
After	3.82	0.40	3.14	2.80	9.95

The actual values are ℘ = 3.85 rad · pixel², Δχ = 0.4 ppm, A = 3.14 pixel², ρ₀ = 10.0, and ρ_0,c = 3.31. The second column lists the magnetic moment. The third column lists the susceptibility value. The fourth column lists the cross-sectional area, A. The fifth column lists the effective spin density inside the object. The sixth column lists the effective spin density outside the object. The results at the third row are before the removal of the local background phase. The results at the fourth row are after the removal of the local background phase, which is calculated from Eq. (10).

3.1.2. Susceptibility quantifications at large orientations

Using the quantified magnetic moment from T_E = 30 ms scaled to that at T_E = 17 ms as an input to Eq. (4), the precision of the measured susceptibility at T_E = 17 ms is improved. The quantified magnetic moment at T_E = 30 ms is 4.86 ± 0.34 rad · pixel², compared to the input value of 4.82 rad · pixel². Table 2 lists the magnetic moment directly quantified from T_E = 17 ms or scaled from T_E = 30 ms, and their associated susceptibilities and cross-sectional areas solved from Eq. (4).

Table 2.

Quantified results from simulated images at T_E = 17 ms and with an orientation of 90°.

	℘	Δχ	A
	rad · pixel2	ppm	pixel2
No scaled	2.63 ± 0.94	0.39 ± 0.12	3.08 ± 1.42
Scaled	2.75 ± 0.19	0.39 ± 0.07	3.25 ± 1.69

The theoretical values of input parameters are given in the caption of Table 1. The second column lists the magnetic moment, ℘. The third column lists the susceptibility value. The fourth column lists the cross-sectional area, A. The magnetic moment in the third row was quantified directly from Eq. (9). The theoretical value of ℘ at T_E = 17 ms is 2.73 rad · pixel². The magnetic moment in the fourth row was scaled by the magnetic moment, 4.86 ± 0.34 rad · pixel², at T_E = 30 ms.

3.1.3. Susceptibility quantifications at low orientations

The results of measured susceptibility values agree with the theoretical value within 5%. The quantified cross-sectional areas of the objects agree with the input value within 8%. These results are shown in Table 3. We also find that this approach is suitable for objects with orientations up to 40°.

Table 3.

Quantified results from simulated images using the low orientation method.

Angle	TE	Δχ	A	ρ0,c	ρ0
Degree	ms	ppm	pixel2
10	17	0.41 ± 0.03 (17/24)	3.27 ± 0.78	4.2 ± 1.6	9.89 ± 0.20
	24		3.15 ± 0.75	3.4 ± 1.6	9.89 ± 0.20
30	17	0.42 ± 0.13 (17/24)	3.14 ± 1.70	4.2 ± 1.7	9.89 ± 0.20
	24		2.96 ± 1.60	4.5 ± 2.8	9.88 ± 0.20
30	17	0.42 ± 0.05 (17/30)	2.89 ± 0.84	4.2 ± 1.2	9.79 ± 0.20
	30		2.96 ± 0.86	2.5 ± 1.4	9.76 ± 0.20

The first column lists the orientation. The second column lists T_E. The third column lists Δχ solved from Eq. (8). Numbers inside parentheses show the two echo times used for calculating the susceptibility. The theoretical value of Δχ is 0.4 ppm and the theoretical cross-sectional area is 3.14 pixel². The chosen radius, R, for solving Eq. (8) is 1.5 pixel. The fourth column lists the cross-sectional area of the cylinder calculated from Eq. (7). The fifth column lists the effective spin density inside the object calculated from the imaginary part used in Eq. (7). The sixth column lists the quantified effective spin density outside the object.

3.1.4. Influence of the high pass filter

For cylindrical objects whose radii are 1 pixel, quantified magnetic moments and phase values are almost the same with or without the application of the high pass filter (see Table 4). It indicates that quantifications of small objects are not affected by the high pass filter. Therefore, our in vivo results are unlikely affected by the chosen size of the high pass filter. We note that due to the partial volume effect, some measured phase values inside objects can be much smaller than the actual phase values. However, quantified susceptibility values using our method still agree well with input values.

Table 4.

Simulated results of magnetic moments of cylindrical objects and phase values inside objects, at different echo times.

		Theory			No high pass filter			High pass filter
a	TE	℘	ϕ90	ϕ0	℘	ϕ90	ϕ0	℘	ϕ90	ϕ0
pixel	ms	rad·pixel2	rad	rad	rad · pixel2	rad	rad	rad · pixel2	rad	rad
1	10	1.61	0.54	−1.07	1.79	0.39	−0.58	1.89	0.35	−0.52
1	20	3.21	1.07	−2.14	3.55	0.55	−1.45	3.54	0.55	−1.41
1	30	4.82	1.61	−3.21	5.16	1.45	−4.53	5.11	1.55	−4.56
1	40	6.42	2.14	−4.28	6.66	1.96	−4.89	6.53	1.95	−5.00
1	50	8.02	2.68	−5.35	8.26	2.32	−5.62	7.99	2.50	−5.30
3	10	14.4	0.54	−1.07	14.9	0.53	−1.05	14.7	0.34	−0.71
3	20	28.9	1.07	−2.14	29.2	1.08	−2.11	27.0	0.59	−1.60
3	30	43.3	1.61	−3.21	43.8	1.59	−3.26	36.1	0.54	−3.27
3	40	57.8	2.14	−4.28	58.2	2.16	−4.32	41.8	0.34	−4.80
3	50	72.2	2.68	−5.35	72.8	2.72	−5.36	45.3	0.10	−5.65

The radii of these objects were 1 pixel and 3 pixels. The orientations of the objects were 90° and 0°. Theoretical values, results without using the high pass filter, and results using the high pass filter are listed. The first column lists the radius a of the object. The second column lists T_E. The third, sixth, and ninth column show the magnetic moments ℘. The fourth, seventh, and tenth column list phase values inside objects perpendicular to the field. The fifth, eighth, and eleventh column list phase values inside objects parallel to the field. Uncertainties of these quantified results are not shown.

For cylindrical objects whose radii are 3 pixels, quantified magnetic moments using our method with or without the application of the high pass filter can become very different when the echo time is 30 ms or longer (see Table 4). In addition, even at T_E = 10 ms, measured phase values (from central pixels completely inside each object) can already be different with the use of the high pass filter. This shows that the high-pass filter can influence susceptibility quantification when an object is slightly large.

With the applications of the high pass filter, if a phantom or a brain does not occupy the entire image, our further simulations show that the phase value inside a cylindrical object can be further reduced. The reduction depends on the phantom size (or the brain size), object size, object orientation, the original phase value inside the object, or the size of the high pass filter. This was the reason why we cropped the human images before we applied the high pass filter.

3.2. Re-examination of the previous phantom images

Table 5 lists phantom results from an object at the low orientation (28.2°). The differences between the quantified susceptibility values and the expected value (0.58 ppm) are less than 10%. However, the differences between the measured cross-sectional areas and the true value (19.0 ± 0.2 mm²) can be up to 30%. The uncertainties of these results are about one third of those results quantified from the previous single echo approach using Eq. (4) [15].

Table 5.

Quantified results from phantom images with an image resolution of 1 mm isotropic, using two different echo times when the object is oriented at 28.2° to the main field.

	Slice number 12				Slice number 16
TE (ms)	Δχ ppm	Area mm2	ρ0,c	ρ0	Δχ ppm	Area mm2	ρ0,c	ρ0
11		23.4 ± 3.7	2241 ± 130	1291 ± 13		23.2 ± 3.7	2239 ± 130	1263 ± 13
17	0.55 ± 0.03a	22.7 ± 2.3	2059 ± 160	1272 ± 13	0.56 ± 0.03a	22.7 ± 2.3	2021 ± 160	1257 ± 13
20	0.55 ± 0.02b	22.6 ± 2.9	1961 ± 120	1261 ± 13	0.54 ± 0.02b	24.8 ± 3.2	2137 ± 120	1262 ± 13

Comments:

^aT_E = 11 ms and 17 ms.

^bT_E = 11 ms and 20 ms.

Two different slices have been analyzed. The theoretical value of Δχ is 0.58 ± 0.05 ppm and the cross-sectional area is 19.0 ± 0.2 mm². The first column lists the echo time. The second and the sixth column list Δχ solved from Eq. (8). The chosen radius, R, for solving Eq. (8) is 3.0 mm. The superscripts, a and b, refer to the two echo times used for quantifying the susceptibility. The third and seventh column list the cross-sectional area of the cylinder calculated from Eq. (7). The fourth and eighth column list the effective spin density inside the object calculated from the imaginary part used in Eq. (7). The fifth and ninth column list the effective spin density outside the object.

3.3. Results from existing human images

Our quantified susceptibility values shown in Table 6a in general agree with values (0.37–0.54 ppm) from other recent work [10,13,11]. However, our susceptibility values of 5 veins in different regions of each volunteer’s brain are close to each other. The typical susceptibility value from a vein of a healthy person is about 0.41 ppm, if we assume an oxygenation level of 70%, a Hemoticrit of 40%, and a susceptibility difference between fully deoxygenated blood and oxygenated blood of 3.39 ppm [19]. From the measured cross-sectional area of each vein in Table 6a, we find that the diameters of analyzed vein range from 1.2 to 3.0 pixels.

Table 6.

Magnetic susceptibility and 4 other unknowns of veins were measured from T_E = 19.2 ms and 11.6 ms at 3.96 T and from T_E = 17.3 ms and 14.3 ms at 2.89 T.

B0	Angle	℘	Δχ	A0	ρ0,c	ρ0
	(Degree)	rad · pixel2	ppm	pixel2
(a)
4	80 ± 3	1.29 ± 0.55	0.46 ± 0.37	1.50 ± 1.79	297 ± 217	279 ± 8
4	90 ± 1	2.01 ± 0.32	0.46 ± 0.16	2.27 ± 1.11	239 ± 98	292 ± 9
4	75 ± 3	2.57 ± 0.31	0.45 ± 0.12	3.14 ± 1.00	384 ± 104	334 ± 10
4	70 ± 3	1.22 ± 0.35	0.48 ± 0.34	1.45 ± 1.39	254 ± 163	323 ± 6
4	70 ± 3	1.35 ± 0.32	0.48 ± 0.31	1.63 ± 1.38	309 ± 185	261 ± 8
3	80 ± 3	2.67 ± 0.45	0.40 ± 0.19	3.94 ± 2.48	242 ± 87	306 ± 9
3	90 ± 1	2.30 ± 0.44	0.38 ± 0.22	3.46 ± 2.11	57 ± 30	303 ± 9
3	80 ± 3	2.03 ± 0.45	0.36 ± 0.22	3.33 ± 2.70	164 ± 64	354 ± 11
3	67 ± 3	3.07 ± 0.31	0.40 ± 0.20	5.15 ± 2.78	198 ± 63	227 ± 7
3	75 ± 3	1.59 ± 0.64	0.39 ± 0.34	2.49 ± 2.99	231 ± 136	338 ± 7
(b)
4	80 ± 3	2.13 ± 0.91	0.43 ± 0.39	1.58 ± 1.57	28 ± 24	227 ± 7
4	90 ± 1	3.32 ± 0.53	0.32 ± 0.13	3.20 ± 1.83	87 ± 54	244 ± 7
4	75 ± 3	4.26 ± 0.51	0.70 ± 0.30	2.01 ± 0.90	143 ± 112	299 ± 7
4	70 ± 3	2.02 ± 0.58	0.37 ± 0.21	1.91 ± 1.51	329 ± 194	281 ± 8
4	70 ± 3	2.23 ± 0.53	0.28 ± 0.15	2.90 ± 2.00	230 ± 108	210 ± 6
3	80 ± 3	3.23 ± 0.55	0.44 ± 0.09	3.53 ± 0.92	214 ± 58	283 ± 8
3	90 ± 1	2.78 ± 0.53	0.33 ± 0.17	3.94 ± 0.62	90 ± 36	286 ± 8
3	80 ± 3	2.46 ± 0.54	0.36 ± 0.19	3.27 ± 1.05	118 ± 67	344 ± 10
3	67 ± 3	3.72 ± 0.37	0.35 ± 0.21	5.90 ± 3.60	168 ± 54	220 ± 7
3	70 ± 3	1.82 ± 0.73	0.35 ± 0.38	2.78 ± 1.78	241 ± 203	318 ± 6

The first column lists the main field strength. The second column lists each vessel’s orientation. The third column lists the magnetic moment of the vessel. Results from (a) show quantified magnetic moments from the longer echo time but other quantified parameters from the shorter echo time, by scaling the measured magnetic moments to values at the shorter echo time. On the other hand, results from (b) show quantified values all from the longer echo time. The fourth column lists Δχ of the venous blood. The fifth column lists the cross-sectional area of each vein. The sixth column lists the effective spin density inside each vein. The seventh column lists the effective spin density outside each vein. The last vein in the tables has different orientations, due to the movement of the volunteer between the two scans. The orientation of this vein in (a) is from the shorter echo time, while the value in (b) is from the longer echo time.

For comparisons, Table 6b lists the results of magnetic moments, susceptibility values, cross-sectional areas, and other variables of veins quantified from the longer echo time of each volunteer’s images. We find that in general the results of susceptibility values, cross-sectional areas, and spin densities inside veins have larger uncertainties than those results in Table 6a. The susceptibility values in highlighted grey areas in Table 6 were estimated using Eq. (6).

For veins at low orientations, we have quantified two vessels with orientations of 20° ± 5° and 29° ± 3° at T_E = 11.6 ms from 3.96 T images. As the volunteer moved between the scans, at T_E = 19.2 ms, the orientation of the latter vein changed from 29° ± 3° to 16° ± 5°, but the orientation of the former vein did not change. The susceptibility value of the former vein is 0.46 ± 0.11 ppm and its cross-sectional area is 1.51 ± 1.23 pixel². The susceptibility value of the latter vein is 0.43 ± 0.03 ppm and its cross-sectional area is 4.37 ± 1.18 pixel². These two susceptibility values are in good agreement with those shown in Table 6a.

We have also estimated susceptibility values of veins at low orientations from 2.89 T. However, the quantified values are about 0.6 ppm. A closer examination reveals that phase values inside those veins are much higher than the expected value at T_E = 14.3 ms, but are about the same as the expected values at T_E = 17.3 ms if a susceptibility of 0.40 ppm is assumed. After we further examine the data, we believe that this problem is due to the combination of multi-channel phase images.

4. Discussions

Our averaged susceptibility values of veins from Table 6a for two volunteers imaged at 3.96 T and 2.89 T are 0.46 ± 0.02 ppm and 0.39 ± 0.02 ppm, respectively. For the purpose of comparing results below from other groups, the calculated standard deviations here have neglected the uncertainty of the susceptibility of each vein. The standard deviation, 0.02 ppm, is smaller than those from other recent results. For example, the averaged susceptibility values of veins in each volunteer for three volunteers in the work by [10] are 0.54 ± 0.13 ppm, 0.49 ± 0.09 ppm, and 0.53 ± 0.09 ppm. Note that these averaged susceptibility values are higher than our values. In addition, the averaged diameter of quantified veins from [10] is 4.5 pixels, compared to a range of 1.2–3.0 pixels from our images.

In the work by [11], the averaged susceptibility value of 48 veins from 8 volunteers (7 of whom are male) is 0.37 ppm. The standard deviation of the susceptibility quantified from 6 cortical veins of each volunteer is between 0.04 ppm and 0.08 ppm (see Fig. 5b of [11]). In another work by [13], the averaged susceptibility value of small veins from 6 subjects is 0.45 ± 0.02 ppm. The phase and the statistical method described in [13] require subjects to breathe in PCO₂ and PO₂ independently at 7 T.

In our previous work [15], when the orientation of the cylindrical object is around the magic angle (54.7°), Eq. (4) cannot solve for the susceptibility of the object. However, for the vein around the magic angle, we may quantify the susceptibility of this vein by obtaining the magnetic moment in the typical gradient echo sequence and measuring the size of this vein by applying the dark blood spin echo sequence.

With uncertainty formulas given in the Appendices of this paper and in Appendix B of [15], we can optimize imaging parameters by minimizing the uncertainties of susceptibilities of small veins but keeping reasonable imaging time of a two-echo 3D gradient echo sequence. The first consideration is the image resolution. If we are interested in veins with diameters similar to those quantified in this work (at least 0.5 mm in diameter), we can reduce the isotropic image resolution to 0.6 mm. Second, if our goal is to maintain uncertainties of the susceptibility less than 35% from a 3 T machine, for most veins with a diameter of at least two pixels, SNR at least 5.7 to 1 from the shorter echo time, and with orientations either larger than 70° or smaller than 30°, we can choose T_E to be 17 ms and 24 ms. The choice of 24 ms is because this value is close to $T_2^{*}$ of the venous blood [20]. The choice of 17 ms is to have some time difference away from 24 ms, but T_E = 17 ms is still long enough such that we have sufficient phase values inside those veins of interest. If we choose T_R to be 28 ms and a transverse scan with a field of view of 256 mm × 192 mm and a slab coverage of 128 mm, the scan time will be about 32 minutes. If we choose T_E to be 17 ms and 30 ms and T_R to be 35 ms, with other parameters being the same, the scan time will be about 40 minutes. However, the uncertainties of the susceptibility for the same veins will be reduced to 16%. This can be seen from results shown in Tables 2 and 3. If a vein has a length to diameter ratio of more than 5:1, depending on the length of the vein, it may be possible to average quantified susceptibility values from several slices. This will further reduce the uncertainty of the measurement.

Another possible way to reduce the uncertainty of the measured susceptibility from a vein at a large orientation is to inject the contrast agent (Gd-DTPA) into subjects. Here we assume that the vessel size does not change before and after the injection. We can first determine the size of the vein from post-contrast images and then calculate the susceptibility of the same vein from pre-contrast images. Our simulations indicate that this approach can lead to an uncertainty less than 15% with the above parameters of the vein and with T_E = 17 ms and 24 ms.

For the consideration of scan time, if a typical neuro protocol has covered the entire brain with either T₁-weighted or T₂-weighted sequence, then we may use these suggested parameters of the 3D gradient echo sequence to cover only a portion of the brain in which susceptibilities of veins are interested to clinicians. If we just cover 64 slices, the scan time will be less than 12 minutes. We may further reduce this scan time by enabling parallel imaging.

5. Conclusion

With the improved procedures that take into account practical issues in MR imaging, we have demonstrated that magnetic susceptibilities and cross-sectional areas of veins at different orientations can be quantified with reasonable accuracy and precision. The susceptibility values of different veins are almost the same for each volunteer, while the susceptibility values differ between the two volunteers in this work. We have also shown that our post processing procedures will not be affected by subject movements between scans.

Appendix A. Derivation of Eq. (6) for the estimation of susceptibility

We estimate the uncertainty of Eq. (5) by deriving the variation of h(Δχ). As the susceptibility has not been solved yet, we do not consider the variation of the susceptibility. We also neglect the uncertainty of ρ₀.

$$\delta h(\mathrm{\Delta }\chi )=[\delta \mathit{\text{Re}}(S)]\text{sin}{\varphi }_{\mathit{\text{in}}}-[\delta \mathit{\text{Im}}(S)]\text{cos}{\varphi }_{\mathit{\text{in}}}-\pi \ell {\rho }_0\text{sin}{\varphi }_{\mathit{\text{in}}}(\delta \wp ){\int }_{\wp /R^2}^{g\prime }dx\frac{J_0(x)}{x^2}+\pi \ell {\rho }_0(\delta \wp )\text{sin}{\varphi }_{\mathit{\text{in}}}\frac{J_0(\wp /R^2)}{\wp /R^2}=\text{sin}{\varphi }_{\mathit{\text{in}}}\left[\right(\pm \sigma \ell \sqrt{\mathrm{\Delta }x\mathrm{\Delta }y\pi R^2})-(\pm \sigma \ell \sqrt{\mathrm{\Delta }x\mathrm{\Delta }y\pi R^2})\text{cot}{\varphi }_{\mathit{\text{in}}}+\pi \ell {\rho }_0(\delta \wp )(\frac{J_0(\wp /R^2)}{\wp /R^2}-{\int }_{\wp /R^2}^{g\prime }dx\frac{J_0(x)}{x^2}\left)\right]$$

Here we only consider the thermal noise in δRe(S) and δIm(S). As δRe(S), δIm(S), and δ℘ are uncorrelated with each other with the proper choices of R₁, R₂, and R₃, the uncertainty of h(Δχ) is

$$\delta h{(\mathrm{\Delta }\chi )}_{\mathit{\text{max}}}=\sqrt{{\left(\sigma \ell \sqrt{\mathrm{\Delta }x\mathrm{\Delta }y\pi R^2}\right)}^2+{(\delta \wp )}^2{\left(\pi \ell {\rho }_0\text{sin}{\varphi }_{\mathit{\text{in}}}\right(\frac{J_0(\wp /R^2)}{\wp /R^2}-{\int }_{\wp /R^2}^{g\prime }dx\frac{J_0(x)}{x^2}\left)\right)}^2}$$

The uncertainty of magnetic moment, δ℘, is calculated from Eq. (15) in [17]. The Gaussian noise, σ, may be measured from the background of magnitude images.

Appendix B. Identifying the object center with the presence of a local uniform field

With an assumed constant local background phase, ϕ_bkg, the MR complex signal, S, becomes Se^iϕ_bkg. With Eq. (B.1) from [17], which shows the second derivatives of the original signal S within a radius R,

$${\mathit{\text{Im}}\frac{{\partial }^{2}S}{\partial x_0^2}|}_{x_0=y_0=0}={-\mathit{\text{Im}}\frac{{\partial }^{2}S}{\partial y_0^2}|}_{x_0=y_0=0}=-2\pi \ell {\rho }_0\left(\frac{\wp }{R^2}\right)J_2\left(\frac{\wp }{R^2}\right)$$ (B.1)

and

$${\mathit{\text{Re}}\frac{{\partial }^{2}S}{\partial x_0^2}|}_{x_0=y_0=0}={\mathit{\text{Re}}\frac{{\partial }^{2}S}{\partial y_0^2}|}_{x_0=y_0=0}=2\pi \ell {\rho }_0\left(\frac{\wp }{R^2}\right)J_1\left(\frac{\wp }{R^2}\right)$$ (B.2)

the real parts of the second derivatives of Se^iϕ_bkg are

$${\mathit{\text{Re}}\frac{{\partial }^{2}S{e}^{i{\varphi }_{bkg}}}{\partial x_0^2}|}_{x_0=y_0=0}=2\pi \ell {\rho }_0\frac{\wp }{R^2}(J_1(\frac{\wp }{R^2})\text{cos}{\varphi }_{bkg}+J_2(\frac{\wp }{R^2})\text{sin}{\varphi }_{bkg})$$ (B.3)

and

$${\mathit{\text{Re}}\frac{{\partial }^{2}S{e}^{i{\varphi }_{bkg}}}{\partial y_0^2}|}_{x_0=y_0=0}=2\pi \ell {\rho }_0\frac{\wp }{R^2}(J_1(\frac{\wp }{R^2})\text{cos}{\varphi }_{bkg}-J_2(\frac{\wp }{R^2})\text{sin}{\varphi }_{bkg})$$ (B.4)

When 0 < |℘/R²| < 2.63, J₁(|℘/R²|) > J₂(|℘/R²|) > 0. In addition, when |ϕ_bkg| < π/4, we have

$$2\pi \ell {\rho }_0\frac{\wp }{R^2}(J_1(\frac{\wp }{R^2})\text{cos}{\varphi }_{bkg}\pm J_2(\frac{\wp }{R^2})\text{sin}{\varphi }_{bkg})=2\pi \ell {\rho }_0\frac{|\wp |}{R^2}(J_1(\frac{\wp }{R^2})\text{cos}{\varphi }_{bkg}\pm J_2(\frac{\wp }{R^2})\text{sin}{\varphi }_{bkg})>0$$ (B.5)

As the real parts of second derivatives are positive, this proves that our searching algorithm for the center of the object is still valid.

Appendix C. Uncertainty of susceptibility quantified from the same image

These formulas are for magnetic moments and susceptibility values quantified from the same image and for cylinders at large orientations. In addition, the area chosen for quantifying the susceptibility, $\pi {R\prime }_3^2$, overlaps part of the area, $\pi (R_2^2-R_3^2)$ (see Fig. 1b). The latter area is one of the annular regions for quantifying the magnetic moment. Because of this overlapping, we need to carefully separate these regions and ensure no correlation between those regions. We only use these formulas in this paper for comparison purpose, and we typically do not suggest having overlapping areas. As in theory, $\mathit{\text{Im}}(S_3^{\prime }-S_3)$ is zero, we have neglected the uncertainty of $\mathit{\text{Im}}(S_3^{\prime }-S_3)$.

$$\frac{\delta \mathrm{\Delta }\chi }{\mathrm{\Delta }\chi }=\frac{\sqrt{\delta {\theta }^2{A}^2+{\left(\frac{\delta \mathit{\text{Re}}(S_3)}{\pi \ell \sigma }\right)}^2{B}^2+{\left(\frac{\delta \mathit{\text{Im}}(S_3)}{\pi \ell \sigma }\right)}^2{C}^2+{\left(\frac{\delta (S_1-S_2)}{\pi \ell \sigma }\right)}^2{D}^2+{\left(\frac{\delta (S_3^{\prime }-S_3)}{\pi \ell \sigma }\right)}^2{E}^2+{\left(\frac{\delta (S_3^{\prime }-S_2)}{\pi \ell \sigma }\right)}^2{F}^2}}{|\wp /g\prime ||\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,\mathrm{c}}{\varphi }_{\mathit{\text{in}}}-\mathrm{S}\mathrm{N}{\mathrm{R}}_0{J}_0(g\prime )\text{sin}{\varphi }_{\mathit{\text{in}}}|}$$ (C.1)

where SNR₀ ≡ ρ₀/σ, σ is the standard deviation of the thermal noise in images, and SNR_0,c ≡ ρ_0,c/σ.

$$A=2\text{cot}\theta \left|\frac{\wp }{g\prime }\right|(\mathrm{S}\mathrm{N}{\mathrm{R}}_0{J}_0(g\prime )\text{sin}{\varphi }_{\mathit{\text{in}}}-g\prime \mathrm{S}\mathrm{N}{\mathrm{R}}_{0,c})$$

$$B=-\text{sin}{\varphi }_{\mathit{\text{in}}}$$

$$C=\text{cos}{\varphi }_{\mathit{\text{in}}}$$

$$D=\text{sin}{\varphi }_{\mathit{\text{in}}}(\frac{h_3^{\prime }}{h_{12}}+\frac{h_{23}\left(\frac{h_3^{\prime }}{h_{12}}\right(\frac{J_0({\varphi }_2)}{{\varphi }_2}-\frac{J_0({\varphi }_1)}{{\varphi }_1})+\frac{J_0({\varphi }_3^{\prime })}{{\varphi }_3^{\prime }})}{h_{12}\frac{J_0({\varphi }_3)}{{\varphi }_3}+h_{23}\frac{J_0({\varphi }_1)}{{\varphi }_1}+h_{31}\frac{J_0({\varphi }_2)}{{\varphi }_2}})$$ (C.2)

$$E=-\text{sin}{\varphi }_{\mathit{\text{in}}}(\frac{h_3^{\prime }(\frac{J_0({\varphi }_2)}{{\varphi }_2}-\frac{J_0({\varphi }_1)}{{\varphi }_1})+h_{12}\frac{J_0({\varphi }_3^{\prime })}{{\varphi }_3^{\prime }}}{h_{12}\frac{J_0({\varphi }_3)}{{\varphi }_3}+h_{23}\frac{J_0({\varphi }_1)}{{\varphi }_1}+h_{31}\frac{J_0({\varphi }_2)}{{\varphi }_2}}+1)$$

$$F=-\text{sin}{\varphi }_{\mathit{\text{in}}}\frac{h_3^{\prime }(\frac{J_0({\varphi }_2)}{{\varphi }_2}-\frac{J_0({\varphi }_1)}{{\varphi }_1})+h_{12}\frac{J_0({\varphi }_3^{\prime })}{{\varphi }_3^{\prime }}}{h_{12}\frac{J_0({\varphi }_3)}{{\varphi }_3}+h_{23}\frac{J_0({\varphi }_1)}{{\varphi }_1}+h_{31}\frac{J_0({\varphi }_2)}{{\varphi }_2}}$$

where $h_3^{\prime }={\int }_{{\varphi }_3^{\prime }}^{|g\prime |}\frac{dx}{x^2}{J}_0(x),{\varphi }_3^{\prime }=|\wp |/{R\prime }_3^2,{\varphi }_i\equiv |\wp |/R_i^2$ i = 1, 2, or 3

$$h_{ij}={\int }_{{\varphi }_i}^{{\varphi }_j}\frac{dx}{x^2}{J}_0(x)$$

$$h_3={\int }_{{\varphi }_3}^{|g\prime |}\frac{dx}{x^2}{J}_0(x)$$

$$\frac{\delta \mathit{\text{Re}}(S_3)}{\pi \ell \sigma }=\sqrt{\frac{\mathrm{\Delta }x\mathrm{\Delta }y{R}_3^2}{\pi }+{\epsilon }_R^2{(\wp h_3\mathrm{S}\mathrm{N}{\mathrm{R}}_0+\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,c}\frac{\wp }{|g\prime |}\text{cos}{\varphi }_{\mathit{\text{in}}})}^2}$$

where ε_R is defined as the percentage difference between the theoretical Re(S₃) and measured Re(S₃) directly summed from simulated images without the Gaussian noise.

$$\frac{\delta \mathit{\text{Im}}(S_3)}{\pi \ell \sigma }=\sqrt{\frac{\mathrm{\Delta }x\mathrm{\Delta }y{R}_3^2}{\pi }+{\epsilon }_I^2{\left(SN{R}_{0,c}\frac{\wp }{g\prime }\text{sin}{\varphi }_{\mathit{\text{in}}}\right)}^2}$$

where ε_I is defined as the percentage difference between the theoretical Im(S₃) and measured Im(S₃) directly summed from simulated images without the Gaussian noise.

$$\frac{\delta (S_i-S_j)}{\pi \ell \sigma }=\sqrt{\frac{\mathrm{\Delta }x\mathrm{\Delta }y}{\pi }|R_i^2-R_j^2|+{\epsilon }_{ij}^2{\left(\wp h_{ij}SN{R}_0\right)}^2}$$

where εij ≡ δ(S_i−S_j)/(S_i−S_j) for i,j = 1,2,3 and the index i or j refers to the circle within which the complex signal is added. Similarly, ε_ij should be interpreted as the percentage difference between the theoretical S_i−S_j (which is a real number) and the real part of S_i−S_j directly summed from images.

$$\frac{\delta {\rho }_0}{{\rho }_0}=\frac{1}{\mathrm{S}\mathrm{N}{\mathrm{R}}_0}\sqrt{{\left(\frac{G}{\wp }\right)}^2{\left(\frac{\delta (S_1-S_2)}{\pi \ell \sigma }\right)}^2+{\left(\frac{H}{\wp }\right)}^2{\left(\frac{\delta (S_2-S_3)}{\pi \ell \sigma }\right)}^2}$$

where

$$\frac{G}{\wp }=\frac{1}{\wp h_{12}}+\frac{\frac{h_{23}}{h_{12}}(h_{12}+\frac{J_0({\varphi }_2)}{{\varphi }_2}-\frac{J_0({\varphi }_1)}{{\varphi }_1})}{\wp (h_{12}\frac{J_0({\varphi }_3}{{\varphi }_3}+h_{23}\frac{J_0({\varphi }_1)}{{\varphi }_1}+h_{31}\frac{J_0({\varphi }_2)}{{\varphi }_2})}$$

$$\frac{H}{\wp }=\frac{-(h_{12}+\frac{J_0({\varphi }_2)}{{\varphi }_2}-\frac{J_0({\varphi }_1)}{{\varphi }_1})}{\wp (h_{12}\frac{J_0({\varphi }_3}{{\varphi }_3}+h_{23}\frac{J_0({\varphi }_1)}{{\varphi }_1}+h_{31}\frac{J_0({\varphi }_2)}{{\varphi }_2})}$$

As the cross-sectional area of the cylinder is defined as A₀ ≡ πa², the uncertainty of the cross-sectional area is

$$\begin{gathered} \frac{\delta A_0}{A_0}={[{(\frac{A}{I}+2\text{cot}\theta )}^2\delta {\theta }^2+{\left(\frac{B}{I}\right)}^2{\left(\frac{\delta \mathit{\text{Re}}(S_3)}{\pi \ell \sigma }\right)}^2+{\left(\frac{C}{I}\right)}^2{\left(\frac{\delta \mathit{\text{Im}}(S_3)}{\pi \ell \sigma }\right)}^2+{(\frac{h_{12}}{J}-\frac{F}{I})}^2{\left(\frac{\delta (S_2-S_3^{\prime })}{\pi \ell \sigma }\right)}^2 \\ +{(\frac{h_{12}}{J}-\frac{E}{I})}^2{\left(\frac{\delta (S_3^{\prime }-S_3)}{\pi \ell \sigma }\right)}^2+{(\frac{h_{23}}{J}+\frac{D}{I})}^2{\left(\frac{\delta (S_1-S_2)}{\pi \ell \sigma }\right)}^2]}^{1/2} \end{gathered}$$

where

$$I=|\wp /g\prime |(\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,c}{\varphi }_{\mathit{\text{in}}}-\mathrm{S}\mathrm{N}{\mathrm{R}}_0{J}_0(g\prime )\text{sin}{\varphi }_{\mathit{\text{in}}})$$

$$J=|\wp |\mathrm{S}\mathrm{N}{\mathrm{R}}_0(h_{12}\frac{J_0({\varphi }_3)}{{\varphi }_3}+h_{23}\frac{J_0({\varphi }_1)}{{\varphi }_1}+h_{31}\frac{J_0({\varphi }_2)}{{\varphi }_2})$$

$$\begin{gathered} \frac{\delta {\rho }_{0,c}}{{\rho }_{0,c}}={[{\left(\frac{\delta \mathit{\text{Im}}(S_3)}{\pi \ell \sigma }\right)}^2{(\frac{1}{a^2\text{sin}{\varphi }_{\mathit{\text{in}}}\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,c}}+\frac{C}{I}(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}}))}^2+{\left(\frac{\delta \mathit{\text{Re}}(S_3)}{\pi \ell \sigma }\right)}^2 \\ {(\frac{B}{I}(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}}))}^2+{\left(\frac{\delta (S_1-S_2)}{\pi \ell \sigma }\right)}^2{K}^2+{\left(\frac{\delta (S_3^{\prime }-S_3)}{\pi \ell \sigma }\right)}^2{L}^2+{\left(\frac{\delta (S_2-S_3^{\prime })}{\pi \ell \sigma }\right)}^2{M}^2 \\ +{(\delta \theta )}^2{(\frac{A}{I}(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})-g\text{sin}2\theta \text{cot}{\varphi }_{\mathit{\text{in}}}+2\text{cot}\theta )}^2]}^{1/2} \end{gathered}$$

where

$$K=\frac{D}{I}(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})+\frac{h_{23}}{J}$$

$$L=\frac{E}{I}(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})-\frac{h_{12}}{J}$$

$$M=\frac{F}{I}(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})-\frac{h_{12}}{J}$$

Appendix D. Uncertainty of susceptibility quantified from different images

The formulas here are suitable for unknowns quantified from different images. In addition, these formulas are particularly for cylinders with orientations larger than 30°. When the susceptibility is quantified from the shorter echo time with S₃, which is enclosed by the radius R₃, the uncertainty of the susceptibility is

$$\frac{\delta \mathrm{\Delta }\chi }{\mathrm{\Delta }\chi }=\frac{\sqrt{\delta {\theta }^2{A}^2+{\left(\frac{\delta \mathit{\text{Re}}(S_3)}{\pi \ell \sigma }\right)}^2{B}^2+{\left(\frac{\delta \mathit{\text{Im}}(S_3)}{\pi \ell \sigma }\right)}^2{C}^2+{\left(\frac{\delta \wp }{\wp }\right)}^2{D}^2+{\left(\frac{\delta (S_1-S_2)}{\pi \ell \sigma }\right)}^2{E}^2}}{|I|}$$

$$D=-|\wp |\mathrm{S}\mathrm{N}{\mathrm{R}}_0(\frac{J_0({\varphi }_3)}{{\varphi }_3}+\frac{h_3}{h_{12}}(\frac{J_0({\varphi }_2)}{{\varphi }_2}-\frac{J_0({\varphi }_1)}{{\varphi }_1}\left)\right)\text{sin}{\varphi }_{\mathit{\text{in}}}$$ (D.1)

$$E=\frac{h_3}{h_{12}}\text{sin}{\varphi }_{\mathit{\text{in}}}$$

$$\frac{\delta {\rho }_0}{{\rho }_0}=\frac{1}{h_{12}}{[{\left(\frac{1}{\wp \mathrm{S}\mathrm{N}{\mathrm{R}}_0}\right)}^2{\left(\frac{\delta (S_1-S_2)}{\pi \ell \sigma }\right)}^2+{(h_{12}+\frac{J_0({\varphi }_2)}{{\varphi }_2}-\frac{J_0({\varphi }_1)}{{\varphi }_1})}^2{\left(\frac{\delta \wp }{\wp }\right)}^2]}^{1/2}$$

where the uncertainty of ρ₀ here is quantified from the image acquired at the shorter echo time, with the choice of two concentric circles, R₁ and R₂.

$$\frac{\delta A_0}{A_0}={[{(\frac{A}{I}+2\text{cot}\theta )}^2\delta {\theta }^2+{\left(\frac{B}{I}\right)}^2{\left(\frac{\delta \mathit{\text{Re}}(S_3)}{\pi \ell \sigma }\right)}^2+{\left(\frac{C}{I}\right)}^2{\left(\frac{\delta \mathit{\text{Im}}(S_3)}{\pi \ell \sigma }\right)}^2+{\left(\frac{E}{I}\right)}^2{\left(\frac{\delta (S_1-S_2)}{\pi \ell \sigma }\right)}^2+{(1-\frac{D}{I})}^2{\left(\frac{\delta \wp }{\wp }\right)}^2]}^{1/2}$$

$$\frac{\delta {\rho }_{0,c}}{{\rho }_{0,c}}={[O^2{(\delta \theta )}^2+P^2{\left(\frac{\delta \mathit{\text{Im}}(S_3)}{\pi \ell \sigma }\right)}^2+Q^2{\left(\frac{\delta \mathit{\text{Re}}(S_3)}{\pi \ell \sigma }\right)}^2+R^2{\left(\frac{\delta \wp }{\wp }\right)}^2+S^2(\frac{\delta (S_1-S_2)}{\pi \ell \sigma }\left)\right]}^{1/2}$$

where

$$O=\frac{A}{I}(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})-g\text{sin}2\theta \text{cot}{\varphi }_{\mathit{\text{in}}}+2\text{cot}\theta$$

$$P=(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})\frac{C}{I}+\frac{1}{a^2\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,c}\text{sin}{\varphi }_{\mathit{\text{in}}}}$$

$$Q=(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})\frac{B}{I}$$

$$R=(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})\frac{D}{I}-1$$

$$S=(1-{\varphi }_{\mathit{\text{in}}}\text{cot}{\varphi }_{\mathit{\text{in}}})\frac{E}{I}$$

Appendix E. Uncertainty of susceptibility for cylinders at small orientations

We derive these uncertainties based on the variations of the susceptibility and cross-sectional area of a cylindrical object from images acquired at two echo times (Eq. (7)). In this Appendix, subscripts 1 and 2 in the following equations refer to the values quantified from echo time T_E1 and T_E2, respectively. If none of the phase values from either echo time is close to multiples of π, then these equations below lead to smaller and more realistic uncertainties than those given in the Appendix B of [15].

$$\begin{gathered} \frac{\delta \mathrm{\Delta }\chi }{\mathrm{\Delta }\chi }=\frac{1}{|𝔼|}{[{({𝔹}_2{𝔽}_1)}^2{\left(\frac{\delta \mathit{\text{Re}}(S_1)}{\pi \ell \sigma }\right)}^2+{({𝔹}_2{𝔾}_1)}^2{\left(\frac{\delta \mathit{\text{Im}}(S_1)}{\pi \ell \sigma }\right)}^2+{({𝔹}_2{𝔻}_1)}^2{\left(\frac{\delta {\rho }_{0,1}}{{\rho }_{0,1}}\right)}^2+{(\delta {\theta }_1)}^2{({𝔹}_2{ℂ}_1)}^2+{({𝔹}_1{𝔽}_2)}^2 \\ {\left(\frac{\delta \mathit{\text{Re}}(S_2)}{\pi \ell \sigma }\right)}^2+{({𝔹}_1{𝔾}_2)}^2{\left(\frac{\delta \mathit{\text{Im}}(S_2)}{\pi \ell \sigma }\right)}^2+{({𝔹}_1{𝔻}_2)}^2{\left(\frac{\delta {\rho }_{0,2}}{{\rho }_{0,2}}\right)}^2+{(\delta {\theta }_2)}^2{({𝔹}_1{ℂ}_2)}^2]}^{1/2} \end{gathered}$$

If the orientation of the object is measured only once from both echo times, the term (δθ₁)² (𝔹₂ℂ₁)² + (δθ₂)²(𝔹₁ℂ₂)² should be replaced by (δθ)²(𝔹₂ℂ₁−𝔹₁ℂ₂)² in the above uncertainty formula.

$${𝔸}_n={\varphi }_{\mathit{\text{in}},n}\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,c,n}+\frac{{g\prime }_n^2}{2}(1-\frac{a^2}{R^2})\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,n}\text{sin}{\varphi }_{\mathit{\text{in}},n}$$

$${𝔹}_n=(1+\frac{{g\prime }_n^2}{4}-\frac{{g\prime }_n^2{a}^2}{2R^2})\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,n}\text{sin}{\varphi }_{\mathit{\text{in}},n}$$

$${ℂ}_n=-a^2{g}_n\text{sin}2{\theta }_n(\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,c,n}+\frac{{g\prime }_n}{2}(1-\frac{a^2}{R^2}\left)\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,n}\text{sin}{\varphi }_{\mathit{\text{in}},n}\right)$$

$${𝔻}_n=(R^2-a^2)(1-\frac{{g\prime }_n^2{a}^2}{4R^2})\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,n}\text{sin}{\varphi }_{\mathit{\text{in}},n}$$

$$𝔼=a^2({𝔹}_2{𝔸}_1-{𝔹}_1{𝔸}_2)$$

$${𝔽}_n=-\text{sin}{\varphi }_{\mathit{\text{in}},n}$$

$${𝔾}_n=\text{cos}{\varphi }_{\mathit{\text{in}},n}$$

$$\frac{\delta \mathit{\text{Re}}(S_n)}{\pi \ell \sigma }=\sqrt{\frac{\mathrm{\Delta }x\mathrm{\Delta }y{R}^2}{\pi }+{\epsilon }_R^2{\left(\frac{\mathit{\text{Re}}(S_n)}{\pi \ell \sigma }\right)}^2}$$

$$\frac{\delta \mathit{\text{Im}}(S_n)}{\pi \ell \sigma }=\sqrt{\frac{\mathrm{\Delta }x\mathrm{\Delta }y{R}^2}{\pi }+{\epsilon }_I^2{\left(\frac{\mathit{\text{Im}}(S_n)}{\pi \ell \sigma }\right)}^2}$$

$$\frac{\delta {\rho }_{0,n}}{{\rho }_{0,n}}=\sqrt{\frac{\mathrm{\Delta }x\mathrm{\Delta }y}{\pi (R_a^2-R_b^2)\mathrm{S}\mathrm{N}{\mathrm{R}}_{0,n}^2}+{\epsilon }_{ab}^2}$$

where ε_ab is the percentage difference between the theoretical spin density and the measured spin density within the annular ring defined by radii R_a and R_b. The subscript n in ρ_0,n or ϕ_in,n refers to each variable obtained at the n^th echo time T_En.

$$\begin{gathered} \frac{\delta A_0}{A_0}=\frac{1}{|𝔼|}{[{({𝔸}_1{𝔾}_2)}^2{\left(\frac{\delta \mathit{\text{Im}}(S_2)}{\pi \ell \sigma }\right)}^2+{({𝔸}_2{𝔾}_1)}^2{\left(\frac{\delta \mathit{\text{Im}}(S_1)}{\pi \ell \sigma }\right)}^2+{({𝔸}_2{𝔽}_1)}^2{\left(\frac{\delta \mathit{\text{Re}}(S_1)}{\pi \ell \sigma }\right)}^2+{({𝔸}_1{𝔽}_2)}^2{\left(\frac{\delta \mathit{\text{Re}}(S_2)}{\pi \ell \sigma }\right)}^2 \\ +{({𝔸}_2{𝔻}_1)}^2{\left(\frac{\delta {\rho }_{0,1}}{{\rho }_{0,1}}\right)}^2+{({𝔸}_1{𝔻}_2)}^2{\left(\frac{\delta {\rho }_{0,2}}{{\rho }_{0,2}}\right)}^2+{(\delta {\theta }_1)}^2{({𝔸}_2{ℂ}_1)}^2+{(\delta {\theta }_2)}^2{({𝔸}_1{ℂ}_2)}^2]}^{1/2} \end{gathered}$$

If the orientation of the object is measured only once from both echo times, the term (δθ₁)²(𝔸₂ℂ₁)² + (δθ₂)²(𝔸₁ℂ₂)² should be replaced by (δθ)²(𝔸₂ℂ₁−𝔸₁ℂ₂)² in the above uncertainty formula.

$$\begin{gathered} \frac{\delta {\rho }_{0,c,n}}{{\rho }_{0,c,n}}={[{(\delta {\theta }_1)}^2{ℍ}^2+{\left(\frac{\delta {\rho }_{0,1}}{{\rho }_{0,1}}\right)}^2{𝕀}^2+{\left(\frac{\delta \mathit{\text{Re}}(S_1)}{\pi \ell \sigma }\right)}^2{𝕁}^2+{\left(\frac{\delta \mathit{\text{Im}}(S_1)}{\pi \ell \sigma }\right)}^2{𝕂}^2+{(\delta {\theta }_2)}^2{𝕃}^2+{\left(\frac{\delta {\rho }_{0,2}}{{\rho }_{0,2}}\right)}^2 \\ {𝕄}^2+{\left(\frac{\delta \mathit{\text{Re}}(S_2)}{\pi \ell \sigma }\right)}^2{\mathbb{N}}^2+{\left(\frac{\delta \mathit{\text{Im}}(S_2)}{\pi \ell \sigma }\right)}^2{𝕆}^2]}^{1/2} \end{gathered}$$

If the orientation of the object is measured only once from both echo times, the term (δθ₁)²(ℍ)² + (δθ₂)²(𝕃)² should be replaced by (δθ)²(ℍ + 𝕃)² in the above uncertainty formula.

$$ℍ=-{\delta }_{n,1}{g}_1\text{sin}2{\theta }_1\text{cot}{\varphi }_{\mathit{\text{in}},1}+({𝔸}_2-{𝔹}_2{\varphi }_{\mathit{\text{in}},n}\text{cot}{\varphi }_{\mathit{\text{in}},n})\frac{{ℂ}_1}{𝔼}$$

$$𝕃=-{\delta }_{n,2}{g}_2\text{sin}2{\theta }_2\text{cot}{\varphi }_{\mathit{\text{in}},2}-({𝔸}_1-{𝔹}_1{\varphi }_{\mathit{\text{in}},n}\text{cot}{\varphi }_{\mathit{\text{in}},n})\frac{{ℂ}_2}{𝔼}$$

where δ_n,1 and δ_n,2 are Kronecker delta functions. The subscript n refers to each variable measured at the n^th echo time T_En.

$$𝕀={𝔻}_1(\frac{{𝔸}_2}{𝔼}-\frac{{𝔹}_2}{𝔼}{\varphi }_{\mathit{\text{in}},n}\text{cot}{\varphi }_{\mathit{\text{in}},n})$$

$$𝕄=-{𝔻}_2(\frac{{𝔸}_1}{𝔼}-\frac{{𝔹}_1}{𝔼}{\varphi }_{\mathit{\text{in}},n}\text{cot}{\varphi }_{\mathit{\text{in}},n})$$

$$𝕁=({𝔸}_2-{𝔹}_2{\varphi }_{\mathit{\text{in}},n}\text{cot}{\varphi }_{\mathit{\text{in}},n})\frac{{𝔽}_1}{𝔼}$$

$$\mathbb{N}=(-{𝔸}_1+{𝔹}_1{\varphi }_{\mathit{\text{in}},n}\text{cot}{\varphi }_{\mathit{\text{in}},n})\frac{{𝔽}_2}{𝔼}$$

$$𝕂=\frac{{\delta }_{n,1}}{a^2\mathrm{S}\mathrm{N}{\mathrm{R}}_{o,c,1}\text{sin}{\varphi }_{\mathit{\text{in}},1}}+({𝔸}_2-{𝔹}_2{\varphi }_{\mathit{\text{in}},n}\text{cot}{\varphi }_{\mathit{\text{in}},n})\frac{{𝔾}_1}{𝔼}$$

$$𝕆=\frac{{\delta }_{n,2}}{a^2\mathrm{S}\mathrm{N}{\mathrm{R}}_{o,c,2}\text{sin}{\varphi }_{\mathit{\text{in}},2}}-({𝔸}_1-{𝔹}_1{\varphi }_{\mathit{\text{in}},n}\text{cot}{\varphi }_{\mathit{\text{in}},n})\frac{{𝔾}_2}{𝔼}$$