Comparison of Normalization Algorithms for Cross-Batch Color Segmentation of Histopathological Images

Abstract

Automated processing of digital histopathology slides has the potential to streamline patient care and provide new tools for cancer classification and grading. Before automatic analysis is possible, quality control procedures are applied to ensure that each image can be read consistently. One important quality control step is color normalization of the slide image, which adjusts for color variances (batch-effects) caused by differences in stain preparation and image acquisition equipment. Color batch-effects affect color-based features and reduce the performance of supervised color segmentation algorithms on images acquired separately. To identify an optimal normalization technique for histopathological color segmentation applications, five color normalization algorithms were compared in this study using 204 images from four image batches. Among the normalization methods, two global color normalization methods normalized colors from all stain simultaneously and three stain color normalization methods normalized colors from individual stains extracted using color deconvolution. Stain color normalization methods performed significantly better than global color normalization methods in 11 of 12 cross-batch experiments (p<0.05). Specifically, the stain color normalization method using k-means clustering was found to be the best choice because of high stain segmentation accuracy and low computational complexity.

Introduction

Histopathology is an integral part of the detection, monitoring, and research of cancer. Digital histopathology slides, also known as whole-slide images (WSIs), are a modern, high-resolution tool to store the information from a tissue sample fixed on a glass slide for later analysis. WSIs have uses in training, healthcare record management, and telemedicine [1]. The availability of large, public banks of WSIs such as the Cancer Genome Atlas (TCGA) has created a growing area of research devoted to the automated analysis of these images [2]. Reliable, accurate, and automatic processing of WSIs has the potential to cut costs, improve patient outcomes, and take modern pathology into environments not previously possible [3].

Before useful automated processing, digital histopathology slides must undergo a number of quality control steps. These quality control steps ensure that no artifacts or technical variations, created during image acquisition, affect the biological data and the performance of image analysis and machine learning algorithms. Due to the great variability that exists between slides processed using different equipment or reagents, color normalization, which will normalize colors across batches, is a vital quality control step in the slide analysis process [4].

Tissue samples are stained to highlight different cellular structures. For instance, in the most common slide staining for histopathology—H&E or hematoxylin and eosin—hematoxylin stains nuclear structures purple or blue, and eosin stains cytoplasmic structures pink. Analysis of WSIs often requires that the contributions from these two stains be extracted and considered separately. For example, nuclear segmentation algorithms may begin by identifying high concentrations of hematoxylin. The shape and texture features of the isolated stain channels have been shown to have diagnostic value in classification problems. Accurate normalization is thus a necessary first step for extracting any features based on color, texture, or stain segmentation. In this paper, the role of color normalization methods in a supervised stain segmentation pipeline is studied.

Researchers have previously studied color normalization methods for histopathological images [4–6]. Among the published research, there are two categories of methods: global color normalization that normalizes colors of all pixels irrespective of their stain and stain color normalization that separates stains and then normalizes each stain individually. The latter category would be ideal if the stains could be separated accurately. However, unsupervised stain segmentation of histopathological images is often not straightforward. Kothari et al. proposed two global color normalization methods that normalize images using quantile normalization of all pixels in the RGB color space and the quantile normalization of the unique color map [4]. Magee et al. proposed a stain color normalization method that roughly separates stains using color deconvolution and clustering and then normalizes each stain individually using Reinhard’s method [6, 7]. In their study, Magee et al. used a variational Bayesian Gaussian mixture model to cluster the areas where each stain is present in deconvolved images and compared original and normalized colors after normalization rather than comparing segmentation performance. However, variational Bayesian methods are computationally complex. Thus, in this study, two additional stain normalization procedures are developed that use the less complex k-means clustering and expectation-maximization methods to identify stain classes, rather than variational Bayesian methods.

In summary, a quantitative comparison of the impact of five normalization algorithms, two global normalization and three stain color normalization methods, on color segmentation performance is presented in this paper.

Methods

Data

Manually curated portions of digital histopathology slides from four separately acquired image batches are used in this study. Two image batches/datasets, ovarian serious adenocarcinoma (OV) and glioblastoma multiforme (GBM), are from The Cancer Genome Atlas (TCGA). Images in these datasets are cropped sections of 1024×1024 pixels. The other two datasets, renal cell carcinoma (RCC1 & RCC2), were acquired at Emory University. Images in renal datasets are cropped sections of 1600×1200 pixels. In total, 204 images are considered, out of which 50 were derived from OV samples, 52 from GBM, 55 from RCC1, and 47 from RCC2.

Ground truth segmentation for all images is obtained using an interactive system, where an experienced user selected sample pixels belonging to one of the four classes: hematoxylin, eosin, erythrocyte, and stain-free regions. Thereafter, a All the image pixels were grouped into one of the four classes based on their Euclidian distance to selected pixels. These ground truth labels are used for training segmentation classifiers and evaluating segmentation performance.

B. Color Normalization Algorithms

Color normalization methods affect the value of color features and performance of color segmentation algorithms. In this paper, performance of color segmentation using five candidate normalization algorithms (as outlined in Fig. 1) is studied. Previous work published color segmentation results using two global color normalization methods: all pixel and color map normalization, and as such, it is used here as a control [4]. The three other methods are derived from the color normalization methods published in [6, 7]. These methods use stain deconvolution as a first step, splitting the sample image into separate channels for hematoxylin and eosin staining. Three different clustering algorithms are then applied to segment those channels into stain is present / is not present regions. After normalizing different stains in a sample image to stains in a reference image, sample image stains are convolved to produce a normalized sample image.

Figure 1.

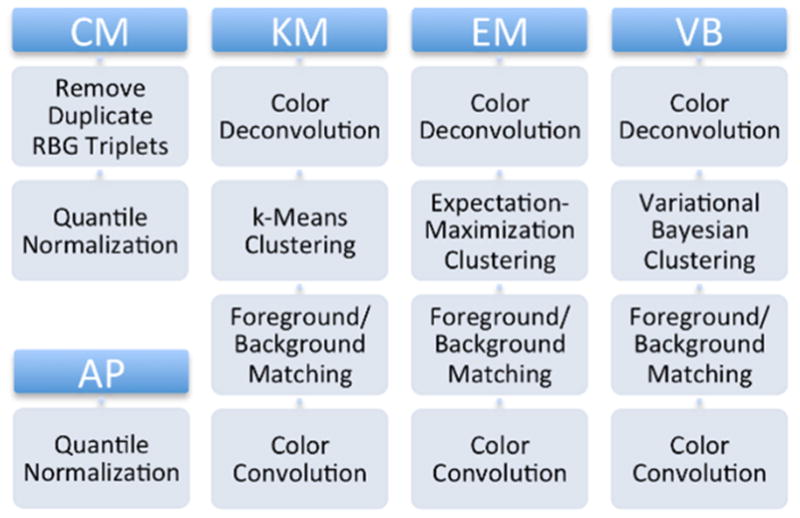
Normalization algorithm candidates. All five candidate algorithms are compared.

Global Color Normalization

All-pixel quantile normalization performs simple quantile normalization of the red (R), green (G), and blue (B) color channel intensity distributions from the sample image to a reference image [4]. In quantile normalization, the largest value from the sample is replaced by the largest value from the reference, the second largest sample value by the second largest reference value, etc. The color distributions of the quantile normalized sample image will then share important statistical properties such as the mean and variance with the color distributions of the reference image.

In color map normalization, a color map is first constructed for the reference image by creating a list of every unique RGB triplet that occurs within the image [4]. This process is repeated with the target image to create its color map. Quantile normalization is then used to normalize individual color channel distributions for the sample color map to the color channel distributions of the reference color map.

Stain Color Normalization

Stain color normalization normalizes each stain separately using the following steps: (1) stain separation, (2) clustering, (3) multimodal color deconvolution (CVD-MM) [5] normalization [5], and (4) stain combination.

Stain Separation

First, the RGB image I produced over the background I0 is broken down into channels representing the contribution from each stain A. This is accomplished using a fixed optical density matrix Q based on the nominal color of each stain: hematoxylin and eosin [5, 8].

$$Q=\left[\begin{array}{ccc}0.65& 0.704& 0.285\\ 0.072& 0.990& 0.105\\ 0.6218& 0& 0.7831\end{array}\right],A={\mathit{log}}_{10}\left(\frac{I}{I_0}\right)Q^{-1}$$

Clustering

Color deconvolution returns grayscale images corresponding to each stain, where intensity at each pixel represents stain intensity. Pixels may have some intensity in each stain channel for one or all stains. Various clustering methods are employed to separate the foreground (strong staining) and background (weak staining) classes for each stain. The three clustering algorithms are employed and compared in this study are k-means, expectation-maximization for a Gaussian mixture, and variational Bayesian inference for a Gaussian mixture. All three clustering techniques were run with the number of classes constrained at k=2.

The k-means algorithm randomly chooses two cluster centers, adds each of the observations to the nearest of those clusters, then updates the cluster center and iterates until it converges to a final solution when the cluster assignments no longer change between iterations [9]. In this implementation, Euclidian distances to cluster centers are used.

The expectation-maximization algorithm used in this study works by estimating the mean and variance parameters of a mixture of two Gaussian distributions that fit the data. The expectation-maximization process consists of two steps. First, the probability that each observation falls into each distribution is determined and, then each observation is assigned a preliminary class based on its the highest probability. The next step assumes that the classes labels assigned in the first are all true, and generates new parameters to best fit those classes. The expectation-maximization EM algorithm used in this study is specifically fitting a Gaussian mixture model, rather than optimizing Euclidian distances to cluster centers as in k-means.

Rather than finding an approximation of the posterior distribution as in expectation-maximization algorithms, the variational Bayesian method attempts to estimate the posterior distribution for all unknown variables [10]. The main difference between variational Bayesian and expectation-maximization is that variational Bayesian calculates the probable distributions of the variables, rather than estimatinges the parameter values (such as Gaussian mixture means) directly. Like expectation-maximization, the variational Bayesian was used with a two Gaussian model.

Fig. 2 shows the color deconvolution and clustering processes for a sample image from RCC1, where the image is first broken down into hematoxylin and eosin “channels” and then foreground and background is clustered before foreground and background clustering.

Figure 2.

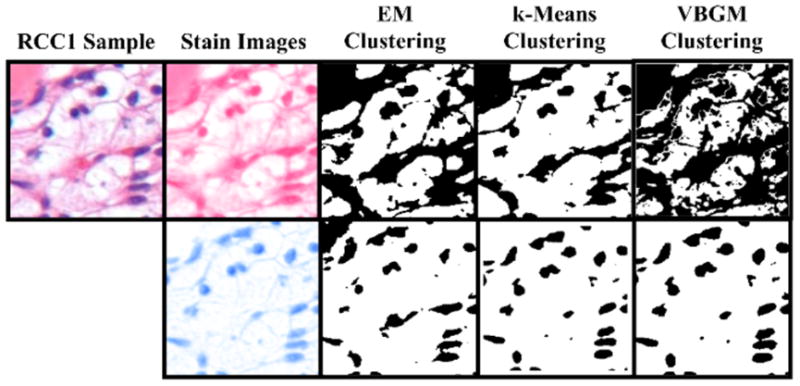
Clustering comparison. A sample image from the RCC1 data set is segmented into hematoxylin and eosin channels. These channels are then separated into foreground (strong staining) background (weak staining) clusters by each of three clustering algorithms.

CVD-MM normalization

A similar deconvolution and clustering takes place for both sample and reference images. Once this is done, the clusters of the sample image are normalized to match the mean and variance of those clusters found in the reference image by the CVD-MM method described by Magee et al. [5], which is conceptually similar to Reinhard’s method [7] implemented in a stain-specific color space.

Reference Gaussian distributions are generated using the means and standard deviations from the clustering step. Background and foreground weights are calculated at each pixel by linear interpolation of the reference Gaussian distributions. A separate saturated-pixel weight is defined such that near-white pixels will not be significantly changed. These weights and reference distributions are combined to yield a normalized stain component pixel [5].

Stain Combination

The normalized stain-domain image is then converted back to the RBG color space using color convolution, in an inverse operation of the deconvolution performed in step (a).

E. Stain Segmentation

Images are segmented using a four-step, supervised color segmentation system [4]. First, a test image is normalized to a standard reference image using one of the five color normalization methods, discussed in the previous section. Second, every pixel in the test image based on its RGB color values is classified as one the of four tissue classes using a supervised classifier. The system uses a 4-class linear discriminant (LDA) classifier, which is trained using ground truth labels and RGB colors values of the reference image. The four tissue classes refer to the hematoxylin, eosin, erythrocyte, and stain-free regions of the image. The first and second steps are repeated with ten different references resulting in ten slightly different segmentations. Ten top references are selected from the same batch using internal cross-validation. More details on cross-validation and validation are described in the next section. Third, the segmentation labels are combined for each pixel using max-voting. Because images have been are segmented in the normalized color space, decision planes for each segmented tissue class are non-uniform may be irregular when transformed into in the original color space. Therefore, in the fourth step Therefore, to refine the segmentation in the original color space, image segmentation is refined by a classifier is trained using the image’s segmentation labels in from the third step and the image’s original RGB color values [4].

F. Validation

The normalization methods are compared using the performance of the color segmentation system, when images are normalized with any method in the first step. The performance is assessed for each binary combination of four batches, where one batch is the train set while another is the test set. In total, 12 cross-batch combinations are assessed during the validation process.

The performance of normalization methods and classifier model depends on the selection of reference images. Therefore, multiple images are selected to avoid bias due to the selection of any single reference image. Cross-validation within a batch is used to select the top ten references for a batch. First, each image within the data set is used as a reference to normalize and segment all of the other images, after which the mean stain segmentation accuracy is recorded. This is repeated for all members of a data set, after which the 10 highest scoring images are saved as the reference set for that batch.

Results and Discussion

Table 1 lists the mean and standard deviation of the segmentation accuracy using two global color normalization methods—all pixel (AP) and color map (CM)— and four stain color normalization methods—k-means (KM), expectation-maximization (EM), and variational Bayesian inference (VB)—for all cross-batch experiments. As reported in previous work as well, among global color normalization methods, CM performs better than AP [4]. However, in most cases stain color normalization methods outperform global color normalization methods. This was expected because stain color normalization normalized each stain separately and prevents color intermixing between stains. To more statistically compare these methods, Student’s t-test was performed between the performances using different normalization methods within each test case, i.e., a train and test batch combination. The following can be concluded based on t-test p-values: (1) There is no statistical difference between stain color normalization methods (KM, EM, and VB) using different clustering methods, (2) In all but one case (RCC2 train set and RCC1 test set), CM performs statistically better than or equivalent to AP, and (2) In all but one case (OV train set and RCC2 test set), KM performs statistically better than or equivalent to CM. Statistical significance was established using p<0.05. Fig. 3 illustrates qualitative differences in the segmentation masks generated by the KM, EM, and VB algorithms.

Figure 3.

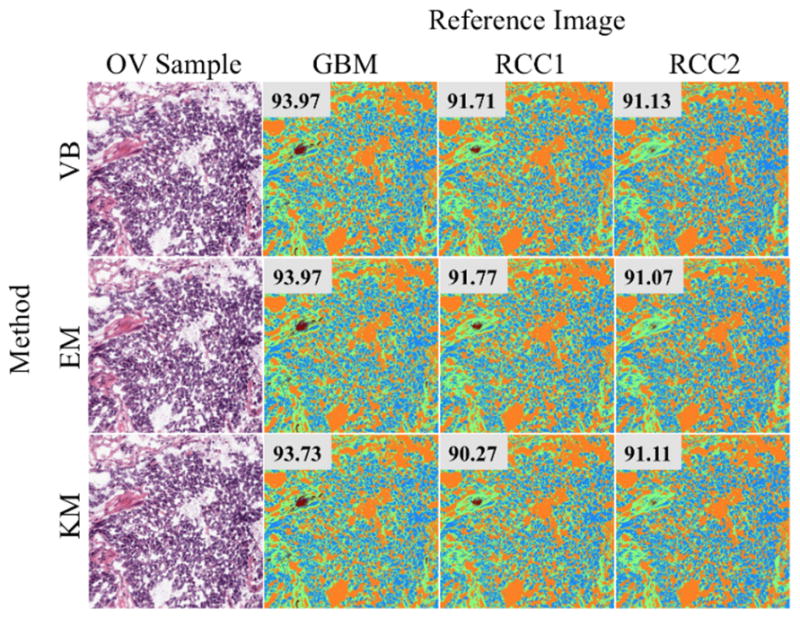
Segmentation accuracy results for a single sample. A single OV sample (left column) is segmented after normalization using three different algorithms (rows) against three different references (columns). Color segmentation accuracy is shown in the top-right of each segmented color map.

Although there was no significant difference in the performance using either of the stain color normalization methods, there was a significant difference in computational complexity between the KM, EM, and VB clustering methods. To quantify the differences in performance between these three algorithms, a single standardized sample from the RCC1 data set was normalized against 10 randomly selected reference images, and the total time elapsed was recorded. The results are reported in Table 3. KM was the fastest, with 10 normalizations taking only 29.28 seconds. It was found to be approximately 6.5x faster than the EM procedure and over 17x faster than VB. Thus, based on our experiments, KM is clearly the ideal choice because it performs better or equivalent to global normalization methods and it is fastest among stain color normalization methods.

Table 3.

Performance comparison for KM, EM, and VB

Method	N	Time (s)
KM	10	29.28
EM	10	190.87
VB	10	511.80

Conclusion

Color normalization is an important quality control step for histopathological images to insure accurate downstream processing of these images. In this work, based on the performance of color segmentation system, five color normalization methods were compared. Among these methods, three methods were previously published but two were novel extensions of an existing method. One of our novel extensions using k-means clustering was found to be the optimal normalization algorithm based on high segmentation accuracy and low computational time. This preliminary study used only four batches of manually curated images. In future work, this work would be extended by evaluating several other normalization methods on more image batches and complete whole-slide images.

Table 2.

Average stain segmentation accuracy using color deconvolution normalization (KM, EM, and VB) and quantile normalization (AP and CM) methods.

	Testing	OV	GBM	RCC1	RCC2
Training	Method	Mean	Mean	Mean	Mean
OV	KM		83 ± 7.2	91 ± 6.4	80 ± 12.6
	EM		83 ± 7.1	91 ± 6.4	80 ± 12.6
	VB		83 ± 7.2	90 ± 6.5	80 ± 12.6
	AP		80 ± 11.1	78 ± 9.4	74 ± 9.2
	CM		85 ± 7.0	87 ± 7.9	84 ± 5.9
GBM	KM	94 ± 6.5		92 ± 7.6	84 ± 10.0
	EM	94 ± 6.5		93 ± 7.5	84 ± 10.0
	VB	94 ± 6.5		92 ± 7.5	85 ± 10.0
	AP	83 ± 7.2		84 ± 6.2	80 ± 7.6
	CM	87 ± 5.8		87 ± 5.5	83 ± 6.1
RCC1	KM	92 ± 4.2	87 ± 6.7		91 ± 6.8
	EM	92 ± 4.2	87 ± 6.7		91 ± 6.8
	VB	92 ± 4.2	85 ± 7.0		91 ± 6.8
	AP	83 ± 7.8	85 ± 7.9		82 ± 7.5
	CM	81 ± 8.9	82 ± 9.2		82 ± 7.3
RCC2	KM	91 ± 4.5	87 ± 6.5	96 ± 9.2
	EM	91 ± 4.5	87 ± 6.5	96 ± 9.2
	VB	91 ± 4.5	87 ± 6.7	95 ± 9.3
	AP	85 ± 7.0	84 ± 8.4	88 ± 6.0
	CM	87 ± 5.2	87 ± 7.5	84 ± 11.4

Performance of KM methods are highlighted in bold red where either (1) performance is significantly better than all other methods for the particular test case, or (2) performance is not significantly different from any other methods. (Student’s t-tests, p-value<0.05).