Abstract
Although the Papanicolaou smear has been successful in decreasing cervical cancer incidence in the developed world, there exist many challenges for implementation in the developing world. Quantitative cytology, a semi-automated method that quantifies cellular image features, is a promising screening test candidate. The nested structure of its data (measurements of multiple cells within a patient) provides challenges to the usual classification problem. Here we perform a comparative study of three main approaches for problems with this general data structure: a) extract patient-level features from the cell-level data; b) use a statistical model that accounts for the hierarchical data structure; and c) classify at the cellular level and use an ad hoc approach to classify at the patient level. We apply these methods to a dataset of 1,728 patients, with an average of 2,600 cells collected per patient and 133 features measured per cell, predicting whether a patient had a positive biopsy result. The best approach we found was to classify at the cellular level and count the number of cells that had a posterior probability greater than a threshold value, with estimated 61% sensitivity and 89% specificity on independent data. Recent statistical learning developments allowed us to achieve high accuracy.
Keywords: cross-validation, DNA ploidy, L1-regularized logistic regression, multilevel classification, quantitative cytology, variable selection
1. INTRODUCTION
The problem treated here may be described as classification of a population given data from a random sample of members and hence could be considered a classification problem using hierarchical data. In our context, the “population” is a patient, and we have measurements on a sample of cells from the patient. More specifically, we want to predict if a patient has cervical neoplasia (cancer or pre-cancer) given quantitative measurements on cells collected by a cervical brushing similar to a Papanicolaou (Pap) smear. Other examples of these types of problems are classifying measurements of cell nuclei from fine needle aspirates to diagnose breast cancer [1], measurements of brushing of cells or mouthwashes for patient diagnosis of oral cancer and periodontal pathogens [2–4], and flow cytometric measurements [5].
We present here a review of new and existing methods for this type of problem and an empirical comparative study of these methods as applied to our specific example. There are three general categories of methods considered. The first one involves producing patient level features from the cell level data, e.g. by summary statistics. For example, one could compute moments of the cell level variables and plug those patient level features into a classification algorithm. The second general approach is to develop a statistical model for the cell level data, and using Bayes theorem or some other method to produce a patient level prediction such as a posterior probability of disease. The third category involves classification at the cell level, and then using some method to predict at the patient level; for example, predict that the patient has disease if the number of cells classified as precancerous is above a threshold. Note that this approach requires cell level ground truth in order to learn the classifier at the cell level. In our data, we do have cell classes obtained by laborious examination of numerous individual cells. These three general categories are not meant to be mutually exclusive and exhaustive – some methods may rightly be considered to belong to more than one of the categories, and new methods may be developed which don’t belong to any.
In the case study presented here, we report on the application of 21 methods from these three categories, including some novel statistical approaches. We use a dataset of 1,728 patients with an average of 2,600 cells per patient (range 30–6,258). The cell level data are produced by a high-resolution automated image cytometer, which consists of an image processing system connected to a microscope. The system produces 104 cell level features for each individual cell that is measured. The objective is to produce a patient level diagnosis that would be used in cervical cancer screening, as the Pap smear is used now for this purpose.
This manuscript is organized as follows. In Section 2.1, we present more details on our application, including some biological motivation for giving special consideration for some of the cell level features. In Section 2.2–2.8, we present the algorithms used in the comparative study, organized according to the three categories introduced above. Section 3 presents the results of our comparative study with an emphasis on finding the most accurate predictor for our specific problem. The discussion section is a summary of our findings to the specific application, and presents some more general discussion of this class of problems.
2. METHODS
2.1 Overview of study procedures
Our specific objective was to develop an automated algorithm for the diagnosis of high-grade pre-cancer (cervical intraepithelial neoplasia [CIN]) or cancer. Thus, we identified a patient as “positive for high-grade CIN” if her cervical tissue had a histological grade of high-grade lesion or worse, including a histology reading of CIN 2, CIN 3, carcinoma in situ, or invasive cancer. A patient was classified as "negative for high-grade CIN” if her cervical tissue had a histological grade that indicated low-grade disease or normal (CIN 1, human papilloma virus [HPV]-related changes, inflammation, atypia, or normal). The study design has been described in the literature [6–8]. Briefly, the patients entered the study in one of two possible categories: patients that never had an abnormal Pap smear (screening patients), and patients who had a history of an abnormal Pap smear (diagnostic patients). High-grade CIN was much more prevalent in the diagnostic than in the screening patients (29% versus 2%).
There were 1,850 total patients in our study, of which 1,728 are included in our analysis. Patients were excluded if the corresponding cytology diagnosis or histology diagnosis was not available. The consensus diagnosis of the patient's histology was regarded as our referent standard. A patient's histology was defined to be the worst histologic grade assigned to any of her biopsy samples [9]. We sought to predict the dichotomized histologic grade (histological grade of high-grade CIN or worse versus low-grade CIN or normal) using information obtained from quantitative cytology.
Details of the quantitative cytology procedures are described in [6,10]. Briefly, the Cytosavant system first acquired images of Feulgen-Thionin stained cells on a slide [11,12]. The cell nucleus images were then segmented and separated to create an individual image for each nucleus [13]. A mask was then created for each nucleus image in order to extract 133 features for each cell [14], generally motivated by known biological changes that take place in the cell in its progression toward cancer. The image processing is only meant to be applied to images of separate single cells. Based on training data sets from previous studies, decision trees were used to sort cell objects into three groups: normal, abnormal, and clumps of cells or debris, which were then confirmed by a cytotechnologist [15]. Only images of individual cells were used in our analyses. Some algorithms used pre-selected variables while others used all 104 features as candidate variables.
2.2 Development of an algorithm for cell classification using quantitative cytology
In the process of selecting the best classifier, a problem may result from the selection of a classifier that is over-trained, that is, it works well on the data set that it was trained on but poorly on an independent data set. A popular solution is to use cross-validation to obtain unbiased estimates of the classifier's performance. We divided the data into three sets: training, validation, and test sets [16]. We chose to randomly sample proportions of 40%, 30%, and 30% for these three data sets, respectively, stratified by the histologic grade. The training set was used to estimate the parameters of a classifier, either by using the whole training set to fit models with no “free” parameters (e.g., logistic regression) or by using 5-fold cross-validation within the training set to choose the model parameters (e.g., the penalization parameter of L1-regularized logistic regression). The validation set was used to obtain estimates of the trained classifier's performance using the parameters estimated from the training set and to select a classifier to apply to the test set. The test set was used to obtain an unbiased estimate of the chosen classifier's performance, re-estimating the classifier’s parameters (since the chosen algorithm had “free” parameters) using 5-fold cross-validation within the combined training and validation sets [16].
We compared all of the methods to the sensitivity and specificity of the Pap smear in the following way. The Pap smear is estimated to have 55% sensitivity and 90% specificity from our validation set (we use the validation data results since we compared the classification methods on this data set). This is consistent with estimates by [6]. The Pap smear sensitivity and specificity varies considerably by setting, with reported sensitivities as low as 20% and as high as 77% [17,18]. Our comparison was based on a population of cancer center providers and thus we expect the comparison to be even more favorable than in a developing country and low-resource settings.
To compare the algorithms, we used receiver operating characteristic (ROC) curve analysis. The main comparison to the Pap smear was performed by computing the sensitivity corresponding to a 90% specificity and comparing the sensitivities among the algorithms. Confidence intervals for proportions were estimated using the normal approximation to the binomial distribution. The area under the ROC curve (AUC), a commonly used summary statistic, summarizes the information over areas of the ROC curve that are clinically unimportant, such as areas with low specificity. A screening test with low specificity for a low-prevalence disease would potentially lead to many unnecessary treatments. To focus on areas of clinical relevance, we calculated the area under a part of the ROC curve. The partial AUC (pAUC) is defined to be the area within the curve between a defined interval of either sensitivity or specificity, discussed in [19]. We identified the area of interest to be between 80% and 100% specificity and used the pAUC to further compare the methods. We averaged the pAUC over the interval by dividing by the length of the interval (thus, the averaged pAUC is equal to pAUC/0.2) and estimated the confidence intervals using bootstrap samples. The averaged pAUC is 1.0 for a perfect test and 0.1 for an uninformative test.
2.3 Feature extraction
A simple and intuitive way of dealing with multilevel data is to summarize the data at the macro level. For example, we may find the means and variances for the cell-level features for each patient and then use those as features to classify at the macro level. Standard classification procedures can be applied to the patient-level feature vector since both the features and the patient biopsy results are at the same level. Summary features may not capture potentially important information about the macro-unit distribution. In our example, the DNA Index is usually bimodal so some potentially important information will be lost if one simply computes the mean and variance. The bimodality features can be captured using a normal mixture model with two modes. Thus, the success of this approach can depend critically on which macro-level features are computed.
To obtain the patient-level features for this class of problem, we (1) calculated summary statistics per patient on the cellular variables, and (2) fit normal mixture models to the cell distribution within a patient, using the parameters of the model as patient-level features [20]. Summary statistics included the mean, standard deviation, skewness, and kurtosis of each variable. Most of the cells within a patient, regardless of the patient’s disease status, are normal cells. There are also some cells that are undergoing cell division at any given time.
The variable DNA Index, which provides an approximate measure of the amount of nuclear DNA in the cells, is one of the most widely used features in quantitative cytology research. The DNA Index may indicate whether the cell is normal (DNA Index is approximately 1), cycling (DNA Index is approximately 2), or potentially abnormal. For the DNA Index, we summarized the distribution using model-based clustering (Mclust function in R) to fit a mixture of Gaussian distributions to each patient with two Gaussian components [20]. One component was fit around DNA Index 1 to represent the normal cells in the sample (with two sets of chromosomes) and another component around DNA Index 2 to represent the cycling or potentially abnormal tetraploid cells (with four sets of chromosomes). The five patient-level features are thus the mean, standard deviation, and weight of the first component and the mean and standard deviation of the second component. In situations where the distribution of the variable has more than two modes or is very skewed, more complicated techniques can be used.
We applied a variety of classification algorithms to the patient-level features, including classification and regression trees (CART), random forests (with 4,000 trees), support vector machines (SVM), K-nearest-neighbors, logistic regression, L1-regularized logistic regression, elastic-net regularized logistic regression, linear discriminant analysis, lasso, ridge regression [16], and regularized linear discriminant analysis using a lasso penalty [21]. For regularization methods, the data were scaled to have mean zero and variance one on the training set so that the L1 and L2 penalty terms were not dominated by features with large relative variance. The training set mean and variance parameters were used to scale the validation and test sets.
2.4 Statistical model
We applied novel statistical models that were developed to account for the nested structure of the data. The cumulative log-odds (CLO) method assumes that given the disease state, the cellular measurements share an identical distribution and are independent of each other, modeled by the posterior log-odds of disease [22]. An extension of this method relaxes the assumption, allowing for heterogeneity of the distributions of the data within a disease state [23]. These methods are briefly described here.
The CLO method assumes that, conditional on the class, the cell feature vectors from the same patient are independent and identically distributed (i.i.d.). Let Y ∈ {0,1} be the binary indicator of the true class of the patient, respectively representing negative and positive for high-grade CIN. Let Si = {xi1, xi2, …, xini} be the unordered ni-tuplet feature vectors measured on the ni cells from patient i, where ni is assumed to be noninformative. The x can be univariate or multivariate features measured on each cell. Si is a vector of variable dimension of the patients’ cell-level measurements. Note that the cells are a sample from the large population of cervical cells in a patient. Let π1 = P(Y = 1) denote the prior probability (prevalence) of class 1 at the patient level and let f (Si|Y = 1) denote the conditional distribution of the feature vector given the class (Y = 1). Let π(Si) = {π1 f (Si|Y = 1)}/{π1 f (Si|Y = 1) + (1 − π1) f (Si|Y = 1) denote the posterior probability of class 1 at the patient level given the cellular features. Thus, the posterior log-odds of class 1 is where the f (xij|Y) are determined using kernel density estimates. This is referred to as the CLO 1 method. This can be rewritten in terms of the cell-level probabilities: . Here, Pr(Y = 1|xij) are the cell-level probabilities and Pr(Y = 1) is the cell-level prior probability of class 1, or the probability that a cell comes from a patient in class 1. We refer to this reformulation as the CLO 2 method.
The extension of the CLO 1 method assumes the existence of an unobserved latent variable U, and that the features are i.i.d. given the class and the latent variable (Yamal et al., 2011). Thus, the log-odds of having the disease given the feature vector is
The latent classes are estimated using K-means clustering [16] of the patient-specific kernel density estimates along a fixed grid. The clustering is used to find the patients that have similar DNA Index distributions; hence, where the CLO method assumption is more likely to hold. Given the estimated latent classes, f (x|u, Y) is estimated for each latent class u and disease state Y using the kernel density estimate of the pooled cells for all patients in that cluster. More details are given in [23].
2.5 Micro-level classification
Our third approach was to perform cell-level classification, and then use the cell-level posterior probabilities in order to conduct classification at the patient level. This method was motivated by clinical pathologists’ search for abnormal cells – if an abnormal cell is found, the pathologist will diagnose the patient as having a disease. A similar simple automated method is the ploidy method of counting the number of cells within a patient that have a DNA Index value greater than 2.5 (hence, are probably abnormal) and using that to conduct the patient classification [6]. The more general class of approaches is to perform the micro-level classification based on more features than DNA Index and various classification methodologies, and then use that information to conduct macro-level classification. For example, one can compute the percentage of the cells that were classified as abnormal and then create a threshold for the patient to be classified as “abnormal” or not. It is important to note that the outcome at the micro level does not have to be the same outcome as the macro-level outcome.
In order to conduct classification at the cellular level, it is necessary to obtain a “ground truth” at the cellular level. We first estimated the cell posterior probability by using the cell’s classification of whether it was an abnormal cell or a negative (including benign and cycling) cell. This classification of cells into abnormal or negative groups was done in the following way. Cells were classified as being negative if their DNA Index was lower than 1.2 to reduce the time that cytotechnologists and cytopathologists reviewed the slides and because most of these cells are likely negative. Cells with a DNA Index between 1.2 and 1.5 were systematically reviewed by an experienced cytotechnologist to classify them into either the abnormal or negative group although none were classified as abnormal. Similarly, cells with a DNA Index higher than 1.5 were reviewed by an experienced cytopathologist to confirm truly abnormal cells.
To train classification algorithms for micro-level classification, we used a subset of the data with cells with a DNA Index value greater than 1.5; although all cells were used in the predictions. This served the purpose of reducing our data set to something more computationally manageable as well as not focusing on the cells that could be automatically classified as being negative anyway at the cellular level. However, these cells may have discriminatory information at the patient level, especially among features other than DNA Index, so we included them in the predictions. There were 53,163 negative cells and 4,004 abnormal cells in this subset of our training data. The estimation of the cell posterior probability was done using random forests (with 4,000 trees), K-nearest-neighbors, elastic-net regularized logistic regression, CART, linear discriminant analysis, regularized discriminant analysis, logistic regression (with and without stepwise variable selection), and L1-regularized logistic regression. Once we had an estimate of the posterior probability of a cell being abnormal, we derived a patient-level feature using the count of cells with a posterior probability above varying thresholds.
We present more details on the L1-regularized logistic regression, elastic-net regularized logistic regression, and CART because these were the most accurate algorithms.
2.6 L1-regularized logistic regression
In logistic regression, the logit transformation of the conditional mean of y given x is modeled using a linear equation: . The model is usually fit using maximum likelihood. L1-regularized logistic regression puts a penalty on the sum of the absolute values of the coefficients: [24]. The λ parameter was estimated using 5-fold cross-validation on the training set.
2.7 The elastic net
The elastic net classifier is a regularization method that performs both regression and variable selection [25]. In contrast to L1-regularized logistic regression which has a penalty term for the sum of the first norm, the elastic-net regularized logistic regression’s penalty term is a weighted sum of the first and second norms: , where 0 ≤ α ≤ 1 is chosen via cross-validation, and |·|1 and |·|2 denote the first and second norms, respectively. The advantage of the elastic net is that it can shrink coefficients down to 0 as (1 − α) increases, effectively performing variable selection, while still encouraging a grouping of correlated variables to have either zero or nonzero coefficients.
The parameters of the elastic net were chosen by searching on a grid of the parameters (11 equally spaced points between 0 and 1 for α; λ ∈ {0, 0.01, 0.1, 1, 10, 100}) and choosing the parameters that had the largest sensitivity for 90% specificity using 5-fold cross-validation of the training data.
2.8 CART
Classification trees partition the feature space into a set of rectangles where we model the response as a constant cm in each region for m = 1, …, M regions [26]. The space is first split into two regions where the mean of y is estimated in each of the regions. The split is found by looking at all possible splits on all variables and finding the split based on the Gini index. Each region Rm with Nm observations is represented by a node m in the tree. The proportion of class k observations in node m is given by p̂mk = 1/(Nm) ∑xi∈Rm I{yi = k}, for k = 0, 1. Observations are classified in node m to class maxk p̂mk, the majority class of the observations in the training data.
2.9 Software
Statistical analysis was performed using the statistical package R version 2.13.1 (R Foundation for Statistical Computing, Vienna, Austria).
3. RESULTS
Histologic grade and the study population (screening or diagnostic) were evenly distributed among the training, validation, and test sets (Table 1). A summary of the accuracies of the trained algorithms on the validation set is shown in Table 2. We see that many of the methods are at least as accurate as clinical cytology. Several algorithms had similar sensitivity and pAUC and were highly correlated with each other (Spearman’s rank correlation coefficients range 0.58–0.99, p<0.001 for all pairwise comparisons of the algorithm prediction scores). The top performers are the classifiers that performed the micro-level classification first, and then counted the number of cells that had a posterior probability over a threshold. The L1-regularized logistic regression, elastic-net regularized logistic regression, and CART cell-level classifiers had the highest sensitivity (66%, 65%, and 65% sensitivity, respectively, for 90% specificity) and the same pAUC (0.61) on the validation set. Logistic regression and the ploidy method also worked well. Of the patient summary-features approaches, the approach that had the best sensitivity and pAUC was deriving features via modeling the DNA Index densities within a patient as a mixture of normal distributions and using logistic regression.
Table 1.
Characteristics of the populations represented in the training, validation, and test sets.
| Characteristic | Training | Validation | Test | Total | |
|---|---|---|---|---|---|
| Normal | 338 (49%) | 266 (52%) | 262 (50%) | 866 | |
| Histology | Low-grade CIN | 239 (34%) | 161 (31%) | 170 (33%) | 570 |
| High-grade CIN & Cancer | 117 (17%) | 86 (17%) | 89 (17%) | 292 | |
| Study group | Screening | 393 (57%) | 274 (53%) | 282 (54%) | 949 |
| Diagnostic | 301 (42%) | 239 (47%) | 239 (46%) | 779 |
CIN = cervical intraepithelial neoplasia
Table 2.
Summary of estimated sensitivities and the partial AUC for detecting high-grade CIN or worse versus low-grade CIN or better on the validation set.
| Approach | Method | Sensitivity (95% CI) for 90% specificity |
Partial AUC for range (80% –100% specificity) (95% CI) |
Candidate features |
|---|---|---|---|---|
| Pathologist | Clinical Cytology | 55% (44%–66%) | 0.47 (0.38–0.56) | - |
| CART | 42% (32%–52%) | 0.37 (0.29–0.46) | All 104 quant cytology | |
| Random Forests | 53% (42%–64%) | 0.48 (0.38–0.58) | All 104 quant cytology | |
| Logistic Regression | 26% (17%–35%) | 0.23 (0.16–0.31) | All 104 quant cytology | |
| Patient summary features | Elastic Nets | 56% (45%–66%) | 0.53 (0.43–0.63) | All 104 quant cytology |
| Lasso | 59% (49%–69%) | 0.54 (0.44–0.64) | All 104 quant cytology | |
| Ridge Regression | 55% (44%–64%) | 0.53 (0.43–0.63) | All 104 quant cytology | |
| SVM | 52% (41%–63%) | 0.51 (0.41–0.61) | All 104 quant cytology | |
| k-Nearest Neighbors | 38% (28%–48%) | 0.38 (0.20–0.37) | All 104 quant cytology | |
| Mclust (DNA Index) | 60% (50%–70%) | 0.54 (0.45–0.63) | DNA Index | |
| CLO Method 1 | 48% (37%–59%) | 0.42 (0.33–0.51) | DNA Index | |
| Model-based | CLO Method 2 | 55% (44%–66%) | 0.47 (0.38–0.58) | All 104 quant cytology |
| Latent Class CLO | 47% (36%–58%) | 0.40 (0.31–0.50) | DNA Index | |
| Cell classification then patient classification | Ploidy Method | 64% (54%–74%) | 0.60 (0.51–0.69) | DNA Index |
| Random Forests | 53% (42%–64%) | 0.59 (0.50–0.69) | All 104 quant cytology | |
| Elastic Net | 65% (55%–75%) | 0.61 (0.51–0.70) | All 104 quant cytology | |
| K-nn | 52% (41%–63%) | 0.47 (0.37–0.56) | All 104 quant cytology | |
| Logistic Regression w variable selection | 63% (53%–73%) | 0.60 (0.51–0.70) | All 104 quant cytology | |
| L1-Regularized Logistic Regression | 66% (56%–76%) | 0.61 (0.52–0.71) | All 104 quant cytology | |
| CART | 65% (55%–75%) | 0.61 (0.52–0.71) | All 104 quant cytology | |
| LDA | 59% (49%–69%) | 0.58 (0.48–0.67) | Top 6 RF variables | |
| Regularized LDA | 62% (52%–72%) | 0.59 (0.49–0.69) | All 104 quant cytology | |
CIN = cervical intraepithelial neoplasia; AUC = area under the receiver operating characteristic curve
We then used the validation set results to find an unbiased estimate of the sensitivity and specificity on our test set by using the threshold selected from the validation set. The top three classifiers were L1-regularized logistic regression, elastic-net regularized logistic regression, and CART. The results on the test set are presented in Table 3.
Table 3.
Summary of estimated sensitivities, specificities, and partial area under the ROC curve on the test set.
| Method | Sensitivity (95% CI) | Specificity (95% CI) | Partial AUC for range (0.8–1 specificity) (95% CI) |
|---|---|---|---|
| Regularized Logistic Regression | 60% (49%–70%) | 89% (86%–92%) | 0.49 (0.40–0.59) |
| Elastic Net | 61% (53%–73%) | 89% (84%–91%) | 0.50 (0.40–0.60) |
| CART | 58% (48%–69%) | 90% (87%–92%) | 0.49 (0.39–0.58) |
ROC = receiver operating characteristic; CART = classification and regression tree
When applying the L1-regularized logistic regression, elastic net algorithm, and CART to the test set to obtain an unbiased estimate of its sensitivity, specificity, and pAUC, we combined the training and validation sets and used 5-fold cross-validation to choose the free parameters. The optimal λ parameter for L1-regularized logistic regression was λ = 1000 and the patient score was calculated by counting if there was more than one cell that had a prediction greater than 0.12. The optimal parameters for the elastic net were α = 0.5 and λ = 0.1, leaving only four variables with non-zero coefficient estimates: DNA Index coefficient = 0.68, Fractal 1 area = 0.10, Fractal 2 area = 0.05, and Average run percent = 0.04. Variable details are provided in [14]. The coefficient estimates are shown in Figure 1. If a patient had more than one cell that had a predicted value greater than 0.1, the patient was predicted to have high-grade CIN with 61% sensitivity and 89% specificity on the cross-validated combined training and validation data.
Figure 1.
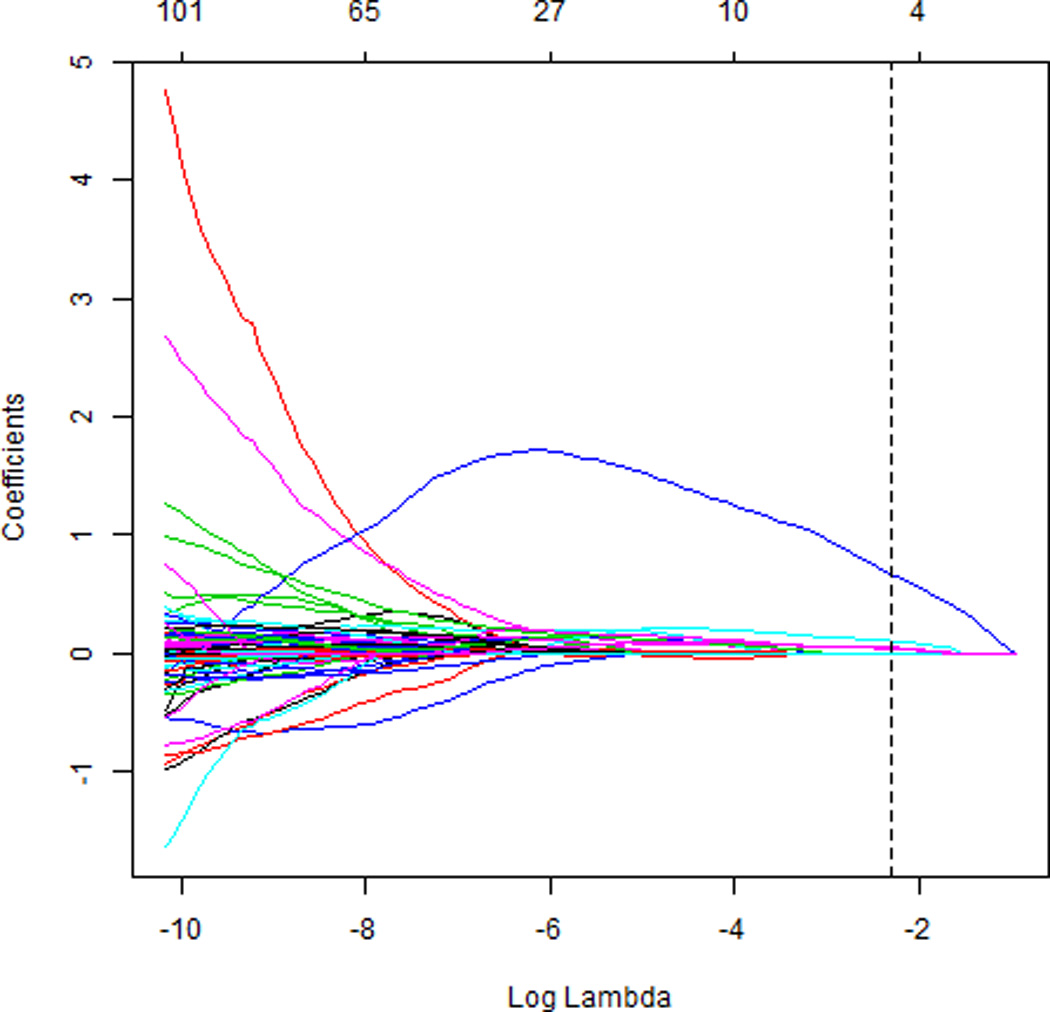
Elastic net coefficient estimates as a function of log(λ) from the combined training/validation set. The optimal λ, a parameter that specifies the amount of shrinkage of the coefficients, was found to be 0.1, and α was found to be 0.5, leaving 4 variables with nonzero coefficients. The top horizontal axis indicates the number of non-zero coefficients for each choice of λ.
We therefore used this same threshold (at least three cells) on the test set. The result was 64% sensitivity (95% CI 54%–74%) and 87% specificity (95% CI 84%–90%) with pAUC 0.50 (95% CI 0.41–0.60). The positive predictive value was 51% (95% CI 42%–60%) and the negative predictive value was 93% (95% CI 90%–95%). The ROC curves for the algorithm applied to the validation and test sets are shown in Figure 2.
Figure 2.
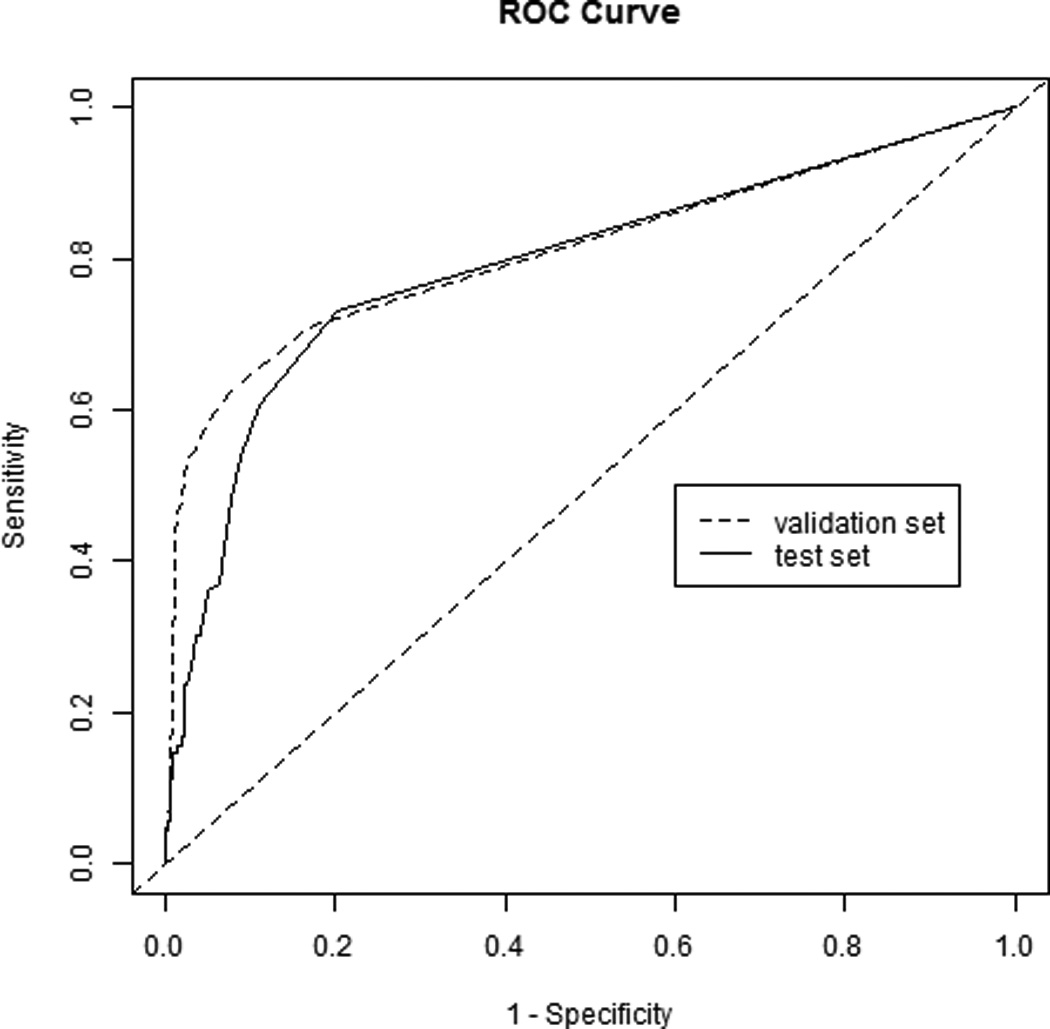
Receiver operating characteristic (ROC) curve of the elastic net algorithm applied to the validation and test sets.
The L1-regularized logistic regression model was used to predict the cell class (as opposed to the patient class) in the test data set. Table 4 gives the cell-level classification confusion matrix where 97% of the cells were correctly classified (87% cell-level sensitivity and 98% cell-level specificity).
Table 4.
Cell-level posterior probability confusion matrix using L1-regularized logistic regression illustrating the classification of each individual cell in the test set.
| True Group | |||
|---|---|---|---|
| Negative | Abnormal | ||
| Predicted Group | Negative | 40,378 | 373 |
| Abnormal | 746 | 2,607 | |
Using the model that was trained on the combined training and validation data, the L1-regularized logistic regression coefficients are given in Table 5. Based on the magnitude of the coefficients (the data were standardized), the top three predictive variables were the DNA Index, area (the area of the nucleus), and low DNA area (the fraction of the total nuclear area that is occupied by low chromatin).
Table 5.
Elastic Net coefficient estimates.
| Variable | Coefficient |
|---|---|
| DNA Index | 0.68 |
| fractal 1 area | 0.10 |
| fractal 2 area | 0.05 |
| average run percent | 0.04 |
The screening sample did not contain many patients who were found to have disease, so were unable to obtain good estimates of the sensitivity and positive predictive value in that population. The specificity in the test screening sample was 96% (95% CI 93%–98%) and the negative predictive value was 97% (95% CI 95%–99%).
4. DISCUSSION
From a statistical standpoint, we have done a comparative study of various methods for classification of data with a hierarchical, nested structure. We found good sensitivity and pAUC in the three general approaches: extracting macro-level features from micro-level data, the use of statistical models that account for the hierarchical structure of the data, and the micro-level classification and counting the number of abnormal cells. The third approach generally had the best accuracy measures when applied to our data but it is not likely to dominate the other approaches for all applications. It is common practice to apply many methods to a classification problem in the search for an algorithm with high predictive accuracy. The presentation of these general approaches provides a framework for the building of a classifier for data with this structure.
We have taken advantage of recent developments in statistical learning for handling high-dimensional data with many features. In some cases, regularization methods were used to perform variable selection, resulting in a more interpretable and parsimonious model. We selected our best performing classifier from among a suite of classfiers from the three basic methodologies that have been used for this type of hierarchical classification. Other promising areas of research in this setting would be to apply ensemble learning methods [27] rather than selecting a single classifier and to use the image itself to conduct classification [28].
The best performing algorithm we found uses the micro-level classification (with elastic net regularized logistic regression) to infer the macro-level class, which mimics the process by which clinicians classify Pap smears, i.e., cytopathologists looking for the abnormal cells on a slide. This general approach was not very sensitive to the choice of the micro-level classifier based on the similarity of the pAUCs and sensitivities in Table 2 and based on >99% agreement of the positive cases in the test set between the top three classifiers in Table 3. Other approaches, including statistical modeling, also had good performance and have promise to improve as new methodologies are developed.
Our best performing algorithm had 61% sensitivity and 89% specificity on the test set – which is approximately the same accuracy as the clinically read Pap smear in our data, and significantly better than reports on the sensitivity and specificity of the Pap smear in some developing countries [29]. Further, the algorithm will give exactly the same score when applied to the same data, whereas pathologists have high intra-observer and inter-observer variability in grading a slide [18,30,31].
Other research groups have developed algorithms for quantitative cytology using only ploidy, i.e., the DNA Index. One such study gave estimates of 54% sensitivity and 97% specificity, based on a diagnostic population of patients who were followed by colposcopic examination [10]. Others have used ploidy subjectively for classification and did not obtain a specific classification algorithm [32–34]. In contrast, we had biopsy results from both screening and diagnostic populations and considered over 100 quantitative cytology features rather than just DNA Index. Because many of the methods we investigated had similar accuracy measures, our results suggest that quantitative cytology is quite robust to the specific classification algorithm chosen.
There are three major strengths of this study. First, this is the first comparative study of methods for classification of hierarchical data that we are aware of. Second, we took great care to obtain unbiased estimates of the performance of the algorithm by using cross-validation techniques. Finally, our algorithm brings improved performance over other quantitative cytology algorithms at no extra cost since it would be employed in the software side of the device. A weakness of the study is the mixed population of screening and diagnostic patients. Training and testing classification algorithms require sufficient numbers of cases and controls. Although quantitative cytology is intended as a screening test, the prevalence of disease is very low in the screening population and training and testing using a screening sample was not practical. Hence, we enriched our sample with more patients likely to have the disease by using a combination of screening and diagnostic populations. A large multi-center trial using screening patients is needed to test any such algorithm. We estimate that it would require 15,000 patients assuming 90% power to detect an increase in the true positive and true negative rates from 50% and 50% to 60% and 90%, respectively [35]. Another possible limitation is some patients had very few cells collected and therefore the utility of such an algorithm in these patients is not clear. However, when stratifying the test set into subsets of patients with <500 cells and in ranges of 500 (e.g., 500–1000, 1000–1500, …, >3500), there was no clear degradation in performance, based on the ROC curves, between the groups. Additionally, more robust estimation of the classifier performance could be obtained by repeating the splitting into training, validation, and test sets.
There are new HPV vaccines, but they do not confer protection against all types of HPV that cause cervical cancer [36]. About 30% of cervical cancers will not be prevented by these vaccines, thus necessitating the continuation of regular screening programs. Furthermore, the uptake of the vaccine has been low, with only 12.5% of eligible women completing the 3-dose HPV vaccine [37]. With increased use of the HPV vaccine, the prevalence of cervical cancer will decrease, resulting in a decreased predictive value of existing screening methods. Thus, if costs and accuracy remain the same, the cost-effectiveness of the currently used screening tests will only decrease. The results of this study show that quantitative cytology provides an alternative with nearly the same accuracy, and, we believe, much lower cost.
Cervical cancer is a preventable disease if it is caught early, especially in the pre-cancerious stage. Thus the key to fighting cervical cancer is screening that is accurate and of low cost. With advances such as the new HPV vaccine and screening process improvements such as those presented in this manuscript, the incidence rates of cervical cancer can be decreased. Further, the expansion of cervical cancer screening to developing nations requires methodologies that are practical in that setting, which is not the case for the current standard of care based on reading of Pap smears by cytopathologists. Quantitative cytology has the potential for high impact in low-resource settings due to its minimal training requirements and being semi-automated which could increase the speed of analysis and potentialy reduce cost [11] and improve patient adherence.
ACKNOWLEDGEMENTS
This work was supported by the National Institutes of Health [grant number P01 CA-82710]. We thank all the patients who participated with the goal of helping other women in future generations.
Footnotes
Financial disclosures: None.
REFERENCES
- 1.Mangasarian O, Street W, Wolberg W. Breast cancer diagnosis and prognosis via linear programming. Operations Research. 1995;43:570–577. [Google Scholar]
- 2.Sciubba J. Improving detection of precancerous and cancerous oral lesions. Journal of the American Dental Association. 1999;130:1445–1457. doi: 10.14219/jada.archive.1999.0055. [DOI] [PubMed] [Google Scholar]
- 3.Christian D. Computer-assisted analysis of oral brush biopsies at an oral cancer screening program. Journal of the American Dental Association. 2002;133:357–362. doi: 10.14219/jada.archive.2002.0175. [DOI] [PubMed] [Google Scholar]
- 4.Boutaga K, Savelkoul P, Winkel E, Van Winkelhoff A. Comparison of subgingival bacterial sampling with oral lavage for detection and quantification of periodontal pathogens by real-time polymerase chain reaction. Journal of Periodontology. 2007;78:79–86. doi: 10.1902/jop.2007.060078. [DOI] [PubMed] [Google Scholar]
- 5.Cadez IV, Mclaren CE, Smyth P, Mclachlan GJ. Hierarchical models for screening of iron-deficient anemia. In: Bratko I, Dzeroski S, editors. Proceedings of the 16th International Conference on Machine Learning. San Francisco, CA: Morgan Kaufmann; 1999. pp. 77–86. [Google Scholar]
- 6.Guillaud M, Benedet J, Cantor SB, Staerkel G, Follen M, Macaulay C. DNA ploidy compared with human papilloma virus testing (Hybrid Capture II) and conventional cervical cytology as a primary screening test for cervical high-grade lesions and cancer in 1555 patients with biopsy confirmation. Cancer. 2006;107(102):309–318. doi: 10.1002/cncr.21993. [DOI] [PubMed] [Google Scholar]
- 7.Cantor SB, Yamal J-M, Guillaud M, Cox D, Atkinson EN, Benedet JL, Miller D, Ehlen T, Matisic J, Van Niekerk D, Bertrand M, Milbourne A, Rhodes H, Malpica A, Staerkel G, Nader-Eftekhari S, Adler-Storthz K, Scheurer M, Basen-Engquist K, West L, Vlastos AT, Tao X, Macaulay C, Richards-Kortum R, Follen M. Accuracy of optical spectroscopy for the detection of cervical intraepithelial neoplasia. International Journal of Cancer. 2011;128(5):1151–1168. doi: 10.1002/ijc.25667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yamal J-M, Zewdie GA, Cox DD, Atkinson EN, Cantor SB, Macaulay CE, Davies K, Adewole I, Buys T, Follen M. Accuracy of optical spectroscopy for the detection of cervical intraepithelial neoplasia without colposcopic tissue information; a step toward automation for low resource settings. Journal of Biomedical Optics. 2012;17(4):047002. doi: 10.1117/1.JBO.17.4.047002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Malpica A, Matisic J, Van Niekirk D, Crum C, Staerkel G, Yamal J-M, Guillaud M, Cox D, Atkinson EN, Adler-Storthz K, Poulin N, Macaulay C, Follen M. Kappa statistics to measure interrater and intrarater agreement for 1790 cervical biopsy specimens amongst twelve pathologists: qualitative histopathologic analysis and methodologic issues. Gynecologic Oncology. 2005;99(3) Supp 1:S38–S52. doi: 10.1016/j.ygyno.2005.07.040. [DOI] [PubMed] [Google Scholar]
- 10.Sun XR, Wang J, Garner D, Palcic B. Detection of cervical cancer and high grade neoplastic lesions by a compbination of liquid-based sampling preparation and DNA measurements using automated image cytometry. Cellular Oncology. 2005;27:33–41. doi: 10.1155/2005/981612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Grohs HK, Husain OAN, editors. Automated cervical cancer screening. New York: Igaku-Shoin; 1994. [Google Scholar]
- 12.Chiu D, Guillaud M, Cox D, Follen M, Macaulay C. Quality assurance system using statistical process control: an implementation for image cytometry. Cellular Oncology. 2004;26:101–117. doi: 10.1155/2004/794021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Anderson G, Macaulay C, Matisic J, Garner D, Palcic B. The use of an automated image cytometer for screening and quantitative assessment of cervical lesions for screening. Columbia Cervical Smear Screening Programme. Cytopathology. 1997;8:298–312. doi: 10.1111/j.1365-2303.1997.tb00554.x. [DOI] [PubMed] [Google Scholar]
- 14.Doudkine A, Macaulay C, Poulin N, Palcic B. Nuclear texture measurements in image cytometry. Pathologica. 1995;87:286–299. [PubMed] [Google Scholar]
- 15.Scheurer ME, Guillaud M, Tortolero-Luna G, Mcaulay C, Follen M, Adler-Storthz K. Human papillomavirus-related cellular changes measured by cytometric analysis of DNA ploidy and chromatin texture. Cytometry Part B: Clinical Cytometry. 2007;72B:324–331. doi: 10.1002/cyto.b.20173. [DOI] [PubMed] [Google Scholar]
- 16.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning, second edition. New York: Springer; 2009. [Google Scholar]
- 17.Schneider A, Hoyer H, Lotz B, Leistritza S, Kuhne-Heid R, Nindl I, Muller B, Haerting J, Durst M. Screening for high-grade cervical intra-epithelial neoplasia and cancer by testing for high-risk HPV, routine cytology or colposcopy. International Journal of Cancer. 2000;89:529–534. [PubMed] [Google Scholar]
- 18.Cuzick J, Szarewski A, Cubie H, Hulman G, Kitchener H, Luesley D, Mcgoogan E, Menon U, Terry G, Edwards R, Brooks C, Desai M, Gie C, Ho L, Jacobs I, Pickles C, Sasieni P. Management of women who test positive for high-risk types of human papillomavirus: the HART study. Lancet. 2003;362:1871–1876. doi: 10.1016/S0140-6736(03)14955-0. [DOI] [PubMed] [Google Scholar]
- 19.Dodd L, Pepe M. Partial AUC estimation and regression. Biometrics. 2003;59:614–623. doi: 10.1111/1541-0420.00071. [DOI] [PubMed] [Google Scholar]
- 20.Fraley C, Raftery AE. Model-based clustering, discriminant analysis, and density estimation. Journal of the American Statistical Association. 2002;97:611–631. [Google Scholar]
- 21.Witten DM, Tibshirani R. Penalized classification using Fisher’s linear discriminant. Journal of the Royal Statistical Society,Series B. 2011;73(5):753–772. doi: 10.1111/j.1467-9868.2011.00783.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Swartz RJ, West LA, Bioko I, Malpica A, Guillaud M, Macaulay C, Follen M, Atkinson EN, Cox DD. Classification using the cumulative log-odds in the quantitative pathologic diagnosis of adenocarcinoma of the cervix. Gynecologic Oncology. 2005;99:S24–S31. doi: 10.1016/j.ygyno.2005.07.038. [DOI] [PubMed] [Google Scholar]
- 23.Yamal J-M, Follen M, Guillaud M, Cox D. Classifying tissue samples from measurements on cells with within-class tissue sample heterogeneity. Biostatistics. 2011;12(4):695–709. doi: 10.1093/biostatistics/kxr010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Park MY, Hastie T. L-1 regularization path algorithm for generalized linear models. Journal of the Royal Statistical Society Series B. 2007;69:659–677. [Google Scholar]
- 25.Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society B. 2005;67:301–320. [Google Scholar]
- 26.Breimann L, Friedman J, Olshen RA, Stone CJ. Classification and Regression Trees. Monterey, California: Wadsworth; 1984. [Google Scholar]
- 27.Rokach L. Ensemble-based classifiers. Artificial Intelligence Review. 2010;33(1–2):1–39. [Google Scholar]
- 28.Wang F, Zhang P, Qian B, Wang X, Davidson I. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM; 2014. Clinical risk prediction with multilinear sparse logistic regression; pp. 145–154. [Google Scholar]
- 29.Ferreccio C, Barriga MI, Lagos M, Ibañez C, Poggi H, Gonzalez F, Terrazas S, Katki HA, Nuñez F, Cartagena J, Van De Wyngard V, Viñales D, Brañes J. Screening trial of human papillomavirus for early detection of cervical cancer in Santiago, Chile. International Journal of Cancer. 2012;132(4):916–923. doi: 10.1002/ijc.27662. [DOI] [PubMed] [Google Scholar]
- 30.Mccluggage WG, Walsh MY, Thronton CM, Hamilton PW, Date A, Caughley LM, Bharucha H. Inter- and intra-observer variation in the histopathological reporting of cervical squamous intraepithelial lesions using a modified Bethesda grading system. BJOG: An International Journal of Obstetrics & Gynaecology. 1998;105:206–210. doi: 10.1111/j.1471-0528.1998.tb10054.x. [DOI] [PubMed] [Google Scholar]
- 31.Woodhouse S, Stastny JF, Styer PE, Kennedy M, Praestgaard AH, Davey DD. Interobserver variability in subclassificaiton of squamous intraepithelial lesions. Archives of Pathology & Laboratory Medicine. 1999;123:1079–1084. doi: 10.5858/1999-123-1079-IVISOS. [DOI] [PubMed] [Google Scholar]
- 32.Lorenzato M, Clavel D, Masure M, Nou J-M, Bouttens D, Evrard G, Bory J-P, Maugard B, Quereux C, Birembaut P. DNA image cytometry and human papillomavirus (HPV) detection help to select smears at high risk of high-grade cervical lesions. Journal of Pathology. 2001;194:171–176. doi: 10.1002/path.874. [DOI] [PubMed] [Google Scholar]
- 33.Bocking A, Nguyen VQ. Diagnostic and prognostic use of DNA image cytometry in cervical squamous intraepithelial lesions and invasive carcinoma. Cancer. 2004;102:41–54. doi: 10.1002/cncr.11889. [DOI] [PubMed] [Google Scholar]
- 34.Baak JPA, Janssen E. DNA ploidy analysis in histopathology. Histopathology. 2004;44:603–620. doi: 10.1111/j.1365-2559.2004.01897.x. [DOI] [PubMed] [Google Scholar]
- 35.Pepe MS. The Statistical Evaluation Of Medical Tests For Classification And Prediction. Oxford: Oxford University Press; 2003. pp. 218–229. [Google Scholar]
- 36.De Vuyst H, Clifford GM, Nascimento MC, Madeleine MM, Franceschi S. Prevalence and type distribution of human papillomavirus in carcinoma and intraepithelial neoplasia of the vulva, vagina and anus: A meta-analysis. International Journal of Cancer. 2008;124(7):1626–1636. doi: 10.1002/ijc.24116. [DOI] [PubMed] [Google Scholar]
- 37.Laz TH, Rahman M, Berenson AB. Human papillomavirus vaccine uptake among 18- to 26-year-old women in the United States. Cancer. 2013;119(7):1386–1392. doi: 10.1002/cncr.27894. [DOI] [PMC free article] [PubMed] [Google Scholar]


