Abstract
Neural oscillations can enhance feature recognition [1], modulate interactions between neurons [2], and improve learning and memory [3]. Numerical studies have shown that coherent spiking can give rise to windows in time during which information transfer can be enhanced in neuronal networks [4–6]. Unanswered questions are: 1) What is the transfer mechanism? And 2) how well can a transfer be executed? Here, we present a pulse-based mechanism by which a graded current amplitude may be exactly propagated from one neuronal population to another. The mechanism relies on the downstream gating of mean synaptic current amplitude from one population of neurons to another via a pulse. Because transfer is pulse-based, information may be dynamically routed through a neural circuit with fixed connectivity. We demonstrate the transfer mechanism in a realistic network of spiking neurons and show that it is robust to noise in the form of pulse timing inaccuracies, random synaptic strengths and finite size effects. We also show that the mechanism is structurally robust in that it may be implemented using biologically realistic pulses. The transfer mechanism may be used as a building block for fast, complex information processing in neural circuits. We show that the mechanism naturally leads to a framework wherein neural information coding and processing can be considered as a product of linear maps under the active control of a pulse generator. Distinct control and processing components combine to form the basis for the binding, propagation, and processing of dynamically routed information within neural pathways. Using our framework, we construct example neural circuits to 1) maintain a short-term memory, 2) compute time-windowed Fourier transforms, and 3) perform spatial rotations. We postulate that such circuits, with automatic and stereotyped control and processing of information, are the neural correlates of Crick and Koch’s zombie modes.
INTRODUCTION
Accumulating experimental evidence implicates coherent activity as an important element of cognition. Since their discovery [7], gamma band oscillations have been demonstrated to exist in hippocampus [8–10], visual cortex [2, 7, 11], auditory cortex [12], somatosensory cortex [13], parietal cortex [14–16], various nodes of the frontal cortex [15, 17, 18], amygdala and striatum [19]. Gamma oscillations sharpen orientation [1] and contrast [20] tuning in V1, and speed and direction tuning in MT [21]. Attention has been shown to enhance gamma oscillation synchronization in V4, while decreasing low-frequency synchronization [22, 23] and to increase synchronization between V4 and FEF [17], LIP and FEF [15], V1 and V4 [24], and MT and LIP [25]; Interactions between sender and receiver neurons are improved when consistent gamma-phase relationships exist between two communicating sites [2].
Theta-band oscillations have been shown to be associated with visual spatial memory [26, 27], where neurons encoding the locations of visual stimuli and an animal’s own position have been identified [26, 28]. Additionally, loss of theta gives rise to spatial memory deficits [29] and pharmacologically enhanced theta improves learning and memory [3].
These experimental investigations of coherence in and between distinct brain regions have informed the modern understanding of information coding in neural systems [30, 31]. Understanding information coding is crucial to understanding how neural circuits and systems bind sensory signals into internal mental representations of the environment, process internal representations to make decisions, and translate decisions into motor activity.
Classically, coding mechanisms have been shown to be related to neural firing rate [32], population activity [33–35], and spike timing [36]. Firing rate [32] and population codes [37–41] are two different ways for a neural system to average spike number to represent graded stimulus information, with population codes capable of faster and more accurate processing since averaging is performed across many fast responding neurons. Thus population and temporal codes are capable of making use of the sometimes millisecond accuracy [36, 42, 43] of spike timing to represent signal dynamics.
Although classical mechanisms serve as their underpinnings, new mechanisms have been proposed for short-term memory [5, 44, 45], information transfer via spike coincidence [4, 46, 47] and information gating [6, 47–50] that rely on gamma- and theta-band oscillations. For example, the Lisman-Idiart interleaved-memory (IM) model [5], and Fries’s communication-through-coherence (CTC) model [47] both make use of the fact that synchronous input can provide windows in time during which spikes may be more easily transferred through a neural circuit. Thus, neurons firing coherently can transfer their activity quickly downstream. Additionally, synchronous firing has been used in Abeles’s synfire network [4, 46, 51–54] giving rise to volleys of propagating spikes.
The precise mechanism and the extent to which the brain can make use of coherent activity to transfer information have remained unclear. Previous theoretical and experimental studies have largely focused on feedforward, synfire chains [51, 53, 55–58]. These studies have shown that it is possible to transfer volleys of action potentials stably from layer to layer, but that the waveform tends to an attractor with fixed amplitude. Therefore, in these models, although a volley can propagate, graded information, in the form of a rate amplitude cannot. Other numerical work has shown that it is possible to transfer firing rates through layered networks when background current noise is sufficient to effectively keep the network at threshold [59]. The disadvantage of this method is that there is no mechanism to control the flow of firing rate information other than increasing or decreasing background noise. Recently, it has been shown that external gating, similar, in principle, to that used in the IM model and to the gating that we introduce below, can stabilize the propagation of fixed amplitude pulses and act as an external factor to control pulse propagation [49, 50].
In the Methods section, we show that information contained in the amplitude of a synaptic current may be exactly transferred from one neuronal population to another, as long as well-timed current pulses are injected into the populations. This mechanism is distinct from the synfire chains mentioned above that can only transfer action potential volleys of fixed amplitude, in contrast to [59], by using current pulses to gate information through a circuit, it provides a neuronal-population-based means of propagating graded information through a neural circuit.
We derive our pulse-based transfer mechanism using mean-field equations for a current-based neural circuit (see circuit diagram in Fig. 1a) and demonstrate it in an integrate-and-fire neuronal network. Graded current amplitudes are transferred between upstream and downstream populations: A gating pulse excites the upstream population into the firing regime thereby generating a synaptic current in the downstream population. For didactic purposes, we first present results that rely on a square gating pulse with an ongoing inhibition keeping the downstream population silent until the feedforward synaptic current is integrated. We then show how more biologically realistic pulses with shapes filtered on synaptic time-scales may be used for transfer. We argue that our mechanism represents crucial principles underlying what it means to transfer information. We then generalize the mechanism to the case of transfer from one vector of populations to a second vector of populations and show that this naturally leads to a framework for generating linear maps under the active control of a pulse generator.
FIG. 1.
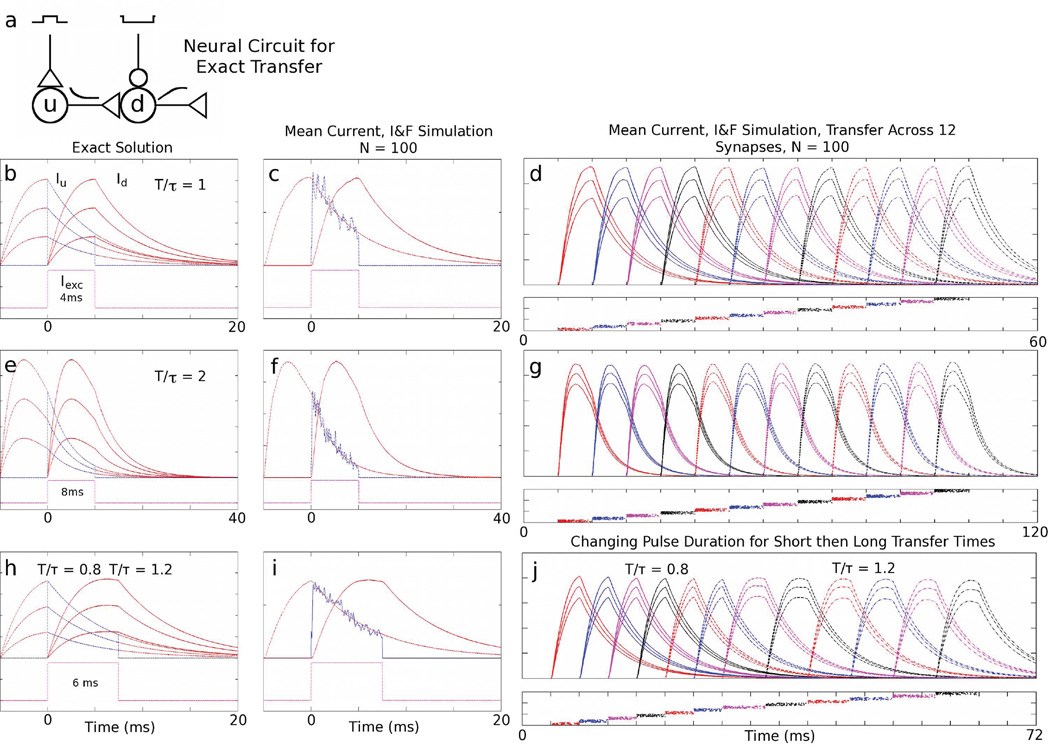
Exact current transfer - Mean-field and I&F: a) Circuit diagram for the current transfer mechanism. Excitatory pulse gating the upstream (u) population and ongoing inhibition acting on the downstream (d) population. The upstream population excites the downstream population and transfers its current. b, e) Dynamics of a single current amplitude transfer with T/τ = 1 and T/τ = 2 with τ = 4 ms. Dashed red traces represent the growth and exponential decay of three different current amplitudes, Iu(t), in the upstream population. Dashed blue traces represent excitatory firing rates of the upstream population. Solid red traces represent the integration and subsequent decay of the downstream current, Id(t). Dashed magenta traces represent the excitatory gating pulse current to the upstream population. Magenta traces are displaced from zero for clarity. c, f) Dynamics of two N = 100 neuron populations of current-based, I&F neurons showing current amplitude transfer averaged over 20 trials. d, g) Mean current amplitudes of twelve current-based, I&F neuronal populations (N = 100 neurons/population, averaged over 20 trials) successively transferring their currents. Below each of these panels is a plot of one realization of the spike times for all neurons in each respective population. h) Dynamics of a single current amplitude transfer between two gating periods, with T/τ = 0.8 and T/τ = 1.2. i) Dynamics of two N = 100 neuron populations showing current amplitude transfer with the same gating periods as in i). j) Five graded current amplitude transfers between six populations with T/τ = 0.8, followed by a transfer to T/τ = 1.2, followed by five equally graded transfers with T/τ = 1.2.
In the Results section, we demonstrate pulse-gated transfer solutions in both mean-field and integrate-and-fire neuronal networks. We demonstrate the robustness of the mechanism to noise in pulse timing, synaptic strength and finite-size effects and show how biologically realistic pulses may be used for gating. We then go on to present three examples of circuits that make use of the framework for generating actively controlled linear maps.
In the Discussion section, we consider some of the implications of our mechanism and information coding framework, and future work.
METHODS
What are the crucial principles underlying information transfer between populations of neurons? First, a carrier of information must be identified, such as synaptic current, firing rate, spike timing, etc. Once the carrier has been identified, we must determine the type of information, i.e. is the information analog or digital? Finally, we must identify what properties the information must exhibit for us to say that information has been transferred. In the mechanism that we present below, we use synaptic current as the information carrier. Information is graded and represented in a current amplitude and thus is best considered analog. The property that identifies information transfer is that the information exhibit a discrete, time-translational symmetry. That is, the waveform representing a graded current or firing rate amplitude in a downstream neuronal population must be the same as that in an upstream population, but shifted in time.
As noted in the Introduction, mechanisms exist for propagating constant activity that have demonstrated time-translational symmetries in both strong [51] and sparsely coupled [57] regimes. Here, we address a mechanism for propagation of graded activity.
An additional consideration for biologically realistic information transfer is that it be dynamically routable. That is, that neural pathways may be switched on the millisecond time scale. This is achieved in our mechanism via pulse gating.
Circuit Model
Our neuronal network model consists of a set of j = 1, …, M populations, each with i = 1, …, N, of current-based, integrate-and-fire (I&F) point neurons. Individual neurons have membrane potentials, υi,j, described by
| (1a) |
and feedforward synaptic current
| (1b) |
with total currents
| (1c) |
and VLeak is the leakage potential. The excitatory gating pulse on neurons in population j is
| (2) |
where θ(t) is the Heaviside step function: θ(t) = 0, t < 0 and θ(t) = 1, t > 0. The ongoing inhibitory current is .
Here, τ is a current relaxation timescale depending on the type of neuromodulator (typical time constants are τAMPA ~ 3 – 11 ms or τNMDA ~ 60 – 150 ms). Individual spike times, , with k denoting spike number, are determined by the time when the voltage υi,j reaches the threshold voltage, VThres, at which time the voltage is reset to VReset. We use units in which only time retains dimension (in seconds) [60]: the leakage conductance is gLeak = 50/sec. We set VReset = VLeak = 0 and normalize the membrane potential by the difference between the threshold and reset potentials, VThres − VReset = 1. For the simulations reported here, we use and . Synaptic background activity is modeled by introducing noise in the excitatory pulse amplitude via ε, where ε ~ N(0, σ2), with σ = 1/sec. The probability that neuron i in population j synapses on neuron k in population j + 1 is Pik = p. In our simulations, pN = 80.
This network is effectively a synfire chain with prescribed pulse input [4, 51, 53, 61, 62].
Mean-field Equations
Averaging (coarse-graining) spikes over time and over neurons in population j (see, e.g. Shelley and McLaughlin [60]) produces a mean firing rate equation given by
| (3) |
where gTotal = gLeak, and
The feedforward synaptic current, Ij+1, is described by
| (4a) |
The downstream population receives excitatory input, mj, with synaptic coupling, S, from the upstream population. As in the I&F simulation, we set, VReset = 0, and non-dimensionalize the voltage using VThres − VReset = 1, so that
| (4b) |
This relation, the so-called f-I curve, can be approximated by
| (5) |
near I ≈ I0, where m′ (I0) ≈ 1 (here the prime denotes differentiation), and letting g0 = m′ (I0) I0 − m(I0) be the effective threshold in the linearized f-I curve.
Exact Transfer
We consider transfer between an upstream population and a downstream population, denoted by j = u and j + 1 = d.
For the downstream population, for t < 0, Id = 0. This may be arranged as an initial condition or by picking a sufficiently large , with
| (6) |
At t = 0, the excitatory gating pulse is turned on for the upstream population for a period T, so that for 0 < t < T, the synaptic current of the downstream population obeys
| (7) |
Therefore, we set the amplitude of the excitatory gating pulse to be to cancel the threshold. Making the ansatz Iu (t) = Ae−t/τ, we integrate
to obtain the expression
| (8a) |
During this time, ongoing inhibition is acting on the downstream population to keep it from spiking, i.e., we have
| (8b) |
For T < t < 2T, the downstream population is gated by an excitatory pulse, while the upstream population is silenced by ongoing inhibition. The downstream synaptic current obeys
| (9a) |
with
| (9b) |
so that we have
| (9c) |
and
| (9d) |
For exact transfer, we need Id (t − T) = Iu (t), therefore we write
| (10) |
So we have exact transfer with
| (11) |
To recap, we have the solution, with Sexact,
| (12a) |
and
| (12b) |
A Synfire-Based Gating Mechanism
In our exact solution, gating pulses have biologically unrealistic instantaneous onset and offset. Therefore, it becomes important to understand how robust graded propagation can be for gating pulses of realistic shape, and is there a natural mechanism for their generation? To test the structural robustness of graded propagation with a known pulse-generating mechanism, we implemented an I&F neuronal network model with two sets of populations, one set had synaptic strengths such that it formed stereotypical pulses with fixed mean spiking profile and mean current waveform [51, 53]. The second set used these pulses, instead of square gating pulses, for current propagation. We call this neural circuit a Synfire-Gated Synfire Chain (SGSC).
Individual I&F neurons in the SGSC have membrane potentials described by
| (13a) |
| (13b) |
| (13c) |
where i = 1, …, Nσ, j = 1, …, M and σ, σ′ = 1, 2 with 1 for the graded chain and 2 for the gating chain; individual spike times, , with k denoting spike number, are determined by the time when reaches VThres. The gating chain receives a noise current, , generated from Poisson spike times, , with strength f2 = 0.05 and rate ν2 = 400 Hz, i.e. a noise current averaging 20/sec that is subthreshold (given by gleak = 50/sec). The current is the synaptic current of the σ population produced by spikes of the σ′ population. In the simulations reported in Results, τ = 5 msec and the synaptic coupling strengths are {S11, S12, S21, S22} = {2.28, 0.37, 0, 2.72}. The probabilities that a neuron in population σ′ synapses on a neuron in population σ are given by {p11, p12, p21, p22} = {0.02, 0.01, 0, 0.8}. The two chains have population size {N1, N2} = {1000, 100}. There was a synaptic delay of 4 ms between each successive layer in the gating chain.
Information Processing Using Graded Transfer Mechanisms
Because for our mechanism current amplitude transfer is in the linear regime, downstream computations may be considered as linear maps (matrix operations) on a vector of neuronal population amplitudes. For instance, consider an upstream vector of neuronal populations with currents, Iu, connected via a connectivity matrix K to a downstream vector of neuronal populations, Id:
| (14) |
With feedforward connectivity, given by the matrix K, the current amplitude, Id, from the mean-field model obeys
| (15) |
where pu(t) denotes a vector gating pulse on layer j. This results in the solution Id(t − T) = PKIu(t), where P is a diagonal matrix with the gating pulse vector, p, of 0s and 1s on the diagonal indicating which neurons were pulsed during the transfer.
For instance, if the matrix of synaptic weights, K, were square and orthogonal, the transformation would represent an orthogonal change of basis in the vector space ℝn, where n is the number of populations in the vector. Convergent and divergent connectivities would be represented by non-square matrices.
This type of information processing is distinct from concatenated linear maps in the sense that information may be dynamically routed via suitable gating. Thus, we can envision information manipulation by sets of non-abelian operators, i.e., with non-commuting matrix generators, that may be flexibly coupled. We can also envision re-entrant circuits or introducing pulse-gated nonlinearities into our circuit to implement regulated feedback.
Information Coding Framework
Our discussion has identified three components of a unified framework for information coding:
information content - graded current, I
information processing - synaptic weights, K
information control - pulses, p
Note that the pulsing control, p, serves as a gating mechanism for routing neural information into (or out of) a processing circuit. We, therefore, refer to amplitude packets, I, that are guided through a neural circuit by a set of stereotyped pulses as “bound” information.
Consider one population coupled to multiple downstream populations. Separate downstream processing circuits may be multiplexed by pulsing one of the set of downstream circuits. Similarly, copying circuit output to two (or more) distinct downstream populations may be performed by pulsing two populations that are identically coupled to one upstream population.
In order to make decisions, non-linear logic circuits would be required. Many of these are available in the literature [61, 63]. Simple logic gates should be straight-forward to construct within our framework by allowing interaction between information control and content circuits. For instance, to construct an AND gate, use gating pulses to feed two sub-threshold outputs into a third population, if the inputs are (0, 0), (0, 1) or (1, 0), none of the combined pulses exceed threshold and no output is produced. However, the input (1, 1) would give rise to an output pulse. Other logic gates, including the NOT may be constructed, giving a Turing complete set of logic gates. Thus, these logic elements could be used for plastic control of functional connectivity, i.e. the potential for rapidly turning circuit elements on or off, enabling information to be dynamically processed.
RESULTS
Exact Transfer
In Fig. 1, we demonstrate our current amplitude transfer mechanism in both mean-field and spiking models. The neural circuit for one upstream and one downstream layer is shown in Fig. 1a. Fig. 1b and e show the exact, mean-field transfer solution for T = τ = 4 ms and T = 2τ = 8 ms. Fig. 1c and f show corresponding transfer between populations of N = 100 current-based, I&F neurons. Fig. 1d and g show mean currents computed from simulations of I&F networks with N = 100. Mean amplitude transfer for these populations is very nearly identical to the exact solution and, as may be seen, graded amplitudes are transferred across many synapses and are still very accurately preserved. Fig. 1h shows the exact mean-field transfer solution between populations gated for T/τ = 0.8 and T/τ = 1.2 with τ = 5 ms. Fig. 1i shows the corresponding transfer between populations of N = 100 I&F neurons. Fig. 1j shows how integration period, T, may be changed within a sequence of successive transfers within an I&F network with a value of Sexact that supports two different timescales.
This mechanism has a number of features that are represented in the analytic solution, Eqns. (11)–(12), and in Fig. 1: 1) Exact transfer is possible for any T and τ. This means that transfer may be enacted on a wide range of time scales. This range is set roughly by the value of Sexact. Roughly, 0.1 < T/τ < 4 gives S small enough that firing rates are not excessive in the corresponding I&F simulations. 2) τ sets the “reoccupation time” of the upstream population. After one population has transferred its amplitude to another, the current amplitude must fall sufficiently close to zero for a subsequent exact transfer. Therefore, synapses mediated by AMPA (NMDA) may allow repeated exact transfers. 3) Pulse-gating controls information flow, not information content. As an example, one upstream population may be synaptically connected to two (or more) downstream populations. A graded input current amplitude may then be selectively transferred downstream depending on whether one, the other, or both downstream populations are pulsed appropriately. This allows the functional connectivity of neural circuits to be plastic and rapidly controllable by pulse generators. 4) Sexact has an absolute minimum at T/τ = 1, and, except at the minimum, there are always two values of T/τ that give the same value of S. This means, for instance, that an amplitude transferred via a short pulse may subsequently be transferred by a long pulse and vice versa (see Fig. 1h,i,j). Thus, not only may downstream information be multiplexed using pulse-based control, but the time scale of the mechanism may also be varied from transfer to transfer.
The means by which the mechanism can fail are also readily apparent: 1) The gating pulses might not be accurately timed. 2) Synaptic strengths might not be correct for exact transfer. 3) The amplitude of the excitatory pulse might not precisely cancel the effective threshold . 4) The mean-field approximation might break down due to too few neurons in the neuronal populations.
Robustness to Variability in Pulse Timing, Synaptic Strength and Finite Size Effects
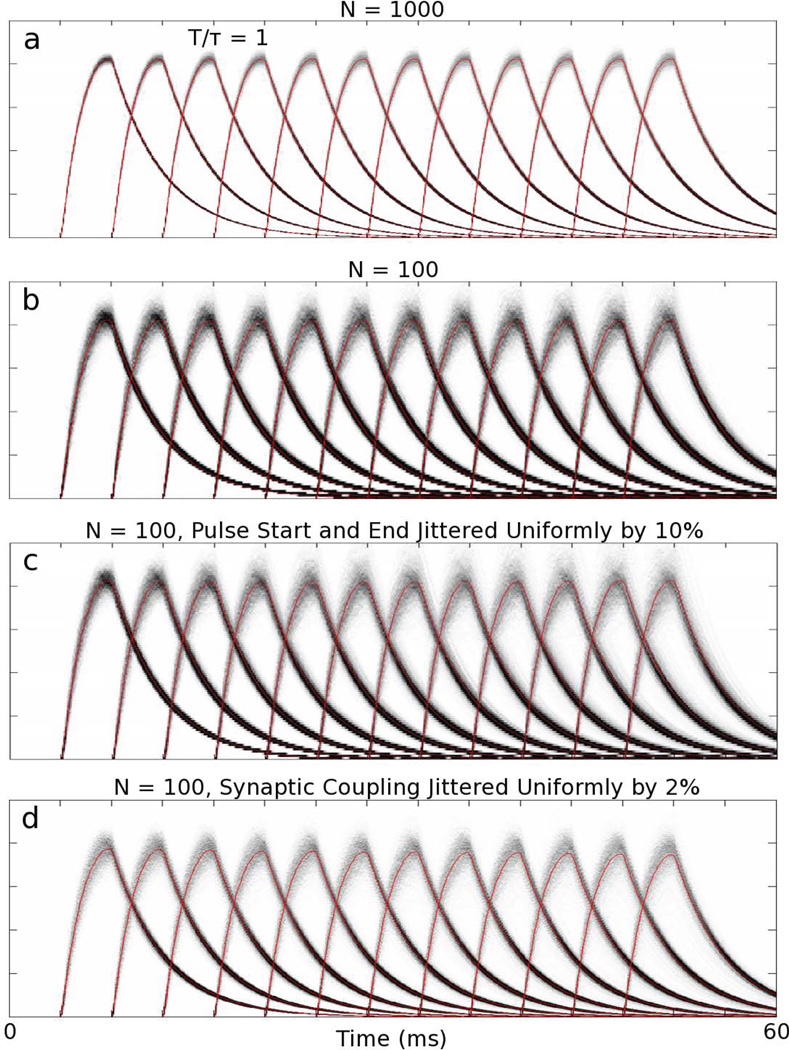
In Fig. 2, we investigate mean current variability for the transfer mechanism in the spiking model due to the modes of failure discussed above for T/τ = 1 with τ = 4 ms. Fig. 2a shows the distribution of mean current amplitudes averaged over populations of N = 1000 neurons, calculated from 1000 realizations. Fig. 2b shows the distribution with just N = 100. Clearly, more neurons per population gives less variability in the distribution. The signal-to-noise ratio (SNR) decreases as the square-root of the number of neurons per population, as would be expected. Thus, for circuits needing high accuracy, neuronal recruitment would increase the SNR. Fig. 2c shows the distribution for N = 100 with 10% jitter in pulse start and end times. Fig. 2d shows the distribution for N = 100 with 2% jitter in synaptic coupling, S. Note that near T/τ = 1, Sexact varies slowly, thus the effect of both timing and synaptic coupling jitter on the stability of the transfer is minimal. Pulse timing, synaptic strengths, synaptic recruitment, and pulse amplitudes are regulated by neural systems. So mechanisms are already known that could allow networks to be optimized for graded current amplitude transfer.
FIG. 2.
Sources of variability in the current transfer mechanism: Distributions of mean current amplitudes from current-based, I&F neuronal simulations. a) N = 1000. b) N = 100. c) N = 100 with the start and end times of each pulse jittered uniformly by 10% of the pulse width. d) N = 100 with synaptic coupling, S, jittered uniformly by 2%. Gray scale: White denotes 0 probability, Black denotes probability maximum. All distributions sum to unity along the vertical axis. Red curves in all panels denote the mean.
A Synfire-Gated Synfire Chain
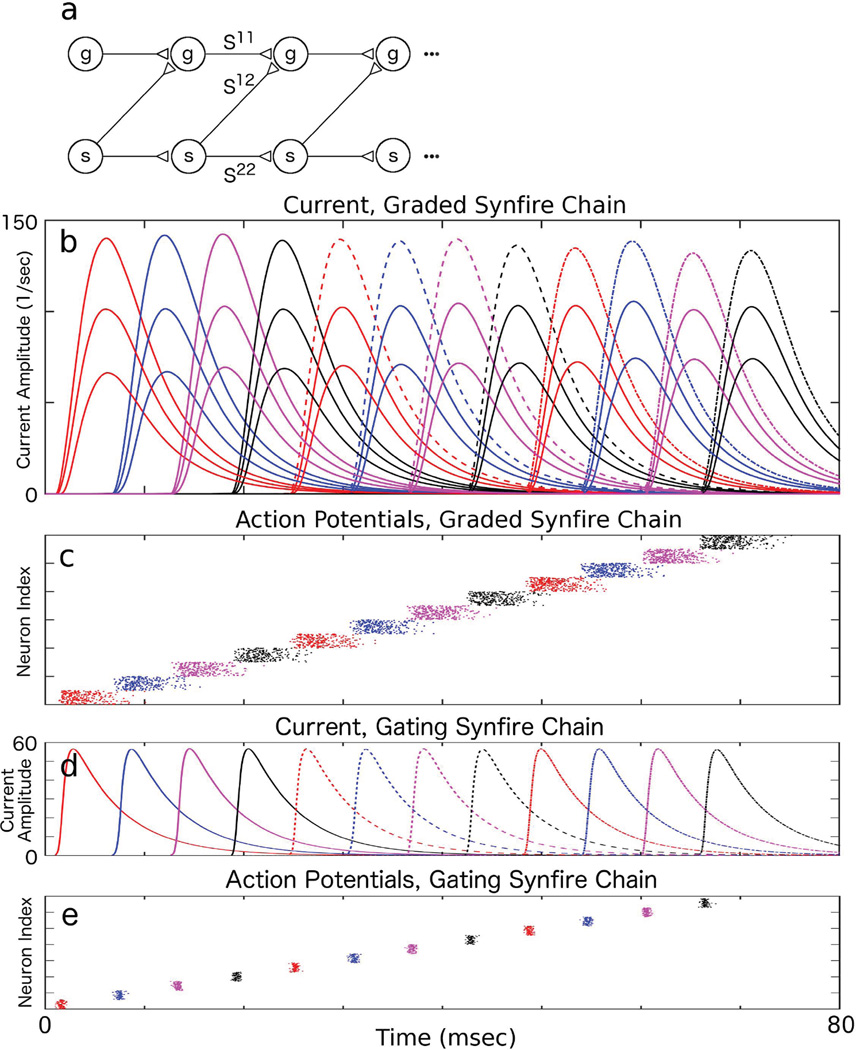
We examine our pulse-gating mechanism in a biologically realistic circuit. Instead of using square gating pulses with unrealistic on- and offset times, we show that we can use the synaptic current generated by a well-studied synfire chain model [51] to gate the synaptic current transfer. In the graded transfer chain, the downstream (d) population receives excitatory synaptic currents from both the upstream (u) population current and from the corresponding synfire (s) population (see Fig. 3a). Note that the synaptic currents generated by the synfire chain play the role of the gating pulse, allowing the upstream population to transfer its current to the downstream population in a graded fashion. In Fig. 3b, we show that our circuit can indeed transfer a stereotypical synaptic current pulse in a graded fashion (3 current amplitudes shown) in an I&F simulation with M = 12 layers. By itself, the gating synfire population is dynamically an attractor, with firing rates of fixed waveform in each layer [51], producing a stereotypical gating current that is repeated across all layers (Fig. 3d). Fig. 3c shows spike times in the populations transferring graded currents and Fig. 3e shows spike times in the gating populations.
FIG. 3.
A Synfire-Gate Synfire Chain (SGSC). a) Neural circuit for an SGSC. b) Mean synaptic current amplitudes (N = 1000 neurons) in a graded synfire chain receiving gating pulses from a synfire chain with coupling set such that it generates constant amplitude pulses (gating synfire chain). c) Action potentials from one realization of the graded synfire chain. d) Mean synaptic current amplitude (N = 100 neurons) from spikes of a gating chain. e) Action potentials from one realization of the gating chain. The mean currents are averaged over 50 realizations.
These results (exact transfer in an analytically tractable mean-field model, the corresponding I&F neuronal network simulations, and the more biologically realistic SGSC model) demonstrate the structural robustness of our graded transfer mechanism. In these cases, a key essential theoretical mechanism was the time window of integration provided by a gating synaptic current (either put in by hand or generated intrinsically by a subpopulation of the neuronal circuit in the SGSC case). We note that, in neural circuits in vivo, time windows provided by gating pulses can be set and controlled by many mechanisms, for instance, time-scales of excitatory and inhibitory postsynaptic currents, absolute and relative refractoriness of individual neurons, time-scales in a high-conductance network state [64, 65] and coherence of the network dynamics. Indeed, different parts of the brain may use different combinations of neuronal and network mechanisms to implement graded current transfer.
A High-Fidelity Memory Circuit
As a first complete example of how graded information may be processed in circuits using pulse-gating, we demonstrate a memory circuit using the mean-field model. Our circuit generalizes the IM model by allowing for graded memory and arbitrary multiplexing of memory to other neural circuits. Because it is a population model, it is more robust to perturbations than the IM model, which transfers spikes between individual neurons. It is different from the IM model in that our circuit retains only one graded amplitude, not many (although this could be arranged) [5]. However, our model retains the multiple timescales that generate theta and gamma oscillations from pulse gating inherent to the IM model [5]. Additionally, other graded memory models based on input integration [45, 66] make use of relatively large time constants that are larger even than NMDA timescales, whereas ours makes use of an arbitrary synaptic timescale, τ, which may be modified to make use of any natural timescale in the underlying neuronal populations, including AMPA or NMDA. Our model is based on exact, analytical expressions, and because of this, the memory is infinitely long-lived at the mean-field level (until finite-size effects and other sources of variability are taken into account).
The circuit has four components, a population for binding a graded amplitude into the circuit (‘read in’), a cyclical memory, a ‘read out’ population meant to emulate the transfer of the graded amplitude to another circuit, and an input population. The memory is a set of n populations coupled one to the other in a circular chain with one of the populations (population 1) receiving gated input from the read in population. Memory populations receive coherent, phase shifted (by phase T) pulses that transfer the amplitude around the chain. In this circuit, n must be large enough that when population n transfers its amplitude back to population 1, population 1’s amplitude has relaxed back to (approximately) zero. The read out is a single population identically coupled to every other population in the circular chain. This population is repeatedly pulsed allowing the graded amplitude in the circular chain to be repeatedly read out.
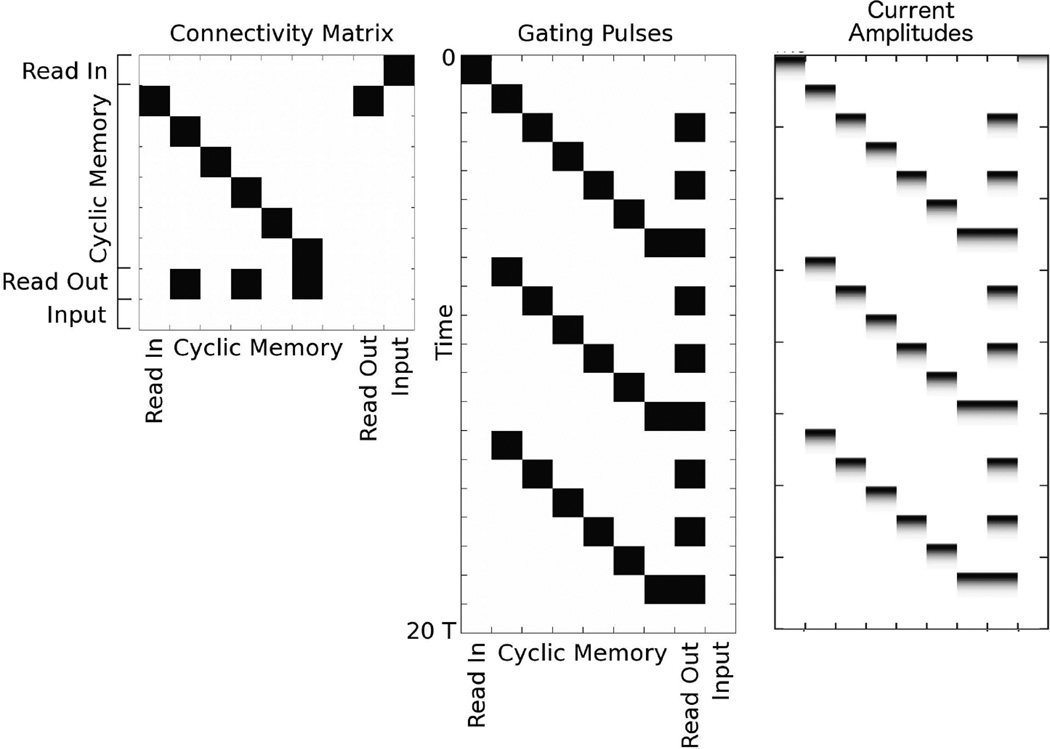
In Fig. 4, we show an example of the memory circuit described here with n = 6. The gating pulses sequentially propagate the graded current amplitude around the circuit. The read out population is coupled to every other population in the memory. Thus, in this example, the oscillation frequency of the read out population is three times that of the memory populations, i.e. theta-band frequencies in the memory populations would give rise to gamma-band frequencies in the read out.
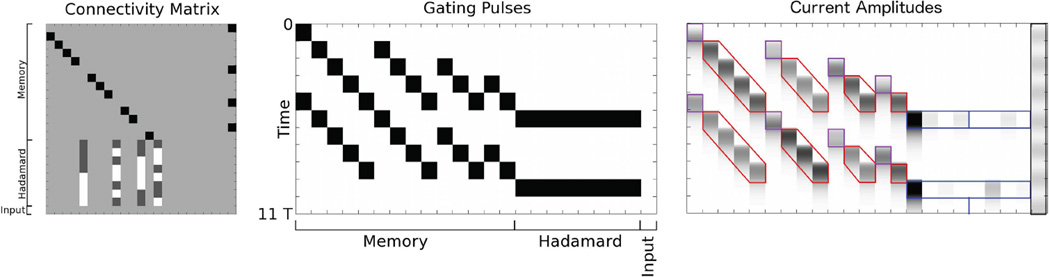
FIG. 4.
Memory circuit maintaining a single graded current amplitude. (Left) Connectivity Matrix. White denotes 0 entries and black denotes 1s. The connectivity matrix is subdivided into four sets of rows. “Input” designates filtered input from an outside source. The first row connects the “Read In” population to the input. The Read In population transduces the filtered input into a graded current packet that then propagates through the memory circuit. The “Cyclic Memory” contains cyclically connected, feedforward populations around which the graded packet is propagated. The “Read Out” population is postsynaptic to every other population in the Cyclic Memory and may be used to transfer graded packets at high frequencies to another circuit. (Middle) Gating Pulses. White denotes 0, black denotes g0, the firing threshold. T/τ = 8. This sequence of gating pulses is used to bind and propagate the graded memory. Time runs from top to bottom. We show three complete cycles of propagation. The initial pulse on the Read In population binds the filtered input. The subsequent pulses within the cyclic memory rotate the packet through the memory populations. The pulses in the Read Out population copy the memory to a distinct population, which could be in another circuit. (Right) Current Amplitudes. White denotes 0, black denotes the maximum for this particular current packet. The input is transduced into the Read In population after time 0 (upper left of panel). The memory is subsequently propagated through the circuit and copied from every other population to the Read Out.
This memory circuit, and other circuits that we present below, has the property that the binding of information is instantiated by the pulse sequence and is independent of the information carried in graded amplitudes and also independent of synaptic processing. Because of the independence of the control apparatus from information content and processing, this neural circuit is an automatic processing pathway whose functional connectivity (both internal and input/output) may be rapidly switched on or off and coupled to or decoupled from other circuits. We propose that such dynamically routable circuits, including both processing and control components, are the neural correlates of automatic cognitive processes that have been termed zombie modes [67].
A Moving Window Fourier Transform
The memory circuit above used one-to-one coupling. It was simple in that information was copied, but not processed. Our second example demonstrates how more complex information processing may be accomplished within a zombie mode. With a simple circuit that performs a Hadamard transform (a Fourier transform using square-wave-shaped Walsh functions as a basis), we show how streaming information may be bound into a memory, then processed via synaptic couplings between populations in the circuit.
A set of read in populations are synaptically coupled to the input. A set of memory chains are coupled to the read in. The final population in each memory chain is coupled via a connectivity matrix that implements a Hadamard transform. Gating pulses cause successive read in and storing in memory of the input until the Hadamard transform is performed once the memory contains all successive inputs in a given time window simultaneously. Because the output of the Hadamard transform may be negative, two populations of Hadamard outputs are implemented, one containing positive coefficients, and another containing absolute values of negative coefficients.
In Fig. 5, we show a zombie mode where four samples are bound into the circuit from an input, which changes continuously in time. Memory populations hold the first sample over four transfers, the second sample over three transfers, etc. Once all samples have been bound within the circuit, the Hadamard transform is performed with a pulse on the entire set of Hadamard read out populations. While this process is occurring, a second sweep of the algorithm begins and a second Hadamard transform is computed.
FIG. 5.
4 × 4 Hadamard transform on a window of input values moving in time. (Left) Connectivity Matrix. White denotes −1/2, light gray denotes 0, dark gray denotes 1/2, and black denotes 1. The connectivity matrix is subdivided into three sets of rows. “Memory” designates Read In and (non-cyclic) Memory populations. “Hadamard” designates populations for the calculation of Hadamard coefficients. Because the packet amplitudes can only be positive, the Hadamard transform is divided into two parallel operations, one that results in positive coefficients and one that results in absolute values of negative coefficients. “Input” designates filtered input from an outside source. (Middle) Gating Pulses. White denotes 0, black denotes g0. T/τ = 2. Time runs from top to bottom. We show the computation for two successive windows, each of length 4T. The pulses transduce the input into four memory chains of length 4T, 3T, 2T and T. Thus, four temporally sequential inputs are bound in four of the memory populations beginning at times t = 4, 8T. Hadamard transforms are performed beginning at t = 5, 9T. Note that the second read in starts one packet length before the Hadamard transform so that the temporal windows are adjacent. (Right) Current Amplitudes. White denotes 0, black denotes the maximum current amplitude. Purple outlines denote Read In, red denote Memory and blue denote Hadamard transform populations. The left four Hadamard outputs are positive coefficients. The right four are absolute values of negative coefficients. The sinusoidal input waveform is shown to the right.
The connectivity matrix for the positive coefficients of the Hadamard transform was given by
and the absolute values of the negative coefficients used the transform −H.
A Re-entrant Spatial Rotation Circuit
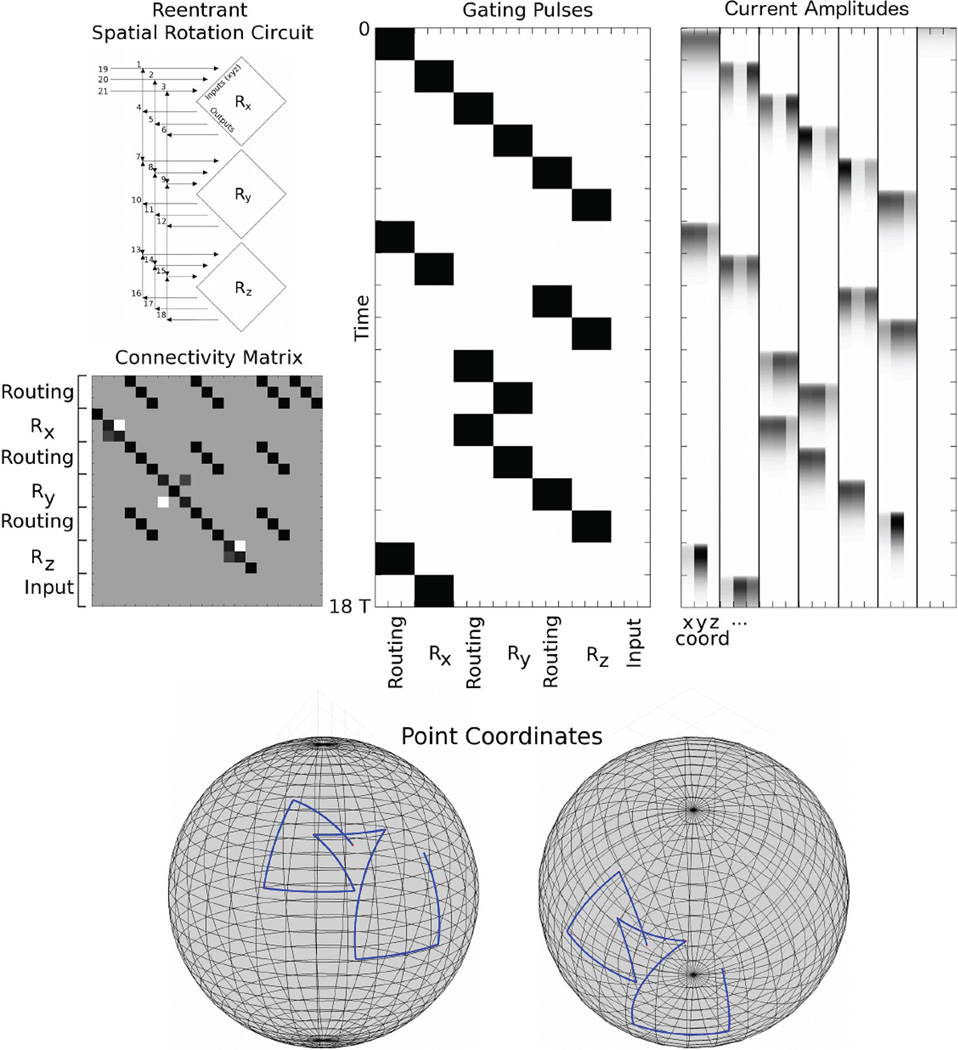
Our final example makes use of plastic internal connectivity to perform an arbitrary set of rotations of a vector on the sphere. Three fixed angle rotations about the x, y and z axes are arranged such that the output from each rotation may be copied to the input of any of the rotations. Because the destination is determined by the pattern of gating pulses, this circuit is more general than a zombie mode with a fixed gating pattern because it is not automatic: manipulation of the rotations would be expected to occur from a separate routing control circuit (here, implemented by hand).
In Fig. 6, initial spatial coordinates of (1, 1, 1) were input to the circuit. The pulse sequence rotated the input first about the x-axis, then sequentially about y, z, x, z, y, y, z, x axes. Views from two angles illustrate the rotations that were performed by the circuit.
FIG. 6.
Spatial rotation of three-dimensional coordinates. (Left, Top) A diagram of the circuit. Diamonds represent spatial rotation about the given axis, x, y, or z, by angle 2π/10. Rx takes coordinates 1, 2 and 3 as input and outputs 4, 5 and 6. Ry takes 7, 8 and 9 as inputs and outputs 10, 11 and 12. And Rz takes 13, 14 and 15 as input and outputs 16, 17 and 18. Outputs may be routed to any of Rx, Ry or Rz giving a reentrant circuit. (Left, Bottom) Connectivity Matrix. Light gray denotes −sin (2π/10), gray denotes 0, dark gray denotes sin (2π/10), black denotes 1, with some black squares representing cos (2π/10) indistinguishable from 1. Input may be read into 1, 2 and 3 only. Outputs of the rotations may be read into any of (1, 2, 3), (7, 8, 9) or (13, 14, 15) and subsequent rotations performed on these amplitudes. (Middle) Gating Pulses. White denotes 0, black denotes g0. T/τ = 3. Time runs from top to bottom. We show read in, then routing of the coordinates through Rx, Ry, Rz, Rx, Rz, Ry, Ry, Rz, and Rx, successively. (Right) Current Amplitudes. Initially uniform coordinates (x, y, z) = (1, 1, 1), are successively rotated about the various axes. (Bottom) Two views of the coordinates connected by geodesics as they are rotated.
This circuit demonstrates the flexibility of the information coding network that we have introduced. It shows a complex circuit capable of rapid computation with dynamic routing, but with a fixed connectivity matrix. Additionally, it is an example of how a set of non-commuting generators may be used to form elements of a non-abelian group within our framework.
DISCUSSION
The existence of graded transfer mechanisms, such as the one that we have found, points toward a natural modular organization wherein each neural circuit would be expected to have 1) sparsely coupled populations of neurons that encode information content, 2) pattern generators that provide accurately timed pulses to control information flow, and 3) regulatory mechanisms for maintaining optimal transfer.
A huge literature now exists implicating oscillations as an important mechanism for information coding. Our mechanism provides a fundamental building block with which graded information content may be encoded and transferred in current amplitudes, dynamically routed with coordinated pulses, and transformed and processed via synaptic weights. From this perspective, coherent oscillations may be an indication that a neural circuit is performing complex computations pulse by pulse.
Our mechanism for graded current transfer has allowed us to construct a conceptual framework for the active manipulation of information in neural circuits. The most important aspect of this type of information coding is that it separates control of the flow of information from information processing and the information itself. This type of segregation has been made use of previously [5, 44, 49, 50] in mechanisms for gating the propagation of fixed amplitude waveforms. Here, by generalizing the mechanism to the propagation of graded information, active linear maps take prominence as a key processing structure in information coding.
The four functions that must be served by a neural code are [31, 68]: stimulus representation, interpretation, transformation and transmission. Our framework serves three of these functions, and we believe is capable of being extended to the fourth. From last to first: the exact transfer mechanisms that we have identified serve the transmission function; synaptic couplings provide the capability of transforming information; the pulse dependent, selective read out of information in part serves the interpretation function. In the examples that we showed above changes in pulse sequences were introduced by hand, but we argued in the Methods section that interaction of pulse chains should be able to achieve fully general decision making. Finally, read in populations, as we demonstrated in our examples, may be used to convert stimulus information into a bound information representation.
The current transfer mechanism is sufficiently flexible that the pulses used for gating may be of different durations depending on the pulse length, T, and the time constant, τ, of the neuronal population involved.
The separation of control populations from those representing information content distinguishes our framework from mechanisms such as CTC, where communication between neuronal populations depends on the co-incidence of integration windows in phase-coherent oscillations. In the CTC mechanism, information containing spikes must coincide to be propagated. In our framework, information containing spikes must coincide with gating pulses that enable communication. In this sense, it is ‘communication through coherence with a control mechanism’.
The separation of control and processing has further implications, one of which is that, as noted above, while a given zombie mode is processing incoming information, one does not expect the pulse sequence to change dependent on the information content. This has been seen in experiment, and presented as an argument against CTC in the visual cortex [69], but is consistent with our framework.
The basic unit of computation in our framework is a pulse gated transfer. Given this, we suggest that each individual pulse within an oscillatory set of pulses represents the transfer and processing of a discrete information packet. For example, in a sensory circuit that needs to quickly and repeatedly process a streaming external stimulus, short pulses could be repeated in a stereotyped, oscillatory manner using high-frequency gamma oscillations to rapidly move bound sensory information through the processing pathway. Circuits that are used occasionally or asynchronously might not involve oscillations at all, just a precise sequence of pulses that gate a specific information set through a circuit. A possible example of such an asynchronous circuit is bat echo-location, an active sensing mechanism, where coherent oscillations have not been seen [70].
An important point to note is that, given a zombie mode that implements an algorithm for processing streaming input, one can straightforwardly predict the rhythms that the algorithm should produce (for instance in our examples, calculate power spectra of the current amplitudes.). This feature of zombie modes can provide falsifiable hypotheses for putative computations that the brain uses to process information.
Since, with our transfer mechanism, information routing is enacted via precisely timed pulses, neural pattern generators would be expected to be information control centers. Cortical pattern generators, such as those proposed by Yuste [71] or hubs proposed by Jahnke, et al. [49], because of their proximity to cortical circuits, could logically be the substrate for zombie mode control pulses. They would be expected to generate sequential, stereotyped pulses to dynamically route information flow through a neural circuit, as has been found in rat somatosensory cortex [72]. Global routing of information via attentional processes, on the other hand, would be expected to be performed from brain regions with broad access to the cortex, such as regions in the basal ganglia or thalamus.
Recent evidence shows that parvalbumin-positive basket cells (PVBCs) can gate the conversion of current to spikes in the amygdala [73]. Also, PVBCs and oriens lacunosum moleculare (OLM) cells have been implicated in precision spiking related to gamma- and theta-oscillations [43] and shown to be involved in memory-related structural-plasticity [74]. Therefore, zombie mode pattern generators would likely be based on a substrate of these neuron types.
Acknowledgements
L.T. thanks the UC Davis Mathematics Department for its hospitality. This work was supported by the Ministry of Science and Technology of China through the Basic Research Program (973) 2011CB809105 (W.Z. and L.T.), by the Natural Science Foundation of China grant 91232715 (W.Z. and L.T.) and by the National Institutes of Health, CRCNS program NS090645 (A.S. and L.T.). We thank Tim Lewis and Antoni Guillamon for reading and commenting on a draft of this paper.
Contributor Information
Andrew T. Sornborger, Department of Mathematics, University of California, Davis, USA, ats@math.ucdavis.edu
Zhuo Wang, Center for Bioinformatics, National Laboratory of Protein Engineering and Plant Genetic Engineering, College of Life Sciences, Peking University, Beijing, China, wangz@mail.cbi.pku.edu.cn.
Louis Tao, Center for Bioinformatics, National Laboratory of Protein Engineering and Plant Genetic Engineering, College of Life Sciences, and Center for Quantitative Biology, Peking University, Beijing, China, taolt@mail.cbi.pku.edu.cn.
References
- 1.Azouz R, Gray CM. Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc. Natl. Acad. Sci. USA. 2000;97:8110–8115. doi: 10.1073/pnas.130200797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- 3.Markowska AL, Olton DS, Givens B. Cholinergic manipulations in the medial septal area: Age-related effects on working memory and hippocampal electrophysiology. J. Neurosci. 1995;15:2063–2073. doi: 10.1523/JNEUROSCI.15-03-02063.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Abeles M. Role of the cortical neuron: Integrator or coincidence detector? Isr. J. Med. Sci. 1982;18:83–92. [PubMed] [Google Scholar]
- 5.Lisman JE, Idiart MA. Storage of 7 ± 2 short-term memories in oscillatory subcycles. Science. 1995;267:1512–1515. doi: 10.1126/science.7878473. [DOI] [PubMed] [Google Scholar]
- 6.Salinas E, Sejnowski TJ. Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci. 2001;2:539–550. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gray CM, König P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- 8.Bragin A, Jandó G, Nádasdy Z, Hetke J, Wise K, Buzsáki G. Gamma (40 – 100 Hz) oscillation in the hippocampus of the behaving rat. J. Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Csicsvari J, Jamieson B, Wise K, Buzsáki G. Mechanisms of gamma oscillations in the hippocampus of the behaving rat. Neuron. 2003;37:311–322. doi: 10.1016/s0896-6273(02)01169-8. [DOI] [PubMed] [Google Scholar]
- 10.Colgin L, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser M, Moser E. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:75–78. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- 11.Livingstone MS. Oscillatory firing and interneuronal correlations in squirrel monkey striate cortex. J. Neurophysiol. 1996;66:2467–2485. doi: 10.1152/jn.1996.75.6.2467. [DOI] [PubMed] [Google Scholar]
- 12.Brosch M, Budinger E, Scheich H. Stimulus-related gamma oscillations in primate auditory cortex. J. Neurophysiol. 2002;87:2715–2725. doi: 10.1152/jn.2002.87.6.2715. [DOI] [PubMed] [Google Scholar]
- 13.Bauer M, Oostenveld R, Peeters M, Fries P. Tactile spatial attention enhances gamma-band activity in somatosensory cortex and reduces low-frequency activity in parieto-occipital areas. J. Neurosci. 2006;26:490–501. doi: 10.1523/JNEUROSCI.5228-04.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat. Neurosci. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- 15.Buschman TJ, Miller EK. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science. 2007;315:1860–1862. doi: 10.1126/science.1138071. [DOI] [PubMed] [Google Scholar]
- 16.Medendorp WP, Kramer GF, Jensen O, Oostenveld R, Schoffelen JM, Fries P. Oscillatory activity in human parietal and occipital cortex shows hemispheric lateralization and memory effects in a delayed double-step saccade task. Cereb. Cortex. 2007;17:2364–2374. doi: 10.1093/cercor/bhl145. [DOI] [PubMed] [Google Scholar]
- 17.Gregoriou GG, Gotts SJ, Zhou H, Desimone R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science. 2009;324:1207–1210. doi: 10.1126/science.1171402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sohal VS, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature. 2009;459:698–702. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Popescu AT, Popa D, Paré D. Coherent gamma oscillations couple the amygdala and striatum during learning. Nat. Neurosci. 2009;12:801–807. doi: 10.1038/nn.2305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Henrie JA, Shapley R. LFP power spectra in V1 cortex: The graded effect of stimulus contrast. J. Neurophysiol. 2005;94:479–490. doi: 10.1152/jn.00919.2004. [DOI] [PubMed] [Google Scholar]
- 21.Liu J, Newsome WT. Local field potential in cortical area MT; Stimulus tuning and behavioral correlations. J. Neurosci. 2006;26:7779–7790. doi: 10.1523/JNEUROSCI.5052-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- 23.Fries P, Womelsdorf T, Oostenveld R, Desimone R. The effects of visual stimulation and selective visual attention on rhythmic neuronal synchronization in macaque area V4. J. Neurosci. 2008;28:4823–4835. doi: 10.1523/JNEUROSCI.4499-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bosman CA, Schoffelen JM, Brunet N, Oostenveld R, Bastos AM, Womelsdorf T, Rubehn B, Stieglitz T, de Weerd P, Fries P. Stimulus selection through selective synchronization between monkey visual areas. Neuron. 2012;75:875–888. doi: 10.1016/j.neuron.2012.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Saalmann YB, Pigarev IN, Vidyasagar TR. Neural mechanisms of visual attention: How top-down feed-back highlights relevant locations. Science. 2007;316:1612–1615. doi: 10.1126/science.1139140. [DOI] [PubMed] [Google Scholar]
- 26.O’Keefe J. Hippocampus, theta, and spatial memory. Curr. Opin. Neurobiol. 1993;3:917–924. doi: 10.1016/0959-4388(93)90163-s. [DOI] [PubMed] [Google Scholar]
- 27.Buzsáki G. Theta oscillations in the hippocampus. Neuron. 2002;33:325–340. doi: 10.1016/s0896-6273(02)00586-x. [DOI] [PubMed] [Google Scholar]
- 28.Skaggs WE, McNaughton BL, Wilson MA, Barnes CA. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus. 1996;6:149–172. doi: 10.1002/(SICI)1098-1063(1996)6:2<149::AID-HIPO6>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 29.Winson J. Loss of hippocampal theta rhythm results in spatial memory deficit in the rat. Science. 1978;201:160–163. doi: 10.1126/science.663646. [DOI] [PubMed] [Google Scholar]
- 30.Quian Quiroga R, Panzeri S. Principles of neural coding. London: CRC Press; 2013. [Google Scholar]
- 31.Kumar A, Rotter S, Aertsen A. Spiking activity propagation in neuronal networks: Reconciling different perspectives on neural coding. Nat. Rev. Neurosci. 2010;11:615–627. doi: 10.1038/nrn2886. [DOI] [PubMed] [Google Scholar]
- 32.Adrian ED, Zotterman Y. The impulses produced by sensory nerve-endings: Part II. The response of a single-end organ. J. Physiol. 1926;61:151–171. doi: 10.1113/jphysiol.1926.sp002281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hubel DH, Wiesel TN. Receptive fields and functional architecture in two non striate visual areas (18 and 19 of the cat. J. Neurophysiol. 1965;28:229–289. doi: 10.1152/jn.1965.28.2.229. [DOI] [PubMed] [Google Scholar]
- 34.Hubel DH, Wiesel TN. Receptive fields and functional architecture of monkey striate cortex. J. Physiol. 1968;195:215–243. doi: 10.1113/jphysiol.1968.sp008455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kaissling KE, Priesner E. Smell threshold of the silkworm. Naturwissenschaften. 1970;57:23–28. doi: 10.1007/BF00593550. [DOI] [PubMed] [Google Scholar]
- 36.Bair W, Koch C. Temporal precision of spike trains in extrastriate cortex of the behaving macaque monkey. Neural Comput. 1996;8:1185–1202. doi: 10.1162/neco.1996.8.6.1185. [DOI] [PubMed] [Google Scholar]
- 37.Knight BW. Dynamics of encoding in a population of neurons. J. Gen. Physiol. 1972;59:734–766. doi: 10.1085/jgp.59.6.734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Knight BW. Dynamics of encoding in a population of neurons: Some general mathematical features. Neural Comput. 2000;12:473–518. doi: 10.1162/089976600300015673. [DOI] [PubMed] [Google Scholar]
- 39.Sirovich L, Knight BW, Omurtag A. Dynamics of neuronal populations: The equilibrium solution. SIAM J. Appl. Math. 1999;60:2009–2028. [Google Scholar]
- 40.Gerstner W. Time structure of the activity in neural network models. Phys. Rev. E. 1995;51:738–758. doi: 10.1103/physreve.51.738. [DOI] [PubMed] [Google Scholar]
- 41.Brunel N, Hakim V. Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Comput. 1999;11:1621–1671. doi: 10.1162/089976699300016179. [DOI] [PubMed] [Google Scholar]
- 42.Butts DA, Weng C, Jin J, Yeh CI, Lesica NA, Alonso JM, Stanley GB. Temporal precision in the neural code and the timescales of natural vision. Nature. 2007;449:92–95. doi: 10.1038/nature06105. [DOI] [PubMed] [Google Scholar]
- 43.Varga C, Golshani P, Soltesz I. Frequency-invariant temporal ordering of interneuronal discharges during hippocampal oscillations in awake mice. Proc. Natl. Acad. Sci. U.S.A. 2012;109:E2726–E2734. doi: 10.1073/pnas.1210929109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jensey O, Lisman JE. Hippocampal sequence-encoding driven by a cortical multi-item working memory buffer. Trends Neurosci. 2005;28:67–72. doi: 10.1016/j.tins.2004.12.001. [DOI] [PubMed] [Google Scholar]
- 45.Goldman MS. Memory without feedback in a neural network. Neuron. 2008;61:621–634. doi: 10.1016/j.neuron.2008.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.König P, Engel AK, Singer W. Integrator or coincidence detector? The role of the cortical neuron revisited. Trends Neurosci. 1996;19:130–137. doi: 10.1016/s0166-2236(96)80019-1. [DOI] [PubMed] [Google Scholar]
- 47.Fries P. A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. Trends Cogn. Sci. 2005;9:474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
- 48.Rubin JE, Terman D. High frequency stimulation of the subthalamic nucleus eliminates pathological thalamic rhythmicity in a computational model. J. Comp. Neurosci. 2004;16:211–235. doi: 10.1023/B:JCNS.0000025686.47117.67. [DOI] [PubMed] [Google Scholar]
- 49.Jahnke S, Memmesheimer RM, Timme M. Hub-activated signal transmission in complex networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2014 Mar;89(3):030701. doi: 10.1103/PhysRevE.89.030701. [DOI] [PubMed] [Google Scholar]
- 50.Jahnke S, Memmesheimer RM, Timme M. Oscillation-induced signal transmission and gating in neural circuits. PLoS Comput. Biol. 2014 Dec;10(12):e1003940. doi: 10.1371/journal.pcbi.1003940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Diesmann M, Gewaltig MO, Aertsen A. Stable propagation of synchronous spiking in cortical neural networks. Nature. 1999;402:529–533. doi: 10.1038/990101. [DOI] [PubMed] [Google Scholar]
- 52.Kremkow J, Aertsen A, Kumar A. Gating of signal propagation in spiking neural networks by balanced and correlated excitation and inhibition. J. Neurosci. 2010;30:15760–15768. doi: 10.1523/JNEUROSCI.3874-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kistler WM, Gerstner W. Stable propagation of activity pulses in populations of spiking neurons. Neural Computation. 2002;14:987–997. doi: 10.1162/089976602753633358. [DOI] [PubMed] [Google Scholar]
- 54.Bienenstock E. A model of neocortex. Network: Comp. in Neural Systems. 1995;6:179–224. [Google Scholar]
- 55.Litvak V, Sompolinsky H, Segev I, Abeles M. On the transmission of rate code in long feedforward networks with excitatory-inhibitory balance. J. Neurosci. 2003 Apr;23(7):3006–3015. doi: 10.1523/JNEUROSCI.23-07-03006.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Reyes AD. Synchrony-dependent propagation of firing rate in iteratively constructed networks in vitro. Nat. Neurosci. 2003 Jun;6(6):593–599. doi: 10.1038/nn1056. [DOI] [PubMed] [Google Scholar]
- 57.Jahnke S, Memmesheimer RM, Timme M. Propagating synchrony in feed-forward networks. Front Comput Neurosci. 2013;7:153. doi: 10.3389/fncom.2013.00153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Feinerman O, Moses E. Transport of information along unidimensional layered networks of dissociated hippocampal neurons and implications for rate coding. J. Neurosci. 2006 Apr;26(17):4526–4534. doi: 10.1523/JNEUROSCI.4692-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.van Rossum MC, Turrigiano GG, Nelson SB. Fast propagation of firing rates through layered networks of noisy neurons. J. Neurosci. 2002 Mar;22(5):1956–1966. doi: 10.1523/JNEUROSCI.22-05-01956.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Shelley M, McLaughlin D. Coarse-grained reduction and analysis of a network model of cortical response: I. Drifting grating stimuli. J Comput Neurosci. 2002;12(2):97–122. doi: 10.1023/a:1015760707294. [DOI] [PubMed] [Google Scholar]
- 61.Vogels TP, Abbott LF. Signal propagation and logic gating in networks of integrate-and-fire neurons. J Neurosci. 2005;25:10786–10795. doi: 10.1523/JNEUROSCI.3508-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Shinozaki T, Okada M, Reyes AD, Cateau H. Flexible traffic control of the synfire-mode transmission by inhibitory modulation: nonlinear noise reduction. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;81:011913. doi: 10.1103/PhysRevE.81.011913. [DOI] [PubMed] [Google Scholar]
- 63.Cassidy AS, Merolla P, Arthur JV, Esser SK, Jackson B, Alvarez-Icaza R, Datta P, Sawada J, Wong TM, Feldman V, Amir A, Rubin DB-D, Akopyan F, McQuinn E, Risk WP, Modha DS. Cognitive computing building block: A versatile and efficient digital neuron model for neurosynaptic cores; Neural Networks (IJCNN), The 2013 International Joint Conference; 2013. Aug, pp. 1–10. [Google Scholar]
- 64.Shelley M, McLaughlin D, Shapley R, Wielaard J. States of high conductance in a large-scale model of the visual cortex. J Comput Neurosci. 2002;13(2):93–109. doi: 10.1023/a:1020158106603. [DOI] [PubMed] [Google Scholar]
- 65.Destexhe A, Rudolph M, Pare D. The high-conductance state of neocortical neurons in vivo. Nat. Rev. Neurosci. 2003 Sep;4(9):739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
- 66.Seung SH, Lee DD, Reis BY, Tank DW. Stability of the memory of eye position in a recurrent network of conductance-based model neurons. Neuron. 2000;26:259–271. doi: 10.1016/s0896-6273(00)81155-1. [DOI] [PubMed] [Google Scholar]
- 67.Crick F, Koch C. A framework for consciousness. Nat. Neurosci. 2003;6:119–126. doi: 10.1038/nn0203-119. [DOI] [PubMed] [Google Scholar]
- 68.Perkel DH, Bullock TH. Neural coding: a report based on an NRP work session. Neurosci Res Program Bull. 1968;6:219–349. [Google Scholar]
- 69.Thiele A, Stoner G. Neuronal synchrony does not correlate with motion coherence in cortical area MT. Nature. 2003;421:366–370. doi: 10.1038/nature01285. [DOI] [PubMed] [Google Scholar]
- 70.Yartsev MM, Witter MP, Ulanovsky N. Grid cells without theta oscillations in the entorhinal cortex of bats. Nature. 2011;479:103–107. doi: 10.1038/nature10583. [DOI] [PubMed] [Google Scholar]
- 71.Yuste R, MacLean JN, Smith J, Lansner A. The cortex as a central pattern generator. Nat. Rev. Neurosci. 2005;6:477–483. doi: 10.1038/nrn1686. [DOI] [PubMed] [Google Scholar]
- 72.Luczak A, Bartho P, Marguet SL, Buzsaki G, Harris KD. Sequential structure of neocortical spontaneous activity in vivo. Proc. Natl. Acad. Sci. U.S.A. 2007;104:347–352. doi: 10.1073/pnas.0605643104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Wolff SB, Grundemann J, Tovote P, Krabbe S, Jacobson GA, Muller C, Herry C, Ehrlich I, Friedrich RW, Letzkus JJ, Luthi A. Amygdala interneuron subtypes control fear learning through disinhibition. Nature. 2014;509:453–458. doi: 10.1038/nature13258. [DOI] [PubMed] [Google Scholar]
- 74.Klausberger T, Magill PJ, Marton LF, Roberts JD, Cobden PM, Buzsaki G, Somogyi P. Brain-state-and cell-type-specific firing of hippocampal interneurons in vivo. Nature. 2003;421:844–848. doi: 10.1038/nature01374. [DOI] [PubMed] [Google Scholar]