Electrical and Optical Activation of Mesoscale Neural Circuits with Implications for Coding

Abstract

Artificial activation of neural circuitry through electrical microstimulation and optogenetic techniques is important for both scientific discovery of circuit function and for engineered approaches to alleviate various disorders of the nervous system. However, evidence suggests that neural activity generated by artificial stimuli differs dramatically from normal circuit function, in terms of both the local neuronal population activity at the site of activation and the propagation to downstream brain structures. The precise nature of these differences and the implications for information processing remain unknown. Here, we used voltage-sensitive dye imaging of primary somatosensory cortex in the anesthetized rat in response to deflections of the facial vibrissae and electrical or optogenetic stimulation of thalamic neurons that project directly to the somatosensory cortex. Although the different inputs produced responses that were similar in terms of the average cortical activation, the variability of the cortical response was strikingly different for artificial versus sensory inputs. Furthermore, electrical microstimulation resulted in highly unnatural spatial activation of cortex, whereas optical input resulted in spatial cortical activation that was similar to that induced by sensory inputs. A thalamocortical network model suggested that observed differences could be explained by differences in the way in which artificial and natural inputs modulate the magnitude and synchrony of population activity. Finally, the variability structure in the response for each case strongly influenced the optimal inputs for driving the pathway from the perspective of an ideal observer of cortical activation when considered in the context of information transmission.

SIGNIFICANCE STATEMENT Artificial activation of neural circuitry through electrical microstimulation and optogenetic techniques is important for both scientific discovery and clinical translation. However, neural activity generated by these artificial means differs dramatically from normal circuit function, both locally and in the propagation to downstream brain structures. The precise nature of these differences and the implications for information processing remain unknown. The significance of this work is in quantifying the differences, elucidating likely mechanisms underlying the differences, and determining the implications for information processing.

Introduction

Artificial stimulation approaches afford the ability to interrogate neural circuit function for basic discovery and potentially replace function lost to trauma or disease by acting as surrogate inputs to the nervous system. Electrical stimulation remains the only clinically viable means of artificial stimulation on fast timescales, whereas optogenetic stimulation has revolutionized the ability to dissect neural circuits experimentally. However, behavioral (Masse and Cook, 2010) and electrophysiological (Logothetis et al., 2010) evidence suggests that neural activity generated by natural and artificial stimuli differentially propagate to downstream structures. The distinct mechanisms by which natural and artificial inputs engage the circuitry are not well understood, and the ultimate coding relevance for the downstream signals remains unknown.

Sensory and artificial stimuli activate neural populations through distinct mechanisms, perhaps most notably in the degree to which neurons are synchronized by artificial stimuli (Boyden et al., 2005; Wagenaar et al., 2005). The degree of synchronization of spiking across a neuronal population significantly affects the faithful propagation of neural activity to downstream structures (Kumar et al., 2010), particularly in driving reliable cortical responses in the early sensory pathways (Bruno and Sakmann, 2006; Wang et al., 2010a). Indeed, the synchrony of early-stage sensory neurons is modulated by the properties of the sensory stimulus (Pinto et al., 2000; Temereanca et al., 2008; Wang et al., 2010b). The regulation of population synchronization has thus been proposed as a mechanism by which information flow is gated in neural pathways (Wang et al., 2010b). In this context, the degree to which sensory or artificial stimuli synchronize neuronal populations may influence how information is coded. We hypothesize that this population synchronization combined with the volumetric effects of current injection or light activation on the tissue together serve as the primary determinants of the activation of downstream structures. However, we further postulate that principled design of artificial stimuli can overcome the distinct mechanisms of circuit engagement to produce functionally relevant patterns of neural activation.

In this study, we measured directly the propagation of neural activity generated by sensory and artificial stimuli, investigated the mechanistic differences in circuit engagement through a computational network model, and established a theoretical framework to evaluate the downstream coding consequences of artificial stimuli as surrogate inputs. Specifically, we used voltage-sensitive dye imaging (VSDI) of primary somatosensory cortex (S1) in the anesthetized rat in response to deflections of the facial vibrissae and electrical or optogenetic stimulation of neurons in the thalamus. For each of the input modalities, we quantified the amplitude, variability, and spatial spread of the cortical response, finding distinct and repeatable differences in the way sensory and artificial inputs activated the cortex. Then, using a model of the thalamocortical circuit, we quantified the relative roles of the magnitude and synchrony of the activation of the input population in predicting the experimentally observed cortical variability. Finally, we explored the coding ramifications of the distinct neural response statistics associated with sensory and artificial stimulation in the context of generating maximally discriminable neural responses in downstream structures.

Materials and Methods

Experimental preparation.

All procedures were approved by the Georgia Institute of Technology Institutional Animal Care and Use Committee and followed guidelines established by the National Institutes of Health. Female Sprague Dawley rats (250–300 g) were initially anesthetized with 4% isoflurane before intraperitoneal injection of Nembutal (50 mg/kg weight) for long-term anesthesia. Subsequent doses of Nembutal were used to maintain a surgical level of anesthesia.

Animals were mounted in a stereotactic device, and a craniotomy was performed over the left parietal cortex (coordinates: 1–4 mm posterior to bregma, 4–7 mm lateral to midline) to expose the barrel representation of the S1 (Paxinos and Watson, 1998). Another craniotomy was performed to allow access to the ventral posteromedial (VPm) region of the thalamus (coordinates: 2–4 mm posterior to bregma, 1.5–2.5 mm lateral to midline, 4.5–5.5 mm depth at a 12° angle to the brain surface).

A subset of the animals underwent an initial survival surgery, during which the viral vector [AAV2–CaMKIIa–hChR2(H134R)–mCherry; University of North Carolina Viral Vector Core, Chapel Hill, NC] was delivered to the thalamus using stereotactic coordinates. The injection was delivered at 0.2 μl/min for 5 min for a total of 1 μl. The animals were allowed to recover for 3–4 weeks, providing time for the channelrhodopsin 2 (ChR2) expression to reach functional levels.

VSDI.

VSDI was used to monitor cortical activation in response to thalamic microstimulation according to methods described previously (Wang et al., 2012). The VSDI data were acquired at 5 ms interframe intervals beginning 200 ms preceding stimulus presentation.

Multiple trials of VSDI data were collected for each stimulus. For each trial, the 40 frames (200 ms) collected before the presentation of the stimulus were averaged to calculate the background fluorescence, against which the activation was measured. For each frame, the background fluorescence was subtracted to produce a differential signal ΔF. Additionally, each frame was divided by the background image to normalize for uneven illumination and staining to produce the signal ΔF/F₀. The initial frame of activation was used for all stimuli. For visual presentation purposes only, the individual trials were averaged together and then filtered with a 9 × 9 pixel (∼200 × ∼200 μm) spatial averaging filter.

The anatomical mapping, acquired through cytochrome oxidase histology, was registered with the functional cortical column mapping from VSDI by solving a linear inverse problem, the details of which have been described previously (Wang et al., 2012). After the functional image registration, the cortical response was discretized, in which each signal corresponds to the average of the pixels contained within a single functional cortical column. An example of the resulting signal is shown in Figure 1B for individual trials (gray lines) and the mean across trials (black), in response to the deflection of a single whisker.

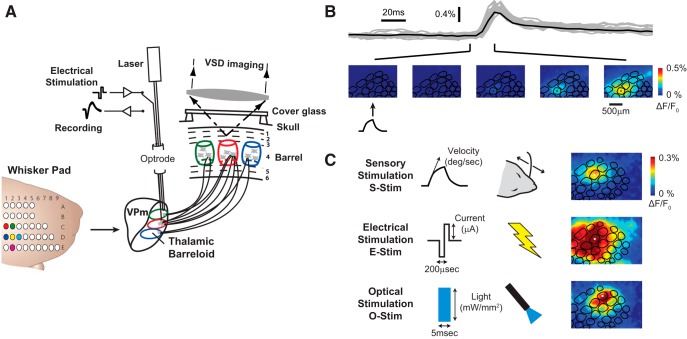
Figure 1.

VSDI captures the cortical response with high spatial and temporal resolution. A, Diagram of the imaging system. The optrode was positioned in a barreloid in the thalamus, a collection of cells that respond most vigorously to a common whisker. Imaging in the cortex captured the response of each cortical column. Histological analysis provides an anatomical map of the cortical column structure (see Materials and Methods). B, The cortical response to whisker stimulation (1200°/s) begins ∼10–15 ms after stimulation, in a focal location before growing in amplitude. C, Trial-averaged examples of the cortical response to whisker (1200°/s), electrical (50 μA), and optical (100 mW/mm²) stimuli delivered within a single experiment.

Whisker stimulation.

Whiskers were trimmed at ∼12 mm from the face and were inserted into a glass pipette fixed to the end of a calibrated multilayered piezoelectric bimorph bending actuator (range of motion, 1 mm; bandwidth, 200 Hz; Physik Instrumente) positioned 10 mm from the vibrissa pad. Vibrissae were always deflected in the rostrocaudal plane. Punctate deflections consisted of exponential rising and falling phases (99% rise time, 5 ms; 99% fall time, 5 ms), with varying angular deflection velocity (75–1200°/s). In a subset of experiments (n = 2), whiskers were stimulated with brief puffs of air as described previously (Ollerenshaw et al., 2012).

Electrical stimulation.

A glass-coated tungsten microelectrode (impedance, 1–2 MΩ at 1 kHz) was advanced to the VPm region of the thalamus using a precision microdrive (David Knopf Instruments). The principal vibrissa was determined by manually deflecting individual whiskers and confirmed using the latency and spike count of single-unit recordings in response to controlled whisker deflection using a piezoelectric actuator. In the event that single-unit recordings could not be achieved, multiunit activity was used.

After electrophysiological determination of the electrode position and its associated principal vibrissa, the electrode was used to deliver microstimulation to the surrounding tissue. The stimulus waveforms were designed using a digital stimulus generator (WPI) and delivered using a current-controlled, optically isolated stimulator (WPI). Individual electrical stimuli were charge-balanced, cathodal-first, biphasic waveforms of 200 μs duration per phase. A series of single electrical stimulation pulses with varying amplitude between 10 and 100 μA was used to test the static nonlinearity of the neural circuit. The current range was chosen to elicit the full range of subthreshold to maximal cortical responses.

Optical stimulation.

For optical stimulation, an “optrode” was used. The optrode consisted of a multimode optical fiber (105 μm core diameter, 125 μm coating diameter, 0.22 numerical aperture; Thorlabs) and one or two quartz-coated platinum–tungsten microelectrodes (80 μm diameter; Thomas Recording). The microelectrodes were pulled and ground to an impedance of 1–2 MΩ at 1 kHz. The optical fiber was also ground to a fine point, producing a spherical, rather than conical, pattern of light delivery.

A diode-pumped solid-state laser (Laserglow Technologies) was used to deliver blue (473 nm) light to the VPm thalamus and stimulate the ChR2-expressing cells. The stimuli were square pulses of 5 ms duration and varying light intensity. The maximum light delivered during the experiments was ∼150 mW/mm², but typically less light was needed to drive neural activity in ChR2-expressing neurons. According to Aravanis et al. (2007), the light intensity at 200 μm from the optical fiber tip was ∼$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$ of the calibrated light at the tip, such that the majority of neurons were activated at <15 mW/mm² (Aravanis et al., 2007).

Thalamic data analysis.

The single-unit thalamic recordings presented here were acquired in a previous study from our laboratory (Wang et al., 2010b) using the same experimental preparation described here. The spiking activity from pairs of thalamic neurons residing in the same barreloid was recorded simultaneously in response to punctate whisker stimuli across multiple independently controlled quartz-insulated platinum–tungsten electrodes (4–6 MΩ, 80 μm diameter, Mini Matrix Microdrive; Thomas Recording). Data were collected using a 32-channel data acquisition system (Plexon) and analyzed using the Plexon OfflineSorter software. Each thalamic single-unit recording was sorted using standard template-matching techniques with physiologically plausible refractory periods. Each thalamic neuron pair was recorded with two electrodes in the same barreloid while stimulating the primary whisker. A cross-correlogram of firing between two simultaneously recorded neurons was computed for spikes fired in response to the sensory stimulus. The synchrony strength was defined as the total number of spikes within a ±5 ms window (N_cc) normalized by the number of spikes from each neuron (N₁, N₂) included in the analysis (Temereanca et al., 2008; Wang et al., 2010b):

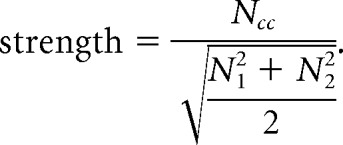The first spike latency on each trial was computed as the first spike within the 30 ms window after the whisker or light stimulation. The jitter was quantified as the SD of the first spike latency values for each stimulus condition across trials.

Computational network model.

A network model was used to investigate the hypothesis that sensory and artificial stimuli differentially activate thalamic neurons, leading to divergent response properties in downstream cortex. Specifically, the development of a model allowed direct and independent manipulation of the magnitude and synchrony of input population activity, whereas direct experimental control of these variables was not possible. Toward this goal, a simple cortical network model was developed, and the thalamic input activity was systematically controlled.

The network was modeled after the thalamocortical circuit of the rodent vibrissa pathway and the extensive anatomical and computational literature for this model system (Kyriazi et al., 1993; Diamond, 2008). The neural circuit consisted of 400 thalamic neurons that project to a downstream cortical population of 800 excitatory neurons and 200 inhibitory neurons. The relative size of the thalamic and cortical populations and the balance of excitation and inhibition in cortex were based off of previous studies (Kyriazi et al., 1993). The thalamic neurons made direct synapses on both the excitatory and inhibitory neurons in the cortex, allowing for feedforward inhibition.

The cortical population was modeled as a collection of quadratic integrate-and-fire neurons (Izhikevich, 2003) according to the following set of equations:

where v is a 1000 × 1 vector of the membrane potential of the cortical neurons, and u is a 1000 × 1 vector describing the recovery variable instituting the nonlinear dynamics of the cortical neurons. Spiking was determined by the membrane potential passing a fixed threshold of 30 mV, denoting the peak of depolarization, at which point v → c and u → u + d to model repolarization of the neuron by resetting the membrane potential, v, and the state variable, u. These parameters were set according to previous work (Izhikevich, 2003). The input, I, delivered to each cell was composed of a membrane noise term, I_m, and summed postsynaptic potentials from the thalamocortical and intracortical activity, I_S, according to the following set of equations:

where W^TC is a 1000 × 400 matrix describing the thalamic synaptic weights, such that W_ij^TC is the strength of the synapse from the jth thalamic neuron on the ith cortical neuron, and H^TC (a 400 × 1 vector) is the thalamic activity from the preceding time step, where H_j^TC is one if the jth thalamic cell spiked in the preceding time sample and 0 otherwise. In a similar manner, W^CC (a 1000 × 1000 matrix) and H^CC (a 1000 × 1 vector) describe the intracortical synaptic activity for the excitatory (800 neurons) and inhibitory (200 neurons) population. I_m is drawn from a normal distribution with mean of 0 and covariance K, producing spatially correlated membrane potential fluctuations in the cortical population (Poulet and Petersen, 2008). The membrane potential fluctuations were also filtered temporally over a 10 ms window. The connectivity and synaptic weights were extrapolated from previous modeling work and updated according to more recent in vivo work (Kyriazi et al., 1993; Bruno and Sakmann, 2006). This type of network has been shown previously to exhibit many of the common response features and rhythms of in vivo cortical circuits (Izhikevich, 2003).

The thalamic input spikes were drawn from an inhomogeneous Poisson process with rate:

where

such that M gave the average number of spikes per neuron per trial in the stimulus window, T, and S determined the synchrony of those spikes. Both S and M were functions of neuron location, such that neurons near the center of the stimulus responded with the greatest synchrony and magnitude, and neurons far from the center of the stimulus responded with low synchrony and magnitude. The fall off of these variables with space was dictated by the following Gaussian shaped functions:

where x gives the location along the linear array of thalamic cells, with x₀ at the center of the stimulus. M_peak and S_peak determine the magnitude and synchrony, respectively, at the center of the stimulus, and σ determines how quickly the magnitude and synchrony fall off with distance from the center of the stimulus. S_peak was systematically varied, whereas M_peak was held constant in Figure 6A, and vice versa for Figure 6B, while σ was set at 100 thalamic neurons to simulate the activation of one barreloid.

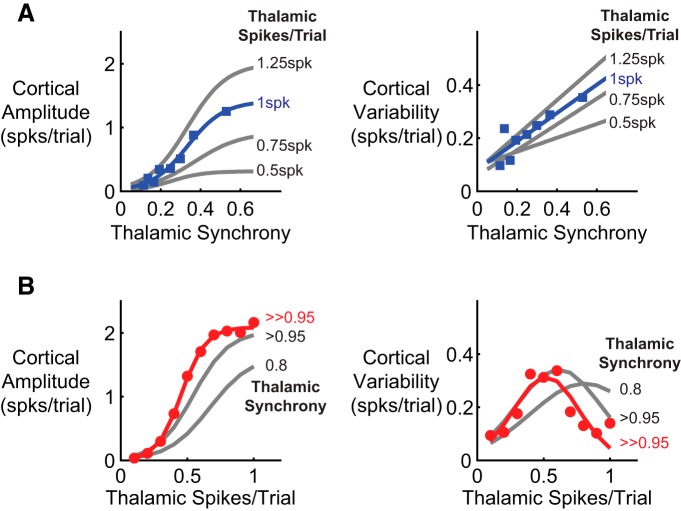
Figure 6.

Extreme synchrony ensures robust response in the face of trial-to-trial variability. The mean amplitude and trial-to-trial variability of the excitatory cortical units were computed for systematic variations in the number and timing of the thalamic input spikes. The gray lines indicate alternate values of synchrony and spike magnitude. A, The cortical response was a nonlinear function of thalamic synchrony, whereas the variability in the response amplitude increased linearly. B, The cortical response amplitude exhibited a similar nonlinear relationship as the magnitude of the thalamic input was increased and synchrony was fixed at a high level. However, the trial-to-trial variability in the cortical response peaked at the threshold magnitude of the thalamic input under high synchrony.

Although S modulates the synchrony of the input spiking activity, this simulation parameter is related inversely to commonly used experimental measures of synchrony such that small S values correspond to large synchrony strength values. Therefore, in all analyses, the synchrony strength of both the experimental and simulation results was calculated according to methods used previously in the literature and described above to permit direct comparisons between the model and the experimental data (Temereanca et al., 2008; Wang et al., 2010b). Briefly, the cross-correlogram was computed for pairs of neurons using the input spikes contributing to the stimulus. The area under the cross-correlogram within a synchrony window (±5 ms), normalized for the number of spikes used to create the cross-correlogram, was calculated for each pairwise combination of the central 20 thalamic neurons and averaged across the permutations to give the synchrony measure. The synchrony strength metric is by definition non-negative, but it does not have an upper bound. In the paradigm presented here, neurons typically fired a maximum of one spike on any given trial in response to a punctate whisker stimulus. With only one spike per thalamic neuron, a synchrony value of 1 means that the stimulus-related spike from each neuron in a simultaneously recorded pair occurs within the synchrony window (±5 ms).

Functional coding analysis.

Distinct trends in the trial-to-trial variability were observed for sensory and artificial stimuli experimentally. In both cases, the variability was response dependent, such that it varied as a function of the cortical response amplitude. To assess the functional relevance of the distinct response-dependent variability trends, we used a theoretical analysis aimed at quantifying and optimizing the discriminability of sensory inputs based on ideal observer analysis of downstream cortical response amplitudes. We framed the optimization of the stimulus as a signal set design problem (Proakis, 1989). The optimization framework involved two components: classification and maximization.

First, the classification was implemented with a standard maximum likelihood classifier. From the perspective of an observer of cortical activity, the discriminability between sensory inputs is a direct function of the discriminability between the corresponding cortical responses, which is derived from the separation of the mean cortical response amplitudes relative to the trial-to-trial variability (quantified here as the SD). For a set of N different stimuli (see Fig. 7A), the distribution of the cortical response r given a presentation of the kth stimulus is denoted as P(r|s_k). As shown in Figure 7B, within a simple maximum likelihood classification framework, the observed response is classified as having arisen from the stimulus for which the conditional probability P(r|s_k) is maximal for the observed cortical response r on that trial. As illustrated in Figure 7B, the performance of such a classifier depends on the overlap between the distributions, which in turn is dictated by the means and variances for each of these example Gaussian distributions. Taking stimulus s₃ as an example, the probability of a correct classification (ŝ = s₃) given the presentation of stimulus s₃ is the area under P(r|s₃) over the region for which it is larger than all other conditional distributions (Fig. 7B, gray shaded region).

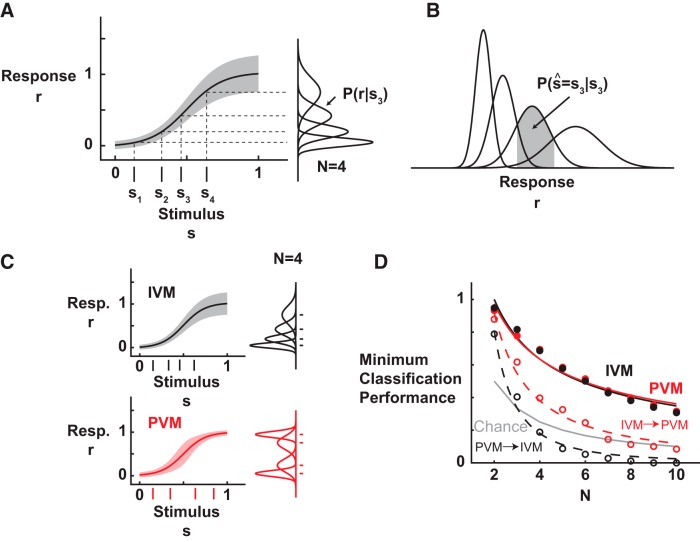
Figure 7.

Optimal stimulus set design. A, Depiction of the theoretical framework for stimulus design. The stimulus set maps to a noisy response set through a nonlinear relationship. B, The optimal set of response distributions was identified by maximizing the minimum probability of correct classification across the stimulus set. In the diagram, the gray region indicates the range of response values for which the response would have been correctly classified, given s₃. C, The trial-to-trial cortical variability was response dependent, and two different models were compared. The IVM modeled the variability as a linear function of the response, similar to the experimental observations for sensory stimuli. The PVM modeled the variability as a Gaussian function of the response, with the peak variability occurring at the threshold, similar to the experimental observations for artificial stimuli. For n = 4, the optimal set of discriminable responses and stimuli are shown for both cases on the vertical and horizontal axes, respectively. D, The performance (minimum probability of correct classification) decreased as the number of distinct stimuli increased. The performance across the IVM and PVM was identical for their optimal stimulus sets, and both were above chance (gray curve). The performance dropped to chance when the optimal stimuli were used in the mismatched variance models (PVM → IVM, dashed black; IVM → PVM, dashed red).

The second part of the optimization was the maximization of the classification performance over a range of possible stimuli to design a set of stimuli/inputs that produce cortical responses that are maximally discriminable. To maximize the discriminability between a pair of stimuli, given a fixed variability, stimuli should be chosen to best separate the mean response amplitudes in downstream cortex. For more than two stimuli and fixed variability, the spacing will depend only on the shape of the nonlinear mapping between the stimulus and response. However, if the response variability also changes as a function of the mean response amplitude, the classification problem and optimization of the input become more complex.

Within our framework based on experimental observations, a unique set of inputs, s = {s₁ … s_N}, precisely defined the set of cortical response distributions P(r|s_k) for k = {1, …, N}. We assumed that each P(r|s_k) was a Gaussian whose mean and SD were dictated by the stimulus s_k, as in Figure 7A. The optimal stimulus set was then the set of stimuli for which the minimum performance across the different classes was maximized:

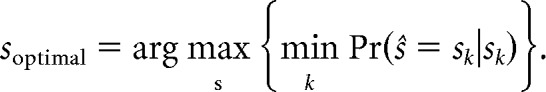We performed the numerical optimization to design stimuli for two different models of the trial-to-trial variability observed experimentally. The variability was found to vary systematically as a function of the mean response amplitude and exhibited distinct trends for sensory and artificial stimuli. For sensory stimuli, the variability increased linearly as a function of the mean response amplitude [increasing variance model (IVM)]. We modeled this as a linear function, shown in the top panel of Figure 7C. For artificial stimuli, the variability peaked at the threshold response amplitude. We modeled this as Gaussian-shaped function of the mean response amplitude, with a peak in the variability at the threshold response amplitude [peak variance model (PVM)], shown in the bottom of Figure 7C. Each of these models was compared with chance performance, given by 1/N, for a range of N. Power law curve fits, given by y = a × N^−b, were used to describe the performance as a function of N in Figure 7D.

Results

To precisely quantify the differential effects of artificial and sensory stimulation on propagation of signals in neural pathways, we specifically compared the propagation of neural activity generated by whisker deflection sensory inputs and electrical and optogenetic stimuli delivered to the thalamus in the vibrissa pathway of the anesthetized rat, in vivo.

The cortical response is highly nonlinear for whisker, electrical, and optical stimuli

All experiments used in vivo VSDI of layer 2/3 in the whisker representation of the S1 with whisker stimuli delivered to an individual whisker on the face and electrical and optical stimuli delivered to the topologically matched “barreloid” in the VPm portion of the thalamus in the anesthetized rodent, as depicted in Figure 1A. Post-experiment cytochrome oxidase staining revealed the anatomical structure of the cortical columns, which was then registered to the VSDI recordings. An example of the spatiotemporal VSDI response to whisker stimulation is shown in Figure 1B with the overlaid anatomical map. In this example, a single punctate deflection was delivered to whisker D2 (cortical column with dot) in the rostrocaudal plane (see Materials and Methods). The cortical response was initially constrained to the principal cortical column, matched to the deflected whisker on the face, before spreading spatially and growing in amplitude. For comparison, Figure 1C shows the onset frame of the cortical response to single-whisker, electrical, and optical stimuli, all from a single experiment. The electrical stimulation consisted of a symmetric biphasic waveform, whereas the optical stimulation was a 5 ms pulse of blue light (see Materials and Methods).

First, the amplitude of the cortical response was quantified for whisker, electrical, and optical stimuli of increasing intensity. To do so, the cortical response was averaged across trials and then averaged spatially within the principal cortical column. An example of the single-trial (gray) and average (black) responses within the principal cortical column is shown in Figure 1B. The mean and SD of the maximum response amplitude was then calculated and plotted as a function of whisker deflection velocity, electrical stimulation current, and optical stimulation light intensity (Fig. 2).

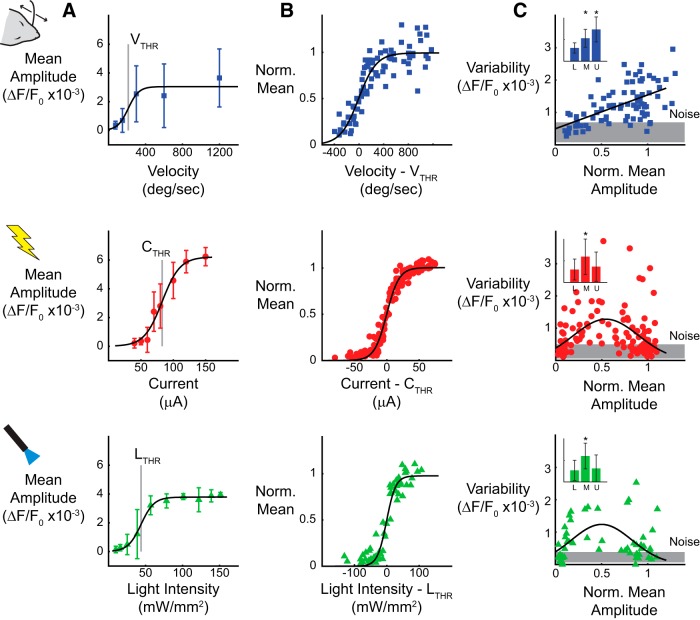
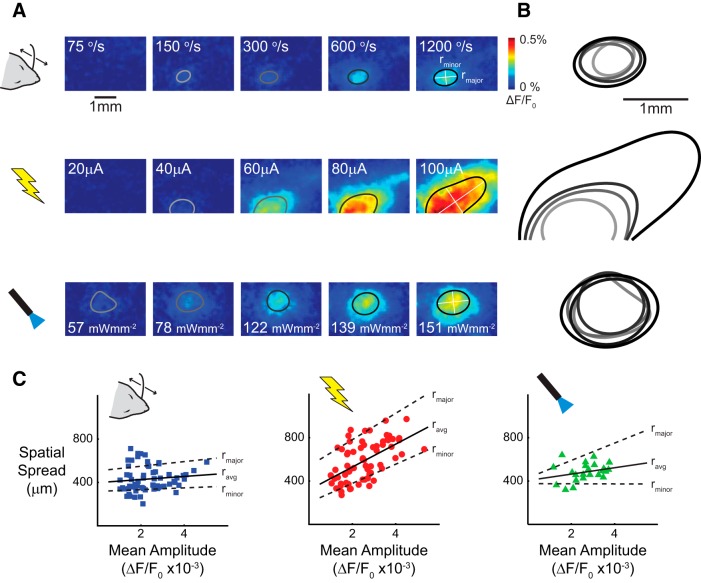
Figure 2.

Whisker stimuli are more sensitive to trial-to-trial variability. A, The response amplitude was quantified as the maximum VSDI signal, after averaging spatially within a single cortical column and across trials, for whisker, electrical, and optical stimuli. B, Tuning curves for velocity (top, n = 12), current (middle, n = 18), and light intensity (bottom, n = 6) across all experiments. Stimulus values from each experiment were normalized relative to the threshold stimulus. Mean response values from each experiment were normalized with respect to the amplitude of the sigmoidal fit. C, The variability in the response amplitude was quantified as the SD of the maximum amplitude across trials, averaged spatially within a single cortical column. The response amplitude variability for whisker stimuli (top) increases as a function of mean response amplitude (n = 12). The response amplitude variability for electrical (middle) and optical (bottom) stimuli peak at the threshold response amplitude (n = 18 for electrical, n = 6 for optical). Inset depicts all data binned into three equally sized groups to demonstrate variability trends (* indicates p < 0.05, two-sided t test with unequal variances).

A representative example of the cortical response to varying intensity of each stimulus type is shown in Figure 2A. For each experiment, the stimulus intensities were chosen to span the range from no response to maximal response. The response amplitude increased monotonically as a function of stimulus intensity for all stimulus types and was well approximated by a sigmoidal function. From the sigmoidal fit, the threshold stimulus intensity was defined as that which produced a half-maximal cortical response amplitude (Fig. 2A, gray vertical line). The average threshold whisker deflection velocity (V_THR) was determined to be 229 ± 139°/s (n = 12 animals, top row), consistent with previous behavioral literature (Stüttgen and Schwarz, 2008; Ollerenshaw et al., 2012). The average threshold current (C_THR) was 54 ± 20 μA (n = 18 animals, middle row), and the threshold light intensity (L_THR) was 87 ± 31 mW/mm² (n = 6 animals, bottom row). Figure 2B presents a compilation of the mean response amplitude across all experiments and all stimulus types. For each experiment, the stimulus intensities are plotted relative to the threshold stimulus, and the response amplitudes are normalized with respect to the amplitude of the sigmoidal fit. The compilation of the data illustrates the consistency and similarity of the nonlinear relationship between cortical response amplitude and the strength of sensory and artificial stimuli.

Sensory-evoked and artificially evoked cortical responses exhibit distinctly different variability

Although the mean cortical response showed similar trends for sensory and artificial stimuli, the trial-to-trial variability did not. The trial-by-trial variability was quantified as the SD of the single-trial maximum response amplitudes for each stimulus type. Figure 2C presents the summary data for all experiments and all stimulus types. Because there is no clear relationship between deflection velocity, microstimulation current, and light intensity, the variability was analyzed as a function of the normalized mean response amplitude. For whisker stimuli, the trial-to-trial variability increased linearly as a function of the response amplitude for each case. At low response amplitudes, the trial-to-trial variability matched the variability in noise trials (trials without sensory stimulation, gray band, mean of variability in the noise ±1 SD across n = 12 experiments), whereas high stimulus intensities exhibited a marked increase in variability. The data were split into three equally distributed bins, the lower (L), middle (M), and upper (U) response amplitudes, corresponding to subthreshold, perithreshold, and suprathreshold responses, respectively, as shown in the inset. The difference in variability for the perithreshold and suprathreshold bins was significantly different from the subthreshold response amplitudes (L vs M, p = 5.0e-4; L vs U, p = 3.3e-10; two-sided t test with unequal variances).

The variability in the cortical response to thalamic microstimulation and optogenetic stimulation followed a different trend. At subthreshold and suprathreshold response amplitudes, the trial-to-trial variability was comparable with that of noise trials (gray band, mean of variability in the noise ±1 SD across n = 18 experiments). However, near the threshold response amplitude, the trial-to-trial variability was significantly higher. When binned in the same manner as the whisker stimuli, only the perithreshold bin was significantly different from the subthreshold variability, indicating that the variability returned to baseline at strong response amplitudes for electrical (L vs M, p = 0.0061; L vs U, p = 0.17; two-sided t test with unequal variances) and optical (L vs M, p = 0.043; L vs U, p = 0.55; two-sided t test with unequal variances) stimuli. Importantly, the distinct trends of trial-to-trial variability for sensory and artificial stimuli have implications for the capacity to generate discriminable cortical responses (see Fig. 7) and influence behavior (see Discussion). Together, the results here strongly suggest that one kind of input cannot simply be “substituted” for another through a simple “lookup table,” because one response property may be achieved at the expense of others.

The cortical response to microstimulation exhibits the greatest spatial spread

In addition, the VSDI modality enabled the quantification of the spatial spread of the cortical response to whisker, electrical, and optical stimuli. Examples of the spatial cortical response to each stimulus type are presented in Figure 3A for varying stimulus intensities. The initial frame of activation was used for all stimuli (see Materials and Methods). The spatial spread was quantified as the length of the major axis, minor axis, and equivalent radius of the contour at 70% of the maximum amplitude. In this way, the spread measurement was normalized for differences in the maximum amplitude across variations in stimulus intensity and stimulus type. Also, the contour was taken from the sum of Gaussians fit to the raw data to provide a smooth estimate to the contour. Qualitatively, for increasing velocity of whisker stimuli (Fig. 3A, top) and light intensity of optical stimuli (bottom), the area of activation remains restricted to a small region of cortex. For increasing current amplitude of the electrical stimuli (middle), the area of activation is initially constrained but spreads farther across cortex for higher current intensities.

Figure 3.

Electrical stimulation activates a significantly larger region of the cortex. A, The spatial spread was quantified as the average radius of the 70% amplitude contour. The initial frame of activation was used, and the contour was taken from a parametrized sum of Gaussians fit to the VSDI data. B, The size of the contours is similar across whisker deflection velocities (top) and optical light intensity (bottom) but increases dramatically for increasing electrical stimulation current (middle). C, The spatial spread increased significantly more as a function of response amplitude for electrical stimuli (n = 17) than for whisker (n = 12) or optical (n = 4) stimuli.

The individual contours for all stimulus intensities are overlaid in Figure 3B for each stimulus type (light gray is the lowest stimulus intensity, black is the strongest). Again, it is clear that the spatial spread grew slightly across varying whisker deflection velocities and optical light intensities, whereas the spatial spread grows more steeply for increasing current of electrical stimulation. The average radius (r_avg) of the contours is plotted as a function of the maximum response amplitude for all experiments in Figures 3C–E, for whisker, electrical, and optical stimuli, respectively, along with the linear fit of the relationship (black line). The linear fits to the trends for the radii on the major (r_major) and minor (r_minor) axes are plotted on the same graph (dashed lines). As in the single-experiment example, the average radius grew weakly as a function of the response amplitude for whisker [slope, 15 μm/unit activity; 95% confidence interval (CI) = −18, 48; n = 12 experiments] and optical (slope, 38 μm/unit activity; 95% CI = −11, 87; n = 4 experiments) stimuli. However, electrical microstimulation exhibited an increasingly large spatial spread as the response amplitude increases (slope, 108 μm/unit activity; 95% CI = 68, 149; n = 18 experiments). For comparison, the radius of a cortical column in the rodent S1 is ∼200 μm. As an example, the average radius of the 70% contour for a strong response (ΔF/F₀ of 0.4%) to whisker (474 μm) and optical (558 μm) stimuli only extends in nearest neighbor cortical columns, whereas the 70% contour for electrical stimuli (770 μm) reaches two cortical columns outside of the principal column, encompassing ∼2.6 times as much cortical surface as the response to whisker stimuli. These observations are consistent with the hypothesis that activation of axons locally in the thalamus leads to increased spatial spread in cortex given that electrical stimuli (Histed et al., 2009), and optical stimuli to a lesser extent (Cruikshank et al., 2010), are known to activate axons near the site of stimulation.

Together, whisker stimuli of increasing velocity produced a nonlinear increase in the mean cortical response amplitude, with high trial-to-trial variability, in a fixed, focal spatial location. Conversely, electrical stimulation of the thalamic input to the cortex produced a highly nonlinear modulation of the cortical response amplitude, with little trial-to-trial variability except at the threshold current, over an increasingly large region of the cortical space. Optical stimulation of thalamic neurons expressing light-sensitive ion channels induced a mixture of the properties observed with whisker and electrical stimuli, in which the nonlinearity of the amplitude and variability of the cortical response closely matched that of electrical stimulation, yet the cortical spatial response properties were more akin to that of whisker stimuli. These experimental observations reinforce the general conclusion from previous work that natural and artificial inputs activate neural circuits in distinct ways but also further elucidate the specific details of the distinction and identify potential mechanistic differences in optical stimulation compared with traditional electrical microstimulation.

Magnitude and synchrony of thalamic input drive cortical response properties

Striking differences were observed in the properties of the cortical response to whisker, electrical, and optical stimuli, which were likely the result of the stimuli activating the thalamus in fundamentally different ways. Two obvious determinants of the cortical response are the extent of the subpopulation of thalamic neurons activated during the sensory and artificial stimulation and the degree to which these projections to cortex are synchronized, both of which have potentially strong influence on the magnitude, variability, and spatial spread of the cortical response.

First, as the current and light spread through the tissue, they recruit an increasing number of neural elements with increasing stimulus intensity (Aravanis et al., 2007; Histed et al., 2009). It is thus likely that increasing strength of the electrical and optical stimulation activates increasing numbers of neurons in the barreloid (functional groupings that principally relay information from a single whisker to the cortex) within which the electrode/fiber is positioned. Furthermore, the artificial stimulation potentially extends beyond the primary barreloid, which would simultaneously activate multiple barreloids in the thalamus. In comparison, the sensory stimuli were delivered to a single whisker on the face and thus primarily activate a single thalamic barreloid. It is possible that this discrepancy in the number of barreloids activated between sensory and artificial stimuli may account for the variability trends described previously.

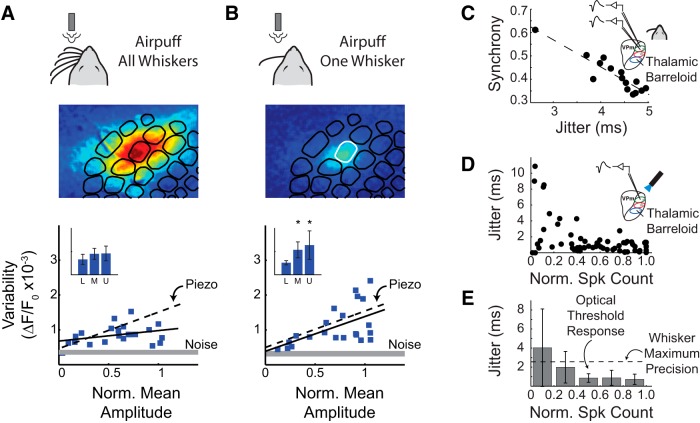
We investigated this further using an air-puff stimulus to simultaneously activate the entire whisker array (Fig. 4A). The response to full whisker array stimulation spreads over a large region in the cortex as in the response to the electrical stimulus, yet the variability in the cortical response magnitude within a single barrel did not peak at the threshold stimulus intensity. Instead, the variability increased linearly with the response amplitude but with a lower slope than was observed with the single-whisker deflection (dashed black line). As a control, all whiskers except one were trimmed, and the same air-puff stimulus was repeated (Fig. 4B). These results mimicked the spatial spread and variability trends observed for the single-whisker deflection in Figures 2 and 3 demonstrating that the air-puff stimuli is not fundamentally different from the precise whisker stimulation used in this study. Although the activation of multiple whiskers may explain the differences in spatial activation in electrical stimulation, the activation of multiple barreloids alone is insufficient to explain the distinct variability trends observed for sensory and artificial stimuli. However, the overall amount of thalamic spiking within a given barreloid remains an important parameter in determining the cortical activation within the corresponding barrel because increasing stimulus amplitudes leads to increasing firing in the thalamus within the aligned barreloid.

Figure 4.

Magnitude and synchrony of thalamic input drive cortical response properties. A, Air-puff stimulation of the full whisker array leads to a greater spatial spread of the cortical response in the onset frame, but the variability of the response amplitude does not peak at threshold stimulus amplitudes (n = 2 animals). Inset depicts all variability data binned into three equally sized groups to demonstrate variability trends (* indicates p < 0.05, two-sided t test with unequal variances). B, Sensory stimulation with an air puff after trimming all but one whisker shows spatial and amplitude variability responses similar to those seen with single whisker stimulation using a piezoelectric actuator (n = 2 animals). Inset depicts all variability data binned into three equally sized groups to demonstrate variability trends (* indicates p < 0.05, two-sided t test with unequal variances). C, Activity from pairs of single neurons residing in the same barreloid were recorded simultaneously in response to whisker deflections. The jitter, calculated as the SD of the first spike latency, was strongly correlated with the synchrony of firing between the two neurons (n = 15 pairs). D, Increasing intensity of optical stimulation of ChR-expressing VPm neurons reduced jitter. E, Beyond the optical threshold response, the jitter in response to optical stimulation was significantly lower than the minimum jitter achieved using whisker stimulation (n = 7 cells).

Second, the cortical response has been shown to be extremely sensitive to the timing of thalamic inputs. Although previous studies have shown that the timing precision and synchrony of population activity in the thalamus are modulated by variations in the strength of a sensory stimulus, the temporal precision of artificially evoked neural activity suggests that electrical and optical stimuli likely synchronize the neurons they activate beyond sensory-evoked synchrony levels (Boyden et al., 2005; Wagenaar et al., 2005). To further elucidate this issue, we used extracellular recordings in the thalamus from a previous study (Wang et al., 2010b) to compare the degree of synchrony produced by sensory and artificial stimuli. First, synchronous activity was measured across pairs of thalamic units in response to whisker stimuli using multielectrode recordings of single-unit activity (Wang et al., 2010b). Synchrony strength was quantified as the integrated area under the spike cross-correlogram of simultaneously recorded VPm single units in a 10 ms window, normalized by the total number of spikes of each unit (see Materials and Methods). The narrow synchrony window implemented in this metric is modeled after the short cortical window of integration whereby thalamic spikes summate effectively before disynaptic feedforward inhibition prohibits additional cortical excitation (Gabernet et al., 2005). If each neuron fires one spike, a synchrony strength of 1 corresponds to all stimulus-related spikes from one neuron occurring within the synchrony window of the stimulus-related spikes from the second neuron, whereas a synchrony strength of 0 corresponds to no synchronous firing activity between the two cells. As shown in Figure 4C, the maximal synchrony strength evoked by whisker stimulation reaches 0.61. Note that the synchrony strength values described here correspond to conditions under barbiturate anesthesia, which we reported previously (Wang et al., 2010b). However, these synchrony strength values are markedly lower than those presented by studies performed under fentanyl anesthesia (Temereanca et al., 2008). The number of elicited thalamic spikes under barbiturate anesthesia varied between 0 and 1 spike on each trial. Although the synchrony measure attempts to normalize between the firing rates of the neurons, neuron pairs with no-response trials (i.e., zero spikes) can have lower synchrony strength relative to neuron pairs that respond on every trial. When we repeated the synchrony analysis of thalamic neurons recorded under sodium pentobarbital with all no-response trials removed, the synchrony strength values (range from 0.8 to 1.0; data not shown) are on the same order of those in the study by Temereanca et al. (2008). As such, we believe that the quantitative difference in synchrony values could be attributable to differences in the firing patterns elicited with varying anesthesia drugs. However, we expect that the relative qualitative shifts in synchrony will be consistent regardless of the anesthetic used.

The jitter in first spike latency for each unit in a pair of thalamic neurons was highly correlated with the computed synchrony strength (Fig. 4C). Although the synchrony strength defined here is limited to pairs of neurons, there has also been evidence that reduced jitter is correlated with greater population synchrony in the VPm thalamus, as quantified by the amplitude of the local field potential (Temereanca and Simons, 2003). Analysis of the thalamic spiking activity used to drive the computational model presented below also demonstrated the same correlation between first spike latency jitter and synchrony strength (data not shown). Together, these findings suggest that first spike latency jitter computed for an individual thalamic neuron is highly correlated with pairwise synchrony between at least two thalamic neurons, suggesting that spike timing precision (jitter) may act as a surrogate for direct measures of synchrony between two neurons in thalamus (Temereanca et al., 2008). However, as information progresses along the sensory pathway, it becomes integrated with additional nonsensory information such that the evoked response is better predicted by the presynaptic activity rather than the stimulus timing alone (Eldawlatly and Oweiss, 2011). Although estimation of population synchrony from single-neuron precision may be a valid method for recordings performed early in the sensory pathway such as sensory thalamus, it may not generalize across areas.

Although spike timing precision could not be measured concurrently with electrical stimulation because of the electrical recording artifact, optical stimulation allowed for quantification of the spike timing precision of artificially evoked thalamic single-unit activity. In agreement with previous results, we found a high degree of spike timing precision in response to optical stimuli (Fig. 4D) relative to whisker stimuli (Fig. 4C; note that the jitter scale is approximately half as large as D). For suprathreshold light intensities, the evoked activity reached submillisecond precision (0.70 ± 0.48 ms), which corresponds to a significantly higher degree of synchronization than the highest degree of precision/synchrony observed for whisker inputs (Fig. 4E).

Computational model of thalamocortical circuit allows direct control of thalamic input

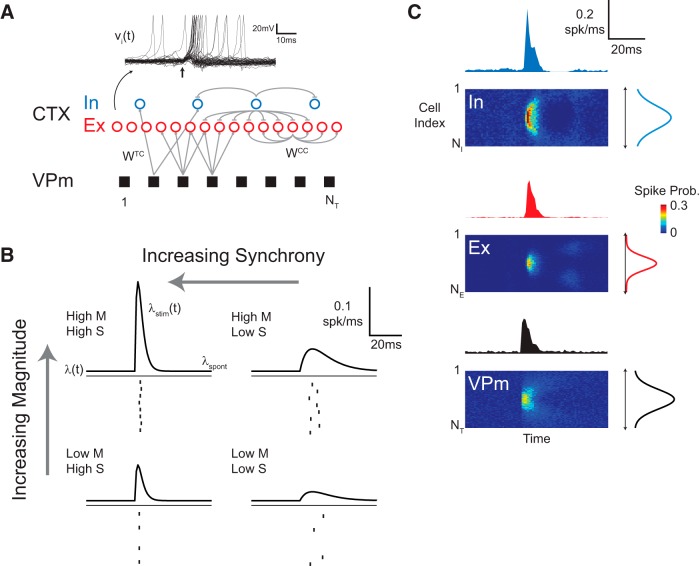
The above analyses point to the possible roles of both the numbers of thalamic projection neurons engaged within a barreloid and the degree to which they are synchronized, but they are best studied in situations in which these parameters can be more directly controlled. To explicitly control the number of thalamic neurons that were activated and the degree of synchronization, we constructed a computational model of the thalamocortical projection. The network connectivity is illustrated in Figure 5A and was based off of previous anatomical and computational studies of the thalamocortical circuit (Kyriazi et al., 1993; Bruno and Sakmann, 2006; Diamond, 2008). The network was a canonical feedforward model, similar to what has been used extensively to explore the propagation of neural activity (Kumar et al., 2010). A population of thalamic neurons formed the input to the network, and the cortical population of interconnected excitatory and inhibitory neurons was the output layer. The synaptic weights and relative connectivity were drawn from previous experimental and computational work in the rodent vibrissa system (see Materials and Methods). However, to retain generality, the neurons in the model were arranged in a linear array, as opposed to the discrete nature of the cortical columns in the rodent barrel cortex. In this way, neighboring thalamic neurons synapsed on overlapping cortical populations. As the distance between thalamic neurons increased, the probability of shared connections to a single cortical neuron decreased, with the individual synaptic weights drawn randomly. The previous modeling work, on which this model was based, used 100 thalamic neurons to model a barreloid. We retain this convention, such that the 400 thalamic neurons modeled in this study corresponds to four barreloids in sequence.

Figure 5.

Computational network model of activity propagation in the thalamocortical circuit. A, The population activity of the VPm thalamus is controlled as the input to the cortical population. The neurons are arranged spatially in a linear array, such that neurons are more likely to be connected to their neighbors. The network promotes feedforward inhibition in that thalamic VPm neurons synapse on both excitatory (Ex) and inhibitory (In) neurons within the cortical population. Example membrane potential traces for a single neuron across multiple trials are shown in the top. CTX, Cortex. B, Diagram illustrating the inhomogeneous rate function used to generate the thalamic spikes. The magnitude and synchrony of the thalamic spiking activity was systematically modulated as the input to the model. C, Spatial PSTH and averaged PSTH for the excitatory (top left) and inhibitory (top right) cortical population in response to the thalamic input (bottom).

Each individual cortical neuron was modeled as a nonlinear dynamical system (Izhikevich, 2003). Specifically, each neuron was described by two state variables: (1) the membrane potential of the neuron; and (2) a recovery variable. The membrane potential evolved according to a quadratic integrate-and-fire model, whereas the recovery variable enforced the relative refractory period of the neuron and overall excitability. Example traces of the membrane potential of a single neuron in response to a simulated stimulus are shown in the top portion of Figure 5A for multiple trials. Noise was added to the membrane potential of each neuron to mimic the in vivo high conductance state (Destexhe et al., 2003; Ratté et al., 2013). The noise was correlated across the cortical neurons, such that neighboring neurons experienced similar fluctuations. The thalamic population activity acted as the input to the cortical population and was generated by the inhomogeneous Poisson rate function, λ(t) = λ_stim(t) + λ_spont, where λ_spont produced a constant rate of background activity and λ_stim(t) was systematically varied to control the magnitude (M) and synchrony (S), as in Figure 5B. Examples of the input thalamic population activity (bottom) and output cortical population activity (inhibitory, top; excitatory, middle) are shown in Figure 5C. For each cell type, the image shows the average activity across the entire population. The peristimulus time histogram (PSTH) for the central 20 neurons is shown above, and the spatial cross-section, averaged across the first 20 ms after the stimulus, is on the right. The illustrated thalamic input to the cortex corresponds spatially to the activation of a single barreloid, with the excitatory response in the cortex being confined spatially to a single barrel in the cortex and the inhibitory response in the cortex extending farther laterally. Using this modeling architecture, we evaluated the same response metrics as the experimental VSDI data, namely the response amplitude and variability.

Magnitude and synchrony of population activity control the nonlinear response in a network model

The magnitude and synchrony of the input thalamic population activity were systematically varied to investigate the relative contributions of these fundamental variables on the response amplitude and variability. For the amplitude and variability, two different input scenarios were used to explore the two extremes in terms of synchrony and magnitude. In Figure 6A, the average number of spikes per trial per thalamic neuron was fixed, but the synchrony of those spikes varied to modulate the intensity of the stimulus. In this way, the average number of thalamic neurons participating in the cortical input was systematically varied independent of synchrony. Conversely, in Figure 6B, the synchrony of the thalamic population spikes was held fixed at a high level, and the average number of spikes per trial per neuron was varied to modulate the intensity of the stimulus. The synchrony of the thalamic input was computed as the area under the cross-correlogram within a synchrony window (see Materials and Methods), as done previously (Wang et al., 2010b; Stanley et al., 2012). Note that this measure saturated for stimuli with unnaturally high synchrony but allowed direct agreement with physiologically relevant values of thalamic synchrony in the rodent vibrissa system.

The cortical response amplitude grew monotonically as a function of the thalamic input synchrony (Fig. 6A, left), whereas the trial-to-trial variability in the cortical response amplitude increased linearly (Fig. 6A, right). These trends mirrored those observed experimentally for whisker stimuli. We then examined the sensitivity of this relationship to the fixed magnitude of the thalamic input activity. Each of the gray curves in Figure 6A give the relationship between the synchrony of the thalamic population input and the amplitude of the cortical response for a fixed magnitude of the thalamic input. The same trends were observed for a range of thalamic input magnitudes, spanning half activation (0.5 spikes/trial for each neuron) to maximal activation (1.25 spikes/trial for each neuron) of a thalamic input population corresponding to a single barreloid.

In comparison, Figure 6B illustrates the simulated cortical response amplitude (left) and trial-to-trial variability (right) as a function of the thalamic input magnitude, for fixed levels of input synchrony. The cortical response increased monotonically with the thalamic input magnitude before saturating for high intensity inputs (Fig. 6B, left), similar to the effect of increasing the thalamic synchrony (Fig. 6A, left). Thus, both magnitude and synchrony of the thalamic input can modulate cortical response amplitude. Unlike the fixed spike count condition presented in Figure 6A, the trial-to-trial variability in the cortical response amplitude for fixed synchrony demonstrated a nonlinear relationship as a function of the thalamic input magnitude (Fig. 6B, right). The two highest levels of synchrony modeled (>0.95 and ≫0.95) saturated the synchrony strength measure derived from previous sensory neurophysiology studies (see Materials and Methods), consistent with the much higher degree of precision observed for optically evoked thalamic spikes in Figure 4E. The peak variability was observed at the threshold input magnitude for the fixed, high input synchrony (red), whereas subthreshold and suprathreshold inputs produced low trial-to-trial variability in the simulated cortical response. The simulated cortical response amplitude and variability for fixed high synchrony reproduced the results observed experimentally for electrical and optical stimulation, suggesting that the extreme synchronization generated by electrical and optical stimuli is responsible for the quenched variability at suprathreshold stimulus intensities.

These computational results support the hypothesis that the nonlinear properties, including the amplitude and variability, of the cortical response are determined by the magnitude and synchrony of the input population. Specifically, the model predicts that strong synchronization of the input increases the slope of the nonlinear transformation in cortex, while simultaneously reducing trial-to-trial variability for suprathreshold inputs. However, the functional ramifications of these observations on neural information processing are unclear.

Coding consequences of nonlinear properties of activity propagation

The distinct ways in which the cortex was activated by sensory and artificial stimuli have profound implications for the ability to use artificial stimuli as a surrogate for sensory inputs. Certainly, it will be difficult for artificial stimuli to exactly mimic the cortical response to sensory inputs given the fundamental experimental observations in Figures 2 and 3. However, it may be sufficient for artificial stimuli to merely deliver information to downstream cortex and rely on some degree of learning to associate the stimuli with meaningful inputs. However, the ability to perform this depends strongly on designing stimuli that yield different/discriminable cortical responses, which is in turn strongly influenced by the variability structure.

Consider an ideal observer tasked with discriminating between the strengths of different stimuli based on the observation of the cortical response amplitude (e.g., integrated activity within a cortical column; Fig. 7A). For a particular stimulus s_k, the distribution of observed responses is given by P(r|s_k). Within a simple maximum likelihood framework, the observer makes an inference by selecting the stimulus for which the likelihood P(r|s_k) is maximized. This maximization is conducted across the stimulus set, for the particular cortical response observed on that trial (see Materials and Methods). The probability of a correct classification is the area under the distribution over a region for which the probability associated with the correct class is larger than all others, as illustrated for s₃ in Figure 7B (shaded region). Therefore, in this simple paradigm, the ability to discriminate between any two inputs is dictated by the separability of the corresponding conditional response distributions.

For a sigmoidal nonlinear relationship between the input stimulus and the cortical response amplitude, and a hypothetically constant trial-to-trial variability, the ability to discriminate between two inputs with a given absolute difference in strength would be highest near the threshold input because of the steep slope of the nonlinearity at this point. However, as previously demonstrated experimentally, the variability is not constant but is instead a function of the stimulus. As a result, the overall performance of the observer in discriminating between a set of stimuli is dependent on both the nonlinearity of the stimulus–response relationship and the corresponding variability.

To demonstrate the functional relevance of the response-dependent variability, we framed this as a signal set design problem (Proakis, 1989). In this framework, the goal was to find the set of N stimuli that produced maximally discriminable cortical response amplitudes, given identical deterministic nonlinear stimulus–response characteristics (i.e., the sigmoid) but different variability structures. In detail, because each stimulus can have a different probability of being classified correctly, the overall criterion here was to find the set of stimuli that maximized the lowest (minimum) probability of correct classification among the set (see Materials and Methods). Figure 7C shows the stimulus–response relationships for the sensory stimulus case, in which there was increasing cortical variability with stimulus strength (IVM; top), and for the artificial stimulus case, in which there was a peak variance for threshold levels of stimulus strength (PVM; bottom). Both of these plots were generated from models based on the observed cortical variability described previously (see Materials and Methods). Shown to the right on the vertical axis are the corresponding sets of conditional response distributions for the optimal set of four distinct stimulus strengths, along with the corresponding set of stimuli as tick marks along the horizontal axis. The difference in variability structure thus leads to a different optimal set of stimuli under the discriminability criterion described here. As expected, the optimal response sets for the IVM are biased toward lower response amplitudes, in which the trial-to-trial variability was lowest. In comparison, the optimal response sets for the PVM are biased toward response amplitudes distant from the threshold, for which the variability is lowest, at both low and high stimulus strength.

For each of the models of variability, as the size of the response set increased, the overlap between the neighboring response distributions obviously increased, reducing the overall performance. Figure 7D presents the minimum probability of correct classification as a function of N for each of the models of response-dependent variability. Chance performance (solid gray curve) was given by 1/N, signifying the probability of correct classification when randomly choosing among the N stimuli. The curve fits to the data were modeled after this relationship (see Materials and Methods). Despite the difference in variability structure and the corresponding optimal stimulus set, the overall level of performance, as quantified by the minimum classification performance among stimuli in the set, was the same when the optimization was performed taking the appropriate variability structure into account (solid black and red curves). The performance was indistinguishable across the two models and well above chance. However, for mismatched cases in which the stimulus set was optimized under an assumption of IVM and evaluated for the PVM case (IVM → PVM, dashed red curve) and vice versa (PVM → IVM, dashed black curve), there was a significant drop in performance, which became increasingly more dramatic for larger number of stimuli. These results demonstrate that, despite the difference in variability structure, the artificial stimulus set could be designed such that it achieved the level of performance of natural stimuli.

These theoretical results highlight the functional relevance of the distinct nonlinear mappings observed experimentally and computationally for sensory and artificial stimuli. The utility of a surrogate input is judged on the amount of information delivered to downstream cortex. In this simple example of encoding information in the cortical response amplitude, we show that the choice of inputs significantly affects the classification performance downstream. However, through knowledge of the input–output nonlinear relationship and the associated trial-to-trial variability, optimal surrogate inputs were chosen that maximized downstream performance. Ultimately, our theoretical results suggest that the optimal response amplitudes will not be the same for sensory and artificial stimuli, but we may be able to design surrogate stimulus sets to maximize performance for artificial stimulation of neural circuits.

Discussion

Critical in the artificial stimulation of neural tissue is the consideration of what cells are being activated. The VPm region of the rodent somatosensory thalamus contains purely excitatory projection neurons organized into functional groups, termed barreloids, that principally relay information from a common facial vibrissa to layer 4 of S1 (Simons and Carvell, 1989). Although an individual barreloid was targeted during placement of the microelectrode and optical fiber, neurons were likely activated across multiple barreloids because of the nonspecific spread of the current/light within the tissue (and broad opsin expression) at the strongest current/light levels. Because sensory stimulation was restricted to the deflection of a single whisker (and thus activating a single barreloid when stimulated under barbiturate anesthesia), it is possible that the artificial activation of multiple barreloids did contribute to the trends observed here. However, as shown in Figure 4, cortical responses from simultaneously deflecting the entire whisker array (and thus activation of multiple thalamic barreloids) suggest that merely recruiting an increased number of neurons does not fully account for the response profiles of natural and artificial stimuli.

It is also the case that the current/light spread could go beyond the neuronal cell bodies in VPm thalamus and reach inhibitory neurons within the nearby nucleus reticularis thalami (nRT), afferent axonal “fibers of passage” projecting from other barreloids within the VPm thalamus to the cortex and even terminals of descending corticothalamic projections. Indeed, electrical microstimulation is indiscriminate and could activate any or all of the above. Electrical stimulation with symmetric, charged-balanced current pulses such as those used here may preferentially activate nearby axons of passage instead of local cell bodies and thus could also engage the circuit through activation of orthodromic and/or antidromic fibers of passage (Wang et al., 2012). However, optical stimulation engages principally cell bodies and, because of the viral transduction methods used, is not capable of antidromically activating the cortex (Cruikshank et al., 2010). Therefore, the increased spatial spread of the cortical response to electrical stimuli, and not whisker or optical stimuli, is consistent with the activation of local fibers of passage by electrical stimulation (Wang et al., 2012) and provides additional support that optical stimuli principally activate cell bodies, and not axons, nearby the light source. Furthermore, opsin expression is cell-type specific to limit functional opsin expression to excitatory neurons. Therefore, although the electrical microstimulation could in principle activate cell bodies within the inhibitory nRT, it would not be activated by the optical stimulus even if sufficient light reached the nucleus. Given the similarity of the nonlinear variability trends between electrical and optical stimuli, neither antidromic activation nor nRT activation likely play a role in the distinct trends for natural and artificial stimuli.

Given that simply activating larger regions of subcortical tissue appears insufficient to account for differences in the relationship between variability and response magnitudes, we hypothesize that the distinct response profiles elicited by sensory and artificial stimulation are driven by differences in the coordination of spiking across neurons. Thalamic neurons are known to make weak, noisy synapses onto downstream cortical neurons (Bruno and Sakmann, 2006), and these connections comprise a relatively small percentage of the incoming synapses compared with intracortical connections (Benshalom and White, 1986; da Costa and Martin, 2009). This anatomical wiring alone has led many to suggest that synchronization of the thalamic neurons be necessary for the reliable activation of downstream cortical neurons (Wang et al., 2010a; Bruno, 2011; Stanley, 2013), whereas experimental and computational work indicates a role for synchrony in driving cortical feature selectivity (Alonso et al., 1996; Temereanca et al., 2008; Wang et al., 2010b; Stanley et al., 2012; Kelly et al., 2014). We believe the degree to which natural and artificial stimuli synchronize the thalamic input to the cortex is responsible for the variability trends observed experimentally. We hypothesize that the relative influence of a thalamic input spike increases with synchrony and may eventually engage the cortex at the level of variability in the cortical baseline membrane potential. In this way, very subtle changes in the thalamic input near threshold may cause large variations in the cortical response, whereas inputs significantly above reliably produce a maximal response regardless of cortical state. Indeed, we found that the temporal precision of thalamic spiking in response to threshold-level optical stimuli was significantly greater than that of even the strongest whisker stimuli, providing support for the hypothesis that the high degree of synchrony generated by artificial inputs is responsible for the distinct variability trends observed experimentally, as confirmed by the computational model.

The agreement in the computational and experimental results supports a conceptual model for the distinct ways in which natural and artificial inputs activate neural circuits. Sensory stimuli modulate thalamic synchrony to drive downstream cortical activity, whereas electrical and optical stimuli activate a population of neurons at a fixed, high synchrony. This dichotomy has direct relevance to the use of electrical and optical stimuli as surrogates for sensory stimuli. As surrogate stimuli, we aim for electrical and optical inputs to reproduce natural patterns of activity in downstream structures when possible. However, if completely natural circuit activation is not achievable, the delivery of inputs that are discriminable is imperative. Previous work has modeled the nonlinear mappings from electrical stimuli to downstream response to control patterns of neural activity (Daly et al., 2012; Millard et al., 2013). Our results here specifically suggest that the variability structure induced by the different types of inputs is a critical component of stimulus design within this context. Importantly, the variability in evoked responses is not only a function of the type of input but is also a function of brain state. Cortical recordings during whisker stimulation from the study by Petersen et al. (2003) found that much of the variability in sensory-evoked responses could be accounted for by interactions with ongoing brain state, specifically in the context of up/down states. Whisker deflections administered during a down state elicit reliable large-amplitude responses, whereas whisker stimulation during an up state results in greater spike timing variability (Petersen et al., 2003; Hasenstaub et al., 2007). This becomes fundamentally important when comparing the variability trends observed in the anesthetized animal, in which the cortex oscillates between up and down states with a significant amount of time spent in down states, to the awake animal, in which up states dominate (McCormick et al., 2015). Furthermore, whisker-evoked responses in the awake mouse have been shown to be significantly more variable than in the isoflurane-anesthetized mouse (Ferezou et al., 2006). Although the increased prevalence of up states in the awake animal will likely have quantitatively distinct effects on the variability trends described here, the fundamentally different patterns of network activation by sensory and artificial stimulation will likely maintain the qualitative nonlinear mappings identified here. From the perspective of an ideal observer, knowledge of these distinct nonlinear mappings from sensory and artificial stimuli to the downstream cortical response can be leveraged to identify optimal stimuli that maximize discriminability. This simple example opens up a class of problems that needs to be more extensively addressed for the optimal design of spatiotemporal patterns of surrogate stimuli.

Implicit in the analysis of cortical activation in this study is the desire to link the cortical response to sensory percepts. The detection of whisker inputs through a Go–No-go paradigm has been investigated, and the sigmoidal cortical activation curves observed here for both sensory and artificial inputs mirror the performance of highly trained animals (Butovas and Schwarz, 2007; Stüttgen and Schwarz, 2008; Ollerenshaw et al., 2012; Bari et al., 2013), despite the fact that the electrophysiological data were obtained in acute, anesthetized settings. For behavioral relevance, surrogate sensory signals must match, if not mimic, information content delivered to the cortex. Sensory and artificial signals activate regions in distinct combinations of size and synchrony, leading to fundamentally different neural responses, and yet, knowledge of the specific mappings from stimulus to response enabled the design of optimal artificial stimuli that matched the theoretical information capacity of sensory stimuli. Behaviorally, this would correspond to an animal that was equally capable of discriminating between two intensities of whisker stimulation on a single whisker or two intensities of artificial stimulation administered in the same spatial location. This simple example points toward extension of these concepts to the design of stimulation profiles and parameters for artificial stimuli and the consideration of spatiotemporal nonlinearities in the mapping from stimulus to response. Optogenetic stimuli afford an expanded parameter space for the design of stimuli compared with electrical stimulation (Wang et al., 2012), in which design of the specific opsin properties or freedom from traditional stimulus constraints (i.e., charge-balancing) may enable more naturalistic mechanisms of neural circuit activation. Meanwhile, the static mappings here are a reduced view of a more complicated nonlinear system (Millard et al., 2013), such that additional identification and control of artificial circuit activation is needed to produce ethologically useful surrogate sensory signals. Ultimately, it is knowledge of the mechanisms by which sensory and artificial stimuli engage neural circuits that will inform these engineering approaches to optimizing the design and implementation of sensory surrogate signals in vivo.