Abstract
Fertilized soils have large potential for production of soil nitrogen oxide (NOx=NO+NO2), however these emissions are difficult to predict in high-temperature environments. Understanding these emissions may improve air quality modelling as NOx contributes to formation of tropospheric ozone (O3), a powerful air pollutant. Here we identify the environmental and management factors that regulate soil NOx emissions in a high-temperature agricultural region of California. We also investigate whether soil NOx emissions are capable of influencing regional air quality. We report some of the highest soil NOx emissions ever observed. Emissions vary nonlinearly with fertilization, temperature and soil moisture. We find that a regional air chemistry model often underestimates soil NOx emissions and NOx at the surface and in the troposphere. Adjusting the model to match NOx observations leads to elevated tropospheric O3. Our results suggest management can greatly reduce soil NOx emissions, thereby improving air quality.
 Soil NOx emissions can significantly impact air quality in agricultural regions, particularly high temperature fertilized systems. Here, the authors investigate NOx emissions in one such system in California and suggest that the NOx emissions are the highest ever observed, with implications for air quality.
Soil NOx emissions can significantly impact air quality in agricultural regions, particularly high temperature fertilized systems. Here, the authors investigate NOx emissions in one such system in California and suggest that the NOx emissions are the highest ever observed, with implications for air quality.
While agriculture in high-temperature environments is widespread and will become increasingly prominent in a future warmer climate1, the impacts of these systems on air quality are poorly constrained2,3. Nitrogen (N) losses to the atmosphere from high-temperature agroecosystems are not well characterized2,4 and are likely higher than temperate systems due to the combination of N fertilization2,5, nonlinear temperature dependence of biological processes6 and pulsed fluxes in response to irrigation—drying cycles7. Soil nitrogen oxide (NOx=NO+NO2) is one important form of N trace gas that can be released from fertilized soils and plays an important role in the formation of tropospheric ozone (O3), a toxic air pollutant. Approximately 1/4 of global NOx production is derived from soils, mostly from fertilized agriculture; however, estimates of global soil NOx emissions vary widely (9–27 Tg per year)8,9,10. Understanding how soil NOx emissions are regulated in high-temperature agroecosystems will help constrain current and future global NOx budgets and quantify the human health and ecosystem impacts of fertilized agriculture in a warming world.
The Southwestern United States of America has been experiencing warmer winter temperatures and more frequent heat waves over the past 100 years11,12 and is considered to be a climate-change hotspot13. The Imperial Valley, CA, is an important agricultural region within the Southwestern United States of America encompassing 200,000 hectares of irrigated agricultural land with air temperatures >40 °C in the summer. The Imperial Valley also suffers from poor air quality that regularly exceeds government O3 standards14, and experiences the highest rates of asthma hospitalizations in California15. To improve air quality in the region, understanding how urban and agricultural sources contribute to O3 formation is necessary. Fossil fuel combustion is likely a dominant source of NOx in the region, as there are small cities within the Imperial Valley (for example, El Centro; population=163,972) and large neighbouring urban areas including Los Angeles, San Diego and Mexicali. However, it is not clear whether agricultural NOx emissions significantly increase O3 formation, as O3 chemistry may be NOx saturated16. On the other hand, if the atmosphere is NOx limited, soil NOx emissions may enhance O3 formation, as observed in agricultural regions in the Midwestern United States of America17. The Imperial Valley is therefore a complex and important location for studying the impact of agriculture on air quality and human health.
Soil NOx emissions vary nonlinearly with environmental and land management factors including temperature, fertilization and soil moisture, but these relationships are not well constrained in high-temperature systems. While most studies have detected exponential increases in soil NOx emissions with temperature, there are contrasting results concerning high-temperature (>30 °C) responses of soil NOx emission18,19. Fertilization and N deposition are known to increase soil NOx emissions; however, the majority of studies are conducted at temperatures below 35 °C (refs 6, 20). In addition, fertilization type, amount and application method are known to influence soil NOx emissions. Side-injected fertilizers (where fertilizer is injected into the soil versus applied to the top) and splitting fertilization into smaller applications (<100 kg N ha−1) can limit NOx emission; however, these factors have mainly been evaluated in temperate environments5. Finally, irrigation and soil moisture are important factors regulating soil NOx emissions. In particular, strong pulse NOx emission responses to rewetting of soils in high-temperature regions are important21,22,23, yet understudied in managed systems. Therefore, measuring soil NOx emissions at high temperatures under different fertilization and soil-moisture conditions is needed to understand the regulation of fluxes, improve management and inform biogeochemical models.
Most chemistry transport models predict soil NOx emissions as a function of temperature, soil moisture and ecosystem type, such as in the Yienger and Levy model24 (hereafter called YL95). Models often assume optimum temperatures for nitrification and denitrification occur at 20–30 °C (refs 25, 26), with soil NOx emissions increasing exponentially before hitting a plateau at 30 °C (refs 8, 9). Within the YL95 paradigm, agricultural systems are assumed to be wet year-round and are assigned an emission factor associated with fertilization, where 1–2% of fertilizer applied is lost as NOx throughout the growing season27,28. Fertilization and irrigation events are generally not considered pulse events in models and are instead interpreted as elevating emissions at a constant rate throughout a growing season (for example, YL95 and the Weather Research and Forecasting with Chemistry model (WRF-Chem)29). Despite updates to YL95 (refs 8, 9), uncertainty associated with NOx pulse emission events and fertilizer-induced agricultural emissions is large8,9,23,27.
Here we aim to identify the environmental (that is, soil temperature, soil volumetric water content and inorganic N availability) and management factors (that is, time since fertilization and fertilization application practices) that regulate soil NOx emission, and its impacts on air quality in a high-temperature agricultural region: the Imperial Valley, California. Soil NOx emission measurements were conducted using the static chamber technique throughout two growing seasons of a high biomass grass, Sorghum bicolor. We use two N-fertilization experiments to evaluate pulse NOx responses to different levels of fertilization (20, 50 and 100 kg N ha−1) and fertilizer application methods (side-injected dry granulated N versus dissolved N). The implications of soil NOx fluxes on regional air quality are evaluated using a regional air chemistry model and local and remote sensing measurements of NO2 at the surface and in the troposphere. In these modelling exercises, we aim to test whether the model assumptions are valid for high-temperature environments. Specifically, we evaluate the model's ability to simulate soil NOx emissions, surface concentrations of NO2 and tropospheric NO2 columns in the Imperial Valley. We also elevate soil NOx emission rates in the model to evaluate the impact of those emissions on regional concentrations of tropospheric O3. We find that soil NOx emissions from this site are among the highest ever observed and respond nonlinearly to increases in fertilization, temperature and soil moisture. We also find that a regional air chemistry model often underestimates soil NOx emissions, surface NO2 concentrations and tropospheric NO2 columns in the Imperial Valley. Finally, we find that increasing cropland soil NOx emissions to match observations leads to elevated surface O3 concentrations.
Results
Environmental drivers of soil NOx emission
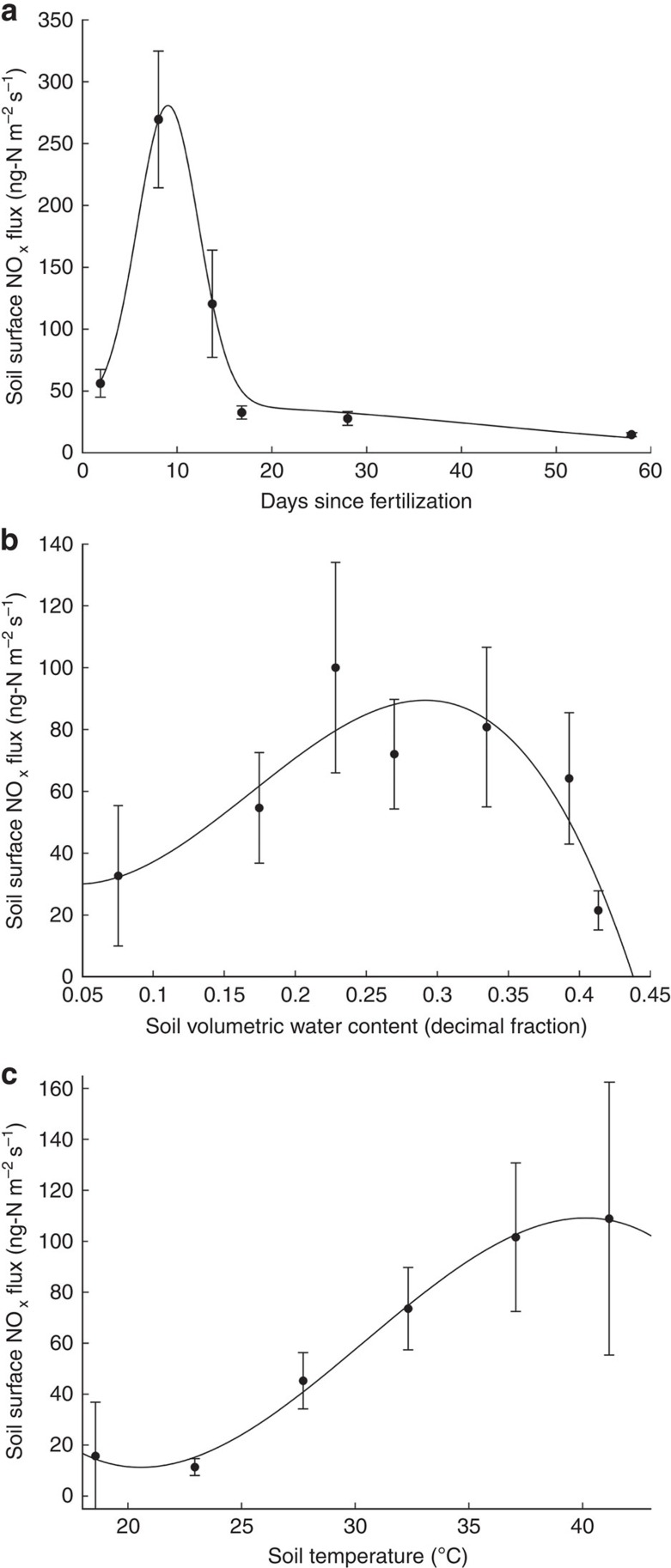
Soil NOx emissions observed in a high-temperature fertilized agricultural region of the Imperial Valley, CA, ranged between −5 and 900 ng N m−2 s−1. The highest NOx fluxes (top 10%) were observed at temperatures between 27–40 °C with moderate soil volumetric water content (0.14–0.40) and within 23 days of a fertilization event. The strongest predictor of NOx flux across all measurements was days since fertilization (F=5.32, P<0.0001; Fig. 1a) followed by soil volumetric water content (averaged across 0–10 cm depth; F=3.55, P=0.00053; Fig. 1b) and soil temperature (averaged between 2 and 10 cm depth; F=2.69, P=0.016; Fig. 1c). The adjusted R2 for the nonlinear model was 0.38, with 48.2% of deviance explained. Inorganic soil N content (NH4 and NO3) was a weak predictor of flux (NH4: F=3.04, P=0.043; NO3: F=2.28, P=0.061).
Figure 1. Environmental variables that regulate soil NOx emission.
Relationship between soil surface NOx flux (ng N m−2 s−1) and (a) days since fertilization, (b) soil volumetric water content (0–10 cm) and (c) soil temperature (average 2 and 10 cm; °C). Measurements were collected across two growing seasons 2012–2013, including measurements made during fertilization experiments (n=241). Data were binned by environmental variable and s.e. bars are shown for each bin. A Gaussian equation (f(x)=a+b*exp(−0.5((x−c)/d)2)) was fitted to the NOx relationship with days since fertilization data (a=18.6, b=254.3, c=8.6 and d=3.4). A third-order polynomial (f(x)=a*x3+b*x2+c*x+d) was fitted to the NOx relationship with soil volumetric water content (a=−8128.3, b=4125.5, c=−333.3 and d=37.4) and soil temperature (a=−0.026, b=2.4, c=−64.6 and d=562.5).
Soil NOx emission responses to fertilization and irrigation
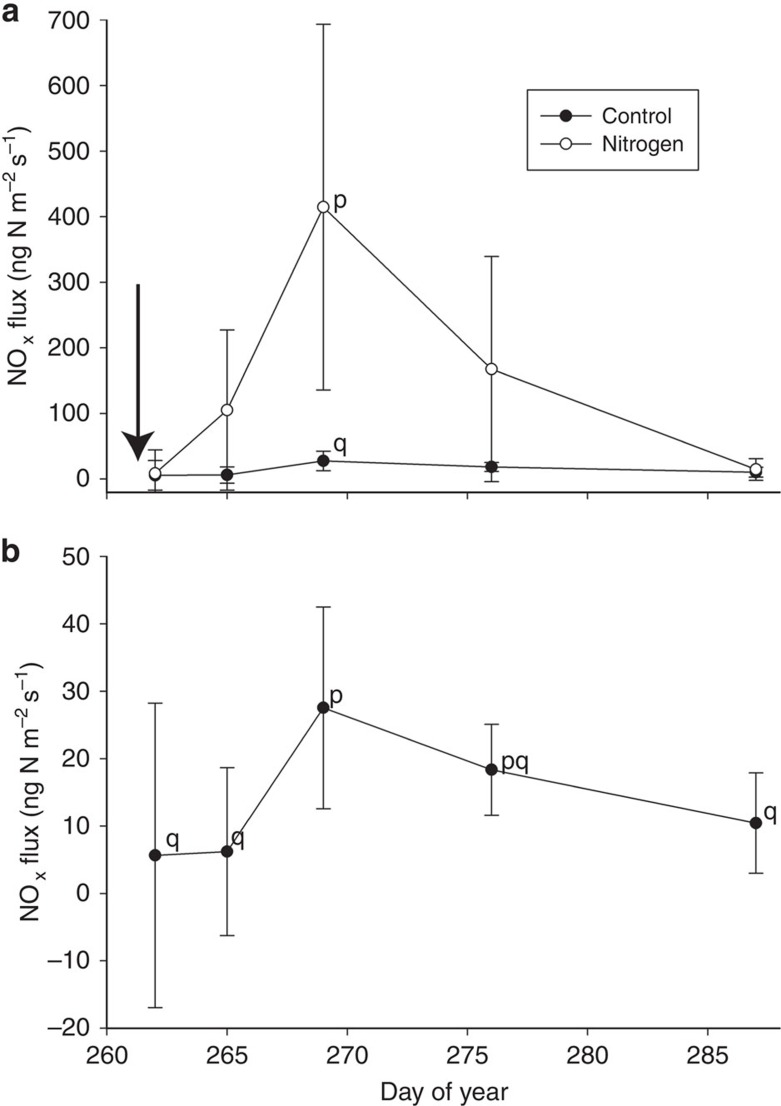
In the first N-fertilization experiment, experimental collars received an irrigation and fertilizer treatment (20 kg N ha−1 dissolved ammonium nitrate) and control collars received irrigation only. During the experiment, soil temperatures at 2 cm depth were on average 30.0 °C (s.d.=4.5 °C), and plant canopy height was on average 152.3 cm (15.8 s.d.). N-fertilization treatment and time had a significant effect on NOx emissions (F=30.56, P<0.0001; F=12.13, P<0.0001 for treatment and time effects, respectively). Pairwise comparisons indicated that the fertilized collars were significantly different from control collars 7 days post treatment (Fig. 2a; P<0.01); all other time points were not significantly different from each other. Numerical integration via the trapezoidal method revealed that treatment collars released 0.13 g N-NOx m−2 on average during the experiment, corresponding to a 6.6% emission factor. Control collars released 0.012 g N-NOx m−2 during the experiment.
Figure 2. Pulse NOx emission responses to dissolved ammonium nitrate fertilization.
(a) Soil NOx fluxes observed during a N-fertilization experiment in 2012 where collars received 20 kg ammonium nitrate-N ha−1 in dissolved form during an irrigation (white circles; n=10) and control collars received irrigation only (black circles; n=10; s.d. bars shown). The irrigation and fertilization event is indicated by an arrow (DOY 262). N treatment significantly increased NOx emissions with peak emissions observed 7 days post fertilization. (b) Control collar NOx fluxes were also evaluated in a separate analysis to investigate the influence of irrigation alone on NOx flux. Control NOx fluxes were significantly affected by time during the experiment in response to irrigation, where fluxes observed during the third measurement (7 days post treatment) were significantly different from all other measurements except for the fourth measurement (14 days post treatment). Significant differences between time points are indicated by letters (p, q) at P<0.05, as determined using pairwise comparisons with Bonferroni adjustment.
To evaluate the importance of rewetting events for NOx emissions without a recent fertilization, we conducted a separate analysis of the above experiment, but only included control collars. These control collars received irrigation only and had not been fertilized for over 30 days. In this separate analysis, NOx fluxes from control collars were significantly affected by time in response to irrigation (Fig. 2b; F=4.01, P<0.01), where the third measurement (7 days post treatment) was significantly different from all previous measurements (P<0.05), but not the fourth measurement (14 days post treatment; Fig. 2b), indicating that pulse soil NOx emission responses to irrigation occur even over 30 days after fertilization.
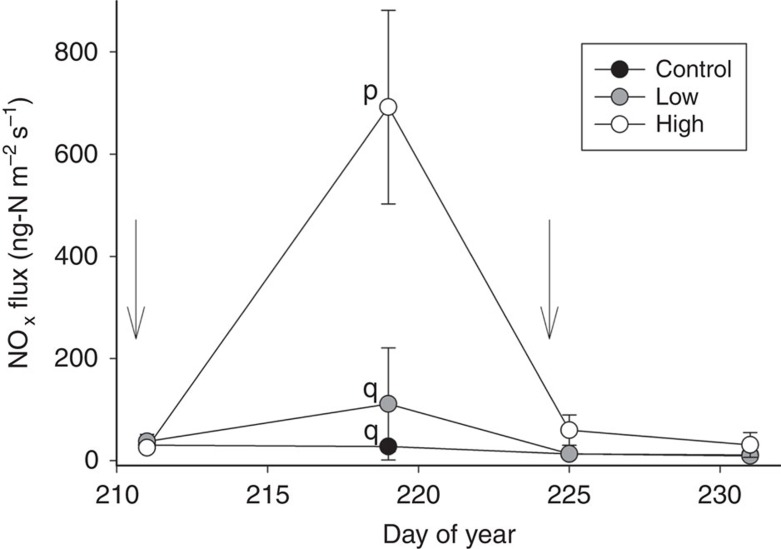
In the second N-fertilization experiment, experimental collars received low (50 kg N ha−1) or high (100 kg N ha−1) fertilizer treatment plus irrigation, while control collars received irrigation only. Fertilizer was applied via a side injection with urea granules. During the experiment, soil temperatures at 2 cm depth were on average 37.7 °C (s.d.=4.2 °C), and plant canopy height was on average 57.8 cm (22.7 s.d.). N-fertilization treatment and time had a significant effect on NOx emissions (F=32.20, P<0.0001, F=36.88, P<0.0001 for treatment and time effects, respectively). Pairwise comparisons indicated that the high-fertilizer treatment collars were significantly different from low-fertilizer treatment and control collars 9 days post treatment (Fig. 3; P<0.05); no differences between treatments were detected at other time points. Numerical integration via the trapezoidal method revealed that while control collars released 0.037 g N-NOx m−2 during the experiment, high-fertilizer treatment collars released 0.46 g N-NOx m−2 on average during the experiment, corresponding to a 4.6% emission factor, and low-fertilizer treatment collars released 0.089 g N-NOx m−2, corresponding to a 1.8% emission factor. Therefore, doubling the fertilization amount (50–100 kg N ha−1) increased integrated fluxes by a factor of 5.
Figure 3. Pulse NOx emission responses to side-injected urea fertilization.
Soil NOx fluxes observed during a fertilization experiment in 2013 with control (0 N), low (50 kg urea-N ha−1) and high (100 kg urea-N ha−1) side-injected fertilization treatments (n=3 collars per treatment; s.d. bars shown). Irrigation events are indicated by arrows. Fertilization occurred on DOY 210. High-fertilizer treatment collars were significantly different from low-fertilizer treatment and control collars at the second time point (9 days post treatment); no differences between treatments were detected at other time points. Significant differences between time points are indicated by letters (p, q) at P<0.05, as determined using pairwise comparisons with Bonferroni adjustment.
Investigating the regional significance of soil NOx emission
To assess the influence of soil NOx emissions on regional air quality, we employed a regional air chemistry model, WRF-Chem, and local and remotely sensed measurements of NO2 in the troposphere. We then increased soil NOx emission rates within the model to reach levels similar to those measured in the field and compared the modelled NO2 (default and elevated simulations) with measured surface NO2 concentrations and tropospheric NO2 columns. Finally, we evaluated the effect of increasing soil NOx emissions on modelled tropospheric O3.
First, we compared soil NOx emissions modelled in WRF-Chem with emissions measured in the field. By default, WRF-Chem estimated surface NOx emissions in the Imperial Valley to be near 2 ng NOx-N m−2 s−1. Across all our measurements, NOx fluxes were on average 66.4 ng NOx-N m−2 s−1 with a median of 20 ng NOx-N m−2 s−1. Across measurements made within 20 days of a fertilization event, NOx fluxes were on average 128.1 ng NOx-N m−2 s−1 with a median of 38 ng NOx-N m−2 s−1. By multiplying WRF-Chem emission rates by factors of 10 and 64.5, we elevated soil NOx emissions in Imperial Valley croplands to be near 20 and 129 ng NOx-N m−2 s−1, which are representative of the range in mean and median flux values collected under both average and recently fertilized conditions in the field.
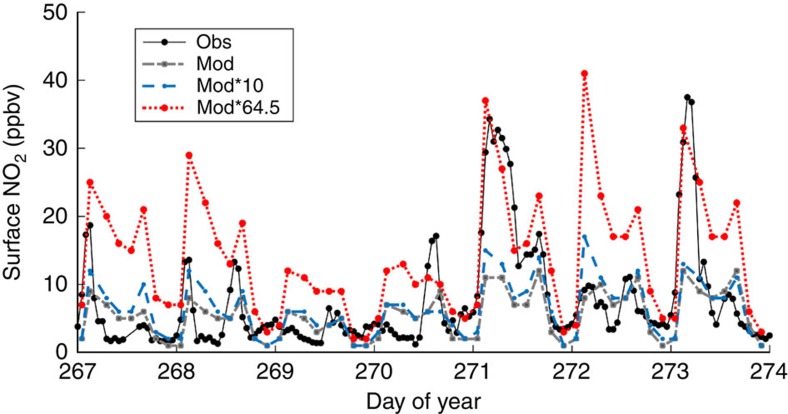
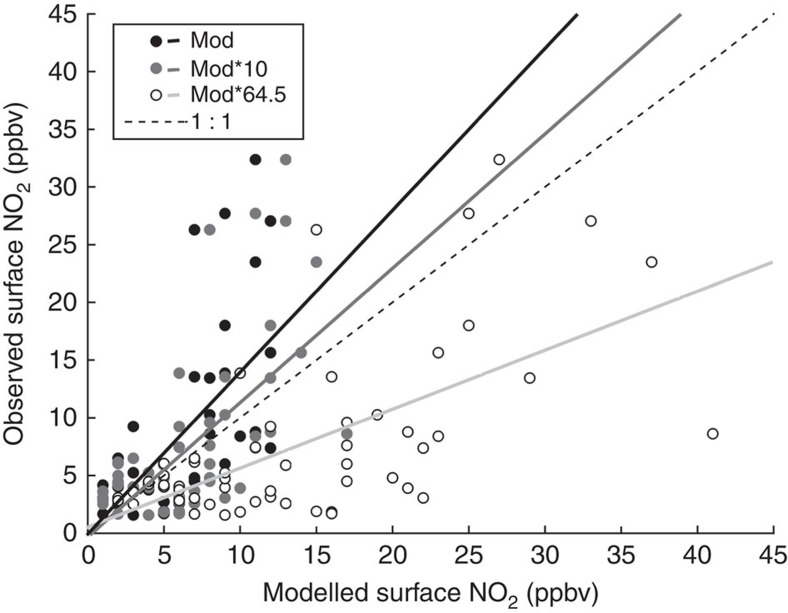
We then compared modelled surface NO2 concentrations in the Imperial Valley with surface NO2 measurements collected at an air quality monitoring site (CA Air Resources Board, El Centro-9th Street, CA; Fig. 4). Meteorological conditions were stable, with no rainfall and consistent temperature and radiation during the simulation period (average air temperature=30.29 °C, s.d.=1.9; average daily net radiation=110.9 W m−2, s.d.=4.1). WRF-Chem default parameterization performed well, especially on days when NO2 surface concentrations were low (for example, day of year (DOY) 269; Fig. 4) and tended to underestimate peak NO2 concentrations early in the morning when the daytime boundary layer was developing and pollutants, including NO2, were not well mixed (for example, DOY 271; Fig. 4; Supplementary Fig. 1). All model simulations explained significant amounts of variation in observed surface NO2 during the simulation period (Fig. 5), with the least amount of bias occurring when soil NOx emissions in the model were increased by an order of magnitude (root mean s.e. (r.m.s.e.)=6.1, 5.7 9.5 p.p.b.v. for model default, model*10 model*64.5, respectively). These results suggest that an improved soil NOx emission factor in WRF-Chem would be close to 10 or 20 × higher than default to match observed surface concentrations of NO2 in the Imperial Valley. When soil NOx emissions were increased 64.5 × , the model overestimated surface NO2 by 81% across the simulation period. An additional analysis was conducted using only data at local time 13:00–16:00 when the boundary layer was well developed at an average of 1,587 m (s.d.=796 m; Supplementary Fig. 1) and overlapping with Ozone-monitoring instrument (OMI) overpass time (12:00–13:30). However, the results were similar to the analysis including all data (Fig. 5) and therefore are not shown.
Figure 4. Comparing time series of modelled and measured surface concentrations of NO2 in the Imperial Valley, CA.
Surface concentrations of NO2 measured at an air quality monitoring station (obs) in El Centro, CA (CA Air Resources Board) and modelled with WRF-Chem (mod) and WRF-Chem with soil NO2 emission rates multiplied by 10 (mod*10) and 64.5 × (mod*64.5). All data are from 23 to 29 September 2012.
Figure 5. Comparing modelled and measured surface NO2 concentrations in El Centro, CA.
Surface concentrations of NO2 (p.p.b.v.) at an air quality monitoring station in El Centro, CA (CA Air Resources Board; obs) and modelled with WRF-Chem (mod) and WRF-Chem with soil NO2 emission rates multiplied by 10 (mod*10) and 64.5 (mod*64.5). All data are from 23 to 29 September 2012. The dashed line represents the 1:1 relationship; all other lines correspond to linear regressions between modelled and observed data (default model r2=0.44, slope=1.4, intercept=0.14; mod*10 r2=0.44, slope=1.1, intercept=0.38; mod*64.5 r2=0.42, slope=0.5, intercept=0.7). All linear regressions were significant at P<0.0001.
While the discrepancies between measured and modelled surface NO2 concentrations may be due to the model underestimating soil NOx emissions from local agricultural fields, they may also be due to mischaracterized local meteorology or underestimated NOx emissions inventories from local biomass burning and/or fossil fuel combustion. To investigate alternative sources of error, we first compared locally measured meteorological variables with simulated meteorological variables and found high agreement between modelled and measured air temperature and wind speed during the simulation period (r2=0.60, r.m.s.e.=2.3 °C and r2=0.80, r.m.s.e.=0.58 m s−1 for air temperature and daily average wind speed, respectively). We also examined the infrared anomaly (fire) data from MODIS and determined that no large biomass burning events had occurred during 20–29 September 2012. The discrepancies between modelled and measured NO2 may also be due to under-represented fossil fuel combustion rates; however, the fossil fuel combustion NOx emission data used in the model are known to overestimate anthropogenic NOx sources by 32% in southern California30.
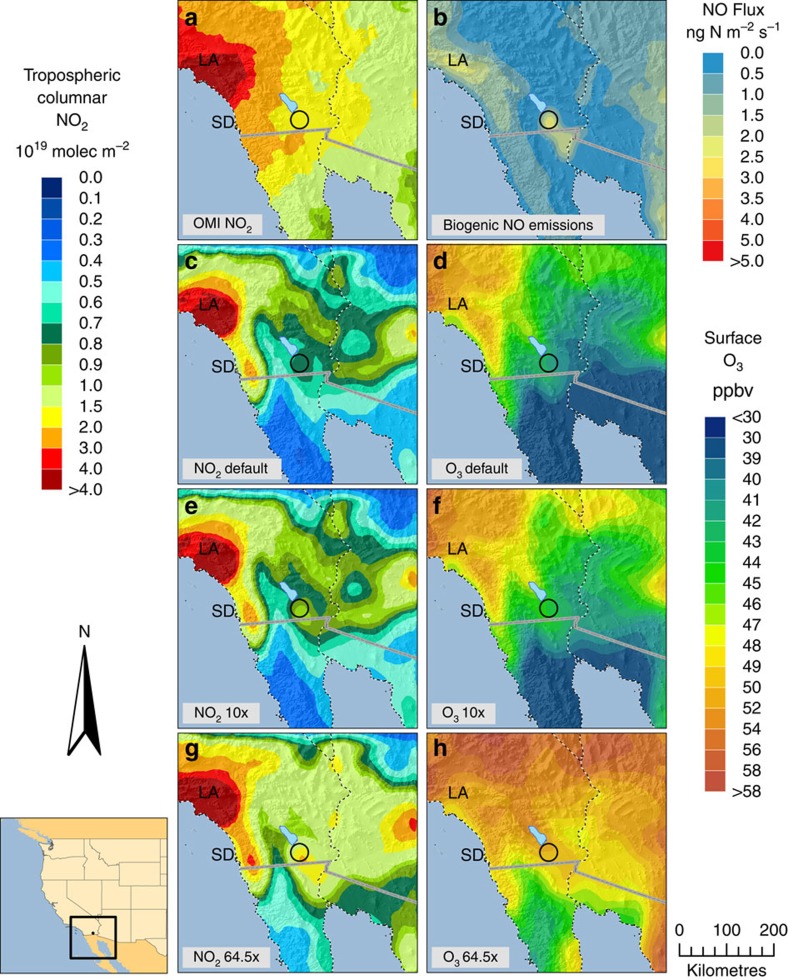
We also compared remotely sensed measurements of tropospheric NO2 columns with WRF-Chem model simulations. The OMI satellite-derived tropospheric NO2 columns suggest that WRF-Chem underestimates NO2 above the Imperial Valley by 63% during the simulation period (0.75 and 2.05*1019 molecules NO2 m−2 for WRF-Chem and OMI, respectively; Fig. 6a,c). Elevating soil NOx emissions by an order of magnitude still resulted in the model underestimating observed tropospheric NO2 columns by 56% (0.90*1019 molecules NO2 per m2 above the Imperial Valley). However, elevating soil NOx emissions by 64.5 × led to good agreement with observed tropospheric NO2 columns (2.0*1019 molecules NO2 per m2 above the Imperial Valley; Fig. 6e,g).
Figure 6. NO2 and O3 distributions from WRF-Chem and OMI above the Imperial Valley.
Distribution of tropospheric columnar NO2 retrieved by (a) OMI across 3 days (25, 28 and 29 September 2012) measured at 12:00–13:30 local time. WRF-Chem (b) surface NO2 emissions (ng N m−2 s−1) and (c) tropospheric NO2 columns are also shown across the same 3 days at 12:00–13:30 local time. Soil NO2 emission rates from cropland were elevated within WRF-Chem (e) 10 × and (g) 64.5 × above default resulting in higher tropospheric NO2 columns. WRF-Chem simulations of surface O3 concentrations (p.p.b.v.) are also shown corresponding to the (d) default, (f) 10 × and (h) 64.5 × elevated soil NO2 emission runs. All tropospheric NO2 column units are in 1019 molecules NO2 per m2. The Imperial Valley study region is circled in black in each panel. Nearby cities are also indicated within each panel as San Diego (SD) and Los Angeles (LA).
WRF-Chem simulations with elevated soil NOx emission rates resulted in significant increases in surface O3 concentration. Under default conditions, WRF-Chem estimates O3 at 41.5 p.p.b.v. in the Imperial Valley across 3 days in September 2012 (Fig. 6d). Increasing soil NOx emissions by 10 and 64.5 × increased O3 levels by 2.2 and 8.5 p.p.b.v., respectively (Fig. 6f,h). These modelled O3 concentrations highlight the sensitivity of air quality to soil NOx emissions in the region and confirm that this air shed is NOx limited.
Discussion
We find that NOx emission rates from high-temperature agricultural soils in the Imperial Valley are some of the highest ever reported8,31. Despite differences in fertilizer type and application method, both fertilization experiments resulted in higher than expected NOx fluxes with emission factors ranging between 1.8 and 6.6% over the course of 20–25 days following treatment. Our approximated emission factors are likely an underestimation, as they were derived from non-continuous short monitoring periods highlighting the need for continuous flux measurements. Overall, our results suggest that commonly applied NOx emission factors (typically 1–2% across an entire growing season5,8,23) are highly uncertain and underestimate NOx emissions in high-temperature agricultural systems.
We also find that NOx emissions are best predicted through nonlinear relationships with time since fertilization, soil temperature and soil moisture. Incorporating nonlinear NOx emission responses to these factors into biogeochemical models is becoming more common. In particular, Hudman et al.9 account for pulse emission responses to fertilization and continuous dependence on soil moisture (instead of distinct wet/dry states) within the Berkeley–Dalhousie Soil NOx Parameterization model, which is available in GEOS-Chem, a global chemistry transport model. However, many models (including the Berkeley–Dalhousie Soil NOx Parameterization model) do not account for NOx emission responses to different levels, chemical species, application methods of fertilization, irrigation events in agricultural systems and nonlinear NOx emission responses to high temperature (>30 °C). Our study highlights these factors as critical functions influencing NOx emissions.
Fertilization management, including the type of fertilizer used and how it is applied, is critical for minimizing the loss of N to the atmosphere in the form of NOx. Our fertilization experiment revealed strong nonlinear increases in flux response to increases in fertilizer amount. This extends previous work suggesting that large fertilization events result in higher than expected NOx emissions and splitting fertilization into smaller amounts can greatly reduce NOx emissions5. Our experiments also demonstrate that using side-injected granular urea-N-fertilizer results in lower NOx emissions than a dissolved NH4NO3-N application. Application of 50 kg urea-N ha−1 induced an integrated flux that was 30% lower than a 20-kg NH4NO3-N ha−1 treatment. Urea is a more complex N source requiring an extra step before it can serve as a substrate in nitrification and denitrification, while ammonium nitrate is a direct substrate for both nitrification and denitrification. This supports previous research conducted in lower-temperature environments, suggesting that side injection and complex N (for example, urea) limit N trace gas emissions5,32. Fertilizer management is therefore a critical factor for minimizing N losses to the atmosphere and reducing adverse effects to air quality in high-temperature agroecosystems.
We find NOx emission pulses in response to irrigation alone, a response consistent with a previously described hypothesis that fertilized soil will continue to exhibit pulse NOx emission behaviour with multiple irrigation events2. Long-term effects of fertilization on soil NOx production may therefore significantly contribute to annual NOx budgets. Models often assume agricultural systems maintain constant soil-moisture conditions33; however, soil surface drying between irrigation events is common in high-temperature arid agroecosystems34. Our results stress the importance of understanding how combined fertilization and irrigation practices influence soil NOx emissions.
Soil NOx models often assume NOx emission exponentially increases with temperature until a plateau is reached above 30 °C (ref. 9). Our results highlight nonlinear responses in NOx emissions above 30 °C, where soil NOx emissions increase 38% on average as soil temperatures increase from 30–35 to 35–40 °C (Fig. 1). While exponential relationships between soil temperature and soil NOx emissions are valuable for predicting flux, these responses need to be parameterized to different environmental conditions. This is especially true in high-temperature environments such as the Imperial Valley where microbial acclimation to high temperature and/or increased contributions of deeper and cooler soil layers (>10 cm) to surface NOx emissions may be significant. While we did not observe inhibition of NOx emissions above 35 °C, higher temperatures than those covered in this study (>40 °C) may reveal inhibition of NOx emissions.
We find evidence that the regional air chemistry model WRF-Chem underestimates soil NOx emissions, tropospheric NO2 columns and, at times, surface NO2 concentrations in the Imperial Valley. Default WRF-Chem simulation of soil NOx emissions from agricultural land was on average 2.0 ng N m−2 s−1 (Fig. 6b), much lower than observed in the Sorghum field (on average 65 ng N m−2 s−1 across all measurements). Model simulations of tropospheric NO2 columns also underestimated observed values. These results agree with previous research showing that satellite-derived (OMI) tropospheric NO2 columns are elevated above agricultural land in the Western United States of America, and that these sources are underestimated in current models23. However, the model did not consistently underestimate surface NO2 (for example, DOY 272; Fig. 4). While increasing soil NOx emission rates by 64.5 × within WRF-Chem led to strong overestimation of surface NO2 observations, it led to good agreement with tropospheric NO2 column observations. Our results therefore indicate that there is no single emission factor that can be used to accurately simulate both tropospheric NO2 columns and NO2 observed at the surface. On the basis of field measurements, soil NOx emissions are highly variable depending on fertilization, soil temperature and soil moisture. We therefore advocate for modifying model structure within WRF-Chem to incorporate these NOx emission dynamics, versus simply increasing emission factors. This is an important area for future research.
High soil NOx emissions are likely contributing to high concentrations of tropospheric O3 in the Imperial Valley. Elevating soil NOx emission rates within the model to the point where better agreement was achieved with observations led to significantly higher concentrations of simulated surface O3. These model simulations suggest that air chemistry in the region is NOx limited and therefore sensitive to soil NOx emissions. Intensive agriculture in the Imperial Valley and associated high soil NOx emissions may therefore be contributing to poor air quality in the region. Soil NOx emissions may also be contributing to the formation of particulate nitrate, another threat to human respiratory health. The management of fertilizers may be a valuable approach for reducing the negative impacts of agriculture on human health in the Imperial Valley.
There are multiple factors that could lead to WRF-Chem underestimating tropospheric NO2 columns and, at times, surface NO2 concentrations in the Imperial Valley. While we investigated some of these factors (for example, poorly constrained soil NOx emissions, meteorology and biomass burning NO2 sources), more intensive evaluation and improved model parameterization will be required to advance predictive skill of NO2 and O3 dynamics in the region. First, to improve regional scale modelling of agricultural NOx emissions, future studies require NOx flux measurements across all dominant crop types in the Imperial Valley paired with spatially explicit management data, including irrigation and fertilization practices. Second, improved model structure informed by relationships presented in Fig. 1 will be required for predicting soil NOx emission responses to temperature, irrigation and fertilization. Third, biogenic volatile organic compound emissions in high-temperature irrigated environments35 and fossil fuel combustion inventories need to be better constrained to more accurately evaluate the significance of soil NOx sources for tropospheric O3 production. This is particularly important as previous work has shown that the EPA's NEI-05 emission data significantly overestimate anthropogenic NOx sources in Southern California30. Improving WRF-Chem performance will therefore require evaluation of both model structure and model input data with regard to multiple sources of agricultural and anthropogenic organic compounds and NOx in the Imperial Valley.
In summary, we find high N losses in the form of NOx from high-temperature agroecosystems that are not well represented by a current air chemistry model. Managing soil NOx emissions should be considered in future efforts to improve regional air quality in the Imperial Valley, a region that regularly exceeds government O3 standards14 and suffers from the highest rates of asthma hospitalizations in California15. Our results suggest that smaller doses of side-injected dry fertilizers with complex N formulations may help reduce NOx emissions and thereby increase nutrient-use efficiency. There is growing concern over the sustainability of agricultural production in regions of the world that have been experiencing higher temperatures and more frequent heat waves1. Results from this study highlight the need for improved understanding of fertilized high-temperature environments, for better representation in air chemistry transport models and for development of sustainable management of agricultural land in a future warmer climate.
Methods
Study location and experimental design
All measurements were conducted in experimental agricultural fields located in the low elevation (−18 m ASL) University of California Desert Research and Extension Center (DREC), Holtville, Imperial County, CA (32°N 48′ 42.6″, 115°W 26′ 37.5″) characterized by deep alluvial soils (42% clay, 41% silt and 16% sand) with 2.34% C and 0.13% N, and a pH of 8.3. The field site experienced historically typical air temperatures during the experiments conducted in 2012 and 2013 (ref. 36). Two N-fertilization studies were conducted under cultivation of a forage cultivar of S. bicolor (cv. Photoperiod LS; Scott Seed Inc.) in adjacent fields. Seed of S. bicolor were planted at 90,000 plants per ha. High-biomass-producing grasses including sorghum, sudangrass and sugarcane are the 4th most common crop type in the Imperial Valley, behind Alfalfa, pasture and vegetables37. These high-biomass-producing grasses typically receive a large fertilizer application at planting (100–150 kg N ha−1) followed by smaller applications (50 kg N ha−1) throughout the growing season, typically following harvests38,39. Fertilizers are often applied by injecting anhydrous fertilizer into the sides of furrows or by broadcasting fertilizer on the soil surface. The cheapest form of fertilizer is dry urea, but ammonium nitrate and ammonia are also used40. The fields were gravity-fed flood irrigated as needed, usually every 10 days or when soil surface volumetric water content fell below 0.10 cm3 cm−3. Gravity-fed flood irrigation is the most prevalent irrigation practice in the Imperial Valley; 70% of irrigated crops using water from the Colorado River use flood irrigation41. Both fields had beds separated by 1.5 m with 20-cm-deep furrows, and have been used for agricultural production at least since the establishment of DREC in 1912. The first experiment was conducted in a large experimental field (5.3 ha) in 2012 and the second in a smaller field (0.4 ha) in 2013.
Large-field measurements
Seed of S. bicolor were planted on 16 February 2012. Urea fertilizer treatments of 90 kg N ha−1 were applied with a 3-m-wide fertilizer spreader on 10 February, 18 June and 16 August 2012, totalling to 270 kg N ha−1 per year. Pesticides were applied at 2.1 l ha−1 on 30 April 2012 (Lorsban insecticide, Dow AgroSciences, Indiana, USA) and herbicides were applied at 0.84 kg ha−1 on 27 March 2012 (Maestro, Nufarm Americas Inc., Illinois, USA). Three harvests were conducted in 2012 on 4 June, 14 August and 12 November (corresponding to DOY 156, 227 and 317, respectively). The second and third growth periods were ratoon crops. The field was left fallow in the winter and was re-seeded on 1 April 2013. Sorghum was planted later in the season in 2013 due to late rains. In 2013, only two harvests were conducted on 19 July and 18 September 2013. Fertilizer treatments were applied on 29 May 2013 at 52 kg N ha−1 (side dressed urea), 20 June at 66 kg N ha−1 (mixture of urea–ammonium nitrate solution (32%) and 8% ammonium nitrate organic solution), and 20 August 2013 as 96 kg N ha−1 (urea–ammonium nitrate 32%), totalling to 214 kg N ha−1 per year. No pesticides or herbicides were applied in 2013.
We installed 20 soil collars on 20 February 2012, split between the northwest and southeast quadrants. In each quadrant, 10 collars were divided between two rows separated by three furrows. Soil NOx measurements were conducted throughout the growing season to assess general trends in NOx emissions (21 March, 22 May, 27 June, 7 August and 20 August corresponding to DOY 81, 143, 179, 220 and 233, respectively) and again in 2013 (9 July, 30 July, 19 August, 22 August, 28 August and 2 September corresponding to DOY 190, 211, 231, 234, 240 and 245, respectively). Due to difficulties with instrumentation, not all collars were measured on every sampling occasion.
In the first N-fertilization experiment in 2012, 10 experimental collars received an irrigation and fertilizer treatment (dissolved 20 kg ammonium nitrate-N ha−1) on 18 September 2012, while 10 control collars received irrigation only (with five collars in the southeast quadrant and five in the northwest quadrant randomly receiving fertilization). Collars were fertilized concurrent with flood irrigation of the entire field. Before the experimental fertilization, the field had not received fertilization for 32 days (at 90 kg urea-N ha−1). During this experiment, each collar was measured on 18 September, 21 September, 25 September, 5 October and 13 October (corresponding to DOY 262, 265, 269, 279 and 287, respectively). Plant canopy height next to each collar was also measured on those dates.
Small-field measurements
A similar N-fertilization experiment was conducted in 2013 in an adjacent Sorghum field (planted on 1 April 2014). We installed soil collars on 23 July 2013 in a randomized block design where the field was split into three blocks each with six rows of control, six rows of low (50 kg urea-N ha−1) fertilizer treatment and six rows of high (100 kg urea-N ha−1) fertilizer treatment. One soil collar was established within each treatment per block (nine soil collars total with three replicates per treatment). Fertilizer granules (urea) were side-injected into the furrows using a tractor, immediately followed by flood irrigation on 29 July 2013 (DOY 210). Before the experimental fertilization, the crop had not received fertilization. Soils in this field had not been fertilized since the cultivation of a previous crop 5 months before. Measurements were collected on 30 July, 7 August, 13 August and 19 August 2013 (corresponding to DOY 211, 219, 225 and 231, respectively). Plant canopy height next to each collar was also measured on those dates.
Soil NOx flux measurements
NOx chamber measurements were conducted using the static chamber technique. Soil collars (made of polyvinyl chloride with a diameter of 20 cm and height of 10 cm) were inserted 4–6 cm into the soil on the top of furrows. A custom-built chamber was set on top of soil collars and set into place using a rubber seal. The chamber was also made from polyvinyl chloride with a mixing fan mounted on the inside and reflective tape covering the outside of the chamber42. Air was pulled from the top of the chamber at 1 l min−1 and routed to a portable NO monitor (Nitric Oxide Monitor Model 410 with NO2 converter Model 401, 2B Technologies, Colorado, USA) where depletion of O3 is measured using UV absorbance (detection range: 2–2,000 p.p.b.; precision: ±1.5 p.p.b.; measurement rate: 0.1 Hz). This system converts all NO2 to NO using a molybdenum converter before sending sample air to the NO monitor, therefore measurements are expressed as NOx flux (NO+NO2). This technique is similar to conventional chemiluminescence analyzers; however, we found our system to be better suited to high-emission environments compared with chemiluminescence instruments in preliminary studies conducted in both field and lab settings. Soil NOx flux was calculated using the rate of increase in NOx concentration within the first 3 min of placing the chamber onto the collar. We used linear regression to determine rates of change from an average of nine points in the regression or 1.5 min of data.
Ancillary soil sampling and inorganic soil N analysis
Each flux measurement was paired with soil temperature, moisture and inorganic N measurements. Soil temperature was measured next to each collar at 2 and 10 cm depth (Fluke 51 II Thermometer (Wilmingtion, NC, USA)). A soil core (1.5 cm diameter) was extracted next to each collar following the NOx measurement (0–10 cm). The core was homogenized in a bag before removing 15 g for measuring soil volumetric water content and 2.5 g for inorganic N extraction at a 1:10 soil weight-to-solution volume ratio using 2 M KCl. Extracts were put on ice until transported back to the lab, where they were processed within 24–48 h. Samples were shaken for 1 h at room temperature, centrifuged and filtered through Whatman no. 40 filter paper (11 μm) and frozen until further processing. Filtrates were acidified and analysed by automated cadmium coil reduction for nitrate/nitrite (Seal Analytical Inc., AQ2 Discrete Analyzer (Mequon, Wisconsin). NO3 and NH4 are expressed in μg N g−1 dry soil.
Statistical analyses
In a comprehensive analysis of all observed NOx fluxes, nonlinear generalized additive modelling was used to assess the influence of environmental parameters on NOx flux via the GAM function in R (v.3.1.1, Vienna, Austria). The model included explanatory variables NO3, NH4, soil temperature (averaged between 2 and 10 cm depth), soil volumetric water content (averaged across 0–10 cm depth) and days since fertilization. The best-fitting parsimonious model was selected using Akaike's information criterion. For visualization, NOx fluxes were binned according to environmental variables (days since fertilization, soil volumetric water content and soil temperature). Third-order polynomials were fitted to the relationships between binned average NOx flux and soil volumetric water content and soil temperature. A Gaussian equation was fitted to the relationship between binned average NOx flux and days since fertilization. All fitting was performed in Matlab (v.R2014a, The Mathworks, Inc. USA). Repeated measures analyses of variance were conducted independently on each N-fertilization experiment to test for significant effects of treatment (fertilized or control) on NOx emissions. Pairwise comparisons using the Bonferroni adjustment were conducted to explore differences between treatments at specific time points. NOx emissions were log transformed to meet homogeneity of variance assumptions. Analysis of variance and Bonferroni tests were performed in R (v.3.1.1, Vienna, Austria). To estimate total N released as NOx in response to treatments, we performed numerical integration via the trapezoidal method in Matlab. These integrated values are only approximate and are most likely an underestimate of total flux, as peak fluxes may not have been captured with discontinuous measurement techniques.
Regional air quality modelling
We evaluated the influence of soil NOx emissions on regional air quality using the WRF-Chem (version 2.0). The WRF-Chem model29,43 is a regional air quality model that can be used for weather forecasting and simulating gas-phase chemistry, including NOx and ozone chemistry at an hourly time step. With its nested grid capability, WRF-Chem-simulated quantities can be more easily compared with a wide range of in situ and remote sensing data collected at different temporal and spatial resolutions. A nested grid configuration was used in this study with the centre in the Imperial Valley, CA. The resolution of fine grid was 12 × 12 km and the outer domain was 36 × 36 km. Table 1 lists the model configuration options employed in this study.
Table 1. WRF-Chem configuration.
| Atmospheric process/inputs | Model option |
|---|---|
| Surface layer | MM5 |
| Land surface | Noah64 |
| Boundary layer | YSU65 |
| Cumulus clouds | G3 (ref. 66) |
| Cloud microphysics | Lin67 |
| Gas-phase chemistry | RADM2 (ref. 68) |
| Aerosol chemistry | MADE69/SORGAM70 |
| Horizontal resolution | 36 km For the outer domain, 12 km for the inner domain |
| Vertical layers | 27 |
WRF-Chem, Weather Research and Forecasting with Chemistry model.
The NARR (North American Regional Reanalysis) data at 0000, 0600, 1200 and 1800 UTC were used for initializing and specifying the temporally evolving lateral boundary conditions. The US National Emissions Inventory emissions data (NEI-05; version 2) was used in the simulation as background emission (US Environmental Protection Agency, 2010). The NEI-05 data are likely a high estimate for anthropogenic NOx sources in the Imperial Valley. Previous work in Los Angeles County has shown that anthropogenic NOx sources in NEI-05 are overestimated by 32% (ref. 30). The land-use data used in this study is the US Geological Survey land-use data. Biogenic emissions of volatile organic compounds and soil NOx emissions are calculated using the Model of Emissions of Gases and Aerosols from Nature (MEGAN v2.0 (refs 44, 45)). In MEGAN, gridded emission factors are based on global data sets of four functional plant types (broadleaf trees, needle-leaf tree, shrubs/bushes and herbs/crops/grasses), where the herbs/crops/grass category has a higher emission factor compared with the other plant types46. In this version of MEGAN, soil N (NO, NO2 and NH3) emissions are a function of temperature only; production and loss of NOx within the canopy is not considered. Previously reported canopy uptake rates are low, ranging up to 3 ng N-NO2 m−2 s−1 under high light and high NO2 concentrations (NO2=5 p.p.b.)47. However, canopy uptake rates in high-emission and high-temperature environments are uncertain and require further research36,47,48,49,50. Pulse NOx emissions following fertilization events are also not considered in the model. The emission factor for agricultural soils is 6 ng N m−2 s−1 at a standard temperature of 273.15 K (ref. 46). Due to assumptions made in the satellite observations, we apply an averaging kernel to the WRF-Chem simulations to allow comparison with the space-borne OMI (described below)51,52.
Modifications to a regional air quality model
To evaluate the sensitivity of air quality to soil NO2 sources in the Imperial Valley, we modified the strength of soil NOx emissions from irrigated agricultural land. Other land types such as surrounding urban and dry native lands were not manipulated. We elevated WRF-Chem emission rates by a factor of 10 and 64.5, resulting in simulated soil NOx emissions in Imperial Valley croplands near 20 and 129 ng N m−2 s−1, which are representative of the range in mean and median flux values collected under both average and recently fertilized conditions in the field. It is important to note that this modelling exercise simply increases emission rates and does not account for the observed nonlinear pulse NOx emission events that occur in response to fertilization.
All simulations were run for 7 days in September 2012 (23–29 September 2012), with several days as spin-up time. These simulations were compared with measurements of surface and tropospheric NO2 columns above the Imperial Valley.
Comparing modelled and measured NO2
Evaluation of WRF-Chem model performance was assessed through comparisons with surface and satellite observations. First, we compared modelled with measured surface NO2 in the Imperial Valley. Surface NO2 concentrations are measured by the California Air Resources Board at an air quality-monitoring site located 11.3 km west of DREC on 9th Street, El Centro, CA (latitude: 32.79222; longitude: −115.563). This site is not near a point source and provides representative concentrations of pollutants for the Imperial Valley. Surface NO2 measurements are made by first reducing all NO2 to NO using heated molybdenum surfaces and then measuring the chemiluminescent reaction of NO with O3 (ref. 53). Comparisons between modelled and measured surface NO2 concentration were made for all WRF-Chem model simulations (default, 10 × and 64.5 × elevated soil NOx emission). WRF-Chem model performance was assessed using linear regression and the coefficient of determination (r2). Model bias was estimated using the absolute r.m.s.e. between modelled and observed surface NO2 concentrations.
To evaluate the model's ability to simulate local meteorology, we compared daily average wind speed (m s−1) and air temperature (°C) measured at the El Centro air quality monitoring station and simulated by the model. Model performance was assessed using the coefficient of determination (r2) and the absolute r.m.s.e.. We evaluated local sources of NOx from biomass-burning events using MODIS images. MODIS images are publically available and were assessed for 20–29 September 2012. We also analysed meteorological data from a weather station located at DREC (managed by the California Irrigation Management Information System, www.cimis.water.ca.gov) to investigate how rainfall (mm), air temperature (°C) and net radiation (W m−2) changed during the simulation period.
We also assess WRF-Chem performance using remotely sensed tropospheric columnar NO2 by OMI on board the Aura satellite. OMI measures radiation in the broad visible spectrum between 264 and 504 nm54. OMI has near daily contiguous global coverage with moderate spatial resolution (60 cross-track ground pixels ranging from 13 × 24 to 128 × 40 km at the edge of a sampling swath). We use the level 2 (version 2.0) KNMI-DOMINO product (Royal Netherlands Meteorological Institute). The KNMI product and its errors are described in detail by Irie et al.55 and Boersma et al.56,57. Briefly, the KNMI-DOMINO product determines the stratospheric portion of the column by assimilating slant columns in the TM4 chemistry transport model, with an uncertainty in the stratospheric NO2 column of near 0.3*1015 molecules per cm2 (ref. 58). The tropospheric air mass factor is determined using the formulation of Palmer et al.59 and Boersma et al.60 to convert slant columns to vertical columns57. The KNMI product is known to compare well with aircraft measurements of NO2 in urban regions (r2=0.67, slope=0.99±0.17)61, while tending to overestimate NO2 in remote regions62,63. When compared with ground-based measurements in China, the biases of the KNMI product were less than 10% (ref. 55). The KNMI product is also known to have less systematic seasonal error compared with the NASA product52. Due to satellite data having irregular grid boxes, we re-gridded to regular grid boxes at a 0.4° resolution using area-weighted average for illustrative purposes (Fig. 6). During the WRF-Chem simulation period, an average of eight OMI pixels fell within the Imperial Valley region. We present OMI data averaged across 25, 28 and 29 September 2012, as these were all days during the WRF-Chem simulation period when OMI data were available, the cloud radiance fraction was <50% and the target region was not on the edge of the swath (excluding pixels with a viewing angle >45°).
Additional information
How to cite this article: Oikawa, P. Y. et al. Unusually high soil nitrogen oxide emissions influence air quality in a high-temperature agricultural region. Nat. Commun. 6:8753 doi: 10.1038/ncomms9753 (2015).
Supplementary Material
Supplementary Figure 1
Acknowledgments
We are grateful to F. Miramontes and F. Maciel and the staff of the University of California Desert Research and Extension Center for skillful assistance, to K. Kitajima, P. Homyak and M. Bell for technical advice, and K. Ricio, A. Contreras and many other dedicated undergraduates for field and laboratory assistance. We thank Robert Johnson for map preparation. We thank Coby Kriegshauser at Scott Seed Co. for providing seeds for these experiments. We thank anonymous reviewers for their helpful comments and suggestions. Participation of C.G. and J.W. was supported by NASA Applied Science Program and Aura Science program, and by Holland Computing Center and Office for Research and Economic Development in University of Nebraska-Lincoln. This work was also supported by the USDA-NIFA Award No. 2011-67009-30045, and by U.C. Riverside.
Footnotes
Author contributions This experiment was designed and implemented by all authors. P.Y.O., G.D.J., D.A.G., L.A.A., L.L.L. and J.R.E. participated in the collection of data at the University of California Desert Research and Extension Center. J.W. and C.G. conducted all WRF-Chem simulations and retrieval of OMI data. All authors contributed to data analysis and editing and revisions of text.
References
- Field C. B. et al. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. (Cambridge, UK and New York, USA (2014).
- Hall S. J., Matson P. A. & Roth P. M. NOx emissions from soil: implications for air quality modeling in agricultural regions. Annu. Rev. Energ. Environ. 21, 311–346 (1996). [Google Scholar]
- Peel J. L., Haeuber R., Garcia V., Russell A. G. & Neas L. Impact of nitrogen and climate change interactions on ambient air pollution and human health. Biogeochemistry 114, 121–134 (2013). [Google Scholar]
- Hall S. J., Huber D. & Grimm N. B. Soil N2O and NO emissions from an arid, urban ecosystem. J. Geophys. Res. 113, G01016 (2008). [Google Scholar]
- Bouwman A. F., Boumans L. J. M. & Batjes N. H. Emissions of N2O and NO from fertilized fields: summary of available measurement data. Glob. Biogeochem. Cycle 16, 6.1–6.13 (2002). [Google Scholar]
- Schindlbacher A., Zechmeister-Boltenstern S. & Butterbach-Bahl K. Effects of soil moisture and temperature on NO, NO2, and N2O emissions from European forest soils. J. Geophys. Res. 109, D17302 (2004). [Google Scholar]
- Davidson E. A. et al. Soil emissions of nitric oxide in a seasonally dry tropical forest of Mexico. J. Geophys. Res. Atmos. 96, 15439–15445 (1991). [Google Scholar]
- Steinkamp J. & Lawrence M. G. Improvement and evaluation of simulated global biogenic soil NO emissions in an AC-GCM. Atmos. Chem. Phys. 11, 6063–6082 (2011). [Google Scholar]
- Hudman R. C. et al. Steps towards a mechanistic model of global soil nitric oxide emissions: implementation and space based-constraints. Atmos. Chem. Phys. 12, 7779–7795 (2012). [Google Scholar]
- Vinken G., Boersma K., Maasakkers J., Adon M. & Martin R. Worldwide biogenic soil NOx emissions inferred from OMI NO2 observations. Atmos. Chem. Phys. 14, 10363–10381 (2014). [Google Scholar]
- Garfin G. et al. in Climate Change Impacts in the United States: The Third National Climate Assessment (eds Melillo, J., Richmond, T., & Yohe, G.) 462–486 (US Global Change Research Program, 2014).
- Hoerling M. P. et al. Assessment of Climate Change in the Southwest United States 74–100Springer (2013). [Google Scholar]
- Diffenbaugh N. S., Giorgi F. & Pal J. S. Climate change hotspots in the United States. Geophys. Res. Lett. 35, (2008). [Google Scholar]
- EPA. Current Nonattainment Counties for all Criteria Pollutants. Green Book. Available at http://www.epa.gov/oaqps001/greenbk/ancl.html , last accessed July 2015 (2014).
- Stockman J. K., Shaikh N., Von Behren J., Bembom O. & Kreutzer R. California County Asthma Hospitalization Chart Book: Data from 1998-2000 Department of Health Services, Environmental Health Investigations Branch (2003). [Google Scholar]
- Jacob D. Introduction to Atmospheric Chemistry Princeton Univ. Press (1999). [Google Scholar]
- Hudman R. C., Russell A. R., Valin L. C. & Cohen R. C. Interannual variability in soil nitric oxide emissions over the United States as viewed from space. Atmos. Chem. Phys. 10, 9943–9952 (2010). [Google Scholar]
- Saad O. & Conrad R. Temperature-dependence of nitrification, denitrification, and turnover of nitric-oxide in different soils. Biol. Fertil. Soils 15, 21–27 (1993). [Google Scholar]
- Gödde M. & Conrad R. Immediate and adaptational temperature effects on nitric oxide production and nitrous oxide release from nitrification and denitrification in two soils. Biol. Fertil. Soils 30, 33–40 (1999). [Google Scholar]
- Maag M. & Vinther F. P. Nitrous oxide emission by nitrification and denitrification in different soil types and at different soil moisture contents and temperatures. Appl. Soil Ecol. 4, 5–14 (1996). [Google Scholar]
- Ghude S. D. et al. NOx emission from India during the onset of the summer monsoon: a satellite perspective. J. Geophys. Res. 115, D16304 (2010). [Google Scholar]
- Harris G. W., Wienhold F. G. & Zenker T. Airborne observations of strong biogenic NOx emissions from the Namibian savanna at the end of the dry season. J. Geophys. Res. 101, 23707–23711 (1996). [Google Scholar]
- Bertram T. H., Heckel A., Richter A., Burrows J. P. & Cohen R. C. Satellite measurements of daily variations in soil NOx emissions. Geophys. Res. Lett. 32, L24812 (2005). [Google Scholar]
- Yienger J. J. & Levy H. Empirical model of global soil-biogenic NOx emissions. J. Geophys. Res. Atmos. 100, 11447–11464 (1995). [Google Scholar]
- Tian H. et al. Spatial and temporal patterns of CH4 and N2O fluxes in terrestrial ecosystems of North America during 1979–2008: application of a global biogeochemistry model. Biogeosciences 7, 2673–2694 (2010). [Google Scholar]
- Li C. & Aber J. A process-oriented model of N20 and NO. J. Geophys. Res. 105, 4369–4384 (2000). [Google Scholar]
- Jaeglé L., Steinberger L., Martin R. V. & Chance K. Global partitioning of NOx sources using satellite observations: relative roles of fossil fuel combustion, biomass burning and soil emissions. Faraday Discuss. 130, 407–423 (2005). [DOI] [PubMed] [Google Scholar]
- Potter C. S., Matson P. A., Vitousek P. M. & Davidson E. A. Process modeling of controls on nitrogen trace gas emissions from soils worldwide. J. Geophys. Res. Atmos. 101, 1361–1377 (1996). [Google Scholar]
- Grell G. A. et al. Fully coupled ‘online' chemistry within the WRF model. Atmos. Environ. 39, 6957–6975 (2005). [Google Scholar]
- Brioude J. et al. Top-down estimate of surface flux in the Los Angeles Basin using a mesoscale inverse modeling technique: assessing anthropogenic emissions of CO, NOx and CO2 and their impacts. Atmos. Chem. Phys. 13, 3661–3677 (2013). [Google Scholar]
- Matson P. A., Naylor R. & Ortiz-Monasterio I. Integration of environmental, agronomic, and economic aspects of fertilizer management. Science 280, 112–115 (1998). [DOI] [PubMed] [Google Scholar]
- Thornton F. C., Bock B. R. & Tyler D. D. Soil emissions of nitric oxide and nitrous oxide from injected anhydrous ammonium and urea. J. Environ. Qual. 25, 1378–1384 (1996). [Google Scholar]
- Wang Y., Jacob D. J. & Logan J. A. Global simulation of tropospheric O3-NOx-hydrocarbon chemistry: 1. Model formulation. J. Geophys. Res. Atmos. 103, 10713–10725 (1998). [Google Scholar]
- Oikawa P. Y. et al. Unifying soil respiration pulses, inhibition, and temperature hysteresis through dynamics of labile soil carbon and O2. J. Geophys. Res. 119, 521–536 (2014). [Google Scholar]
- Sindelarova K. et al. Global data set of biogenic VOC emissions calculated by the MEGAN model over the last 30 years. Atmos. Chem. Phys. 14, 9317–9341 (2014). [Google Scholar]
- Oikawa P. Y., Jenerette G. D. & Grantz D. A. Offsetting high water demands with high productivity: Sorghum as a biofuel crop in a high irradiance arid ecosystem. GCB Bioenergy 7, 974–983 (2015). [Google Scholar]
- Resources CDoW. Irrigated Crop Acres and Water Use. Available at http://www.water.ca.gov/landwateruse/anaglwu.cfm , last accessed July 2015 (2010).
- Wright S. D., Collar C. A., Klonsky K. & De Moura R. L. Sample Costs to Produce Sorghum Silage. http://coststudyfiles.ucdavis.edu/uploads/cs_public/f8/b1/f8b125ac-f70c-42ff-97d2-4caa93121510/sudansilagevs09.pdf (Extension UoCC, 2009).
- Mayberry K. S. Sample Cost to Establish and Produce Sudangrass http://coststudyfiles.ucdavis.edu/uploads/cs_public/a2/ba/a2ba6644-27fc-4e2a-b70e-611d9c23d636/sudangrass04.pdf , last accessed October 2015 (Extension UoCC, 2000).
- Jackson L., Fernandez B., Meister H. & Spiller M. Small grain production manual 8164, University of California Division of Agriculture and Natural Resources (2006). [Google Scholar]
- California Department of Water Resources.. http://www.water.ca.gov/landwateruse/surveys.cfm Statewide Irrigation Methods Survey (2010).
- Parkin T. B. & Venterea R. T. in Sampling Protocols (ed. Follett, R. F.) 3-1 to 3-39. Available at www.ars.usda.gov/research/GRACEnet (USDA-ARS, 2010). .
- Fast J. D. et al. Evolution of ozone, particulates, and aerosol direct radiative forcing in the vicinity of Houston using a fully coupled meteorology-chemistry-aerosol model. J. Geophys. Res. Atmos. 111, D21305 (2006). [Google Scholar]
- Guenther A. et al. Estimates of global terrestrial isoprene emissions using MEGAN (Model of Emissions of Gases and Aerosols from Nature). Atmos. Chem. Phys. 6, 3181–3210 (2006). [Google Scholar]
- Guenther A. et al. The model of emissions of gases and aerosols from nature version 2.1 (MEGAN2. 1): an extended and updated framework for modeling biogenic emissions Geosci. Model Dev. 5, 1471–1492 (2012). [Google Scholar]
- Grell G. A. et al. Application of a multiscale, coupled MM5/chemistry model to the complex terrain of the VOTALP valley campaign. Atmos. Environ. 34, 1435–1453 (2000). [Google Scholar]
- Chaparro-Suarez I., Meixner F. & Kesselmeier J. Nitrogen dioxide (NO2) uptake by vegetation controlled by atmospheric concentrations and plant stomatal aperture. Atmos. Environ. 45, 5742–5750 (2011). [Google Scholar]
- Raivonen M. et al. Compensation point of NOx exchange: Net result of NOx consumption and production. Agric. For. Meteorol. 149, 1073–1081 (2009). [Google Scholar]
- Hereid D. P. & Monson R. K. Nitrogen oxide fluxes between corn (Zea mays L.) leaves and the atmosphere. Atmos. Environ. 35, 975–983 (2001). [Google Scholar]
- Teklemariam T. A. & Sparks J. P. Leaf fluxes of NO and NO2 in four herbaceous plant species: the role of ascorbic acid. Atmos. Environ. 40, 2235–2244 (2006). [Google Scholar]
- Eskes H. & Boersma K. Averaging kernels for DOAS total-column satellite retrievals. Atmos. Chem. Phys. 3, 1285–1291 (2003). [Google Scholar]
- Herron-Thorpe F., Lamb B., Mount G. & Vaughan J. Evaluation of a regional air quality forecast model for tropospheric NO2 columns using the OMI/Aura satellite tropospheric NO2 product. Atmos. Chem. Phys. 10, 8839–8854 (2010). [Google Scholar]
- Demerjian K. L. A review of national monitoring networks in North America. Atmos. Environ. 34, 1861–1884 (2000). [Google Scholar]
- Levelt P. F. et al. The ozone monitoring instrument. IEEE Trans. Geosci. Remote Sensing 44, 1093–1101 (2006). [Google Scholar]
- Irie H. et al. First quantitative bias estimates for tropospheric NO2 columns retrieved from SCIAMACHY, OMI, and GOME-2 using a common standard. Atmos. Meas. Tech. 5, 3953–3971 (2012). [Google Scholar]
- Boersma K. et al. Near-real time retrieval of tropospheric NO2 from OMI. Atmos. Chem. Phys. 7, 2103–2118 (2007). [Google Scholar]
- Boersma K. et al. An improved tropospheric NO2 column retrieval algorithm for the Ozone Monitoring Instrument. Atmos. Meas. Tech. 4, 1905–1928 (2011). [Google Scholar]
- Dirksen R. J. et al. Evaluation of stratospheric NO2 retrieved from the Ozone Monitoring Instrument: intercomparison, diurnal cycle, and trending. J. Geophys. Res. Atmos. 116, D08305 (2011). [Google Scholar]
- Palmer P. I. et al. Air mass factor formulation for spectroscopic measurements from satellites: application to formaldehyde retrievals from the Global Ozone Monitoring Experiment. J. Geophys. Res. Atmos. 106, 14539–14550 (2001). [Google Scholar]
- Boersma K., Eskes H. & Brinksma E. Error analysis for tropospheric NO2 retrieval from space. J. Geophys. Res. Atmos. 109, D04311 (2004). [Google Scholar]
- Boersma K. et al. Validation of OMI tropospheric NO2 observations during INTEX-B and application to constrain NOx emissions over the eastern United States and Mexico. Atmos. Environ. 42, 4480–4497 (2008). [Google Scholar]
- Bucsela E. et al. Comparison of tropospheric NO2 from in situ aircraft measurements with near-real-time and standard product data from OMI. J. Geophys. Res. Atmos. 113, D16S31 (2008). [Google Scholar]
- Russell A. et al. A high spatial resolution retrieval of NO2 column densities from OMI: method and evaluation. Atmos. Chem. Phys. 11, 8543–8554 (2011). [Google Scholar]
- Chen F. & Dudhia J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: model implementation and sensitivity. Mon. Weather Rev. 129, 569–585 (2001). [Google Scholar]
- Hong S.-Y., Noh Y. & Dudhia J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 134, 2318–2341 (2006). [Google Scholar]
- Grell G. A. & Dévényi D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 29, 38-31–38-34 (2002). [Google Scholar]
- Lin Y.-L., Farley R. D. & Orville H. D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 22, 1065–1092 (1983). [Google Scholar]
- Stockwell W. R., Middleton P., Chang J. S. & Tang X. The second generation regional acid deposition model chemical mechanism for regional air quality modeling. J. Geophys. Res. Atmos. 95, 16343–16367 (1990). [Google Scholar]
- Ackermann I. J. et al. Modal aerosol dynamics model for Europe: Development and first applications. Atmos. Environ. 32, 2981–2999 (1998). [Google Scholar]
- Schell B., Ackermann I. J., Hass H., Binkowski F. S. & Ebel A. Modeling the formation of secondary organic aerosol within a comprehensive air quality model system. J. Geophys. Res. Atmos. 106, 28275–228293 (2001). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figure 1