Reproducibility of Quantitative Susceptibility Mapping in the Brain at Two Field Strengths From Two Vendors

Abstract

Purpose

To assess the reproducibility of brain quantitative susceptibility mapping (QSM) in healthy subjects and in patients with multiple sclerosis (MS) on 1.5 and 3T scanners from two vendors.

Materials and Methods

Ten healthy volunteers and 10 patients were scanned twice on a 3T scanner from one vendor. The healthy volunteers were also scanned on a 1.5T scanner from the same vendor and on a 3T scanner from a second vendor. Similar imaging parameters were used for all scans. QSM images were reconstructed using a recently developed nonlinear morphology-enabled dipole inversion (MEDI) algorithm with L1 regularization. Region-of-interest (ROI) measurements were obtained for 20 major brain structures. Reproducibility was evaluated with voxel-wise and ROI-based Bland–Altman plots and linear correlation analysis.

Results

ROI-based QSM measurements showed excellent correlation between all repeated scans (correlation coefficient R ≥ 0.97), with a mean difference of less than 1.24 ppb (healthy subjects) and 4.15 ppb (patients), and 95% limits of agreements of within −25.5 to 25.0 ppb (healthy subjects) and −35.8 to 27.6 ppb (patients). Voxel-based QSM measurements had a good correlation (0.64 ≤ R ≤ 0.88) and limits of agreements of −60 to 60 ppb or less.

Conclusion

Brain QSM measurements have good interscanner and same-scanner reproducibility for healthy and MS subjects, respectively, on the systems evaluated in this study.

Quantitative susceptibility mapping (QSM) is an emerging magnetic resonance imaging (MRI) method for quantifying magnetic susceptibility of compounds in the human body including iron, blood products, and calcification.^1–4 There is an increasing number of clinical applications of QSM including the assessment of cerebral microbleeds and hematoma volume,^5–7 calcifications, hemorrhages, cavernous malformations,^3,8,9 the study of multiple sclerosis (MS), Alzheimer’s and Wilson’s disease,^9–11 and the visualization of subthalamic nuclei for deep brain stimulation.^12,13 QSM has also been used to perform quantitative measurements of perfusion and oxygenation, opening the door for applications such as tumor characterization and treatment evaluation, stroke assessment, and functional neuroimaging.^14,15

Although QSM measurements in the brain have been widely reported,¹⁶ there is limited data on QSM reproducibility when performed on the same scanner or on different scanners, particularly those made by different manufacturers. Such information is valuable for accurate clinical interpretation of longitudinal QSM changes and important in the design of multisite studies. A recent QSM reproducibility study was limited to healthy volunteers and 3T field strength, and conventional measures of reproducibility such as those obtained by linear regression analysis and Bland–Altman plots were not reported.¹⁷ Furthermore, a linear inversion algorithm with L2 regularization was used, which can be less effective than the recently developed nonlinear morphology-enabled dipole inversion (MEDI) algorithm with L1 regularization.^18,19 Although linear QSM may be appropriate for healthy volunteers, it may not be ideal for diseased subjects because brain lesions can be areas of low signal-to-noise ratio (SNR) that require nonlinear reconstruction to correctly account for phase noise and unwrapping errors, and iterative reweighting for robust fitting.¹⁸ The purpose of this study was to assess the reproducibility of nonlinear MEDI-based QSM measurements in both healthy volunteers and patients for scanners from two different manufacturers and at both 1.5T and 3T field strengths.

Materials and Methods

This human study was approved by the local Institutional Review Board and all subjects provided written consent prior to imaging. Three commercial scanner platforms were studied: GE Signa HDxt TwinSpeed 1.5T and 3T (GE Healthcare, Waukesha, WI; 40 mT/m maximum gradient amplitude, 120 T/m/s slew rate, HD16.0 software), and Siemens Magnetom Trio 3T (Siemens Healthcare, Erlangen, Germany; 50 mT/m maximum gradient amplitude, slew rate 150 T/m/s, Syngo VB17 software). These scanners will be referred to in this work as 1.5T Vendor 1, 3T Vendor 1, and 3T Vendor 2, respectively.

To determine the reproducibility of brain QSM, 10 healthy volunteers (eight men, two women, mean 32 ± 6 years of age) were scanned twice on 3T Vendor 1. These scans will be referred to as Scan 1 and Scan 2. For SNR measurements, an intervening scan, referred to as Scan 1A, was performed after Scan 1 without delay. Scan 1 and Scan 2 were separated by an interval of 10 minutes during which subjects exited and reentered the scanner to be repositioned for the second examination. To determine interscanner reproducibility as well as to measure SNR, Scan 1 and Scan 1A were repeated on 1.5T Vendor 1 and 3T Vendor 2 on the same subjects.

To assess the reproducibility of brain QSM in a patient population, two scans were performed on 10 MS patients (nine women, one man, age range of 35–63 years and disease duration of 0–3 years), with interscan interval between 1 and 14 months (average, 6 months) using 3T Vendor 1. A 3D multiecho spoiled gradient echo (SPGR) product sequence was used for QSM data acquisition. The data acquisition parameters for all acquisitions on both the healthy subjects and patients were similar across different scanners: field of view (FOV) = 24 cm, partial FOV factor = 0.8, acquisition matrix size = 384 × 384 × 64 (healthy subjects) and 416 × 384 × 64 (patients), number of averages = 0.75, flip angle = 20°, slice thickness = 2 mm, TR = 52–57 msec, number of echoes = 11, first TE = 4.1 msec, echo spacing = 4.4 msec. Parallel imaging was used to accelerate the QSM data acquisition on both GE (ASSET factor = 2) and Siemens (iPAT factor = 2) scanners, resulting in a scan time of ~8 minutes. For imaging healthy volunteers, an 8-channel high-resolution brain coil (Invivo, Gainesville, FL) and a 12-channel head matrix coil (Siemens Healthcare), both product coils provided by the vendors, were used on the GE and Siemens scanners, respectively. For imaging MS patients on the GE scanner, either the 8-channel high-resolution brain coil, a multichannel head and neck coil (HDNV), or an 8-channel head, neck and spine (HNS) coil was used. Subject heads were positioned in the neutral position.

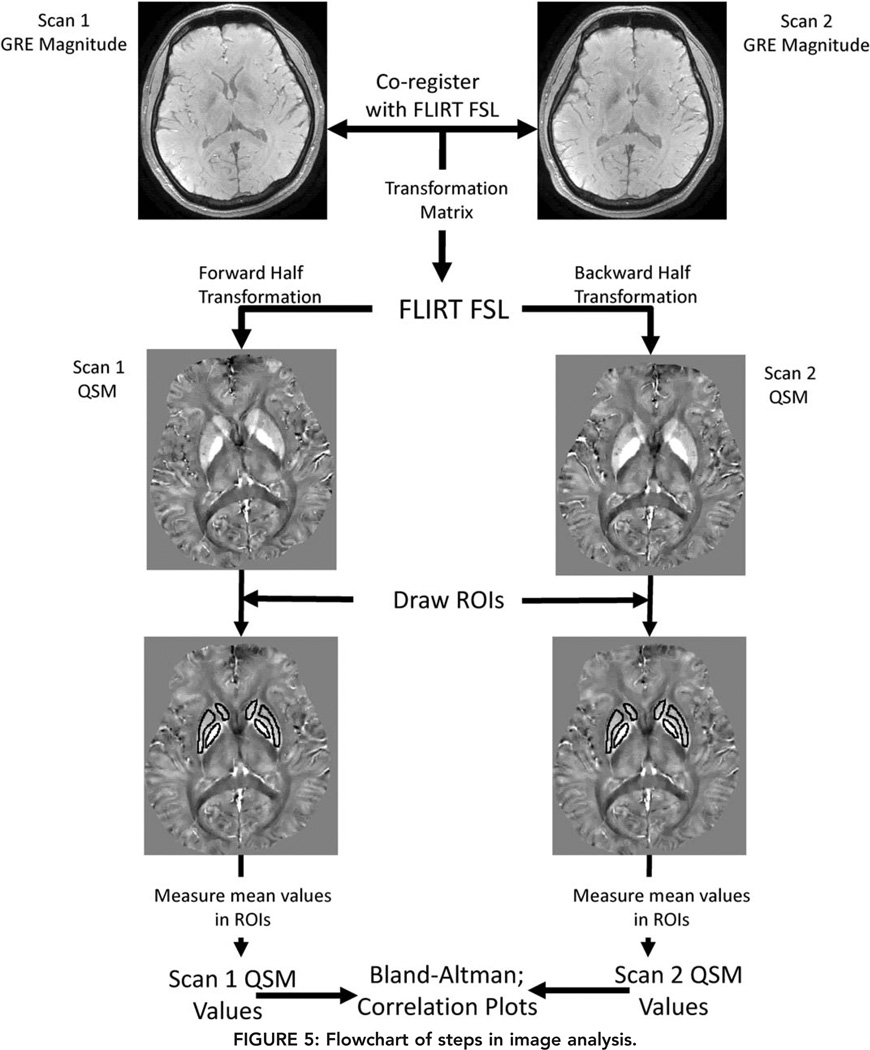
QSM images were reconstructed from real and imaginary DICOM files using a C++ program implementation of the nonlinear morphology-enabled dipole inversion (nonlinear MEDI) algorithm.¹⁸ This program performed a nonlinear estimation of the phase map, followed by phase unwrapping and dipole inversion to calculate the susceptibility maps. Background field removal was implemented using a differential approach and integrated into the dipole inversion step.^4,20,21 All processing steps were fully automated with the MEDI regularization parameter fixed to 1000 for all QSM reconstructions. QSM images were aligned by coregistering the corresponding SPGR magnitude images using the FLIRT algorithm, which is part of the FSL software package,²² and applying the resulting transformations to the QSM images.

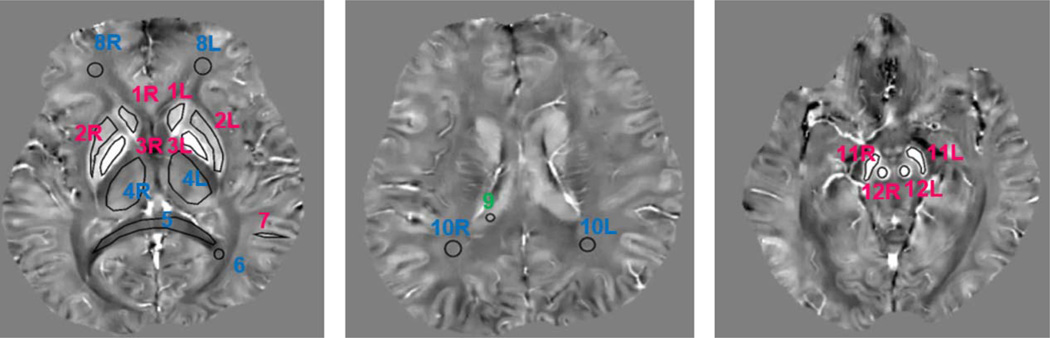
Qualitative and quantitative assessments of QSM reproducibility were performed in separate reading sessions by two neuroradiologists, Y.Z. (4 years of experience) and I.K. (more than 20 years of experience), both blinded to the patients’ and volunteers’ clinical information. The qualitative assessment was performed by visual inspection of corresponding image pairs where the readers were asked to give an overall assessment of agreement (good, moderate, none), while quantitative assessment was performed by constructing Bland–Altman plots and linear regression analysis on all voxels in the brain volume and on measurements obtained from 20 regions of interest (ROIs) covering major structures in gray matter (red nucleus, substantia nigra, caudate nucleus, putamen, globus pallidus, thalamus, cortical gray matter in occipital lobe) and white matter (splenium of corpus callosum, frontal white matter, occipital white matter), as well as cerebrospinal fluid (CSF) within the lateral ventricle (Fig. 1). The ROIs, ranging in size from about 20 to 980 mm³, were described and measured using two image processing programs, ImageJ and ITK-SNAP.^23,24 For each pairwise comparison, the images from the first acquisition were selected and ROIs were manually drawn on the slices where these structures were the most prominent. Next, these ROIs were copied to the corresponding image of the second acquisition. The mean tissue susceptibility within each ROI was recorded and referenced to CSF for analysis.

FIGURE 1.

Example of ROIs in the white matter (red), gray matter (blue), and CSF (green) that were used in reproducibility analysis (1 = caudate nucleus, 2 = putamen, 3 = globus pallidus, 4 = thalamus, 5 = splenium of corpus callosum, 6 = occipital white matter, 7 = cortical gray matter in occipital lobe, 8 = frontal white matter, 9 = CSF, 10 = occipital white matter, 11 = substantia nigra, 12 = red nucleus).

For same-scanner reproducibility assessment, Scan 1 and 2 from 3T Vendor 1 were compared. For interscanner reproducibility assessment, Scan 1 obtained on each of the three scanners for the healthy volunteers was used. For linear regression analysis, the regression line, X₂ = k_X1 + b, where X₁ and X₂ are the repeated susceptibility measurements, k the slope and b the offset, and the Pearson correlation coefficient, R, were computed.²⁵ To assess agreement, Bland–Altman plots were used to calculate the mean difference (bias) I and 95% limits of agreement D (1.96 times the standard deviation of the difference) between the repeated measurements.²⁶ For SNR comparison, the NEMA standard method^27,28 was applied to a region of interest placed within the globus pallidus in the susceptibility maps obtained from Scan 1 and Scan 1A. SNR was calculated as √2 times the mean susceptibility within the ROI of Scan 1 divided by the standard deviation of the susceptibility difference between the two scans measured within the same ROI.

Finally, interobserver variability was measured by performing Bland–Altman and correlation analysis to compare the QSM values from the ROIs placed by I.K. to those placed by Y.Z., in 10 patients.

Results

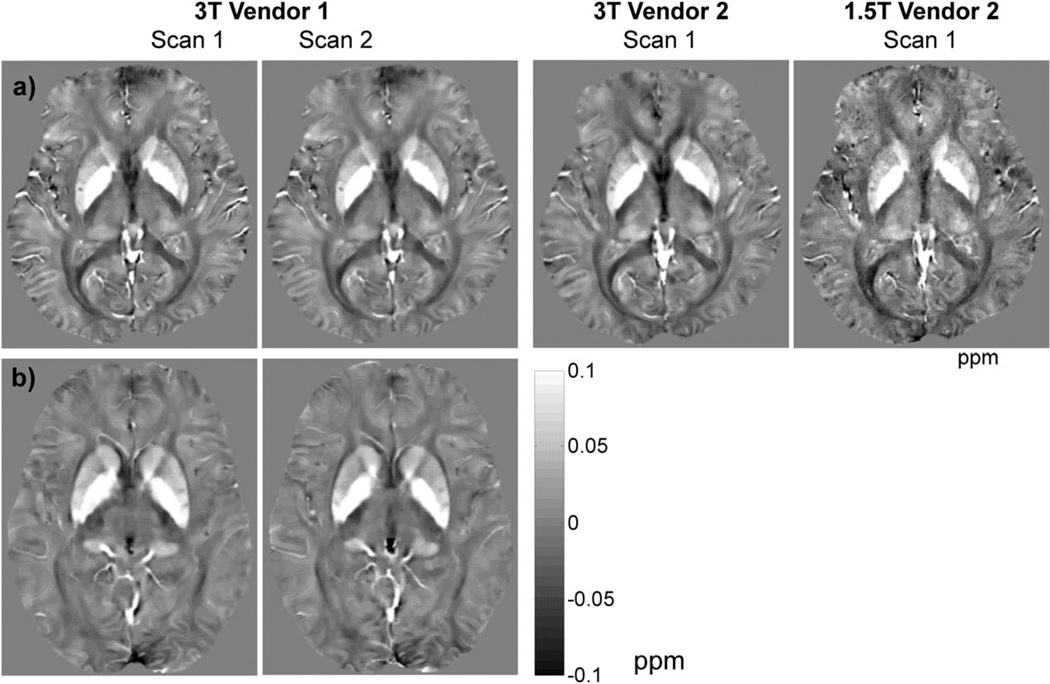
All scans were completed successfully. Figure 1a shows representative brain QSM images obtained on three different scanners from a single healthy subject and Fig. 1b shows an example of QSM images of an MS patient scanned on 3T Vendor 1. While the readers rated the visual agreement between all repeated scans as good, they noted that the QSM images obtained at 3T provided an improved depiction of brain structures compared to those obtained at 1.5T. This observation was reflected by a 51% increase in mean apparent SNR measured in the globus pallidus at 3T compared to 1.5T (23.4 vs. 15.5, P = 0.01, N = 10).

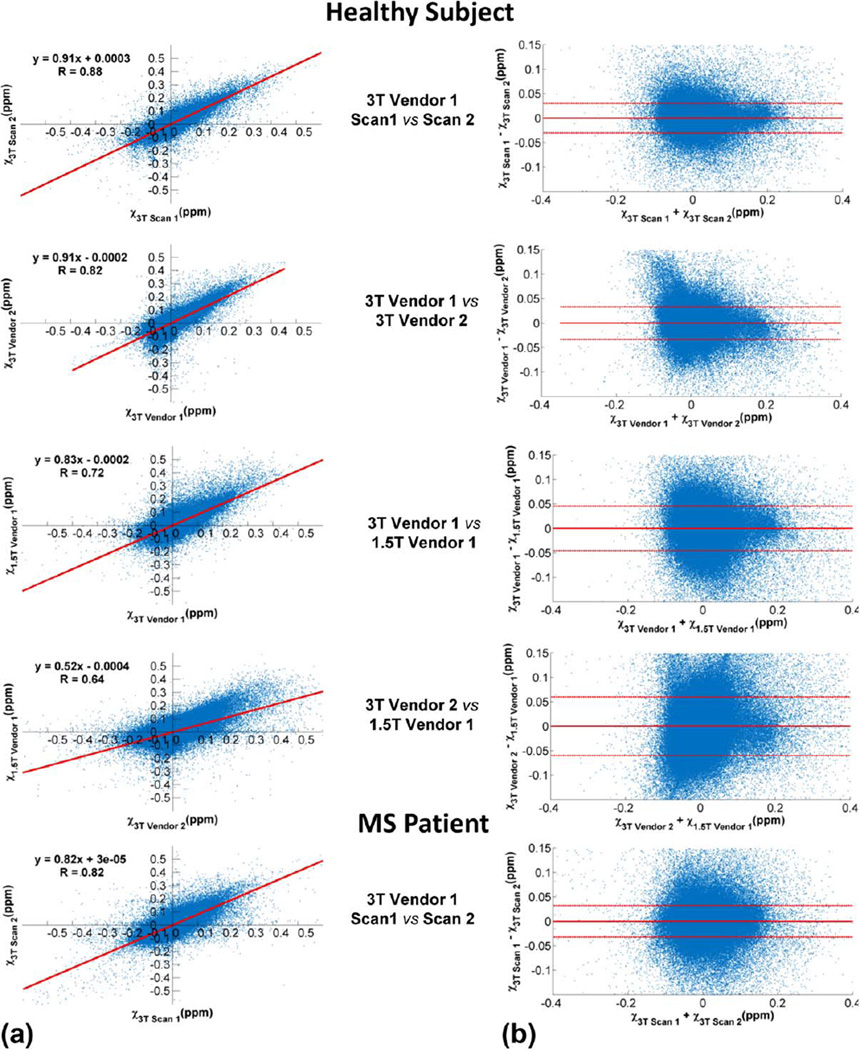
Figure 3 shows the scatter and Bland–Altman plots comparing repeated whole brain voxel-wise QSM measurements obtained for the healthy subject and MS patient in Fig. 1. The regression slope (k) and correlation coefficient (R) were the highest for same-scanner comparison (k = 0.91 and R = 0.88) and decreased with increasing dissimilarity between the platforms being compared (k = 0.91, 0.83, 0.77 and R = 0.88, 0.82, 0.78 for 3T Vendor 1 vs. 3T Vendor 2, 3T Vendor 1 vs. 1.5 T Vendor 1 and 3T Vendor 2 vs. 1.5 T Vendor 1 respectively). Conversely, the 95% limits of agreement (I) became larger with increasing difference in the platforms being compared, from the smallest lower/upper limits of −31.1/30.7 ppb for same-scanner comparison to the largest of −50.2 /50.6 ppb for the comparison of 3T Vendor 2 to 1.5 T Vendor 1. Same-scanner comparison for MS patient gave slightly lower values of k = 0.85 and R = 0.83 than that obtained for the healthy subject, and slightly wider limits of agreement of −32.3/34.6 ppb in the Bland–Altman plot.

FIGURE 3.

Examples of scatter (a) and Bland–Altman (b) plots comparing whole brain voxel-wise QSM measurements obtained from the healthy subject and MS patient shown in Fig. 1.

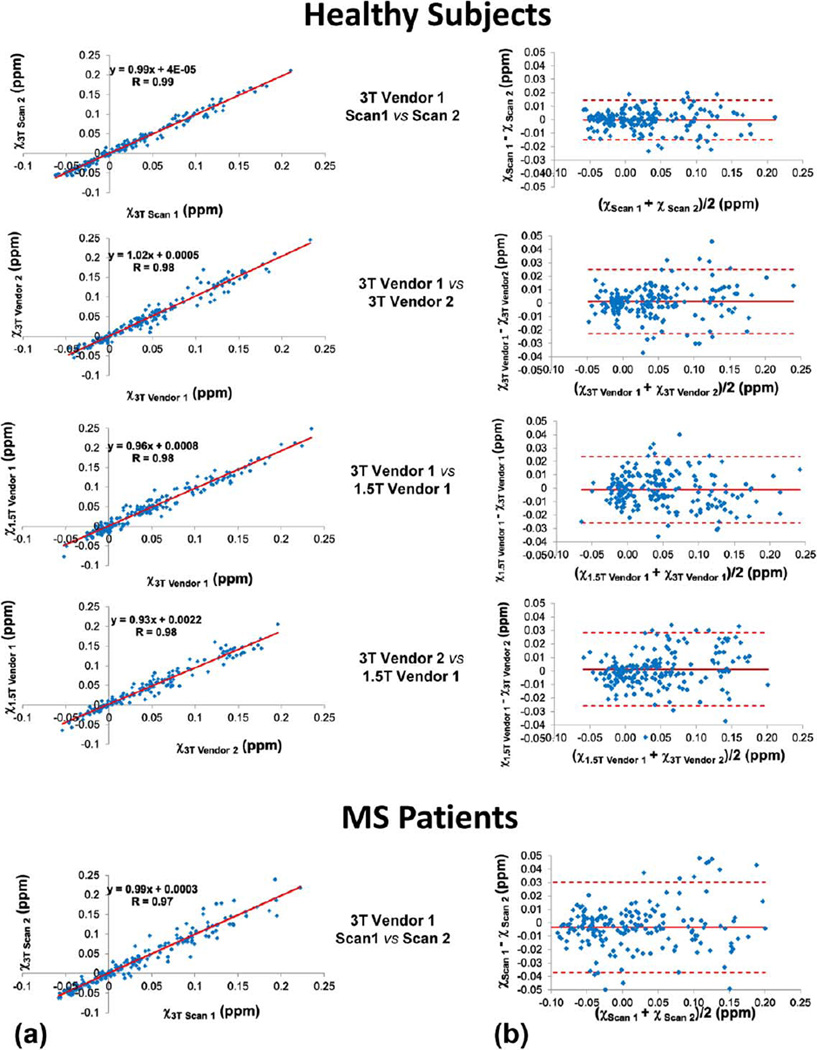
Data analysis using ROI measurements from all healthy subjects showed excellent reproducibility (3T Vendor 1, Scan 1 vs. Scan 2 in Fig. 2) with correlation coefficient R = 0.99 and regression slope k deviating from unity by less than 1%. The Bland–Altman plots showed a negligible bias of ~0.02 ppb and a narrow limits of agreement −10.5 to 13.4 ppb for 3T Vendor 1. A slightly lower correlation coefficient (R = 0.97) was obtained for the same analysis using MS patient data. Among different scanners, the brain QSM was also found to be highly reproducible for healthy subjects with a linear correlation coefficient larger than 0.975, although the agreement between the two 3T scanner was slightly better than between the 1.5T and each of the 3T scanners, as indicated by the slope of the regression lines (Fig. 3). This trend was confirmed by the Bland–Altman plots, which also show a negligible bias within 1 ppb and small limits of agreement (−19.2 to 21.6 ppb for 3T Vendor 1 vs. 3T Vendor 2, −26.3 to 24.1 ppb for 1.5T Vendor 1 vs. T Vendor 1, −23.9 ppb to 25.9 ppb for 1.5T Vendor 2 vs. 3T Vendor 2). Results of both voxelwise and ROI comparisons are summarized in Table 1.

FIGURE 2.

Axial QSM maps obtained by repeated scans on a healthy subject using three different scanners (a), and an MS patient using 3T Vendor 1 (b), demonstrating good to excellent visual similarity in depicting major gray matter and white matter brain structures, and MS lesions.

TABLE 1.

Summary Statistics (Mean ± Standard Deviation) of Brain QSM Reproducibility Metrics Obtained by Linear Regression Analysis (Slope (k) and Correlation Coefficient (R)) and Bland-Altman Plots (Mean Difference (D) and 95% Limits of Agreement (I)) for Voxel- and ROI-Based Comparisons on Scanners From Vendor 1 (V1) and Vendor 2 (V2)

		Healthy subjects (N = 10)				MS patients (N = 10) 3T V1/V1
		3T V1/V1	3T V1/V2	3T V1/1.5T V1	3T V2/1.5T V1
Voxel	k	0.86 ± 0.03	0.75 ± 0.07	0.80 ± 0.04	0.52 ± 0.03	0.76 ± 0.05
	R	0.86 ± 0.03	0.73 ± 0.04	0.72 ± 0.04	0.64 ± 0.01	0.77 ± 0.05
	D (ppb)	−0.20 ± 0.44	0.22 ± 0.42	0.07 ± 0.50	0.21 ± 0.98	−0.03 ± 0.44
	I (ppb)	−31.1 ± 3.8 to 30.7 ± 3.8	−42.0 ± 4.4 to 42.5 ± 4.8	−47.4 ± 3.6 to 47.6 ± 3.8	−50.2 ± 1.1 to 50.6 ± 1.4	−39.5 ± 3.8 to 39.5 ± 4.3
ROI	k	0.99 ± 0.05	1.01 ± 0.01	0.96 ± 0.03	1.04 ± 0.07	1.00 ± 0.11
	R	0.99 ± 0.00	0.98 ± 0.01	0.98 ± 0.01	0.98 ± 0.02	0.98 ± 0.01
	D (ppb)	0.23 ± 3.22	−1.22 ± 2.31	1.09 ± 3.11	−1.24 ± 1.96	−4.2 ± 15.7
	I (ppb)	−12.8 ± 2.6 to 13.3 ± 6.4	−23.8 ± 7.7 to 21.4 ± 8.21	−23.2 ± 5.3 to 25.4 ± 2.97	−25.5 ± 8.7 to 25.0 ± 7.4	−35.8 ± 30.6 to 27.6 ± 9.13

For the interobserver reproducibility assessment, the correlation coefficient was 0.98, while the Bland–Altman plot had a mean difference of 1.2 ppb and limits of agreement of −24.3 to 26.7 ppb.

Discussion

A systematic comparison of nonlinear MEDI-based QSM measurements in the brain was performed at the two clinically most relevant field strengths of 1.5T and 3T in healthy volunteers and MS patients. Our data show that QSM has good to excellent reproducibility across three different platforms using commercially available pulse sequences and scanner hardware. Compared to the only QSM reproducibility study published so far,¹⁶ which reported the standard error of repeated QSM measurements as a reproducibility metric in five regions of the basal ganglia, slightly better same-scanner and cross-scanner reproducibility were obtained (data not shown). The improved QSM performance may be attributed to the use of the L1-based nonlinear MEDI reconstruction algorithm, as demonstrated previously.^18,19

The high degree of QSM reproducibility can be understood by the high performance of modern MRI scanners. The susceptibility sources in the measured QSM values in our healthy subjects are largely from ferritin in tissue, deoxyhemoglobin in veins, and myelin in white matter tracts, all of which are not expected to change during the short duration of the study on healthy volunteers. QSM measures these tissue magnetic sources by deconvolving the magnetic field that is estimated from MRI signal phase. MRI phase measurement has long become very reliable on modern superconducting magnets with very high field stability (B₀ shifts < 0.01 ppm).²⁹ The agreements of QSM measurements obtained among different scanners were similar to but tended to be slightly lower than that obtained on the same scanner. The larger QSM variation may be attributed to differences in vendor-specific implementation of pulse sequences and image reconstruction algorithms, as well as to increased difficulty in coregistering images obtained in different imaging sessions (eg, due to different head positioning and orientation) compared to those obtained within the same session.

In this study, QSM imaging parameters were matched as closely as possible across different scanners. This was done to mitigate the effect of discretization error on the comparison between the different QSM reconstructions, which depends on voxel size.² We chose the same imaging parameters for both 1.5T and 3T scanners, including the same imaging matrix, TE/TR, and scan time. We acknowledge this as a limitation of the study since the same scan parameters on 1.5 and 3T did not result in the same phase shift. An alternative choice may be to double the TEs/TR and scan time at 1.5T for the same amounts of phase as 3T, but prolonged scan time may introduce additional motion artifacts. Because white matter tracts have susceptibility anisotropies that make susceptibility depend on orientation,^30–32 subject heads were positioned in the same neutral position to minimize this effect. QSM values may also depend on field-to-susceptibility dipole inversion algorithms and background field removal methods.² Accordingly, this study used the same nonlinear MEDI processing algorithm¹⁸ with a fixed regularization parameter across field strengths and vendors.

In the evaluation of agreements among different scans, we used both voxel-based and region-based regressions. The voxel-based comparison is prone to errors, including those caused by imperfection in image registration and orientation-dependence of white matter susceptibility. Another source of error is the orientation dependence in the background field removal that is determined by the geometry of the brain.³³ These errors are minimized by averaging in regions, selecting only regions of white matter fairly independent of head positioning in the scanner, and avoiding regions near the brain boundary where the background field removal is more prone to the orientation-dependent error.³³ Inspection of the boundaries of the images in Fig. 2 reveals differences in the frontal lobes that lead to low measurement reproducibility in that region.

Repeated QSM measurements in MS patients were similar to but tended to be slightly more variable than measurements from healthy subjects. The repeat scan interval in patients was larger than that for healthy subjects. There may be greater differences in head positions and consequently larger amount of image registration errors. Changes in the disease status may also be a contributing factor, as the disease duration for the patients (0–3 years) correspond to a period during which measurements on MS brains have been show to give increasing susceptibility values.^11,34 QSM reproducibility in MS patients might be closer to that in healthy subjects if the scan interval were much shorter and if there was no major disease activity in the interval.

This preliminary study on QSM reproducibility has several limitations. Only three scanners from two MRI vendors at a single site were included. Due to the large number of MRI scans performed within a relatively short period of 1 week, only young healthy volunteers were enrolled for the comparison of different field strengths and vendors. Also, the patient study examined reproducibility only in MS patients and was performed only on scanners from 3T Vendor 1, and not on the other scanners or field strength. Recent developments in QSM technology have resulted in new data acquisition methods and a number of QSM reconstruction algorithms.^35–39 This work used the nonlinear MEDI reconstruction algorithm,^2,40 because it has been shown to produce improved QSM maps in simulations and in vivo.² Finally, the acquisition and reconstruction parameters that were used in this study are those that have been reported as optimal for detecting susceptibility with GRE sequences in the gray matter of the brain.² In this study, 11 echoes were used in the GRE data acquisition. Reducing this number may reduce the computational cost of the nonlinear MEDI reconstruction not significantly, since most of the computations occur in the susceptibility mapping after the calculation of the field map. Since a long echo time is desired to achieve the high phase SNR needed for the adequate reconstruction of small susceptibility differences, no significant shortening of the scan time would be possible without affecting QSM quality. The design of a TE acquisition scheme with equivalent QSM quality but minimal number of echoes remains an open problem. Therefore, the reproducibility of QSM with a reduced number of echoes was not attempted in this work but requires further study.

In conclusion, brain QSM measurements have good to excellent reproducibility over the same scanner and over different scanners at 1.5T and 3T for the two manufacturers evaluated.

FIGURE 4.

Scatter (a) and Bland–Altman (b) plots of ROI-based QSM measurements obtained from repeated scans in all subjects, demonstrating excellent correlation, a negligible bias, and 95% limits of agreement of approximately ±30 ppb or less.

FIGURE 5.

Flowchart of steps in image analysis.