Valuing QALYs in Relation to Equity Considerations Using a Discrete Choice Experiment

Abstract

Background

To judge whether an intervention offers value for money, the incremental costs per gained quality-adjusted life-year (QALY) need to be compared with some relevant threshold, which ideally reflects the monetary value of health gains. Literature suggests that this value may depend on the equity context in which health gains are produced, but the value of a QALY in relation to equity considerations has remained largely unexplored.

Objective

The objective of this study was to estimate the social marginal willingness to pay (MWTP) for QALY gains in different equity subgroups, using a discrete choice experiment (DCE). Both severity of illness (operationalized as proportional shortfall) and fair innings (operationalized as age) were considered as grounds for differentiating the value of health gains.

Methods

We obtained a sample of 1205 respondents, representative of the adult population of the Netherlands. The data was analysed using panel mixed multinomial logit (MMNL) and latent class models.

Results

The panel MMNL models showed counterintuitive results, with more severe health states reducing the probability of receiving treatment. The latent class models revealed distinct preference patterns in the data. MWTP per QALY was sensitive to severity of disease among a substantial proportion of the public, but not to the age of care recipients.

Conclusion

These findings emphasize the importance of accounting for preference heterogeneity among the public on value-laden issues such as prioritizing health care, both in research and decision making. This study emphasises the need to further explore the monetary value of a QALY in relation to equity considerations.

Electronic supplementary material

The online version of this article (doi:10.1007/s40273-015-0311-x) contains supplementary material, which is available to authorized users.

Key Points for Decision Makers

In a study estimating the social marginal willingness to pay (MWTP) for QALY gains among the general public, we observed distinct preference patters with respect to the allocation of healthcare resources.

Among a considerable proportion of the public, MWTP per QALY was sensitive to the severity of illness. It was not at all sensitive to the age of care recipients.

These findings emphasize the importance of accounting for heterogeneity in preferences among the public on value-laden issues such as prioritizing health care, both in research and decision making.

Findings about equity considerations are, however, not consistent across studies. This underlines the need to further explore the monetary value of a QALY in relation to equity considerations.

Introduction

Cost-utility analysis is increasingly used to inform allocation decisions about scarce healthcare resources. To evaluate whether an intervention yields good value for money, the incremental costs per gained QALY (quality-adjusted life-year) must be judged against some monetary threshold value. The nature of this threshold is a matter of debate. One stream of literature considers it as the opportunity costs of spending within a fixed healthcare budget, while the other considers it to represent the consumption value of health gains [1]. Here, we take the latter view and, more precisely, consider the appropriate threshold to reflect the social willingness to pay (WTP) for a QALY gain [2–4]. In other words, the threshold expresses the maximum acceptable cost to society for a QALY gained through an intervention. Without such a threshold the results of a cost-utility analysis are of limited value to healthcare decision makers. Somehow, they must judge whether a treatment with a cost-per-QALY ratio of, say, €50,000 offers value for money and should be reimbursed [5]. It need not surprise that this threshold has generated much debate. Societally, the idea of using a threshold expressing the value of health in monetary terms to decide about funding treatments has been contested [2]. Scientifically, the debate is especially about how to set a threshold, and whether there should be a fixed threshold or one that could vary with societal preferences for QALYs.

Regarding the latter issue, it is important to acknowledge that accumulating evidence suggests that the public prefers some QALY gains over others (e.g., those in young children over those in elderly) [6–9]. This suggests that the social value of a QALY does not exist [10] but that this value may vary with, for example, characteristics of the disease and the beneficiaries of treatment [11]. The use of a single threshold in judging the results from economic evaluations would therefore not align with societal preferences. The distributional preferences of society can be incorporated in the decision framework by applying a more flexible threshold or, under a fixed threshold, by applying equity weights to QALYs [5, 12, 13].

Although in most countries the threshold is still rather implicit, differentiation between QALY gains of different types or to different beneficiaries already exists in actual decision making. In the UK, the National Institute for Health and Care Excellence (NICE) recently formulated a decision rule explicitly giving higher value to costly life-prolonging end-of-life drugs. Under the assumption that all QALY gains should be valued equally, these interventions would probably have exceeded the threshold range. The new decisions rule explicitly considers the “magnitude of the additional weight that would need to be assigned to the QALY benefits… for the cost-effectiveness of the technology to fall within the current threshold range” [14]. This exception may prove to represent a first step in defining more general rules using a flexible threshold, depending on the context in which QALYs are gained [15]. The Netherlands has developed a decision-making framework in which the relationship between equity considerations and the value of a QALY has been made more explicit. The value of a QALY increases with the severity of illness in the target population, the latter being expressed using the concept of proportional shortfall [12, 16].

A fundamental question in the development of a decision framework using a flexible threshold is which equity principle(s) should be the basis for differentiation. In literature, the equity principles ‘severity of illness’ and ‘fair innings’ have been regularly proposed as suitable candidates. The principle of severity of illness considers severity at the time of intervention and expected severity—including death—in future years in case of non-intervention [17, 18]. The fair innings approach, advocated by Alan Williams [20], is based on the assumption that everyone is entitled to some ‘normal’ span of life or lifetime health achievement. As a result, a relatively high priority would be given to those who fall short of this norm and a relatively low priority to those who exceed this norm. Although obviously not without problems, age is often taken as a proxy for lifetime health achievement. Whether severity of illness or fair innings better reflects the distributional preferences of society is still a matter of debate, but both principles rely on justified normative arguments [12]. Proportional shortfall, the equity principle used in the Netherlands, is based on the proportion of remaining lifetime health lost due to some disease [16] and could therefore also be seen as a measure of severity of illness [12, 19]. Proportional shortfall measures the fraction of QALYs lost due to illness relative to remaining life expectancy in absence of the disease, on a scale from 0 (no loss) to 100 (complete loss of remaining health) [16].

Empirical studies show mixed findings with respect to the direction and strength of the preferences for age and severity. These variations might be caused by the framing of the concepts, or by context and methodological differences between studies [19, 21]. Moreover, often only particular aspects of potential value are investigated (e.g. only age or only severity) rather than, arguably more relevant, combinations. This hampers not only definite conclusions about support for specific decision rules, but also about the exact values (weights) attached to different QALY gains.

In that context, it also needs noting that the monetary value of a QALY and equity weights have both received quite some attention in the literature, but typically not jointly in one study [22]. Most WTP studies focus on the individual perspective, asking respondents to value changes in their own health, thus ignoring equity considerations. In the context of healthcare allocation decisions it seems to be more appropriate to consider the social value of a QALY, defined by the amount of their own consumption individuals are willing to forego in order to contribute to a health gain achieved in society [13]. Other studies have explored public preferences for a variety of equity principles and characteristics of the beneficiary or the disease, but these studies have not addressed the monetary valuation [23, 24]. To illustrate, a recent systematic review by Whitty et al. [21] shows an exponential growth in choice-based studies to elicit public preferences with respect to healthcare priority setting. However, most of these studies have not translated preferences into equity weights, let alone included the monetary valuation of QALYs for different equity considerations [6, 7, 21, 25].

The objective of the current study is to contribute to the existing literature by estimating the social WTP for QALY gains in different equity subgroups. More precisely, we aim to estimate the marginal WTP (MWTP) for a QALY at different levels of proportional shortfall, in different age groups. The study was framed in such a way that it could be directly helpful in further shaping the (Dutch) decision-making framework and build on previous studies in this area [12, 22, 26]. Public preferences were elicited using a discrete choice experiment (DCE), which is currently the most commonly applied method to elicit public preferences [21]. Respondents were asked to act as social decision makers. We included both the equity principles ‘severity of illness’ (operationalized as proportional shortfall) and ‘fair innings’ (operationalized as age) in one experiment. In order to arrive at MWTP per QALY estimates, we used the payment vehicle of increases in insurance premiums, which is the common financing mechanism in The Netherlands. In light of the diversity in the literature in terms of methods and results, we need to be modest in our aim. While we want to inform the (Dutch) debates regarding appropriate equity weights and thresholds, the current experiment was especially designed to learn how respondents solve the dilemmas they are confronted with, and to better understand support for differentiating QALY values between groups.

Methods

Discrete Choice Experiment

DCEs are based on the assumption that a good can be described by its characteristics and that the relative importance of these characteristics can be identified in isolation. This makes the DCE a valuable method to explore the preferences for healthcare allocation in relation to equity considerations [21, 27, 28]. DCEs are modelled according to random utility theory, which assumes that a respondent asked to choose between multiple options always chooses the alternative with the highest utility for her/him. The utility of an alternative for respondent n, U_n, can be decomposed in an observable component of utility, V_n, which reflects the utility effect of the characteristics of the alternative, and an unobserved component, ɛ_n, which reflects the utility not captured by these characteristics, such that

$$U_n=\mathit{\lambda }{V}_n+{\mathit{\epsilon }}_n$$ 1

where λ is the scale parameter which presents the variance of the unobserved component.

Identification and Presentation of Attributes and Levels

The main objective of this study was to estimate the MWTP for a QALY at different levels of proportional shortfall, in different age groups. Therefore, the following attributes were included: quality of life if untreated, age of death if untreated, gain in quality of life, gain in life expectancy and cost of treatment. The quality of life attribute was presented on a scale from 0 to 100, with 0 representing the worst imaginable health state and 100 representing perfect health. The cost attribute was operationalized as an increase in the mandatory health insurance premium for all Dutch adult citizens for a period of 1 year. To be able to explore fair innings (or ageism), we designed three versions of the questionnaire considering different age groups: 10 year olds, 40 year olds and 70 year olds. The levels of the attributes quality of life if untreated, gain in quality of life and costs of treatment were identical for all age groups. However, in order to present a comprehensible and plausible range of proportional shortfall in each of the three age groups to respondents, the levels of the attributes age at death if untreated and gain in life expectancy differed between age groups.

Next, to compensate for the smaller absolute health gains in the older age groups, we differentiated the number of people at risk between the age groups. The number of affected people in the Dutch population was 2000 people in the 10-year-old age group (age group 10), 4000 people in the 40-year-old age group (age group 40) and 12,000 in the 70-year-old age group (age group 70). An overview of the attributes and levels is presented in Table 1. (Note that it has been found that people may prefer larger gains in fewer people over smaller gains in more people, even when the two add up to the same total [9]).

Table 1.

Overview of attributes and levels

Attributes	Levels
Quality of life without treatment (scale 0–100)	45, 65, 85
Age at death if untreated (scale 0–80)  Age group 10  Age group 40  Age group 70	30, 50, 70 50, 62, 74 73, 76, 79
Gain in quality of life	5, 15, 25, 35
Gain in life expectancy  Age group 10  Age group 40  Age group 70	5, 10, 15, 20 2, 6, 10, 14 0.5, 1, 1.5, 2
Increase of health insurance premium (euro)	6, 12, 18, 24

Affected people: 2000 in age group 10, 4000 in age group 40 and 12,000 in age group 70

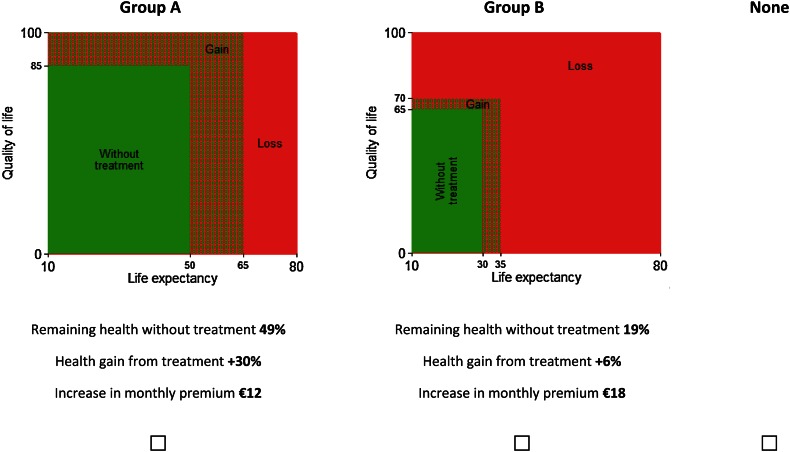
Following the approach adopted by Lancsar et al. [29], we used both words and diagrams to present the choice sets, as shown in Fig. 1. Each scenario was represented by a graph with ‘quality of life’ on the vertical axis (on a scale from 0 to 100) and age on the horizontal axis (on a scale from current age until 80 years old) as shown in Fig. 1. The green area shows the health prospect without treatment, the red area combined with the green-and-red shaded area shows the health loss without treatment (proportional shortfall). The green-and-red shaded area shows the potential health gain from treatment. Below the graphs, the percentages of remaining health without treatment, potential health gain from treatment and the increase in monthly premium were presented. Given the complexity of the graphs we first showed a step-by-step introduction of the graphs to respondents.

Fig. 1.

Question 1. Age group 10, version 1, choice set 1. Which of the groups below do you, as a decision maker, think should be treated?

The attributes, levels and presentation of choice sets were pilot-tested in a small sample of 75 respondents for each age group version. This resulted in adjustment of the level ranges of three attributes: age at death without treatment, gain in life expectancy and costs of treatment. In addition, to improve the clarity of the graphs we added the colours green for remaining health without treatment, red for health loss and shaded green-and-red for potential health gain instead of the blue colours of Lancsar et al. [29].

Questionnaire

Respondents were instructed to imagine themselves being in the position of a decision maker facing allocation decisions in healthcare. They were then asked to imagine that tomorrow an illness will strike two groups of people from the Dutch population that would have otherwise lived in perfect health until death at 80 years of age. The demographic characteristics of the groups were the same, but the illness and the treatment could affect the groups differently, and the costs of treatment could also differ between the groups. The illness would reduce the length and quality of life of the groups of people. There was a treatment available for each group, which would restore some, or all, of the health loss due to the illness. However, the treatment was not yet included in the basic benefit package. Therefore, it would have to be financed through an increase in the mandatory health insurance premium for all Dutch adult citizens for the period of 1 year. The respondents were asked which of the two groups of people they, as decision makers in the healthcare sector, would prefer to treat. An opt-out option was included in order to get valid WTP values [30].

The program Ngene 1.1 was used to generate efficient multinomial logit designs for the main study. An efficient design minimizes the predicted standard errors of the parameters in order to optimize the information obtained from each choice set. The efficiency of the designs was determined by the D-error, which is the most widely used measure of efficiency [31]. Since the levels of the attributes were adjusted after the pilot study we could not use the estimates of the pilot study as Bayesian priors for the main study, but only the signs of the estimates. Bayesian priors are more robust to misspecification because they optimize on prior distributions instead of on fixed parameters [31].

Since certain combinations of levels of attributes resulted in implausible scenarios, we imposed some constrains in the design (e.g., the gain in life expectancy added to the age at death if untreated could not exceed the maximum age of 80 years). Furthermore, interaction effects between quality of life if untreated and age at death if untreated were included to be able to consider the additional effect of proportional shortfall. For each age group we used 1000 Halton sequence draws [32].

For each age group, designs with 24 choice sets were generated. The choice sets were divided over three versions using a blocking variable. This resulted in a total of nine blocks (and versions of the questionnaire) each with eight choice tasks. The alternatives were unlabelled, meaning that the scenarios only varied by the included attributes, and the choice sets were randomized within blocks to avoid order biases in the results. Two control questions were added to each block to detect inconsistent respondents: one dominant choice set was presented as first choice set in all blocks. In a dominant choice set, the attribute levels of one scenario (the dominant scenario) are superior to the levels of the other scenario (the dominated scenario) on each attribute. Therefore, respondents who carefully consider the choice set may be expected to opt for the dominant scenario. Furthermore, the fifth choice set was repeated as the tenth choice set, but now left and right scenarios reversed. Respondents carefully considering the choice sets are expected to choose the same scenario in both questions, independent of its positioning left or right. Altogether, each respondent received 10 choice tasks for one age group. If a respondent chose the dominated scenario in the first choice (i.e. the first control question) and reversed preferences in the tenth choice (i.e. the second control question), the respondent was removed from the data set. Furthermore, based on the distribution of completion times in the pilot study and a quickest possible reading and responding test by three researchers, we determined a minimum completion time for the ten choice sets of 150 s.

In April 2013, the questionnaire was distributed by a professional Internet survey company to a representative sample of the adult population of the Netherlands in terms of gender, age and level of education. The DCE questions were the first part of a larger questionnaire that also contained three contingent valuation questions (as the second part) and questions about socio-demographic characteristics (as the third part). Each respondent was randomly assigned to one of nine versions of the questionnaire (i.e., three age groups times three blocks of choice sets). For an English copy of the questionnaire refer to the electronic supplementary material.

Analyses

To be able to estimate the MWTP per QALY gain for different levels of proportional shortfall the initial model included the following parameters: total QALY gain, proportional shortfall and the increase in health insurance premium. These parameters were calculated from the original attributes using the following equations:

$$\text{Total QALY gain}=(\text{QG}\times (\text{AD}-\text{AO}))+(\text{YG}\times (\text{QOL}+\text{QG}))$$

where QG represents the gain in quality of life, AD represents age of death without treatment, AO is age of onset, YG is life years gained, $\text{QOL}$ the quality of life before treatment. Proportional shortfall was calculated using the following formula.

$$\text{Proportional shortfall}=((\text{MQ}-\text{QOL})\times (\text{AD}-\text{AO}))+((\text{MY}-\text{AD})\times 100))/(\text{MY}-\text{AO})$$

where MQ represents the maximum quality of life (100) and MY the maximum life expectancy, which was set at 80 years of age.

To determine the social MWTP, the QALY gains were multiplied by the size of the risk group and the increase in monthly premium was multiplied by 12 monthly instalments and the number of health insurance payers in the Netherlands (i.e. 13,260,000). The deterministic components of the elemental alternatives for each age group were represented by:

$$\begin{array}{c}\hfill V_{\text{A}}/{\mathit{\lambda }}_{\text{s}}={\mathit{\beta }}_1\text{QALYGAIN}+{\mathit{\beta }}_2\text{PS}+{\mathit{\beta }}_3\text{COST}\\ \hfill V_{\text{B}}/{\mathit{\lambda }}_{\text{s}}={\mathit{\beta }}_1\text{QALYGAIN}+{\mathit{\beta }}_2\text{PS}+{\mathit{\beta }}_3\text{COST}\\ \hfill V_{\text{C}}/{\mathit{\lambda }}_{\text{s}}={\mathit{\beta }}_0\\ \hfill \end{array}$$

where V is the observed component of the random utility function for alternative A, B or C (opt-out), λ_s is the scale parameter and β are the parameters to be estimated. The constant term represents the expected utility for no treatment over treatment. Likelihood ratio tests were used to test different specifications of the utility functions (categorical or numerical attribute levels and interaction effects between QALY gain and proportional shortfall).

In our attempt to find appropriate explanations for the observed patterns in the data, we estimated numerous models. To allow for preference heterogeneity among the population, panel mixed multinomial logit (MMNL) models with correlated coefficients were used to analyse the data. All parameters were included as random parameters. MWTP per QALY values were computed as

$${\text{MWTP}}_a=\frac{{\mathit{\beta }}_a}{{\mathit{\beta }}_{\text{cost}}}$$ 2

However, including the cost parameter as a random parameter in MMNL model may cause problems with respect to the WTP calculations. When a normal distribution for a price coefficient overlaps zero it will result in undefined moments of WTP since dividing by zero is impossible. Furthermore, divisions by numbers arbitrarily close to zero results in very large WTP estimates. Different solutions have been proposed in the literature to tackle this issue, such as WTP space models, MMNL model with a fixed parameter for the cost attribute or constrained distributions like lognormal or triangular distributions [33–35]. All these specifications have been tested for the current models. WTP space models did not fit our data. Different parameter distributions were tested combined with large numbers of Halton draws (i.e. up to 3000), but we were not able to find a model fit. Therefore, different specifications of the MMNL model were estimated and compared using Log Likelihood ratio tests and examining the Akaike and Bayesian information criteria. The MMNL model were estimated with 1000 Halton draws, the statistical results of this process are presented in Table 4. As this table shows, the random parameters with restricted distributions for the costs parameter did not result in better model fits than the specification of a fixed coefficient for the cost attribute. Besides, it should be noted that the specification of a constrained distribution for the cost attribute would still complicate the calculation of the WTP estimates and related confidence intervals. Therefore, in our models cost was specified as a fixed parameter [33–35].

Table 4.

Results from mixed logit and latent class models original attributes

	Age 10				Age 40				Age 70
	MMNL	Latent class			MMNL	Latent class			MMNL	Latent class
		Class 1	Class 2	Class 3		Class 1	Class 2	Class 3		Class 1	Class 2	Class 3
Health gain (%)	0.110**	0.090**	0.090**	0.051**	0.097**	0.084**	0.087**	0.046**	0.117**	0.075**	0.137**	0.054**
Remaining health without treatment (%)	0.028**	0.070**	−0.035**	0.015*	0.032**	0.082**	−0.013**	0.022**	0.022**	0.052**	−0.046**	−0.001
Increase in premium (€/month)	−0.063**	−0.042**	−0.049**	−0.119**	−0.052**	−0.016*	−0.054**	−0.123**	−0.074**	−0.060**	−0.050**	−0.133**
Constant	−0.494	1.263**	−1.877**	1.286**	−0.752**	1.652**	−1.254**	1.450**	−0.863**	−0.011	−1.646**	0.427
SD random parameters
Health gain (%)	0.059**				0.043**				0.081**
Remaining health without treatment (%)	0.084**				0.062**				0.066**
Constant	3.383**				2.931**				2.755**
Probability of class membership		0.476**	0.407**	0.117**		0.400**	0.496**	0.104**		0.567**	0.304**	0.130**
LL at convergence	−2219.3	−2288.5			−2194.2	−2233.7			−2054.0	−2124.1
MWTP for a QALY (per class)		€243.635	€208.072	€48.793		€533.015	€160.695	€37.271		€165.784	€366.749	€53.873
MWTP for a QALY (95 % CI)	€197.663	€206.408 (€125.993–€286.823)			€184.893	€296.756 (€37.281–€556.233)			€209.588	€212.322 (€136.454–€288.190)

LL log likelihood, MMNL mixed multinomial logit model, SD standard deviation, MWTP marginal willingness to pay

** p < 0.001, * p < 0.1

The MMNL model based on the above-mentioned attributes did not behave as expected. As shown later on in the Sect. 3, counterintuitive results were found with respect to proportional shortfall (i.e. scenarios with higher proportional shortfall were less likely to be chosen, c.p.). Moreover, all standard deviations of the random parameters were significant, which implies a substantial amount of preference heterogeneity within the sample. To further explore these results and understand the preference structure of respondents, we searched for decision patterns within the data. For that reason, we relaxed our assumptions with respect to proportional shortfall and absolute QALY gains to explain respondents’ preferences and used the attributes as presented to the respondents instead. Latent class models were estimated to identify different subgroups in the population based on unobserved characteristics that affect their preferences. It is assumed that preferences are homogeneous within the classes but differ between classes [36]. The optimal number of classes was determined by examining the Akaike and Bayesian information criteria of different numbers of classes and the standard errors of the corresponding parameters. The latter is a valid additional argument in this context, because an increasing number of classes may lead to extremely large standard errors of several parameters, complicating the interpretability of the model. Latent class models with four classes showed extremely large standard errors in age groups 10 and 40, and insignificant coefficients—and consequently meaningless WTP estimates—in age group 70. Thus, in all three age groups the number of classes was limited based on the standard errors of the corresponding parameters, despite the fact that accepting more classes would have improved model fit [33, 37].

The results of the latent class models provided additional insights in respondents’ preferences compared with the MMNL model. Therefore, the latent class models were chosen as a starting point for further analyses.

Overall MWTP values were estimated as the weighted average of conditional class MWTPs. Confidence intervals for MWTP estimates were estimated using the Delta method [29, 36, 33].

Analyses were performed in Nlogit 5.0 (Econometric Software Inc.).

Results

The final dataset included 1205 respondents representative of the adult population of the Netherlands with respect to age (mean 45.0 years), gender (50.8 % female) and education level (25.5, 42.1, and 32.4 % had lower, middle, and higher education, respectively). Demographic statistics of the sample are presented in Table 2. The completion time for the ten DCE questions was, on average, 5.2 min.

Table 2.

Demographic statistics (N = 1205)

Variable	Mean	SD	Min	Max
Age	45.0	15.0	18	86
Gender (% female)	50.8
Partner (% yes)	67.0
Children (% yes)	58.3
Monthly income (%)
Group 1 (<€1000)	23.5
Group 2 (€1000–€1999)	31.5
Group 3 (€2000–€3499)	32.3
Group 4 (≥€3500)	12.7
Education status (%)
Elementary school	25.5
High school	42.1
University	32.4
Health status
VAS (0–100)	80.1	15.0	15	100
Opt-out (%)	10.9

Number of observations per version of the questionnaire: 411 for age group 10; 410 for age group 40; 384 for age group 70; General population statistics: 45 years of age (18+), 50.9 % female (18+) and 33.0 % elementary school, 40.2 % high school, 26.8 % university (15+) [http://statline.cbs.nl/Statweb/?LA=en]

SD standard deviation, VAS visual analogue scale

The results of the panel MMNL model for the three age groups are presented in Table 3. As already briefly discussed in the Sect. 2, we strongly questioned whether this model accurately represents respondents’ preferences. The results with respect to proportional shortfall were counterintuitive and the standard deviations of the random parameters were all statistically significant with relatively large coefficients, which suggest a substantial heterogeneity in preferences in the sample.

Table 3.

Results from MNL and MMNL models with QALY gain and proportional shortfall

	Age 10		Age 40		Age 70
	MNL	MMNL	MNL	MMNL	MNL	MMNL
Health gain from treatment (QALY)	0.092**	0.133**	0.170**	0.243**	0.735***	1.178**
Proportional shortfall	−0.016**	−0.025**	−0.021**	−0.032**	−0.016***	−0.022**
Increase in health insurance premium (€/month)	−0.027**	−0.055**	−0.036**	−0.052**	−0.048***	−0.075**
Constant	−1.251**	−3.324**	−1.693**	−3.875**	−1.554***	−3.053**
SD random parameters
Health gain from treatment (QALY)		0.007		0.107**		0.810**
Proportional shortfall		0.076**		0.063**		0.066**
Constant		6.366**		5.479**		6.050**
Log-likelihood at convergence	−2723.392	−2244.898	−2590.386	−2193.658	−2466.932	−2054.220

MNL multinomial logit model, MMNL mixed multinomial logit model, SD standard deviation

** p < 0.001, * p < 0.1

Table 4 presents the results of the MMNL model and latent class models using the attributes as presented to the respondents, that is, health gain as a percentage, remaining health without treatment (%) and the increase in health insurance premium. The MMNL model were comparable to the MMNL model of Table 3 with respect to preference heterogeneity and counterintuitive results for health state before treatment (i.e. an average preference was observed to treat people who already were relatively healthy). Although the MMNL model had a slightly better model fit than the latent class models, we preferred to use the latent class models since they seem to provide additional insight in the heterogeneous preference structures of the respondents. The results for the selection of number of classes are presented in Sect. 5. For all three age groups, the most appropriate model consisted of three classes (as explained in the Sect. 2).

Respondents belonging to the first latent class of age group 10 had a relatively strong preference not to choose between one of the groups of patients as indicated by the positive significant constant term. In case respondents were willing to treat one of the groups of patients, more remaining health without treatment increased the probability to receive treatment. Remarkably, the coefficients of health gain from treatment and remaining health without treatment were comparable in magnitude and sign. This indicates that these respondents did not really differentiate between these two attributes. The increase in monthly health insurance premium was the least important attribute in this class. The significant negative constant term in class two of age group 10 indicates a general preference toward treating one of the groups of patients. Respondents belonging to this class were more likely to treat patients with larger health gains and a more severe health state before treatment. Larger increases in monthly health insurance premium decreased the probability to be chosen. Respondents belonging to the third class preferred not to choose between the groups of patients. The increase in health insurance premium had the largest marginal effect on respondents’ choice. Probabilities of class membership were 47.6, 40.7 and 11.7 %, respectively.

A similar preference structure was found for age group 40, although the highest probability was to be assigned to class 2 (49.6 %), implying a preference to treat patients with more severe health states before treatment.

Somewhat distinct preferences were observed for age group 70. The insignificant constant terms in the first and third classes indicate that respondents did not have a general preference for either choosing between groups of patients, or not. Respondents had a 57 % probability to be in first class in which health gain was the most important attribute, followed by the increase in health insurance premium. Respondents belonging to this class preferred to treat patients with a relatively good health state before treatment which is different from what we expected but in line with the other age groups. Respondents had a 30 % probability to be in class 2. These respondents were willing to choose between groups of patients and preferred to treat patients with a more severe health state before treatment. Respondents in class 3 seemed to be mainly driven by the increase in health insurance premium in their decision. Remaining health without treatment did not significantly influence respondents’ preferences.

The probability weighted MWTP values ranged from €206,408 in age group 10 to €296,756 in age group 40, but were not significantly different between the age groups. This indicates that we did not find a significant age effect in our data. Interaction effects between health state before treatment and health gain were not significant and therefore not included in the final models. This indicates that, statistically, the value of a health gain was not different for different levels of severity. However, the main effect of severity was significant, which indicates that severity did influence preferences between groups.

Discussion

It is increasingly recognized that a monetary threshold value against which health gains from an intervention can be evaluated should vary with distributional preferences in society. However, most WTP per QALY studies so far have focused on the individual perspective and have not incorporated such equity considerations. Studies exploring public preferences for QALYs, on the other hand, rarely translate these preferences into equity weights or subgroup-specific QALY values. Therefore, the aim of this study was to contribute to the existing literature by estimating the social MWTP for QALY gains in different equity subgroups, considering the equity principles severity of illness (operationalized as proportional shortfall) and fair innings (operationalized as age). Our results show substantial preference heterogeneity among members of the public. As discussed further below, this finding may be helpful in explaining the mixed findings in literature with respect to the value of a QALY in relation to severity of illness and age of care recipients.

Before the results are discussed in more detail, our approach to the data analysis warrants further discussion. A variety of model specifications were tested to analyse the data. Given the aim of this study, levels of proportional shortfall and QALY gains were calculated from the original attributes and included in MMNL model. The results (Table 3) showed substantial preference heterogeneity and counterintuitive results: we found that respondents were less likely to choose patients with higher levels of proportional shortfall. It should be noted that, although counterintuitive, this finding is consistent with Lancsar et al. [29], Dolan and Tsuchiya [38] and Skedgel et al. [36].

In order to better understand how respondents made their decisions, latent class models were estimated with the attributes as presented to respondents. These latent class models demonstrated distinct preference structures in the data, which seem plausible and were helpful in clarifying some of the counterintuitive results we found in the mixed models. It is often suggested that different views exist in society regarding the distribution of health and health care [11]. Exploring mean preferences may therefore not be most insightful in the context of such value-laden issues. We suggest that future studies in this area should account for these heterogeneous preferences in society by considering multiple models to explore possible decision patterns underlying the data.

The results of the latent class models (Table 4) showed some interesting decision patterns with respect to equity considerations in healthcare allocation decisions, which were more or less consistent across the different age groups.

The first class of each age group showed aforementioned counterintuitive preferences for treating persons who were already in a relatively good health state before treatment (i.e. less severe diseases). In addition, in the first class of age group 40, respondents reported fairly equal preferences for health state without treatment and health gain (and also in age groups 10 and 70 the differences were relatively small). This might indicate that respondents in this class were driven by the best health state after treatment, irrespective of whether this was a consequence of the health state before treatment or the health gain from treatment. Other studies also have found that respondents consider health state after treatment more important than health state before treatment [21]. However, it is also possible that this finding was (partly) induced by the presentation of the scenarios in our study. A closer look at the graphs of the scenarios (Fig. 1) shows that the best end state after treatment automatically coincides with the smallest health loss, indicated by the red area in the graph. It is conceivable that some respondents just opted for the smallest health loss (i.e. the smallest red area). Using graphs to clarify the scenarios might thus be helpful in presenting complex choice problems to respondents, but at the same time unintentionally influence their choices. As the use of such graphs is relatively new in this field, this deserves further study, and future studies should be aware of this issue when they consider using graphs to present their attributes to respondents.

The second latent class of all age groups aligned with the principle of proportional shortfall, thus expressing concerns for severity of illness. These respondents were the only ones willing to choose between the groups of patients and, ceteris paribus, preferred to treat patients with a relatively more severe health state without treatment. The probabilities of membership of this class were considerable, which highlights considerable support for considering severity in healthcare priority setting in the general public.

Respondents assigned to class 3, the smallest class of each age group, seemed to consist of individuals with a general aversion to prioritising patients based on the health characteristics included in the study. The remaining health state without treatment attribute was not significant in age group 70, and only marginally significant in age group 40, suggesting that differences in health state without treatment were not a relevant argument for them to prioritise between different groups of patients. Moreover, the constant term indicated that these respondents generally preferred not to choose between patients, and when they did choose, their decision was mainly driven by the change in monthly health insurance premium.

In other words, in each age group we found two latent classes with a general preference not to choose between patients, and one class that was willing to choose and displayed preferences that aligned with what was expected from the theory of proportional shortfall. The first two classes represented the majority of respondents in all three age groups, but a substantial minority thus supports accounting for severity in priority setting.

Interaction effects between remaining health without treatment and health gain were found not to be significant. This indicates that, statistically, severity did not influence the value of a QALY itself in our sample. Nevertheless, the significant coefficients of the main effects suggest that health state before treatment does influence respondents’ choices. However, theoretically, these two cannot be valued separately since a certain health gain is always accompanied by a certain health state before treatment (or proportional shortfall). This suggests that at least indirectly the MWTP for a QALY depends on the health state without treatment. Overall, it seems worthwhile to investigate these preferences with respect to severity in more detail, in particular taking the preference heterogeneity within the general public into consideration.

No clear support was found for the fair innings argument in this study, since the MWTP per QALY estimates did not significantly differ between age groups—although the value in age group 40 appears considerably higher (Table 4). The confidence interval of the MWTP estimate of age group 40 was large, which may be due to the low significance of the health insurance premium attribute in the first class. The relatively small coefficient for health insurance premium in this class resulted in a fairly high MWTP for a QALY estimate (€533.015), which in turn (given the substantial probability to be part of group 1) led to a relatively high MWTP estimate for age group 40.

Apart from the common limitations that come with DCEs and online surveys, the following limitations of this study need to be mentioned. First of all, as discussed here, a possible explanation for part of the preference heterogeneity observed in this study might relate to the graphical presentation of the scenarios. Such graphs, also used before by Lancsar et al. [29], Shah et al. [39] and Brazier et al. [40], may unintentionally give room to different interpretations of the scenarios by respondents, and therefore may not be the best way to present the attributes to respondents. How respondents perceive the information contained in such graphs deserves further study, for instance using a think-aloud procedure.

Second, finding that fair innings is of no relevance for the value of a QALY may be a result of framing, since age was part of the scenario description and not an attribute in the choice set. This implies that respondents did not trade age against other characteristics of the recipients, which may have given a different meaning to age in the choices made. In the literature there has been a growing interest in the context and framing of studies in order to improve the consistency and comparability between studies. Our results are in line with those reported by Lancsar et al. [29] and Diederich et al. [41]. It would be interesting for future research to investigate whether a DCE with a fixed level of severity in each scenario and age included as an attribute would result in opposite findings.

Concluding, this study aimed to contribute to the existing literature by bridging the gap between WTP per QALY studies from an individual perspective and the growing literature exploring societal preferences for health and health care. A recent review of Whitty et al. [21] underlined the importance of multi-criteria studies and the translation of public preferences into equity weights that can be used for policy making. In this study, we estimated MWTP per QALY for different age groups and found no support for the fair innings argument, or for prioritizing based on health characteristics more generally. We did find support for considering severity of illness among a substantial minority of the public, but since interaction terms between health state without treatment and QALY gains were not significant, we cannot say that the MWTP per QALY estimates differed statistically significantly for different levels of severity of illness.

While some of our results may be related to the design of our study, including the graphical presentation of the scenarios, they are insightful and, most of all, highlight the importance of accounting for heterogeneity in preferences among the public on value-laden issues such as prioritizing health care, both in research and in decision making.

Appendix: Selection number of classes in the latent class models

	Number of classes	Log Likelihood	AIC	BIC
Age group 10	1	−2723.39212	5454.8	5479.2
	2	−2473.78587	4965.6	5020.5
	3	−2288.50549	4605.0	4690.4
	4	−2271.26754	4580.5	4696.4
	5	−2225.79214	4499.6	4645.9
	6	−2202.77079	4463.5	4640.4
	7	−2184.51031	4437.0	4644.4
	8	−2178.68425	4435.4	4673.2
	9	−2178.71372	4445.4	4713.7
	10	–	–	–
Age group 40	1	−2590.38614	5188.8	5213.2
	2	−2342.04598	4702.1	4757.0
	3	−2233.72689	4495.5	4580.8
	4	−2186.88956	4411.8	4527.6
	5	−2168.02966	4384.1	4530.4
	6	−2157.85377	4373.7	4550.5
	7	−2152.86299	4373.7	4581.0
	8	−2131.83972	4341.7	4579.4
	9	−2130.30804	4348.6	4616.8
	10	−2120.76759	4339.5	4638.2
Age group 70	1	−2466.93212	4941.9	4966.0
	2	−2224.51394	4467.0	4521.3
	3	−2124.14160	4276.3	4360.7
	4	−2080.06128	4198.1	4321.7
	5	−2052.04820	4152.1	4296.8
	6	–	–	–
	7	−2017.28796	4102.6	4307.6
	8	−1993.56204	4065.1	4300.3
	9	−1994.84877	4077.7	4343.0
	10	−2002.77934	4103.6	4399.0

AIC Akaike Information Criterion; BIC Bayesian Information Criterion

Compliance with Ethical Standards

This study was financially supported by Zorgonderzoek Nederland (ZonMW), Netherlands Organization for Health Research and Development (project number 152002038). The usual disclaimer applies.

Liesbet van de Wetering, Job van Exel, Ana Bobinac and Werner Brouwer declare that they have no competing interests.

This study has not been approved by an ethics committee because this is not required in the Netherlands for population-based studies.

The data sampling of this study was conducted by a professional panel company (Survey Sampling International, http://www.surveysampling.com). People voluntarily subscribe to these panels and regularly participate in a variety of online surveys. All panel members agreed with the privacy statements of Survey Sampling International. After completion of the survey, a small donation is made to the participant’s charity of choice.