Abstract
Capping protein (CP), which caps the growing ends of actin filaments, accelerates actin-based motility. Recent experiments on biomimetic beads have shown that CP also enhances the rate of actin filament nucleation. Proposed explanations for these phenomena include i) the Actin Funneling Hypothesis (AFH), in which the presence of CP increases the free-actin concentration, and ii) the Monomer Gating model, in which CP binding to actin filament barbed ends makes more monomers available for filament nucleation. To establish how CP increases the rates of filament elongation and nucleation on biomimetic beads, we perform a quantitative modeling analysis of actin polymerization, using rate equations that include actin filament nucleation, polymerization and capping, as modified by monomer depletion near the surface of the bead. With one adjustable parameter, our simulation results match previously measured time courses of polymerized actin and filament number. The results support a version of the AFH where CP increases the local actin monomer concentration at the bead surface, but leaves the global free-actin concentration nearly constant. Because the rate of filament nucleation increases with the monomer concentration, the increased local monomer concentration enhances actin filament nucleation. We derive a closed-form formula for the characteristic CP concentration where the local free-actin concentration reaches half the bulk value, and find it to be comparable to the global Arp2/3 complex concentration. We also propose an experimental protocol for distinguishing branching nucleation of filaments from spontaneous nucleation.
Keywords: Actin filaments, networks, branching, nucleation, capping protein, Arp2/3 complex
1 Introduction
The Actin Funneling Hypothesis (AFH) was proposed by Carlier and Pantaloni [1–3] to explain how capping protein CP accelerates the motility of cells [4] and intracellular pathogens [5]. CP caps free barbed ends of actin filaments and thus prevents them from polymerizing [6]. According to the AFH, increased CP reduces the number of uncapped filaments, so that fewer actin monomers are consumed and thus the monomer concentration increases, enhancing motility. This provides a straightforward qualitative explanation of the effects of CP on motility.
Previous theoretical works argue in favor of the AFH in several different geometries. Ref. [7] modeled lamellipodial protrusion using a model incorporating capping/uncapping processes at the leading edge, coupled with depletion of actin monomers resulting from actin polymerization. The analysis showed that with increasing capping rate, the protrusion velocity initially grows, and subsequently drops. The initial growth resulted from an increase in the actin monomer concentration at the leading edge caused by capping, consistent with the AFH. Ref. [8] further showed that in a filopodial geometry, a reduction in the number of uncapped filaments can lead to faster protrusion, because the actin concentration at the tip is increased. Subsequent studies have reinforced these findings using increasingly realistic descriptions of the actin network and monomer diffusion. In a study of the actin-based propulsion of a disk [9] by freely diffusing filaments, based on explicit filament coordinates, CP accelerated the disk motion by increasing the local free-actin concentration at the disk. Subsequent studies of the effects of CP on lamellipodial protrusion [10–12] treated a rigid actin network, and combined a three-dimensional stochastic treatment of the network’s growth with an explicit treatment of monomer diffusion. They also found that protrusion is accelerated by the increased free-monomer concentration resulting from capping.
However, we are not aware of modeling studies quantitatively testing the AFH by comparing predictions of actin polymerization and nucleation with well-characterized experimental observations. The work of Akin and Mullins [13] provides an opportunity for such a test. They measured actin filament nucleation and polymerization on biomimetic beads coated with the actin nucleator ActA, for varying concentrations of CP and Arp2/3 complex. ActA is one of a number of “Nucleation Promoting Factors” (NPFs) that activate the Arp2/3 complex to generate new filaments as branches on existing filaments. The mechanism of NPFs activating Arp2/3 complex involves events such as NPFs binding to Arp2/3 complex and actin monomers, as well as Arp2/3 complex binding to filaments [14–17]. Ref. [13] measured the growth of actin networks generated by large (3 μm radius) and small (220 nm radius) beads. For the larger beads, time courses of actin subunit count and filament number were measured after they were placed in a solution of actin monomers, Arp2/3 complex, and CP. Several stages of growth and movement driven by actin polymerization were observed. In the first stage, the actin network grew with spherical symmetry. The bulk monomer concentration in this stage did not increase with CP, so alternatives to the AFH were investigated. It was proposed that the faster motility caused by CP results from a more effective growth geometry caused by increased branching. CP was also found to increase the number of actin filaments on the beads, and this effect was explained via a Monomer Gating model in which the competition between barbed ends and Arp2/3 complex for monomers is modulated by CP.
Here we use a set of detailed calculations based on physically motivated rate equations to study the the effects of CP on actin polymerization and nucleation. We focus on the data of Ref. [13], because to our knowledge this is the only measurement of the time courses of total actin count and actin filament number for biomimetic beads. Using a model with one adjustable parameter, we obtain good fits to the measured time courses. We find that a variant of the AFH, based on the local monomer concentration at the bead surface, can explain the actin polymerization and nucleation data. The calculations show that CP significantly increases the local actin concentration, enhancing the rates of both polymerization and filament nucleation. Using analytic theory, we show that in general the concentration of CP required to raise the local actin concentration to roughly half its bulk value is comparable to the concentration of Arp2/3 complex. Finally, we suggest an experimental protocol for distinguishing branching nucleation from spontaneous nucleation of actin filaments.
2 Model
2.1 Physical mechanisms and equations
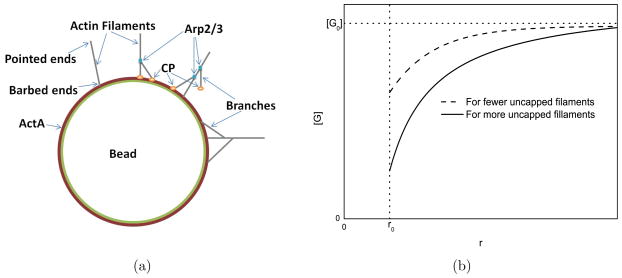
In the model (Fig. 1(a)), actin filaments grow on a bead of radius r0 = 3 μm coated with a nucleation promoting factor (ActA), which nucleates new filaments and anchors them to the bead [18]. The key physical mechanism underlying the model is the reduction of the local actin concentration [G] at the surface of the bead relative to the bulk concentration [G0]. Such depletion effects have previously been analyzed in Ref. [19]. To demonstrate the magnitude of the effect, we note (see Supporting Material A) that [G]/[G0] is reduced by a fraction
Figure 1.
Schematics of a) actin filaments on a bead and b) the monomer concentration profile.
| (1) |
where I is the monomer current to the bead and Dm = 70μm2s−1 [20] is the actin monomer diffusion coefficient. This result is quite rigorous because it depends only on Fick’s law of diffusion, and not on any assumptions about actin nucleation mechanisms. We estimate I in the later part of the time courses Fig. 5b of Ref. [13], as a numerical time derivative based on the difference between the 60s points and the 45s points, averaged over all the curves. This gives I ≃ 2.2 × 106s−1. Furthermore, inspection of Fig. S6B of [13] shows that G0 < 1.8μM. Using these values in Eq. 1 gives a value of 0.8. Therefore [G]/[G0] is reduced by at least 80%, as illustrated in Fig. 1(b). Thus inclusion of local depletion is crucial for the modeling.
In the literature it is generally assumed that Arp2/3 mainly creates new filaments on preexisting filaments, but here we also treat the possibility that Arp2/3 generates filaments by spontaneous nucleation at the bead. Uncapped filaments can be capped by capping protein CP, but uncapping events on capped filaments are neglected, since the uncapping rate (Ref. [21]) is extremely small on the 60-s time scale of the experiments. Incorporation of new subunits into the actin network results from polymerization on uncapped filaments.
This model is analyzed via three sets of equations. The first set, Eqs. (2–4), treats the dynamics of capped and uncapped filaments, and polymerized-actin subunits. The variables and parameters are defined in Tables 1 and 2 respectively.
Table 1.
Simulation Variables
| Symbol | Definition |
|---|---|
|
| |
| Nf | Number of uncapped filaments in the network |
| Nc | Number of capped filaments in the network |
| N | Total number of filaments in the network; N = Nf + Nc |
| F | Number of actin subunits in the network |
| [G] | local (bead surface) monomer concentration |
| [CP] | local (bead surface) capping protein concentration |
| [Arp] | local (bead surface) Arp2/3 complex concentration |
| [ ] | Real-time bulk monomer concentration |
| [ ] | Real-time bulk CP concentration |
| [ ] | Real-time bulk Arp2/3 complex concentration |
Table 2.
Simulation Inputs
| Symbol | Definition | Value | References |
|---|---|---|---|
|
| |||
| δ | Actin monomer size | 2.7 nm | [22] |
| r0 | Bead radius | 3 μm | [13] |
| Dm | Actin Monomer diffusion coefficient | 70 μm2s−1 | [20] |
| Dc | Capping protein diffusion coefficient | 61 μm2s−1 | This article |
| Da | Arp2/3 complex diffusion coefficient | 40 μm2s−1 | This article |
| kon | Monomer on-rate constant | 11.6 μM−1s−1 | [23] |
| kcap | Capping rate | 8 μM−1s−1 | [21] |
| ksp | Nucleation rate | Varies | This article |
| kbr | Branching rate | Varies | This article |
| kd | Decay rate | 1.8 ×103s−1 | [21] |
| [G0] | Initial bulk monomer concentration | 1.4 – 3.0μM | [13] |
| Gc | Barbed-end critical concentration | 0.07 μM | [21] |
| [CP0] | Initial bulk capping protein concentration | 15 – 128 nM | [13] |
| [Arp0] | Initial bulk Arp2/3 complex concentration | 48 – 96 nM | [13] |
| [Arpc] | Crossover Arp2/3 complex concentration | 1 – 10 nM | This article |
| V0 | Solution volume per bead | 3.3 × 105 μm3 | Calculated from [13] |
| (2) |
| (3) |
| (4) |
Eq. (2) describes nucleation of new filaments either by branching from existing filaments or by spontaneous nucleation, and subsequent capping. The [G]-dependence of the nucleation rates is based on the form used in Ref. [21], where the second power gave the optimal fit to time courses of actin polymerization in the presence of activated Arp2/3 complex and capping protein. Eqs. (3) and (4) describe capping and polymerization/depolymerization events, where depolymerization is described by the term proportional to Gc. In each of these equations we also include a term describing filament detachment, and assume that this is the main mode of disassembly, so that the same rate enters all the equations. We find that the results are quite insensitive to the value of this relatively uncertain term. These equations are similar to those used in Ref. [21]. The key difference is the presence of the Arpc factor. This factor results from assuming i) that [Arp0] is not the rate-limiting factor for nucleation over the range of concentrations studied, as suggested by Ref. [13], but also ii) that when [Arp0] becomes extremely small, it must become rate-limiting. The functional form of Eq. 2 is based on a binding equilibrium between Arp2/3 complex and a small number of potential binding sites; Arpc is defined as the concentration where the binding sites are half filled.
The second set, Eqs. (5–7), describes how the local concentrations [G], [CP], and [Arp] at the bead surface are depleted relative to their bulk values , and , by protein incorporation into the actin network. The extent of depletion is calculated in Supporting Material A, using a quasi-static approximation based on the assumption that the free-protein distributions change much faster than the actin network properties, giving
| (5) |
| (6) |
| (7) |
The second term in [G] includes the contribution of actin depolymerization at the bead surface; for [CP] and [Arp] only assembly is included. Note that [Arp] appears on both sides of Eq.(7). Therefore we solve explicitly for [Arp] in terms of the other quantities. These equations are analogous to those used previously in studies of actin monomer depletion in a lamellipodium geometry [7], in which the diffusion profile was taken to have its steady-state form.
Finally, the third set Eqs. (8–10), describes how the bulk concentrations are depleted by incorporation of the proteins into the actin network. We assume that each capped filament has an associated CP and that each filament has an associated Arp2/3 complex.
| (8) |
| (9) |
| (10) |
where V0 is the solution volume per bead.
2.2 Key simplifying approximations
The validity of most of the assumptions underlying the model is discussed in Supplementary Material B. Here we discuss two the most substantial approximations.
Opposing force
The equations of motion do not explicitly include the effect of opposing force on barbed-end polymerization. This would also slow capping [24–27], because the capping process involves the addition of capping protein at the end of the filament similar to the addition of a new subunit. In addition, branching would be slowed if, as suggested by Ref. [28], new branches form on the side of the filament adjacent to the obstacle. The main physical mechanisms causing opposing force in the bead geometry are the following:
Pulling forces on membrane-attached filaments that must be overcome by the growing filaments [29–31].
Inwards forces caused by stretching of the actin gel.
Refs. [30] and [31] showed that the competition between populations of attached and detached filaments can modify the force-velocity relation, and also lead to new active behaviors, such as oscillations. Such oscillations were not seen in Ref. [13], but the average rates of polymerization, branching, and capping could be reduced if i) only some of the filaments are free to polymerize and ii) their polymerization is slowed by forces from attached, non-growing filaments. Ref. [32] treated the effects of filament attachments within a different model of an actin network pushing on a disk, and found that the growth velocity is essentially constant up to a certain value of the attachment strength, at which point it begins to drop. In the simplest picture, the competition between attached and detached filaments could be treated by reducing kon, kcap, and kbr, assuming a fixed ratio of attached to detached filaments. Accordingly, we have performed additional simulations in which kon and kcap are reduced by 50%, and kbr is refitted. We find that in this case the key qualitative features of the results are preserved, but the quantitative agreement with experiment is worsened. For example, the increase in filament number at t = 60s induced by increasing [CP0] from 21 nm to 52 nm is 38% in the baseline model, but is only 25% when kon and kcap are reduced. We are not able to predict the effect of changes in the relative proportions of detached and attached filaments.
Ref. [33] showed that gel-stretching forces are proportional to the shear modulus of the gel, which is enhanced by crosslinking, and to the square of the gel thickness. Unlike the cell-extract system of Ref. [33], the pure-protein system of Ref. [13] had no crosslinking proteins, so the effects of the gel-stretching forces should be smaller. In addition, gel-stretching forces would cause polymerization to slow over time as the gel thickness grows and the filament density increases. However, no significant slowing was seen in Ref. [13] under the conditions that give the maximum number of filaments. Therefore the effect of the gel-stretching forces is probably small.
To further evaluate the possible impact of gel-stretching forces, we have developed a simple modification of our model, based on the proportionality of the opposing force to the square of the gel thickness [33]. Assuming that i) the thickness is proportional to F, ii) the number of filaments is reasonably constant over the later parts of the polymerization process, and iii) polymerization is slowed by a “Brownian ratchet” exponential factor [34], we multiply the polymerization, branching, and capping rates by a factor exp(−αF2), with α chosen so that the exponent is −1 at the end of the time courses. The fits to the data were repeated using this term. We find that inclusion of the exponential factor changes the F-actin and filament number time courses by 3–5%.
Filament nucleation mechanisms
We assume that filament nucleation is dominated by Arp2/3-based branching as opposed to CP-based nucleation in solution. CP is known to nucleate actin filaments in vitro [13,35]. These filaments slowly polymer-ize at the pointed ends rather than at barbed ends. In the system of Ref. [13], such filaments could diffuse to the bead surface and contribute to the filament count. We thus estimate the upper limit of the number of bead-bound filaments that could result from such a process. We define Δ[CP] and Δ[G], respectively, as the differences between the initial and final bulk concentrations of CP and actin monomers measured in Ref. [13]. To estimate the maximum filament number from this process, we assume that all of Δ[CP ] and Δ[G] are due to CP-induced nucleation and subsequent polymerization, and that the bead is a perfect absorber for the filaments. Then the concentration of CP-nucleated filaments is Δ[CP].
In Supplemental Material C we prove that the number Ntouch of CP-nucleated filaments attached to the bead is less than
| (11) |
where Dm is the monomer diffusion coefficient, Lmin and Lmax are the lengths of the shortest and longest filaments (measured in subunits), respectively, and tf is the accumulation time. For the case of an initial CP concentration of 56 nM, Fig. S6a of Ref. [13] shows a final CP concentration of approximately 15 nM. This means that the upper limit of Δ[CP] is 41 nM; the actual value is smaller since not all of the CP is free at the beginning of the time course. We take Δ[G] to be the global concentration of polymerized actin on the beads, estimated below in Parameterization and Fitting Procedure as 0.8μM. This gives 〈L〉 = Δ[G]/Δ[CP] = 20 and (using Lmin = 3) Lmax = 37, so that C0 = 41 nM/34 = 1.2 nM . Using these values in Eq. 11, along with Dm = 70μm2s−1 [20], we obtain . This is much lower than the filament number measured in Ref. [13], which is about 2 × 106.
The actual number of CP-nucleated filaments on a bead will be even less than , for three reasons. First, the derivation of Eq. 11 does not include the slowing of filament accumulation due to global depletion of the number of filaments. Second, the bead is probably not a perfect absorber. Third, we used an upper bound for ΔCP, and the actual value will be smaller. Therefore it is reasonable to assume that most of the filaments on the bead are generated by Arp2/3-based branching on the bead rather than by CP-induced nucleation in solution.
3 Parameterization and Fitting Procedure
The parameters not given previously, and whose values are not fitted in the calculations, are obtained as follows. For the diffusion coefficient Da of Arp2/3 complex, we note that the Arp2/3 complex molecular mass is approximately 220 kDa (Ref. [36]), and the actin molecular mass is 42 kDa. Treating the complex as a sphere, assuming that the molecular mass is proportional to the third power of the protein radius, and that D is inversely proportional to the radius [37], we obtain Da ~ (42/220)1/3 Dm ~ 40 μm2s−1. Similarly, Dc ~ (42/65)1/3 Dm ~ 61 μm2s−1, since the molecular mass of CP is ~ 65 kDa (Ref. [38]). The value of ksp is not fitted in the baseline model; rather it is given a value so that less than 5% of the filaments are generated by spontaneous nucleation; the results are found to be insensitive to its precise value. The value of kbr is obtained from the simulations, by matching the experimental data using a least-squares procedure. We minimized the sum of all the squared errors between the predictions and the experimental data at all time points for N given in Ref. [13] divided by the squared experimental values of N, for each of the experimental [Arp0] and [CP0] values.
We obtained the initial G0 as the final of about 1.4μM (obtained from Fig. S6B of Ref. [13]) plus a contribution from the subunits on the beads. To calculate this contribution, we used the bead surface area density per unit volume of 1010 μm2/mL = 10−2μm−1 (Ref. [13], Supplementary Material) and the bead radius of r0 = 3 μm, to infer a bead density of (1/30) × 10−2μm−1/(4π × 32μm2) = 3 × 10−6/μm3, since the solution was diluted 1:30. Thus, the solution volume per bead is V0 ≃ 3.3 × 105 μm3. We use 1.5 × 108 (Fig. 5c of Ref. [13]) as a typical number of actin subunits on the bead. The global concentration of actin on the beads is thus ~ 1.5 × 108/3.3 × 105 μm3 = 0.8μM, giving an initial G0 = 2.2μM . This is lower than the value suggested by the stoichiometry of the solution, presumably because of polymerization induced by CP [13,35]. Similar calculations for [CP0] yield initial values [CP0]=21 and 52 μM, corresponding to the final values of 15 and 30 μM respectively. The final value of [Arp0] after the experiment was not given in Ref. [13], so we use the quoted initial value. For Arpc, we find that values less than 10 nM reproduce the weakness of the Arp2/3 effect measured in Ref. [13].
4 Results
There are several possible variations of the model, and a priori it is not clear which combination of assumptions describes the system best. For this reason, we first present a baseline model, which makes the assumptions that we feel are most plausible. In this model, the contribution from spontaneous nucleation is assumed to be much less than (< 5%) that from branching, but not completely negligible. We also assume that Arpc ≪ Arp0. We then present results for two modifications of the baseline model, describe the basic mechanisms by which CP enhances polymerization and nucleation, and propose experiments to distinguish between branching nucleation and spontaneous nucleation.
4.1 Baseline model
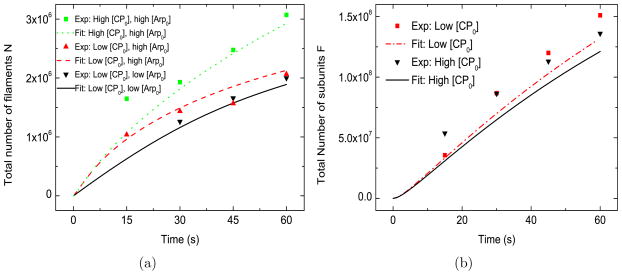
This model (Fig. 2(a)) matches several aspects of the filament-number measurements well: i) the general trend of the time courses; ii) the weak effect of [Arp2/3] on N; and iii) the strong positive effect of CP on N. When [CP0] is increased, the resulting increase in N grows with time. In contrast, when [Arp0] is varied, the change in N becomes smaller at later times. The main discrepancies between the baseline model and the experimental data are in the the initial stage (< 15 s) of the growth of actin networks for higher values of the CP concentration. However, only one datum is available within the first 15 s of the experiment, so the significance of the discrepancy between the experiments and the fit is not clear.
Figure 2.
Baseline model. [G0] =2.2 μM, kbr=0.65 μM−2s−1, ksp=1.0 ×104 μM−2s−1, [Arpc] = 2 nM . Low [CP0] = 21 nM , high [CP0] = 52 nM . Low [Arp0] = 48 nM , high [Arp0] = 96 nM . In this and following figures, an estimate of the nonspecific association of CP to the beads was subtracted from filament numbers quoted in Ref. [13]. This was obtained by linear interpolation of the data in Fig. S5 of Ref. [13].
The time courses of the number of subunits F are also matched well for different CP concentrations (Fig. 2(b)). Consistent with the experiments, we find that CP has a weak effect on the number of actin subunits incorporated into network. This is because the large density of uncapped filaments causes the actin gel to act essentially as a perfect absorber. The total polymerization rate is thus limited not by the number of uncapped filaments, but rather by diffusion of actin monomers to the region of the bead. CP enhances the growth rate of individual uncapped filaments, but also reduces the fraction of filaments that are uncapped, and these effects compensate in such a way that the total rate of actin assembly is almost independent of CP. Again, the largest fractional discrepancies between the baseline model and the experimental data are within the first 15 s of the experiment.
4.2 Model with only spontaneous nucleation
Since the relative importance of branching and spontaneous nucleation for bead-induced actin polymerization is not known, we have also studied a variant of the model in which spontaneous nucleation is the only source of new filaments. In Figure 3(a) and 3(b), we see that the results of this model are almost indistinguishable from those of the baseline model. Another variation of the model, with no spontaneous nucleation (see Supporting Material D), also differs only slightly from the baseline model. Thus there is no obvious way to differentiate spontaneous nucleation from branching on the basis of the data considered here. Section 4.6 describes an experimental protocol that can distinguish between the nucleation modes.
Figure 3.
Model with only spontaneous nucleation. [G0] =2.2 μM, kbr = 0, ksp = 4.3 × 105 μM−2s−1, [Arpc] = 2 nM . Low [CP0] = 21 nM , high [CP0] = 52 nM . Low [Arp0] = 48 nM , high [Arp0] = 96 nM.
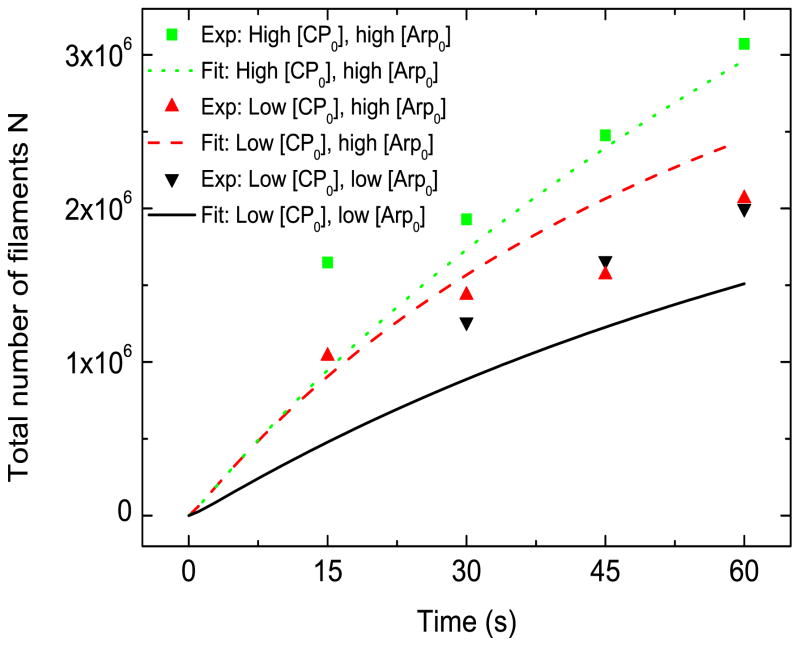
4.3 Model without [Arpc] term
We found that the [Arpc] term, in Eqs. (2) and (7) is needed to reproduce the small effect of [Arp2/3] on N. In Fig. 4, we present results for the case when the factor 1/([Arp] + [Arpc]) in Eqs. (2) and (7) is dropped. It is seen that in this case lowering [Arp0] shifts the high-Arp2/3 (dashed) curve away from the low-Arp2/3 (solid) curve, and the gap between them does not decrease with time. Both of these behaviors are inconsistent with the experimental findings. In contrast, in Figs. 3 and 4 where the [Arpc] correction is included, the calculated time courses of N for different [Arp0] eventually converge, despite an early-time difference.
Figure 4.
Model without [Arpc] term. [G0] =2.2 μM, kbr=18.5 μM−3s−1, ksp=1.0 × 105 μM−3s−1, [Arpc] = 2 nM. Low [CP0] = 21 nM , high [CP0] = 52 nM . Low [Arp0] = 48 nM , high [Arp0] = 96 nM.
This suggests that a factor other than Arp2/3 complex is the rate-limiting factor for nucleation, as pointed out by Akin and Mullins [13]. Instead, it is possible that the limited amount of the actin nucleator ActA attached to the bead surface is the rate-limiting factor. This contention is supported by previous work, which showed that the rate of motion of of certain viruses in limited by the release of actin filaments from nucleation-promoting factors [18]. Mechanical effects, as suggested by Ref. [13], could also be important. In Supporting Material E we discuss how such effects might influence the gel thickness.
4.4 How CP enhances actin polymerization and nucleation
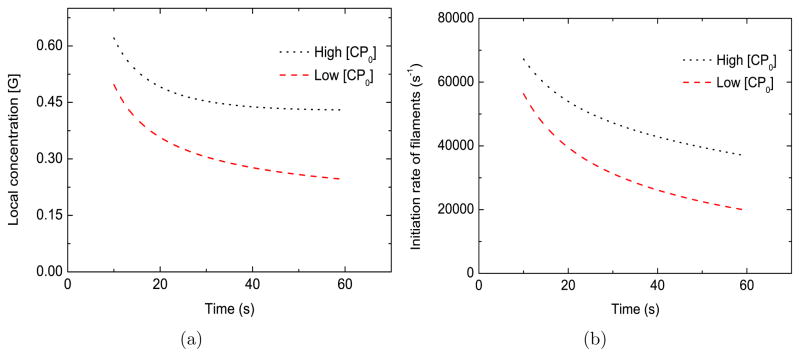
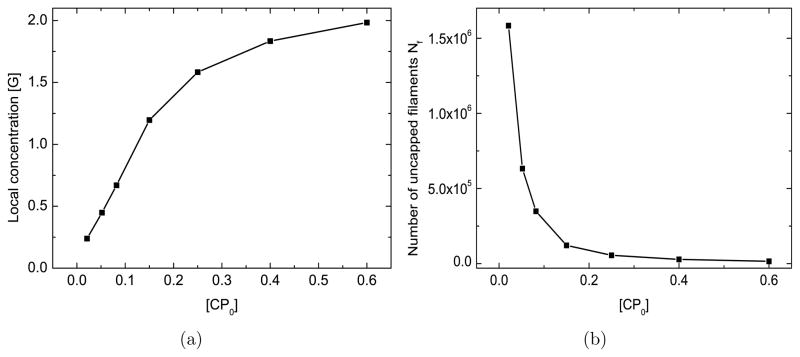
In this and the following subsections, we investigate the basic biophysical mechanisms embodied in the model and make proposals for future experiments. To simplify the theoretical analysis, we keep the bulk concentrations at constant values ( ). The heart of the mechanism by which CP enhances motility and filament number is seen in Fig. 5(a), where the local monomer concentration [G] at the bead increases by approximately 80% when [CP0] increases from 21 nM to 52 nM. The dependence of the asymptotic value of [G] on [CP ], shown in Fig. 6(a), shows a monotonic climb. This will accelerate elongation. The increase occurs because CP reduces the number of uncapped filaments (see Fig. 6(b)), which would otherwise have lowered the local actin concentration [G] by consuming monomers. Since the nucleation rate of new actin filaments increases strongly with [G], CP increases this rate as well, as shown in Fig. 5(b). This mechanism for CP enhacing motility and filament nucleation makes only two key assumptions: that the number of uncapped filaments is reduced by CP, and that the nucleation rate grows with the free-actin concentration. The same basic mechanism is present in the spontaneous-nucleation model (SN) discussed above and the branching-only model discussed in Supporting Material B, both of which also fit the data well.
Figure 5.
Effect of [CP] on the local monomer concentration [G] (frame a) and the initiation rate of new actin filaments (frame b). [G0] = 2.2 μM, kbr=0.65 μM−2s−1, ksp=1.0 × 104 μM−2s−1, [Arpc] = 2 nM , [Arp0] = 96 nM . Low [CP0] = 21 nM , high [CP0] = 52 nM.
Figure 6.
Effect of [CP ] on asymptotic values of [G] (frame a) and Nf (frame b). [G0] = 2.2 μM, kbr=0.65μM−2s−1, ksp=1.0 × 104 μM−2s−1, [Arpc] = 2 nM, [Arp0] = 96 nM.
Our finding that CP reduces the number of uncapped filaments and increases the filament elongation rate differs from that of Ref. [13], where the number of uncapped filaments and the elongation rate were found to be independent of CP. We believe the reason for the difference is that Ref. [13] used the global CP and actin concentrations to evaluate the number of uncapped filaments and the elongation rate, while here we use the local concentrations at the bead.
It is not clear whether the mechanism is important for the smaller beads considered by Ref. [13]. The use of a more complex motility medium and the lack of measured N values for this case make it difficult to assess the extent of local depletion of proteins around the beads.
4.5 The characteristic CP concentration for raising the free-actin concentration
For interpreting the results of motility experiments, it is useful to estimate the characteristic value CPc of [CP0] where the local actin concentration at the bead reaches half the bulk value: [G] ≥ 0.5[G0]. To calculate CPc, we consider relatively late times, when the number of uncapped filaments has reached steady state (i.e., dNf /dt = 0). We obtain from Eq. (2)
| (12) |
if we assume that i) branching dominates over spontaneous nucleation and ii) the decay term is negligible. We define a dimensionless filament number nf = konNf/4πr0Dm, so that (from Eq. 5) [G] = [G0]/(1 + nf), and nf = 1 corresponds to [G] = 0.5[G0]. Then Eq.(6) can be rewritten as
| (13) |
From Eq.(7) (again ignoring the spontaneous nucleation term), we obtain
| (14) |
From our numerical results, the first term of the denominator is negligible when 0.25[G0] ≤ [G] ≤ 0.5[G0], so we obtain
| (15) |
Putting nf = 1 and Eqs. (13),(15) into (12), we obtain
| (16) |
For our parameters, and [Arp0] = 96 nM, Eq. (16) yields [CP0] ≃ 0.14 μM. This theoretical estimate is essentially identical to the numerically obtained value [CP0] = 0.14 μM value corresponding to [G] = 1.1 μM = 0.5[G0] in Fig. 6(a).
If we assume that the currents of Arp2/3 and CP to the bead are close to being diffusion-limited, then this result is consistent with the physical intuition that the rate of CP flow to the bead should at least equal the rate Arp2/3 flow, so that all filaments will eventually be capped. Eq.(16) is also consistent with the finding of Loisel et al [5] that the optimal [CP0] value and [Arp0] values for actin-propelled pathogens are nearly the same.
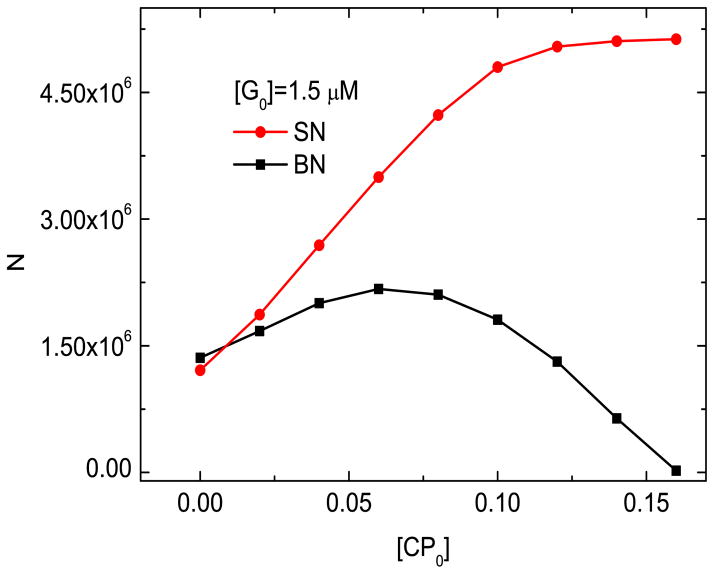
4.6 A method for distinguishing branching from spontaneous nucleation in the growth of actin networks
In Sections 4.1 and 4.2, we showed that the the available data does not determine whether branching nucleation (BN) or spontaneous nucleation (SN) dominate. Here we show that modifying the design of the experiments of Ref. [13] to measure the total number of filaments at t = 60 s as a function of [CP0], using lower [G0] values, can differentiate between the BN and SN models. Figure 7 shows the number of filaments as a function of [CP0] for the two models. In the SN model, N increases monotonically with [CP0]. In contrast, in the BN model N increases to a peak but diverges from the SN results by turning over and eventually approaching zero at long times. The reason for these differences is the following: in the BN model, dNf/dt = keff Nf, where keff = kbr[Arp]([G] − Gc)2/([Arpc] + [Arp]) − kcap[CP ] − kd. If [CP ] is large enough, keff will be negative and Nf will thus approach zero at long times, at which point no new filaments can be initiated by branching. However, in the SN model,
Figure 7.
N vs [CP0] in branching nucleation (BN) and spontaneous nucleation (SN) models. kbr=0.65 μM−2s−1, ksp=1.0 × 104 μM−2s−1.
| (17) |
Adding Eq. (17) to Eq. (3), we obtain dN/dt = ksp[Arp]([G] − Gc)2/([Arpc] + [Arp]) − kd(Nf + Nc). If the small kd term is ignored, this quantity depends on [CP ] only via [G]; since [G] increases with increasing [CP ], so will dN/dt.
5 Discussion
We have performed a quantitative modeling study of the effect of CP and Arp2/3 complex on motility and and actin filament nucleation, using a model based on the local concentrations of key proteins at biomimetic beads. The main conclusions are the following:
Increasing CP concentration leads to a larger number of filaments because filaments are nucleated at a higher rate. The mechanism is that the nucleation rate of actin filaments grows with the local monomer concentration, which is increased by lowering the number of uncapped filaments through increased CP. A kinetic model based on this effect fits the experimental data of Ref. [13] well, with only one adjustable parameter. The characteristic CP concentration CPc where the local actin concentration at the bead reaches half the bulk value is related to the bulk Arp2/3 complex concentration [Arp0] as follows: CPc ~ 1.5[Arp0]. This estimate is roughly consistent with the concentrations at which Listeria was found to reach its maximum velocity in Ref. [5].
In order to reproduce the relatively small effect of Arp2/3 complex on the number of filaments, it was necessary to introduce a term based on [Arpc] that weakens the Arp2/3-dependence of the nucleation rates. This suggests that a factor other than Arp2/3 complex is rate-limiting for actin filament nucleation.
We have suggested a feasible method of determining whether spontaneous nucleation (SN) or branching nucleation (BN) is the dominant mechanism of filament initiation in the bead polymerization assay. This method is based on measuring the number of filaments N as a function of [CP0]. For SN, N increases monotonically, but for BN, it reaches a peak and turns over.
Our study reinforces findings from previous calculations of actin polymerization in lamellipodia and filopodia, that used either rate equations and analytic theory [7,8] or explicit 2d or 3d modeling of the actin network [9–12,39]. These works found that the actin monomer concentration is depleted near the leading edge; this effect is reduced by capping protein. Ref. [7] showed that depletion can be understood straightforwardly from the density nf of uncapped filaments per unit area at the leading edge. If one treats the lamellipodium as a rectangular strip of width W (perpendicular to the leading edge) having a density (per unit area) of free filaments nf at its front, the free-monomer density is reduced by a factor 1/(1 + konWnf/Dm). Here we have treated a similar physical effect in the geometry of a biomimetic spherical bead, where the reduction factor [19] is 1/(1 + konr0nf /Dm). Having access to published curves of filament number and subunit count [13] in a biomimetic system allowed us to quantitatively establish effect of capping protein on the actin monomer concentration and actin filament nucleation, in a system with few unknown parameter values.
The importance of the depletion effects for intracellular pathogens such at Listeria depends on the number of free filaments at the pathogen surface. It is clear from the form of the reduction factor above that the depletion effects will be significant if . We treat Listeria as as sphere of radius r0 ~ 1μm. Using the same kinetic constants as for the lamellipodium case, we obtain . We do not know the value of nf for Listeria, but if it is comparable to the measured value for lamellipodia the depletion effects will be important.
How could one experimentally distinguish between the present local-depletion model and the monomer gating model of Ref. [13]? The clearest distinction would be obtained by direct measurement of the protein concentrations near the bead, which should be much lower than the bulk concentrations if the local-depletion model holds. This could be accomplished via fluorescence correlation spectroscopy (FCS) [40], using a laser spot placed near the bead together with functional fluorescently labeled proteins. Because FCS uses the high-frequency components of the fluorescence signal, one can in principle separate the proteins in solution from those bound to the bead. Nevertheless, the experiment would be challenging, since the background concentration of proteins bound to the bead is much higher than that in solution. This difficulty might be remedied by pulse-chase experiments in which the color of the fluorophore is abruptly changed. If the imaging were performed quickly enough, the ratio of bound to free protein of the second color could be reduced significantly.
Alternatively, one could photobleach circular regions containing the beads, and measure the fluorescence recovery. The earliest stages of recovery would be dominated by actin monomers diffusing in from the edge of the bleached region. The initial magnitude of the recovery would thus depend on the monomer concentration at the edge. If one varied the radius of the photobleached region, one could then obtain an estimate of monomer concentration as a function of distance, and see how it varies with CP. Performing such measurements would require using a plane of focus through the bead, and eliminating out-of-focus light. This could be accomplished by using confocal microscopy to image beads attached to a surface.
Supplementary Material
Acknowledgments
We appreciate informative conversations with Dyche Mullins and John Cooper. This work was supported by the National Institutes of Health under Grant Number R01 GM107667.
References
- 1.Carlier Marie-France, Pantaloni Dominique. Control of actin dynamics in cell motility. Journal of molecular biology. 1997;269(4):459–467. doi: 10.1006/jmbi.1997.1062. [DOI] [PubMed] [Google Scholar]
- 2.Pantaloni Dominique, Le Clainche Christophe, Carlier Marie-France. Mechanism of actin-based motility. Science. 2001;292(5521):1502–1506. doi: 10.1126/science.1059975. [DOI] [PubMed] [Google Scholar]
- 3.Le Clainche Christophe, Carlier Marie-France. Regulation of actin assembly associated with protrusion and adhesion in cell migration. Physiological reviews. 2008;88(2):489–513. doi: 10.1152/physrev.00021.2007. [DOI] [PubMed] [Google Scholar]
- 4.Hug Christopher, Jay Patrick Y, Reddy Indira, McNally James G, Bridgman Paul C, Elson Elliot L, Cooper John A. Capping protein levels influence actin assembly and cell motility in dictyostelium. Cell. 1995;81(4):591–600. doi: 10.1016/0092-8674(95)90080-2. [DOI] [PubMed] [Google Scholar]
- 5.Loisel Thomas P, Boujemaa Rajaa, Pantaloni Dominique, Carlier Marie-France. Reconstitution of actin-based motility of listeria and shigella using pure proteins. Nature. 1999;401(6753):613–616. doi: 10.1038/44183. [DOI] [PubMed] [Google Scholar]
- 6.Edwards Marc, Zwolak Adam, Schafer Dorothy A, Sept David, Dominguez Roberto, Cooper John A. Capping protein regulators fine-tune actin assembly dynamics. Nature Reviews Molecular Cell Biology. 2014;15(10):677–689. doi: 10.1038/nrm3869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mogilner Alex, Edelstein-Keshet Leah. Regulation of actin dynamics in rapidly moving cells: a quantitative analysis. Biophysical journal. 2002;83(3):1237–1258. doi: 10.1016/S0006-3495(02)73897-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mogilner Alexander, Rubinstein Boris. The physics of filopodial protrusion. Biophysical journal. 2005;89(2):782–795. doi: 10.1529/biophysj.104.056515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee Kun-Chun, Liu Andrea J. New proposed mechanism of actin-polymerization-driven motility. Biophysical journal. 2008;95(10):4529–4539. doi: 10.1529/biophysj.108.134783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hu Longhua, Papoian Garegin A. Mechano-chemical feedbacks regulate actin mesh growth in lamellipodial protrusions. Biophysical journal. 2010;98(8):1375–1384. doi: 10.1016/j.bpj.2009.11.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hu Longhua, Papoian Garegin A. How does the antagonism between capping and anti-capping proteins affect actin network dynamics? Journal of Physics: Condensed Matter. 2011;23(37):374101. doi: 10.1088/0953-8984/23/37/374101. [DOI] [PubMed] [Google Scholar]
- 12.Hu Longhua, Papoian Garegin A. Molecular transport modulates the adaptive response of branched actin networks to an external force. The Journal of Physical Chemistry B. 2013;117(42):13388–13396. doi: 10.1021/jp405179e. [DOI] [PubMed] [Google Scholar]
- 13.Akin Orkun, Dyche Mullins R. Capping protein increases the rate of actin-based motility by promoting filament nucleation by the Arp2/3 complex. Cell. 2008;133(5):841–851. doi: 10.1016/j.cell.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Machesky Laura M, Dyche Mullins R, Higgs Henry N, Kaiser Donald A, Blanchoin Laurent, May Robin C, Hall Margaret E, Pollard Thomas D. Scar, a wasp-related protein, activates nucleation of actin filaments by the arp2/3 complex. Proceedings of the National Academy of Sciences. 1999;96(7):3739–3744. doi: 10.1073/pnas.96.7.3739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pollard Thomas D, Borisy Gary G. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112(4):453–465. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 16.Beltzner Christopher C, Pollard Thomas D. Pathway of actin filament branch formation by arp2/3 complex. Journal of Biological Chemistry. 2008;283(11):7135–7144. doi: 10.1074/jbc.M705894200. [DOI] [PubMed] [Google Scholar]
- 17.Smith Benjamin A, Padrick Shae B, Doolittle Lynda K, Daugherty-Clarke Karen, Corrêa Ivan R, Xu Ming-Qun, Goode Bruce L, Rosen Michael K, Gelles Jeff. Three-color single molecule imaging shows WASP detachment from Arp2/3 complex triggers actin filament branch formation. Elife. 2013;2:e01008. doi: 10.7554/eLife.01008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Co Carl, Wong Derek T, Gierke Sarah, Chang Vicky, Taunton Jack. Mechanism of actin network attachment to moving membranes: barbed end capture by N-WASP WH2 domains. Cell. 2007;128(5):901–913. doi: 10.1016/j.cell.2006.12.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dickinson Richard B, Purich Daniel L. Diffusion rate limitations in actin-based propulsion of hard and deformable particles. Biophysical journal. 2006;91(4):1548–1563. doi: 10.1529/biophysj.106.082362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lanni F, Ware BR. Detection and characterization of actin monomers, oligomers, and filaments in solution by measurement of fluorescence photobleaching recovery. Biophysical journal. 1984;46(1):97–110. doi: 10.1016/S0006-3495(84)84002-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Carlsson AE, Wear MA, Cooper JA. End versus side branching by Arp2/3 complex. Biophysical journal. 2004;86(2):1074–1081. doi: 10.1016/S0006-3495(04)74182-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dominguez Roberto, Holmes Kenneth C. Actin structure and function. Annual review of biophysics. 2011;40:169. doi: 10.1146/annurev-biophys-042910-155359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pollard Thomas D. Rate constants for the reactions of ATP-and ADP-actin with the ends of actin filaments. The Journal of cell biology. 1986;103(6):2747–2754. doi: 10.1083/jcb.103.6.2747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Carlsson Anders E. Growth of branched actin networks against obstacles. Biophysical journal. 2001;81(4):1907–1923. doi: 10.1016/S0006-3495(01)75842-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bieling P, Li TD, Mullins RD, Fletcher DA. Molec Biol Cell. Vol. 23. Amer. Soc. Cell Biol; 8210 Woodmont Ave, Ste. 750, Bethesda, MD 20814-2755 USA: 2012. The mechanobiochemistry of dendritic actin network assembly. [Google Scholar]
- 26.Zimmermann Juliane, Falcke Martin. On the existence and strength of stable membrane protrusions. New Journal of Physics. 2013;15(1):015021. [Google Scholar]
- 27.Zimmermann Juliane, Falcke Martin, Aspenstrom Pontus. Formation of transient lamellipodia. PLoS one. 2014;9(2):e87638. doi: 10.1371/journal.pone.0087638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Risca Viviana I, Wang Evan B, Chaudhuri Ovijit, Chia Jia Jun, Geissler Phillip L, Fletcher Daniel A. Actin filament curvature biases branching direction. Proceedings of the National Academy of Sciences. 2012;109(8):2913–2918. doi: 10.1073/pnas.1114292109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mogilner Alex, Oster George. Force generation by actin polymerization ii: the elastic ratchet and tethered filaments. Biophysical journal. 2003;84(3):1591–1605. doi: 10.1016/S0006-3495(03)74969-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Enculescu Mihaela, Falcke Martin. Actin-based propulsion of spatially extended objects. New Journal of Physics. 2011;13(5):053040. [Google Scholar]
- 31.Falcke M, Zimmermann J. Polymerization, bending, tension: What happens at the leading edge of motile cells? The European Physical Journal Special Topics. 2014;223(7):1353–1372. [Google Scholar]
- 32.Banigan Edward J, Lee Kun-Chun, Liu Andrea J. Control of actin-based motility through localized actin binding. Physical biology. 2013;10(6):066004. doi: 10.1088/1478-3975/10/6/066004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Noireaux V, Golsteyn RM, Friederich Evelyne, Prost J, Antony C, Louvard D, Sykes C. Growing an actin gel on spherical surfaces. Biophysical journal. 2000;78(3):1643–1654. doi: 10.1016/S0006-3495(00)76716-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Peskin Charles S, Odell Garrett M, Oster George F. Cellular motions and thermal fluctuations: the Brownian ratchet. Biophysical journal. 1993;65(1):316–324. doi: 10.1016/S0006-3495(93)81035-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cooper John A, Pollard Thomas D. Effect of capping protein on the kinetics of actin polymerization. Biochemistry. 1985;24(3):793–799. doi: 10.1021/bi00324a039. [DOI] [PubMed] [Google Scholar]
- 36.Millard Thomas H, Sharp Stewart J, Machesky Laura M. Signalling to actin assembly via the WASP (Wiskott-Aldrich syndrome protein)-family proteins and the Arp2/3 complex. Biochem J. 2004;380:1–17. doi: 10.1042/BJ20040176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Berg Howard C. Random Walks in Biology. Princeton University Press; 1993. [Google Scholar]
- 38.Wear Martin A, Cooper John A. Capping protein: new insights into mechanism and regulation. Trends in biochemical sciences. 2004;29(8):418–428. doi: 10.1016/j.tibs.2004.06.003. [DOI] [PubMed] [Google Scholar]
- 39.Schaus Thomas E, Borisy Gary G. Performance of a population of independent filaments in lamellipodial protrusion. Biophysical journal. 2008;95(3):1393–1411. doi: 10.1529/biophysj.107.125005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Elson Elliot L. Fluorescence correlation spectroscopy: past, present, future. Biophysical journal. 2011;101(12):2855–2870. doi: 10.1016/j.bpj.2011.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.