Soft Polydimethylsiloxane Elastomers from Architecture-driven Entanglement Free Design

Abstract

We fabricate soft, solvent-free polydimethylsiloxane (PDMS) elastomers by crosslinking bottlebrush polymers rather than linear polymers. We design the chemistry to allow commercially available linear PDMS precursors to deterministically form bottlebrush polymers, which are simultaneously crosslinked, enabling a one-step synthesis. The bottlebrush architecture prevents the formation of entanglements, resulting in elastomers with precisely controllable elastic moduli from ~1 to ~100 kPa, below the intrinsic lower limit of traditional elastomers. Moreover, the solvent-free nature of the soft PDMS elastomers enables a negligible contact adhesion compared to commercially available silicone products of similar stiffness. The exceptional combination of softness and negligible adhesiveness may greatly broaden the applications of PDMS elastomers in both industry and research.

Polydimethylsiloxane (PDMS) elastomers are widely used in both industry and research; for example, they are contained in personal care products, applied as sealants, and used as materials for microfluidic devices and stretchable electronics.^{[1, 2]} PDMS elastomers are typically formed by crosslinking entangled linear polymers; such conventional elastomers are intrinsically stiffer than a threshold value set by the density of entanglements that act as effective crosslinks. Making PDMS elastomers softer would allow their deformation with less energy, enabling uses that require them to easily comply with the shape of objects they contact, broadening potential applications. To make the elastomer softer, the density of crosslinks must be lowered; this goal can be easily achieved by swelling the elastomer with solvent. However, the solvent may leach out; moreover, such a PDMS gel is adhesive, which is unacceptable for applications requiring the separation of PDMS from another surface. Therefore, silicone gels intrinsically cannot be soft and nonsticky. The stickiness is lower for elastomers without solvents; however, conventional ‘dry’ PDMS elastomers cannot have shear moduli lower than 200 kPa, the threshold set by entanglements.^{[3, 4]} A multiple-step, complex chemical synthesis circumvents this threshold by avoiding the entanglements, but results in elastomers with uncontrollable storage and loss moduli.^[5] It remains a challenge to develop soft, solvent-free PDMS elastomers with controllable viscoelastic properties through a simple approach.

Here we report soft PDMS elastomers fabricated by crosslinking bottlebrush rather than linear polymers. The bottlebrush architecture prevents the formation of entanglements, enabling soft, yet solvent-free PDMS elastomers with precisely controllable elastic moduli ranging from ~1 to ~100 kPa, much softer than typical PDMS elastomers. We find that the elastic moduli are in excellent agreement with theoretical predictions based on classical rubber elasticity: The modulus is linearly proportional to the density of crosslinking chains. Remarkably, in addition to prescribed stiffness, the bottlebrush structure enables independent control over the loss modulus. We measure the difference in adhesiveness between the soft PDMS elastomers and commercial silicone products of similar stiffness. We find that the soft PDMS elastomers are far less adhesive due to their significantly smaller amount of uncrosslinked, free molecules as quantified by Soxhlet extraction. Importantly, the fabrication of soft PDMS elastomers is a one-step process, as easy as that for commercial silicone elastomer kits.

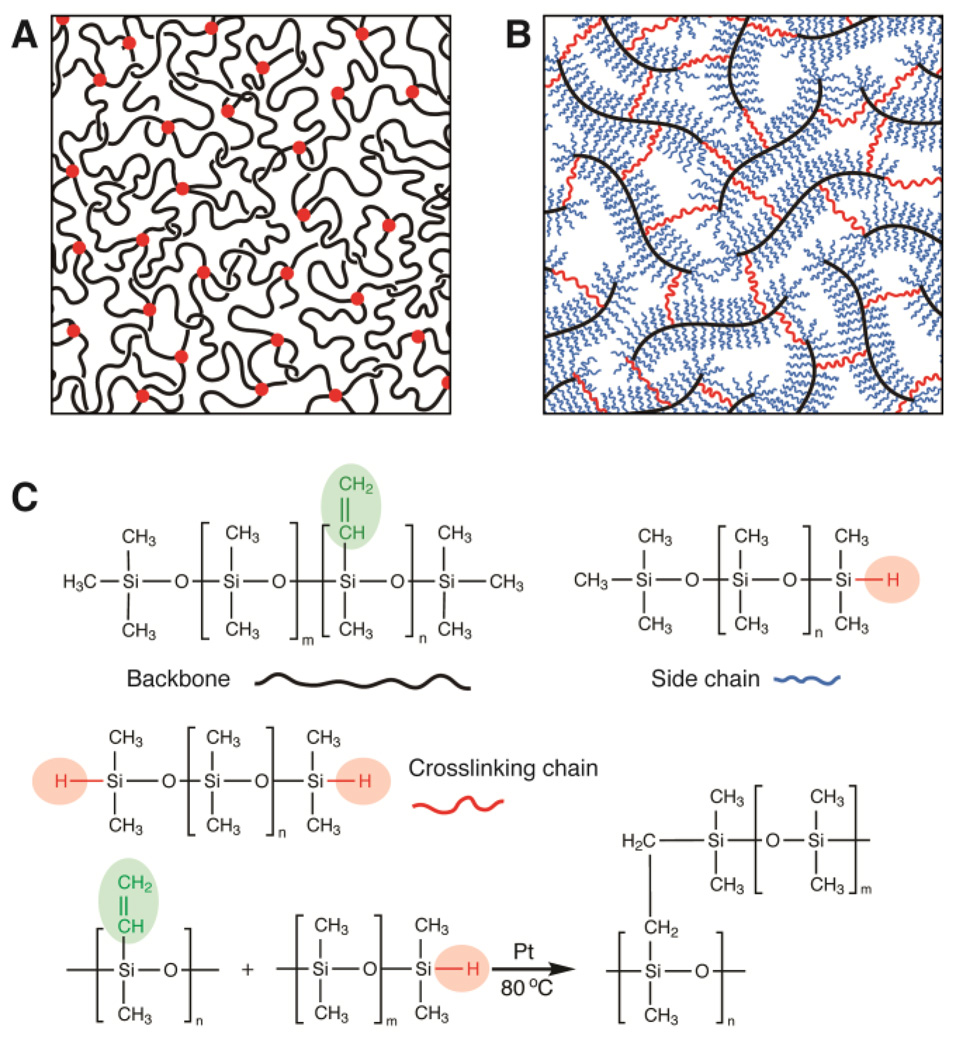
To overcome the intrinsic stiffness threshold of elastomers, the density of entanglements must be reduced. To this end, the entanglement molecular weight must be significantly increased. However, this requirement is impossible to meet for linear polymers in a melt, as they entangle at relatively low molecular weight.^{[4, 6, 7]} An elastomer formed by such a linear polymer melt, containing both entanglements and covalent crosslinks, is illustrated by Figure 1A. For linear PDMS polymers the entanglement molecular weight is ~10⁴ g/mol.^[3] Unlike a linear polymer, a bottlebrush molecule has many relatively short linear side chains chemically attached to a long linear backbone.^[8] Such a bottlebrush molecule can be considered a ‘thick’ linear polymer; it has an entanglement molecular weight easily exceeding 10⁷ g/mol, orders of magnitude higher than that of linear polymers (SI text). Therefore, using bottlebrush polymers rather than linear polymers enables the elimination of entanglements in a polymer melt. An elastomer formed by such a bottlebrush polymer melt, containing covalent crosslinks but no entanglements, is illustrated by Figure 1B.

Figure 1. Molecular design of soft elastomers.

(A) Schematic view of a conventional elastomer formed by crosslinking linear polymers: Red circles denote chemical crosslinks, and knots denote entanglements. (B) Schematic view of a soft elastomer fabricated by crosslinking bottlebrush polymers: A multifunctional linear polymer chain acts as backbone (black); it is grafted by many side chains (blue), which are relatively short, mono-functional linear polymers carrying one reactive site, and crosslinking chains (red), which are di-functional linear polymers. (C) Three types of precursor reactive linear PDMS polymers form the structure illustrated by (B) through hydrosilylation reactions with the aid of platinum catalyst at 80°C.

We synthesize bottlebrush PDMS polymers through hydrosilylation,^[9] which proceeds by the addition of silicone hydride to unsaturated vinyl groups. We use a multiple-functional linear PDMS copolymer, trimethylsiloxy terminated vinylmethylsiloxane–dimethylsiloxane, as the backbone of bottlebrush molecules; this copolymer carries about 300 methyl-vinyl siloxane units, allowing multiple hydrosilylation reactions per chain. To form a bottlebrush molecule, many mono-functional linear PDMS polymers, mono-hydride terminated polydimethylsiloxane, each carrying one terminal hydride group, are grafted to a backbone, acting as side chains. To simultaneously crosslink bottlebrush molecules, we use di-functional linear PDMS polymers, dihydride-terminated polydimethysiloxane, as covalent crosslinks; they bridge the backbones of bottlebrush molecules to form a network. Importantly, the copolymer structure of the backbone allows its miscibility with other PDMS polymers; half of the units in the backbone are dimethylsiloxane groups which favorably interact with other PDMS units on both the side chains and crosslinking polymers.^[10] The reactions for forming and crosslinking bottlebrush polymers are both hydrosilylations, as shown in Figure 1C; this feature enables a one-step synthesis of soft PDMS elastomers.

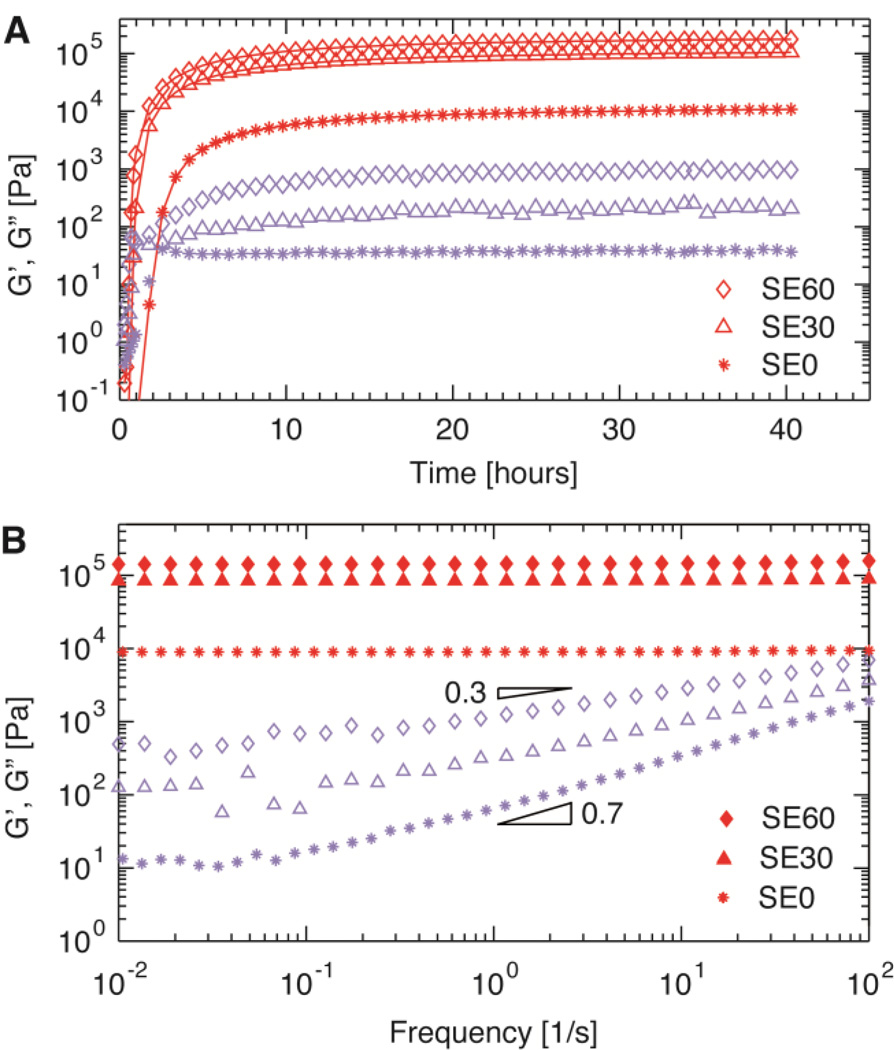
To fabricate soft PDMS elastomers, we mix the three types of precursor linear PDMS polymers at prescribed ratios, add platinum catalyst, and elevate the temperature to 80°C to accelerate polymerization. To determine the kinetics of polymerization, we measure the viscoelastic properties of the mixture in situ using a rheometer. The shear storage modulus increases significantly within the first a few hours, exceeding the shear loss modulus, as shown in Figure 2A and S1. After about 40 hours, the storage modulus reaches a stable value.

Figure 2. Rheological and mechanical properties.

(A) Dependence of viscoelastic properties of representative soft PDMS elastomers on curing time measured at 80°C, 1 Hz, and a fixed strain of 0.5%. (B) Frequency dependence of the storage (red symbols, G') and loss (blue symbols, G″) moduli of representative soft elastomers measured at 20°C at a fixed strain of 0.5%. Different symbols show soft elastomers corresponding to different number of crosslinking chains per bottlebrush molecule: Diamonds – SE60, triangles – SE30, and stars – SE0. Recipe of each sample is listed in Table 1.

The elastomers exhibit nearly frequency-independent shear storage moduli, reminiscent of a perfect rubber.^[4] Upon changing oscillatory shear frequency by four orders of magnitude, from 10⁻² to 10² Hz, the amplitude of storage moduli varies by less than 10%, as shown for different samples in Figure 2B and S2. Therefore, we take the value of G' at the lowest frequency, 10⁻² Hz, as the equilibrium modulus, G, of the network. Remarkably, the values of G for all elastomers formed by crosslinking bottlebrush PDMS are lower than the plateau modulus, 200 kPa, of entangled linear PDMS melts.

To explore the range of moduli achievable for soft PDMS elastomers, we vary the density of crosslinks by adjusting the number of crosslinking chains. To keep the molar ratio between vinyl and hydride groups constant at 2:1 as we increase the amount of di-functional crosslinking chains, we simultaneously reduce the number of mono-functional side chains. This method ensures the same condition for polymerization of different samples. Moreover, it ensures an excess amount of vinyl groups; this is important for completion of the crosslinking process which slows at the end of polymerization due to increases in steric hindrance from the densely grafted side chains. By tuning the concentration of crosslinking chains, we successfully produce a wide range of elastic moduli from ~1 to ~100 kPa, as listed in Table 1.

Table 1.

Recipe for fabrication of soft PDMS elastomers presented as molar ratio of each polymer component. The mixture is polymerized with the addition of Karstedt’s Catalyst at concentration of 5 µl/g. Equilibrium shear storage modulus is taken as the measured value at oscillatory frequency of 0.01Hz, temperature of 20°C, and fixed strain of 0.5%.

Sample name	Backbone (50,000 g/mol)	Side chain (4,750 g/mol)	Crosslinking chain (17,200 g/mol)	Extension chain (10,000 g/mol)	Shear storage modulus (Pa)	Gel fraction (wt%)
SE60	1	30	60	0	132,000	93.8
SE30	1	90	30	0	84,100	–
SE10	1	130	10	0	34,700	85.6
SE5	1	140	5	0	20,400	80.3
SE1	1	148	1	0	11,800	–
SE0	1	150	0	0	8,940	78.0
SEL	1	150	0	150	7,430	76.2

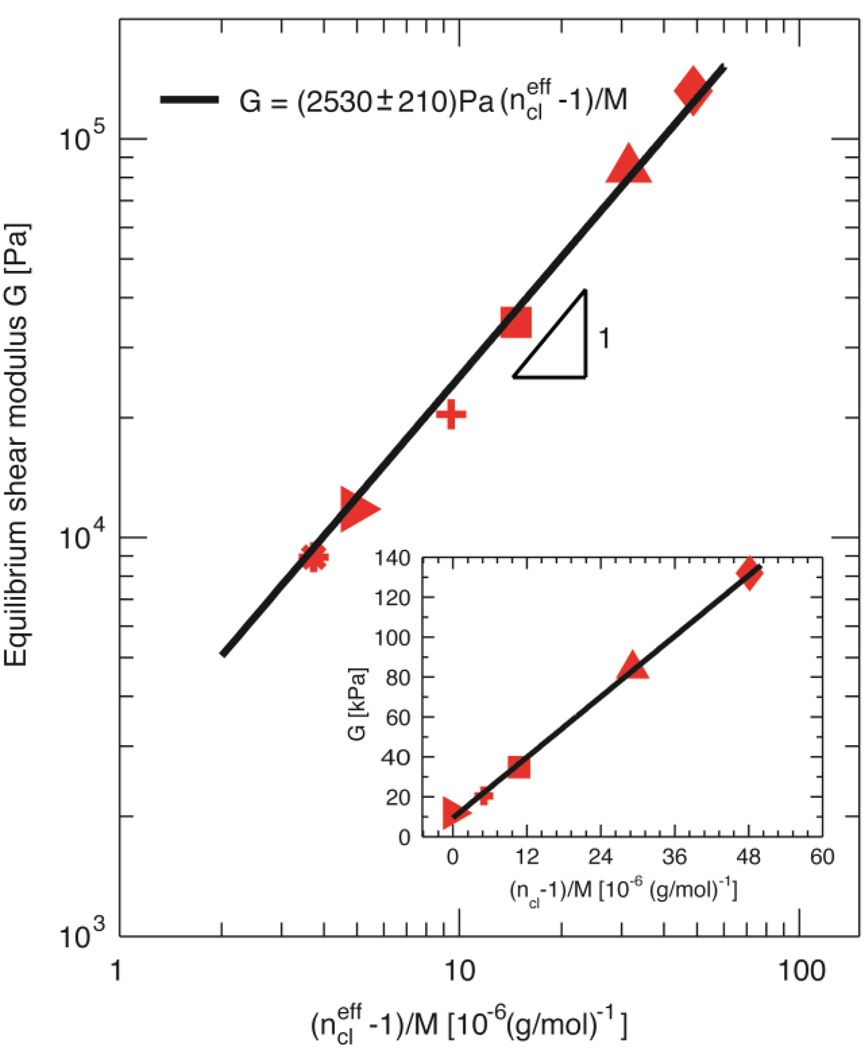
To quantitatively understand the dependence of elastic moduli on concentration of crosslinking chains for soft PDMS elastomers, we apply the classic estimate for elasticity of a rubber without entanglements.^[11] The equilibrium modulus G of an unentangled network is proportional to the concentration of elastically effective network strands under the assumption of affine deformation where the relative deformation of each network strand is the same as the macroscopic relative deformation imposed on the whole network. This assumption is valid when the ends of network strands are attached to a fixed elastic background. In real networks, however, the ends of network strands are attached to other network strands at crosslinks. These crosslinks are not fixed in space; instead, they fluctuate around their average positions. These fluctuations lead to reduced stretching of the network strands; as a result, the shear modulus is lower than that of an affine network. Indeed, it is described by the phantom network model: G = k_BT(ν−μ), where k_B is the Boltzmann constant, T is absolute temperature, ν and μ are the number densities of elastically effective network strands and crosslinks respectively.^{[4, 12]} To estimate the relation between ν, µ and the number density of crosslinking chains, we consider a soft PDMS elastomer with on average n_cl fully reacted, bridging crosslinking chains per bottlebrush molecule. These di-functional crosslinking chains contribute 2n_cl crosslinks, dividing the backbone of the bottlebrush molecules into 2n_cl−1 network strands. Taking into account that the crosslinking chains themselves are network strands, there are 3n_cl−1 network strands and 2n_cl crosslinks per bottlebrush molecule (SI text and Figure S3). Therefore, the modulus of a soft PDMS elastomer is expected to be

$$G=k_{B}T(\nu -\mu )=k_{B}T\rho (n_{cl}-\mathit{1})/M,$$ (1)

in which ρ = 0.97 g/cm³ is the density of PDMS,^[13] and M is the mass of the bottlebrush molecule that includes backbone polymer, side chain, and crosslinking chain.

To test this estimate, we plot the modulus of soft elastomers as a function of (n_cl−1)/M as suggested by equation (1). Consistent with the prediction of equation (1), we find that the modulus is linearly proportional to the number of crosslinking chains per bottlebrush molecule, as shown by the solid line in the inset of Figure 3. The slope of this linear dependence, 2530±210 Pa, is in good agreement with the predicted value, k_BTρ/(10⁶ g/mol) = 2400 Pa, corresponding to the modulus for one crosslinking chain per PDMS bottlebrush molecule of molecular weight 10⁶ g/mol. However, the modulus is still finite when there is on average one crosslinking chain per brush molecule, appearing inconsistent with the prediction from equation (1). This discrepancy suggests the possibility of di-functional chains – crosslinking chains in the commercially available mono-functional side chains. To estimate the fraction of these di-functional chains, we measure the equilibrium modulus of sample SE0 that contains only backbone polymers and side chains with molar ratio 1:150. Its modulus is G=8940 Pa, which gives the number fraction of di-functional polymers in side chains: f_ip = [GM/(ρk_BT)+1]/n_sc = 2.56×10⁻², where n_sc = 150 is the number of side chains per bottlebrush molecule. Including these di-functional chains, we calculate the effective number of fully reacted, bridging crosslinking chains per bottlebrush molecule using n_cl^eff ≡ n_cl+n_scf_ip, and re-plot the modulus of soft elastomers as a function of (n_cl^eff −1)/M. The re-plotted data is in good agreement with the classic phantom network prediction by equation (1), G = (2530±210) Pa (10⁶ g/mol) (n_cl^eff −1)/M, as shown by the red symbols and solid line in Figure 3.

Figure 3. Control over elastic modulus.

Dependence of equilibrium shear modulus on density of crosslinking chains for soft PDMS elastomers; the equilibrium moduli are taken as the values measured at frequency of 0.01 Hz, temperature of 20°C, and strain of 0.5%. The density of crosslinking chains is presented by (n_cl^eff −1)/M, in which M is the molecular weight of a bottlebrush molecule, and n_cl^eff is the effective number of crosslinking chains per bottlebrush molecule by taking into account contributions from crosslinking chains and “impurities” – a small fraction of di-functional crosslinking chains in commercially available side chains and chain extensions. Solid line represents the best fit using equation (1): G = (2530 Pa)/(10⁶ g/mol) [(n_cl^eff −1)/M]. Inset: The density of crosslinking chains calculated based on the assumption that all crosslinking chains successfully bridge neighboring bottlebrush molecules and there are no “impurities” in side chains. Solid line represents the best fit to the data: G = (2530 Pa)/(10⁶ g/mol) [(n_cl−1)/M] + 9370 Pa.

The excellent agreement between our measurements and the theoretical prediction (equation 1) suggests the modulus of soft PDMS elastomers can be tuned in a predictable way by changing the density of crosslinking chains. Indeed, we have successfully fabricated elastomers with shear modulus from ~7 to ~100 kPa using solely commercially available PDMS polymers through a one-step synthesis. This simple synthesis is in contrast to fabrication of soft elastomers using a multiple-step approach, which makes it more difficult to control the network architecture; as a result, the properties of the final product are less controllable.^{[5, 14]} Moreover, the storage modulus, G', of soft PDMS elastomers is 10² – 10³ times of the loss component, G″, at relatively low shear frequency of 1Hz, as shown in Figure 2B. The noise in the viscous modulus, G″, at very low frequencies, <0.1Hz, is due to the difficulty in precisely determining very small (<10⁻³) phase angle, δ = tan⁻¹(G″/G').^[15] The magnitude of the loss modulus for soft PDMS elastomers is determined by the amount and relative molecular weight distribution of network imperfections, which are mostly dangling chains. This correlation suggests that it may be possible to develop elastomers with controllable loss modulus by tuning the amount of network imperfections.

The ability to control the loss modulus is important for improving the fabrication of damping materials.^[16] In addition, recent evidence shows that the loss modulus of the substrate is likely to play an important role in determining cell behavior.^{[17, 18]} To change the amount of network imperfections, we introduce another type of commercially available linear polymer, monovinyl-monohydride terminated PDMS (Materials and Methods). These polymers effectively act as extension chains; they either directly graft to backbone molecules, or react with short, mono-functional side chains, forming longer side chains that can also graft to backbone molecules, as illustrated in Figure S4. Compared to sample SE0, in which the molar ratio of backbone to side chain is 1:150, in sample SEL the molar ratio of backbone, side chain, and extension chain is 1:150:150, as listed in Table 1. This recipe enables the average molecular weight of side chains in sample SEL to be three times that in sample SE0, as the molecular weight of an extension chain is twice that of a short side chain. Interestingly, compared to sample SE0, we find that the frequency-dependent loss modulus, G″(ω), for sample SEL is shifted up while maintaining a constant slope of ~0.75, as shown in Figure S5. In particular, at 1 Hz, the loss modulus increases by more than a factor of three from ~60 Pa to ~200 Pa. By contrast, the storage modulus of sample SEL is almost the same as that of sample SE0 as the density of crosslinking chains is nearly constant (SI Text and Figure S6). Therefore, tuning the amount of side chains enables control over the magnitude of loss modulus for soft PDMS elastomers without altering its frequency-dependent behavior.

Interestingly, the loss modulus for soft PDMS elastomer is very small, nearly two orders of magnitude smaller than that of storage modulus. Nevertheless, it is clearly measurable, and exhibits a power-law dependence on frequency: G′′(ω)~ ω^α. Remarkably, the value of the exponent α exhibits a strong dependence on the network elastic modulus; it increases from ~0.3 to ~0.7 as the elastic modulus decreases from ~100 kPa to ~10 kPa in the frequency range of 0.1 – 100 Hz, as shown by the empty symbols in Figure 2B; this behavior is in sharp contrast to that of conventional elastomers with a fixed value of the exponent (Figure S7). In soft PDMS elastomers, the reaction between multi-functional backbone polymers and di-functional crosslinking polymers can result in the formation of long dangling polymers that are only connected to the network framework on one end, as illustrated in Figure S8. The concentration of these long dangling polymers decreases exponentially with their length; moreover, they are constrained by the network mesh and exhibit logarithmically slow relaxation dynamics.^[7] The combination of the exponential and logarithmic forms yields a power-law stress relaxation in time, and thus a power-law dependence of loss modulus on frequency (SI text).^[19] The value of the exponent α describes the change in the magnitude of loss modulus with frequency: The less change of loss modulus, the smaller value of α. Indeed, the value of α is correlated to the crosslink density of soft PDMS elastomers. As the density of crosslinks increases, the network mesh size decreases; meanwhile, the probability of forming long dangling polymers becomes smaller, thus changing the length distribution of dangling polymers. However, the length of dangling polymers decreases slightly slower compared to the network mesh size due to the presence of side chains in soft PDMS elastomers; this behavior is in contrast to conventional elastomers where both the length of dangling polymers and the network mesh size decrease in the same manner (Figure S9 and SI text). As a result, for soft PDMS elastomers, the dangling polymers are subjected to more constraints at higher crosslink density, and it takes a longer time for dangling polymers to relax to equilibrium. Thus, within a certain time interval, the change in the amount of relaxed dangling polymers is less, reflected by a smaller change in the magnitude of loss modulus within the corresponding frequency range. Consequently, the value of the exponent α for the frequency dependence of loss modulus decreases with the increase of crosslink density, as shown in Figure S10.

Importantly, the value of α describes the relative rather than absolute change in the magnitude of loss modulus. For instance, for soft elastomer samples SE0 and SEL, both with nearly the same crosslink density, their relative change in loss modulus is the same, reflected by the same value of α~0.75; by contrast, the absolute magnitude of loss modulus is different due to different amount of dangling polymers, as shown in Figure S5. Nevertheless, the amount of long dangling polymers in soft PDMS elastomers is very small, as evidenced by very small loss tangent, tan δ = G″/G'~10⁻³, at frequency of 1Hz.

In addition to the effect of long dangling polymers, the exponent α may be also affected by the sol fraction, which is uncrosslinked, free polymers. By removing the sol fraction, the network mesh size becomes smaller; therefore, the dangling polymers should be subjected to more constraints from the network mesh and have slower relaxation dynamics, resulting in a smaller value of the exponent α. Indeed, the exponent α of loss modulus for a soft PDMS elastomer with storage modulus of 20 kPa decreases from 0.70 to 0.65 after the sol fraction extracted, as shown in Figure S11. Inspired by this correlation between sol fraction and the behavior of loss modulus, we also quantify the sol fraction for other soft PDMS elastomers. To do so, we perform Soxhlet extraction for 60 hours using acetone/n-hexane (50:50) to remove the unreacted polymers, and measure the remaining mass after drying (Materials and Methods and SI Methods).^[20] The ratio of the remaining to the initial mass is termed gel fraction. As the modulus for soft PDMS elastomers decreases from ~100 kPa to ~7 kPa, the gel fraction decreases from 94% (wt/wt) to 76%, as listed in Table 1; this decrease in gel fraction provides further support for the increase of the exponent of the frequency dependence of loss modulus when elastomers becomes softer. Interestingly, compared to commercial silicone products of similar moduli, we find that the soft PDMS elastomers have remarkably higher gel fraction. For instance, at G~ 7 kPa, the gel fraction is ~76% for soft PDMS elastomer, which is significantly higher than ~50% for Sylgard^® 184 PDMS products. Moreover, upon a decrease in stiffness, the gel fraction only reduces slightly for soft PDMS elastomers (Table 1); by contrast, it decreases dramatically to a very small value, ~2%, for Sylgard^® 184 PDMS elastomers (Table S1).

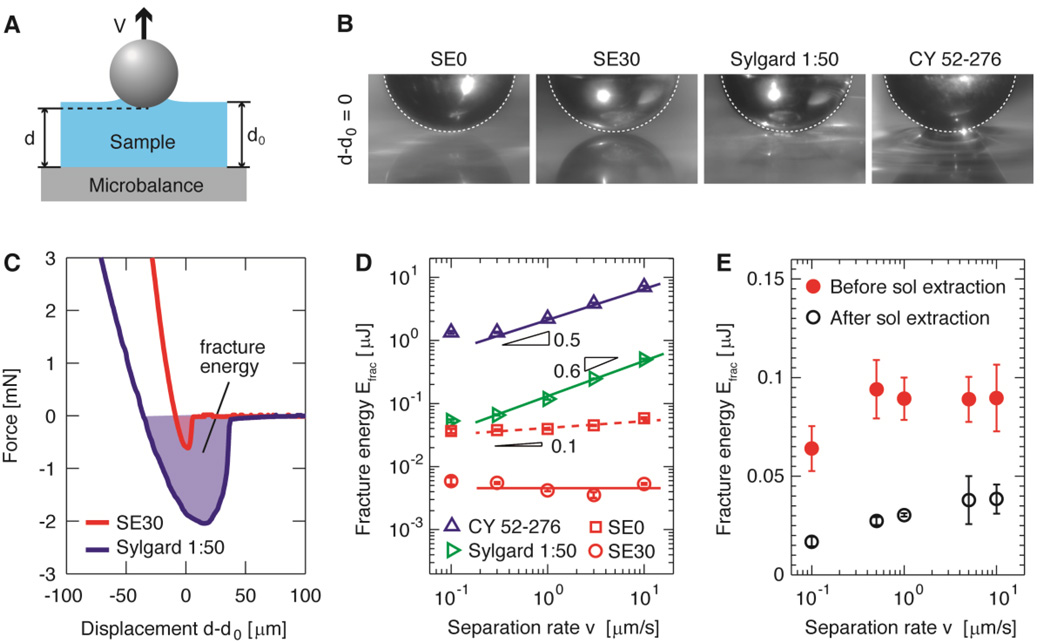
The importance of gel fraction in PDMS elastomers may be highlighted by its correlation to a material property, adhesiveness, a critical measure when involving direct contact of PDMS elastomers to objects, such as ingredients for personal care products.^[21] To characterize the adhesiveness of soft PDMS elastomers, we perform adhesion measurements by bringing a spherical stainless steel ball and a flat PDMS sample into contact.^[22] The adhesive force, acting across the ball-elastomer interface, tends to deform the elastomer and thus increases the area of their contact, as illustrated schematically in Figure 4A. Since this deformation is opposed by the elastic restoring force, the contact area is higher for elastomers of larger adhesion, provided that they are of the same elastic modulus. For similar moduli, we find that the deformation of soft PDMS elastomers is smaller compared to commercial Sylgard^® 184 PDMS products and silicone gel CY 52–276, as shown in Figure 4B and SI Movies. The relatively smaller deformation of soft PDMS elastomers suggests they are less adhesive compared to commercial silicone products of similar stiffness.

Figure 4. Adhesion.

(A) Schematic of adhesion test by retracting a steel ball with diameter 3.55mm from elastomer films at a controlled velocity, ν, after indentation. The adhesive force between the ball and the PDMS sample is measured by a microbalance underneath the film. (B) Representative images showing the contact between the different elastomers and ball at zero displacement d-d₀=0 for the ball is retracted at 1µm/s. (C) Representative curves for retracting the ball at ν=1µm/s from elastomer samples after indentation. The shadowed area represents the fracture energy required to separate the ball from the elastomer sample. (D) Dependence of fracture energy on ball-film separation rate for soft PDMS elastomers (circles and squares) and commercially available silicone products (triangles). (E) Fracture energy for a soft PDMS elastomer sample with modulus of 20 kPa (SE5) before and after the sol fraction extracted. Data are shown as mean ± SD with the number of samples n≥3.

To quantify the adhesive properties, we measure the force applied to the flat PDMS sample as the steel ball retracts from it with a controlled velocity. This force is initially positive, due to the elastic restoration of the compressed sample. As the ball retracts, the sample becomes less compressed and thus the elastic restoration force decreases. The elastic restoration is balanced by adhesive force at a certain displacement. As the displacement, d, increases beyond this point, the adhesive force dominates and thus the force becomes negative until the ball separates from the elastomer, at which point the ball is above position d₀, the surface of the undeformed PDMS sample, as illustrated in Figure 4A. This adhesive force-dominated window is presented by the shadowed area in the force profile, as shown in Figure 4C. This area represents the work, termed fracture energy, E_frac(ν), required to separate the ball from the PDMS sample at a rate, ν. Consistent with the material deformation apparent in Figure 4B, we find that E_frac for SE0 at ν = 10µm/s is about one order of magnitude lower than that for the Sylgard^® 184 product mixed at a ratio 1:50 and of similar modulus, as shown by the symbols close to the right in Figure 4D. Moreover, compared to another commercial silicone product, CY 52–276, the fracture energy for soft PDMS elastomer, SE0, is lower by more than two orders of magnitude at ν=10µm/s.

The lower fracture energy of soft PDMS elastomers can be qualitatively understood based on energy dissipation, which accounts for the excess amount of energy to separate two surfaces in addition to surface energy. The amount of dissipated energy at a certain separation rate is lower for elastomers with lower loss modulus. Consistent with this understanding, the loss modulus of soft PDMS elastomers is much lower than that of commercial silicone products. To further explore the role of loss modulus, we measure the fracture energy at different separation rates. The fracture energy for soft PDMS elastomers is almost independent of separation rate; by contrast, the commercial silicone products have fracture energy increasing with separation rate, with a power of 0.6, as shown by the triangles and lines in Figure 4D. This result for commerical silicone products is consistent with that observed for viscoelastic polymers, which have dissipated energy typically proportional to the separation rate with a power between 0.4 and 1.^[23] Indeed, the viscoelastic behavior of commerical silicone products is reminiscent of viscoelastic polymers; their loss modulus becomes comparable to the storage modulus at relatively high frequency, as shown in Figure S7. Moreover, the fracture energy for soft PDMS elastomers is lower after the sol fraction extracted, as shown in Figure 4E; this result provides direct evidence that less sol fraction corresponds to less energy dissipation and thus lower adhesiveness. Collectively, our results demonstrate that soft PDMS elastomers are different from commercial silicone products of similar stiffness in their significantly lower adhesiveness.

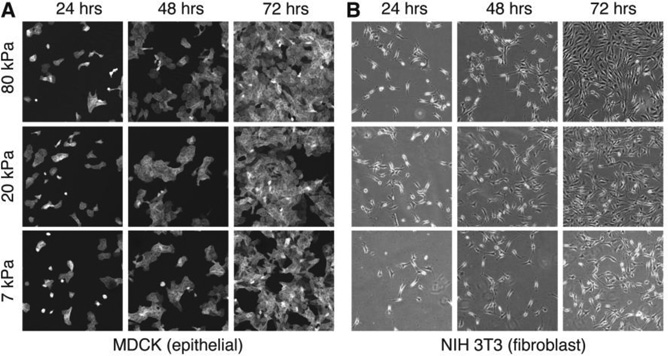
The independent control over storage and loss moduli could allow soft PDMS elastomers to be used as a unique substrate material to study cell behavior.^{[24, 25, 26]} In addition to stiffness, the loss modulus is being realized as a crucial property of materials when being used as substrates to study cell-substrate interactions.^{[18, 24, 27]} To demonstrate the applicability of soft PDMS elastomers for studying cell-substrate interactions, we test the cultivation of cells on substrates made of the soft PDMS elastomers of different moduli (Materials and Methods). We monitor the growth of MDCK epithelial and NIH/3T3 fibroblast cells and find that both cell types spread on the substrates after 24 hours, and are confluent within 72 hours, as shown in Figure 5. This result highlights that soft PDMS elastomers can be used to study cell growth and proliferation on substrates of different stiffness. Interestingly, we find that these cell types appear to proliferate faster on stiffer substrates without a change in spreading area (Figure S12), contrary to similar work using hydrogel substrates.^[28] This difference may be a consequence of the negligible loss modulus for soft PDMS elastomers, which is qualitatively different from hydrogels. However, further understanding of cell responses, such as spreading area, volume, proliferation rate and differentiation on substrates made of soft PDMS elastomers is beyond the scope of this paper and will be the subject of further explorations.

Figure 5. Biocompatibility.

Fluorescence and phase contrast images showing the proliferation of (A) MDCK epithelial and (B) NIH/3T3 fibroblast cells at 24, 48, and 72 hours on substrates formed by soft PDMS elastomers with storage moduli of 7kPa (SEL), 20kPa (SE5), and 80kPa (SE30). Images are 750µm×750µm.

We have developed soft PDMS elastomers by crosslinking bottlebrush polymers through a one-step synthesis; they have storage moduli below the lower limit of typical PDMS elastomers fabricated by crosslinking linear polymers. The stiffness of soft PDMS elastomers described here is comparable to that of hydrogels;^[29] moreover, in principle, extremely low moduli, <100 Pa, are achievable by using longer backbone and side chain polymers without impurities (SI text). Unlike commercial soft silicone products, soft PDMS elastomers have substantially less soluble fraction and significantly lower adhesiveness. The exceptional combination of softness and negligible adhesiveness may enable the application of soft PDMS elastomers in ultrasensitive, flexible pressure sensors.^[30] In addition, the simplicity of synthesis, the commercial availability of raw ingredients, and the flexibility of choosing the backbone/side chain/crosslinking chain ratio provide a useful tool with which to precisely tune the mechanical properties of soft PDMS elastomers. This versatility, together with the biocompatibility of soft PDMS elastomers, provides an asset for industrial development of critical ingredients for personal care products,^[2] designing soft materials for biomedical research and engineering^[26], and enabling materials for stretchable electronics.^[31] In addition, soft PDMS elastomers offer a model system for understanding the challenging physics of unusual elasticity, dynamics and relaxations of soft elastomers. Finally, the one-step fabrication method proposed here is not restricted to PDMS; it should be general and will enable exploration of soft elastomers made of other polymers.

Materials and Methods

Reagents

All chemicals are purchased from Sigma-Aldrich (St. Louis, MO) unless otherwise noted. All reactive PDMS polymers are purchased from Gelest^® Inc. (Philadelphia, PA) and used as received. Backbone: vinylmethylsiloxane–dimethylsiloxane copolymer, trimethylsiloxy terminated, ~300 vinyl groups per molecule, MW~50,000 g/mol (VDT-5035). Side chain: mono-hydride terminated polydimethylsiloxane, MW~4,750 g/mol (MCR-H21). Crosslinking chain: hydride-terminated polydimethysiloxane, MW~17,200 g/mol (DMS-H25). Extension chain: α-monovinyl-Ω-monohydride terminated polydimethylsiloxane, MW~10,000 g/mol (DMS-HV22).

Bulk rheology

The PDMS linear polymers are mixed at a predetermined mass ratio to achieve different density of crosslinking chains. Catalyst, 2% platinum in xylene, so called Karstedt’s catalyst, is added at the concentration of 5 µl/g, The mixture is cured at 80°C for 40 hours to reach a steady shear storage modulus. Rheological experiments are carried out on a stress controlled rheometer (MCR501, Anton Paar) with 50 mm plate-plate geometry at a gap of 750 µm. Frequency sweeps are performed from 10² to 10⁻² Hz at 0.5% stain at temperatures 80°C, 20°C, and −20°C. Changes in normal force due to a gap contraction with temperature are alleviated by adjusting the gap height.

Gel fraction

To quantify the gel fraction of soft elastomers, we use standard Soxhlet method to remove unreacted molecules in the polymerized PDMS-catalyst mixture. We perform the extraction in acetone/n-hexane (50:50) for 60 hours, and then dry the swollen PDMS gel in a vacuum oven at 80°C for 24 hours; after that the mass of PDMS does not decrease. The mass of the insoluble gel fraction is divided by the total mass before extraction and the values are listed in Table 1. The actual value of gel fraction may be larger than the measured value due to possible breakage of bonds upon swelling; swelling soft PDMS elastomers by a large extent leads to a large tension along network strands that may cause bond scission.

Cell growth

To prepare substrates for mammalian cell growth, we place 150µl of the PDMS-catalyst mixture in each well of a 24-well plate and polymerize at the same condition above. We then add 1ml of 1M KOH to each well for 1hr to gently treat the surface of soft PDMS elastomer instead of using plasma oxidation, which can crosslink the surface of PDMS, yielding a stiffer substrate^[32]. The surface is silanized by adding 500µl of 1% (v/v) glycidyl propyl trimethoxysilane (Gelest^® Inc.) in ethanol, and 500µl 1% (v/v) ammonium solution in water sequentially to each well. After 10 minutes, the surface is cleaned using ethanol, and then 1× phosphate buffered saline (PBS), twice. We add 500 µl of 0.1 mg/ml type 1 collagen to each well and store the plate at 4°C to prevent collagen polymerization but allow the collagen to react to the glycidyl group on the silanized PDMS surface. We repeat the above procedure with fluorescently labeled type 1 collagen^[33] and find that the surface coverage of collagen is homogeneous and uniform in fluorescent intensity across all PDMS substrates of different stiffness. The collagen coated surfaces are washed with 1× PBS twice, then culture media: 10% fetal bovine serum (FBS) with 1% pen-strep in Dulbecco’s modified eagle medium (DMEM). 1 ml of culture media is placed in each well and warmed to 37°C. Two cell types are used: Madin-Darby canine kidney (MDCK) epithelial cells (NBL-2, ATCC^® CCL-34™), which have been stably transfected with plasmid pCMV LifeAct–TagGFP2 (Ibidi), and NIH/3T3 fibroblasts (ATCC^® CRL-1658™). We place trypsinized MDCK epithelial and NIH/3T3 fibroblast cells on the collagen functionalized substrates at an initial concentration of ~20 cells/mm². We use fluorescence microscopy to image the fluorescent actin of MDCKs and phase contrast microscopy to image NIH/3T3s. Cell growth is monitored at 37°C over 72 hours at the same location of the substrate surface; culture media is not exchanged.

Adhesion measurement

To quantify the adhesiveness of soft PDMS elastomers, we use a customized adhesion apparatus consisting of an analytical balance (Mettler Toledo™ AT261) and a linear translation stage (Newport™ LTA-HL) remotely controlled by a motion control software (Newport™ Controller ESP300). The balance records mass with the rate of 1/sec, and the translation stage drives a smooth stainless steel ball with diameter of 3.55 mm moving at a resolution of 0.0074µm. To perform an adhesion test, we lower the ball to a position about 100µm above the surface of a soft PDMS elastomer sample that is placed on the balance; the sample is molded in a Petri dish with diameter of 35mm (Nunc™ Petri Dishes) and has a thickness of ~5mm. After that, the ball is driven at a certain rate by the linear translation stage towards the surface of soft PDMS, and indents the sample with a distance ~100 µm. The ball is held at its maximum indentation, waiting 20 minutes for the relaxation of stress due to the compression of soft PDMS sample, and then retracted at the same rate. During the course of indentation and retraction, the force and displacement outputs are collected by customized MATLAB data acquisition software. The adhesion measurement at a certain rate is repeated at least 5 times; between each measurement, the steel ball is cleaned with hexane to remove possible residuals adhered to the ball surface.