New Additions to the Toolkit for Forward/Inverse Problems in Electrocardiography within the SCIRun Problem Solving Environment

Abstract

Cardiac electrical imaging often requires the examination of different forward and inverse problem formulations based on mathematical and numerical approximations of the underlying source and the intervening volume conductor that can generate the associated voltages on the surface of the body. If the goal is to recover the source on the heart from body surface potentials, the solution strategy must include numerical techniques that can incorporate appropriate constraints and recover useful solutions, even though the problem is badly posed. Creating complete software solutions to such problems is a daunting undertaking. In order to make such tools more accessible to a broad array of researchers, the Center for Integrative Biomedical Computing (CIBC) has made an ECG forward/inverse toolkit available within the open source SCIRun system. Here we report on three new methods added to the inverse suite of the toolkit. These new algorithms, namely a Total Variation method, a non-decreasing TMP inverse and a spline-based inverse, consist of two inverse methods that take advantage of the temporal structure of the heart potentials and one that leverages the spatial characteristics of the transmembrane potentials. These three methods further expand the possibilities of researchers in cardiology to explore and compare solutions to their particular imaging problem.

1. Introduction

Cardiac electrical imaging often requires the examination of different forward and inverse problem formulations in order to find the methods that best suit the problem of observing a physiological event that is otherwise inaccessible or unethical to explore. One limitation of such modeling methods is that they often require complex models and numerical solutions strategies that are not always available to researchers in cardiology without the advanced computational background required. Additionally, there are further challenges that these methods face associated with the need for detailed geometric models, acquisition of data, and proper validation. Thus additional researchers and groups often develop their own in-house software with years of development incorporated cross-method comparison becomes difficult. These challenges significantly impede research progress in this area and thus its successful application in clinical practice.

To facilitate the access of researchers (and industry) to such methods, the Center for Integrative Biomedical Computing CIBC maintains and expands SCIRun [1]. SCIRun is an open source, problem solving environment that allows access to complex models and algorithms to users through a visual and intuitive programming interface. In particular, the Forward/Inverse Toolkit of SCIRun provides a wide variety of algorithms and sample networks to researchers in the field of cardiology [2].

2. Forward/Inverse Toolkit

The forward problem in electrocardiography computes the potentials that would propagate to the body surface given a specific electrical distribution in the heart. The inverse problem in electrocardiography uses solutions of the forward problem and measurements on the body surface to estimate the cardiac source [3, 4].

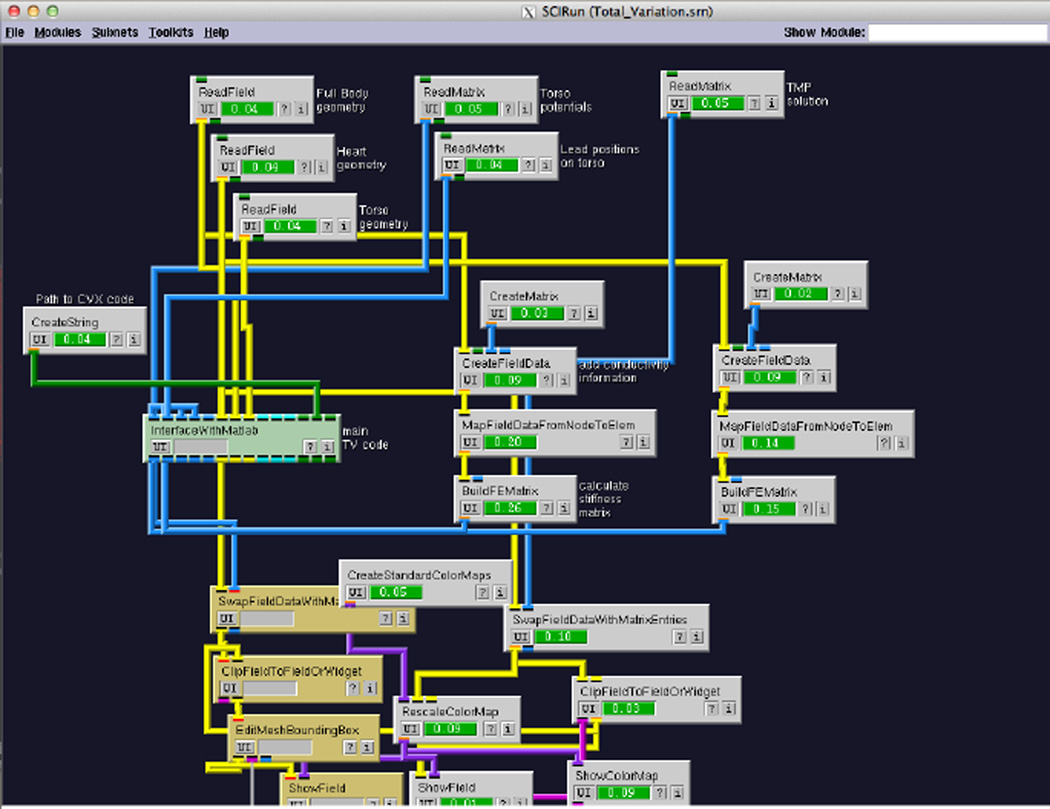
The objective of the Forward/Inverse Toolkit is to make available to researchers in cardiology a suit of tools to solve these computational problems. More generally, the SCIRun framework supplies an extensible interface module based environment, where researchers can visually program their algorithms by linking individual modules and pre-existing complex networks. An example of SCIRun in action is shown in Figure 1, with modules that have completed their processes (grey), are currently active (green), and are waiting to execute (yellow).

Figure 1.

Example of network in SCIRun. The links connecting modules indicate flow of data between them. The color of the modules indicate if they are done with computations, active or waiting for input (grey, green and yellow).

The toolkit currently provides several methods, both as SCIRun modules and through the built-in MATLAB interface, that solve the computational problems using potential and activation based source models, boundary element (BEM) and finite element methods (FEM) for the numerical approximations, as well as multiple computational and regularization methods for the inverse problem. A summary of the current suite of tools is shown in Table 1.

Table 1.

Current tools within the Forward/Inverse Toolkit.

Forward Tools	Inverse Tools
Potential-based (FEM/BEM)	Potential-based (FEM/BEM)
Activation-based (FEM/BEM)	Activation-based (FEM/BEM)
FEM Lead field Calculations	Regularization Methods
Stiffness Matrix Calculation	-Isotropy Method Gauss-Newton Method Wavefront-based Method Tikhonov Tikhonov SVD Truncated SVD Total Variation Non-decreasing TMP Spline-based Method

To demonstrate the utility of the Forward/Inverse Toolkit, we describe three new additions to the suite. These additions implement three inverse algorithms, two of which can be applied to any dataset given a forward matrix and one that uses an FEM specific implementation. Each one of these algorithms implements a different regularization of the inverse and is solved with a different optimization method.

3. New Additions

As described in Section 2, the inverse problem in electrocardiography tries to solve for the potentials on the heart from the corresponding body surface potentials (BSPs) at time t (y_t) and a forward model (A). The difficulties in solving this problem reside in the fact that it is ill-posed and thus highly sensitive to noise. For this reason there is need of introducing regularization to obtain meaningful solutions. Regularization can be introduced through parametrization of the solutions or as an added term in the function to be optimized, but in any case, it should be designed based on the spatial and temporal characterization of the potentials on the heart.

The inverse algorithms implemented in SCIRun that we will discuss in this section use different source models and characterizations of the potentials during the QRS segment. The first one, implements an FEM-based inverse that imposes sparsity on the spatial gradient of the potentials. The other two algorithms take different approaches to the regularization. One imposes non-decreasing transmembrane potentials (TMPs) in time, while the other parametrizes the temporal behavior of the heart surface potentials (HSPs) with a spline approximation.

3.1. Total Variation Inverse

The Total Variation algorithm is a general regularization method for ill-posed problems [5]. These is an implementation based on the work of Wang et al. [6], uses a FEM discretization of the heart and torso geometries to solve for the TMPs on the heart. The assumption behind the application of Total Variation to the inverse problem in electrocardiography is that the potentials on the heart at each time instance can be divided into two areas with a sharp transition between them: an activated zone with positive potentials V⁺ and a resting zone with negative potentials V⁻. This spatial characterization of the potentials leads to spatial gradients that are 0 everywhere except for the narrow wavefront where they take relatively high values, thus, these are sparse. This sparse constraint can be implemented by adding a regularization term that also minimizes the l1 norm of the gradient estimation (Equation 1).

$$\underset{x_t}{\text{min}}{\Vert y_t-A{x}_t\Vert }_2^2+\lambda {\Vert TV(x_t)\Vert }_1$$ (1)

$$TV(•)=\text{gradient estimation}$$

The network from Figure 1 is the example implementation of Total variation in SCIRun. It is an example of how the tools in SCIRun facilitate creating new pipelines to compute inverse solutions, since it uses multiple modules in SCIRun which, together with the Total Variation algorithm in the MATLAB interface allows to automatically obtain the inverse solutions from a torso and heart geometries and the BSP measurements.

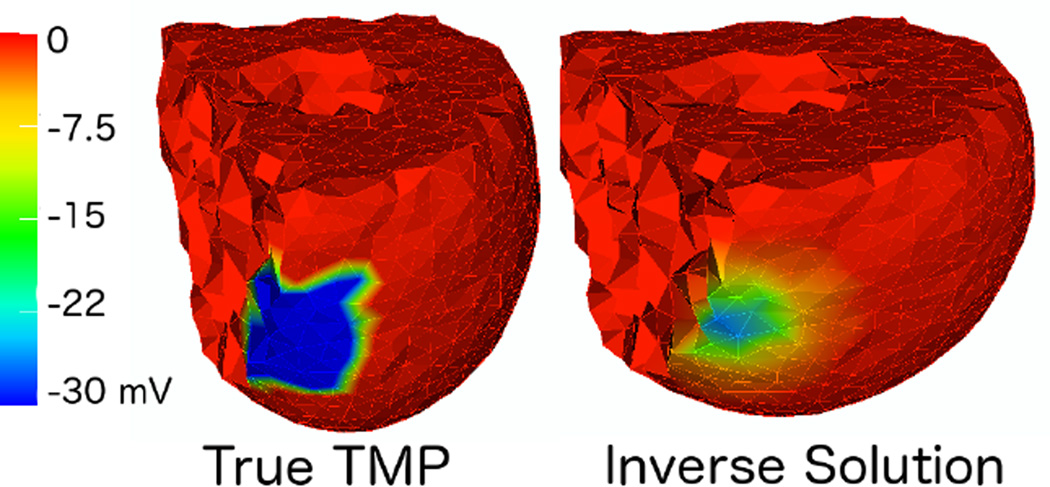
An example of the solutions obtained from this algorithm are shown in Figure 2. Even though the solutions of this algorithm do not have the sharp transitions of real TMPs (on the right), standard Tikhonov regularization methods produce smoother results than those shown here [7].

Figure 2.

Example of solution obtained with Total Variation compared against the true transmembrane potentials (right and left respectively).

3.2. Non-Decreasing TMP Inverse

The Non-Decreasing TMP is a BEM-based inverse method that differently from the Total Variation method, considers the time characteristics of the TMPs to regularize the inverse solutions. This algorithm is based on the method introduced by Messnarz et al. in [8]. In their algorithm the authors pose a Tikhonov objective function with the non-decreasing temporal constraint as in (Equation 2), which uses the same notation as in Equation 1.

$$\underset{x_t}{\text{min}}{\Vert y_t-A{x}_t\Vert }_2^2+\lambda {\Vert x_t\Vert }_1$$

$$st.b_{\mathit{\text{min}}}\le x_1$$ (2)

$$st.x_t\le x_{t+1}$$

$$st.x_T\le b_{\mathit{\text{max}}}$$

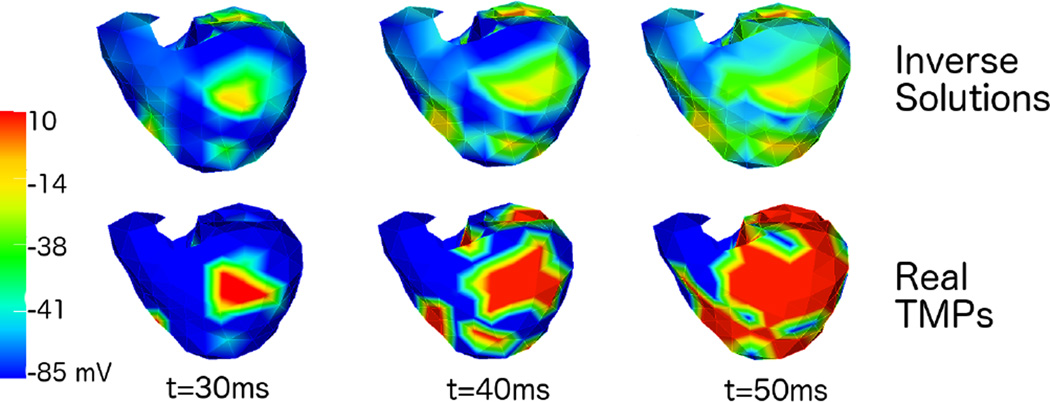
In the original paper, the authors used a standard convex solver. However, for memory efficiency, the current SCIRun implementation of this method uses a tailored ADMM solver in MATLAB [9]. This optimization algorithm allows us to iteratively compute the inverse solutions without prohibitive memory requirements. Solutions from this method present sharp increases in potential at their time of activation in most of the heart, while it also shows well marked wavefronts in space. An example of the potentials obtained is shown in Figure 3.

Figure 3.

Example of solution obtained with Non-Decreasing TMP inverse at 3 time instances. Upper row shows the inverse solutions, bottom row shows the real TMPs.

3.3. Spline Based Inverse

Finally, the Spline-Based method, based on [10], also uses temporal characterization of the heart surface potentials to obtain the inverse solutions. It assumes that the evolution of HSPs and the BSPs can be approximated by a smooth curve in a high dimensional space where the potential at each lead represents a single dimension. Given this description of the potentials, a spline fitting in this high dimensional space smooths out the potentials, eliminating high frequency components that correspond to noise [11]. With the further assumption that the temporal dynamics are preserved from HSPs to BSPs, by just estimating the inverse solutions at the knot points, the algorithm is capable of reconstructing the full time course of the HSPs. Thus the method is implemented in three steps: spline approximation of the BSPs, inverse calculation of the knot points using Tikhonov and reconstruction of full HSPs using the inverse estimated knot points and the temporal dynamics from the initial spline approximation. A typical result is shown in Figure 4. As observed, the solutions from this inverse method are smooth in space and time but show an activation wavefront moving from the early activation nodes to the last ones.

Figure 4.

Example of solution obtained with the Spline Inverse method for consecutive time instances.

4. Conclusions

These three algorithms exemplify how, with SCIRun, different approaches to the inverse problem in electrocardiography can be tested without requiring advanced knowledge in computational strategies. The interactive programming of SCIRun allows researchers to test distinct approaches that may not have been available to them previously. The Forward/Inverse Toolkit is extensible and is not limited to these algorithms and access to the multiple tested forward and inverse methods listed in Table 1. Moreover, the continuous collaborative efforts and the compatibility of SCIRun with major industry and educational software packages—such as CHASTE [12], CARP [13] and ECGSIM [14] — maintain SCIRun as a generalizable and useful tool for research (and industry) in the future.

CIBC continues expanding and developing the Forward/Inverse Toolkit in SCIRun to give access to researchers to a large body of tools to improve scientific knowledge in cardiac electrophisiology.