B₁ and T₁ mapping of the breast with a reference tissue method

Abstract

Purpose

To develop a method for mapping the B1 field using a reference signal from a tissue with known T1.

Methods

Flip angle correction factors were calculated in a region with a known ‘gold standard’ T1; by comparing T1 values from a variable flip angle (VFA) sequence to the ‘gold standard’ and correcting the value of the Ernst angle. The resulting partial B1 map was interpolated for all other regions. In the breast, fat is an ideal reference tissue because its T1 is spatially homogeneous and inter-patient variability is low. This method was tested with scans of phantoms and patients (n=4) on a 3T magnet. The performance of the method was evaluated by comparing the results of VFA T1 mapping with and without B1 correction to inversion recovery (IR) T1 maps.

Results

Phantom data determined that a linear inverse distance weighted interpolation accurately recovered the full B1 map. Use of interpolated maps to correct the VFA data in-vivo, reduced the average difference in the T1 of parenchyma between VFA and IR results from 58% to 8%.

Conclusions

This proof-of-principle study showed that it is possible to recover a full and accurate map of the B1 field in the breast by using a reference tissue (fat) with an accurately measured T1.

Introduction

Dynamic contrast enhanced MRI (DCE-MRI) is a highly sensitive method for the detection of breast cancer (1–3). During a DCE-MRI exam a series of T₁-weighted images are acquired before and after the intravenous injection of paramagnetic contrast media. The contrast agent preferentially accumulates in lesions due to their increased blood flow and fenestrated (leaky) vasculature, increasing their signal intensity in a T₁-weighted image. Routine analysis of DCE-MRI of the breast involves the tracking of signal increase and decrease in tissues indicative of the uptake and washout of contrast media (4).

B₁ inhomogeneity is especially notable in breast MRI, due to the large fields-of-view (FOV) required for bilateral breast imaging, and the off-center positioning of patients in the coil. Kuhl et al. reported significant differences in the B₁ field across the FOV, with differences of nearly a factor of two between the left and right breasts (5). These differences can lead to variations in image intensity across the FOV (e.g. shading), as well as spatial variations in the signal enhancement in lesions after the administration of a contrast agent. Azlan et al. mapped the B₁ field in several healthy volunteers at 3 Tesla (T) and simulated differences in enhancement in a phantom study (6). They found significant differences between the right and left breasts, and reductions of more than 50% of the nominal B₁ in some cases. They also showed that a reduction in B₁ leads to a reduction of the enhancement ratio (ER), possibly reducing the conspicuity of a breast lesion.

Dual source, parallel radiofrequency (RF) excitation has been proposed as a method of reducing variations in the B₁ field (7). Rahbar et al. compared B₁ maps acquired in the breast using both single and dual source RF excitation (8). They found that while the use of dual source parallel excitation reduced differences in the whole breast mean B₁ value between the right and left breasts compared to single source excitation, significant differences remained at some locations even when parallel excitation was used.

B₁ field inhomogeneity has a significant effect on the estimation of quantitative parameters in DCE-MRI (9). Estimations of native T₁’s of tissues, using a variable flip angle approach, rely on the accurate knowledge of the flip angles used. Knowledge of the native T₁ as well as the actual flip angle is necessary for an accurate estimate of post contrast T₁ based on signal enhancement in DCE-MRI. Measurements of contrast agent concentration are obtained from the native and post-contrast T₁’s, and thus are affected by the errors in the estimated flip angle in the region-of-interest (ROI). In fact, when the repetition time is short, and a low flip angle is used; a small error in the flip angle can lead to a large bias in concentration. In DCE-MRI of the breast it is common to use protocols with these conditions (at our institution for example standard protocols include a TR of 5 ms and flip angle of 10°). For this reason accurate knowledge of the actual flip angle is essential for accurate measurements of contrast media concentration, a necessary step in the measurement of pharmacokinetic parameters of lesions (e.g. K_trans, v_e, and k_ep) (10,11).

The issues outlined above demonstrate the need for methods for accurate mapping of the B₁ field in vivo for research applications and clinical evaluation of DCE-MRI images. The actual flip angle imaging (AFI) method can be used to measure B₁ maps in vivo (12). In this approach the ratio of the signal at two different repetition times (TRs) is used to derive the actual flip angle in each voxel. When implementing this sequence one must ensure that the transverse magnetization is adequately spoiled, and that the steady state has been achieved, otherwise the accuracy of the AFI technique is affected (13). Additionally, large flip angles are required when implementing this sequence, this leads to a reduced signal-to-noise ratio, potential artifacts from stimulated echoes, and a distortion of slice profiles. Furthermore, this sequence may not be available depending on the particular vendor/scanner used and its implementation may require pulse programming knowledge. Other methods for in vivo B₁ mapping include the saturated double-angle method (SDAM) (14), dual refocusing echo acquisition mode (DREAM) (15), and mapping by Bloch-Siegert shift (16). In a study by Nehrke et al. RF shimming with DREAM, AFI and SDAM was compared (17). The authors found that DREAM outperformed the other methods while significantly reducing acquisition time. Bloch-Siegert shift B₁ mapping offers the advantage of insensitivity to factors such as TR, T₁, and flip angle (DREAM has a weak dependence on T₁ and T₂). In fact, there is potential to combine DREAM and Bloch-Siegert approaches to produce a new and more accurate method. One drawback of the DREAM and Bloch-Siegert B₁ mapping methods is that they require specialized sequences that are implemented through research software patches (which are not widely available).

Here we present an approach for accurately mapping B₁ and T₁ values in the breast, with a variable flip angle (VFA) sequence and use of adipose tissue in the breast as a reference tissue. As demonstrated by Sung et al. fat is an ideal T₁ reference tissue for breast imaging (18). Rakow-Penner et al. used a fast spin-echo inversion recovery technique to accurately measure the T₁ of fat in the breast and found a mean value of 367 ms ± 8 ms at 3T (19). Merchant et al. also reported a low standard deviation in the T₁ of fat in the breast at 1.5T, with an average value of 265 ms ± 2 ms (20). Graham et al. measured the fat T₁ in ex-vivo samples and found an average value of 230 ms ± 10 ms (21). The relatively low standard deviation in these studies suggests a low variability in the T₁ value of fat, both inter-patient and across the breast (values at 3T were measured in several ROIs in each patient). By measuring the T₁ of the fat in the breast of a patient, or, assuming low inter-patient variability, using a population based value for the T₁ of fat, it is possible to find the actual flip angle in each fat voxel. The method presented here allows for B₁ mapping of the breast based on standard T₁ mapping sequences.

Methods

Theory

T₁ was estimated by fitting variable flip angle (VFA) data from each voxel to the spoiled gradient echo signal model (22):

$$S=M\sin \alpha \frac{1-e^{-TR∕T_1}}{1-\cos \alpha e^{-TR∕T_1}}$$ (1)

The optimal fits based on the nominal flip angles (those prescribed at the scanner console) provide an estimate of T₁ in each voxel. In the presence of an inhomogeneous B₁ field differences between the estimated and actual T₁ can be attributed, in part, to differences between the nominal and actual flip angles. In each voxel in the reference tissue (where the actual T₁ is known) a proportionality factor ‘A’ can be calculated to correct for differences in the flip angles:

$${\alpha }^{\prime }=A\alpha$$ (2)

Where α’ is the actual flip angle, α is the nominal flip angle. A is assumed to be constant at a particular location for the range of relatively small flip angles used here, and proportional to B₁ (23). ‘A’ can be defined as the ratio of the Ernst angle for the true T₁ to the Ernst angle for the measured T₁ from the fit to equation (1) with the nominal flip angles:

$$\mathrm{A}=\frac{{\theta }_{\mathrm{Et}}}{{\theta }_{\mathrm{Em}}}=\frac{{\cos }^{-1}\left({\mathrm{e}}^{-\mathrm{TR}∕{\mathrm{T}}_{1\mathrm{t}}}\right)}{{\cos }^{-1}\left({\mathrm{e}}^{-\mathrm{TR}∕{\mathrm{T}}_{1\mathrm{m}}}\right)}$$ (3)

Where θ_E is the Ernst angle and the subscripts t and m denote the true and measured T₁ values, respectively.

The map of ‘A’ or B₁ must then be estimated for all image voxels to obtain a correction to the nominal flip angle. To do this we developed the interpolation procedure outlined below.

B₁ map interpolation

After a VFA volume is acquired and fit to the spoiled gradient echo signal model, as detailed above, the following steps were taken to obtain a B₁ map for the whole breast.

1. Segment the fat in the image by thresholding the uncorrected T₁ map (since the T₁’s of glandular tissue are significantly longer than those of fat). A signal intensity threshold can also be used on one of the VFA images where there is good visual differentiation between fat and glandular tissue. Segmentation was supervised to account for signal intensity variation due to the inhomogeneous B₁ fields of the excitation and receiver coil.

2. A T₁ for fat can be measured very accurately at a few points using spectroscopic ‘recovery from inversion’ methods. Since the fat T₁ is very homogeneous, the T₁ found in a few (or one) fat regions can be assumed to apply to all fat voxels. In principle a ‘population’ value for the fat T₁ can be used as a reference.

3. Solve Equation (3) for each fat voxel, using the uncorrected T₁ values, and the gold standard value for the fat T₁.

4. Identify the regions with missing B₁ values (i.e. non-fatty regions of the breast) using a region labeling algorithm.

5. For each voxel in the regions of the B₁ map that need to be filled, identify the nearest ‘N’ neighbors with B₁ values in each 8-connected direction, along with the Euclidean distance between the voxel and each of the neighbors.

6. Interpolate to estimate the missing B₁ value B₁(x,y) from its nearest neighbors using inverse distance weighting.

   $${\mathit{B}}_1(x,y)=\frac{{\Sigma }_{i=1}^N{w}_i(x,y)B_1(x_i,y_i)}{{\Sigma }_{i=1}^N{w}_i(x,y)}$$ (4)

   Where N is the number of neighbors being used, x_i are the voxel locations with known B₁ values B₁(x_i,y_i) and w_i are the distance weights being used and given by:

   $$w_i=\frac{1}{{d_i}^P}$$ (5)

   d_i is the Euclidean distance between voxels (x,y) and (x_i,y_i) and P is the power of the distance weighting.

7. Repeat steps 5 and 6 for all voxels and regions.

8. Apply an averaging filter to the resulting map to smooth the B₁ map.

The optimal values of N (number of neighbors used in the interpolation) and P (the power of the distance weighting) were determined in phantom scans described below. Segmentation of the fat in the image must be performed with care so as not to include partial volume voxels at the boundaries between fat and glandular tissue as this could lead to artificially large gradients in the B₁ map at these locations.

The result of this algorithm is a complete B₁ map of the whole breast, where the values of B₁ in glandular tissue were interpolated from the values in the surrounding fat voxels.

Phantom Scans

All scans were performed on a Philips Achieva 3.0T TX scanner (Philips Healthcare, Best, The Netherlands) using a 16-channel bilateral breast coil (MammoTrak), and dual source parallel RF excitation (MultiTransmit).

To investigate the feasibility of the approach outlined above, and to determine adequate values for ‘N’ and ‘p’ in equations (4) and (5), respectively, we scanned a breast flood phantom. The flood phantom consisted of a mixture of water and CuSO₄. Previous experiments on this phantom showed a gradient in the B₁ field ranging from roughly 70% to 130% of the prescribed flip angle, thus the phantom provides a reasonable test for this method. The T₁ of the phantom was measured using a single voxel PRESS preceded by an inversion pulse and the following acquisition parameters: 5 mm isotropic voxel; TR/TE = 5100/36 ms; inversion delays of 50 ms, 200 ms, 500 ms, 1000 ms and 3000 ms; number of samples averaged (NSA) = 4. This sequence was repeated at four different locations in the flood phantom. The VFA sequence consisted of a 3D spoiled gradient echo (fast field echo), TR/TE = 10/2.4 ms; 2 mm isotropic acquisition voxels; NSA = 2; flip angles = 5°, 10°, 15°, 20°. An actual flip angle (AFI) B₁ map was also acquired using a dual TR acquisition with TR₁ = 10 ms; TR₂ = 50 ms; voxel size 5 mm × 5mm; 10 mm slice thickness; and a flip angle of 60°.

Data analysis was performed in Matlab (MathWorks, Natick, MA) with in-house built software. The VFA data were fit to the signal model shown in Equation (1), and a T₁ map of the flood phantom was generated. This map, along with the true T₁ from the spectroscopic sequence were then used to create a B₁ map by solving Equation (3) for each voxel. The flip angle of the inversion pulse was assumed to be fixed at 180° when fitting the IR data. Because the phantom being scanned consisted of a uniform solution, the resulting map included the whole phantom.

To evaluate the accuracy of an interpolated map, regions were drawn and zeroed out from the B₁ map of the phantom. The B1 map of the remainder of the phantom was then interpolated using the code described above, with varying values of the power of the inverse distance weights (P) and the number of neighbors used for the interpolation (N) of each voxel. The resulting interpolated maps were then compared to the original full B₁ map to determine the best combination of P and N. Values of N tested ranged from 1 to 8, while the P’s tested were 1, 2 and 3. This was repeated for regions of different sizes and shapes.

We built a second phantom to mimic the magnetic properties of tissues in the breast, as described by Liney et al. (24). The phantom consisted of lard and gelatin, to mimic breast fat and parenchymal tissue, respectively. In the middle of the phantom, we placed a small vial containing a mixture of water and gadobutrol (Gadavist, Bayer, Whippany, NJ). The phantom was placed into the right breast cup of the bilateral breast coil. Cross-sections of this phantom can be seen in Figure 1. A VFA sequence was acquired, with the same acquisition parameters as described for the flood phantom. An inversion recovery fast spin-echo (IR-FSE) sequence was also acquired with the following parameters: TR/TE = 9000/36 ms; 2 mm isotropic voxels; inversion times: 50, 150, 300, 600, 1000, 3000 and 4000 ms. In this phantom, the lard was used as the reference “tissue”. Its true T₁ value was calculated from the inversion recovery sequence. The B₁ map was created from the VFA data as described above, using the lard as the reference signal and interpolated in the other areas, and used to correct the VFA T₁ map. The accuracy of the corrected T₁ map (using the interpolated B₁ map) was evaluated using the inversion recovery T₁’s as the gold standard.

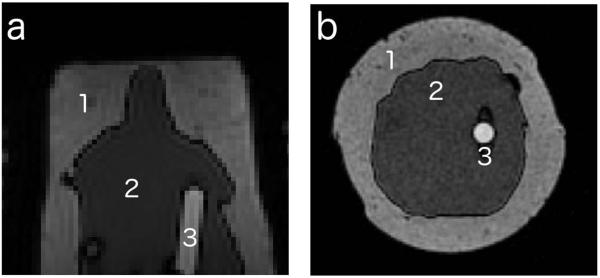
Figure 1.

Cross-sections of the non-uniform phantom in the (a) axial and (b) coronal planes, 3 regions can be seen in each one: (1) lard, (2) gelatin, and (3) water + contrast media

In vivo Scans

The methods presented here were evaluated in four patient scans (ages: 23, 28, 51, and 52), with the same scanner and coil used in the phantom scans. Informed consent was obtained under an IRB-approved, HIPAA-compliant protocol. A 3D VFA volume was acquired with the following acquisition parameters: 1 mm isotropic voxels; TR/TE = 10/2.4 ms; flip angles = 5°, 10°, 15°, and 20°; acquisition time of roughly 1.5 min for each flip angle. An IR-FSE sequence was acquired with: TR/TE = 5000/32 ms; inversion times = 50, 150, 300, 600, 1000, 3000 ms; acquisition time of roughly 1.7 min per inversion time (single slice). The acquisition times are given for bilateral axial scans; in one patient the data were acquired in the sagittal plane. B₁ maps were interpolated using data from a single slice (i.e. 2D approach), as described above, from the partial fat B₁ map obtained by calculating the correction factor in Equation (3). The true T₁ of fat was measured using a spectroscopic inversion recovery sequence acquired in voxels containing mostly fat. The IR-PRESS sequences had a TR of 3100 ms, and inversion times of 100, 650, 1050, and 2500 ms, in a 5 mm isotropic voxel, NSA = 4, and an acquisition time of 2.5 min. The accuracy of the T₁ maps obtained from the VFA sequence corrected for variations in B₁ using the reference tissue method was evaluated by comparing the T₁ values in a few regions of interest (ROIs) (drawn in the glandular tissue) to the values for the same ROIs in the maps generated from the IR-FSE data. Scatter plots were formed by plotting the IR T₁ data on one axis and the VFA T₁ on the other, for both uncorrected and B₁ corrected data, on a voxel-by-voxel basis for each patient. A linear function was then fit to the data. The slopes of the resulting fits provided another measure of the performance of the correction. The root-mean-square error (RMSE) for each fit was calculated to assess the spread of the T₁ data relative to the IR vs. VFA fit.

To determine whether there are significant variations in the T₁ values of breast fat in different patients, single-voxel spectroscopic inversion recovery sequences were acquired in ten patients, using the same acquisition parameters as listed above. The amplitude of the main peak (CH2) of the fat spectrum as a function of inversion time was fit to the inversion recovery signal model to obtain an estimate for the T₁ of adipose tissue in the breast, using in-house software.

In order to estimate the effect of using a population average for the T₁ of fat on the flip angle correction factor ‘A’, the following equation was solved:

$$\frac{\delta {\mathrm{A}}_{\mathrm{T}1\mathrm{t}}}{\mathrm{A}}=\frac{\delta {\mathrm{T}}_{1\mathrm{t}}}{\mathrm{A}}\frac{\partial \mathrm{A}}{\partial {\mathrm{T}}_{1\mathrm{t}}}=-\frac{\delta {\mathrm{T}}_{1\mathrm{t}}{\mathrm{TRe}}^{-\mathrm{TR}∕{\mathrm{T}}_{1\mathrm{t}}}}{{{\mathrm{T}}_{1\mathrm{t}}}^2{\cos }^{-1}\left({\mathrm{e}}^{-\mathrm{TR}∕{\mathrm{T}}_{1\mathrm{t}}}\right)\sqrt{1-{\mathrm{e}}^{-2\mathrm{TR}∕{\mathrm{T}}_{1\mathrm{t}}}}}$$ (6)

Where δA_T1t is the bias in A from a bias in the assumed true T₁ of fat (δT_1t).

Results

Flood phantom

From the spectroscopic inversion recovery data (PRESS-IR), the T₁ of the flood phantom was determined to be 217.3 ms ± 10.3 ms. The T₁ map obtained from the VFA data was used to generate a B₁ map from Equation (3), using the inversion recovery result as the true T₁.

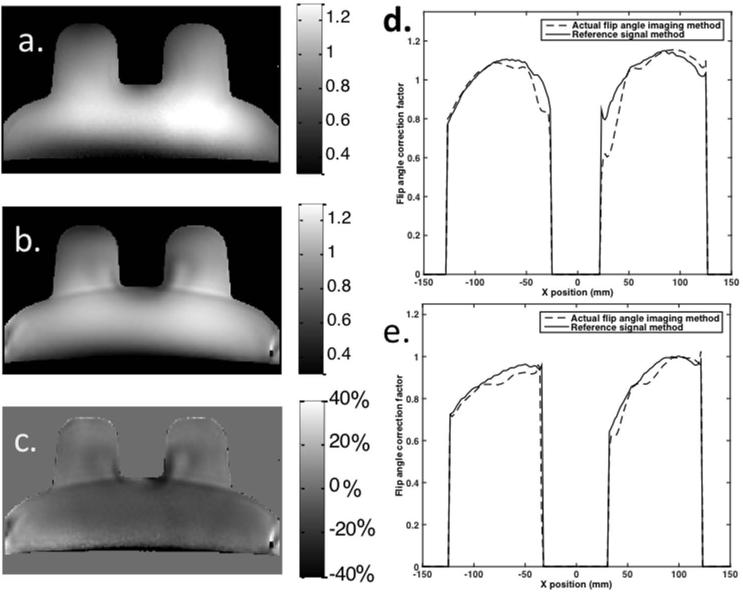
The reference signal B₁ map and the one obtained from the dual TR ‘Actual Flip angle Imaging’ (AFI) sequence can be seen in Figure 2. Plots of the profile of the map in a medial and posterior line through the phantom ‘breasts’ can also be seen in the figure. While both B₁ maps generally follow the same trend there are significant differences in their magnitudes in some locations. For the portion of the phantom that corresponds to the breasts only, the absolute difference, averaged across all voxels, between the reference signal B₁ map and the dual TR AFI map was 5.4% ± 5.3%, with an average difference in the top tenth percentile of 17.1% ± 4.4%.

Figure 2.

B₁ maps for a flood phantom from (a) reference signal method and (b) dual TR actual flip angle imaging sequence, along with a percent difference image (c) between the two (scale for a and b corresponds to the correction factor between the nominal and actual flip angle). On the right, profile plots of the B₁ maps obtained in a flood phantom for lines through the (d) central and (e) posterior section of the ‘breasts’

The interpolated maps from the flood phantom tests were compared to the full B₁ map by calculating the mean absolute differences between the full reference signal B₁ map and the interpolated map in the voxels in the regions that were zeroed out (taking the average over all interpolated voxels). Two of the realizations of this experiment are depicted in Figure 3, where the original map, the zeroed out regions, and the resulting interpolated maps (with N = 6, P = 1, 2, 3) can be seen. In these examples the mean absolute difference between the original and interpolated maps are shown for each interpolated map. When the power of the inverse distance-weighting algorithm (Equation 5) was increased, the calculated maps deviated further from the original maps. We determined that linear inverse distance weighting (P = 1) resulted in the most accurate maps in the interpolated regions. For example, in one case the mean differences between the original and interpolated maps (across all zeroed out voxels) were 5.6%, 6.2% and 6.7%; for P’s 1, 2, and 3, respectively. The value of N did not have as large an effect as P on the resulting maps, an N of 6 was selected as it offered a good combination of accuracy and computational efficiency. For example, the mean absolute difference between the original and interpolated maps varied by 0.6% between N values of 1 and 8.

Figure 3.

Examples of the interpolation tests in a flood phantom for two different simulated fat distributions. Top row: maps with zeroed-out regions. The bottom 3 rows depict percent difference images between the original and interpolated maps, for different values of the power of the inverse distance weighting (P). The value of Δ is the mean absolute difference (in the zeroed-out regions) between the original and interpolated maps (± standard deviations)

Multiple “tissue” phantom

T₁ values from the inversion recovery, uncorrected and B1-corrected VFA measurements can be seen in Table 1. The results shown in Table 1 are the means (and standard deviations) from all the voxels of that “tissue” type in the slice measured. The compartments were segmented based on signal intensity in the VFA series as well as T₁’s resulting from the fits of the uncorrected VFA data. It can be seen that use of the reference tissue B₁ map to correct flip angles reduced the difference between the VFA and IR T₁’s in the gelatin and water with contrast media compartments.

Table 1.

T₁ measurements (before and after B₁ correction) from the multiple compartment phantom

		Uncorrected		B1 corrected
Compartment	IR T1 (ms)	VFA T1 (ms)	Difference	VFA T1 (ms)	Difference
Lard	246.9 ± 11.9	267.4 ± 45.4	8.3%	256.3 ± 13.8	3.8%
Gelatin	2009.2 ± 44.9	2543.6 ± 295.9	26.6%	2070.5 ± 235.3	3.1%
Water + CA	708.1 ± 27.9	903.61 ± 31.5	27.6%	803.5 ± 28	13.5%

In-vivo scans

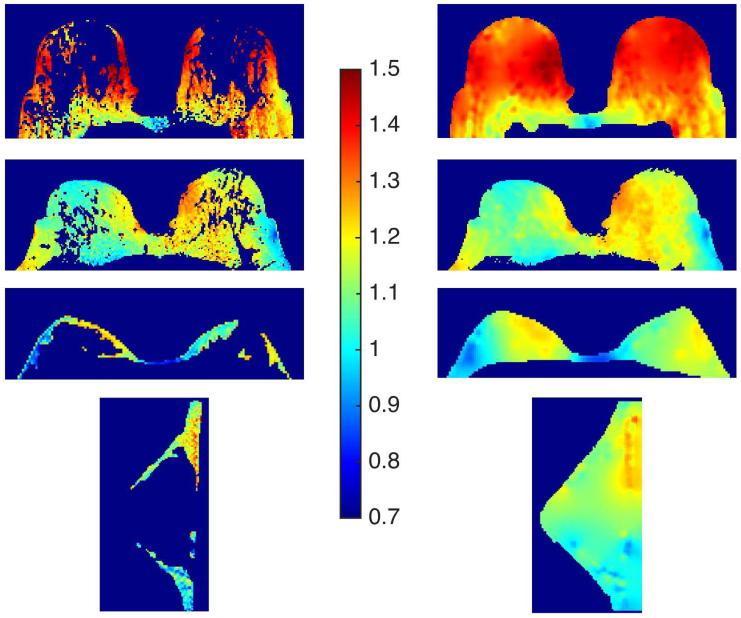
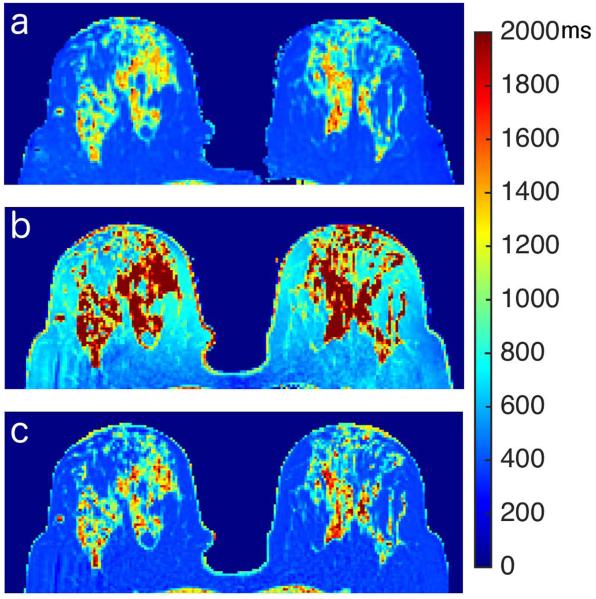
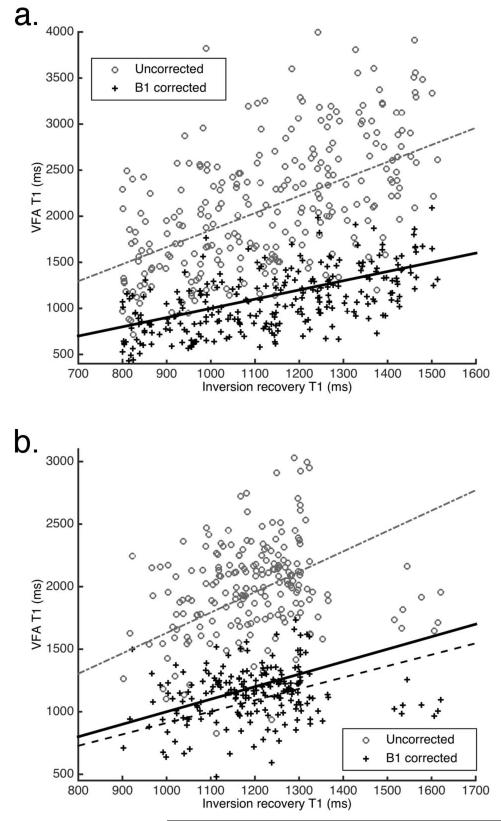
Reference tissue and interpolated B₁ maps are shown in Figure 4. T₁ maps from one of the cases can be seen in Figure 5. In this figure the overestimation of T₁ values in the parenchyma by the uncorrected VFA data is clearly seen. This figure also shows that the T₁ map produced from the VFA data corrected for local variations in flip angle is closer to the IR map than the uncorrected T₁ map. Results from the four patient scans are summarized in Table 2. The use of interpolated reference tissue B₁ maps for calculations of T₁ from VFA data significantly reduced the difference between the measured ‘gold standard’ inversion recovery and VFA T₁ values in glandular tissue. Before correction the average absolute difference between VFA and IR values was 58% ± 21% (p < 0.05); after correction the absolute difference was reduced to 8.1% ± 7.8% (p > 0.05). In the voxels with the top 10% of differences the average was 170% ± 53% without B₁ correction and 28% ± 13% after B₁ correction. In the IR vs. VFA linear fits of the T₁ values in the ROI’s analyzed (two examples can be seen in Figure 6), the slope of the B₁ corrected data was closer to 1 for all cases. The root-mean-square error (RMSE) in the VFA vs IR fits was also reduced in all cases following the flip angle correction from the reference tissue B₁ maps, indicating a reduction in the spread of the T₁ values. The average intra-patient standard deviation in the fat T₁ values, as measured from the IR sequence, was 7.9% of the mean.

Figure 4.

In vivo results, B₁ maps for the reference tissue (left column) and interpolated maps for the whole breast (right column); displayed in terms of the flip angle correction factor (‘A’). The bottom row were acquired from a unilateral sagittal scan, all others were acquired axially.

Figure 5.

T₁ maps from an in vivo scan: a) inversion recovery T₁ map; b) uncorrected VFA T₁ map; c) VFA T₁ map corrected with interpolated B₁ map

Table 2.

In vivo T₁ measurements performed at 3T for: inversion recovery, VFA (before and after B₁ correction) and fit parameters for IR vs VFA scatter-plots.

						IR T1 vs VFA T1 fits
#	IR T1 (ms)	VFA T1 (ms)		% Difference in T1		Slope		RMSE (ms)
		No correction	B1 corrected	No correction	B1 corrected	No correction	B1 corrected	No correction	B1 corrected
1	1145 ± 228	2119 ± 751	1147 ± 401	85.1%	0.2%	1.85	1.00	622	335
2	1145 ± 123	1878 ± 345	1049 ± 226	64.0%	−8.4%	1.63	0.91	348	236
3	942 ± 239	1269 ± 508	894 ± 420	34.7%	−5.1%	1.32	1.15	483	403
4	1074 ± 219	1610 ± 451	1274 ± 323	49.9%	18.6%	1.49	1.18	335	225

Figure 6.

Scatter-plots of VFA T₁ data (before and after B1 correction) vs. inversion recovery T₁ data. Dotted lines correspond to linear fits to data, solid line is the line of equality (lines overlap in a). Parameters for the fits are included in Table 2 (a. case 1, b. case 2)

Spectroscopic fat measurements

The mean fat T₁ value from the spectroscopic measurements in ten patients was 341.3 ms with a standard deviation of 31 ms. Equation 6 was solved to estimate of the bias introduced in ‘A’ from differences between the true T₁ value in a particular patient, and the population average. A 10% error in the assumed true T₁ of fat led to a relative bias of 5% in the estimate of the flip angle correction factor ‘A’. A difference of 10% was chosen due to the fact that the standard deviation in the T₁’s measured was 9% of the mean. This relative bias increases with the error in the assumed true T₁.

Discussion and Conclusions

The method proposed here, using a reference signal from a region (or regions) with a known T₁, produced B₁ maps that successfully reduced the variation between T₁ values measured using a variable flip angle and an inversion recovery sequence in the breast parenchyma in vivo and in phantom studies.

Significant differences were observed between B₁ maps obtained from solving Equation 3 and the AFI method in some locations in a flood phantom. This is likely due to inadequate spoiling in the implementation of the AFI sequence causing off-resonance artifacts (13).

A linear inverse distance weighted interpolation was shown to accurately recover a full B₁ map when starting with a partial map from a reference region. This was determined in phantom scans using acquisition parameters equivalent to those used in other in-vivo studies.

In a non-uniform phantom built to mimic the T₁ values of breast tissues, a B₁ map was generated by interpolation from the data of one compartment alone (the ‘fat’ compartment). This map significantly reduced the difference between the T₁’s measured with a VFA sequence and the IR results in the gelatin (‘parenchyma’) compartment. In a third compartment containing an aqueous solution of contrast media, the variability between the VFA and IR results was also reduced, however the remaining difference after correction was larger than in the gelatin compartment. This could be due to local variations in the B₁ field caused by the different dielectric properties of the water and contrast agent compartment, compared to those of the water and gelatin used.

Data from the in vivo scans showed a reduction in the difference between IR and VFA T₁’s, when the flip angles are corrected using the method presented here. The T₁ values of the parenchyma were overestimated by the non-corrected VFA data in every case. This is likely due to both the deviation from the nominal flip angles, and the difficulty of estimating a relatively long T₁ from VFA data acquired with a short TR. While overall differences between the corrected and IR maps were reduced to 8%; in one of the cases a mean difference greater than 18% remained in the T₁’s. In this study we employed a 2D approach for the interpolation of the full map, using data from a single slice to interpolate the B₁ map. Incorporating data from contiguous slices, adding more directions in the interpolation, could potentially increase the accuracy of the method proposed.

Segmentation of the fat in the breast was achieved by using thresholds for signal intensity and the uncorrected T_1. This had the drawback of requiring supervision to avoid errors in segmentation caused by non-uniformity in the signal intensity of fat. An automatic algorithm such as Fuzzy C-means clustering could increase the accuracy of the segmentation (25).

Obtaining a B₁ map using the current approach requires knowledge of the T₁ of a reference tissue, in this case fat. A spectroscopic inversion recovery sequence in a voxel placed in the fat was used to measure the T₁ value in several patient scans. The relatively low standard deviation across all patient scans in this study and previous measurements suggest low inter-patient variability of the T₁ of fat. This suggests that one could forego the measurement of the T₁ of fat in each patient and use a population average when generating a B₁ map with this approach. This could also be useful in correcting data retrospectively in studies where a T₁ map was acquired but the B₁ field was not mapped. A simple simulation showed that the flip angle correction factor estimated with this method is relatively sensitive, but not overly sensitive, to differences between the actual true T₁ of fat and an assumed value (i.e. population average), with the parameters used here.

Other methods for combined T₁/B₁ mapping have focused on novel acquisition techniques. Treier et al. proposed a method based on a VFA approach incorporating data from a dual TR (AFI) acquisition (26). In this study the authors optimized the acquisition parameters for a dual flip angle VFA for a range of T₁ values (100 – 800 ms) while keeping acquisition times short. Their results showed increased accuracy in T₁ mapping with this approach, and demonstrated its usefulness in DCE-MRI applications. Hurley et al. showed that this method increases the accuracy of T₁ mapping even in the presence of short T₁’s, as long as adequate spoiling is performed (27). However, the accuracy of this method may be somewhat limited in areas of the body with a large range of T₁’s, such as the breast (28). Due to the reliance of this method on the AFI technique, it also suffers from the shortcomings of the AFI above. Another approach based on the AFI, the multiple TR B₁/T₁ mapping (MTM) method was proposed by Voigt et al. (29). In the MTM the pair of TR’s used by the AFI is substituted with a series of TR’s; this yields both B₁ and T₁ estimates. The additional TR’s increased the accuracy of the AFI method but resulted in increased acquisition times. Another method for the acquisition of combined B₁/T₁ maps, DESPOT1-HIFI, produced combined maps by adding an inversion prepared SPGR image along with the multi flip angle SPGR data acquired in DESPOT1 (30). However this method’s accuracy may be limited in areas with long T₁’s and affected by error in the inversion pulse it employs. In contrast to these combined B₁/T₁ mapping methods, the reference tissue method proposed here, as well as related methods proposed by Sung et al. (18), relies on post processing of a VFA T₁ map, eliminating the need for specialized acquisitions. However the reference tissue method requires the presence of a tissue with a known, homogeneous T₁ in the field-of-view, ideally surrounding a tissue or area of interest. The abundance and wide distribution of fat makes the breast well suited for this method. The method may also be effective in other regions of the body, e.g. cerebral spinal fluid (CSF) in the brain could be used as a ‘reference tissue’. One must exercise caution when selecting a reference tissue so as to avoid partial volume effects, especially in the case of CSF. In some regions use of this approach might be more challenging due to lack of an optimal reference tissue.

In conclusion, we present a method that allows mapping of the B₁ field in a reference region or tissue with a known T₁; the data from this reference tissue can then be used to interpolate the B₁ map in the rest of the tissue of interest. This approach was validated in phantom scans and tested in in vivo breast scans. The maps generated with this method reduced the variability in the T₁ values measured with a variable flip angle sequence when compared to inversion recovery values. Accurate knowledge of the flip angle across the field of view is important not only in the quantitation of T₁ values, but also in the quantitative analysis of DCE-MRI data. This method provides a new alternative for mapping the B₁ field in the breast, and requires only the T₁ of the reference tissue, either from direct measurements or from a population average. While related methods have shown promise, this is the first study that has quantitatively validated a reference tissue post-processing method.