Optimizing 1-μs-Resolution Single-Molecule Force Spectroscopy on a Commercial Atomic Force Microscope

Abstract

Atomic force microscopy (AFM)-based single-molecule force spectroscopy (SMFS) is widely used to mechanically measure the folding and unfolding of proteins. However, the temporal resolution of a standard commercial cantilever is 50–1000 μs, masking rapid transitions and short-lived intermediates. Recently, SMFS with 0.7-μs temporal resolution was achieved using an ultrashort (L = 9 μm) cantilever on a custom-built, high-speed AFM. By micromachining such cantilevers with a focused ion beam, we optimized them for SMFS rather than tapping-mode imaging. To enhance usability and throughput, we detected the modified cantilevers on a commercial AFM retrofitted with a detection laser system featuring a 3-μm circular spot size. Moreover, individual cantilevers were reused over multiple days. The improved capabilities of the modified cantilevers for SMFS were showcased by unfolding a polyprotein, a popular biophysical assay. Specifically, these cantilevers maintained a 1-μs response time while eliminating cantilever ringing (Q ≅ 0.5). We therefore expect such cantilevers, along with the instrumentational improvements to detect them on a commercial AFM, to accelerate high-precision AFM-based SMFS studies.

Over the last 50 years, elucidating the process by which proteins fold into their complex structures has blossomed into a large, interdisciplinary field.¹ Single-molecule techniques have provided unique insights into protein folding.²⁻¹² Force-induced unfolding has proven particularly powerful, as the application of a constant force (F) lowers the height of the energy barrier (ΔG^‡) at the transition state (Δx^‡) by FΔx^‡, effectively “tilting” the folding energy landscape. The resulting folding dynamics can be quantitatively modeled as thermal activation across a barrier.¹³⁻¹⁶ Enhancements in the temporal resolution of single-molecule force spectroscopy (SMFS) have been critical to the protein-folding field, detailing short-lived (<1 ms) on-pathway and misfolded intermediates.^17,18 The transition time—the time it takes to cross the barrier—occurs on even faster scales, ∼1–10 μs for typical globular proteins.^12,19,20 To better understand these dynamics, the folding of individual molecules should be measured with 1-μs resolution and in a manner consistent with the theoretical framework used to model the folding process. Specifically, the instrumentally applied force should tilt the energy landscape but not add a high-frequency force modulation. Such a modulation is not modeled in traditional SMFS theories,^13,16,21,22 yet it is expected to significantly perturb a protein’s average unfolding rate, which varies exponentially with F. Indeed, we note that even sub-pN changes in applied F are detectable.^18,23,24 Hence, the optimum force probe for SMFS should respond on the 1-μs time scale while avoiding Brownian-motion-induced oscillation (or “ringing”) of the force probe inherent in probes that are underdamped (Q > 0.5).

Standard SMFS assays have a temporal resolution of 50–1000 μs,^25,26 with advanced statistical techniques capable of probing the 10-μs regime.²⁷ Optical-trapping-based SMFS has resolved the transition path time of exceptionally slow (∼500 μs) misfolding transitions.²⁸ However, the transition path time in an individual SMFS record remains unresolved for a typical globular protein, the foundation of protein-folding studies. Ultimately, the temporal resolution of SMFS is limited by the mechanical response time (τ) of the probe in liquid.

High-precision atomic force microscopy (AFM)-based SMFS has often favored long, soft cantilevers (Figure 1a) (e.g., long BioLever, Olympus (L = 100 μm; k = 6 pN/nm)),^29,30 but these cantilevers offer relatively slow time resolution (τ ≈ 450 μs).³¹ One way around this limitation is to use shorter cantilevers. Shorter cantilevers have reduced hydrodynamic drag (β) and increased stiffness (k) and hence respond to changes in force more rapidly (τ = β/k when overdamped (Q ≪ 0.5)). Moreover, it has long been known that smaller cantilevers also have improved force precision due to lower β.³² Recently, Rico et al. used a custom-built high-speed Ando-style AFM³³ to achieve high-velocity SMFS with 0.7-μs temporal resolution using ultrashort Olympus BioLever Fast cantilevers (Figure 1b) (L = 9 μm; k = 100 pN/nm).³⁴

Figure 1.

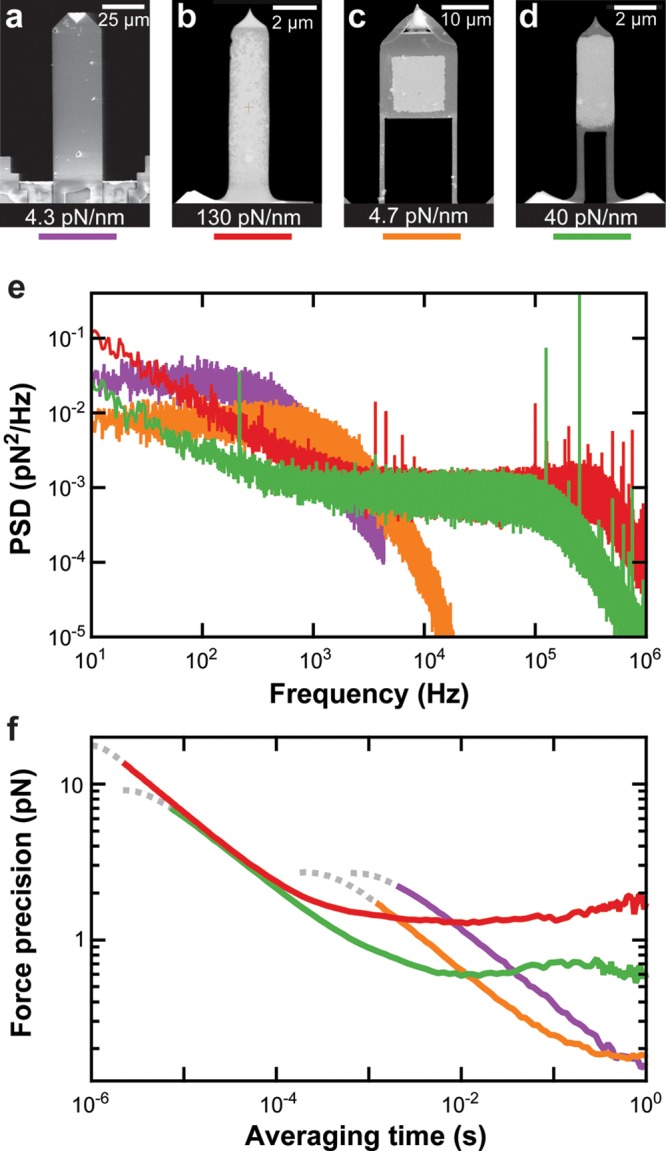
Comparison of the mechanical properties of various cantilevers in liquid. Scanning electron microscopy (SEM) images of (a) an uncoated long BioLever (L = 100 μm); (b) a gold-coated BioLever Fast (L = 9 μm); (c) an FIB-modified BioLever Mini (L = 40 μm); and (d) an FIB-modified BioLever Fast. Each cantilever’s measured spring constant is indicated. (e) The force power spectral density (PSD) of each cantilever in liquid is plotted as a function of frequency. The data were taken at 50 nm over the surface. The color coding is indicated below each cantilever’s image in panels a–d. (f) Force precision for each cantilever was calculated from the Allan deviation⁴⁶ σ_x(T) = (1/2⟨(x̅_i+1 – x̅_i)²⟩_T)^1/2, where x̅_i is the mean value of the data over the ith time interval T. The Allan deviation represents the average force noise over a given averaging time derived from the same set of data used in panel e. We note that, at the very shortest times, the motion of the cantilever becomes correlated, distorting the Allan deviation. This region of the curve is de-emphasized using a dotted line.

Notwithstanding the pioneering nature of this work,³⁴ three aspects of the BioLever Fasts are not optimal for SMFS. First, ultrashort cantilevers are not overdamped (Q ≤ 0.5), violating an underlying assumption that forms the basis of traditional force spectroscopy analyses.^13,16,21,22 Specifically, traditional force spectroscopy analyses assume a uniform probability for unfolding over a sufficiently short period, whereas an oscillating cantilever exponentially modulates that unfolding probability at the resonance frequency of the cantilever (∼500 kHz for a BioLever Fast). Second, these cantilevers are inherently stiffer than long cantilevers, leading to increased force noise (δF = k δx) due to low-frequency positional noise (δx) in the optical detection systems.^31,35,36 Finally, such tiny cantilevers are difficult to detect on commercially available AFMs, decreasing usability and throughput. We therefore sought to optimize SMFS with 1-μs temporal resolution by developing soft but ultrashort cantilevers along with the instrumentational improvements to detect them on a commercial AFM.

To generate such an overdamped ultrashort cantilever, we needed to modify k and β and thereby Q. Within the damped simple harmonic oscillator model, these quantities are interconnected by Q = k/(2π f_vac β), where f_vac is the resonance frequency of the cantilever in the absence of damping.³⁷ Reduced β also increases short-term force precision as a consequence of the fluctuation–dissipation theorem ΔF = (4k_BTΔfβ)^1/2, where ΔF is the force precision, k_BT is the thermal energy, and Δf is the bandwidth of the measurement.³² Also, as discussed earlier, reduced k increases long-term force stability given the fixed amount of instrumental positional noise (δx) in the optical detector system (δF = kδx).^31,35,36 However, while shorter cantilevers have reduced β,³² shorter cantilevers are inherently stiffer (k ∝ 1/L³). Recently, we circumvented this scaling relation by using an efficient method to modify a short cantilever (L = 40 μm; BioLever Mini (Olympus)) with a focused ion beam (FIB) (Figure 1c).³¹ By this technique, we equally reduced β and k so that the modified cantilever’s response time (τ ≈ 80 μs) remained similar to that of an unaltered BioLever Mini. We also mitigated the adverse effect of a cantilever’s gold coating on force stability³⁰ by removing the gold coating everywhere except a small area at the end of the cantilever.³¹ Together, these modifications yielded sub-pN force precision over five decades of bandwidth (0.01–1000 Hz).

In this Letter, we extended FIB-modification to ultrashort cantilevers (Figure 1d). This work required overcoming two critical challenges. First, we developed a modification process that eliminated the significant bending observed when FIB-modifying ultrashort cantilevers (Supporting Information, Figure S1). Second, we retrofitted our commercial AFM with a home-built detection module to achieve a 3-μm circular spot size for increased sensitivity (Supporting Information) since the modified cantilevers were only marginally detectable even on a state-of-the-art commercial AFM (Cypher, Asylum Research). The resulting precise detection of our new soft but ultrashort cantilevers showed that they have excellent properties for SMFS including being overdamped (Figure 1e) and having a force precision of 1.1 pN in a 200-μs window (Figure 1f). This force precision is just ∼50% larger than state-of-the-art optical-trapping experiments,¹⁷ despite a substantially larger force probe. We next applied these cantilevers to a traditional SMFS assay, the mechanical unfolding of a polyprotein. Analysis of the force decay after the protein’s detachment from the cantilever yielded the cantilever’s response time. The response time varied from 0.4–1.8 μs as we tuned the cantilever’s k and Q. Importantly, a practiced practitioner can modify 4–8 of these cantilevers in 2 h, and individual modified cantilevers were reused over multiple days. We therefore expect ultrashort cantilevers optimized for SMFS, along with the instrumentational improvements to detect them on a commercial AFM, to accelerate the mechanical studies of protein folding and unfolding with 1-μs resolution.

The first step in the cantilever optimization process was to cut a rectangular area (∼4 × 1.3 μm²) from the base of the cantilever with an FIB (Figure 1d).³¹ Unfortunately, this modification led to detection problems due to significant upward bending of the cantilever (Supporting Information, Figure S1). Ultrashort cantilevers bent by more than ∼5° were typically undetectable on our AFM. Fortuitously, we observed that FIB-induced thinning of the two narrow cantilever supports bent the cantilevers downward, allowing us to counteract the upward bending. To implement this bend compensation, we imaged the cantilever in real-time with a scanning electron microscope during the thinning process and stopped the thinning upon achieving a straight cantilever (Supporting Movie S1). Thinning the cantilevers after cutting dramatically increased the yield of useable cantilevers and further reduced k, for a total reduction of 3–8-fold.

A significant drawback of the modified cantilevers, however, was that they were only marginally detectable on our commercial AFM, even with its small-spot-size module (9 × 3 μm²). We therefore developed a home-built detection laser module (Figure 2a) with an even smaller spot size for detecting the modified cantilevers. Using a commercial AFM instead of an AFM optimized for high-speed imaging brings two significant benefits: enhanced ease of use and higher throughput. This modification of our commercial AFM to support a custom-detection module was straightforward but necessarily specific to this particular AFM. In general, this simplicity arises from modifying a commercial AFM that features a sufficiently powerful objective (e.g., NA = 0.45, LUCPLFLN 20X, Olympus) coupled with an optical isolator (formed by a polarizing beam splitter and a quarter-wave plate) to separate the incoming from the reflected cantilever-detection laser beam.³⁸ The new detection laser module generated a ∼3-μm circular spot size (Figure 2b), considerably smaller than that generated by the commercial small spot-size module (Figure 2c). Such small spot sizes have been previously developed for high-speed AFM imaging.³⁹ To achieve such a tight focus using our AFM’s existing objective, we needed a circular laser beam with a 4 mm diameter in a TEM₀₀ mode. We achieved these specifications while minimizing the modifications inside the commercial AFM using a triplet collimator (TC-18APC, Thorlabs) to introduce a laser via a single-mode polarization-maintaining fiber. The fiber was supported mechanically to minimize motion-induced pointing noise of the laser beam, similar to methods used previously to enhance stability in optical traps.^40,41 These modifications required raising a single electronics board inside the AFM by using an adaptor board. Importantly, the full optical path of the commercial AFM remained unmodified (including the detector and its associated electronics) after the introduced triplet collimator, which used an existing mounting interface for different detection modules. The hardware modifications were accompanied by a simple modification to the control software that assured proper initialization in the absence of the standard laser module.

Figure 2.

Detecting FIB-modified ultrashort cantilevers on a commercial AFM. (a) Schematic of the custom-built small-spot-size detection module integrated with a commercial AFM. A diode laser (λ = 853 nm) passes through an acousto-optic modulator (AOM) before being coupled into a single-mode polarization-maintaining fiber. Following a 50/50 fiber-based splitter, one output arm is used to measure the laser intensity using a photodiode (PD) and thereby stabilize the laser intensity using feedback to the AOM. The other fiber output is coupled into the AFM using a triplet collimator. A pre-existing polarizing beam splitter (PBS) and quarter-wave plate (λ/4) within the AFM act as an optical isolator to direct the reflected laser light onto the quadrant photodiode (QPD). Acronyms represent the following: optical isolator (OI) and neutral density filter (ND). (b, c) Optical images comparing the spot size generated by (b) our custom small spot-size module and (c) the commercial small spot-size module reflecting off a BioLever Mini for image clarity. (d) The positional power spectral density (PSD) plotted as a function of frequency for a modified BioLever Fast cantilever at 50 nm over the surface in liquid when using the commercial (red) and custom (green) detection module. The estimated noise floor (black) for detecting modified cantilevers with this custom-detection module is ∼20-fold lower than the commercial one. (e) Sensitivity for detecting modified ultrashort cantilever using the commercial (red) and custom (green) detection modules determined by pushing the cantilever into a hard surface. Note that an optical-interference artifact leads to a sinusoidal modulation in the deflection signal as a function of the cantilever’s height over the surface. The voltage amplitude of this artifact for both detection modules was similar, implying at least a three-fold reduction in this artifact when deducing force and displacement with our custom-built module due to its higher sensitivity.

Two other improvements were made to optimize the detection of ultrashort cantilevers. First, optical interference between laser light reflecting off the cantilever and the sample surface produced a sinusoidal artifact in the deflection signal, a common complication that is exacerbated when the detection laser spot size is larger than the cantilever.³⁴ To reduce this effect, we modulated the laser diode current at 460–500 MHz,⁴² typically achieving a 50% reduction in the magnitude of the artifact (Supporting Information, Figure S2). Second, we stabilized the laser intensity after coupling the laser into the fiber since coupling a free-space laser into a single-mode fiber converts pointing and mode noise into intensity noise. To do so while also minimizing the optics inserted into the commercial AFM, we used a 50/50 fiber-splitter where one of output fibers went to the AFM and the other to a photodiode (Figure 2a). The resulting custom-detection module integrated well with our commercial AFM and could be swapped in and out of the system in 20 min.

This custom-detection module was essential to using our modified ultrashort cantilevers. Application of the standard small spot-size module to characterize the modified cantilevers was not only technically challenging, but also failed to yield interpretable thermal calibrations. Specifically, the power spectral density (PSD) of modified ultrashort cantilevers was corrupted by instrumental noise in a manner inconsistent with thermally limited detection (Figure 2d, red), presumably due, in part, to the very low sensitivity of detecting these cantilevers (1.5 mV/nm). In contrast, the detection sensitivity using our custom-detection module was typically 3–5-times better (Figure 2e) because of increased reflection from the cantilever. More importantly, the resulting PSD showed an extended flat section consistent with thermally limited detection of an overdamped cantilever (Figure 2d, green), enabling proper thermal calibration of the stiffness. We estimated the noise floor of our custom-built detection module by positioning the laser on the cantilever chip next to the base of the cantilever and scaled the resulting signal by the measured sensitivity. This analysis showed a 20-fold reduction in the instrumental noise compared to the commercial small spot-size module (Figure 2d, black vs red).

Precise PSD measurements also provided insight into the suitability of a modified cantilever for SMFS. In particular, analysis of a cantilever’s thermal motion yielded a characteristic frequency (f_c) and a quality factor (Q). The temporal resolution of the cantilever can be estimated using τ_calc ≈ Q/(πf_c), similar to prior work.³⁴ Traditional SMFS analysis assumes the motion of the force probe is overdamped and therefore not applying a high-frequency force modulation to the biomolecule. Cantilever ringing is absent when the cantilever is overdamped, which is the case if Q ≤ 0.5 (not Q < 1), a well-established result for a damped simple harmonic oscillator⁴³ that has previously been shown to apply to AFM.⁴⁴

Both f_c and Q are affected by the proximity of the cantilever to the surface since squeezed film damping increases β.⁴⁵ It is therefore important to characterize the cantilever at a typical displacement used in SMFS experiments. Hence, we recorded the thermal fluctuations of the cantilever at 50 nm above the surface. In additional to computing the positional PSD, it is helpful to compute the force PSD (Figure 1e) since the latter metric allows for direct comparison between cantilevers of different k, f_c, and β values.

To place the performance of our modified ultrashort cantilever into context, we compared an FIB-modified BioLever Fast to three other cantilevers recently used in advancing AFM-based SMFS: an uncoated long BioLever that achieved sub-pN force stability (Figure 1a);³⁰ a standard gold-coated BioLever Fast used in the pioneering high-speed SMFS (Figure 1b);³⁴ and an FIB-modified BioLever Mini that achieved sub-pN performance over a significantly broader time scale (Figure 1c).³¹ The properties of these cantilevers are summarized in Table 1. Of particular importance, the modified BioLever Fast had a τ_calc of 0.7 μs, suggesting 1-μs-scale temporal resolution. Moreover, since both the modified and the standard BioLever Fast had a lower β value than the other cantilevers, they also had better force precision per unit bandwidth in the thermally limited regime (Figure 1e). Finally, the modified BioLever Fast had a two-fold lower f_c compared to an unmodified BioLever Fast, resulting in a slower estimated τ_calc (Table 1). Despite this modest reduction in temporal resolution of the modified cantilevers, this cantilever now exhibited a Q ≤ 0.5 and thereby fulfilled a fundamental assumption of traditional SMFS analyses.

Table 1. Mechanical Properties of Cantilevers.

type of cantilever	L (μm)a	k (pN/nm)b	fc (kHz)c	Qc	τcalc (μs)d	τ (μs)e
Long BioLever	100	4.3	1.2 ± 0.1	0.32 ± 0.02	86	450f
Modified BioLever Mini	38	4.7	4.1 ± 0.1	0.325 ± 0.004	25	53f
BioLever Fast	9	130	444 ± 2	0.847 ± 0.003	0.6	0.4
Stiff modified BioLever Fast	9	40	240 ± 6	0.52 ± 0.01	0.7	1.2
Soft modified BioLever Fast	9	20	175 ± 3	0.43 ± 0.01	0.8	1.8

^aTypical length provided by manufacturer.

^bSpring constant measured for each cantilever as described in Supporting Information.

^cExtracted from a fit of the simple harmonic oscillator equation to the power spectral densities measured 50 nm above the surface in liquid.

^dτ_calc ≅ (Q/πf_c).³⁴ However, this metric should be used with caution since it differed substantially from the measured relaxation time τ.

^eMeasured τ determined from exponential fit to the tip–sample detachment during SMFS experiments.

^fSee ref (31).

Modified BioLever Fast cantilevers were not universally better for all SMFS applications; their enhanced temporal resolution and force precision came at the expense of not only an increased optical-interference artifact, but also decreased force stability, particularly in comparison to the softer FIB-modified BioLever Mini (Figure 1f).³¹ Such a trade-off would not exist if the detected motion of the cantilevers was thermally limited over all time scales since the force precision per unit bandwidth is set by β, which favors smaller cantilevers.³² Unfortunately, the measured motion of the cantilevers was not thermally limited, but it also included instrumental noise in the optical lever arm.^31,35,36 This instrumental noise led to an increase in the positional PSD at low frequency (Figure 2d). As introduced previously, instrumental positional noise (δx) leads to larger force noise in stiffer cantilevers (δF = kδx) (Figure 1e). Our preferred metric for analyzing the trade-off between force precision and stability is the Allan variance⁴⁶ (or more specifically the Allan deviation) in which the mean force precision is computed over a given averaging time. As shown in Figure 1f, softer cantilevers had significantly better force precision over long periods, with the two softest cantilevers performing best. The choice of the optimum cantilever therefore depends on the particular application. For example, the transition time depends only logarithmically on the force,^47,48 as opposed to the exponential force dependence of transition rates. Enhancing temporal resolution at the expense of force stability is thus a valuable trade-off for such measurements.

As a biophysical demonstration of the advantages of modified ultrashort cantilevers, we used them to mechanically unfold a polyprotein, a widely used AFM-based SMFS assay. Specifically, we compared the performance of two modified BioLever Fasts of different stiffnesses (k = 20 and 40 pN/nm) to that of an unmodified BioLever Fast (k = 130 pN/nm). The polyprotein consisted of four repeats of NuG2,⁴⁹ a computationally derived fast-folding variant of the protein G B1 domain (GB1) (Figure 3a). The polyprotein was covalently anchored to a polyethylene glycol (PEG)-coated surface at one end and attached via biotin to a streptavidin-coated tip at the other end. The protein was unfolded by retracting the cantilever at constant velocity (400 nm/s) while simultaneously measuring F at 50 kHz and 5 MHz. After the adverse optical interference was computationally subtracted off (Supporting Information, Figure S2),³⁴ the resulting force–extension curves displayed the classic sawtooth pattern associated with sequential unfolding (Figure 3b). Analysis of the force–extension curves using a worm-like chain (WLC) model yielded a change in contour length (ΔL₀ = 17.6 nm) consistent with prior results for unfolding of NuG2.^31,50,51 We also observed an increased deviation between the data and the WLC fit at higher forces. We speculate that this deviation arises, in part, from a known structural change in PEG at higher forces⁵² and difficulty in calibrating the stiffness and sensitivity of ultrashort cantilevers.

Figure 3.

Optimizing SMFS using FIB-modified ultrashort cantilevers. (a) A cartoon of the assay showing a polyprotein composed of four domains of NuG2 being mechanically stretched. (b) Force–extension records showing the mechanical unfolding of the NuG2 polyprotein at 400 nm/s with a standard BioLever Fast (k = 130 pN/nm, red), a stiff modified BioLever Fast (k = 40 pN/nm, green), and a soft modified BioLever Fast (k = 20 pN/nm, blue). Data recorded at 50 kHz. Gray dashed lines represent worm-like chain fits to the data, yielding a change in contour length (ΔL₀) of 17.3–17.9 nm, in agreement with previous results.^31,50,51 Traces were laterally aligned and vertically displaced for clarity. (c) Force-versus-time record detailing the response of each cantilever used in panel b as the polyprotein detaches from the tip. Data recorded at 5 MHz. Time constants were determined by exponential fits (black) to each record. (d) An underdamped cantilever adds a time-varying tilt to a simple one-dimensional energy landscape for protein unfolding. Such a perturbation rapidly modulates the barrier height during a SMFS experiment. (e) Force-versus-time records while stretching the fully unfolded polyprotein at ∼60 pN. Histograms show the distribution in measured forces after a linear subtraction, with RMS deviations of 24, 11, and 6.8 pN for the red, green, and blue curves, respectively. Data recorded at 5 MHz. (f) Force power spectral densities (PSDs) for the three different cantilevers calculated from the data in panel e. Both the stiff and soft FIB-modified BioLever Fasts were nonresonant (Q = 0.58 and Q = 0.50 respectively) during the SMFS experiment, whereas this analysis shows a clear resonance peak for the unmodified BioLever Fast (Q = 0.88), consistent with the periods of oscillatory force fluctuations shown in panel e.

We next directly measured the cantilever response time in a protein-unfolding assay. To do so, we analyzed the force decay after the protein detached from the cantilever (Figure 3c). This is our preferred metric for reporting a cantilever’s response time because it makes no model-dependent assumptions and includes the effects of squeezed-film damping. The force decay for both of the modified cantilevers was well fit by a single exponential (Figure 3c, green and blue), with relaxation times of 1.2 and 1.8 μs for cantilevers with k of 40 pN/nm and 20 pN/nm, respectively. In contrast, the force decay for an unmodified cantilever was three-fold faster (0.4 μs) but showed some ringing (Figure 3c, red). Interestingly, the force-vs-time traces for the two modified cantilevers also showed significantly lower force noise. Such improved force precision arises, in part, from decreasing Q to achieve an overdamped cantilever (Q ≤ 0.5).

To illustrate the impact of an underdamped cantilever, consider a simple one-dimension energy landscape for unfolding of a protein (Figure 3d). The application of a constant force tilts the landscape, as shown. Thermal fluctuations lead to crossing the energy barrier separating the folded and unfolded state. The resulting rate of barrier crossing is exponentially sensitive to the applied F, and even sub-pN changes in applied force can be detected.^18,23,24 An underdamped cantilever adds a high-frequency force modulation on top of the average force. Although such a force modulation is not modeled in traditional SMFS theories,^13,16,21,22 it is expected to have a significant effect due to the exponential sensitivity of rates to F. Indeed, a simple back of the envelope calculation within the context of the Bell–Evans model²¹ highlights this adverse effect. We assume the high-frequency modulation generates a peak-to-peak variation in F of 60 pN. The unfolding transition state (Δx^‡) for NuG2 was recently measured to be 0.42 nm.⁵¹ The difference between the unfolding rate at force peak relative to a force valley is then given by exp(FΔx^‡/k_BT) where the thermal energy k_BT equals 4.1 pN-nm. This calculation yields a ∼450-fold variation in the unfolding rate during half an oscillatory cycle of the force probe.

Do such oscillatory-like cantilever-driven force fluctuations actually arise while stretching a protein? To check, we compared force-versus-time records over a short time window (40 μs) for the two modified and one unmodified cantilevers while stretching a completely unfolded polyprotein at ∼60 pN (Figure 3e). This force corresponded to the approximate mean unfolding force for NuG2 at this stretching velocity (400 nm/s).⁵¹ Periods of force fluctuations at the resonant frequency of a standard BioLever Fast are clearly seen (Figure 3e, red). Moreover, the fluctuations are large: 30–90 pN peak-to-peak around an average force of 60 pN. In contrast, both modified BioLever Fast cantilevers exhibited much smaller fluctuations (Figure 3e, green and blue). The stiffer modified BioLever Fast showed RMS force fluctuations were reduced from 24 to 11 pN relative to the unmodified cantilever, whereas the softer modified BioLever Fast had even lower force fluctuations (6.8 pN). These improvements in force precision arise not only from reducing Q, but also from the slower response time of the modified cantilevers. In essence, the cantilever itself acts like an analog low-pass filter smoothing the measurement of both the thermal motion and the step-response function.

To quantify this observation, we plotted the force PSDs from these records (Figure 3f). The results demonstrate that the unmodified BioLever Fast was still marginally resonant even while stretching an unfolded protein. The force PSD shows a slight peak around f_c (Figure 3f, red). Analysis of the PSD yielded Q = 0.88 (Supporting Information, Table S1). In contrast, neither of the modified cantilevers showed a pronounced peak in the force PSD, consistent with their reduced Q values (0.58 and 0.50) (Supporting Information, Table S1). The softer cantilever had the lower Q, as expected. FIB-modification of ultrashort cantilevers was thus critical to avoiding an unwanted high-frequency oscillatory component added to the force applied to the system under study.

In summary, AFM-based SMFS using ultrashort cantilevers provides a unique capability: probing a single individual protein with sub-μs temporal resolution.³⁴ However, commercially available ultrashort cantilevers are optimized for tapping-mode imaging not SMFS. As a result, commercial cantilevers not only exhibit relatively poor long-term stability, but also undergo underdamped motion, which increases measurement noise and modulates the unfolding landscape in a way not modeled by traditional SMFS analysis. By FIB-modifying ultrashort cantilevers, we optimized their mechanical performance for SMFS. The modified cantilevers were 3–8-times softer and showed significantly reduced force fluctuations during SMFS. Lower force noise results partially from eliminating cantilever ringing and also from reducing the cantilever’s characteristic frequency, which acts as a low-pass filter. Nonetheless, such modified cantilevers achieved a 1.2-μs mechanical response time as measured during protein-unfolding experiments. Further, the mechanical properties of these cantilevers can be tuned to suit the needs of a particular experiment. For instance, cantilevers can be made softer (e.g., 20 pN/nm vs 40 pN/nm) at the cost of temporal resolution (1.8 μs vs 1.2 μs). Importantly, the modification process was not unduly time-consuming; a skilled undergraduate modified 4–8 cantilevers in 2 h, and modified cantilevers could be reused for SMFS over multiple days. Finally, by developing a 3-μm circular spot-size detection module, we merged the excellent mechanical properties of these cantilevers with the ease-of-use and throughput of a commercial AFM. Looking forward, we expect that these modified ultrashort cantilevers, together with the instrumentational improvements for detecting them on a commercial AFM, will significantly accelerate high-resolution SMFS studies of protein folding.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.5b03166.

• Detailed description of FIB-modification protocol, custom-detection module, cantilever calibration and characterization, and SMFS experiments and analysis; mechanical properties of cantilevers during SMFS experiments; FIB-modification parameters; SEM images of FIB-modification process; reduced interference artifact with current modulation; stability comparison of detection lasers; improved detection sensitivity of unmodified cantilevers (PDF)

• SEM movie of FIB-modification process (AVI)

Author Present Address

M.S.B., Department of Applied Physics, Stanford University, Stanford, CA 94305, United States.

Author Contributions

D.T.E., M.S.B., and T.T.P. designed the experiment. D.T.E., J.K.F., A.W.S., and M.S.B. optimized and performed FIB-modification. D.T.E. and T.T.P. designed and built the detection system. R.W., M.A.L., M.C.S., and T.T.P. conceived and optimized the protein and substrate preparation. D.T.E. performed the AFM experiments. D.T.E. and T.T.P. analyzed the SMFS data. D.T.E. and T.T.P. wrote the manuscript, which was reviewed and approved by all of the authors.

This work was supported by a fellowship from the National Research Council (D.T.E.), an NIH biophysics training grant (M.A.L., T32 GM065103), the National Science Foundation (DBI-135398 to T.T.P.; Phys-1125844), NIH (R01 AI080709 to M.C.S.), a Butcher Grant (to T.T.P.), and NIST. Mention of commercial products is for information only; it does not imply NIST’s recommendation or endorsement. T.T.P. is a staff member of NIST’s Quantum Physics Division.

The authors declare no competing financial interest.