Partial correlation analyses of global diffusion tensor imaging-derived metrics in glioblastoma multiforme: Pilot study

Abstract

AIM: To determine existing correlates among diffusion tensor imaging (DTI)-derived metrics in healthy brains and brains with glioblastoma multiforme (GBM).

METHODS: Case-control study using DTI data from brain magnetic resonance imaging of 34 controls (mean, 41.47; SD, ± 21.94 years; range, 21-80 years) and 27 patients with GBM (mean, SD; 48.41 ± 15.18 years; range, 18-78 years). Image postprocessing using FSL software calculated eleven tensor metrics: fractional (FA) and relative anisotropy; pure isotropic (p) and anisotropic diffusions (q), total magnitude of diffusion (L); linear (Cl), planar (Cp) and spherical tensors (Cs); mean (MD), axial (AD) and radial diffusivities (RD). Partial correlation analyses (controlling the effect of age and gender) and multivariate Mancova were performed.

RESULTS: There was a normal distribution for all metrics. Comparing healthy brains vs brains with GBM, there were significant very strong bivariate correlations only depicted in GBM: [FA↔Cl (+)], [FA↔q (+)], [p↔AD (+)], [AD↔MD (+)], and [MD↔RD (+)]. Among 56 pairs of bivariate correlations, only seven were significantly different. The diagnosis variable depicted a main effect [F-value (11, 23) = 11.842, P ≤ 0.001], with partial eta squared = 0.850, meaning a large effect size; age showed a similar result. The age also had a significant influence as a covariate [F (11, 23) = 10.523, P < 0.001], with a large effect size (partial eta squared = 0.834).

CONCLUSION: DTI-derived metrics depict significant differences between healthy brains and brains with GBM, with specific magnitudes and correlations. This study provides reference data and makes a contribution to decrease the underlying empiricism in the use of DTI parameters in brain imaging.

Core tip: Diffusion tensor imaging (DTI)-derived metrics depict specific magnitudes and correlations; and significant differences between healthy brains and brains with glioblastoma multiforme (GBM). For example, only 5 bivariate correlations in GBM depicted significant very strong association: [FA↔Cl (+)], [FA↔q (+)], [p↔AD (+)], [D↔MD (+)], and [MD↔RD (+)]. Among 56 pairs of correlations, only seven were significantly different. Diagnosis showed a main effect [F-value (11, 23) = 11.842, P ≤ 0.001], with a large effect size (partial eta squared = 0.850); a similar result was observed for age. This study makes a contribution to decrease the empiricism in the use of DTI parameters in brain imaging.

INTRODUCTION

In the last decade, advanced magnetic resonance (MR) techniques have been adopted for the diagnosis and follow-up of intra-axial brain tumors[1], with a rising interest in novel diffusion tensor imaging (DTI)-derived metrics showing clinical applicability either in a tumor-region assessment (ROIs measurements in the cystic cavity, enhancing rim, edema, and normal-appearing white matter regions)[2-4]; or in a global approach (whole-brain selected values of DTI-derived biomarkers are able to assemble a predictive model for the diagnosis of glioblastoma multiforme)[4].

Conventional MR evaluation of glial tumors reporting qualitative and quantitative findings in the T₁-w post gadolinium, Flair and T₂-w sequences represents a caveat in the pathologic and regional evaluation of astrocytomas grades II to IV, as evidence suggest these tumors should received a global instead of regional brain assessment: glial tumors can depict manifold regions with different histologic grading, conditioning that biopsies reviewed by the neuropathologist may not reflect higher malignancy degrees in supplemental tumor regions, which may lead to underrating pathology reports[5]. There is a low correlation between visible margins of tumoral areas on conventional MR images with the true areas of tumor infiltration[5] this is due to microscopic invasion of white matter (WM) regions[6,7], extending dozens of millimeters from conspicuous areas of viable tumor[8].

Several combinations of the terms of the diagonalized diffusion tensor, that is, the eigenvalues λ₁, λ₂, and λ₃, have been reported as scalar measures of diffusion, such as: fractional (FA) and relative anisotropy (RA); pure isotropic (p) and anisotropic diffusions (q), total magnitude of diffusion (L); linear (Cl), planar (Cp) and spherical tensors (Cs); mean (MD), axial (AD) and radial (RD) diffusivities[2,3,9-11]; Table 1. However, to best of our knowledge, there is currently neither a clear understanding of the expected measurements among these variables, nor existing studies reporting their correlations; likewise there is a lack of consensus about which of the tensor metrics available should be used in the evaluation of brain tumors.

Table 1.

Diffusion tensor imaging-derived tensor metric formulas

MD

MD = D = (λ1 + λ2 + λ3)/3

FA

FA = [(3/2) × (q/L)]1/2 = (3/2)1/2{[(λ1 - D)2+(λ2 - D)2+(λ3 - D)2]/(λ12 + λ22 + λ32)}1/2

RA

RA = q/p = {[(λ1 - D)2 + (λ2 - D)2+(λ3 - D)2]1/2}/[31/2D]

RD

RD = (λ2 + λ3)/2

AD

AD = λ1

Cs

Cs = 3λ3/(λ1 + λ2 + λ3)

p

p = 31/2D = (λ1 + λ2 + λ3)/31/2

q

q = [(λ1 - D)2 + (λ2 - D)2 + (λ3 - D)2]1/2

L

L = (p2 + q2)1/2 = (λ12 + λ22 + λ32)1/2

Cl

Cl = (λ1 - λ2)/(λ1 + λ2 + λ3)

Cp

Cp = 2(λ2 - λ3)/(λ1 + λ2 + λ3)

MD: Mean diffusivity; FA: Fractional anisotropy; RA: Relative anisotropy; RD: Radial diffusivity; AD: Axial diffusivity; Cs: Spherical tensor; p: Pure isotropic diffusion; q: Pure anisotropic diffusion; L: Total magnitude of the diffusion tensor; Cl: Linear tensor; Cp: Planar tensor.

In this study we (1) used a global approach, that is, a single measure of the whole brain for each metric aimed to determine the normal limits (magnitudes) of previously reported DTI-derived tensor metrics in healthy brains and brains of patients with glioblastoma multiforme (GBM); (2) assessed the statistical significance between DTI values in these groups; and (3) analyzed the DTI-metrics correlates considering the influence of clinical diagnosis (healthy vs GBM brains).

MATERIALS AND METHODS

Subjects

Case-control study design; inclusion criteria considered preoperative brain MR examinations between January 2010 and September 2012 of patients with at first (suspected) diagnosis and later pathology confirmation of astrocytoma grade IV, GBM according to the World Health Organization. Exclusion criteria applied to corticosteroid or antibiotic treatment, lesions with areas related to calcification and/or haemorrhage and previous brain surgery. A control group included young and elderly healthy volunteers recruited among the enrolled interns and medical residents of the hospital as well as elderly subjects from our Geriatric unit. All volunteers received detailed health examinations; exclusion criteria considered major neurological, psychiatric, or cardiovascular diseases. A radiologist interpreted the MR images blinded to the patient’s history. MR examinations with other structural abnormalities were excluded. The local Institutional Review Boards approved the study (Project #2011.044), patients and also volunteers gave “informed consent”.

Brain image acquisition

MR sequences included conventional axial T₂-w imaging, axial FLAIR, axial SPGR, DWI and axial T₁-w imaging, using 0.1 mmol/kg of Magnevist (Schering, Berlin, Germany); healthy volunteers did not received endogenous contrast. DTI was performed using a SS SE EPI sequence. DTI sequence was acquired with 25 directions, a b-value of 1000 s/mm² and with b-value of 0 s/mm²; axial plane included 40 contiguous slices with 2.4 mm thickness, no intersection gap, TR 17000, TE 80 ms, with parallel imaging to reduce off-resonance artifacts (PI factor was 2); FOV 25 cm × 25 cm, and matrix size 128 × 128. Images were acquired using a 3T clinical scanner (GE Healthcare, HDxt Signa, Waukesha, WI, United States); and a 8-channels head coil (Invivo, Gainesville city, Florida).

Image postprocessing and data analysis

The methodology for calculation of global DTI-derived tensor metrics has been recently described[4]; each one of the eleven metrics in this study (Cl, Cp, Cs, RA, AD, RD, MD, FA, p, q, L) represent a single global measure of a whole-brain taking into account the higher (λ1), medium (λ2), and lower (λ3) eigenvalues of DTI[12].

Statistical analysis

Sample size: With the intention to run a Mancova analysis to investigate whether mean differences between healthy brains and brains of patients with GBM (combining different variables) occurred randomly, we followed Pallant’s recommendation for sample size[13], the absolute minimum of cases to have in each cell must equal at least the number of dependent variables; in our study, we had twenty-two cells (two levels of our independent variable: healthy brains/brains with GBM, and eleven dependent variables for each). The study was run in 34 controls and 27 patients; this numbers also follow the recommendation of Tabachnick and Fidell[14], for whom a minimum of 20 cases in each cell should ensure a “robustness” analysis. Assumptions testing included normality, multicollinearity and homogeneity tests[13,15]. We performed a partial correlation analysis to calculate association values between each pair of parameters. Considering the age range and the gender of the subjects in our study, this method allowed us to calculate correlations among tensor metrics without the effect of age and gender; independent analyses were carried out for each group (healthy brains vs brains with GBM). Each correlation coefficient was interpreted as very strong (at least of 0.8), moderately strong (0.6 up to 0.8), fair (0.3 up to 0.6) and poor (less than 0.3). Squaring r-values represented the coefficient of determination, the proportion of variance that each two compared variables had in common[16]. We additionally tested the statistical significance of the difference between r coefficients from both groups by converting each pair of r-values into a standard z scores, then using the formula proposed by Pallant[17]: Observed Z value ≤ -1.96 or ≥ 1.96 were considered statistically significantly different.

A two-way Mancova identified diagnosis and gender differences in tensor metrics measurements[18]. The eleven tensor-metrics represented the dependent variables used; independent variables were the diagnosis and gender; the effect of age was controlled. The effect size was obtained using the Eta squared value[19]: 0.01 to 0.06 represents small effect, 0.06 to 0.14 medium and > 0.14 shows a large effect[20]. A P-value < 0.05 depicted a significant difference.

Software: All analyses were carried out using the IBM^® SPSS^® Statistics software (version 22.0.0.0 IBM Corporation; Armonk, NY).

RESULTS

Demographic data and quantitative DTI tensor maps

The study was conducted in 61 subjects; 27 patients: 13 females (mean age 50.0 ± 15.4 years, range 31-73 years) and 14 males (mean age 46.93 ± 15.4 years, range 18-78 years); and 34 controls: 26 females (mean age 41.04 ± 22.3 years, range 21-80 years) and 8 males (mean age 42.88 ± 21.89 years, range 24-72 years). Tensor maps generated using the FSL software, added up to 671 tensor-metrics measurements. Figure 1 shows an example of some of the MR sequences and tensor-metric maps included in the data analyses.

Figure 1.

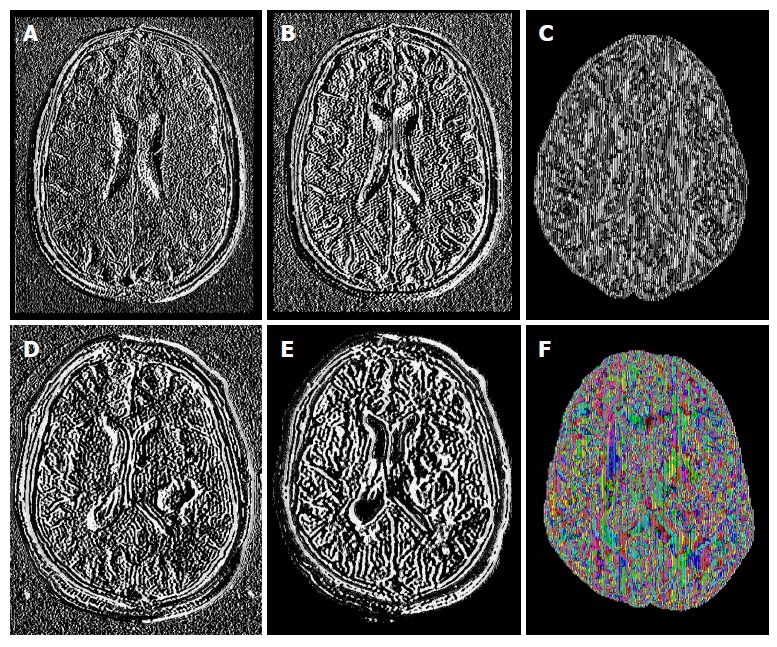
Example of some sequences and diffusion tensor imaging maps from healthy brains (upper row) and brains with glioblastoma multiforme (lower row): T1-postgadolinium images (A and D), Flair sequence (B and E); pure isotropic diffusion (C), color map of the V1-vector (F).

Normality tests, magnitudes of means and SD

There was a normal distribution for all metrics. In order to understand the corresponding magnitudes of each DTI biomarker (previously not reported), we counted the number of decimal places to the right of the decimal point: five tensor metrics reported mean values within the tenths place: Cs, FA, RA, Cp and Cl; none tensor measurement fell in the hundredths place; five tensors values fell in the thousandths place: L, p, AD, MD and RD; and one tensor metrics had values in the ten thousandths place: q. Table 2 shows the means and SD ordered by descending means.

Table 2.

Means, SD and correlations (controlled for the effect of age and gender) in healthy brains

Tensor metric													Mean	SD
		Cs											0.756690	0.032259
FA	Pearson’s R	-0.456	FA										0.284317	0.018917
	P-value	0.029
RA	Pearson’s R	-0.992	0.434	RA									0.224873	0.029523
	P-value	0.000	0.039
Cp	Pearson’s R	-0.979	0.460	0.938	Cp								0.133346	0.017086
	P-value	0.000	0.031	0.000
Cl	Pearson’s R	-0.946	0.442	0.978	0.855	Cl							0.111574	0.016583
	P-value	0.000	0.024	0.000	0.000
L	Pearson’s R	0.372	-0.115	-0.416	-0.317	-0.186	L						0.002275	0.000100
	P-value	0.117	0.578	0.076	0.200	0.408
p	Pearson’s R	0.179	-0.095	-0.214	-0.020	-0.014	0.945	p					0.002096	0.000087
	P-value	0.477	0.652	0.395	0.938	0.953	0.000
AD	Pearson’s R	0.322	-0.012	-0.348	-0.287	0.019	0.804	0.761	AD				0.001553	0.000056
	P-value	0.179	0.952	0.144	0.249	0.933	0.000	0.000
MD	Pearson’s R	0.181	-0.096	-0.215	-0.022	-0.014	0.945	1.000	0.762	MD			0.001210	0.000050
	P-value	0.473	0.649	0.391	0.934	0.953	0.000	0.000	0.000
RD	Pearson’s R	0.053	-0.297	-0.119	0.426	-0.131	0.877	0.954	0.628	0.954	RD		0.001046	0.000072
	P-value	0.821	0.132	0.606	0.054	0.542	0.000	0.000	0.001	0.000
q	Pearson’s R	-0.077	0.698	0.019	0.257	0.138	0.138	0.153	0.393	0.152	0.406	q	0.000445	0.000055
	P-value	0.721	0.000	0.929	0.225	0.492	0.502	0.466	0.047	0.467	0.029

FA: Fractional anisotropy; RA: Relative anisotropy; Cp: Planar tensor; p: Pure isotropic diffusion; q: Pure anisotropic diffusion; L: Total magnitude of the diffusion tensor; Cl: Linear tensor; MD: Mean diffusivity; RD: Radial diffusivity; AD: Axial diffusivity.

Partial correlation analyses

A scatterplot for each group showed no serious violation of the assumptions of linearity, homoscedasticity, and outliers (Figure 2). In healthy brains, significant very strong bivariate correlations were observed for: [Cs↔RA (-)], [Cs↔Cp (-)], [Cs↔L (-)], [RA↔Cp (+)], [RA↔Cl (+)], [Cp↔Cl (+)], [L↔p (+)], [L↔AD (+)], [L↔MD (+)], [L↔RD (+)], [p↔MD (+)], [p↔RD (+)] and [MD↔RD (+)]; and moderately strong significant correlations were calculated for: [FA↔q (+)], [p↔AD (+)], [AD↔MD (+)] and [AD↔RD (+)].

Figure 2.

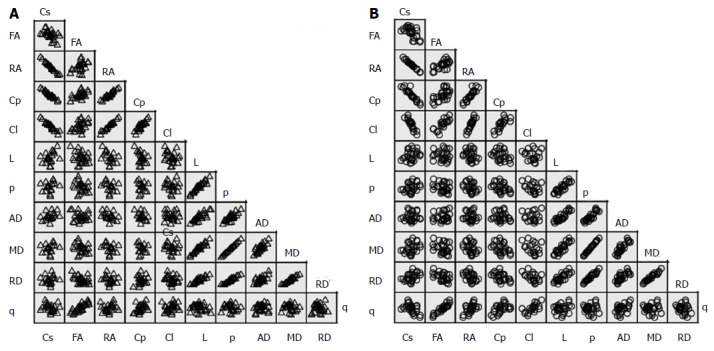
Scatter matrix of the variable’s data grouped by diagnosis. A: Normal brains; B: Brains with GBM. MD: Mean diffusivity; FA: Fractional anisotropy; RA: Relative anisotropy; RD: Radial diffusivity; AD: Axial diffusivity; Cs: Spherical tensor; p: Pure isotropic diffusion; q: Pure anisotropic diffusion; L: Total magnitude of the diffusion tensor; Cl: Linear tensor; Cp: Planar tensor; GBM: Glioblastoma multiforme.

In brains with GBM, the corresponding significant very strong bivariate correlations included: [Cs↔RA (-)], [Cs↔Cp (-)], [Cs↔L (-)], [FA↔Cl (+)], [FA↔q (+)], [RA↔Cp (+)], [RA↔Cl (+)], [Cp↔Cl (+)], [L↔p (+)], [L↔AD (+)], [L↔MD (+)], [p↔AD (+)], [p↔MD (+)], [p↔RD (+)], [AD↔MD (+)], and [MD↔RD (+)]; the moderately strong significant correlations were observed in: [Cl↔q (+)], [AD↔RD (+)] and [AD↔q (+)]. Table 3 present the correlations among the global tensor-metrics controlled for the effect of age and gender.

Table 3.

Means, SD and correlations (controlled for the effect of age and gender) in brains with glioblastoma multiforme

Tensor metric													Mean	SD
		Cs											0.771562	0.066812
FA	Pearson’s R	-0.570	FA										0.253531	0.028425
	P-value	0.003
RA	Pearson’s R	-1.000	0.592	RA									0.201778	0.053287
	P-value	0.000	0.002
Cp	Pearson’s R	-0.936	0.576	0.901	Cp								0.133265	0.043503
	P-value	0.000	0.003	0.000
Cl	Pearson’s R	-0.904	0.819	0.969	0.803	Cl							0.098462	0.011929
	P-value	0.000	0.000	0.000	0.000
L	Pearson’s R	0.096	0.151	0.009	-0.159	0.182	L						0.002111	0.000140
	P-value	0.648	0.472	0.967	0.446	0.469
p	Pearson’s R	0.156	-0.129	-0.094	-0.216	-0.177	0.834	p					0.001961	0.000123
	P-value	0.456	0.540	0.664	0.299	0.482	0.000
AD	Pearson’s R	-0.111	0.343	0.191	0.053	0.173	0.871	0.881	AD				0.001397	0.000080
	P-value	0.596	0.094	0.372	0.803	0.492	0.000	0.000
MD	Pearson’s R	0.154	-0.125	-0.090	-0.215	-0.173	0.837	1.000	0.883	MD			0.001132	0.000071
	P-value	0.462	0.550	0.675	0.303	0.491	0.000	0.000	0.000
RD	Pearson’s R	0.305	-0.411	-0.260	-0.360	-0.395	0.706	0.954	0.699	0.953	RD		0.000999	0.000073
	P-value	0.139	0.041	0.219	0.077	0.105	0.000	0.000	0.000	0.000
q	Pearson’s R	-0.484	0.928	0.539	0.466	0.736	0.430	0.187	0.629	0.191	-0.114	q	0.000363	0.000048
	P-value	0.014	0.000	0.007	0.019	0.001	0.032	0.371	0.001	0.361	0.588

MD: Mean diffusivity; FA: Fractional anisotropy; RA: Relative anisotropy; RD: Radial diffusivity; AD: Axial diffusivity; Cs: Spherical tensor; p: Pure isotropic diffusion; q: Pure anisotropic diffusion; L: Total magnitude of the diffusion tensor; Cl: Linear tensor; Cp: Planar tensor.

From the 55 pairs of bivariate correlations in each a group, statistical significances of the difference between r coefficients were observed in only seven pairs of variables: [Cs↔Cp], [FA↔Cl], [FA↔q], [RA↔q], [C↔q], [L↔p] and [L↔MD].

Mancova analysis

After adjusting for age, there was not interaction effect between the gender and clinical diagnosis [F (11, 23) = 1.115, P = 0.394]. There was not main affect of gender [F (11, 23) = 2.060, P = 0.069]; however, the main effect of diagnosis was statistically significant [F (11, 23) = 11.842, P < 0.001], corresponding to a large effect size (partial η² = 0.850). The age also had a significant influence as a covariate [F (11, 23) = 10.523, P < 0.001], and large effect size (partial η² = 0.834). Table 4 and Figure 3 depict the estimated marginal means; the age was controlled at the value of 43.92 years.

Table 4.

Estimated marginal means SE and CI of diffusion tensor imaging-derived tensor metrics (the effect of age was controlled at the value of 43.92 yr)

Tensor metric	Healthy brains				Brains with GBM
	Mean	SE	95%CI		Mean	SE	95%CI
			Lower	Upper			Lower	Upper
Cs	0.739511	0.009798	0.719577	0.759446	0.766043	0.007824	0.750126	0.781960
FA	0.290160	0.005721	0.278520	0.301799	0.255660	0.004568	0.246366	0.264954
RA	0.241025	0.008008	0.224734	0.257317	0.211498	0.006394	0.198490	0.224506
Cp	0.141366	0.007941	0.125210	0.157522	0.137961	0.006341	0.125061	0.150860
Cl	0.119041	0.003243	0.112443	0.125638	0.099495	0.002589	0.094227	0.104763
L	0.002287	0.000029	0.002227	0.002347	0.002103	0.000024	0.002055	0.002151
p	0.002122	0.000027	0.002068	0.002177	0.001946	0.000021	0.001903	0.001990
AD	0.001558	0.000020	0.001518	0.001598	0.001395	0.000016	0.001363	0.001426
MD	0.001225	0.000015	0.001194	0.001257	0.001124	0.000012	0.001099	0.001149
RD	0.001059	0.000015	0.001029	0.001089	0.000988	0.000012	0.000964	0.001012
q	0.000454	0.000011	0.000432	0.000476	0.000371	0.000009	0.000354	0.000389

MD: Mean diffusivity; FA: Fractional anisotropy; RA: Relative anisotropy; RD: Radial diffusivity; AD: Axial diffusivity; Cs: Spherical tensor; p: Pure isotropic diffusion; q: Pure anisotropic diffusion; L: Total magnitude of the diffusion tensor; Cl: Linear tensor; Cp: Planar tensor; GBM: Glioblastoma multiforme.

Figure 3.

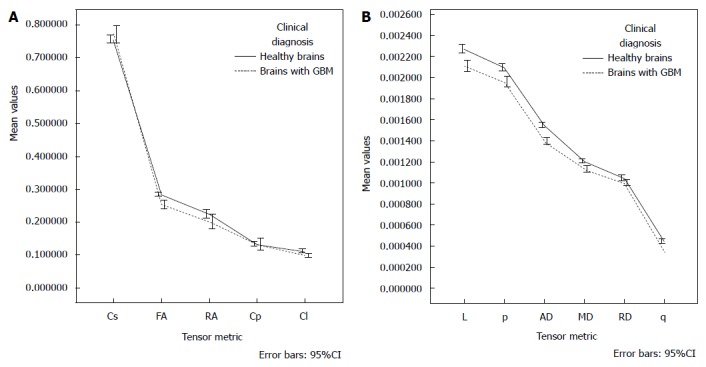
Graphs of the estimated marginal means for each tensor metric, the influence of age was controlled at the value of 43.92 years. MD: Mean diffusivity; FA: Fractional anisotropy; RA: Relative anisotropy; RD: Radial diffusivity; AD: Axial diffusivity; p: Pure isotropic diffusion; q: Pure anisotropic diffusion; L: Total magnitude of the diffusion tensor; Cl: Linear tensor; Cp: Planar tensor; GBM: Glioblastoma multiforme.

DISCUSSION

It is still not completely understood a priori which are the magnitudes and associations among DTI measurements observed in the evaluation of brain tumors[9]. The clinical relevance of these associations has been supported by several studies in the MR-DTI literature: Cs, Cp, Cl, FA and MD, have been related with brain abscesses, GBM and brain metastasis[2]; p, q and L measurements have also been previously applied to the evaluation of GBM and brain metastasis[3,21]; AD has been reported in encephalomyelitis of the spinal cord[22], AD and RD have been correlated with brain development[23], infantile spasm[24], amyotrophic lateral sclerosis[25], schizophrenia[26], and brain tumors[27]; with only one recent study integrating a tumor-region diagnostic evaluation of 11 DTI-metrics[4]. MD is understood as a synonym of the coefficient of diffusion in different space guidelines[28]. FA measures the directional movement of water molecules in the brain[29], it is an index of anisotropic diffusivity reflecting the integrity of myelinated axons[30].

One advantage of using a global approach is that not the only the size of the viable tumor is included (enhanced regions with Gadolinium), but also the non-apparent regions that undergo microscopic infiltration (edema and increased-size regions). Additionally, by using a global approach, all the inhomogeneity nature of GBM is included in a global measurement, a situation missed in a regional approach.

Some interesting associations are worthy to be noted: for example, there is no consensus of normal parameters between fractional anisotropy and mean diffusivity in a day-to-day basis[3]; traditionally, MD and FA showed negative correlation with increased MD and decreased FA in high signal-intensity perilesional regions when compared with normal axonal areas[31]; we observed a poor-negative non-significant correlation when controlling the effect of age and gender. One explanation might be that, different to MD that quantifies the degree of water molecules motion which is independ of myelinated axons; FA directly measures movement of water molecules along myelinated axons, it is a weighted anisotropic diffusion average[10]. The absence of partial correlation analyses in previous reports could explain some conflicts of diffusivity and anisotropy values characterizing tumoral regions[3,32]. For MD, the highest-significant correlation (r = 1) was observed with p and RD, a positive correlation between RD and MD have been previously observed in human brains[33]. We found an inverse relationship between MD with Cp, which seems opposite to previously suggested direction measuring MD, FA and the shape tensor metrics (Cp, Cs, Cl) between tumoral brain tissue, metastasis and abscesses[2]. FA’s mechanisms of decreasing its value in brain tumors are still unclear: it might represents neuronal and axonal infiltration with widening of extracellular space[32]; or tumoral substitution with decrement of extracellular space (this would explain the negative association between fractional anisotropy and tumoral cells)[34]. The FA can also be calculated by dividing q over L[9]; the q parameter could depict a comprehensive profile of brain tumor activity, in our study this parameter showed the highest-significant strength of correlation with FA (r = 0.928) in brains with GBM, it would seem an expected finding from its formula (ratio of q/L); however, our findings differ from other authors who observed no significant changes of q measurements in metastatic regions; this finding suggests that L instead of q, might be the main factor influencing the variability of FA. The inverse correlation between FA and RD observed in our study had been reported[33], although there are not statements of the expected magnitudes among these correlations.

For most of the correlates observed in this study, there was a decrease in the strength of the linear relationship after controlling the effect of age and gender. Poor correlations should be interpreted cautiously; in clinical settings these measurements might have the physiological implication to represent independent biological biomarkers. We do not have an explanation for the differences in the strength and directions of the observed correlations between normal and GBM brains, it is possible that the detailed info from the tumor may be obscured by the global measurement; the gender variable neither had interaction nor main effect in the observed measurements of DTI metrics; however, age did have a significant effect that should be controlled by researchers, as this variable could affect the p-value of the results.

As we mentioned in the results, there where some very strong, significant correlations observed only in brains with GBM (despite we use a global approach): [FA↔Cl (+)], [FA↔q (+)], [p↔AD (+)], [D↔MD (+)], and [MD↔RD (+)]; these findings were an indicator for us that, these parameters might be among the most useful for clinical diagnosis and/or treatment planning.

Comparing healthy brains vs brains with GBM, there were significant very strong bivariate correlations only depicted in GBM: [FA↔Cl (+)], [FA↔q (+)], [p↔AD (+)], [D↔MD (+)], and [MD↔RD (+)].

Our data might represent useful information for radiologist and/or bio imaging researchers trying to explain the relationships between tensor metrics to clinicians (neurologists, neurosurgeons, psychiatrist, neuro-oncologists, etc.) as well as in the preparation of prospective studies with clinical application. Further studies should address the significant differences we found in the correlations between healthy brains and brains with GBM, none of these results have been previously reported. It will be interesting to know the data analyses from other research groups that help validate and support the clinical significance of the results presented in this study.

Several limitations in our study and factors that influence the clinical application of DTI-metrics need to be addressed: our decision to evaluate a single, global measure for each tensor-metric relationships came up from reports depicting absence of P < 0.05 differences in fractional anisotropy between enhanced and not enhanced tumoral areas[35]; not significant differences between FA and MD measurements in tumor regions with distinct T₂-w signal-intensities[36], and findings of increased variability of FA measurements amont diverse brain areas[3], making all them a patent lack of agreement between investigators. Also, some studies have evaluated only selected ROIs within the tumors, missing major components of viable tumor and perilesional infiltration zones; other studies reporting ROIs only of the whole viable tumor mass, excluded many times peritumoral regions, wasting the opportunity to identify areas of severe infiltration within axons[3].

Although conventional sequences for the evaluation of GBM include the use of contrast enhancement agents (gadolinium), two situations could be observed in the managing assessment of these tumors: some regions of GBM could not depict enhancement because the tumor has not damaged enough the blood brain barrier, and second, there might be patients not able to receive gadolinium because chronic kidney failure; in both cases a global measurement of brain tissue would take into account non-evident abnormalities of the brain architecture.

Nowadays, there is still scarce evidence regarding the potential of these DTI biomarkers, for example, besides the clinical acceptance of FA; some studies have showed a significant increment of p (mean 68%) with evident decrement of q (mean 42%) in infiltrated axons[37]. Also, some proved parameters, for example, the increase of RD as a marker of demyelination and axonal loss has not had generalization in its use[33]. These facts reflect the limited acceptance of DTI by the medical community; it has not attained the same anatomic validation of structural myelin studies and so far does not discrimiante individual tracts or complex functional linkages among synapses[38]. DTI-derived tensor metrics intricacies to characterize brain tissue in health and disease might be affected among other variables by the quotient of extracellular to intracellular compartments; blood vessels density, abnormal accumulation of fluid in the interstitium, microscopic cysts, and the extracellular meshwork of proteins and carbohydrates that binds cells together[39]. The clinical value of our findings has yet to be determined, and the biological impact of the different metrics should be explained in more detail in clinical journals.

In conclusion, a comprehensive understanding of the currently available DTI-derived parameters will help researchers in the decision of which one to include in the diagnosis and treatment planning of brain tumors, researchers could know a priori expected relationships in a prospective analysis decreasing the underlying empiricism in this area. It is possible that several tensor metrics answer different questions; also, variations in DTI measures are not specific of one histologic type of tumor, which broaden the application of these biomarkers to a wider variety of intracranial pathologies. Given the increased availability of open source software in MRI units around the world, it is anticipated that measurements of DTI-derived tensor metrics may become a low-cost and common used approach.

COMMENTS

Background

In the last decade, advanced magnetic resonance techniques have adopted the use of diffusion tensor imaging (DTI)-derived metrics in the evaluation of glioblastoma multiforme. However, to best of our knowledge, there is currently neither a clear understanding of the expected measurements among these variables, nor existing studies reporting their correlations; likewise there is a lack of consensus about which of the tensor metrics available should be used in the evaluation of brain tumors.

Research frontiers

This study reports measurement of eleven DTI-derived tensor metrics which have only recently been described in the litarature: fractional (FA) and relative anisotropy (RA); pure isotropic (p) and anisotropic diffusions (q), total magnitude of diffusion (L); linear (Cl), planar (Cp) and spherical tensors (Cs); mean (MD), axial (AD) and radial (RD) diffusivities.

Innovations and breakthroughs

Compared with previous studies, this report provides novel quantitative data of DTI-derived metrics in normal brains and brain with glioblastoma multiforme, its main aim is to decrease the underlying empiricism involving these parameters. Additionally, innovation is depicted in the use of a global approach (whole-brain) instead of the conventional tumor-region assessment; this approach warrants the inclusion of all tumor regions (ROIs measurements in the cystic cavity, enhancing rim, edema, and normal-appearing white matter regions).

Applications

Data in this study might represent useful information for radiologist and/or bio imaging researchers trying to explain the relationships between tensor metrics to clinicians (neurologists, neurosurgeons, psychiatrist, neuro-oncologists, etc.) as well as in the preparation of prospective studies with clinical application. The authors believed that the very strong, significant correlations observed only in brains with glioblastoma multiforme (GBM) (despite the authors use a global approach): [FA↔Cl (+)], [FA↔q (+)], [p↔AD (+)], [D↔MD (+)], and [MD↔RD (+)]; might be among the most useful parameters for clinical in diagnosis and/or treatment planning. Furthermore, the gender variable neither had interaction nor main effect in the observed measurements of DTI metrics; however, age did have a significant effect that should be controlled by researchers, as this variable could affect the P-value of the results. One advantage of using a global approach is that not the only the size of the viable tumor is included (enhanced regions with Gadolinium), but also the non-apparent regions that undergo microscopic infiltration (edema and increased-size regions). As this DTI-derived metrics do not require the use of a constrat agent (gadolinium), the proposed global approach takes into account non-evident abnormalities of the brain architecture which occurs in some regions of GBM without enhancement because the tumor has not damaged enough the blood brain barrier, and also, this approach can be used in patients not able to receive gadolinium because chronic kidney failure.

Terminology

The DTI-derived metrics reported in this study were calculated from the below described formulas:

MD = D = (λ₁ + λ₂ + λ₃)/3

FA = [(3/2)(q/L)]^1/2

= (3/2)^1/2{[(λ₁ - D)²+(λ₂ - D)²+(λ₃ - D)²]/(λ₁² + λ₂² + λ₃²)}^1/2

RA = q/p = {[(λ₁ - D)² + (λ₂ - D)² + (λ₃ - D)²]^1/2}/[3^1/2D]

RD = (λ₂ + λ₃)/2

AD = λ₁

Cs = 3λ₃/(λ₁ + λ₂ + λ₃)

Pure Isotropic Diffusion (p)

p = 3^1/2D = (λ₁ + λ₂ + λ₃)/3^1/2

Pure Anisotropic Diffusion (q)

q = [(λ₁ - D)²+(λ₂ - D)²+(λ₃ - D)²]^1/2

Total Magnitude of the Diffusion Tensor (L)

L = (p² + q²)^1/2 = (λ₁² + λ₂² + λ₃²)^1/2

Linear Tensor (Cl)

Cl = (λ₁ - λ₂)/(λ₁ + λ₂ + λ₃)

Planar Tensor (Cp)

Cp = 2(λ₂ - λ₃)/(λ₁ + λ₂ + λ₃)

Peer-review

The authors studied the relationships of 11 DTI-derived tensor metrics between healthy brains and brains with GBM. They used a noval technique, i.e., a single global measure of the whole brain for each metric rather than a conventional approach of measuring the entire tumor or some regions.