Mechanical and energetic consequences of reduced ankle plantar-flexion in human walking

ABSTRACT

The human ankle produces a large burst of ‘push-off’ mechanical power late in the stance phase of walking, reduction of which leads to considerably poorer energy economy. It is, however, uncertain whether the energetic penalty results from poorer efficiency when the other leg joints substitute for the ankle's push-off work, or from a higher overall demand for work due to some fundamental feature of push-off. Here, we show that greater metabolic energy expenditure is indeed explained by a greater demand for work. This is predicted by a simple model of walking on pendulum-like legs, because proper push-off reduces collision losses from the leading leg. We tested this by experimentally restricting ankle push-off bilaterally in healthy adults (N=8) walking on a treadmill at 1.4 m s⁻¹, using ankle–foot orthoses with steel cables limiting motion. These produced up to ∼50% reduction in ankle push-off power and work, resulting in up to ∼50% greater net metabolic power expenditure to walk at the same speed. For each 1 J reduction in ankle work, we observed 0.6 J more dissipative collision work by the other leg, 1.3 J more positive work from the leg joints overall, and 3.94 J more metabolic energy expended. Loss of ankle push-off required more positive work elsewhere to maintain walking speed; this additional work was performed by the knee, apparently at reasonably high efficiency. Ankle push-off may contribute to walking economy by reducing dissipative collision losses and thus overall work demand.

Summary: Ankle push-off plays an important role of the energy expenditure of human walking, which can be explained by the mechanical work performed by the lower extremity joints.

INTRODUCTION

During human walking, the ankle produces the highest mechanical power among the joints, in a burst late in the stance phase termed push-off. Its importance is illustrated by cases of impaired or reduced push-off, which generally require considerably more metabolic energy expenditure to walk at the same speed (Doets et al., 2009; van Engelen et al., 2010; Waters and Mulroy, 1999). If walking were only a matter of supplying a requisite amount of forward propulsion, then other joints might be expected to supply a greater proportion of the mechanical work to offset reduced push-off work, and not necessarily at higher metabolic cost. The actual energetic penalty suggests that the normal push-off conveys some unique advantage, perhaps in its timing or spatial location, that is not presently understood. To gain insight into this matter, we proposed and tested a mechanistic explanation for the disadvantages of reduced ankle push-off.

Ankle push-off appears to be important to walking economy. The ankles normally produce a burst of positive push-off power, peaking at more than 2.5 W kg⁻¹ (e.g. Zelik and Kuo, 2010). That peak is more than three times the maximum power produced by the other joints, but is reduced considerably in pathological gait. For example, the peak can be reduced by more than half in patients with multiple sclerosis, those recovering from stroke (Bregman et al., 2011) and individuals with ankle arthrodesis or arthroplasty (Singer et al., 2013). The energetic penalty varies considerably with severity and condition, but typically entails an increase of 30% or more in net metabolic power (subtracting the cost of upright standing from gross power) to walk at the same speed (Doets et al., 2009; Torburn et al., 1995; Waters and Mulroy, 1999). There are surely many pathology-specific contributors to that penalty, but here we examined fundamental costs that may potentially stem from altered mechanics during push-off.

The energy expenditure of walking is explained in part by the mechanical work performed in the transition between pendulum-like steps (Kuo et al., 2005). The body center of mass (COM) is located near the pelvis and moves in an arc determined by the pendulum-like stance leg (Fig. 1). The COM velocity must be redirected upward between the end of one pendulum phase and the beginning of the next (Adamczyk and Kuo, 2009; Kuo, 2002). This entails negative, dissipative work by the leading leg's ground collision, which is ameliorated by positive push-off work from the trailing leg, especially if it is initiated earlier than collision (Kuo, 2002). In humans, the positive and negative work overlap during double support (Donelan et al., 2002a), but with earlier phasing for push-off (Adamczyk and Kuo, 2009). Indeed, in cases of total ankle arthroplasty, patients produce less push-off, resulting in greater collision losses and greater metabolic energy expenditure at a given speed (Doets et al., 2009). But one discrepancy is that overall positive work performed on the COM is not observed to increase (Doets et al., 2009), as would be expected from the imbalance between push-off and collision. The theory of step-to-step transitions would therefore appear to only partially explain the effects of reduced push-off. Investigation at the joint level rather than COM may reveal whether the total positive work performed by lower extremity joints can explain the energetic cost of walking with reduced push-off.

Fig. 1.

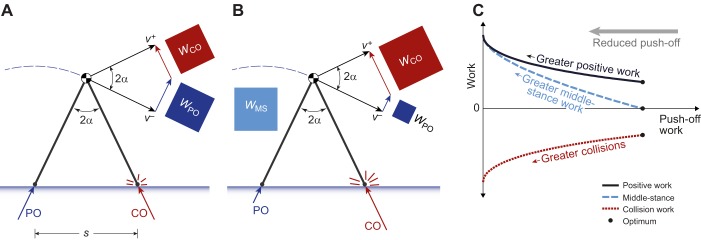
Dynamic walking model predicts effects of reduced push-off work. (A) Normal optimum . The model has pendulum-like legs supporting body center of mass (COM), whose velocity must be redirected from a downward-and-forward v⁻ at the end of one pendulum's stance phase to an upward-and-forward v⁺ at the beginning of the next pendulum-like stance phase. This is most economical when positive push-off work is performed impulsively just before and in equal magnitude to the leading leg's negative collision work. Ideal impulses PO (push-off) and CO (collision) perform work W_PO and W_CO proportional to the square of impulse magnitude (Kuo, 2002). In the model, PO and CO occur sequentially in an instant between the two pendulum-like stance phases. (B) Reduced push-off. For the same speed and step length, restricted push-off should result in greater collision and more energy dissipation. The COM velocity must be increased during the rest of the step, requiring net positive ‘middle-stance’ work, W_MS, and greater positive work overall. (C) Compensatory work. Model prediction of collision and middle-stance work as a function of push-off work, for walking at fixed speed and step length. Starting from the most economical case (right-most point on the plot), reduced push-off work leads to greater magnitudes of negative collision work and positive middle-stance work. s, step length; 2α, inter-leg angle.

There are two potential explanations for this discrepancy. The first is that the muscles might perform additional mechanical work not observed in previous studies. Work performed on the COM is an indicator of overall work from an entire limb, convenient for showing when the two limbs simultaneously perform positive and negative work (Donelan et al., 2002b). But it is also an incomplete measure, because it does not indicate when one joint performs work cancelling out another joint within the single limb (Donelan et al., 2002a). It is possible that reduced push-off does indeed increase the overall positive work performed during a step, if measured at the joints instead of the limbs. The alternative possibility is that there is nothing special about push-off so long as propulsion with a requisite amount of work is performed elsewhere in the body. The energetic penalty associated with reduced push-off might instead be explained by poor efficiency of the muscles performing the same amount of propulsive work, rather than the mechanics of COM motion as we have theorized. This might be the case with co-morbidities accompanying limb loss or joint fusion. For example, Wutzke et al. (2012) have proposed that the hip muscles may be less efficient when replacing the work normally performed at the ankle, without having to perform more work overall. However, in the case of stroke patients, the elevated metabolic cost of walking appears to be explained by greater mechanical work (Detrembleur et al., 2003), without differences in muscle efficiency (Stoquart et al., 2005, 2012).

List of symbols and abbreviations

AFO

ankle–foot orthoses

COM

center of mass

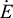
net metabolic rate

f

step frequency

ground reaction force

g

gravitational acceleration

L

leg length

M

body mass

P_COM

instantaneous center of mass work rate

P_joint

summed joint power

s

step length

v

walking speed

center of mass velocity

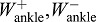
ankle joint work per stride (positive, negative)

W_CO

center of mass work during collision

hip joint work per stride (positive, negative)

sum of joint work per stride (positive, negative)

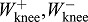
knee joint work per stride (positive, negative)

W_MS

center of mass work during middle-stance

W_PO

center of mass work during push-off

In the present study, we addressed these questions in two ways. First, we used a simple dynamic walking model (Kuo, 2002) to demonstrate the theoretical effects of bilaterally reduced push-off for a fixed walking speed. Although the model does not predict how the joints will compensate for reduced push-off, it does suggest that overall work will increase, even if not captured by work performed on the COM. Second, we experimentally tested human subjects walking with artificially constrained ankle push-off (Fig. 2). To focus only on the mechanical effects of reduced push-off, we tested healthy subjects and did not consider the many co-morbidities of pathological conditions. Our experiment allowed for continuous adjustment of the degree of constraint, which facilitates identification of trends associated with reduced push-off, thus enabling a test of whether the overall amount of mechanical work by the joints increases with artificially reduced push-off as predicted by the step-to-step transition hypothesis, or whether the energetic penalty is explained better by poor efficiency of the joints that perform compensatory work.

Fig. 2.

Method for experimentally reducing push-off. (A,B) An ankle–foot orthosis (AFO) was modified with steel cables restricting plantar-flexion motion on both sides. (C) The relative lengths of cables (25–29 cm) for five constraint conditions experienced by human subjects walking at constant speed (1.40 m s⁻¹).

MATERIALS AND METHODS

Model

We used a dynamic walking model (Fig. 1) to predict the effects of reduced push-off on locomotion dynamics and energetics. In the ‘simplest walking model’ (Kuo, 2002), the legs behave like ideal pendulums, with the body COM moving in an inverted pendulum arc atop the stance leg. With each footfall, an impulsive collision redirects the COM velocity to a new arc determined by the leading leg. This collision performs negative work on the COM, and requires positive work to offset the loss. The most economical solution is an impulsive push-off just prior to, and equal in magnitude to, the leading leg collision (Fig. 1A). This reduces the collision loss and maintains walking speed with the least positive work. These principles have been tested experimentally and been found to predict the mechanical and energetic effects of walking with, for example, greater step lengths (Donelan et al., 2002a) and step widths (Donelan et al., 2001). Here, we applied the same model, but explicitly computed the effect of reduced push-off.

There are several consequences if optimal push-off is restricted (Fig. 1B). First, reduced push-off increases the leading leg's ensuing collision. Second, the imbalance in push-off and collision work requires more positive work to be performed in the interval after collision and before the next push-off, referred to here as the middle-stance phase (Adamczyk and Kuo, 2014). Third, the imbalance also requires more positive work overall from the push-off and middle-stance phases. All of these effects are predicted quantitatively by models described previously (Adamczyk and Kuo, 2009; Kuo, 2002; Kuo et al., 2005), as summarized in the Appendix. The overall result is that collision work W_CO is predicted to change with push-off work W_PO according to:

(1)

where s denotes step length, L leg length, M body mass and v walking speed. To ensure zero net work over a gait cycle, the stance phase work between collision and push-off, termed middle-stance work W_MS, is:

(2)

When push-off work is restricted, the magnitudes of collision and middle-stance work both increase for a given walking speed and step length (Fig. 1B). These effects are approximately linear for push-off work reductions up to about 50% (Fig. 1C), for conditions similar to those of the experiment described below (equivalent to dimensionless speed of 0.44 and step length 0.78, using M, L and gravitational acceleration g as base units). Although this model is quite crude compared with the complexity of actual human walking, it yields predictions that can be tested experimentally.

Experimental method

We tested the hypotheses informed by the model by measuring the work performed by healthy adults while they walked with restricted ankle plantar-flexion at a fixed speed. Rather than control push-off explicitly, we found it more practical to control kinematic displacement of the ankle. We therefore tested whether this restriction was indeed able to affect ankle work as intended, and in turn create the predicted increases in overall positive mechanical work and overall metabolic cost demonstrated by the model.

During the experiment, eight subjects walked at 1.40 m s⁻¹ while wearing bilateral ankle–foot orthoses (AFO, Bledsoe Brace System, Grand Prairie, TX, USA) modified to restrict ankle plantar-flexion range of motion (Fig. 2). This was achieved through the addition of steel cables between the shank and forefoot. We applied five controlled conditions with different cable lengths (including one with no restriction). For comparison, a separate normal shod condition, in which subjects wore their normal street shoes, was conducted. Subjects were young adults (aged 21–27 years, 6 males and 2 females) with body mass M of 76.6±8.8 kg (mean±s.d.) and leg length L of 0.95±0.06 m. All subjects provided written informed consent prior to the study, according to Institutional Review Board procedures. To facilitate comparison between conditions, all data were collected at the same controlled walking speed.

The data collected included joint kinematics and kinetics, mechanical work performed on the COM, and metabolic energy expenditure. Subjects walked on a split-belt instrumented treadmill (Bertec, Columbus, OH, USA) that yielded ground reaction forces from the individual legs. Lower extremity kinematic data were recorded using a marker-based motion-capture system (Phasespace, San Leandro, CA, USA). We measured oxygen consumption and carbon dioxide production using a wireless portable respirometry system (CareFusion, Vernon Hills, IL, USA).

These data were used to quantify mechanical work performed on the COM and by the lower extremity joints. The instantaneous COM work rate P_COM was calculated as the inner product of ground reaction force of each leg and COM velocity (Donelan et al., 2002b), where the velocity was computed by integrating the total ground reaction force, subject to constraints on periodicity. The stride was defined as starting and ending at consecutive same-side heelstrikes and was examined in terms of three phases defined by COM work rate zero-crossings: collision (about 0–18%), middle-stance (about 18–49%) and push-off (about 49–66%). The work rate was integrated over each of these intervals (W_CO, W_MS and W_PO, respectively), and separately over the positive intervals to yield positive work per stride, W⁺. The middle-stance work includes two phases we have previously referred to as rebound and pre-load (Donelan et al., 2002a); these were lumped together here because the model only predicts trends in overall work between collision and push-off. Another possible compensation for restricted push-off would be to change gait parameters, for example walking with shorter steps while maintaining the same speed. We did not specifically predict such effects, but tested for these changes by examining gait parameters such as step length, step time and double support time.

Joint kinematics and kinetics were computed from ground reaction force and motion capture data using standard methods. Commercial software (Visual3D, Germantown, MD, USA) was used to calculate joint angles, moments and powers for the ankle, knee and hip, in three dimensions. As a simple summary of power from an entire leg, we calculated summed joint power P_joint by adding together the powers from ankle, knee and hip of one leg. Positive (negative) joint work per stride was defined as the integral of positive (negative) intervals of each joint power. We also calculated the positive (negative) summed joint work per stride 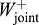() by adding together the positive (negative) ankle, knee and hip work of one leg. For simplicity, only sagittal plane angles and moments are plotted here, although power and work quantities were calculated in three dimensions.

We estimated the net metabolic rate of energy expenditure from oxygen consumption and carbon dioxide production data. These data were collected over walking trials of at least 6 min, with only the final 3 min of each trial retained for analysis to ensure steady state. Gross metabolic energy expenditure (in W) was calculated using standard conversion factors (Brockway, 1987). Net metabolic rate was defined as the gross metabolic rate for walking minus that for quiet standing (110±22 W).

To account for differences in subject body size and facilitate comparison with the model, measurements were normalized to dimensionless form, using base units of body mass M, standing leg length L (ground to greater trochanter) and gravitational acceleration g. The mean normalization constant for force was therefore Mg (average 751.87 N), for work MgL (717.10 J) and for power Mg^1.5L^0.5 (2299.82 W). We performed statistical tests to check three main predictions. The first was to determine whether kinematic ankle restriction could reduce push-off work, examined through repeated measures ANOVA across conditions. We then tested whether the following work quantities increased with reduced push-off work: collision work W_CO, middle-stance work W_MS, and total positive work W⁺. Finally, an increase in total positive work should lead to an increase in net metabolic rate 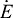as a function of push-off work. These were all tested with linear regression against push-off work W_PO, with a significant slope indicated by its 95% confidence interval and individual offset for each subject. The threshold of significance for all tests was set at α=0.05. We also examined several other quantities such as joint work measures, but there were no specific predictions other than that total joint work should increase with reduced push-off.

RESULTS

Restricted ankle plantar-flexion had a substantial effect on the mechanics and energetics of walking at fixed speed. We found that the ankle constraints did reduce push-off work as intended, which in turn led to increases in positive work performed elsewhere, as well as greater metabolic cost. These effects occurred despite no statistically significant differences in step length, step frequency f and double support time (see Table 1), which could potentially affect energy expenditure if they were to change appreciably. Below, we first describe some qualitative observations of the effects of the restricted ankle motion on time-varying variables, followed by quantitative summaries of the mechanical and energetic effects over an entire stride. A stride was defined as starting and ending at consecutive same-side heelstrikes, and examined in three phases defined by zero-crossings of COM work rate: collision (about 0–18%), middle-stance (about 18–49%) and push-off (about 49–66%).

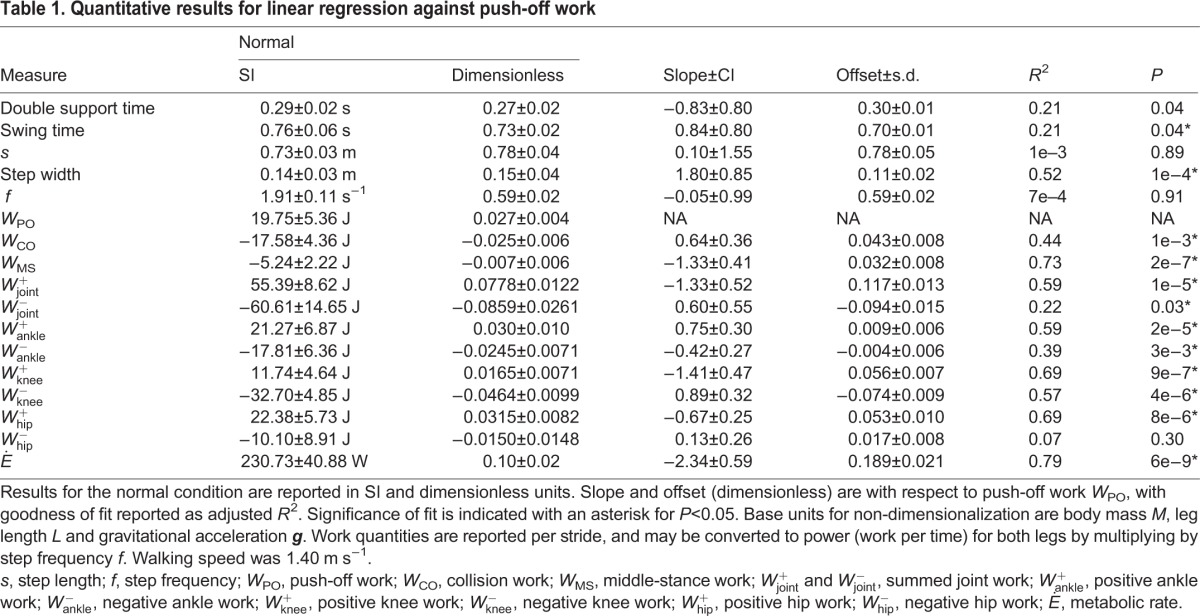
Table 1.

Quantitative results for linear regression against push-off work

A number of qualitative trends from the ankle restrictions were subjectively observed in the experimental data. Examining the ankle (Fig. 3), angular displacement was reduced by as much as 40 deg, and peak power was substantially reduced during push-off (particularly near 60% stride). The ankle moment trajectory was relatively unaffected despite the restriction, as it is governed by the forward progression of the center of pressure (Adamczyk et al., 2006; Bregman et al., 2011; Vanderpool et al., 2008; Zelik et al., 2014). While the constraints were generally effective in reducing plantar-flexor motion in a controlled manner, depending on their normal range of ankle motion and alignment of the AFO some subjects were relatively unaffected by the two least restrictive conditions. There were also effects on the force and power trajectories (Fig. 4). The first peak of the vertical ground reaction force tended to increase with greater restriction, whereas the second peak tended to decrease (Fig. 4A). The anterior–posterior force exhibited decreasing amplitude with greater ankle restriction (Fig. 4B). This caused corresponding changes in instantaneous COM work rate: the amplitude of push-off work rate decreased while collision amplitude increased with greater restriction (Fig. 4C). During the normal shod condition, subjects performed positive and then negative work during middle-stance, yielding slightly negative work overall. With increasing ankle restriction, the middle-stance work shifted toward positive. This was true for both the positive and negative intervals of this phase, which are termed rebound and pre-load, respectively (Donelan et al., 2002a; Kuo et al., 2005). The summed joint power, defined as the sum of ankle, knee and hip power, had a similar trend during middle-stance, also shifting to the positive, an indication of more positive work overall (Fig. 4D).

Fig. 3.

Ankle angle, moment and power versus stride time for all experimental conditions. Shown are averaged trajectories across subjects (N=8) over one full stride (defined by same-side heelstrikes), with increasing push-off restriction (solid line to dotted lines), as well as normal shod walking (solid gray line), all at 1.40 m s⁻¹. Moment and power are shown in terms of dimensionless units (left-hand vertical axes), using body mass, leg length and gravitational acceleration as base units, and with equivalent SI units (right-hand axes). Ext., extension; Flex., flexion.

Fig. 4.

Effect of ankle restriction on ground reaction forces and power measures. (A) Vertical ground reaction force and (B) horizontal (fore–aft) ground reaction force versus stride time. (C) Instantaneous COM work rate (dot product of COM velocity with ground reaction force from one leg) versus time. Zero-crossings of COM work rate define collision, middle-stance and push-off phases of stride (CO, MS and PO, respectively). Middle-stance is an interval including both positive rebound and negative pre-load work (RB and PL). (D) Summed joint power (sum of ankle, knee and hip powers) versus time. Left-hand vertical axes show dimensionless units, and right-hand vertical axes show equivalent dimensional SI units. Data are trajectories averaged across subjects (N=8) walking at 1.40 m s⁻¹.

The observations above are supplemented by statistical examination of the mechanical work performed on the COM (Fig. 5). Significant differences were observed in COM push-off, middle-stance and collision work across ankle restriction conditions (repeated-measures ANOVA, P=1e−12, 7e−3 and 1e−9, respectively). With increasing restriction, push-off decreased from about 19.1 J to 11.8 J, middle-stance work increased from about −2.7 J to 6.8 J, and collision work increased from about −19.4 J to −23.1 J. Individual joint contributions are reported further below.

Fig. 5.

Summary of work performed on COM as a function of ankle restriction. Shown are COM work per step during collision, middle-stance and push-off phases (W_CO, W_MS and W_PO, respectively), at 1.40 m s⁻¹. Error bars denote s.d., asterisks indicate statistically significant differences across conditions (P<0.05, repeated-measures ANOVA). Vertical axes are shown with dimensionless and SI units (left- and right-hand sides, respectively).

We next examined work as a continuous function of COM push-off work (rather than discrete conditions; see Table 1 for quantitative summary). In terms of COM work per stride, reduced push-off led to more collision work (Fig. 6A), as evidenced by a significant linear trend between the two, with slope 0.64 (change in collision work divided by change in push-off work). Correspondingly, reduced push-off also led to more middle-stance work (i.e. it became more positive; Fig. 6A), with slope −1.32. Total positive COM work did not change significantly with reduced push-off work. The positive sum of joint work per stride increased with reduced push-off, with a slope of −1.33 (Fig. 6B). Negative summed joint work increased in magnitude with reduced push-off, with slope 0.60.

Fig. 6.

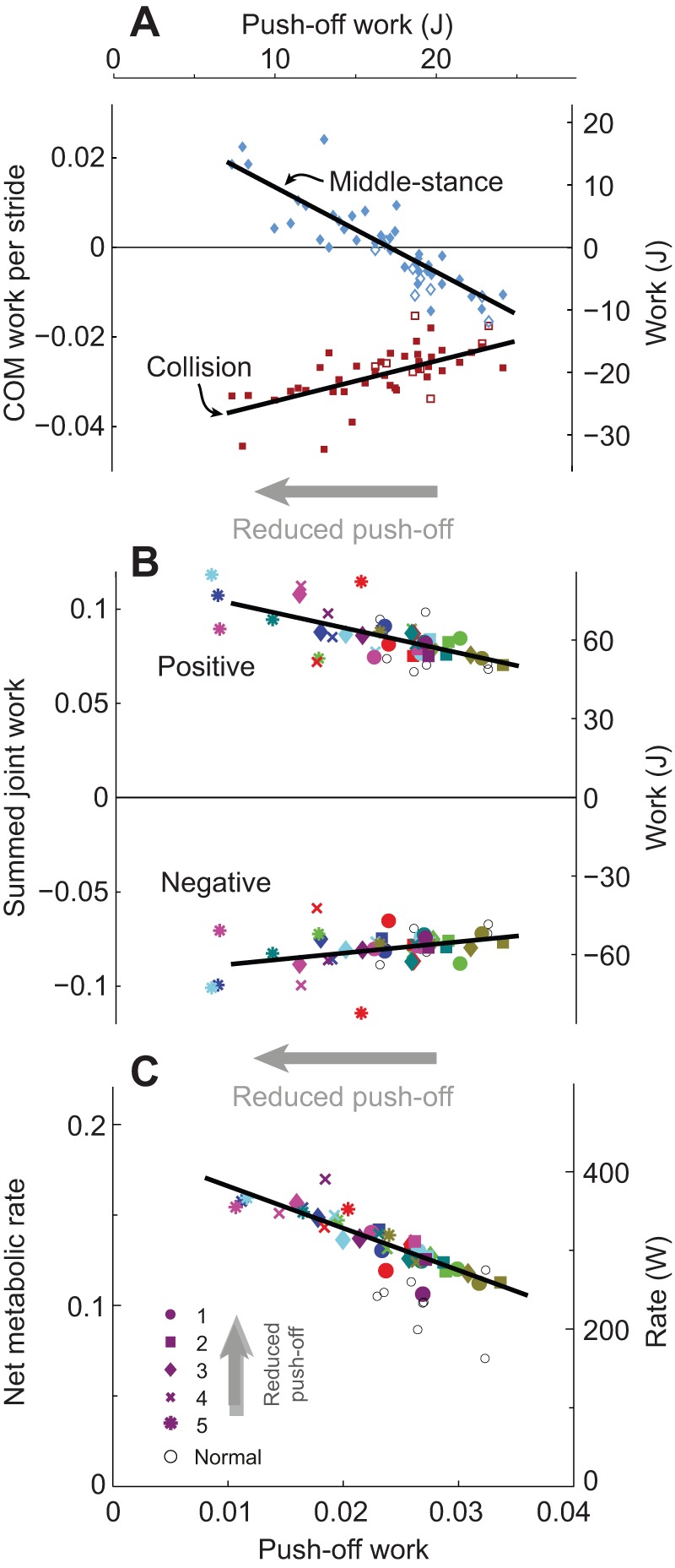
Effect of reduced push-off work on overall mechanical work on COM, summed joint powers and metabolic energy expenditure. (A) Collision work and middle stance work per stride (W_PO and W_CO, respectively) as a function of COM push-off work. (B) Positive and negative summed joint work per step versus push-off work. Summed joint work is defined as the integral of positive and negative intervals of summed joint powers (see Fig. 4D). (C) Net metabolic rate as a function of COM push-off work. Data are shown for each subject and experimental condition (denoted by color and symbol, respectively), along with linear fits (all statistically significant, P<0.05). Vertical axes are shown with dimensionless and SI units (left- and right-hand axes, respectively).

Net metabolic rate also increased with reduced push-off (Fig. 6C). The non-dimensional slope of the change was −2.34 (change in metabolic rate divided by change in push-off work per step). Comparing rates directly (change in metabolic rate divided by change in push-off work rate across both legs), the equivalent slope was −3.94. Similarly, the change in metabolic rate per change in positive summed joint work rate for the two legs was 2.91.

Reduced push-off also affected the work performed by the individual joints (Fig. 7). As push-off was reduced, positive ankle work and negative work per stride decreased significantly in magnitude (quantitative summary in Table 1). The ankle restrictions also had slightly less effect on ankle work itself than on COM push-off, with a slope of 0.75 (change in positive ankle work per change in COM push-off). At the knee, both positive and negative work increased significantly in magnitude with reduced push-off, with slope −1.41 and 0.89. At the hip, only positive work increased significantly with reduced push-off, with slope −0.67.

Fig. 7.

Lower extremity joint kinematics and kinetics as a function of ankle restrictions. (A) Angle, moment and power trajectories versus time for ankle, knee and hip. Data shown are trajectories averaged across subjects (N=8). Angles and moments are defined as positive in extension (Ext.) and negative in flexion (Flex.). (B) Positive and negative joint work per stride for ankle, knee and hip, as a function of push-off work. Data points are shown for each subject and each condition (denoted by color and symbol, respectively), all at 1.40 m s⁻¹. Moment, power and work are shown with dimensionless and SI units (left- and right-hand vertical axes, respectively).

DISCUSSION

This study tested mechanisms by which reduced push-off leads to increased energetic cost during walking. A simple model (Kuo, 2002) predicts that reduced push-off work from the trailing leg should lead to greater collision losses at the leading leg, which must be offset with more positive work elsewhere in the gait cycle to maintain the same walking speed. We experimentally applied a kinematic restriction to the ankles, which achieved the aim of reducing the push-off work produced by healthy subjects. This was accompanied by more dissipative collision work, more positive work by the joints over the entire stride, and increased overall metabolic energy expenditure. These results are consistent with the proposed mechanistic link between ankle push-off and overall energy expenditure. The results also yield insight into strategies used by the subjects to compensate for reduced push-off, with possible implications for patient groups with similar deficits.

Reduced push-off resulted in more work performed elsewhere in the gait cycle, and greater dissipation during the opposite leg's collision. For each 1 J of reduced push-off work, subjects performed an additional 0.64 J of dissipative collision work (from the slope of linear fits in Fig. 6), which was compensated by 1.33 J more work during middle-stance. The dissipation was somewhat less than predicted by the model (about 0.74 J more collision, 1.74 J more middle-stance work for equivalent speed and step length), suggesting that subjects were able to adjust their gait to avoid increased collision to some degree. They nevertheless paid a 33% penalty in positive work for not performing the positive work at push-off. No such penalty would be expected if walking were solely a matter of performing a constant amount of positive, propulsive work. Our results agree with the model prediction, that a properly timed push-off can reduce the energy dissipated by collision (Eqn 1), which then reduces the amount of positive work needed over a stride (Eqn 2).

There were several ways that subjects compensated for reduced push-off. The COM work rate during middle-stance shifted positively, in terms of both greater positive rebound work and less negative pre-load work. Here, COM measures are limited in their resolution, and closer examination of joint kinetics reveals that the knee bears the brunt of the compensations for reduced ankle push-off. When ankle push-off was restricted, the knee experienced greater flexion while producing a considerably greater extension moment during much of the stance phase. The net effect was to contribute substantially more work during most of middle-stance, and particularly during rebound. Further, knee power remained positive for part of the (net negative) pre-load phase, exhibiting simultaneous positive and negative work within the limb that is not captured by examining COM work.

There were also subtler compensations at the other joints. For example, the ankle appeared to contribute less negative work, particularly during pre-load. This is largely consistent with the expectation that a smaller range of motion should reduce the amount of both negative and positive work at the ankle. A separate model of walking, including series elasticity at the ankle, suggests that elastic pre-load can enhance push-off work through passive dynamics (Zelik et al., 2014). Thus, we would not consider reduced ankle pre-load to be energetically advantageous, even though it contributed to the positive shift in middle-stance work. Separate from that effect, the ankles also appeared to perform slightly less negative work immediately following heelstrike, and the hip performed slightly more positive work over a stride. Our subjects therefore redistributed work across joints and throughout the gait cycle, and performed more of it overall, to compensate for reduced push-off.

A primary consequence of these changes in work was greater metabolic energy expenditure. We observed about an extra 2 W of metabolic power for each 1 W reduction in push-off work. For reference, a 50% reduction in push-off resulted in an energetic penalty comparable to carrying an extra load of about 10 kg (Huang and Kuo, 2014). As discussed above, no increase of metabolic energy expenditure would be expected if walking were merely a matter of supplying sufficient work. Instead, we observed more total joint work (especially at the knee) with reduced push-off, indicating that the benefit of push-off is not only performing positive work but also reducing the total work requirement.

Our findings regarding bilateral push-off may be compared with unilateral effects. For example, unilateral amputees compensate for asymmetric push-off with greater middle-stance work and greater positive work overall (Adamczyk and Kuo, 2014). In contrast, another study by Wutzke et al. (2012) examining the effects of unilaterally fixing the ankle with a brace found greater work at the hip and greater metabolic energy expenditure, similar to our observations. But they did not find greater work at the knee, or greater mechanical work overall. It is, however, difficult to interpret those results because the unilaterally fixed condition was compared against a control case where the unilateral ankle brace was worn but not fixed, which resulted in substantial asymmetry in hip power even in the control case. It is possible that a comparison between the fixed ankle and a more symmetric control condition would have yielded greater overall joint work, or greater middle-stance work, as we would expect.

While these results demonstrate a clear link between push-off and economical gait, there are opposing opinions regarding ankle push-off. Others have proposed that push-off aids initiation of the swing phase (Bajd et al., 1997; Meinders et al., 1998), more so than redirection of the COM (Lipfert et al., 2014). Reduced push-off might then be expected to adversely affect swing initiation. This would be expected to result in either a slower swing phase or the avoidance of slow swing through compensations such as greater moments and powers at the hip and knee. In fact, swing phase appeared slightly faster, not slower, with reduced push-off (as indicated by a positive correlation between swing time and push-off work; Table 1). We did not observe significant change in hip and knee moments and powers. Our data therefore do not suggest a strong detriment in swing phase initiation due to reduced push-off.

The findings presented here are subject to a number of limitations. We reduced push-off work with an artificial kinematic constraint. This may have had unintended consequences, such as causing subjects to exaggerate knee flexion (and thus negative work) during collision (Fig. 7). A more direct approach might have been to constrain ankle kinetics more explicitly, for example with mechanical damping, or more invasively through a nerve block to the plantar-flexor muscles, albeit with potential side-effects. And despite considerable ankle restrictions, subjects still performed considerable push-off with parts of the body other than the ankle, including directions outside the sagittal plane. We restricted the ankle because its power production coincides well with push-off (COM work rate; Fig. 4), although hip and knee contribute as well, albeit to lesser degree. Our model is concerned only with reducing total push-off and not with particular joints (see Fig. 7). There may therefore be other ways to experimentally reduce push-off that may be more effective, or better model-specific pathologies. Depending on the pathology, the actual effect on push-off in patients, and associated co-morbidities, could potentially be quite different from the constraint applied here. For example, persons with reduced walking economy may tend to prefer slower walking speeds rather than expending more energy (Waters and Mulroy, 1999). They may also prefer shorter steps for a given speed, a potential adaptation we did not observe in healthy subjects. To examine fundamental, mechanistic effects, we focused on able-bodied individuals under relatively controlled conditions, with a model that also predicts effects at slower speeds not tested here. Future studies might benefit from experimental models more similar to actual pathologies affecting push-off, and overground rather than treadmill walking.

Another challenge we encountered was the quantification of mechanical work. Our model only predicts broad trends in work without the ability to predict how it might be redistributed among the joints. The measurements were similarly broad, with COM and summed joint work both characterizing the overall work performed on the body in roughly similar ways (Fig. 3). But positive COM work over a stride appears not to capture the increased work demands resulting from reduced push-off (Doets et al., 2009), which appear to be met by the knee and hip (Fig. 7). Increased positive joint work may cancel negative work at other joints, for example the ankle during pre-load, and therefore appear as less negative work on the COM rather than more positive work. We thus found it more suitable to examine the COM work specifically during the middle-stance phase (including both rebound and pre-load phases), which did yield more work with greater ankle restriction, as expected. Middle-stance work is actually more relevant to the simple model, which does not predict the separate effects on rebound and pre-load phases.

We also caution that all of the empirical work measures are incomplete. Although we found COM work to be a helpful measure for testing some hypotheses (e.g. Adamczyk et al., 2006; Donelan et al., 2001, 2002a; Zelik and Kuo, 2010), it does not quantify work performed peripheral to the COM (Zelik and Kuo, 2012; Zelik et al., 2015). Summed joint work appears more suitable for that purpose, and the individual joint powers also help to determine compensation for reduced push-off. But joint powers, like all other non-invasive measures practical for human locomotion, are also only indirect indicators of work that cannot distinguish between the active work of muscle fascicles and the passive elastic work of series tendons or parallel ligaments. For example, the knee's positive work could be powered elastically to some degree, as a consequence of the immediately preceding collision (Shamaei et al., 2013), hence our term ‘rebound’ (Donelan et al., 2002a). There is, however, no direct quantification of knee elasticity, again because of limitations in experimental work measures.

We also consider it likely that there are compensations for reduced push-off not considered in our model. The energetic penalty predicted by the model does not take into account the myriad degrees of freedom that humans could potentially employ to improve economy. There are also other measures to alter economy, for example by physically changing the foot bottom shape, which can greatly influence collision losses (Adamczyk and Kuo, 2013; Adamczyk et al., 2006). An appropriate shape can even reduce collisions such that the energetic penalty may be avoided despite reduced push-off (Vanderpool et al., 2008), although this entails a different shoe rather than a coordinative change. However, with respect to gait adaptations alone, we expect that most compensations will typically result in greater collision losses, and therefore more work, even if to lesser degree than the present model predicts.

Despite these limitations, our findings may have implications for patient groups with reduced push-off. Both the amount and timing of push-off appear important for energy economy, as also suggested by studies of ankle fusion (Doets et al., 2009; van Engelen et al., 2010), ankle exoskeletons (Malcolm et al., 2013; Sawicki and Ferris, 2008), ankle orthoses (Bregman et al., 2011) and lower limb prosthetics (Collins and Kuo, 2010; Zelik et al., 2011). If push-off cannot be restored, an alternative is to reduce the collision loss, for example with arc-shaped foot bottoms (Adamczyk and Kuo, 2013; Adamczyk et al., 2006; Vanderpool et al., 2008; van Engelen et al., 2010). Such interventions might help to mitigate the disadvantages of impaired ankle strength or power.

Appendix

Here, we briefly summarize details of the dynamic walking model, which comprises pendulum-like legs and concentrated mass at the pelvis (Kuo, 2002). During stance phase, the COM moves in an inverted pendulum arc atop the stance leg. The COM moves down-and-forward with a velocity v⁻ just before heelstrike, and must be redirected to up-and-forward for the next leg's inverted pendulum arc (denoting velocity v⁺). The COM velocity is redirected by a pre-emptive push-off impulse and a heelstrike collision impulse. Because all the mass is concentrated at the COM, the push-off and collision impulses can only point to the COM, and are perpendicular to v⁻ and v⁺, respectively. The COM velocity after push-off and before collision is denoted v_­mid. The push-off work W_PO can be derived as:

(A 1)

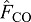where M is total mass and is the push-off impulse. Similarly, the dissipative work by the collision impulse is:

(A 2)

The relationship between the collision impulse and v_­mid is:

(A 3)

where α is the angle between each leg and vertical during the step-to-step transition, and β is the angle between v_­mid and v⁻. Using geometry, we have:

(A 4)

(A 5)

This yields collision impulse:

(A 6)

Substituting Eqns 4–6 into Eqn 2:

(A 7)

Assuming small angle approximations and that v⁻ is close to the average walking speed v:

(A 8)

(A 9)

where s is step length and L leg length. Then we have our final formula for dissipative collision work:

(A 10)

For typical human walking speeds, W_PO is quite small, and so W_CO will generally be dominated by the two terms of lowest order, yielding Eqn 1.