Power amplification in an isolated muscle–tendon unit is load dependent

ABSTRACT

During rapid movements, tendons can act like springs, temporarily storing work done by muscles and then releasing it to power body movements. For some activities, such as frog jumping, energy is released from tendon much more rapidly than it is stored, thus amplifying muscle power output. The period during which energy is loaded into a tendon by muscle work may be aided by a catch mechanism that restricts motion, but theoretical studies indicate that power can be amplified in a muscle–tendon load system even in the absence of a catch. To explore the limits of power amplification with and without a catch, we studied the bullfrog plantaris muscle–tendon during in vitro contractions. A novel servomotor controller allowed us to measure muscle–tendon unit (MTU) mechanical behavior during contractions against a variety of simulated inertial-gravitational loads, ranging from zero to 1× the peak isometric force of the muscle. Power output of the MTU system was load dependent and power amplification occurred only at intermediate loads, reaching ∼1.3× the peak isotonic power output of the muscle. With a simulated anatomical catch mechanism in place, the highest power amplification occurred at the lowest loads, with a maximum amplification of more than 4× peak isotonic muscle power. At higher loads, the benefits of a catch for MTU performance diminished sharply, suggesting that power amplification >2.5× may come at the expense of net mechanical work delivered to the load.

Summary: Power amplification in a compliant muscle-tendon unit is maximal for intermediate inertial-gravitational loads and can be enhanced by a trigger and catch mechanism for small loads.

INTRODUCTION

The mechanical output of skeletal muscle is bound by an intrinsic power limit, defined by the force–velocity properties of the contractile elements. These muscle properties can potentially limit fast movements, which often require brief periods of high power output (e.g. jumping, prey capture, feeding). Many animals overcome this potential constraint by using elastic mechanisms that store the energy of muscular contraction relatively slowly, then release it rapidly to provide a brief burst of power (de Groot and van Leeuwen, 2004; Lappin et al., 2006; Deban et al., 2007; Van Wassenbergh et al., 2008; Patek et al., 2011; Roberts and Azizi, 2011). In some arthropods, the storage and release of elastic energy is facilitated by an explicit anatomical ‘catch’ that holds an appendage in place while muscle contraction loads strain energy into elastic tissues (Gronenberg, 1996; Patek et al., 2011). Elastic strain energy is released when the catch is disengaged by a trigger mechanism. Several vertebrates also appear to use an elastic mechanism to amplify muscle power output. Studies of feeding and prey capture in pipefish (Van Wassenbergh et al., 2008), salamanders (Deban et al., 2007), chameleons (de Groot and van Leeuwen, 2004) and toads (Lappin et al., 2006), and jumping in humans, galagos and frogs, have all observed power outputs that exceed the power-producing capacity of the muscles involved, thereby providing evidence of power amplification by an elastic mechanism (Bobbert et al., 1986; Marsh and John-Alder, 1994; Aerts, 1998; Astley and Roberts, 2012). In jumping, ‘dynamic catch mechanisms' including the inertial/gravitational load of the body, a shifting mechanical advantage of muscle–tendon units (MTUs) during movement and reaction torques from proximal joints have recently been shown to contribute to the loading of elastic structures (Astley and Roberts, 2014), but no direct evidence of a trigger-like anatomical catch mechanism in these jumpers has been produced.

It is clear how an explicit anatomical catch in the form of a latch can allow muscles to temporarily store elastic energy that is later used to power movement in a similar manner to a catapult. The latch prevents motion of the load while high muscle forces are developed to store energy in the stretch of elastic elements. But theoretical studies indicate that power amplification can occur in a muscle–tendon system even in the absence of a latch-like catch (Alexander, 1995; Galantis and Woledge, 2003; Paluska and Herr, 2006). Analytical models of a Hill-type muscle operating in series with an elastic tendon (Galantis and Woledge, 2003) and a muscle-like actuator in series with a spring (Paluska and Herr, 2006) show that when a load is accelerated, the inertia of the load itself can be sufficient to allow significant tendon loading and subsequent power amplification when the energy is released. In computer simulations, the magnitude of power amplification varies depending on the size of the load, the forces acting on it (e.g. inertia only versus inertia plus gravity) and the stiffness of the in-series spring (Galantis and Woledge, 2003; Paluska and Herr, 2006). For muscle-like actuators, the highest simulated power outputs correspond to ∼1.8× the peak isotonic power output of the muscle contractile component (Galantis and Woledge, 2003). A model meant to represent the interaction of limb muscles and body forces in jumping bullfrogs also found that power could be amplified above maximal muscle power, up to a value of about 1.2×, without a catch mechanism (Roberts and Marsh, 2003). These studies and more recent experiments in jumping frogs suggest that power amplification can occur in the simplest system, that of a MTU accelerating a load, providing a potential explanation for locomotor performance observed among vertebrate jumpers (Astley and Roberts, 2012, 2014). However, the maximum amplification in simulations, 1.8× peak muscle power, falls well below the maximum amplification calculated for jumping, which can be as high as 7× in some species (Peplowski and Marsh, 1997; Roberts et al., 2011).

List of symbols and abbreviations

E_s

Hookean approximation of strain energy stored in series elastic tissues

EMA

effective mechanical advantage

F_load

gravitational force resulting from a given simulated mass applied by the ergometer to the MTU

F_max

maximum force of the MTU in a 300 ms ‘fixed-end’ contraction

F_o

maximum force of the MTU in a 100 ms ‘fixed-end’ contraction

FEC

fixed-end compliance

L_o

muscle fascicle length corresponding to F_max

MTU

muscle–tendon unit

PCSA

muscle physiological cross-sectional area

PL

plantaris longus

P_{max(Fload/Fo)}

peak mechanical power output of the MTU during contractions against a dynamic load

P_{max iso}

peak isotonic mechanical power output of the muscle during an isotonic contraction

v_max

maximum velocity of the muscle (i.e. zero force crossing)

The goal of the present study was to test empirically the idea that a muscle–tendon system can develop power outputs exceeding maximum muscle power when accelerating a load, and to explore the limits of amplification. We measured the mechanical performance of an isolated bullfrog plantaris MTU contracting to accelerate a simulated inertial/gravitational load. The load was simulated by a feedback loop to control servomotor position based on the measured force. We measured performance over a range of simulated loads both with and without a simulated catch mechanism. We hypothesized that power amplification in the no-catch condition would be load dependent, as observed in simulations (Galantis and Woledge, 2003). We also hypothesized that power amplification would increase when the muscle operated with a simulated catch.

MATERIALS AND METHODS

Animals

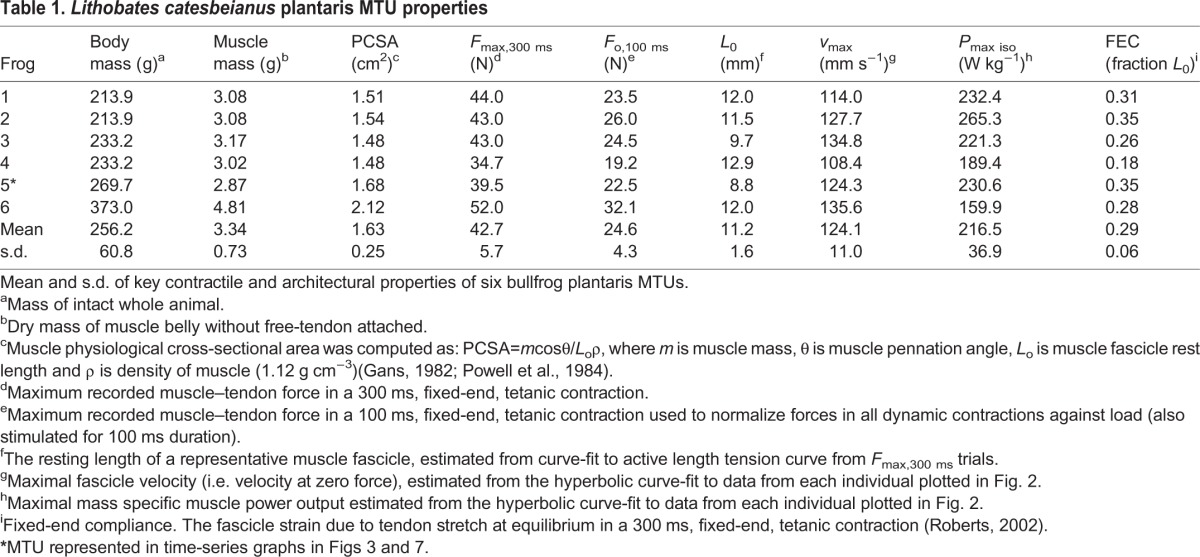
Four adult bullfrogs (Lithobates catesbeianus Shaw 1802) ranging in body mass from 214 to 373 g were purchased from a licensed vendor and housed in the Brown University Animal Care facility in large aquaria with both an aquatic region and a terrestrial platform. Animals were fed large vitamin-enriched crickets ad libitum twice weekly. Animals were given at least 1 week to acclimate before they were used in an experiment. Frogs were euthanized by a double pithing procedure. All animal procedures were approved by the Brown University Institutional Animal Care and Use Committee.

In vitro preparation

Six plantaris longus (PL) muscle–tendons were isolated post mortem by careful dissection under oxygenated amphibian Ringer's solution (100 mmol l⁻¹ NaCl, 2.5 mmol l⁻¹ KCl, 2.5 mmol l⁻¹ NaHCO₃, 1.6 mmol l⁻¹ CaCl, 10.5 mmol l⁻¹ dextrose) and kept at room temperature (∼22°C). The PL, the primary ankle extensor, is a large and particularly compliant MTU that serves as a critical power source during jumping (Azizi and Roberts, 2010; Astley and Roberts, 2012). The proximal origin of the muscle was left attached at the knee joint and the muscle was freed from the ankle and tibiofibula, taking care to preserve the series elastic tissues including both the superficial aponeurosis and the free tendon up to its distal insertion at the toes. Measurements of muscle morphological properties (muscle mass, fiber length and pennation angle) were taken from the isolated PL MTU upon completion of contractile property measurements (Table 1). Muscle physiological cross-sectional area (PSCA) was calculated following Nelson and Roberts (Nelson et al., 2004).

Table 1.

Lithobates catesbeianus plantaris MTU properties

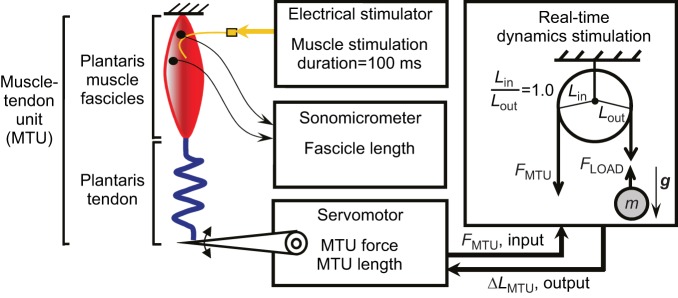
Once the muscle and bony origin were freed from the leg, the sciatic nerve was dissected away from surrounding tissue and a bipolar electrode nerve cuff, constructed of two silver wires and plastic tubing (7 mm length, 1.5 mm inner diameter), was gently placed around the nerve just proximal to the plantaris origin on the knee. To stimulate the muscle, wire leads from the nerve cuff were connected to a Grass S48 stimulator (Grass Technologies, West Warwick, RI, USA). In addition, sonomicrometry transducers (1 mm, Sonometrics Inc., London, Ontario, CA, USA) were implanted along a proximal fascicle of the plantaris muscle and secured using gauge 6-0 silk to directly measure length changes in the contractile tissues of the MTU (Fig. 1).

Fig. 1.

Schematic of in vitro experimental setup to study MTU contractions against ‘real-world’ loads. An isolated plantaris MTU is attached from a rigid ground plate to the lever of an instrumented ergometer. A cuff electrode on the sciatic nerve stimulates the muscle to contract and accelerate a computer-simulated inertial-gravitational load. Ergometer length is controlled using a feedback system involving real-time force measurements (sample time=0.0005 s) from the muscle–tendon attached to the ergometer. These force values are used in conjunction with the equations of motion of the simulated mechanical system to calculate the change in position of the load, which is then converted across a simulated pulley transmission to control the position of the ergometer/MTU. Nine simulated loads were tested, ranging from a normalized weight (F_load=W=m·g) of 0.175 to 1.0×F_o, where F_o was the maximum force recorded in a 100 ms isometric contraction. MTU force and length were recorded from the ergometer and muscle fascicle length was measured from surgically implanted sonomicrometry crystals.

The isolated knee joint, including sections of the femur and tibiofibula, was then securely fastened to a plexiglass platform that was bolted to the bottom of a chamber containing oxygenated Ringer's solution and maintained at room temperature (22°C). The distal end of the plantaris free tendon was attached to a custom-made friction clamp, and the clamp was connected by a stiff stainless steel cable to a servomotor (310 B-LR, Aurora Scientific Inc., Cambridge, MA, USA) (Fig. 1). The servomotor was used to measure muscle–tendon force and length in order to characterize muscle contractile properties (i.e. force–length, force–velocity relationships) as well as MTU mechanical performance during contractions against various dynamic loads. The servomotor also controlled muscle–tendon length during simulated load experiments.

In vitro data collection: characterizing muscle properties

First, to determine the optimum stimulation voltage, the twitch force of a MTU was monitored as the voltage was increased by 1 V increments. The voltage that resulted in maximum twitch force was increased by 1 V and used to supramaximally stimulate the muscle for all subsequent contractions in a given experiment (∼5–7 V).

We then used 4–5 ‘fixed-end’ tetanic contractions at varying muscle–tendon lengths set by the servomotor position to characterize the muscle's active force–length properties. Each tetanic stimulation was performed using 0.2 ms pulses, at 100 pulses s⁻¹ for 300 ms. Effects of muscle fatigue were minimized by allowing a rest period of at least 5 min between successive tetanic contractions. The passive force–length properties were also quantified using the sonomicrometer-measured muscle fascicle length and servomotor force prior to stimulation. All data were collected at 1000 Hz using a 16-bit A/D converter (National Instruments USB- 6251, Austin, TX, USA). Peak force, F_max, was recorded and the fascicle length at F_max on the length–tension curve was used to estimate L₀ (Table 1). Subsequent measurements of force–velocity properties were taken within ±10% of this length. For each preparation, we also used sonomicrometer recordings of fascicle length change during an isometric tetanus to calculate the fixed-end compliance (FEC) of the tendon. FEC was calculated as the amount of fascicle strain against tendon elongation at a fixed muscle–tendon length, with the fascicle starting at ∼L₀ (Roberts, 2002).

Next, a series of 5–7 tetanic isotonic contractions over a range of set forces clamped by the servomotor controller were used to characterize each muscle's force–velocity curve. Force and length values were measured after the muscle was fully active (i.e. stimulation duration ≥100 ms) and force reached a plateau to be sure that only muscle fascicles and not series elastic elements were contributing to MTU length changes. Contraction velocity (mm s⁻¹) was determined by differentiating MTU length measured by the servomotor. Then, each muscle's force–velocity curve was characterized by fitting the data with a Hill-type equation:

(1)

where F is force normalized F_max and v is shortening velocity in L₀ s⁻¹. The equation for this hyperbola was used to solve for each muscle's theoretical unloaded maximum velocity (v_max) (Table 1). Finally, muscle power was calculated as the product of force and velocity from the hyperbola for each muscle, plotted against shortening velocity and used to determine the peak isotonic muscle power (P_{max iso}) (Table 1, Fig. 2).

Fig. 2.

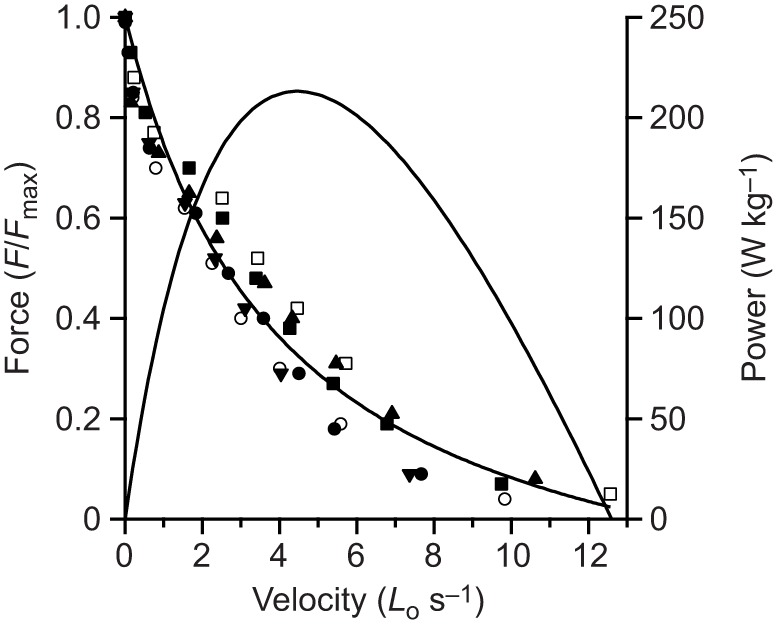
Force–velocity and power–velocity characteristics for six Lithobates catesbeianus plantaris muscle preparations. Different symbols represent different individuals.

In vitro data collection: dynamic contractions in simulated mass/gravity

Next, we performed a series of 7 dynamic contractions over a range of ‘real-world’ inertial/gravitational loads (F_load=m·g). For all contractions, we used a 100 ms stimulation period and a starting length of 1.3 L₀ to be consistent with contractile conditions that have been observed in vivo during frog jumps (Roberts and Marsh, 2003; Azizi and Roberts, 2010; Astley and Roberts, 2012). To select simulated loads, we first determined the maximum force each muscle could develop under jumping conditions (100 ms stimulation and 1.3 L₀ starting length) by measuring peak force in an isometric contraction (F_{o,100 ms}, Table 1). Then, using F_o, we calculated the mass of the load that would yield static equilibrium across the lever system (i.e. m=1.0×F_o/g). Following that, the scaled masses were computed corresponding to 0.175, 0.25, 0.375, 0.5, 0.625, 0.75 and 0.875 of m=1.0× F_o/g, corresponding to each target F_load/F_o. We then applied the loads in randomized order to prevent systematic effects of muscle fatigue.

To simulate dynamic loading conditions in vitro, we programmed a custom servomotor controller (LabView, National Instruments Inc., Austin, TX, USA, sample time=0.0005 s) to enforce a simplified dynamic model meant to capture the essential features of the load experienced by the hindlimb extensor MTUs during a rapid acceleration (Fig. 1). The controller commanded ‘real-time’ servomotor position in accordance with the equations of motion for a circular pulley system (i.e. a fixed mechanical advantage) with a mass in gravity on the output side (F_load=m·g) and muscle–tendon force on the input side (F_MTU) (Eqns 2–6):

(2)

(3)

(4)

(5)

(6)

where dt in Eqn 5 is equal to the sample time set by the control software.

A typical control loop proceeded as follows: (1) servomotor force, F_MTU, was recorded via the servomotor at the muscle–tendon attachment; (2) F_MTU was used to compute F_load based on a user-selected fixed mechanical advantage L_in/L_out (Eqn 2); (3) F_load was used to compute a_load (Eqn 3); (4) a_load was numerically integrated to yield v_load (Eqn 4); (5) v_load was used to compute the load displacement, Δx_load (Eqn 5); and finally, (6) Δx_load was converted back to a muscle–tendon length change, ΔL_MTU (Eqn 6) that was applied by the servomotor to the biological muscle–tendon. For all dynamic contractions in this study, we set L_in/L_out=1 (see Discussion for rationale).

For each dynamic loading condition, we started the system at rest with the mass on a ‘virtual table’ (i.e. in static equilibrium) and the muscle–tendon under passive tension (∼5–10% F_max) to maintain fascicles at ∼1.3 L₀ (Azizi and Roberts, 2010). Then, we supramaximally stimulated the muscle for 100 ms (Azizi and Roberts, 2010) and when F_MTU produced the condition F_load>m·g, the mass and MTU began to accelerate in gravity according to Eqn 3. For each trial, we recorded muscle–tendon force and length as well as fascicle length (via sonomicrometry) for 200 ms, which was long enough to capture the full power stroke of the MTU during all loading conditions.

We also simulated dynamic loading conditions with an anatomical ‘catch’ that could effectively hold the load in place while muscle contraction loaded strain energy into elastic tissues (Patek et al., 2011). To do this, we implemented a ‘catch force’ by enforcing the rule: a_load=0 for F_MTU<F_catch=0.95×F_o. That is, the system was held still until the MTU produced force exceeding the anatomical catch force. Using this approach, we simulated catch contractions for loads with m·g equivalent to 0.175, 0.375 and 0.50×F_o in four of the six preparations.

For all dynamic contractions, we implemented a software fault to prevent damage to the MTU during the recoil following the power stroke. If the servomotor lever velocity ever exceeded 40 mm s⁻¹ upward (i.e. muscle–tendon lengthening), the system would slowly return to its initial position.

The effects of muscle fatigue were minimized by randomizing the order of trials and allowing a rest period of at least 5 min between successive contractions. In addition, isometric contractions at 300 ms train duration were recorded at the beginning and end of the length–tension, force–velocity and dynamic load portions of the experiments to check for potential declines in maximum isometric force due to muscle fatigue. Maximum isometric force (F_max) did not change significantly during any experiment.

Data analysis

All MTU force and length (from servomotor) and fascicle length (from sonomicrometry) data were processed and analyzed using custom Matlab software (Mathworks Inc., Natick, MA, USA). Sonomicrometry data required post processing to remove easily identified level-shifts using a custom algorithm. Then we smoothed all raw data (MTU force, MTU length, muscle fascicle length) using a fourth-order Butterworth filter with low-pass cutoff frequency=25 Hz. To compute the velocity of the MTU and the fascicles, we took the first derivative of servomotor and sonomicrometry length change data, respectively. Then, we computed the mass-specific mechanical power output (W kg⁻¹) over time for the MTU and the muscle fascicles by multiplying force (N) and velocity (mm s⁻¹) time-series and dividing by muscle mass. Our calculation of muscle fascicle mechanical power output based on MTU force likely represents an underestimate of actual power output of the contractile elements because force at the fascicles is reduced relative to the muscle force output (measured by the servomotor) due to the effects of fiber pennation angle (Azizi et al., 2008).

In each preparation, based on the time-series data for MTU force (N) and MTU and muscle fascicle length (mm), velocity (mm s⁻¹) and mechanical power output (W kg⁻¹), we computed a number of metrics to test our hypotheses. All metrics were calculated over the ‘power stroke’, defined as the time window from stimulation onset until muscle shortening ceased (i.e. the time of maximum MTU excursion; ∼125–175 ms). For the MTU, we calculated peak force, peak shortening velocity, muscle peak mass-specific mechanical power and mass-specific net work (J kg⁻¹) performed. To compute MTU net work, we integrated the MTU mechanical power time-series data over the ‘power stroke’. For the muscle fascicles, we calculated peak shortening velocity. Finally, for all of these metrics, we computed mean and standard error of the mean (s.e.m.) of values for all conditions across all preparations (N=6; N=4 for anatomical ‘catch’ contractions).

Statistical tests

To compare performance metrics between experimental conditions, we used a series of repeated measures analysis of variance (ANOVA) tests (JMP Statistical Software, SAS Inc., Cary, NC, USA). First, we tested significance of the main effect, dynamic loading condition (load), on the following key MTU outcome measures: (1) peak force, (2) peak shortening velocity, (3) mass-specific net mechanical work, and (4) peak mechanical power output. To do this we used a one factor (load: 7 levels between 0.175–0.875×F_load/F_o) repeated measures (N=6 preparations) ANOVA with α=0.05. For outcomes where the effect of load was significant, we performed post hoc pairwise t-tests to determine specific differences between loads, and reported those only when relevant to primary hypotheses. We note, for the outcome-variable peak mechanical power output, in order to assess whether there was power amplification (i.e. P_{max(Fload/Fo)}/P_{max iso}>×1) we included an additional load, isotonic at P_{max iso}, as a condition in the ANOVA (i.e. load: 8 levels).

Next, to assess the effects of adding an anatomical ‘catch’ mechanism on each of the four key muscle–tendon outcome measures, we performed a two-factor (load, catch) repeated measures (N=4 preparations) ANOVA with an interaction effect (catch×load) and α=0.05. As before, for outcomes with a significant main and/or interaction effect, we performed post hoc pairwise t-tests to determine specific differences between loads/catch, and report those only when relevant to primary hypotheses. Also, as described above, we added an additional load condition in the ANOVA for peak mechanical power output.

RESULTS

Force, velocity and power output for frog plantaris were determined for each muscle from a series of isotonic contractions. Peak isometric stress averaged for the six muscle preparations was 26.32±2.8 N cm⁻². Force–velocity data were well fit by a Hill equation (Eqn 1, Fig. 2). The constants a and b were determined by best fit to the pooled data for all individuals to be a=0.30±0.07 (s.d.) and b=4.13±0.47. The theoretical unloaded maximal shortening velocity for the pooled data was calculated by extrapolation from the Hill curve to be 13.8 L₀ s⁻¹. Peak isotonic power output was calculated from the Hill equation fit to each individual, and was 216.5±36.9 W kg⁻¹. The value calculated for peak power for the pooled data was 213.1 W kg⁻¹, indistinguishable from the average of individually calculated peak power values (Table 1, Fig. 2).

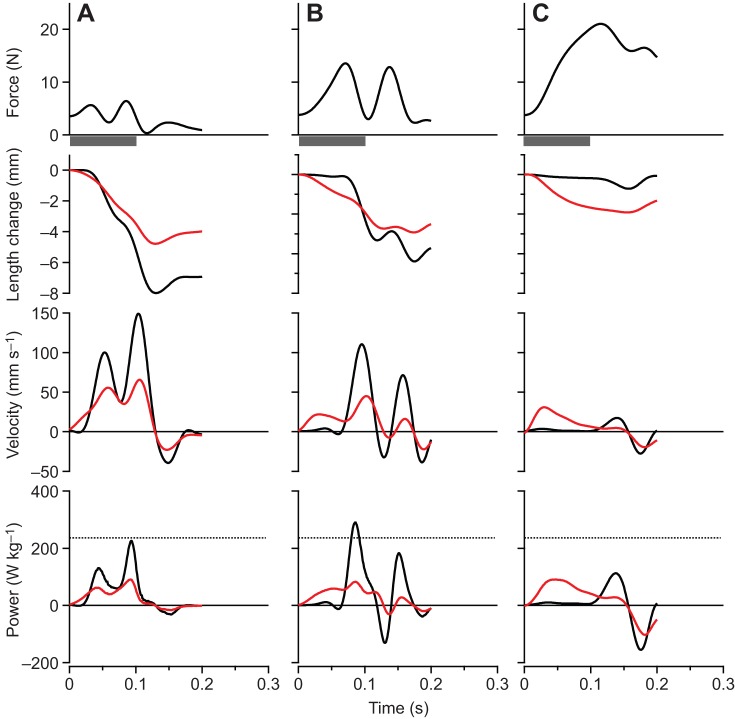
The maximum force, velocity and power as well as the net work of contraction all varied significantly with the simulated load [ANOVA (load), P<0.0001 for all dependent variables]. Representative contractions from one of the preparations are shown in Fig. 3. At low loads (Fig. 3A), rapid acceleration of the virtual mass resulted in high muscle velocities and low forces, due to force-velocity effects. High forces were developed at high loads (Fig. 3C), but because of relatively low mass accelerations, the velocity of the muscle and the virtual mass was low. The highest power outputs occurred at intermediate loads (Fig. 3B), and peak instantaneous power output of the MTU (P_{max(Fload/Fo)}) exceeded the peak isotonic power of the muscle (P_{max iso}) at these loads (Fig. 3B and Fig. 4). We found evidence of load-dependent power amplification [ANOVA (load), P<0.0001], with P_{max(Fload/Fo)}/P_{max iso} greater than 1× in only the F_load/F_o=0.375 (1.35×) and F_load/F_o=0.5 (1.28×) conditions (post hoc paired t-tests: P<0.05) (Fig. 4). The total net work performed in a contraction (Fig. 5) paralleled changes in peak power output as a function of the virtual load. Apparent in the representative contractions is a regular cyclic fluctuation of force and velocity during the contraction (Fig. 3). This fluctuation was due to the natural oscillation of the spring–mass system formed by the tendon spring and virtual load.

Fig. 3.

Contractions from a single plantaris muscle preparation for a range of simulated loads. (A) A light (F_load/F_o=0.175), (B) an intermediate (F_load/F_o=0.375) and (C) a heavy (F_load/F_o=0.875) simulated load. Black traces are for the whole MTU, while red traces indicate values for fascicles. The highest powers occur at intermediate loads, and peak power output at this load exceeds the muscle's maximum isotonic power (denoted by the dashed line, bottom panel). At low loads velocities are high but forces are low, whereas at high loads forces are high but velocities are too low to achieve significant power. The ‘double-humped’ pattern of force and velocity results from oscillation of the muscle–spring–mass system during acceleration of the virtual load. The time of stimulation was 100 ms for all contractions, as indicated by the gray bar below the top panel.

Fig. 4.

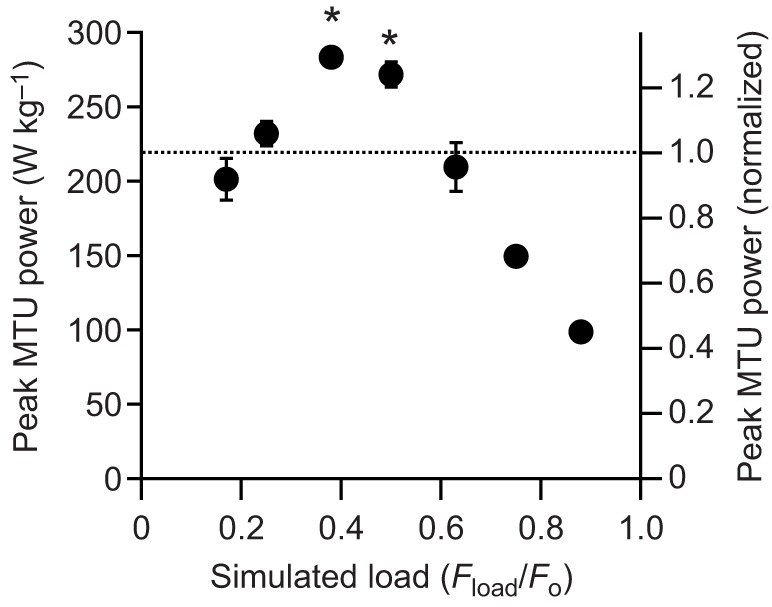
Peak power output during muscle contractions against simulated loads. At intermediate loads, peak power output developed by the MTU exceed the peak isotonic power of the muscle contractile apparatus (dotted line). Simulated load (x-axis) is the ratio of the gravitational force on the simulated mass (F_load=m·g), to the muscles’ peak isometric force in a 100 ms contraction, F_o. The right-hand y-axis is the peak power expressed as a proportion of the peak isotonic power output of the muscle. Values are means±s.e.m., N=6. Asterisks indicate significant difference (post hoc pairedt-test; P<0.05) with respect to the peak isotonic power of the muscle contractile apparatus (dotted line).

Fig. 5.

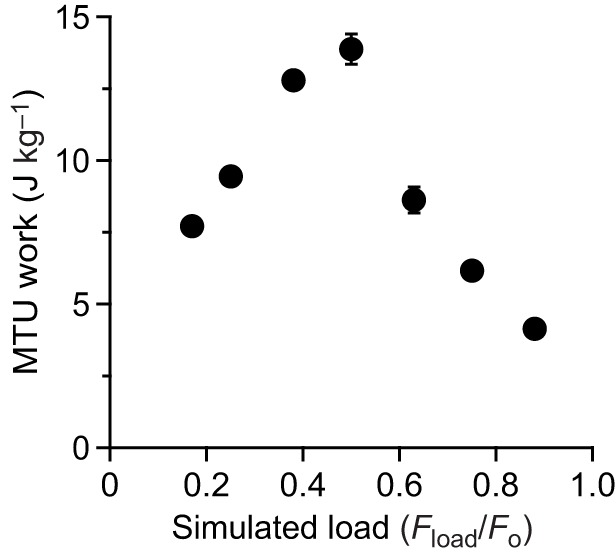
Net work performed by the MTU during muscle contractions against simulated loads. Loads at which high powers develop also correspond to high values of net work. Values are means±s.e.m., N=6.

The force developed in a contraction increased significantly with increasing simulated load [ANOVA (load), P<0.0001] (Fig. 6A). Peak force was higher, as a proportion of the simulated load, in light load contractions because of higher load accelerations. At high loads, accelerations were lower and the peak muscle force approached the force of gravity on the load (Fig. 6A, dotted line). The peak velocity of the whole MTU and the load decreased with increasing load [ANOVA (load), P<0.0001] (Fig. 6B, black). Muscle fascicle velocity also varied significantly with load [ANOVA (load), P<0.0001] (Fig. 6B, red). For low loads, peak muscle fascicle velocity was proportional to the load. At higher loads peak fascicle velocity reached a plateau, because at the higher loads the peak fascicle velocity occurred during early tendon stretch, which was identical in the early part of the contractions.

Fig. 6.

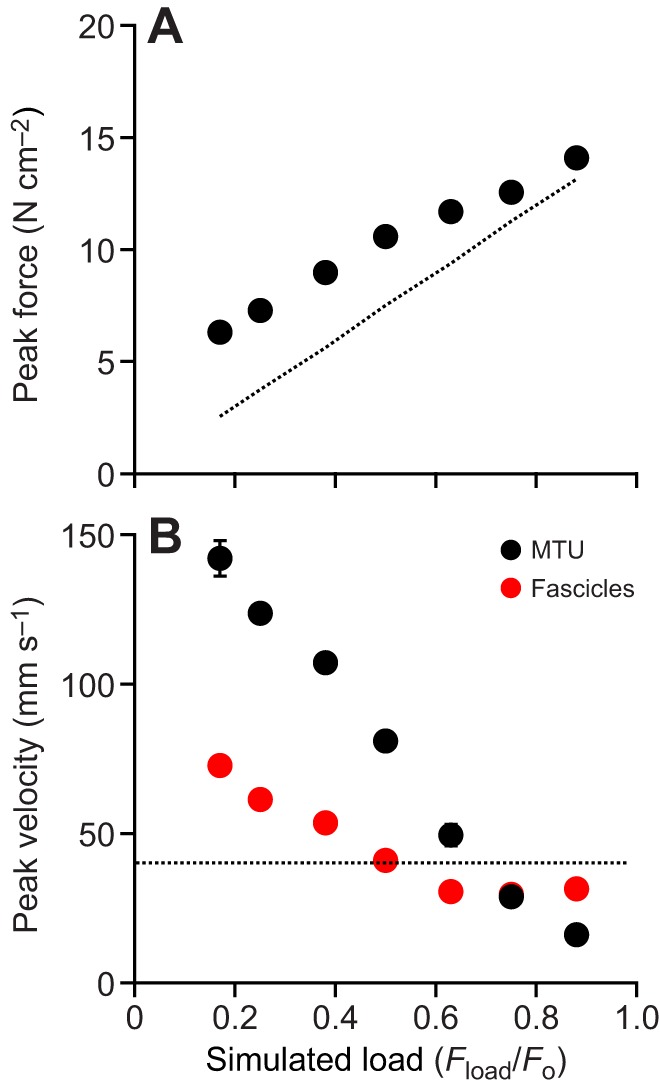
Peak force and velocity developed during contractions for a range of loads. (A) Forces at low loads exceed the force required to counteract gravity only (dotted line) because there is significant acceleration, while at high loads forces developed by the muscle are close to the gravitational force. (B) MTU velocity is low for high loads and high for low loads, and is close to the velocity corresponding to the muscle's maximum power output at intermediate loads (dashed line). Peak fascicle velocities follow the same trend as MTU velocity at low loads, but at high loads they plateau at a value fixed by the rate of MTU shortening against tendon early in the contraction.

Contractions with a catch resulted in significantly higher power outputs than contractions with no catch, and this was load dependent [ANOVA (catch×load), P<0.0001]. Representative contractions show that a simulated catch mechanism that held the MTU isometric for the first 100 ms of contraction allowed relatively high forces to be developed. High power outputs occurred later, during rapid load acceleration following release of the catch (Fig. 7). A catch significantly increased power output at low loads (e.g. a ∼5.7-fold increase at F_load/F_o=0.175 and a ∼1.7-fold increase at F_load/F_o=0.375; post hoc paired t-tests: P<0.05), but had no significant effect at higher loads (e.g. F_load/F_o=0.5; post hoc paired t-tests: P>0.05) (Fig. 8A).

Fig. 7.

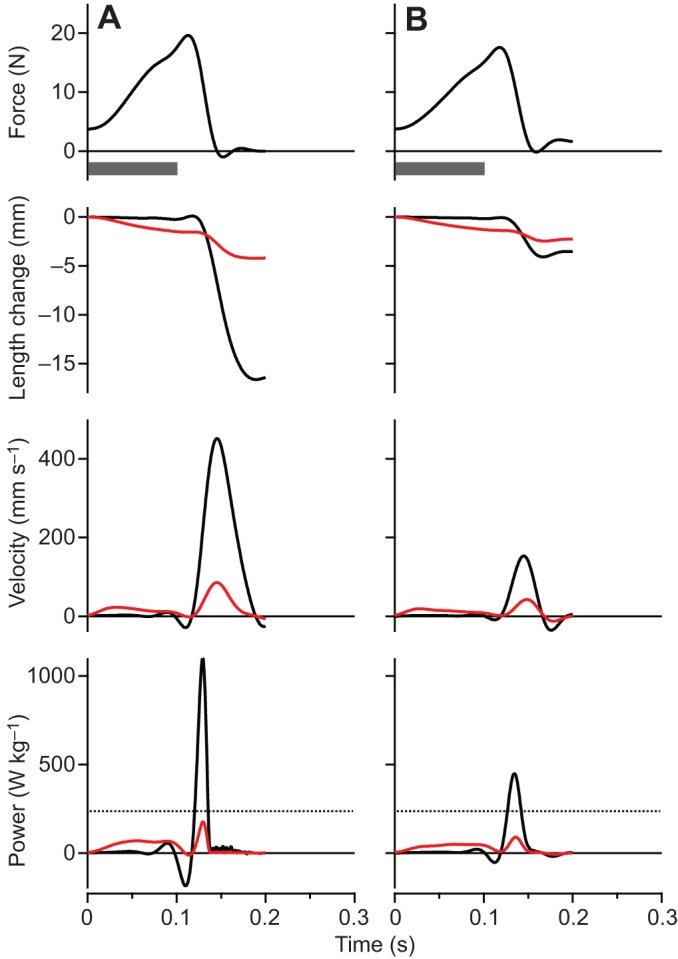
Contractions from a single plantaris muscle preparation operating with a simulated anatomical catch mechanism to accelerate simulated loads. (A) A light (F_load/F_o=0.175) and (B) an intermediate (F_load/F_o=0.375) simulated load. The MTU was held isometric until 100 ms into the contraction, when it was released to accelerate the simulated load. The highest power outputs occur in the light load condition, and exceed the peak isotonic power (dashed line, bottom panel) by several fold.

Fig. 8.

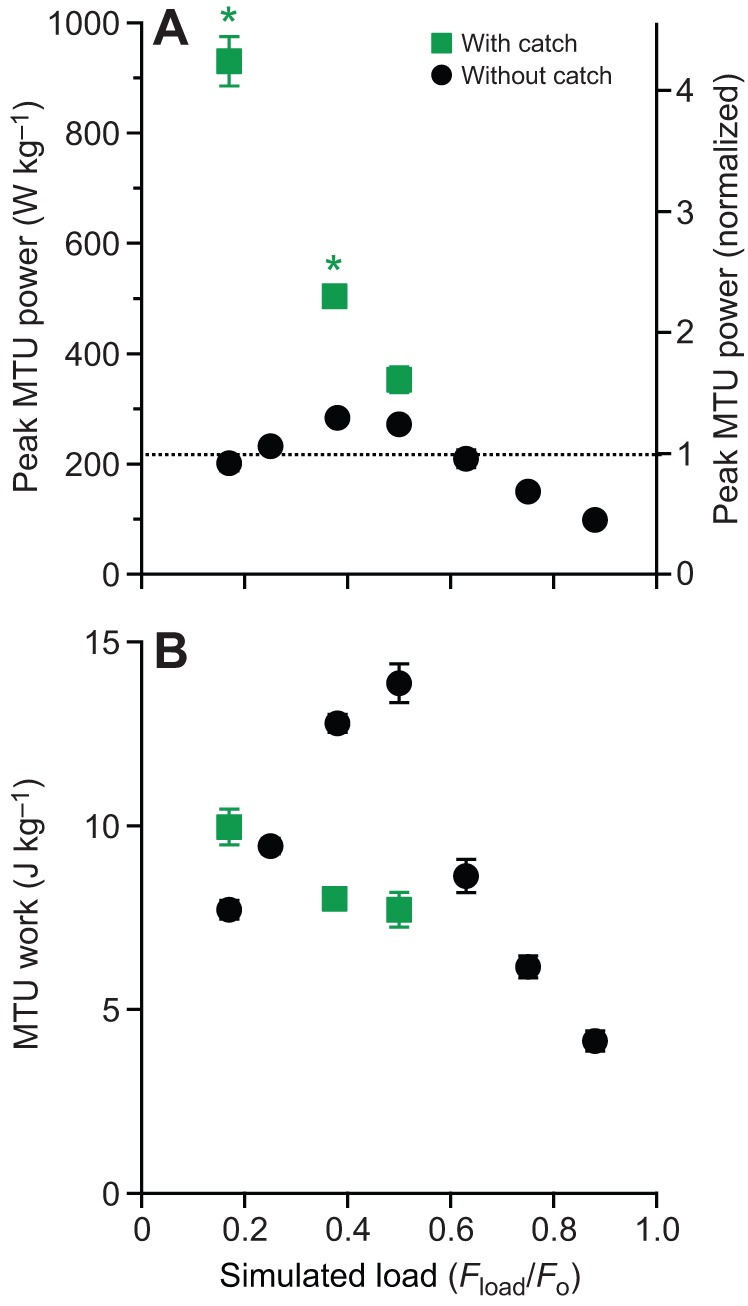
Power and work developed in the MTU during contractions without and with a simulated anatomical catch mechanism. (A) Anatomical catch mechanisms substantially increase the peak power output. Dotted line indicates the peak isotonic power output of the muscle. (B) Anatomical catch mechanisms sometimes (low loads), but not always (intermediate loads), result in high net work outputs. Asterisks indicate significant difference (post hoc paired t-test; P<0.05) with respect to the peak isotonic power of the muscle contractile apparatus (dotted line) in trials with a simulated anatomical catch mechanism.

All contractions with a catch demonstrated peak power outputs that were greater than the peak isotonic muscle power (i.e. power amplification, P_{max(Fload/Fo)}/P_{max iso}>1×, of 4.59×, 2.57× and 1.71× as the load increased from F_load/F_o=0.175 to 0.375 to 0.5, respectively), indicating that the majority of the power developed during load acceleration was due to recoil of elastic strain energy stored during the MTU-isometric portion of the contraction (Fig. 8A). In spite of this, power amplification was only significantly enhanced with versus without a catch at low loads [ANOVA (catch×load), P<0.0001]. More specifically, a catch increased power amplification from 0.81× to 4.59× at F_load/F_o=0.175 and 1.48× to 2.57× at F_load/F_o=0.375 (post hoc paired t-tests: P>0.05), but only 1.38× to 1.71× at F_load/F_o=0.5 (post hoc paired t-test: P>0.05) (Fig. 8A).

The effect of the catch on net work was also load dependent [ANOVA (catch×load), P=0.0009]. At lower loads, a catch produced significantly more net work than without a catch (e.g. 9.9 versus 6.6 J kg⁻¹ at F_load/F_o=0.175; post hoc paired t-tests: P<0.05). At higher loads, a catch actually reduced net MTU work, because contractions with a catch produced significantly less net work than without a catch (e.g. 7.7 versus 14.5 J kg⁻¹ at F_load/F_o=0.175; post hoc paired t-tests: P<0.05) (Fig. 8B).

DISCUSSION

The aim of this study was to empirically test the theoretical limits for power amplification of a muscle–tendon system working to accelerate a mass in the presence of gravity. Based on the predictions of simple models (Galantis and Woledge, 2003; Roberts and Marsh, 2003), we hypothesized that power amplification would be load dependent, and would increase when the MTU operated with a catch mechanism in place.

Our data from frog plantaris working on simulated loads of varying magnitude support both hypotheses. We observed maximum power amplification of ∼1.35× that occurred at an intermediate load (F_load/F_o=0.375) and decreased for loads above and below that value (Fig. 4). For contractions with a simulated catch set to release at F_o of the muscle, power amplification was much higher when compared with a no-catch contraction, especially for the lowest loads (e.g. 4.59× versus 0.80× at F_load/F_o=0.175) (Fig. 8A). These results confirm that a muscle–tendon system accelerating a load can produce power outputs that exceed the power-producing capacity of the contractile apparatus, and also that this amplification of power can be much greater if a catch and trigger mechanism is present to facilitate tendon energy storage and release.

Empirical versus theoretical limits of MTU power amplification

Drawing comparisons between empirical results and predictions from simple muscle–tendon models can help reveal factors that drive power amplification in systems with real biological MTUs driving ‘real-world’ loads. Our results from contractions without a catch mechanism are in qualitative agreement with the prediction of Galantis and Woledge that optimal power amplification occurs at intermediate inertial-gravitational (m·g) loads (Fig. 4). However, our measured peak amplification of 1.35× is lower than the 2.0× ‘best case’ predicted for systems with very compliant tendons (i.e. when Γ>100) (Galantis and Woledge, 2003), where performance can be classified using the non-dimensional gravitational constant, 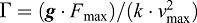, based on peak muscle force (F_max) and velocity (v_max), as well as the series tendon stiffness (k).

A rough calculation using estimates of tendon stiffness, v_max and F_o from the plantaris MTUs used in this study yields Γ=∼1.5 and would place the predicted optimal power amplification at ∼1.5× for a m·g load (F_load) corresponding to ∼½ F_o muscle; a bit higher than our measured value at that load. This is a remarkably close agreement given all of the simplifications in the Galantis and Woledge model that do not hold for real muscle–tendons. These include: no modeled muscle force–length relationship, activation–relaxation dynamics, shortening-dependent force depression or elastic tissue hysteresis, which are all effects that would act to reduce potential for power amplification. A similar model of plantaris muscle–tendon during frog jumping that did include force–length predicted power amplification of ∼1.2×, but the load applied to the MTU was only a portion of m·g, in line with observed changes in body orientation during real jumps (Roberts and Marsh, 2003). Future research, especially on the empirical side, should resolve how variations in muscle properties (force–length, force–velocity, force–activation), MTU architecture (i.e. compliance), leverage and load type (e.g. mass with no gravity, viscous) influence the limits of power amplification.

Our results for contractions with a catch mechanism are also in qualitative agreement with predictions from simple models. Galantis and Woledge only report results for simulated contractions with catches on inertial loads without gravity (m only) (Galantis and Woledge, 2003). Even so, they clearly demonstrate that for loads that diminish towards zero mass, MTU power amplification approaches very large values. In a similar fashion, our experimental results demonstrate that for m·g loads with a catch mechanism set to release near maximum muscle force, power amplification increases from 1.7 at F_load=0.5×F_o to 4.6 at F_load=0.175×F_o. This result suggests that when the primary goal is to maximize power amplification, a catch mechanism is beneficial for m·g loads ≤0.5×F_o.

The role of series compliance in muscle power enhancement and conditions for the special case of power amplification

Our results highlight the fact that directly coupling a muscle to a dynamic load via series elastic structures is sufficient for mechanical power enhancement, the condition when instantaneous power output of an MTU exceeds the instantaneous power output of the muscle (Fig. 3). Furthermore, in a muscle–tendon system, if the load is sized appropriately, we observe a special case of enhancement, termed amplification (Richards and Sawicki, 2012), when the instantaneous power of the MTU exceeds the upper limit of power output for the muscle alone, as dictated by its force–velocity relationship. Our data based on the force–velocity relationship determined from isotonic contractions indicate an upper limit of 216.5 W kg⁻¹ for the plantaris muscles tested in this study (Table 1, Fig. 2). During contractions against intermediate dynamic loads, the plantaris MTU produced instantaneous powers in excess of the muscle upper limit (Fig. 3B and Fig. 4).

Power enhancement in muscle–tendon systems results from series elastic tissues that serve to decouple the movement of the muscle from the movement of the whole MTU and thus, the load. This decoupling, makes possible a ‘catapult mechanism’ whereby elastic energy can be stored slowly in tendon stretch and then released rapidly at a later time; a feature that makes it possible to briefly exceed the power limits of muscle alone (Roberts and Azizi, 2011; Richards and Sawicki, 2012). The ‘catapult’ action leads naturally to the definition of two key phases of a contraction that can be evaluated in understanding how the magnitude of the load influences power enhancement/amplification in a muscle–tendon system: (1) the energy storage phase and (2) the energy release phase.

Our data indicate that intermediate loads allow for an optimal compromise between a large amount of elastic energy storage and effective release of the stored energy to power the load (e.g. Fig. 3B). In the F_load/F_o=0.375–0.5 conditions, relatively large amounts of energy are transferred from muscle to tendon during storage. Then upon release, the load accelerates in a manner that keeps muscle fascicles operating over a range of velocities ideal for continued high muscle power output that adds to the energy recovered from elastic structures, enhancing total power output beyond what is possible from muscle alone (Fig. 4) and at the same time delivering large amounts of net work to the load (Fig. 5). We note, in contractions where there is power amplification, the power output of the muscle fascicles remains nearly constant even as power transmitted to the load fluctuates (Fig. 3B). In fact, in the contractions with highest muscle–tendon power output, muscle fascicles operate at velocities consistent with the upper limit of muscle power output [i.e. ∼⅓ v_max=∼30 mm s⁻¹ (Azizi et al., 2008)] (Fig. 4 and Fig. 6B).

To catch or not to catch?

Our data indicate that, if net work of the task is of primary importance (e.g. jumping), an anatomical catch mechanism may only be beneficial for muscle–tendon systems working on relatively small loads (e.g. F_load/F_o<∼0.2) (Fig. 8). An anatomical catch can significantly increase the amount of elastic energy stored early in a contraction for small loads, because the amount of energy stored is not load dependent. That is, the limit of energy stored in series elastic structures E_s=½ (F²/k) is determined by F_o of the muscle and k of the tendon (i.e. F=F_o), rather than the size of the load and the effective mechanical advantage (i.e. F=m·g/EMA). However, while the very high shortening velocities that develop upon rapid release of the stored elastic energy generate very large instantaneous power outputs, contractile conditions are quite poor for ongoing muscle force production (Fig. 7A,B), ultimately limiting the amount of net work transferred to the load (Fig. 8). It may be possible to circumvent this trade-off by using catches that are less discrete in nature (i.e. not all or none latches based on bony anatomical structures). Possibilities beyond anatomical catch mechanisms include ‘dynamic catches' that could be implemented using antagonist muscle forces (Gronenberg, 1996), dynamically changing lever ratios (Roberts and Marsh, 2003) or moments from proximal joints (Astley and Roberts, 2014). In many systems the velocity of the movement is of primary importance and maximizing net energy transfer to the load may be secondary (e.g. time-sensitive feeding/prey capture). In these cases, where very high peak powers develop because of extremely high velocities of relatively small inertial loads (e.g. tongues) (de Groot and van Leeuwen, 2004), our data suggest that using an explicit anatomical catch with a latch and trigger mechanism is highly beneficial over a larger range of loads (e.g. F_load/F_o<∼0.5).

The role of leverage in accelerating loads with muscle–tendon systems

The ratio of the moment arm lengths on the input versus output side of a lever or pulley transmission [i.e. leverage or effective mechanical advantage (EMA)], determines the magnitude and timing of the trade-off between force and velocity of an MTU and its load. In the current study, we chose to start with the simple case of a constant leverage=1 throughout our simulated contractions to isolate the effect of load independent of leverage on MTU mechanical performance during acceleration. It is unlikely that the value of the EMA, as long as it is constant, will significantly influence the observed magnitude of the peak MTU power output, or the general effect that there is an optimal intermediate load that maximizes MTU power output. However, it will shift the load at which the peak power occurs; with lower values of EMA (i.e. higher gears) tending to shift the power–load relationship ‘leftward’ on the load axis towards lower values (Galantis and Woledge, 2003). An EMA that varies throughout a contraction can also have a significant influence on energy storage and recovery, but we did not attempt to simulate a variable EMA in the present study.

Unexpectedly, setting the value of the EMA fixed at L_in/L_out=1 highlighted the fact that the mechanical and neural components within muscle–tendon systems must be set up to deal with the ‘real-world’ dynamics of forced spring–mass systems. Our data revealed an interesting ‘double-hump’ feature in muscle–tendon and fascicle force and velocity during accelerations of inertial–gravitational loads spanning a wide range from very light to very heavy (Fig. 3).

The bi-phasic pattern of muscle shortening was similar to that seen in vivo during bullfrog jumps (Roberts and Marsh, 2003; Azizi and Roberts, 2010; Astley and Roberts, 2012), but with a more-exaggerated pattern and in the absence of a bi-phasic pattern of muscle stimulation (Fig. 3). Spring–mass systems (e.g. muscle–tendons) with lever or pulley transmissions (Fig. 1) have a natural frequency of oscillation approximated by:

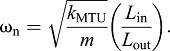(7)

Furthermore, fluctuations in muscle–tendon velocity (Fig. 3) are proportional to accelerations of the load transmitted to the input side of the lever (i.e. accelerations of the muscle–tendon, a_MTU) and can be expressed as:

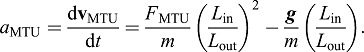(8)

As can be seen from these relationships, the presence (Eqn 7) and severity (Eqn 8) of these oscillations depends heavily on the muscle–tendon EMA, L_in/L_out. For example, natural oscillations due to impulsive loading can only occur within the period of a jump when the EMA, L_in/L_out, is high (i.e. at low gears), and can be avoided when the EMA, L_in/L_out, is small enough (i.e. at high gears) to make a resonant cycle longer than the period of application of force to the load (e.g. before ‘take-off’ in a jump). This is likely the case in jumping frogs where L_in/L_out is quite small (∼0.1) compared with the baseline value used in this study (L_in/L_out=1.0).

In addition, to help keep muscle–tendon force high during the energy storage phase of jump, relatively poor leverage (i.e. low EMA/high gear ratio) may also help to alleviate oscillations during the energy release phase of a jump.

Applications to locomotor performance

Power outputs exceeding the isotonic capacity of limb muscles or muscle groups have been observed in jumping bushbabies, frogs and humans, providing evidence that elastic energy storage and recovery contributes to the high power requirements for these movements (Bobbert et al., 1986; Marsh, 1994; Aerts, 1998). Running accelerations in turkeys also involve very high power outputs that suggest that an elastic-power-amplifying mechanism is involved (Roberts and Scales, 2002). Our results from isolated muscle–tendons provide some insight into how these mechanisms work.

First, the observation that a small amount of power amplification can occur even without a catch mechanism demonstrates how this might occur in systems that would not be considered specialized for high power output. During maximal running accelerations in turkeys, peak instantaneous hindlimb power output exceeds the power-producing capacity of the hindlimb muscles by about 1.2× (Roberts and Scales, 2002). This level of power amplification is well within the range that can be achieved in an MTU operating without a catch, according to the present results.

Second, the present results also support the idea that the very high power outputs observed in systems specialized for power output require some sort of catch mechanism. Power output during jumping in Cuban tree frogs has been estimated to be 3–7× the peak isotonic power output of the hindlimb musculature (Peplowski and Marsh, 1997; Roberts et al., 2011) and power amplification of up to 15× has been observed for some muscle groups in jumping bushbabies (Aerts, 1998). Our results confirm the conclusion of previous modeling studies (Galantis and Woledge, 2003; Roberts and Marsh, 2003) that this level of power amplification is not possible without a catch mechanism to facilitate the storage of elastic energy early in the contraction. Recent work suggests that frogs use a variable mechanical advantage as well as proximal–distal sequence of joint action to facilitate elastic energy storage and release (Astley and Roberts, 2014). Such ‘dynamic catch mechanisms’ may provide an effective alternative to the anatomical catch and trigger systems observed in many invertebrates (Patek et al., 2011).

Study limitations

The present study tests the mechanism of power amplification on a real muscle–tendon system operating against a simulated inertial–gravitational load. This approach holds some advantages over modeling studies (Alexander, 1995; Roberts, 2002; Galantis and Woledge, 2003), because any model must make assumptions about the many parameters that define muscle contractile performance. At the same time, an advantage of modeling studies is that they make the exploration of a wide range of combinations of variables practical. We tested muscle–tendon–load interactions for a particular muscle–tendon (frog plantaris), operating on a mass in a 1 g environment with an EMA set to a constant at a value of L_in/L_out=1, with a particular muscle stimulation pattern (100 ms of stimulation). Some of our results, for example, the exact magnitude of power amplification during catch and no-catch conditions, would probably vary with changes in these parameters. However, we are confident that the pattern of load dependence of power amplification observed in this study can be generalized to reflect a range of muscles and load types. In particular, alteration of our stimulation pattern would not have influenced our conclusions. At heavier loads, a longer stimulation would have served to maintain a high force for a longer duration. However, because that force was not sufficient to significantly accelerate the load, the ultimate reabsorption of tendon energy by muscle lengthening would still have occurred.

We chose to simulate a 1 g environment, whereas other studies have simulated accelerations with no gravitational force (Galantis and Woledge, 2003; Paluska and Herr, 2006). Our simulations most closely represent the pattern of load that would be experienced in a strictly vertical jump. An animal jumping at an angle to the vertical would experience only a vector component of gravity in the direction of acceleration – a condition for future study that lies somewhere in between a pure inertial (m) and pure inertial-gravitational (m·g) load. Based on the work of Galantis and Woledge, we would expect that muscle–tendon peak power output would shift to lower magnitude and require larger masses if the influence of gravity is reduced (Galantis and Woledge, 2003). We also did not simulate the poor leverage with which limb muscles typically operate (e.g. L_in/L_out=0.1 in some frogs) (Roberts and Marsh, 2003). Although changes in leverage might alter the load at which power output is maximal, we do not expect it to drastically alter the absolute magnitude of peak power output across loads (Galantis and Woledge, 2003). Despite these potential limitations, the our data support the conclusion that power amplification from dynamic interaction of the MTU and load, whether inertial and/or gravitational, is possible but relatively small (<∼2.0×) in the absence of an anatomical catch mechanism.

The independent measurement of muscle fascicle length from sonomicrometry and MTU length from muscle servomotor displacements allowed us to observe the length trajectory of the contractile element independent of any length changes in the series elastic element. In a parallel-fibered muscle, the length of the series elastic element could be calculated as the difference between the MTU length and the fascicle length. However, the plantaris is pennate, and thus the difference between MTU length changes and fascicle length changes are due not only to the action of series elastic elements, but also to the influence of fascicle pennation (Azizi et al., 2008). Thus, while the qualitative comparison of fascicle and MTU length can reveal the influence of series elasticity, it should be noted that muscle pennation angle also contributes to these differences. Similarly, as detailed in the Materials and methods, our estimate of muscle fascicle power output (e.g. Figs 3 and 7, red) is prone to error associated with the effects of muscle pennation and variable gearing (Azizi et al., 2008).

In conclusion, power amplification in a compliant MTU during dynamic contractions against a mass in gravity is load dependent. Intermediate loads produce the highest muscle–tendon mechanical power output and net mechanical work. The highest MTU peak power we observed was 1.35× above that which is possible from the muscle alone. For low loads, it is possible to overcome the load-dependent constraint on power amplification using a catch mechanism and still perform large amounts of net work on the load. At higher loads, the benefits of a catch mechanism on MTU mechanical performance vanish, especially the ability to maintain a high level of net work transfer to the load. These results give some insight into how muscle–tendon systems might be ‘tuned’ to their loads (e.g. body mass) in order to prioritize maximization of peak power output, net mechanical work, or both.