Dermal Absorption of Finite Doses of Volatile Compounds

Abstract

Laplace domain solutions to a previously published finite dose skin diffusion model are presented. The purpose of the current analysis is to derive a simple algebraic expression quantifying the total mass that is systemically absorbed at infinite time after exposure, relative to the applied mass. The resulting expression is a function of two dimensionless parameters: f, the fractional depth within the skin surface through which the permeant is initially deposited, and Χ, the ratio of maximum evaporation flux to maximum dermal flux. The result may be useful for dermal risk assessment as well as in the evaluation of cosmetic and pharmaceutical product performance.

INTRODUCTION

The importance of understanding the disposition of small doses of volatile compounds in contact with skin is broadly appreciated. Cosmetic applications of skin care products, and occupational and environmental exposures to toxic chemicals, benefit from such understanding in the evaluation of product performance and risks associated with exposure. Kasting and Miller¹ presented solutions to skin permeation models that track the disposition through absorption and evaporation over time, following finite dose exposures. An important result of finite dose models is the calculation of the total absorbed amount at infinite time following exposure. A dermal risk assessment, for example, might primarily be concerned with this quantity and less interested in the time course of absorption. Solutions presented by Kasting and Miller¹ permit such calculation, but the equations are cumbersome in that they require infinite series solutions of transcendental equations. On the contrary, Laplace domain solutions to the model equations, derived herein, lead to a compact algebraic expression for total absorbed amount.

THEORY

Kasting and Miller’s Case 1 model¹ posits an initial applied finite dermal dose, M₀ (mass/area), to be less than or equal to the saturation dose, which may be understood as the maximum capacity of the stratum corneum for a given compound. In its simplest form, amenable to an analytical solution, the stratum corneum is taken as a uniform effective medium of thickness h, occupying the space between x = 0 (skin surface) and x = h (bottom of tissue). The permeant has an effective diffusivity D that does not vary with position or time. Permeant transport is governed by the one-dimensional diffusion equation:

$$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial x^2},0\le x\le h$$ (1)

with the initial condition

$$C(x,0)=C_0\left(x\right)=\left\{\begin{array}{cc}\hfill \frac{M_0}{fh},\hfill & \hfill 0\le x\le fh\hfill \\ \hfill 0,\hfill & \hfill fh<x\le h\hfill \end{array}\right\},$$ (2)

and boundary conditions

$$\begin{array}{cc}\hfill C(h,t)& =0\hfill \\ \hfill D\frac{\partial C}{\partial x}{\mid }_{x=0}& =\gamma C(0,t),\hfill \end{array}$$ (3)

where

$$\gamma =\chi \frac{D}{h}.$$ (4)

The first member of Eq. 3 expresses the assumption of effectively perfect clearance at the bottom of the tissue; the second member specifies the flux of permeant at the skin’s surface. The time domain solution to an analogous problem for heat conduction was presented by Carslaw and Jaeger² and was adapted by Kasting and Miller¹ for application to diffusion within skin.

The dimensionless parameters f and Χ will prove to be crucial in the subsequent analysis. f is the fractional depth within the stratum corneum through which the permeant is initially deposited, and corresponds to the fractional thickness of the desquamating region of the stratum corneum. The applied dose rapidly penetrates this accessible region, presenting a constant initial concentration therein. Χ is a ratio comparing rates of evaporation and absorption of a permeant. For Χ »1, permeants will largely evaporate from the skin surface, whereas for Χ «1, they will be largely absorbed. Consult Kasting and Miller¹ for complete discussions of these parameters.

METHODS

The solution to Eq. 1 with associated initial and boundary conditions was undertaken using the method of Laplace transforms. Solutions for concentration distribution, flux, and cumulative mass absorption were obtained. The final value theorem was then applied to obtain total mass absorption at infinite time.

RESULTS

The initial concentration profile (Eq. 2) may be represented by a Fourier series:

$$C_0\left(x\right)=\frac{M_0}{h}\left[1+\frac{2}{\pi f}\sum _{n=1}^{\infty }\frac{1}{n}\text{sin}(n\pi f)\text{cos}(n\pi x∕h)\right].$$ (5)

Taking the Laplace transform of Eq. 1, one finds:

$$\frac{d^2\widehat{C}\left(x\right)}{d{x}^2}-{\lambda }^2\widehat{C}\left(x\right)=-\frac{C_0\left(x\right)}{D},$$ (6)

with ^ indicating a function of the Laplace variable s, and

$$\lambda =\frac{s}{D},$$ (7)

and taking the Laplace transform of Eq. 3, one obtains:

$$\begin{array}{cc}\hfill \widehat{C}\left(h\right)& =0\hfill \\ \hfill \gamma \widehat{C}\left(0\right)-D\frac{d\widehat{C}}{dx}{\mid }_{x=0}& =0.\hfill \end{array}$$ (8)

The solution of Eq. 6 with specified initial (Eq. 5) and boundary (Eq. 8) conditions is:

$$\widehat{C}\left(x\right)=\frac{R_0\text{sinh}(\lambda [h-x])+R_h[\gamma \text{sinh}(\lambda x)+\lambda D\text{cosh}(\lambda x)]}{-\lambda D\text{cosh}(\lambda h)-\gamma \text{sinh}(\lambda h)}+{\widehat{C}}_p\left(x\right),$$ (9)

with

$${\widehat{C}}_p\left(x\right)=\frac{M_0}{h}\left[\frac{1}{s}+\frac{2}{\pi fD}\sum _{n=1}^{\infty }\frac{1}{n}\text{sin}(n\pi f)\frac{\text{cos}(n\pi x∕h)}{{(n\pi ∕h)}^2+{\lambda }^2}\right],$$ (10)

$$\begin{array}{cc}\hfill R_0& =\gamma {\widehat{C}}_p\left(0\right)\hfill \\ \hfill & =\frac{\gamma M_0}{h}\left[\frac{1}{s}+\frac{2}{\pi fD}\sum _{n=1}^{\infty }\frac{1}{n}\frac{\text{sin}(n\pi f)}{{(n\pi ∕h)}^2+{\lambda }^2}\right],\hfill \end{array}$$ (11)

$$\begin{array}{cc}\hfill R_h& ={\widehat{C}}_p\left(h\right)\hfill \\ \hfill & =\frac{M_0}{h}\left[\frac{1}{s}+\frac{2}{\pi fD}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\frac{\text{sin}(n\pi f)}{{(n\pi ∕h)}^2+{\lambda }^2}\right].\hfill \end{array}$$ (12)

In the Laplace domain, the flux into the skin at any position x is given by:

$$\begin{array}{cc}\hfill & \widehat{F}\left(x\right)=-D\frac{d\widehat{C}}{dx}\hfill \\ \hfill & =D\left[\frac{R_h[s\text{sinh}(\lambda x)+\lambda \gamma \text{cosh}(\lambda x)]-R_0\lambda \text{cosh}(\lambda [h-x])}{\lambda D\text{cosh}(\lambda h)+\gamma \text{sinh}(\lambda h)}-\frac{d{\widehat{C}}_p}{dx}\right],\hfill \end{array}$$ (13)

with

$$\frac{d{\widehat{C}}_p}{dx}=\frac{-2M_0}{f{h}^{2}D}\sum _{n=1}^{\infty }\frac{\text{sin}(n\pi f)}{{(n\pi ∕h)}^2+{\lambda }^2}\text{sin}(n\pi x∕h).$$ (14)

The flux specifically at x = h is:

$$\widehat{F}\left(h\right)=D\left[\frac{R_h[s\text{sinh}(\lambda h)+\lambda \gamma \text{cosh}(\lambda h)]-R_0\lambda }{\lambda D\text{cosh}(\lambda h)+\gamma \text{sinh}(\lambda h)}\right],$$ (15)

and mass accumulation at x = h is given by:

$$\widehat{M}=\frac{\widehat{F}\left(h\right)}{s}.$$ (16)

The final value theorem allows the determination of the total absorbed amount after infinite time from its Laplace transform:

$$m_{abs}\left(\infty \right)=\underset{s\to 0}{\text{lim}}s\widehat{M}=\underset{s\to 0}{\text{lim}}\widehat{F}\left(h\right).$$ (17)

The evaluation of the limit is somewhat cumbersome but straightforward. The procedure is to (i) expand the hyperbolic functions in infinite series:

$$\begin{array}{cc}\hfill & \text{cosh}(\alpha )=1+\frac{{\alpha }^2}{2!}+\frac{{\alpha }^4}{4!}+\cdots \hfill \\ \hfill & \text{sinh}(\alpha )=1+\frac{{\alpha }^3}{3!}+\frac{{\alpha }^5}{5!}+\cdots ,\hfill \end{array}$$ (18)

(ii) keep only the terms in Eq. 15 with the lowest order of s, and (iii) then take the limit (Eq. 17). Algebraic manipulation eventually leads to:

$$\frac{m_{\text{abs}}\left(\infty \right)}{M_0}=\frac{D+\frac{\gamma h}{2}-\frac{4\gamma h}{{\pi }^{3}f}\sum _{n=1}^{\infty }\frac{\text{sin}([2n-1]\pi f)}{{(2n-1)}^3}}{D+\gamma h}.$$ (19)

With Χ = γh/D, multiplying numerator and denominator by 2/D, one obtains

$$\frac{m_{\text{abs}}\left(\infty \right)}{M_0}=\frac{2+\chi -\frac{8\chi }{{\pi }^{3}f}\sum _{n=1}^{\infty }\frac{\text{sin}([2n-1]\pi f)}{{(2n-1)}^3}}{2+2\chi }.$$ (20)

It can be shown that

$$\frac{8}{{\pi }^{3}f}\sum _{n=1}^{\infty }\frac{\text{sin}([2n-1]\pi f)}{{(2n-1)}^3}=1-f,0\le f\le 1,$$ (21)

which follows from the fact that $\frac{8}{{\pi }^{3}f}{\sum }_{n=1}^{\infty }\frac{\text{sin}([2n-1]\pi f)}{{(2n-1)}^3}$ is the Fourier expansion of the expression f (1 − f ) over the interval 0 ≤ f ≤ 1. Thus, Eq. 20 simplifies to:

$$\frac{m_{\text{abs}}\left(\infty \right)}{M_0}=\frac{2+f\chi }{2+2\chi }.$$ (22)

Figure 1 displays cumulative absorption at infinite time as a function of fractional deposition depth for a range of volatilities (Eq. 22).

Figure 1.

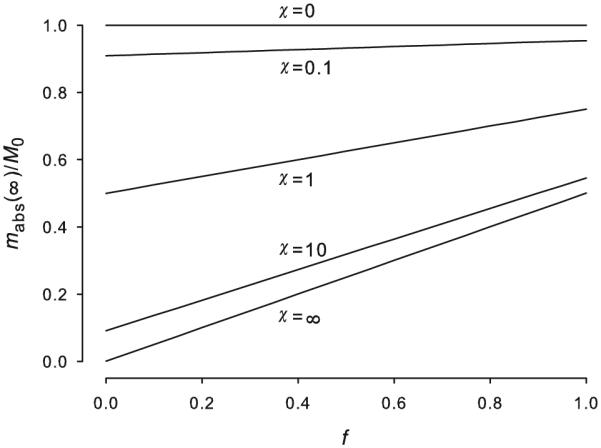
Cumulative absorption at infinite time as a function of fractional deposition depth for range of volatilities (Eq. 22). Compare with Kasting and Miller’s¹ Figure 3.

Because at infinite time the entire applied dose is either absorbed or evaporated, the total evaporated mass is readily obtained:

$$\frac{m_{\text{evap}}\left(\infty \right)}{M_0}=1-\frac{m_{\text{abs}}\left(\infty \right)}{M_0}=\frac{2\chi -f\chi }{2+2\chi }.$$ (23)

DISCUSSION

For practical applications of Eqs. 22 and 23, Kasting and Miller¹ suggest that a reasonable value of f for stratum corneum is 0.1. Values for Χ follow from its definition as the ratio of the maximum evaporation flux to the maximum steady-state dermal flux. Both quantities may be measured or estimated from various algorithms, as outlined by Kasting and Miller.¹ Their Eq. 40 is reproduced here only as one example to illustrate the kinds of inputs that are required:

$$\chi =3.4\times {10}^{-3}{u}^{0.78}\frac{P_{\text{vap}}{\text{MW}}^{3.4}}{K_{0\mathrm{w}}^{0.76}{S}_{\mathrm{w}}},$$ (24)

where u is ambient air speed (m/s), P_vap is the permeant’s vapor pressure (torr), MW its molecular weight, K_ow its octanol–water partition coefficient, and S_w its aqueous solubility (μg/cm).

A potential hurdle to the adoption of Eqs. 22 and 23 is determining whether the applied dose M₀ falls within the small-dose range for which the equations apply. For guidance, Kasting and Miller¹ define a saturation dose, M_sat, as the mass (per unit area) of applied chemical required to saturate the desquamating layers of the stratum corneum, which constitute the region that is freely accessible to the applied dose. Its value may be estimated as:

$$M_{\text{sat}}=fh{K}_{\mathrm{sc}∕\mathrm{w}}{S}_{\mathrm{w}},$$ (25)

where K_sc/w is the effective stratum corneum–water partition coefficient of the permeant. For applied loads that exceed M_sat, excess permeant resides in a pool on the skin’s surface that is gradually depleted through absorption and evaporation. Strictly, Eqs. 22 and 23 apply to cases where M₀ ≤ M_sat. Kasting and Miller¹ argue convincingly that for large doses, the absorbed amount can be estimated as:

$$\frac{m_{\text{abs}}\left(\infty \right)}{M_0}=\frac{1}{1+\chi },$$ (26)

which also corresponds to the limit of Eq. 22 for small f. This large-dose limit would appear to apply for all values of f, as the initial distribution of permeant becomes irrelevant after a long time. For intermediate doses, say M_sat < M₀ < 10 × M_sat, asymptotic analysis seems intractable. Numerical investigations were therefore undertaken using the Finite Dose Skin Permeation Calculator,³ which implements numerical solutions to Kasting and Miller’s model.¹ Results from intermediate doses, not shown here, also support the use of Eq. 26 for small f. For larger f, a smooth transition between Eqs. 22 and 26, as applied load increases through the small- to large-dose range, seems a reasonable postulate. However, as stated above, small f is representative of stratum corneum. Therefore, for practical applications of the results presented here, a precise determination of M_sat may not crucial: m_abs(∞)/M₀ reverts to the small-f limit of Eq. 22 for small, large, and intermediate doses.

Equation 22 thus provides a simple, usable expression for evaluating the fractional total mass absorbed from finite dose exposures. This expression may be useful for dermal risk assessment as well as in the evaluation of skin cosmetic and pharmaceutical product performance.