Inward Leakage Variability between Respirator Fit Test Panels – Part I. Deterministic Approach

Abstract

Inter-panel variability has never been investigated. The objective of this study was to determine the variability between different anthropometric panels used to determine the inward leakage (IL) of N95 filtering facepiece respirators (FFRs) and elastomeric half-mask respirators (EHRs). A total of 144 subjects, who were both experienced and non-experienced N95 FFR users, were recruited. Five N95 FFRs and five N95 EHRs were randomly selected from among those models tested previously in our laboratory. The PortaCount Pro+ (without N95-Companion) was used to measure IL of the ambient particles with a detectable size range of 0.02 to 1 μm. The Occupational Safety and Health Administration standard fit test exercises were used for this study. IL test were performed for each subject using each of the 10 respirators. Each respirator/subject combination was tested in duplicate, resulting in a total 20 IL tests for each subject. Three 35-member panels were randomly selected without replacement from the 144 study subjects stratified by the National Institute for Occupational Safety and Health bivariate panel cell for conducting statistical analyses. The geometric mean (GM) IL values for all 10 studied respirators were not significantly different among the three randomly selected 35-member panels. Passing rate was not significantly different among the three panels for all respirators combined or by each model. This was true for all IL pass/fail levels of 1%, 2%, and 5%. Using 26 or more subjects to pass the IL test, all three panels had consistent passing/failing results for pass/fail levels of 1% and 5%. Some disagreement was observed for the 2% pass/fail level. Inter-panel variability exists, but it is small relative to the other sources of variation in fit testing data. The concern about inter-panel variability and other types of variability can be alleviated by properly selecting: pass/fail level (IL 1–5%); panel size (e.g., 25 or 35); and minimum number of subjects required to pass (e.g., 26 of 35 or 23 of 35).

INTRODUCTION

In 1972, Los Alamos National Laboratory (LANL) developed recommendations for test panels to evaluate respirator fit, which, based on a 1967–68 USAF survey, led to the LANL proposal of 25-subject fit test panels.^(1–2) Following criticisms of the LANL specifications,⁽³⁾ the National Institute for Occupational Safety and Health (NIOSH) initiated a study to develop an anthropometric database more representative of civilian respirator users⁽⁴⁾ and produce a panel more representative of the age and racial/ethnic distributions of the current civilian work force. Based on the NIOSH anthropometric survey, Zhuang et al.^(5–7) defined two new test panels, including: (1) the NIOSH bivariate Respirator Fit Test Panel (NRFTP) with ten cells based on face length and face width; and (2) the Principal Component Analysis (PCA) Panel, which was defined from the first two principal components (which are the independent linear combinations that explain the maximum degree of variance) from 10 dimensions of face size.

In 1995, the fit testing of respirators equipped with particle filters and filtering facepiece respirators was abandoned in the certification standard with the transition to a new respirator approval regulation because of the difficulty (i.e., particulate respirators had to be modified to remove iso-amyl acetate) and lack of appropriate fit testing techniques. Later, as NIOSH attempted to revise its respirator approval standard, new certification requirements for half-mask air-purifying particulate respirators in the approval process were proposed.⁽⁸⁾ This proposed rule would establish approval requirements for an alternate class of half-mask air-purifying respirators, for which the performance of the respirator in preventing inward leakage (IL) of contaminants through the face seal and non-filter components would be evaluated, supplementing existing requirements for testing the performance of the filter.

The goal of any fit test criterion would be to demonstrate the ability of a respirator to fit the facial sizes and shapes for which it was designed. In order to achieve this, it is necessary for the method to be able to reject a high percentage of ineffective respirators, while still passing a high percentage of highly effective respirators. A simple binomial approach was proposed to simultaneously determine both the required sample size and the optimal cut-off for the number of subjects needed to achieve a passing result.⁽⁹⁾ The method essentially conducts a global search of the Type I and Type II errors under different null and alternative hypotheses, across the range of possible sample sizes, to find the lowest sample size which yields at least one cut-off satisfying or approximately satisfying all pre-determined limits for the different error rates. Benchmark testing of 98 respirators (conducted by NIOSH) is used to illustrate the binomial approach and show how sample size estimates from the random effects model can vary substantially depending on estimated variance components.⁽⁹⁾ For the binomial approach, probability calculations show that a sample size of 35–40 yields acceptable error rates (i.e., Type I error of 0.05 for falsely passing a respirator and Type II error of 0.20 for falsely failing a respirator) under different null and alternative hypotheses. Overall, despite some limitations, the binomial approach represents a highly practical approach with reasonable statistical properties.

The 2009 Notice of Proposed Rulemaking (NPRM) proposed a 35-member panel for a respirator intended to fit the civilian work force.⁽⁸⁾ One of the comments received on this NPRM was concerned about panel variability. Specifically, manufacturers are located throughout the US and the world. They would be required to use the NIOSH bivariate panel to recruit 35 subjects and conduct IL tests and then submit their IL test results to NIOSH as part of their submission for approval. NIOSH would also conduct IL tests on a panel of 35 subjects in Pittsburgh, PA and test results would be used to determine if a respirator is approved or not. Would NIOSH get the same results as the results obtained by the manufacturers? NIOSH usually recruits three times more subjects than the panel size. Would IL test results differ from one panel to another at NIOSH?

Variability in fit test data has been recognized for a long time. The most commonly recognized variabilities are the inter- and intra-subject variabilities.^(10–14) To address inter-subject variability, NIOSH has developed a more representative respirator fit test panel than the LANL panel to select representative subjects for IL test. Multiple donnings are used to address intra-subject variability. The inter-panel variability needs to be determined to adequately address the comment expressed by the stakeholders about the variability inherent in the test panel proposed by NIOSH for the IL test.

The objective of this study was to determine the variability between different anthropometric panels when used to determine the IL of N95 filtering facepiece respirators (FFRs) and elastomeric half-mask respirators (EHRs). The specific aims were: (1) to determine if geometric mean ILs were significantly different among different respirator fit test panels; (2) to estimate the coefficient of variation (CV) for inter-panel variability; (3) to determine if passing rates were significantly different among different respirator fit test panels; (4) to determine if passing/failing a respirator (one size only or more than one size system or family) in IL test was consistent among different respirator fit test panels; and (5) to investigate how different pass/fail parameters affect the inter-panel variability. This was a first-of-its kind study to address this important issue. This article only reports the study results based on a deterministic approach, i.e., randomly selecting three different panels and investigating differences in geometric mean (GM) IL value, passing rate (percent of subjects passing IL test), and passing a respirator in IL test (at least 26 of 35 subjects passing the IL test) among them. Subsequent papers will report the results based on a probabilistic approach (i.e., bootstrapping or data-based resampling) and the effect of sample size on inter-panel variability.

METHODS

Study Subjects

In this study, 144 study subjects were recruited by first asking for volunteers from the pool of experienced N95 FFR users who regularly participate in NIOSH certification testing, followed by recruitment of inexperienced N95 users. Among the 144 study subjects, 62 were experienced and 82 were inexperienced N95 FFR users. Subjects from the pool of certification testing participants undergo a yearly physical at Jefferson Regional Medical Center (Pittsburgh, PA). The inexperienced test subjects completed a health history questionnaire as well as a physical exam by a medical officer. Exclusion criteria for the study included a history of uncontrolled chronic asthma, pneumonia, and high blood pressure.

Three 35-member fit-test panels were randomly selected without replacement from the 144 study subjects stratified by the NIOSH bivariate panel cell, as shown in Table I. Each subject could be a member of only one panel. The number of subjects for each cell was determined by the distribution of the US civilian work force. Subjects in Cells 3, 4, and 7 were all assigned to one of the three panels. Nine of the 12 subjects in Cell 8 were assigned. Only 6 subjects for the remaining 6 cells were not assigned because there were 12 subjects and only 6 subjects were needed. Individuals who chose to participate signed a consent form. This study was approved by the NIOSH human subject review board.

TABLE I.

Randomized Assignment of Three 35-member Panels from 144 Study Subjects

		No. of randomized subjects
Bivariate panel cell	No. of all subjects	Panel I	Panel II	Panel III	Total
1	12	2	2	2	6
2	12	2	2	2	6
3	12	4	4	4	12
4	27	9	9	9	27
5	12	2	2	2	6
6	12	2	2	2	6
7	21	7	7	7	21
8	12	3	3	3	9
9	12	2	2	2	6
10	12	2	2	2	6
Total	144	35	35	35	105

Respirators

Five N95 FFRs and five N95 EHRs were randomly selected from among models tested previously in our laboratory. The FFRs were: 3M 1860/1860S (cup-shaped, NIOSH approval number: TC-84A-0006), Gerson 1730 (cup-shaped, TC-84A-0160), Kimberly Clark Tecnol PFR95 (flat, TC-84A-0299), Willson N9510F (flat, TC-84A-1165), and Sperian HCNB295F (flat fold, TC-84A-4371). The EHRs were: MSA Comfo with 816291 filters (TC-84A-1514), Moldex 8000 with 8910 N95 filter (TC-84A-1343), Sperian Respiratory Protection USA, LLC Premier Plus T-Series with 1060N95 filter (TC-84A-1426), 3M 7500 with 5N11 filter (TC-84A-0376), and North Safety Products 7700 with 7506N95 filters (TC-84A-1099). The five FFRs were randomly assigned labels A–E, while the five EHRs were randomly assigned labels F–J. A new respirator for each FFR model was provided to each subject since FFRs may typically be designed for limited number of donning/doffings. Because the EHRs had to be reused, the elastomeric facepiece were cleaned and disinfected per the manufacturers’ instructions and the filters were replaced before being worn by another subject.

The FFRs were available in one or two sizes and all five EHRs were available in three sizes. The one size respirators were tested by all subjects from cells 1–10. For two-size respirators, the small size facepiece was tested by subjects in cells 1–5 and the large size facepiece was tested by subjects in cells 6–10. For three-size respirators, the small size facepiece was tested by subjects in cells 1–3, the medium size facepiece was tested by subjects in cells 4–7, and the large size facepiece was tested by subjects in cells 9–10.

Inward Leakage Measurement

The Occupational Safety and Health Administration (OSHA) standard for quantitative fit testing accepts the use of the TSI PortaCount, which counts the particle concentration in the ambient air outside the respirator and the particle concentration inside the respirator facepiece. The ratio of the ambient particle sample to the respirator particle sample is used to determine a fit factor. The PortaCount Pro+ 8038 without N95-Companion was used to measure IL (i.e., face seal leakage and filter penetration of the ambient particles with a detectable size range of 0.02–1 μm). By evaluating a larger size range of particles, a more conservative estimate of fit is achieved and the detection limit increases to a maximum fit factor value of 10,000. The OSHA standard fit test exercises were used for this study: normal breathing, deep breathing, breathing while moving their head from side to side, breathing while moving their head up and down, reciting the rainbow passage, reaching floor to ceiling, grimacing (not included in calculations) and normal breathing. Subjects were asked to don a respirator, wait 5 min for the concentration of particles inside the respirator facepiece to reach a steady state, and complete the IL test. The particle concentration was considered to be in the steady state when the particle count inside the respirator showed no fluctuation while the test subject was not performing any activities. The overall fit factor was recorded.

Prior to conducting the test, the User Instructions provided by the manufacturer were reviewed to verify that the instructions for facepiece size selection were easily understood, easily followed, and practical. Test subjects were asked to familiarize themselves with the manufacturer’s selection, donning and fitting procedures for the respirator. Each test subject performed a user seal check in accordance with the manufacturer’s User Instructions. Since this protocol investigated inter-panel variability, any test subject not being able to successfully perform a user seal check, in his or her opinion, was allowed to continue the test, but the fact that a seal check could not be performed was noted. The intention was to have a wider variety of fit factors, and it was not intended to find the best fitting respirator or only those that would pass all the testing.

Each respirator was probed for purposes of measuring concentrations of aerosol inside the facepiece. For filtering face-piece respirators, the optimum sampling probe position is flush with the inside of the facepiece at the point of quadrilateral symmetry of the mouth and nose, i.e., midway between the nose and upper lip. For the elastomeric facepieces, the appropriate test adapter was used. The test adapter is a circular fitting that is inserted between the facepiece and filter. The PortaCount sampling tube is attached to the fitting from the exterior. A sampling tube attached to the interior of the fitting extends into the facepiece to measure the particle count.

Inward leakage tests were performed for each subject using each of the 10 respirators. The testing order for the respirators was randomized for each subject. Each respirator/subject combination was tested in duplicate, resulting in 20 IL tests for each subject. After the completion of the first respirator, the subject removed the respirator, returned it to the test operator who returned the head straps and/or noseband as appropriate to their original condition (as the respirator came from the manufacturer), rested for two minutes and then repeated the IL test. The subjects were not allowed to know if they passed or failed the test or see the IL value.

Statistical Analysis

The fit factor computed by the PortaCount was converted to IL by taking its reciprocal. The IL was log-transformed for conducting statistical analyses due to it log-normal distribution. Geometric mean (GM), geometric standard deviation (GSD), and 95th percentile (P95) of the percent IL were calculated for each panel. For each respirator, the GMs were compared among three panels using analysis of variance (ANOVA). The SAS PROC GLM procedure was used to determine if ILs between panels were statistically different. Log-transformed IL was the dependent variable. Panel and subject were the independent variables with subject nested within each panel.

Tests of hypotheses used the Type III MS for subject within panel as an error term. The inter-panel variability, intra- and inter-subject variability were calculated through a variance component model (PROC VARCOMP). Since the IL data were log-transformed, the CV was calculated by using the standard deviation (SD) of the log-transformed data in the following equation:⁽¹⁵⁾

$$\text{CV}=\text{sqrt}(exp(\text{SD}\ast \text{SD})-1).$$

A subject was considered to pass the IL test if one of the two IL values was less than or equal to a given passing level of 1%, 2%, and 5%. Only one passing test was required to prove that it was possible for the subject to obtain an acceptable fit using that respirator. The passing rate for each respirator was calculated as the percentage of subjects who passed the IL test. For each respirator, a Chi-Square test was used to investigate difference of the passing rates among the three panels.

All analyses were conducted using SAS version 9.3 (SAS Institute Inc., Cary, NC). All P values were two sided.

RESULTS

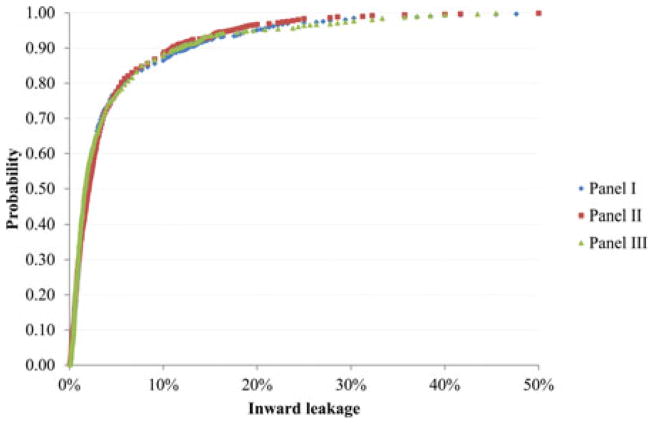
Figure 1 shows the IL data for all 10 models by panel. Each panel had 35 subjects, two tests each, and 10 respirators, resulting in 700 data points. The minimum IL was close to zero percent, whereas the maximum IL was about 50%. About 90% of the IL values were less than 10%. The three curves for three panels gave very similar distributions.

FIGURE 1.

Probability of inward leakage (i.e., the percentage of inward leakage measurements < the indicated inward leakage) for all respirators by panel.

Table II presents the GM, GSD and P95 of each respirator for all 144 subjects. The GM and P95 ranged from 0.47% (EHR-F) to 5.88% (FFR-B) and 2.94% to 37.93%, respectively. These data provide an estimate of how they fit the population and their effectiveness. The effectiveness will then be shown to affect inter-panel variability.

TABLE II.

Descriptive Statistics of Inward Leakage for the 144 Study Subjects by Respirator

	All subjects (N = 144)
Respirator	No. of Tests	GM (%)	GSD	P95 (%)
FFR-A	288	1.65	2.85	9.25
FFR-B	288	5.88	3.01	36.04
FFR-C	288	4.24	2.87	24.05
FFR-D	288	1.98	3.04	12.34
FFR-E	288	5.40	3.27	37.93
EHR-F	288	0.47	3.05	2.94
EHR-G	288	1.48	2.37	6.10
EHR-H	288	1.45	2.72	7.52
EHR-I	288	1.43	2.24	5.37
EHR-J	288	1.00	2.84	5.54
Total	2880	1.90	3.60	15.66

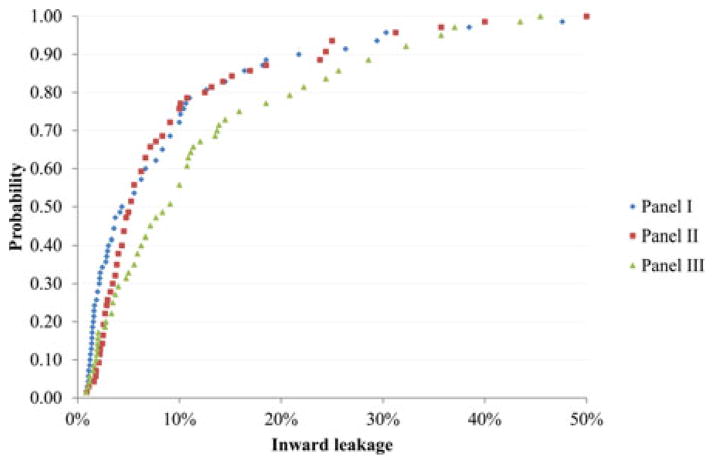
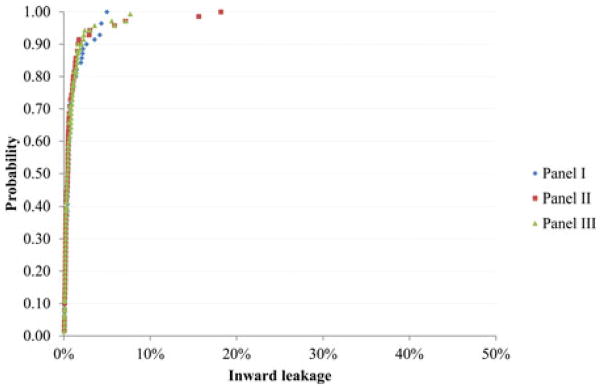
The GM and P95 values for each respirator and panel can be seen in Table III. The ANOVA results did not indicate significant GM difference among the three panels for all respirators. Figure 2 shows the distribution of IL for FFR-B by panel. As Table II shows, FFR-B is the respirator with highest overall GM IL. The IL ranged from ~0% to ~50%. About 90% of the IL values were less than 30%. The curves of panel I and II were similar, but somewhat different from panel III. Figure 3 shows the distribution of IL for the respirator with lowest GM IL (EHR-F) by panel. The IL ranged from ~0% to ~20%. About 90% of the IL values were less than 3%. The three curves were very similar.

TABLE III.

Comparison of Inward Leakage for Each 35-member Panel by Respirator

	Panel I			Panel II			Panel III
Respirator	No. of Tests	GM (%)	P95 (%)	No. of Tests	GM (%)	P95 (%)	No. of Tests	GM (%)	P95 (%)
FFR-A	70	1.59	10.62	70	1.60	8.37	70	2.20	13.54
FFR-B	70	4.93	30.02	70	5.88	25.52	70	7.76	42.46
FFR-C	70	5.59	27.26	70	3.75	18.87	70	4.27	25.19
FFR-D	70	2.12	16.11	70	2.44	10.66	70	1.89	13.28
FFR-E	70	6.00	37.96	70	5.22	37.39	70	4.71	33.08
EHR-F	70	0.52	3.39	70	0.46	3.42	70	0.49	3.13
EHR-G	70	1.47	4.42	70	1.51	7.22	70	1.47	6.01
EHR-H	70	1.58	8.72	70	1.70	11.67	70	1.22	4.63
EHR-I	70	1.53	5.35	70	1.56	6.78	70	1.26	4.14
EHR-J	70	0.92	4.60	70	1.12	7.52	70	0.99	3.96
Total	700	1.99	16.18	700	1.98	15.86	700	1.93	15.66

Note: GM, geometric mean; P95, the 95th percentile.

FIGURE 2.

Probability of inward leakage (i.e., the percentage of inward leakage measurements < the indicated inward leakage) for respirator with the highest geometric mean inward leakage (FFR-B) by panel.

FIGURE 3.

Probability of inward leakage (i.e., the percentage of inward leakage measurements < the indicated inward leakage) for respirator with the lowest geometric mean inward leakage (EHR-F) by panel.

Variance components for inter-panel variability were obtained from the variance component model for only four respirators (FFR-A, FFR-B, FFR-C, and EHR-H). For the other six respirators, the variance components for inter-panel variability were too small to estimate from the variance component model. The ANOVA table for Respirator FFR-A is summarized in Table IV as an example. There was no significant difference in IL among the three panels (p-value > 0.05). There were significant differences in IL among subjects (p-value < 0.05). The corresponding variance component estimates for respirator FFR-A are summarized in Table V. Variance is also expressed as SD, GSD, and CV. The variance for subject (inter-subject variability) was the largest (CV = 130%). The variance for the inter-panel (CV = 5.1%) was the smallest. Intra-subject variability was in between with a CV of 48.5%. The inter-panel CVs for all respirators are summarized in Table VI.

TABLE IV.

Analysis of Variance (ANOVA) Table for Respirator FFR-A

Source	Degrees of Freedom	Expected Mean Square	F Value	P Value
Panel	2	σ2 + 2σs2 + 35 σp 2	1.08	> 0.05
Subject (Panel)	102	σ2 + 2σs2	10.37	< 0.05
Error	105	σ2

Note: Tests of hypotheses using the Type III MS for subject within panel as an error term.

TABLE V.

Variance Component Estimates for Respirator FFR-A

Variance Component	Variance	Standard Deviation	Geometric Standard Deviation	Coefficient of Variation
Var(Panel), Σαi2	0.002607	0.0511	1.1	5.1%
Var(subject(Panel)),σs2	0.989568	0.9948	2.7	130%
Var(Error), σ2	0.211286	0.4597	1.6	48.5%

TABLE VI.

Inter-panel Variability Estimated as Coefficient of Variation

	Method 1 – Variance Component Estimates			Method 2 – Using Means for Each Panel
Respirator	Standard Deviation	Overall Mean Log(IL)	Coefficient of Variation	Standard Deviation	Overall Mean Log(IL)	Coefficient of Variation
FFR-A	0.0511	−4.0303	5.1%	0.1841	−4.0303	18.6%
FFR-B	0.1612	−2.7998	16.2%	0.2289	−2.7999	23.2%
FFR-C	0.1259	−3.1065	12.6%	0.2033	−3.1065	20.5%
FFR-D	N/AA			0.1281	−3.8445	12.9%
FFR-E	N/A			0.1213	−2.9406	12.2%
EHR-F	N/A			0.0564	−5.3145	5.6%
EHR-G	N/A			0.0138	−4.2091	1.4%
EHR-H	0.0460	−4.2094	4.6%	0.1741	−4.2094	17.5%
EHR-I	N/A			0.1177	−4.2369	11.8%
EHR-J	N/A			0.0980	−4.6016	9.8%

^AN/A – variance component was so small that it could not be estimated.

In addition to obtaining CVs from variance component estimates, CVs were also calculated using a second method. The mean log-transformed IL values were first calculated for each panel. The three mean values were then used to calculate the overall mean log-transformed IL and SD which was further used to calculate inter-panel variability as CV. These results are also summarized by respirator in Table VI. These CVs tend to be larger than those estimated by Method 1 because inter-and intra-subject variability was accounted for in Method 1, but not in Method 2. Method 2 may have overestimated inter-panel variability.

Table VII shows the passing rate for each respirator among all 144 subjects. We considered the three passing levels of 1%, 2%, and 5%. The passing rate of each respirator with passing level of 1% ranged from 5.6% (FFR-B) to 86.8% (EHR-F). The ranges were from 27.1% (FFR-B) to 97.2% (EHR-F) and 54.9% (FFR-B) to 98.6% (EHR-F) for the passing levels of 2% and 5%, respectively.

TABLE VII.

Passing Rates for the 144 Study Subjects by Passing Level and Respirator

	Relative Frequency of Passing (N = 144)
Respirator	≤1% (%)	≤2% (%)	≤5% (%)
FFR-A	45.8	75.7	90.3
FFR-B	5.6	27.1	54.9
FFR-C	13.2	34.0	69.4
FFR-D	31.3	67.4	88.2
FFR-E	11.8	29.9	59.7
EHR-F	86.8	97.2	98.6
EHR-G	34.7	73.6	95.1
EHR-H	42.4	66.7	94.4
EHR-I	36.8	77.8	97.2
EHR-J	61.1	84.0	94.4
Total	36.9	63.3	84.2

Note: Data are expressed as relative frequency (i.e., percent of subjects passing).

The comparison of passing rates for each 35-member panel by passing level and respirator is presented in Table VIII. In another study to determine sample size for respirator fit test panel, respirators with passing rate of 80% or higher were considered effective, 60% or less were ineffective.⁽⁹⁾ For the passing level 1%, only EHR-F was an effective respirator if using at least 26 of 35 subjects passing the IL test as a criterion; whereas all remaining respirators failed the IL test. However, all three panels resulted in the same results for passing or failing a respirator. For the passing level 2%, EHR-F and EHR-J were effective respirators; FFR-B, FFR-C, and FFR-E were still ineffective respirators; FFR-A, FFR-D, EHR-G, EHR-H, and EHR-I were in between. Using the above criterion, effective respirators EHR-F and EHR-J passed the IL test for all three panels; the three ineffective respirators FFR-B, FFR-C, and FFR-E failed the IL test for all three panels; for respirators with passing rate between 60% and 80%. For the passing level 5%, FFR-A, FFR-D, EHR-F, EHR-G, EHR-H, EHR-I, and EHR-J were effective respirators; FFR-B was still an ineffective respirator; and respirators FFR-C and FFR-E were in between. Using the above-mentioned criterion, all effective respirators passed the IL test; the ineffective respirator failed the IL test; and the remaining respirators failed one or more panels. The above results showed little inter-panel variability for passing level 1%, but suggested a little inter-panel variability for passing level 2% and 5%; nonetheless, the Chi-Square test did not indicate any statistically significant difference in passing rates among the three panels (all P > 0.05).

TABLE VIII.

Comparison of Passing Rates for Each 35-member Panel by Passing Level and Respirator

	Inward leakage ≤1%				Inward leakage ≤2%				Inward leakage ≤5%
Respirator	Panel I (%)	Panel II (%)	Panel III (%)	P value	Panel I (%)	Panel II (%)	Panel III (%)	P value	Panel I (%)	Panel II (%)	Panel III (%)	P value
FFR-A	48.6	42.9	37.1	0.63	80.0	74.3	57.1	0.09	91.4	91.4	82.9	0.58
FFR-B	5.7	2.9	2.9	1.00	37.1	14.3	22.9	0.08	62.9	60.0	40.0	0.15
FFR-C	5.7	14.3	11.4	0.62	25.7	34.3	37.1	0.57	65.7	74.3	68.6	0.80
FFR-D	28.6	20.0	40.0	0.18	65.7	60.0	62.9	0.88	85.7	88.6	85.7	1.00
FFR-E	5.7	14.3	14.3	0.48	34.3	25.7	22.9	0.54	57.1	65.7	60.0	0.82
EHR-F	82.9	85.7	82.9	0.93	94.3	94.3	100.0	0.35	100.0	94.3	100.0	0.33
EHR-G	31.4	31.4	34.3	0.96	65.7	68.6	74.3	0.73	100.0	94.3	94.3	0.54
EHR-H	37.1	45.7	48.6	0.60	60.0	57.1	80.0	0.09	88.6	91.4	97.1	0.53
EHR-I	37.1	40.0	34.3	0.88	77.1	68.6	82.9	0.37	97.1	94.3	100.0	0.77
EHR-J	57.1	57.1	68.6	0.53	88.6	82.9	82.9	0.74	97.1	94.3	100.0	0.77
Total	34.0	35.4	37.4	0.64	62.9	58.0	62.3	0.35	84.6	84.9	82.9	0.74

Note: Data are expressed as relative frequency (i.e., percent of subjects passing). P-values are for the Chi-Squared Test.

DISCUSSION

The results from this study show that the GM IL values for the 10 studied respirators were not significantly different among the three randomly selected 35-member panels. For passing rate this trend was true for all 10 respirators. Passing level may be an important factor that could affect inter-panel variability. Results in this study are consistent with the findings by Landsittel et al., who calculated rejection probabilities for a panel of 25 subjects for respirators with different passing rates.⁽⁹⁾ Using at least 19 of 25 subjects passing the IL test as a criterion, effective respirators pass the IL test with high probability. Ineffective respirators are rejected at a high probability. For respirators with passing rate between 60% and 80%, rejection probability is moderate. Passing rate affected inter-panel variability. For effective respirators (passing rate of 80% or higher) and ineffective respirators (passing rate of 60% or lower), different panels will give similar results. For respirators with passing rates between 60% and 80%, disagreements between test panels are expected.

Landsittel et al. also demonstrated that if the number of subjects required to pass is decreased, more of the respirators with passing rate between 60% and 80% will pass the test.⁽⁹⁾ If there are many respirators with passing rate between 60% and 80% and we want most of them to pass, we can lower the number of subjects required to pass. Alpha error is the probability of rejecting effective respirators and beta error is the probability of passing ineffective respirators (1 – probability of rejecting ineffective respirators). For the binomial approach, probability calculations show that a sample size of 35–40 yields acceptable error rates under different null and alternative hypotheses.

Previous studies have also shown that variability is inherent to fit testing research. Oestenstad and Zwissler performed 3 fit tests per respirator type on 45 subjects wearing natural silicone and rubber half-mask respirators. The GSD ranged from 1.06–17.09 for silicone facepieces and 1.06–5.68 for natural rubber facepieces.⁽¹⁰⁾ Similar results have been found in other research associated with re-useable halfmask respirators.^(11–13) da Roza et al. found reproducibility is more easily achieved when tests are given on the same day than when fit tests are conducted on different days.⁽¹¹⁾

Recently, NIOSH conducted a study to assess respirator fit and facial dimension changes as a function of time to improve the scientific basis for decisions on the periodicity of fit testing. A pilot study (n = 10) was conducted to investigate the variation in fit test data collected in accordance with the study protocol.⁽¹⁴⁾ That pilot study first quantified variability associated with different respirator samples for the same model (CV = 35.3%) in addition to estimating between subjects (inter) and within each subject (intra) variability (CVs of 41.8% for inter- and 40.0% for intra-subject variability). The pilot study found that between visit variability (CV = 12.4%) was not significant. In this current study, CVs for inter- and intra-subject variability based on data from one subject were 130% and 48.5%. Inter-panel variability (CV = 5.1%) was not significant. Therefore, the findings in this study were consistent with findings in the previous pilot study.

Fit testing is not error free and is associated with the fitting characteristics of a given respirator as well as the accuracy of the fit-testing method.⁽¹⁶⁾ Two studies investigated the alpha (failing a fit-test in error) and beta (passing a fit test in error) errors associated with various fit testing methods. A comparison of Bitrex, Saccharin and TSI PortaCount Plus with N95 Companion showed beta errors (falsely passing) of 8%, 8%, and 9%, respectively, and alpha errors (falsely failing) of 71%, 68%, and 40%, respectively.⁽¹⁷⁾ A comparison of those same fit testing methods, as well as the ambient aerosol method using the TSI PortaCount Plus and the generated aerosol method with corn oil found that when the errors are combined, the TSI PortaCount Plus had the lowest percentage of wearers being assigned a poor-fitting respirator.⁽¹⁸⁾

CONCLUSIONS

This study found that the GM IL values for the 10 studied respirators were not significantly different among the three randomly selected 35-member panels. Passing rate was not significantly different among the three panels for all respirators combined or by each model. This was true for all IL pass/fail levels of 1%, 2%, and 5%. Using 26 or more subjects to pass the IL test, all three panels had consistent passing/failing results for pass/fail levels of 1% and 5%. Some disagreement was observed for 2% pass/fail level. Pass/fail level is an important factor affecting inter-panel variability.

Inter-panel variability exists, but it is small relative to the other sources of variation in fit testing data. The concern about inter-panel variability and other types of variability can be alleviated by properly selecting: pass/fail level (IL 1–5%); panel size (e.g., 25 or 35); and minimum number of subjects required to pass (e.g., 26 of 35 or 23 of 35). Further resampling analyses can be conducted to estimate the probability that two panels will both pass or fail a respirator and to investigate the effect of pass/fail level and sample size on the probability.