Accurate estimation of influenza epidemics using Google search data via ARGO

Significance

Big data generated from the Internet have great potential in tracking and predicting massive social activities. In this article, we focus on tracking influenza epidemics. We propose a model that utilizes publicly available Google search data to estimate current influenza-like illness activity level. Our model outperforms all available Google-search–based real-time tracking models for influenza epidemics at the national level of the United States, including Google Flu Trends. Our model is flexible, self-correcting, robust, and scalable, making it a potentially powerful tool that can be used for estimation and prediction at multiple temporal and spatial resolutions for other social events.

Abstract

Accurate real-time tracking of influenza outbreaks helps public health officials make timely and meaningful decisions that could save lives. We propose an influenza tracking model, ARGO (AutoRegression with GOogle search data), that uses publicly available online search data. In addition to having a rigorous statistical foundation, ARGO outperforms all previously available Google-search–based tracking models, including the latest version of Google Flu Trends, even though it uses only low-quality search data as input from publicly available Google Trends and Google Correlate websites. ARGO not only incorporates the seasonality in influenza epidemics but also captures changes in people’s online search behavior over time. ARGO is also flexible, self-correcting, robust, and scalable, making it a potentially powerful tool that can be used for real-time tracking of other social events at multiple temporal and spatial resolutions.

Big data sets are constantly generated nowadays as the activities of millions of users are collected from Internet-based services. Numerous studies have suggested great potential of these big data sets to detect/manage epidemic outbreaks [influenza (1–6), Ebola (7), dengue (8)], predict changes in stock prices (9, 10) and housing prices (11), etc. In 2009, Google Flu Trends (GFT), a digital disease detection system that uses the volume of selected Google search terms to estimate current influenza-like illnesses (ILI) activity, was identified by many as a good example of how big data would transform traditional statistical predictive analysis (12). However, significant discrepancies between GFT’s flu estimates and those measured by the Centers for Disease Control (CDC) in subsequent years led to considerable doubt about the value of digital disease detection systems (13). Although multiple articles have identified methodological flaws in GFT’s original algorithm (14–16) and have led to incremental improvements (14, 16) (see also googleresearch.blogspot.com/2014/10/google-flu-trends-gets-brand-new-engine.html), a statistical framework that is theoretically sound and capable of accurate estimation is still lacking. Here we present such a framework that culminates in a method that outperforms all existing methodologies for tracking influenza activity using internet search data.

Influenza outbreaks cause up to 500,000 deaths a year worldwide, and an estimated 3,000–50,000 deaths a year in the United States (17). Our ability to effectively prepare for and respond to these outbreaks heavily relies on the availability of accurate real-time estimates of their activity. Existing methods to predict the timing, duration, and magnitude of flu outbreaks remain limited (18). Well-established clinical methods to track flu activity, such as the CDC’s ILINet, report the percentage of patients seeking medical attention with ILI symptoms (www.cdc.gov/flu/). Although CDC’s %ILI is only a proxy of the flu activity in the population, it can help officials allocate resources in preparation for potential surges of patient visits to hospital facilities. See refs. 19–21 for further discussion.

CDC’s ILI reports have a delay of 1–3wk due to the time for processing and aggregating clinical information. This time lag is far from optimal for decision-making purposes. To alleviate this information gap, multiple methods combining climate, demographic, and epidemiological data with mathematical models have been proposed for real-time estimation of flu activity (18, 21–25). In recent years, methods that harness Internet-based information have also been proposed, such as Google (1), Yahoo (2), and Baidu (3) Internet searches, Twitter posts (4), Wikipedia article views (5), clinicians’ queries (6), and crowdsourced self-reporting mobile apps such as Influenzanet (Europe) (26), Flutracking (Australia) (27), and Flu Near You (United States) (28). Among them, GFT has received the most attention and has inspired subsequent digital disease detection systems (3, 8, 29–32). Interestingly, Google has never made their raw data public, thus making it impossible to reproduce the exact results of GFT.

We highlight three limitations of the original GFT algorithm, previously identified in refs. 15 and 16. First, it was shown that a static approach, which does not take advantage of newly available CDC’s ILI activity reports as the flu season evolves, produced model drift, leading to inaccurate estimates. Second, the idea of aggregating the multiple query terms (the independent variables in the GFT model) into a single variable did not allow for changes in people’s Internet search behavior over time (and thus changes in query terms’ abilities to track flu) to be appropriately captured. Third, GFT ignored the intrinsic time series properties, such as seasonality of the historical ILI activity, thus overlooking potentially crucial information that could help produce accurate real-time ILI activity estimates.

Our Contribution

The methodology presented here produces robust and highly accurate ILI activity level estimates by addressing the three aforementioned shortcomings of the multiple GFT engines. In addition, we provide a theoretical framework that, for the first time to our knowledge, justifies the prevailing use of linear models in the digital disease detection literature by incorporating causality arguments through a hidden Markov model. This theoretical framework contains, as a special case, the model developed in ref. 16. Our model not only achieves the goal of (i) dynamically incorporating new information from CDC reports as it becomes available and (ii) automatically selecting the most useful Google search queries for estimation as in ref. 16, but also largely improves estimation by (iii) including the long-term cyclic information (seasonality) from past flu seasons on record as input variables and (iv) using a 2-y moving window (which immediately precedes the desired date of estimation) for the training period to capture the most recent changes in people’s search patterns and time series behavior (33). Our methodology efficiently builds a prediction model from individual search frequency as well as the past records of ILI activity. It uses both sources of information more efficiently than simply combining GFT with autoregressive terms as suggested in ref. 15, because GFT is not optimally aggregated to provide additional information on top of time series information. Furthermore, we provide a quantitative efficiency metric that measures the statistical significance of the improvement of our methodology over other alternatives. For example, our method is twice as accurate as the method that combines GFT with autoregressive terms. Finally, even though we use as input only the publicly available, low-quality data from the Google Correlate and Google Trends websites, our method has significant improvement over the latest version of GFT.

We name our model ARGO, which stands for AutoRegression with GOogle search data. Statistically speaking, ARGO is an autoregressive model with Google search queries as exogenous variables; ARGO also employs $L_1$ (and potentially $L_2$) regularization to achieve automatic selection of the most relevant information.

Results

Retrospective estimates of influenza activity (ILI activity level, as reported by the CDC) were produced using our model, ARGO, for the time period of March 29, 2009 through July 11, 2015, assuming we had access only to the historical CDC’s ILI reports up to the previous week of estimation. We compared ARGO’s estimates with the ground truth: the CDC-reported weighted ILI activity level, published typically with 1- or 2-wk delay, by calculating a collection of accuracy metrics described in Materials and Methods. These metrics include the root-mean-squared error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), correlation with estimation target, and correlation of increment with estimation target. For comparison, we calculated these accuracy metrics for (i) GFT estimates (accessed on July 11, 2015), (ii) estimates produced using the method of Santillana et al. (6, 16), (iii) estimates produced by combining GFT with a lag-3 autoregressive model, AR(3), as suggested in ref. 15, (iv) estimates produced with an AR(3) autoregressive model (4, 15), and (v) a naive method that simply uses the value of the prior week’s CDC ILI activity level as the estimate for the current one. For fair comparison, all benchmark models (ii–iv) are dynamically trained with a 2-y moving window.

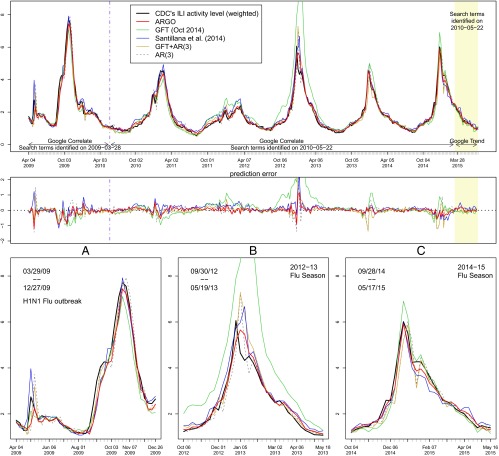
Table 1 summarizes these accuracy metrics for all estimation methods for multiple time periods. The “Whole period” column shows that ARGO’s estimates outperform all other alternatives, in every accuracy metric for the whole time period. The other columns of Table 1 show the performance of all of the methods for the 2009 off-season H1N1 flu outbreak, and each regular flu season since 2010. Fig. 1 displays the estimates against the observed CDC-reported ILI activity level.

Table 1.

Comparison of different models for the estimation of influenza epidemics

	Whole period (Mar 29, 2009 to Jul 11, 2015)	Off-season flu H1N1	Regular flu seasons (week 40 to week 20 next year)
			2010–2011	2011–2012	2012–2013	2013–2014	2014–15
RMSE
ARGO	0.608	0.640	0.596	0.807	0.687	0.306	0.438
GFT (Oct 2014)	2.216	0.773	1.110	3.023	4.451	0.986	0.700
Ref. 16	0.915	0.833	0.881	2.027	1.090	0.446	0.663
GFT+AR(3)	0.912	0.580	0.602	1.382	1.279	0.993	0.906
AR(3)	0.957	0.813	0.794	1.051	1.191	0.969	0.928
Naive	1 (0.348)	1 (0.600)	1 (0.339)	1 (0.163)	1 (0.499)	1 (0.350)	1 (0.465)
MAE
ARGO	0.649	0.584	0.574	0.748	0.650	0.391	0.530
GFT (Oct 2014)	1.834	0.777	1.260	3.277	5.028	0.891	0.770
Ref. 16	1.052	0.719	1.010	2.211	1.029	0.610	0.820
GFT+AR(3)	0.888	0.570	0.613	1.308	1.016	1.034	0.839
AR(3)	0.925	0.777	0.787	0.951	0.988	0.917	0.934
Naive	1 (0.201)	1 (0.425)	1 (0.259)	1 (0.135)	1 (0.325)	1 (0.212)	1 (0.295)
MAPE
ARGO	0.787	0.620	0.663	0.770	0.719	0.453	0.620
GFT (Oct 2014)	1.937	0.721	1.394	3.442	5.419	0.892	0.895
Ref. 16	1.381	0.765	1.380	2.306	1.251	0.754	0.958
GFT+AR(3)	1.037	0.683	0.698	1.407	0.986	1.062	0.828
AR(3)	1.003	0.894	0.814	0.947	0.939	0.891	0.916
Naive	1 (0.090)	1 (0.139)	1 (0.105)	1 (0.081)	1 (0.110)	1 (0.084)	1 (0.097)
Correlation
ARGO	0.986	0.985	0.989	0.928	0.968	0.993	0.993
GFT (Oct 2014)	0.875	0.989	0.968	0.833	0.926	0.969	0.986
Ref. 16	0.971	0.967	0.983	0.927	0.956	0.985	0.984
GFT+AR(3)	0.967	0.986	0.985	0.879	0.929	0.945	0.957
AR(3)	0.964	0.968	0.971	0.877	0.903	0.927	0.945
Naive	0.961	0.951	0.954	0.887	0.924	0.923	0.937
Correlation of increment
ARGO	0.758	0.806	0.810	0.286	0.527	0.938	0.912
GFT (Oct 2014)	0.706	0.863	0.702	0.484	0.502	0.847	0.918
Ref. 16	0.690	0.776	0.693	0.510	0.367	0.915	0.889
GFT+AR(3)	0.512	0.708	0.708	0.165	0.141	0.534	0.587
AR(3)	0.385	0.585	0.569	0.077	0.011	0.404	0.493
Naive	0.436	0.602	0.570	0.095	0.134	0.406	0.514

GFT+AR(3) stands for the model $p_t=\mu +{\alpha }_1{p}_{t-1}+{\alpha }_2{p}_{t-2}+{\alpha }_3{p}_{t-3}+\beta \text{GFT}\left(t\right)$, where the GFT estimate is treated as an exogenous variable. Boldface highlights the best performance for each metric in each study period. RMSE, MAE, and MAPE are relative to the error of naive method; that is, the number reported is the ratio of error of a given method to that of the naive method. The absolute error of the naive method is reported in parentheses. All comparisons are based on the original scale of ILI activity level.

Fig. 1.

Estimation results. (Top) The estimated ILI activity level from ARGO (thick red), contrasting with the true CDC’s ILI activity level (thick black) as well as the estimates from GFT (green), method of ref. 16 (blue), GFT plus AR(3) model (dark yellow), and AR(3) model (dashed gray). The two background shades, white and yellow, reflect two data sources, Google Correlate and Google Trends, respectively. The dash-dotted purple vertical line separates Google Correlate data with search terms identified on March 28, 2009 and May 22,2010. (Middle) The estimation error, defined as estimated value minus the CDC’s ILI activity level. (Bottom) Zoomed-in plots for estimation results in different study periods. (A) The H1N1 flu outbreak period. (B) The 2012–2013 regular flu season. (C) The 2014–2015 regular flu season. A regular flu season is defined as week 40 of one year to week 20 of the following year.

Close inspection shows that, in the post-2009 regular flu seasons, ARGO uniformly outperformed all other alternative estimation methods in terms of RMSE, MAE, MAPE, and correlation. ARGO avoids the notorious overshooting problem of GFT, as seen in Fig. 1. During the 2009 off-season H1N1 flu outbreak, ARGO had the smallest MAPE. In terms of RMSE and MAE, ARGO (relative RMSE = 0.640, relative MAE = 0.584) had the second best performance, underperforming slightly only the GFT+AR(3) model (relative RMSE = 0.580, relative MAE = 0.570). In terms of correlation, ARGO (r = 98.5%) had similar performance to the (potentially in-sample data of) GFT (r = 98.9%) (14) and GFT+AR(3) models (r = 98.6%) and outperformed all of the other alternatives.

To assess the statistical significance of the improved prediction power of ARGO, we constructed a 95% confidence interval for the relative efficiency of ARGO compared with other benchmark methods. The relative efficiency of method 1 to method 2 is the ratio of the true mean-squared error of method 2 to that of method 1 (34), which can be estimated by its observed value (see Eq. 4); its confidence interval can be constructed by stationary bootstrap of the error residual time series (35). Table 2 shows that ARGO is estimated to be at least twice as efficient as any other alternative, and the improvement in accuracy is highly statistically significant.

Table 2.

Estimate of relative efficiency of ARGO compared with other models with 95% confidence interval (CI)

	Point estimate	95% CI
GFT (Oct 2014)	12.85	[5.18, 91.82]
Ref. 16	2.02	[1.36, 2.83]
GFT+AR(3)	2.17	[1.23, 4.53]
AR(3)	2.40	[1.56, 3.69]

Relative efficiency being larger than 1 suggests increased predictive power of ARGO compared with the alternative method. The estimates and the bootstrap confidence intervals are constructed based on data from March 29, 2009 to May 17, 2015.

It is well known that CDC reports undergo revisions, weeks after their initial publication, that respond to internal consistency checks and lead to more accurate estimates of patients with ILI symptoms seeking medical attention. Thus, the available historical CDC information, in a given week, is not necessarily as accurate as it will be. We tested the effect of using (potentially inaccurate) unrevised information by obtaining the historical unrevised and revised reports, and the dates when the reports were revised, from the CDC website for the time period of our study. We used only the information that would have been available to us, at the time of estimation, and produced a time series of estimates for the whole time period described before. We compared our estimates to all other methods and found that ARGO still outperformed them all. Moreover, the values of all five accuracy metrics for ARGO essentially did not change, suggesting a desirable robustness to revisions in CDC’s ILI activity reports. The results are shown in Table S1.

Table S1.

Comparison of different models for the estimation of influenza epidemics, with weekly CDC’s ILI activity level that excludes forward-looking information from ILI activity report revision

		Off-season flu	Regular flu seasons (week 40 to week 20 next year)
	Whole period:	H1N1:	2010–2011:	2011–2012:	2012–2013:	2013–2014:	2014–2015:
	Mar 29, 2009 to Jul 11, 2015	Mar 29, 2009 to Dec 27, 2009	Oct 3, 2010 to May 22, 2011	Oct 2, 2011 to May 20, 2012	Sep 30, 2012 to May 19, 2013	Sep 29, 2013 to May 18, 2014	Sep 28, 2014 to May 17, 2015
RMSE
ARGO	0.565	0.630	0.509	0.608	0.622	0.298	0.434
GFT (Oct 2014)	2.003	0.702	0.971	1.878	4.387	0.885	0.714
Ref. 16	0.897	0.858	0.760	1.179	1.248	0.373	0.691
GFT+AR(3)	0.825	0.530	0.616	0.680	1.168	0.981	0.898
AR(3)	0.963	0.805	0.986	1.136	1.087	0.946	0.931
Naive	1.000 (0.385)	1.000 (0.661)	1.000 (0.388)	1.000 (0.263)	1.000 (0.506)	1.000 (0.391)	1.000 (0.456)
MAE
ARGO	0.557	0.595	0.483	0.555	0.627	0.339	0.501
GFT (Oct 2014)	1.465	0.670	1.093	2.026	5.082	0.747	0.787
Ref. 16	0.865	0.723	0.875	1.283	1.087	0.472	0.847
GFT+AR(3)	0.790	0.485	0.672	0.643	1.000	1.036	0.890
AR(3)	0.999	0.808	0.982	1.158	1.094	0.943	0.920
Naive	1.000 (0.252)	1.000 (0.494)	1.000 (0.299)	1.000 (0.218)	1.000 (0.322)	1.000 (0.253)	1.000 (0.289)
MAPE
ARGO	0.587	0.587	0.511	0.560	0.588	0.350	0.582
GFT (Oct 2014)	1.350	0.603	1.163	2.163	4.827	0.688	0.906
Ref. 16	0.970	0.709	1.141	1.363	1.143	0.545	0.937
GFT+AR(3)	0.848	0.599	0.749	0.669	0.819	1.068	0.964
AR(3)	1.067	0.915	1.051	1.169	1.050	0.945	0.935
Naive	1.000 (0.129)	1.000 (0.166)	1.000 (0.126)	1.000 (0.129)	1.000 (0.123)	1.000 (0.108)	1.000 (0.095)
Correlation
ARGO	0.985	0.979	0.988	0.911	0.971	0.992	0.992
GFT (Oct 2014)	0.875	0.989	0.968	0.833	0.926	0.969	0.986
Ref. 16	0.965	0.956	0.985	0.937	0.938	0.987	0.973
GFT+AR(3)	0.971	0.984	0.983	0.853	0.931	0.943	0.960
AR(3)	0.961	0.965	0.955	0.815	0.921	0.920	0.953
Naive	0.956	0.943	0.946	0.828	0.928	0.910	0.945
Correlation of increment
ARGO	0.742	0.751	0.772	0.262	0.633	0.898	0.892
GFT (Oct 2014)	0.706	0.863	0.702	0.484	0.502	0.847	0.918
Ref. 16	0.625	0.680	0.719	0.619	0.293	0.917	0.837
GFT+AR(3)	0.536	0.703	0.703	0.155	0.220	0.514	0.621
AR(3)	0.420	0.562	0.554	0.067	0.106	0.360	0.549
Naive	0.455	0.552	0.556	0.162	0.247	0.345	0.586

The estimation target is the finalized CDC’s ILI activity level. RMSE, MAE, and MAPE are relative to the error of the naive method. The absolute error of the naive method is reported in parentheses. Boldface highlights the best performance for each metric in each study period.

We faced an additional challenge in producing real-time estimates for the latest portion of the 2014–2015 flu season. At the time of writing this article, the only data available to us for the week of March 28, 2015 and later came from the Google Trends website. The information from Google Trends has even lower quality than from Google Correlate and changes every week. These undesired changes affected the quality of our estimates. To assess the stability of ARGO in the presence of these variations in the data, we obtained the search frequencies of the same query terms from Google Trends website on 25 different days during the month of April 2015 and produced a set of 25 historical estimates using ARGO. The results of the accuracy metrics associated to these estimates are shown in Table S2. This table shows that, despite the observed variation in the Google Trends data, ARGO is threefold more stable than the method of ref. 16, and still outperforms on average any other method.

Table S2.

Mean and SD of accuracy metrics when using Google Trends data accessed at different dates

	RMSE	MAE	MAPE	Correlation	Correlation of increment
Mean
ARGO	0.226	0.304	0.079	0.981	0.831
GFT (Oct 2014)	0.262	0.366	0.089	0.985	0.920
Ref. 16	0.306	0.398	0.116	0.973	0.803
GFT+AR(3)	0.303	0.482	0.090	0.948	0.581
AR(3)	0.332	0.492	0.096	0.936	0.492
SD
ARGO	0.013	0.017	0.005	0.002	0.016
GFT (Oct 2014)	0.000	0.000	0.000	0.000	0.000
Ref. 16	0.029	0.049	0.013	0.005	0.050
GFT+AR(3)	0.000	0.000	0.000	0.000	0.000
AR(3)	0.000	0.000	0.000	0.000	0.000

The common study period is 2014–2015 partial season (September 28, 2014 to March 29, 2015). At the time of first submitting this article, Google Correlate data covered only up to February 2014, which inspired us to study the robustness of ARGO with respect to Google Trends data variability on the 2014–2015 season.

Discussion

Strength of ARGO.

The results presented here demonstrate the superiority of our approach in terms of both accuracy and robustness, compared with all existing flu tracking models based on Google searches. The value of these results is even higher given the fact that they were produced with low-quality input variables. It is highly likely that our methodology would lead to even more accurate results if we were given access to the input variables that Google uses to calculate their estimates.

The combination of seasonal flu information with dynamic reweighting of search information appears to be a key factor in the enhanced accuracy of ARGO. The level of ILI activity last week typically has a significant effect on the current level of ILI activity, and ILI activity half a year ago and/or 1 y ago could provide further information, as shown in Fig. S1, which reflects a strong temporal autocorrelation. The integration of time series information leads to a smooth and continuous estimation curve and prevents undesired spikes. However, simply adding GFT to an autoregressive model is suboptimal compared with ARGO, because simply treating GFT as an individual variable does not allow adjustment for time series information at the resolution of individual query terms, and many terms included in GFT may no longer provide extra information once time series information is incorporated. In fact, once the time series information is included, fewer Google search query terms remain significant. For example, among 100 Google Correlate query terms, ARGO selected 14 terms, on average, each week, whereas the method of ref. 16 and GFT (1) selected 38 and 45 terms, respectively, each week on average. The combination of ARGO’s smoothness and sparsity lead to a substantial reduction on the estimation error, as observed in Tables 1 and 2, where ARGO shows improved performance in all evaluation metrics over the whole time period and is twice as efficient as GFT+AR(3).

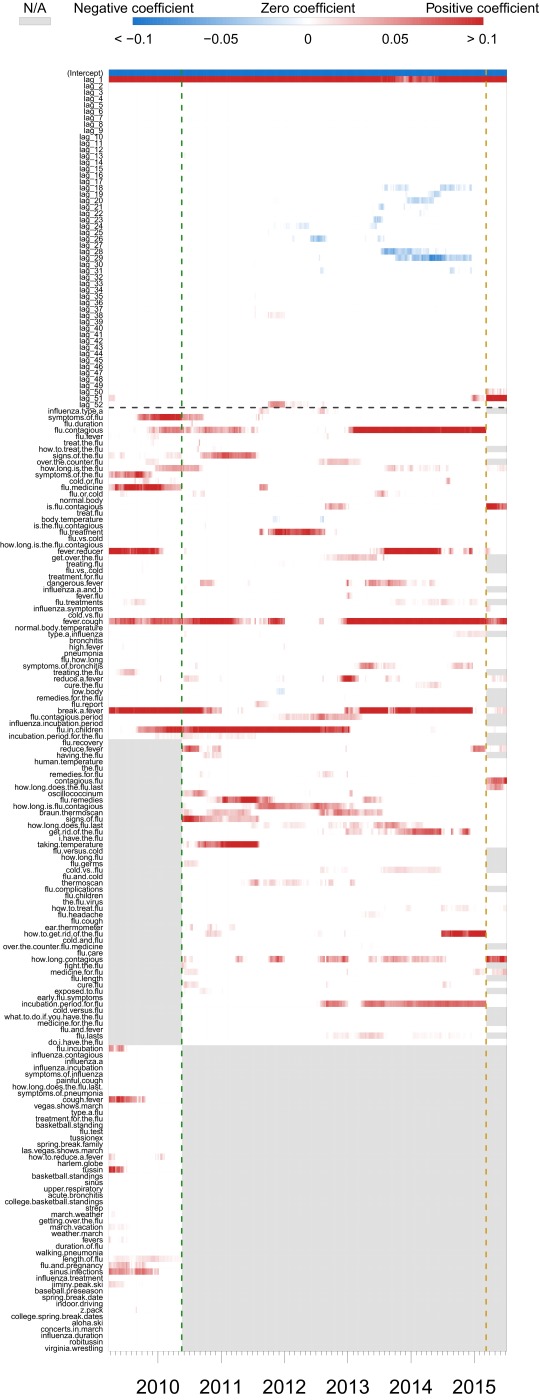
Fig. S1.

Dynamic coefficients for ARGO. Red color represents positive coefficients, blue color represents negative coefficients, white color represents zero, and gray color represents missing values. Missing values can be the result of (i) query terms not identified by Google Correlate and (ii) Google Trends data not available for particular query terms. Black horizontal dashed line separates Google query queries from autoregressive lags. Yellow vertical dashed line separates coefficients trained on Google Correlate data from those trained on Google Trends data, and green vertical dashed line separates query terms identified on March 28, 2009 from those identified on May 22, 2010.

Our methodology allows us to transparently understand how Google search information and historical flu information complement one another. Time series models tend to be slow in response to sudden observed changes in CDC’s ILI activity level. The AR(3) model shows this “delaying” effect, despite its seemingly good correlation. Google searches, on the other hand, are better at detecting sudden ILI activity changes, but are also very sensitive to public’s overreaction.

To investigate further the responsiveness (comovement) of ARGO toward the change in ILI activity, we calculated the correlation of increment between each estimation model and CDC’s ILI activity level. The correlation of increment between two time series $a_t$ and $b_t$ is defined as $\mathrm{Corr}\left(a_t-a_{t-1},b_t-b_{t-1}\right)$, which measures how well $a_t$ captures the changes in $b_t$. Table 1 shows that ARGO has similar capability to that of GFT and the method of ref. 16 in capturing the changes in ILI level, and outperforms the time series model AR(3) uniformly.

Time series information (seasonality) tends to pull ARGO’s estimate toward the historical level. This was evident at the onset of the off-season H1N1 flu outbreak (week ending at May 2, 2009), which resulted in ARGO’s underestimation. ARGO self-corrected its performance the following week by shifting a portion of model weights from the time series domain to the Google searches domain. Inversely, at the height of 2012–2013 season, ARGO, GFT, and the method of ref. 16 all missed the peak due to an unprecedented surge of search activity. ARGO achieved the fastest self-correction by redistributing the weights not only across Google terms but also across time series terms, missing the peak by only 1 wk, as opposed to 2 wk for ref. 16 and about 4 wk for GFT. It is important to note that although we have used CDC’s ILI as our gold standard for influenza activity in the US population, and data from Google Correlate/Trends as our independent variables, our methodology can be immediately adapted to any other suitable ILI gold standard and/or set of independent variables.

Limitations and Next Steps.

Although ARGO displays a clear superiority over previous methods, it is not fail-proof. Because it relies on the public’s search behavior, any abrupt changes to the inner works of the search engine or any changes in the way health-related search information is displayed to users will affect the accuracy of our methodology (36, 37). We expect that ARGO will be fast at correcting itself if any such change takes place in the future. As in any predictive method, the quality of past performance does not guarantee the quality of future performance. In this article, we fixed the search query terms after 2010 so as to directly compare our results with GFT, which has kept the same query terms since 2010; future application of ARGO may update search terms more frequently. ARGO can be easily generalized to any temporal and spatial scales for a variety of diseases or social events amenable to be tracked by Internet searches or services (3, 4, 8, 9, 29, 30, 38, 39). Further improvements in influenza prediction may come from combining multiple predictors constructed from disparate data sources (40). After the initial submission of this article in May 2015, Google announced that GFT would be discontinued and that their raw data would be made accessible to selected scientific teams. This announcement happened soon after the GFT team published a manuscript that proposed a new time series-based method for the (now discontinued) GFT engine (41). This new development makes our contribution timely and useful in providing a transparent method for disease tracking in the future.

Materials and Methods

All data used in this article are publicly available. Therefore, IRB approval is not needed.

Google Data.

To avoid forward-looking information in our out-of-sample predictions, and to make the search term selection in our approach consistent with the main revision to GFT (14) immediately after the H1N1 pandemic, we obtained the highest-correlated terms to the CDC’s ILI using Google Correlate (www.google.com/trends/correlate) for two different time periods. For the first time period (pre-H1N1 period), we inserted only CDC’s ILI data from January 2004 to March 28, 2009 into Google Correlate, and used the resulting most highly correlated search terms as independent variables for our out-of-sample predictions for the time period April 4, 2009 through May 22, 2010. For the second time period (post-H1N1), we inserted only CDC’s ILI data from January 2004 to May 22, 2010 into Google Correlate to select new search terms, as done in ref. 14. These last search terms were used as independent variables for all subsequent predictions presented in this work. Tables S3 and S4 show all query terms identified. For the pre-H1N1 period (the first time period), the terms from Google Correlate include spurious (or overfitted) terms like “march vacation” or “basketball standings,” as discussed in ref. 15. However, Fig. S1 shows that these spurious terms were often not selected by ARGO, i.e., ARGO would give them zero weights, demonstrating its robustness. For the post-H1N1 time period, the updated query terms from Google Correlate include mostly flu-related terms (see Table S4). This suggests that spurious terms were “filtered out” by including off-season flu data. For the time period of March 28, 2015 up to the date of submission of this article, we acquired search frequencies for this set of query terms from Google Trends (www.google.com/trends; date of access: July 11, 2015) as Google Correlate only provides data up to March 28, 2015 at the time of writing this article.

Table S3.

All search phrases identified by Google Correlate using data as of March 28, 2009

influenza.type.a	painful.cough	treatment.for.the.flu	weather.march
flu.incubation	fever.flu	basketball.standing	fevers
bronchitis	over.the.counter.flu	flu.test	duration.of.flu
influenza.contagious	pneumonia	tussionex	flu.contagious.period
flu.fever	how.long.is.the.flu	reduce.a.fever	cold.vs.flu
influenza.a	flu.how.long	how.long.is.the.flu.contagious	cure.the.flu
influenza.incubation	treatment.for.flu	treat.flu	walking.pneumonia
flu.contagious	fever.cough	spring.break.family	flu.vs..cold
treating.the.flu	flu.medicine	las.vegas.shows.march	length.of.flu
type.a.influenza	dangerous.fever	how.to.reduce.a.fever	influenza.a.and.b
symptoms.of.the.flu	high.fever	flu.or.cold	flu.and.pregnancy
influenza.symptoms	is.flu.contagious	incubation.period.for.the.flu	sinus.infections
flu.duration	normal.body	harlem.globe	influenza.treatment
flu.report	normal.body.temperature	tussin	jiminy.peak.ski
symptoms.of.flu	how.long.does.the.flu.last.	basketball.standings	baseball.preseason
influenza.incubation.period	symptoms.of.pneumonia	sinus	spring.break.date
how.to.treat.the.flu	signs.of.the.flu	upper.respiratory	indoor.driving
treat.the.flu	flu.vs.cold	get.over.the.flu	z.pack
symptoms.of.bronchitis	low.body	acute.bronchitis	college.spring.break.dates
flu.treatment	cough.fever	body.temperature	aloha.ski
symptoms.of.influenza	vegas.shows.march	college.basketball.standings	concerts.in.march
treating.flu	is.the.flu.contagious	strep	break.a.fever
flu.in.children	type.a.flu	march.weather	influenza.duration
fever.reducer	flu.treatments	getting.over.the.flu	robitussin
cold.or.flu	remedies.for.the.flu	march.vacation	virginia.wrestling

Table S4.

All search phrases identified by Google Correlate using data as of May 22, 2010

influenza.type.a	get.over.the.flu	type.a.influenza	flu.care
symptoms.of.flu	treating.flu	i.have.the.flu	how.long.contagious
flu.duration	flu.vs..cold	taking.temperature	fight.the.flu
flu.contagious	having.the.flu	flu.versus.cold	reduce.a.fever
flu.fever	treatment.for.flu	bronchitis	cure.the.flu
treat.the.flu	human.temperature	how.long.flu	medicine.for.flu
how.to.treat.the.flu	dangerous.fever	flu.germs	flu.length
signs.of.the.flu	the.flu	cold.vs..flu	cure.flu
over.the.counter.flu	remedies.for.flu	flu.and.cold	exposed.to.flu
how.long.is.the.flu	influenza.a.and.b	thermoscan	low.body
symptoms.of.the.flu	contagious.flu	flu.complications	early.flu.symptoms
flu.recovery	how.long.does.the.flu.last	high.fever	remedies.for.the.flu
cold.or.flu	fever.flu	flu.children	flu.report
flu.medicine	oscillococcinum	the.flu.virus	incubation.period.for.flu
flu.or.cold	flu.remedies	how.to.treat.flu	break.a.fever
normal.body	how.long.is.flu.contagious	pneumonia	flu.contagious.period
is.flu.contagious	flu.treatments	flu.headache	influenza.incubation.period
treat.flu	influenza.symptoms	flu.cough	cold.versus.flu
body.temperature	cold.vs.flu	ear.thermometer	flu.in.children
is.the.flu.contagious	braun.thermoscan	how.to.get.rid.of.the.flu	what.to.do.if.you.have.the.flu
reduce.fever	fever.cough	flu.how.long	medicine.for.the.flu
flu.treatment	signs.of.flu	symptoms.of.bronchitis	flu.and.fever
flu.vs.cold	how.long.does.flu.last	cold.and.flu	flu.lasts
how.long.is.the.flu.contagious	normal.body.temperature	over.the.counter.flu.medicine	incubation.period.for.the.flu
fever.reducer	get.rid.of.the.flu	treating.the.flu	do.i.have.the.flu

Google Correlate standardizes the search volume of each query to have mean zero and SD 1 across time and contains data only from 2004 to March 2015. To make Google Correlate data compatible with Google Trends data, we linearly transformed the Google Correlate data to the same scale of 0–100 in our analysis. We used Google Correlate data up to its last available date, and then switched to Google Trends data afterward. This is indicated in Fig. 1 by different shades of the background. We used the latest version of GFT (fourth version, revised in October 2014) weekly estimates of ILI activity level as one of our comparison methods. GFT is available at www.google.org/flutrends/about (date of access: July 11, 2015).

CDC’s Data.

We use the weighted version of CDC’s ILI activity level as the estimation target (available at gis.cdc.gov/grasp/fluview/fluportaldashboard.html; date of access: July 11, 2015). The weekly revisions of CDC’s ILI are available at the CDC website for all recorded seasons (from week 40 of a given year to week 20 of the subsequent year). For example, ILI report revision at week 50 of season 2012–2013 is available at www.cdc.gov/flu/weekly/weeklyarchives2012-2013/data/senAllregt50.htm; ILI report revision at week 9 of season 2014–2015 is available at www.cdc.gov/flu/weekly/weeklyarchives2014-2015/data/senAllregt09.html.

Formulation of Our Model.

Our model ARGO is motivated by a hidden Markov model. The logit-transformed CDC-reported ILI activity level $\left\{y_t\right\}$ is the intrinsic time series of interest. We impose an autoregressive model with lag N on it, which implies that the collection of vectors ${\left\{y_{\left(t-N+1\right):t}\right\}}_{t\ge N}$ is a Markov chain (this captures the clinical fact that flu lasts for a period, but not indefinitely). The vector of log-transformed normalized volume of Google search queries at time t, ${\mathit{X}}_t$, depends only on the ILI activity at the same time, $y_t$ (this follows the intuition that flu occurrence causes people to search flu-related information online). The Markovian property on block $y_{\left(t-N+1\right):t}$ leads to the (vector) hidden Markov model structure.

$$\begin{array}{ccccccc}{y}_{1:N}& \to & y_{2:\left(N+1\right)}& \to & \cdots & \to & y_{\left(T-N+1\right):T}\\ \downarrow & & \downarrow & & & & \downarrow \\ {\mathit{X}}_N& & {\mathit{X}}_{N+1}& & & & {\mathit{X}}_T\end{array}$$ [1]

Our formal mathematical assumptions are

• (assumption 1) $y_t={\mu }_y+{\displaystyle {\sum }_{j=1}^N{\alpha }_j{y}_{t-j}+{\mathit{ϵ}}_t},{\mathit{ϵ}}_t\stackrel{iid}{\sim }\mathcal{N}\left(0,{\sigma }^2\right)$

• (assumption 2) ${\mathit{X}}_t|y_t\sim {\mathcal{N}}_K\left({\mathit{\mu }}_x+y_t\mathit{\beta },\mathit{Q}\right)$

• (assumption 3) conditional on $y_t$, ${\mathit{X}}_t$ is independent of $\left\{y_l,{\mathit{X}}_l:l\ne t\right\}$

where $\mathit{\beta }={\left({\beta }_1,{\beta }_2,\dots ,{\beta }_K\right)}^{\mathrm{⊺}},{\mathit{\mu }}_x={\left({\mu }_{x_1},{\mu }_{x_2},\dots ,{\mu }_{x_K}\right)}^{\mathrm{⊺}}$, and $\mathit{Q}$ is the covariance matrix. To make the variables more normal, we transform the original ILI activity level $p_t$ from $\left[\mathrm{0,1}\right]$ to $\mathrm{ℝ}$ using the logit function, obtaining the $y_t$, and transform the Google search volumes from $\left[\mathrm{0,100}\right]$ to $\mathrm{ℝ}$ using the log function, obtaining ${\mathit{X}}_t$. The log function is appropriate because Google search frequencies usually have an exponential growth rate near peaks and are artificially scaled to $\left[\mathrm{0,100}\right]$ by dividing the running maximum. Because Google Trends is in integer scale from 0 to 100, we add a small number $\delta =0.5$ before the transformation to avoid taking the log of 0. The predictive distribution $f\left(y_t|y_{1:\left(t-1\right)},{\mathit{X}}_{1:t}\right)$ is normal with mean linear in $y_{\left(t-N\right):\left(t-1\right)}$ and ${\mathit{X}}_t$ and constant variance (see Supporting Information). This observation leads to Eq. 2, which defines the ARGO model.

The ARGO Model.

Let $y_t=\mathrm{logit}\left(p_t\right)$ be the logit-transformed CDC’s (weighted) ILI activity level $p_t$ at time t, and $X_{i,t}$ the log-transformed Google search frequency of term i at time t. Our ARGO model is given by

$$y_t={\mu }_y+{\displaystyle \sum _{j=1}^N{\alpha }_j{y}_{t-j}}+{\displaystyle \sum _{i=1}^K{\beta }_i{X}_{i,t}+{\mathit{ϵ}}_t},\hspace{1em}{\mathit{ϵ}}_t\stackrel{iid}{\sim }\mathcal{N}\left(0,{\sigma }^2\right),$$ [2]

where ${\mathit{X}}_t$ can be thought of as the exogenous variables to time series $\left\{y_t\right\}$.

Parameter Estimation of ARGO Model.

We chose $N=52$ (weeks) to capture the within-year seasonality in ILI activity, and $K=100$ (Google search terms) following the data availability from Google Correlate. Because we have more independent variables than the number of observations, the usual maximum likelihood estimate (ordinary least squares) method will fail. Therefore, we impose regularities for parameter estimation. In general we have three kinds of penalties, $L_1$ penalty (42), $L_2$ penalty (43), and a linear combination of $L_1$ and $L_2$ penalties (44). All parameters are dynamically trained every week with a 2-y (104-wk) rolling window.

In a given week, the goal is to find parameters ${\mu }_y$, $\mathit{\alpha }=\left({\alpha }_1,\dots ,{\alpha }_{52}\right)$, and $\mathit{\beta }=\left({\beta }_1,\dots ,{\beta }_{100}\right)$ that minimize

$$\begin{array}{r}{\displaystyle \sum }_t{(y_t-{\mu }_y-{\displaystyle \sum _{j=1}^{52}{\alpha }_j{y}_{t-j}}-{\displaystyle \sum _{i=1}^{100}{\beta }_i{X}_{i,t}})}^2\\ +{\lambda }_{\alpha }{\Vert \mathit{\alpha }\Vert }_1+{\eta }_{\alpha }{\Vert \mathit{\alpha }\Vert }_2^2+{\lambda }_{\beta }{\Vert \mathit{\beta }\Vert }_1+{\eta }_{\beta }{\Vert \mathit{\beta }\Vert }_2^2\end{array}$$ [3]

where ${\lambda }_{\alpha },{\lambda }_{\beta },{\eta }_{\alpha }$, and η_β are hyperparameters. Ideally, we would like to use cross-validation to select all four hyperparameters. However, because we have only 104 training data points at a given week due to the 2-y moving window, the cross-validation result is highly noisy. Thus, we need to prespecify some of the hyperparameters. For model simplicity and sparsity, combining with the evidence seen from cross-validation, we set ${\eta }_{\alpha }={\eta }_{\beta }=0$, leading to $L_1$ penalization on both autoregressive and Google search terms. With the remaining ${\lambda }_{\alpha }$ and ${\lambda }_{\beta }$, the cross-validation results still have considerable variance. By the same sparsity and simplicity consideration, we further constrained ${\lambda }_{\alpha }={\lambda }_{\beta }$. Therefore, the ARGO model we finally propose is Eq. 3 with constraint ${\eta }_{\alpha }={\eta }_{\beta }=0$ and ${\lambda }_{\alpha }={\lambda }_{\beta }$. A detailed discussion of our specification of the hyperparameters is provided in Supporting Information (see Table S5).

Table S5.

Comparison of different specifications of hyperparameters for in-sample study period

	Whole in-sample period: Jan 7, 2007 to Mar 29, 2009	2006–2007 partial season: Jan 7, 2007 to May 20, 2007	2007–2008 season: Sep 30, 2007 to May 18, 2008	2008–2009 partial season: Sep 28, 2008 to Mar 29, 2009
RMSE
ARGO w/ same $L_1$	0.644	0.697	0.602	0.653
ARGO w/ sep. $L_1$	0.658	0.672	0.637	0.629
ARGO w/ same $L_2$	1.165	0.817	1.175	1.243
ARGO w/ sep. $L_2$	1.010	0.740	0.946	1.173
ARGO w/ ElasticNet	0.669	0.757	0.585	0.766
Naive	1.000 (0.316)	1.000 (0.286)	1.000 (0.473)	1.000 (0.304)
MAE
ARGO w/ same $L_1$	0.678	0.651	0.584	0.634
ARGO w/ sep. $L_1$	0.691	0.671	0.621	0.593
ARGO w/ same $L_2$	1.223	0.836	1.094	1.469
ARGO w/ sep. $L_2$	1.149	0.753	0.943	1.401
ARGO w/ ElasticNet	0.738	0.718	0.613	0.780
Naive	1.000 (0.206)	1.000 (0.245)	1.000 (0.335)	1.000 (0.226)
Correlation
ARGO w/ same $L_1$	0.987	0.977	0.983	0.977
ARGO w/ sep. $L_1$	0.986	0.980	0.980	0.976
ARGO w/ same $L_2$	0.969	0.984	0.976	0.955
ARGO w/ sep. $L_2$	0.979	0.987	0.983	0.967
ARGO w/ ElasticNet	0.987	0.984	0.986	0.975
Naive	0.965	0.949	0.950	0.935
Correlation of increment
ARGO w/ same $L_1$	0.779	0.643	0.857	0.646
ARGO w/ sep. $L_1$	0.708	0.545	0.758	0.697
ARGO w/ same $L_2$	0.828	0.793	0.864	0.799
ARGO w/ sep. $L_2$	0.845	0.795	0.881	0.824
ARGO w/ ElasticNet	0.814	0.835	0.852	0.738
Naive	0.623	0.473	0.756	0.322

“ARGO w/ same $L_1$” is ARGO with the same $L_1$ penalty for Google search terms and autoregressive lags (specification 1). “ARGO w/ sep. $L_1$” is ARGO with separate $L_1$ penalties for Google search terms and autoregressive lags (specification 2). “ARGO w/ same $L_2$” is ARGO with the same $L_2$ penalty for Google search terms and autoregressive lags (specification 3). “ARGO w/ sep. $L_2$” is ARGO with separate $L_2$ penalties for Google search terms and autoregressive lags (specification 4). “ARGO w/ ElasticNet” is ARGO with the same elastic net penalty for Google search terms and autoregressive lags (specification 5). The first column is for the entire in-sample study period. The second column is for 2006–2007 partial season; 2006–2007 full season is not available because data before January 2007 are used for training. The third column is for 2007–2008 full season. The fourth column is for 2008–2009 partial season; 2008–2009 full season is not available because our out-of-sample study period starts in April 2009. RMSE and MAE are relative to the error of the naive method. The absolute error of the naive method is reported in parentheses.

Accuracy Metrics.

The RMSE, MAE, and MAPE of estimator $\widehat{p}$ to the target ILI activity level p are defined, respectively, as $\text{RMSE}\left({\widehat{p}}_t,p_t\right)={\left[\left(1/n\right){\displaystyle {\sum }_{t=1}^n{\left({\widehat{p}}_t-p_t\right)}^2}\right]}^{1/2}$, $\text{MAE}\left({\widehat{p}}_t,p_t\right)=\left(1/n\right){\displaystyle {\sum }_{t=1}^n\left|{\widehat{p}}_t-p_t\right|}$, and $\text{MAPE}\left({\widehat{p}}_t,p_t\right)=\left(1/n\right){\displaystyle {\sum }_{t=1}^n\left|{\widehat{p}}_t-p_t\right|/p_t}$. The correlation of estimator $\widehat{p}$ to the target ILI activity level p is their sample correlation coefficient. The correlation of increment between ${\widehat{p}}_t$ and $p_t$ is defined as

$$\text{Corr}.\hspace{0.17em}\text{of}\hspace{0.17em}\text{increment}\left({\widehat{p}}_t,p_t\right)=\text{Corr}\left({\widehat{p}}_t-{\widehat{p}}_{t-1},p_t-p_{t-1}\right).$$

The relative efficiency of estimator ${\widehat{p}}^{\left(1\right)}$ to estimator ${\widehat{p}}^{\left(2\right)}$ is $e\left({\widehat{p}}^{\left(1\right)},{\widehat{p}}^{\left(2\right)}\right)={\text{MSE}}_{\text{true}}^{\left(2\right)}/{\text{MSE}}_{\text{true}}^{\left(1\right)}$, where ${\text{MSE}}_{\text{true}}^{\left(i\right)}=\mathbb{E}\left[{\left({\widehat{p}}^{\left(i\right)}-p\right)}^2\right]$, which can be estimated by

$$\widehat{e}\left({\widehat{p}}^{\left(1\right)},{\widehat{p}}^{\left(2\right)}\right)=\frac{{\text{MSE}}_{\text{obs}}^{\left(2\right)}}{{\text{MSE}}_{\text{obs}}^{\left(1\right)}}\hspace{1em}\text{where}\hspace{1em}{\text{MSE}}_{\text{obs}}^{\left(i\right)}=\frac{1}{n}{\displaystyle \sum _{t=1}^n{\left({\widehat{p}}_t^{\left(i\right)}-p_t\right)}^2}.$$ [4]

The 95% confidence interval can be constructed by the time series stationary bootstrap method (35), where the replicated time series of the error residual is generated using geometrically distributed random blocks with mean length 52 (which corresponds to 1 y). We obtain the basic bootstrap confidence interval for $\log \left\{e\left({\widehat{p}}^{\left(1\right)},{\widehat{p}}^{\left(2\right)}\right)\right\}$ and then recover the original scale by exponentiation. The nonparametric bootstrap confidence interval takes the autocorrelation and cross-correlation of the errors into account, and is insensitive to the mean block length.

SI Materials and Methods

Details of our methodology are presented as follows. First, the predictive distribution in the formulation of the ARGO model and the corresponding assumptions are described; second, the statistical strategy to determine the hyperparameters of the ARGO model is explained; third, the results of two sensitivity analysis aimed at testing the robustness of the ARGO methodology—(i) with respect to subsequent revisions of CDC’s ILI activity reports and (ii) with respect to observed variation of the input variables coming from Google Trends data—are presented; fourth, the exact search query terms identified by Google Correlate with different data access dates are presented; and fifth, a heat map showing the coefficients for the time series and Google search terms dynamically trained by ARGO is included.

The R package that implements the ARGO method is available at the authors' websites (www.people.fas.harvard.edu/∼skou/publication.htm).

SI Predictive Distribution in the Formulation of ARGO Model

To improve normality for both the input variables and the dependent variables, the CDC-reported ILI activity level was logit-transformed, and the linearly normalized volume of Google search queries were log-transformed. To avoid taking the log of 0, we add a small number $\delta =0.5$ before the log transformation. These transformations led to two sets of variables, the intrinsic (influenza epidemics activity) time series of interest $\left\{y_t\right\}$ and the (Google search) variable vector ${\mathit{X}}_t$ at time t (that depends only on $y_t$). Our formal mathematical assumptions are

• (assumption 1) $y_t={\mu }_y+{\displaystyle {\sum }_{j=1}^N{\alpha }_j{y}_{t-j}+{\mathit{ϵ}}_t},{\mathit{ϵ}}_t\stackrel{iid}{\sim }\mathcal{N}\left(0,{\sigma }^2\right)$

• (assumption 2) ${\mathit{X}}_t|y_t\sim {\mathcal{N}}_K\left({\mathit{\mu }}_x+y_t\mathit{\beta },\mathit{Q}\right)$

• (assumption 3) conditional on $y_t$, ${\mathit{X}}_t$ is independent of $\left\{y_l,{\mathit{X}}_l:l\ne t\right\}$

where $\mathit{\beta }={\left({\beta }_1,{\beta }_2,\dots ,{\beta }_K\right)}^{\mathrm{⊺}},{\mathit{\mu }}_x={\left({\mu }_{x_1},{\mu }_{x_2},\dots ,{\mu }_{x_K}\right)}^{\mathrm{⊺}}$, and $\mathit{Q}$ is the covariance matrix. The predictive distribution $f\left(y_{t+1}|y_{1:t},{\mathit{X}}_{1:\left(t+1\right)}\right)$ is given by

$$\begin{array}{l}f\left(y_{t+1}|y_{1:t},{\mathit{X}}_{1:\left(t+1\right)}\right)\\ \sim \mathcal{N}\left({\left(\frac{1}{{\sigma }^2}+{\mathit{\beta }}^{\mathrm{⊺}}{\mathit{Q}}^{-1}\mathit{\beta }\right)}^{-1}\left(\frac{{\mu }_y+{\mathit{\alpha }}^{\mathrm{⊺}}{y}_{\left(t-N+1\right):t}}{{\sigma }^2}+{\mathit{\beta }}^{\mathrm{⊺}}{\mathit{Q}}^{-1}\left({\mathit{X}}_{t+1}-{\mathit{\mu }}_x\right)\right),{\left(\frac{1}{{\sigma }^2}+{\mathit{\beta }}^{\mathrm{⊺}}{\mathit{Q}}^{-1}\mathit{\beta }\right)}^{-1}\right),\end{array}$$ [S1]

which is a normal distribution, whose mean is a linear combination of $y_{\left(t-N\right):\left(t-1\right)}$ and ${\mathit{X}}_t$, and whose variance is a constant.

SI Determination of the Hyperparameters for ARGO

The optimized parameters of the ARGO model, ${\mu }_y$, $\mathit{\alpha }=\left({\alpha }_1,\dots ,{\alpha }_N\right)$, and $\mathit{\beta }=\left({\beta }_1,\dots ,{\beta }_K\right)$, are obtained by

$$\begin{array}{r}\underset{{\mu }_y,\mathit{\alpha },\mathit{\beta }}{\text{arg}\hspace{0.17em}\text{min}}{\displaystyle \sum _t{\left(y_t-{\mu }_y-{\displaystyle \sum _{j=1}^{52}{\alpha }_j{y}_{t-j}}-{\displaystyle \sum _{i=1}^{100}{\beta }_i{X}_{i,t}}\right)}^2}\\ +{\lambda }_{\alpha }{\Vert \mathit{\alpha }\Vert }_1+{\eta }_{\alpha }{\Vert \mathit{\alpha }\Vert }_2^2+{\lambda }_{\beta }{\Vert \mathit{\beta }\Vert }_1+{\eta }_{\beta }{\Vert \mathit{\beta }\Vert }_2^2.\end{array}$$ [S2]

The training period consists of a 2-y (104-wk) rolling window that immediately precedes the desired date of estimation. The hyperparameters are ${\lambda }_{\alpha },{\lambda }_{\beta },{\eta }_{\alpha }$, and η_β. We tested the performance of ARGO with the following specifications of hyperparameters: (specification 1) restrict ${\eta }_{\alpha }={\eta }_{\beta }=0$ and ${\lambda }_{\alpha }={\lambda }_{\beta }$, cross-validate on ${\lambda }_{\alpha }$. This is our proposed ARGO with the same $L_1$ penalty for Google search terms and autoregressive lags; (specification 2) restrict ${\eta }_{\alpha }={\eta }_{\beta }=0$, cross-validate on $\left({\lambda }_{\alpha },{\lambda }_{\beta }\right)$. This is ARGO with separate $L_1$ penalties for Google search terms and autoregressive lags; (specification 3) restrict ${\eta }_{\alpha }={\eta }_{\beta }$ and ${\lambda }_{\alpha }={\lambda }_{\beta }=0$, cross-validate on ${\eta }_{\alpha }$. This is ARGO with the same $L_2$ penalty for Google search terms and autoregressive lags; (specification 4) restrict ${\lambda }_{\alpha }={\lambda }_{\beta }=0$, cross-validate on $\left({\eta }_{\alpha },{\eta }_{\beta }\right)$—this is ARGO with separate $L_2$ penalties for Google search terms and autoregressive lags; and (specification 5) restrict ${\lambda }_{\alpha }={\lambda }_{\beta },{\eta }_{\alpha }={\eta }_{\beta }$, cross-validate on $\left({\lambda }_{\alpha },{\eta }_{\alpha }\right)$. This is ARGO with the same elastic net (both $L_1$ and $L_2$) penalty for Google search terms and autoregressive lags.

Table S5 summarizes the in-sample estimation performance for our proposed ARGO, together with the other specifications of hyperparameters. It is apparent from the table that the $L_1$ penalty generally outperforms the $L_2$ penalty. The $L_1$ penalty tends to shrink the coefficients of unnecessary independent variables to be exactly zero, and thus eliminates redundant information; on the other hand, the $L_2$ penalty can only shrink the coefficients to be close to zero. As a result, $L_2$ penalized coefficients are not as sparse as their $L_1$ counterparts. Furthermore, from Table S5, we see that ARGO with separate $L_1$ penalties (specification 2) outperforms ARGO with separate $L_2$ penalties (specification 4), in terms of both RMSE and MAE. Similarly, ARGO with the same $L_1$ penalty (specification 1) outperforms ARGO with the same $L_2$ penalty (specification 3), in terms of both RMSE and MAE.

The elastic net model, which combines $L_1$ penalty and $L_2$ penalty, does not provide any error reduction. In the cross-validation process of setting $\left({\lambda }_{\alpha },{\eta }_{\alpha }\right)$ for the elastic net model, 70 wk out of 116 in-sample weeks showed that the smallest cross-validation mean error when restricting ${\eta }_{\alpha }=0$ (i.e., zero $L_2$ penalty) is within 1 SE of the global smallest cross-validation mean error, suggesting that restricting $L_2$ penalty term to be zero (i.e., ${\eta }_{\alpha }=0$) will introduce little bias. Therefore, for the simplicity and sparsity of the model, we drop the $L_2$ penalty terms and use only the $L_1$ penalty.

Next, we want to decide between the remaining two specifications, ARGO with separate $L_1$ penalties (specification 2) and ARGO with the same $L_1$ penalty (specification 1). One might argue that Google search terms and autoregressive lags are different sources of information and thus should have different $L_1$ penalties. However, empirical evidence in Table S5 shows that, again, giving extra flexibility to $\left({\lambda }_{\alpha },{\lambda }_{\beta }\right)$ does not generate improvement compared with fixing ${\lambda }_{\alpha }={\lambda }_{\beta }$. In the cross-validation process of setting $\left({\lambda }_{\alpha },{\lambda }_{\beta }\right)$ for separate $L_1$ penalties, 99 wk out of 116 in-sample weeks showed that the smallest cross-validation mean error when restricting ${\lambda }_{\alpha }={\lambda }_{\beta }$ (i.e., same $L_1$ penalty) is within 1 SE of the global smallest cross-validation mean error. This may well be due to the gain from variance reduction when imposing the restriction ${\lambda }_{\alpha }={\lambda }_{\beta }$. Based on the same simplicity and sparsity consideration, we finally decided to restrict ${\eta }_{\alpha }={\eta }_{\beta }=0$ and ${\lambda }_{\alpha }={\lambda }_{\beta }$ in the setting of hyperparameters for ARGO.

SI Revision of CDC’s ILI Activity Reports

Within a flu season, CDC reports are constantly revised to improve their accuracy as new information is incorporated. Thus, CDC’s weighted ILI figures displayed in previously published reports may change in subsequent weeks. As a consequence, in a given week, the available CDC ILI information from the most recent weeks may be inaccurate. To test the robustness of ARGO in the presence of these revisions and mimic the real-time tracking in our retrospective predictions, we trained ARGO and all other alternative models based on the following schedule.

Suppose $z_{i,j}$ is the CDC-reported ILI activity level of week i accessed at week j. Since CDC’s ILI activity report is often delayed for 1 wk, on week j, the historical ILI activity-level data we have are $\left\{z_{i,j}:i\le j-1\right\}$. Due to revisions, ILI activity level of week i accessed at different weeks $z_{i,i+1},z_{i,i+2},\dots$ may be different but will converge to a finalized value $z_{i,\infty }$ eventually. Hence, to avoid using forward-looking information, in week j, we train all models with the ILI activity level accessed at that week, $\left\{z_{i,j}:i\le j-1\right\}$. In this sense, any future revision beyond week j will not be incorporated in the training at week j. However, for the accuracy metrics, the estimation target remains the finalized the ILI activity level ($z_{i,\infty },i=\mathrm{1,2},\dots$).

Table S1 shows the estimation results when using the aforementioned schedule. Note that ARGO still outperforms all other alternative models. Moreover, the absolute values of all four accuracy metrics for ARGO trained this way essentially do not change compared with ARGO trained with finalized ILI activity level as studied in Table 1 of the main text, indicating the robustness of ARGO.

The weekly revisions of CDC’s ILI activity reports are available at the CDC website from week 40 of the year to week 20 of the subsequent year for all seasons studied in this article. For example, ILI activity level revisions at week 50 of season 2012–2013 are available at www.cdc.gov/flu/weekly/weeklyarchives2012-2013/data/senAllregt50.htm; ILI activity report revision at week 9 of season 2014–2015 is available at www.cdc.gov/flu/weekly/weeklyarchives2014-2015/data/senAllregt09.html (the webpage has suffix “htm” for seasons before 2014–2015 and suffix “html” for 2014–2015 season). In this retrospective case study, when the revisions of ILI activity level were not available for a particular week during the off-season period, the finalized ILI activity level was used instead.

SI Variations of Google Trends Data

Google Trends historical data constantly change as a consequence of renormalizations and algorithm updates. To study the robustness of ARGO to Google Trends data revisions, we obtained the search frequencies of the search query terms identified by Google Correlate on May 22, 2010 (see Fig. S1 and Table S4) from the Google Trends website (www.google.com/trends) on 25 different days in April 2015. We studied the variability of ARGO’s performance when using these 25 different versions of Google Trends data as input variables for the common time period of September 28, 2014 to March 29, 2015. We studied the 2014–2015 flu season only partially (up to March 2015) because this is the longest study period covered by all of the obtained versions of Google Trends data, at the time (May 1, 2015) of the first submission of this article. We want to emphasize that Google Correlate data were only available up to February 2014 when accessed in April 2015.

Despite the inevitable variation to the revision of the low-quality data from Google Trends, ARGO still achieves considerable stability compared with the method of Santillana et al. (16) during this time period. Table S2 suggests that ARGO is threefold more robust than the method of ref. 16. The incorporation of time series information helps ARGO achieve stability. As an extreme example, the AR(3) model focuses entirely on the time series information and is thus independent of Google Trends data revisions. GFT, formulated with the original search variables as inputs, is, by construction, insensitive to the changes in Google Trends data. For this portion of the study, we included the signal from GFT for context only, and we treat it as exogenous in our analysis. Based on the results from previous time periods, it is highly likely that if we had access to Google’s internal raw data (i.e., historical search volume for disease-related phrases), we would have achieved the same stability as well. However, even with these low-quality data, ARGO outperforms GFT uniformly on all versions of data in terms of both RMSE and MAE.

Detailed Description of Google Correlate Data.

Tables S3 and S4 list the search query phrases identified by Google Correlate as of March 28, 2009 and May 22, 2010, respectively. The March 2009 version included spurious terms such as “college.basketball.standings,” “march.vacation,” “aloha.ski,” “virginia.wrestling,” etc. These spurious terms did not appear in the May 2010 version.

Dynamic Coefficients for ARGO.

Fig. S1 shows the coefficients for the time series and Google search terms dynamically trained by ARGO via a heat map. The level of ILI activity last week is seen to have a significant effect on the current level of ILI activity, and ILI activity half a year ago and/or 1 y ago could provide further information, as the figure shows. Among Google Correlate query terms, ARGO selected 14 terms out of 100, on average, each week.