Chromatin extrusion explains key features of loop and domain formation in wild-type and engineered genomes

Significance

When the human genome folds up inside the cell nucleus, it is spatially partitioned into numerous loops and contact domains. How these structures form is unknown. Here, we show that data from high-resolution spatial proximity maps are consistent with a model in which a complex, including the proteins CCCTC-binding factor (CTCF) and cohesin, mediates the formation of loops by a process of extrusion. Contact domains form as a byproduct of this process. The model accurately predicts how the genome will fold, using only information about the locations at which CTCF is bound. We demonstrate the ability to reengineer loops and domains in a predictable manner by creating highly targeted mutations, some as small as a single base pair, at CTCF sites.

Abstract

We recently used in situ Hi-C to create kilobase-resolution 3D maps of mammalian genomes. Here, we combine these maps with new Hi-C, microscopy, and genome-editing experiments to study the physical structure of chromatin fibers, domains, and loops. We find that the observed contact domains are inconsistent with the equilibrium state for an ordinary condensed polymer. Combining Hi-C data and novel mathematical theorems, we show that contact domains are also not consistent with a fractal globule. Instead, we use physical simulations to study two models of genome folding. In one, intermonomer attraction during polymer condensation leads to formation of an anisotropic “tension globule.” In the other, CCCTC-binding factor (CTCF) and cohesin act together to extrude unknotted loops during interphase. Both models are consistent with the observed contact domains and with the observation that contact domains tend to form inside loops. However, the extrusion model explains a far wider array of observations, such as why loops tend not to overlap and why the CTCF-binding motifs at pairs of loop anchors lie in the convergent orientation. Finally, we perform 13 genome-editing experiments examining the effect of altering CTCF-binding sites on chromatin folding. The convergent rule correctly predicts the affected loops in every case. Moreover, the extrusion model accurately predicts in silico the 3D maps resulting from each experiment using only the location of CTCF-binding sites in the WT. Thus, we show that it is possible to disrupt, restore, and move loops and domains using targeted mutations as small as a single base pair.

The human genome is over 2 m long, yet it must fold up to fit inside a nucleus that is only a few microns wide. At the smallest scale, this folding is well characterized: dsDNA helices wrap around histone proteins, forming a nucleosome every ∼200 bp (a beads-on-a-string configuration known as the “10-nm fiber”) (1). At larger scales, the physical structure of chromatin is more mysterious.

One common hypothesis is that the 10-nm fiber is organized into a higher order structure known as the “30-nm fiber,” which has been observed in vitro but not in vivo (2). In the most well-known model, individual nucleosomes are wound about a central cavity that runs axially along the fiber’s length. Every six nucleosomes (roughly 1 kb) correspond to a full turn about this axial cavity, creating a solenoidal structure with a 30-nm diameter.

Another common notion, dating back to the 1970s, is that the human genome is partitioned into domains. These studies have relied on many experimental modalities, such as chromatin sedimentation (3); fluorescence microscopy (4); and, in the past several years, genome-wide DNA proximity ligation data generated using Hi-C (5–8). The internal structure of domains is not well understood (5–10).

A third feature of chromatin folding is the formation of loops, which bring pairs of genomic sites that lie far apart along the linear genome into close spatial proximity (8, 11). Many aspects of chromatin looping are poorly understood, including how loops form.

We recently reported new contact maps of the human genome with a resolution of 1 kb (8). These maps were created by using in situ Hi-C, which couples DNA-DNA proximity ligation in intact nuclei (nuclear ligation assay) (12) with high-throughput sequencing (Fig. 1A). The maps, containing over 15 billion contacts, allowed us to annotate over 9,000 contact domains (median length = 185 kb), which are contiguous genomic intervals in which there is an enhanced probability of contact among all loci. The maps also allowed us to annotate nearly 10,000 loops. These loops typically lie between CCCTC-binding factor (CTCF) motifs in the convergent orientation (i.e., the motifs point toward one another), suggesting a “convergent rule” for loop formation. Notably, we found that many contact domains are also “loop domains,” that is, contact domains whose boundaries are demarcated by the end points of a loop.

Fig. 1.

Chromatin is bendable at the kilobase scale. (A) In situ Hi-C maps DNA-DNA contacts occurring in intact nuclei. Reprinted with permission from ref. 8. (B) Probability that a restriction fragment will bend to form a cycle as a function of fragment length. Results are shown for four restriction enzymes. The 30-nm fiber predicts a peak around 30 kb (Right, yellow shading), whereas the 10-nm fiber is consistent with the peak observed around 1 kb (Left, yellow shading).

Here, we use our new maps to explore the physical structure of chromatin fibers, contact domains, and loops. First, we demonstrate that chromatin fibers are bendable at the kilobase scale, casting doubt on the widespread existence of 30-nm fibers in vivo. Next, we combine Hi-C data, molecular dynamics simulations, and a novel analog of McKean’s dimension-doubling theorem for Brownian motion (13) to explore how chromatin fibers fold inside contact domains. After considering a series of models, we find that the data are best explained by a model where loops form through the extrusion of flexible chromatin fibers by a CTCF- and cohesin-associated complex. This model has many appealing features, and explains why loops tend not to overlap and why they only form between convergent CTCF motifs.

Finally, we use clustered regularly interspaced short palindromic repeat (CRISPR)-mediated genome editing to manipulate CTCF motifs at loop anchors (14). In all 13 cases examined, we find that the convergent rule correctly predicts which loops will disappear. Moreover, the extrusion model accurately predicts in silico the contact maps resulting from these loop engineering experiments, including the conditions under which domains disappear.

Results

Chromatin Is Bendable at the Kilobase Scale, Far Less Stiff than Predictions Based on a 30-nm Fiber.

The stiffness of a fiber can be characterized by the Kuhn length, the minimum fiber length such that it is possible for the beginning and the end of the fiber segment to point in the same direction. Published estimates suggest a Kuhn length in the range of 30–60 kb for a 30-nm fiber (15).

To measure the Kuhn length of human chromatin in vivo experimentally, we examined the tendency of cross-linked chromatin fragments, formed during Hi-C’s restriction digestion step, to form single-fragment DNA cycles during the subsequent proximity ligation step (16). Restriction fragments shorter than 200 bp (the size of a nucleosome) rarely formed cycles, suggesting that they were too stiff. Cyclization probability increased sharply for 200- to 800-bp fragments, and was relatively constant thereafter (Fig. 1B). The results were similar regardless of the restriction enzyme used in Hi-C (MboI, DpnII, HindIII, and NcoI), and with and without cross-linking or harsh detergents (SI Appendix, Fig. S1). These results suggest a Kuhn length of roughly 1 kb for chromatin fibers.

The results of cyclization analysis were consistent with two other approaches. First, we measured the probability, I(s), of contact between two loci as a function of the genomic distance, s, between them. I(s) is maximal at the Kuhn length of a polymer and decreases monotonically as s increases. Using our in situ Hi-C data, we were able to measure I(s) reliably for the human genome at all distances larger than 5 kb (i.e., distances much longer than the typical 4-cutter fragment). The function declines monotonically at all distances probed, implying that the Kuhn length of chromatin is less than 5 kb (SI Appendix, Fig. S2A). Second, 40-kb-long loops were visually obvious in our initial report. At the specific loci involved, kilobase-length chromatin fibers must thus be capable of bending.

The Kuhn length observed in our data (≈1 kb) is incompatible with previous estimates of the Kuhn length for the 30-nm fiber. These results suggest that 30-nm fibers, if they exist, are rare in human nuclear chromatin in vivo. One important caveat should be noted: Our Hi-C protocol might disrupt the structure of the 30-nm fiber (e.g., due to use of nonphysiological ion concentrations.)

Measurements of Contact Probability Using Genome-Wide Averages Are Inconsistent with an Ordinary Polymer at Equilibrium.

In our original Hi-C study (5), we characterized the behavior of chromatin at the megabase scale by analyzing the contact probability function, I(s), described above, based on Hi-C data, analytical estimates, and in silico studies. The data for human chromatin showed a power-law relationship of the form I(s) ∝ s^−ɣ between 500 kb and 7 Mb, with ɣ = 1.08. We showed that values of ɣ can be used to discriminate among distinct polymer states. Specifically, ɣ = 1.08 is inconsistent with the classic structure of a globular polymer at equilibrium (an “equilibrium globule,” which has ɣ = 1.5), but is consistent with a dense, scale-invariant, isotropic, long-lived polymer state known as the fractal globule (5). Because the fractal globule’s unknotted topology makes it easier to access individual genomic loci, it furnishes an appealing model for chromatin structure.

When we repeated the above analysis on our new, kilobase-resolution maps, we observed a scaling of ɣ = 1.27 between 300 kb and 3 Mb (SI Appendix, Fig. S2A). This slightly higher value is consistent with our previous conclusion that chromatin does not fold into an equilibrium globule, and falls within the range we predicted for a fractal globule (17).

Genome-Wide Measurements of Chromatin Folding Inside Individual Contact Domains Reveal a Polymer State Characterized by ɣ ≈ 0.75.

In our original study, we could not discern local folding features at scales smaller than ∼1 Mb. With our new maps, which contain 200- to 1,000-fold more data, we had the opportunity to study folding within contact domains, which are contiguous genomic intervals in which there is an enhanced probability of contact among all loci (Fig. 2A). We found that folding measurements differ sharply within contact domains vs. across contact domains.

Fig. 2.

Contact domains exhibit a contact probability scaling with ɣ ≈ 0.75. (A, Left) Contact domains from a region on chromosome 4 of GM12878 lymphoblastoid cells. (A, Right) Number of contacts (Top) incident on a 50-kb window at the center of a domain (Bottom). (B) Contact probability vs. genomic distance for 473 individual domains, measured with respect to a 50-kb locus at the domain’s center. A power law (reference slope of −0.75, gray dashed line) is consistently observed inside domains, whose boundary is indicated by a vertical dashed line. A single black line shows contact probability for the domain from A. Domains are grouped by size; each group is vertically shifted by an order of magnitude for visual clarity. (Inset) Contact probability vs. genomic distance, excluding pairs of loci that lie in different contact domains. A power-law (ɣ = 0.76) is seen over two orders of magnitude. (C) Histogram of ɣ values for contact domains across six human cell types. (Inset) Representative microscopy images (maximum Z projections) of four cell types, showing chromatin (blue, DAPI stain) and cytoplasm (red, CellTracker CMTPX dye [Thermo Fisher]). (Scale bar: 10 μm.)

We began by calculating I_same(s) using our genome-wide averaging technique, but only including pairs of loci that were in the same contact domain. We obtained a markedly lower value: ɣ = 0.76 (Fig. 2B).

Next, we measured the decline in contact probability with distance relative to a fixed DNA locus. For loci longer than 50 kb, the results were highly reproducible (SI Appendix, Fig. S2G). We focused on 1,057 distinct 50-kb loci, each situated at the midpoint of a contact domain. The resulting contact probability plots consistently exhibited two distinct regimes. Contact frequency within a domain exhibited a power-law decline whose ɣ was centered on 0.75 (SD = 0.05) and always smaller than 1 (Fig. 2B and SI Appendix, Fig. S2D). Outside the domain, the power-law regularity was replaced by a more heterogeneous monotonic decline (Fig. 2B and SI Appendix, Fig. S2E).

Our findings suggest that because the frequency of contact between two loci declines markedly when a contact domain boundary is crossed, I(s), which is calculated predominantly using pairs of loci separated by such a boundary, tends to overestimate ɣ for contact domains (SI Appendix, Fig. S2B).

To check whether ɣ depended on nuclear volume, we compared four human cell types using confocal microscopy and in situ Hi-C. Despite threefold variation in nuclear volume (from smallest to largest, GM12878: 237 ± 84 μm³, IMR90: 381 ± 157 μm³, NHEK: 440 ± 90 μm³, HMEC: 728 ± 307 μm³), the intradomain ɣ measurements were indistinguishable (Fig. 2C and SI Appendix, Table S1). The results were also similar in different nuclear compartments (A/B) (5) and subcompartments (A1/A2/B1/B2/B3) (8) (SI Appendix, Fig. S2C), in mouse (CH12-LX lymphoblasts), and in experiments with and without cross-linking (SI Appendix, Table S2).

Because site-directed recombination relies on the spatial proximity of DNA sites, we reexamined published experiments probing the relationship between flippase recombination frequency and genomic distance in humans (18). Interestingly, we noted a power-law scaling with ɣ = 0.75 (SI Appendix, Fig. S2F).

Taken together, these results suggest that chromatin in contact domains is characterized by ɣ ≈ 0.75. Next, we sought to understand the implications of this exponent.

New Mathematical Theorem Indicates That Chromatin Folding Inside Contact Domains Is Not Strictly Fractal.

A difficulty in interpreting ɣ is the uncertainty about which ɣ values are consistent with a fractal globule. Approximate methods and physical simulations suggested values ranging from 1 to 1.33 (5, 17). However, no rigorous bounds are known. We therefore sought to derive such bounds.

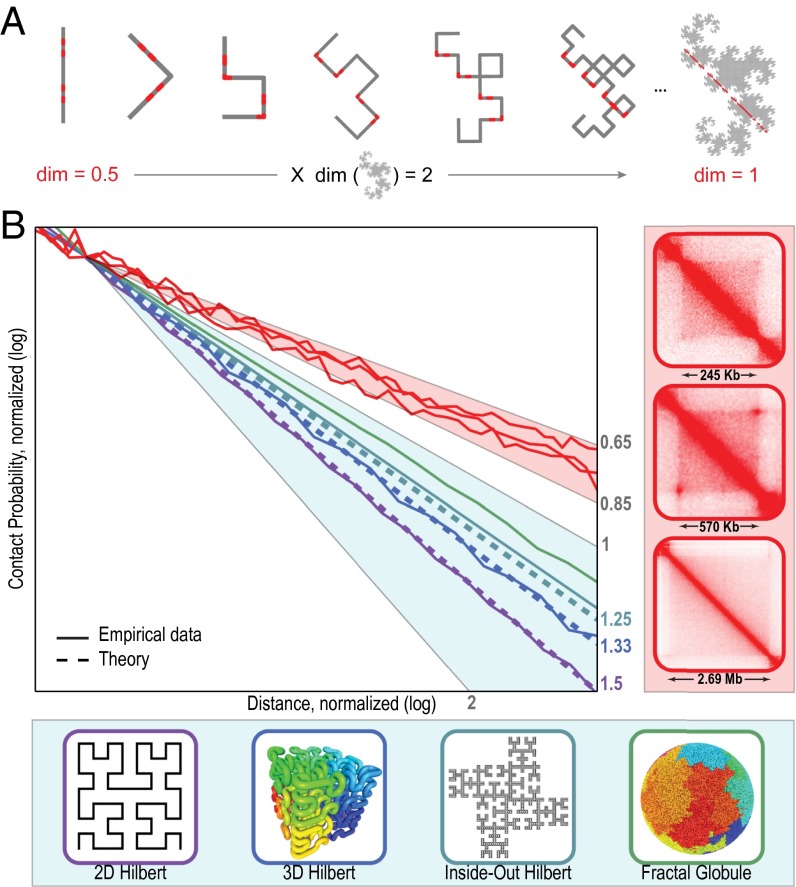
We proved mathematically that ɣ must lie between 1 and 2 for any fractal structure. To prove this result, we analyzed mathematical functions (denoted f) that continuously map (in other words, fold) the unit segment [0,1] into a higher dimensional space. We focused on fractal curves, which are generated by applying a simple folding rule to a simple initial state and repeating ad infinitum. When the folding rule is applied identically at all scales, the resulting fractal curves have no characteristic length scale. Because such curves continuously transform a 1D segment into a higher dimensional object, they have been of interest to mathematicians ever since the first space-filling curves, which map the unit segment onto the unit square, were discovered by Giuseppe Peano (the “Peano curve” in 1890) and David Hilbert (the “Hilbert curve” in 1891). If the repetition process is terminated after a finite number of steps, the resulting curve corresponds to a physically realizable polymer chain. For this reason, finite iterations of fractal curves are often used to model the fractal globule (5). By bounding the values of ɣ that can be obtained from fractal curves, we can test whether our experimental data are consistent with a strict fractal globule.

When characterizing a fractal curve, a commonly used measure is the Minkowski (or “box-counting”) dimension, denoted dim(X), which generalizes the common notion of dimension to non-integer values. Just as the number of line segments with width 1/N needed to cover the 1D unit segment scales as N¹ and the number of squares with width 1/N needed to cover the 2D unit square scales as N², dim(X) is defined so that the number of boxes with width 1/N needed to cover X scales as N^dim(X). For instance, the Minkowski dimension of a crumpled sheet of paper (≈2.51) provides a measure of its packing density (19). The Minkowski dimension of Great Britain’s coastline (≈1.25) is a measure of its roughness (20). The Minkowski dimension can also be less than 1: The set of points in [0,1] without an odd digit in their decimal expansion (i.e., 0.86, 0.22222) has dimension 0.699.

We proved that folding the 1D unit segment [0,1] into a d dimensional fractal curve scales the Minkowski dimension of all subsets of [0,1] by a factor of d; that is, any k-dimensional subset of the unit segment will fold into a k * d dimensional shape. Our results can be summarized in the following theorem and corollary, whose proofs appear in SI Appendix:

• Theorem: For any self-similar fractal curve f([0,1]), $\dim f\left(X\right)=d\cdot \dim X$ for any $X\subseteq \left[\mathrm{0,1}\right]$.*

• Corollary: The contact probability of a fractal curve satisfies I(s) ∝ s^−ɣ with ɣ = 2 − (d_surf/d), where s is the linear distance along the curve, d_surf is the Minkowski dimension of the curve’s surface (i.e., its surface roughness), and d is the Minkowski dimension of the curve as a whole.

An illustration of the theorem is the 2D Dragon curve, which doubles the Minkowski dimension of all subsets in its domain (Fig. 3A). Mathematically, our result is a deterministic analog of Henry McKean’s well-known “dimension-doubling” theorem, which states that Brownian motion doubles the dimension of subsets (13).

Fig. 3.

New mathematical theorem demonstrates that chromatin folding inside contact domains is not strictly fractal. (A) Successively applying a simple folding rule transforms a 1D line segment (Left) into a 2D Dragon curve (Right). Our theorem reveals that just as the curve doubles the dimension of the line segment, it doubles the dimension of all subsets of the line segment. Thus, when we intersect the Dragon curve with a line to create a 1D feature, the corresponding points in the original segment must have a Minkowski dimension of 1/2. A corollary of this theorem makes it possible to calculate the contact probability scaling exponent ɣ for any fractal curve. (B) Contact probability vs. distance for various structures. Our corollary predicts that ɣ for fractal curves satisfies ɣ = 2 − (d_surf/d), where d_surf is the dimension of the curve’s surface and d is the dimension of its interior. (Left) Comparing simulations (solid lines) with theoretical predictions (dashed lines). Two-dimensional Hilbert curve (purple; d_surf = 1, d = 2, ɣ = 1.5), 3D Hilbert curve (blue; d_surf = 2, d = 3, ɣ = 1.33), inside-out Hilbert curve, rank 3 (teal; d_surf = 1.5, d = 2, ɣ = 1.25), and fractal globule (green). As the rank of an inside-out Hilbert curve increases, its boundary becomes nearly 2D and its ɣ draws asymptotically close to 1. (Right, Top to Bottom) Three contact domains: chromosome 12: 46.2–46.4 Mb, chromosome 4: 21.8–22.4 Mb, and chromosome 5: 2.1–4.8 Mb.

The corollary may be illustrated by measuring ɣ for classic fractal curves, such as the 2D Hilbert curve (d_surf = 1, d = 2, ɣ = 3/2; Fig. 3B, purple), the 3D Hilbert curve (d_surf = 2, d = 3, ɣ = 4/3; Fig. 3B, blue), and many others (SI Appendix, Fig. S3 and Table S3). The corollary also implies that for curves with extremely rough surfaces (d_surf close to d), ɣ can draw arbitrarily close to unity. Because no such curves are known, we generalized the Hilbert curve, constructing a class of “inside-out” Hilbert curves (Fig. 3B, teal) whose boundaries are arbitrarily rough and whose ɣ values come arbitrarily close to 1 (SI Appendix, Figs. S6 and S7).

Because 0 ≤ d_surf/d < 1, the corollary proves that ɣ for a fractal curve must lie between 1 and 2. Thus, our measurements of ɣ ≈ 0.75 inside contact domains (Fig. 3B, red) are inconsistent with the hypothesis that contact domains tend to form fractal globules.

Physical Simulations Suggest That ɣ = 0.75 Is Consistent with an Unknotted, Nonequilibrium State That Is Anisotropic Rather than Fractal.

Another way of exploring the significance of a particular value of ɣ is by computationally modeling chromatin as a polymer comprising many identical monomers, each of which represents a fixed number of bases. By simulating the dynamics of a condensing polymer chain and the surrounding mixture under various physical assumptions, it is possible to test whether a particular set of conditions leads to a realistic ɣ value.

In our original models, we simulated a condensation process in which the collapse of the polymer was driven by external forces (i.e., the crowding of a stretch of chromatin by other components of the nucleoplasm). Through an excluded volume interaction, these components crush the polymer chain. Such forces can be modeled using a potential function that attracts all monomers equally toward a single point (5). Because this potential has no characteristic length scale, the resulting dynamics are scale-invariant, and the polymers collapse isotropically into a fractal globule.

Notably, our earlier models did not examine the effects of interactions among the monomers on polymer condensation. Attractive forces between individual nucleosomes have been observed in vitro by many groups (2), and effective attractions between monomers are seen in all polymer globules, arising when a polymer is immersed in a poor solvent (21). Therefore, in the present study, we incorporated attractive forces between monomers using the classic Lennard–Jones potential. This model of intermolecular attractions was originally developed to study van der Waals effects and is commonly used to describe the attractive forces between nucleosomes (15, 22). We examined a class of systems in which both intermonomer attractions and external crushing forces are present during condensation. The ratio of these forces is given by a single parameter, R, which we varied across eight orders of magnitude.

We probed these systems using Langevin dynamics simulations, in which random collisions between the solvent and the polymer are accounted for implicitly through parameters for viscosity and temperature. We ran our simulations using LAMMPS (23), accelerated using graphical processing units (24). Each monomer represented 1 kb (matching the above estimates of Kuhn length). The polymer chain contained up to 10,000 monomers, or 10 Mb. For each condition, we ran at least 100 simulations from randomized starting configurations.

Our simulations revealed a family of nonequilibrium states (Fig. 4A). When internal forces are weak (R << 1), polymer condensation closely resembles the isotropic dynamics observed with pure external forces (R = 0) and results in a fractal globule. Because intermonomeric attractions decay as monomers move apart, internal forces introduce a length scale into the system. When they are sufficiently strong (R >> 1), condensation transitions into an anisotropic regime. First, tiny globules form along an extended chain; tension along the chain then causes the globules to concatenate in a linear fashion (Fig. 4B). This model of polymer condensation was first postulated by de Gennes (21). The resulting state, which we dub a “tension globule,” is not scale-invariant. Instead, it contains long intervals in which genomic position is correlated with spatial position along a linear axis (SI Appendix, Fig. S8 D and E).

Fig. 4.

Value of ɣ obtained using Hi-C is consistent with a tension globule in which loops form by diffusion. (A) Value of ɣ for a polymer after condensation varies as the ratio of internal to external forces, R, is changed. (B) Condensation of a 10-Mb tension globule over time. (C) Contact probability vs. distance for 450 simulated tension globules with a length of 10 Mb. In each case, a power law is seen for distances between 20 kb and 800 kb. Mean ɣ = 0.73, SD = 0.07. (D) Simulation of a region of chromosome 4 in GM12878 (chromosome 4: 20.3–22.6 Mb). The experimental data exhibit four loop domains (Left) and can be recapitulated (Right) using a tension globule containing four loops (black arcs) which is tethered at both ends (SI Appendix). Contact domains form spontaneously.

Importantly, the values of ɣ differ depending on the regime. When R is small, ɣ(R) is slightly larger than unity, consistent with our earlier fractal globule simulations. When R is large, ɣ(R) is roughly 0.72, consistent with our observations for contact domains (Fig. 4C and SI Appendix, Fig. S8A). In-between, ɣ(R) exhibits intermediate values. Interestingly, all of the states in this family are dense and largely unknotted (SI Appendix, Fig. S8F).

Our findings were robust to variations in numerous simulation parameters: chain length and initial configuration, solvent temperature, viscosity, and simulation time (SI Appendix, Fig. S9 and Table S4). They were also robust to the mechanism underlying the internal forces. They did not change significantly when we replaced the Lennard–Jones potential with a Yukawa potential, a model of screened electrostatic forces, in which the attractions decay much more rapidly with distance (SI Appendix, Fig. S10 and Table S4).

Our simulations again suggest that the structure of nuclear chromatin inside contact domains is not consistent with a fractal globule. However, the ɣ value is consistent with a tension globule resulting from condensation amid strong internal attractions between monomers.

Condensation of a Tension Globule Results in Spontaneous Formation of Contact Domains Between the Anchors of a Loop.

One of the most surprising features of our in situ Hi-C maps is that contact domains often correspond to loops, that is, the domain boundaries lie at the loop’s two anchor loci.

We used our physical simulations to explore the effects of bringing together two anchor points followed by condensation into a tension globule. Notably, the formation of a loop led to enhanced contact frequency between all pairs of loci in the interval demarcated by the two loop anchors (i.e., a contact domain) (Fig. 4D). These contact domains exhibited values of ɣ (0.77 ± 0.08) that match our experimental observations (0.75 ± 0.05; SI Appendix, Fig. S11B).

Simulation Results for a Tension Globule Match Intradomain Distances Measured by 3D-FISH.

We next examined whether the tension globule model recapitulates the spatial distances observed experimentally. We studied four pairs of loci using 3D-FISH (8). Each pair lay in a single domain; the genomic distance between the loci ranged from 320 kb to nearly 1 Mb. We measured at least 50 3D distances for each locus pair. We compared these values with distributions obtained using our tension globule simulations (SI Appendix, Fig. S13B). The simulated distributions matched the experimental distributions as closely [Kolmogorov–Smirnov (K-S) statistic = 0.15] as experimental replicates matched one another (K-S statistic = 0.18).

Taken together, our findings show that the tension globule model accounts for three important features of genome folding observed in our 3D maps: the value of the contact probability scaling ɣ, the formation of contact domains between loop anchors, and the distribution of 3D distances between pairs of loci.

Tension Globule Model Fails to Explain Other Key Features of 3D Folding.

Although the tension globule model can explain the general scaling properties of our data, it does not explain many other facets, particularly those facets related to loop formation. In a tension globule model, loop formation would occur via diffusion. Looping proteins (e.g., CTCF) would initially bind to DNA anchor motifs. When diffusion brings two anchors into close spatial proximity, the proteins would dimerize, forming a chromatin loop.

This diffusive process inevitably leads to loops that overlap (i.e., a point in the interior of one loop is anchored to a point outside the loop), thus creating chromatin entanglements. By contrast, our experimental data show that pairs of loops rarely overlap. It is also hard to understand, in a diffusive model, why the CTCF motifs at pairs of loop anchors must lie in the convergent orientation. We therefore considered alternative models.

Loop Formation by Extrusion Complexes Would Explain Key Features of 3D Folding.

Nasmyth proposed a model based on an “extrusion complex” containing two DNA-binding subunits that are physically tethered together (25, 26). This complex is loaded onto chromatin at a single locus. Initially, its subunits are bound to nearby DNA elements, forming a tiny chromatin loop. Next, DNA is extruded through the subunits such that the two tethered subunits move in opposite directions with respect to the genome: one forward and one reverse. As a result, the loop continues to grow, without knotting. Eventually, the extrusion complex dissociates from DNA (Fig. 5A, i–iii).

Fig. 5.

Model based on loop extrusion makes it possible to recapitulate Hi-C maps accurately using only CTCF ChIP-Seq results. (A, i and ii) Extrusion complex loads onto the fiber at a random locus, forming an extremely short-range loop. (A, iii) As the two subunits move in opposite directions along the fiber, the loop grows and the extruded fiber forms a domain. (A, iv) When a subunit detects a motif on the appropriate strand, it can stop sliding. Unlike diffusion, extrusion cannot mediate co-location of motifs on different chromosomes. (B) Three-dimensional rendering of a 3-Mb extrusion globule from the ensemble described below. Convergent CTCF anchors (orange spheres) lead to an unknotted loop spanning a compact, spatially segregated contact domain (highlighted in blue). (C) Contact probability vs. distance for 12 domains with a length of 1 Mb, created in silico using loop extrusion, measured from a 100-kb locus at the center of the domain. In each case, a power law is seen for distances between 5 kb and 400 kb. Mean ɣ = 0.72, SD = 0.06. (D) We use loop extrusion to model a 2.3-Mb region on chromosome 4 of GM12878. CTCF ChIP-Seq signals are normalized and converted into binding probabilities for the simulated extrusion complex. Each peak is assigned a forward (green) or reverse (red) orientation based on the strand of the underlying CTCF motif. Extrusion simulations yield an ensemble of 3D polymer configurations; contact maps for the simulated ensemble (Top) recapitulate the features observed in our kilobase-resolution Hi-C experiments (Bottom), including the position of domains and loops.

We explored the behavior of extrusion complexes in our simulations as follows. As before, we began with a condensing polymer. Extrusion complexes are bound to the polymer at a density that depends on their concentration and dissociate at a rate that depends on their processivity. The complexes cannot pass through one another; if they collide, one must fall off.

We then added one novel feature to Nasmyth’s model (19), based on our observations about the role of CTCF motifs. We assume that each subunit of the extrusion complex recognizes the presence of a particular motif on a particular DNA strand, such as an appropriately oriented CTCF motif, by binding tightly and halting the extrusion process through the subunit. We therefore designated certain monomers in our simulated polymer as anchors, assigning each a forward or reverse orientation. In our simulations, the forward subunit’s progress may be halted by a forward anchor, but not by a reverse anchor; the reverse subunit may be halted by a reverse anchor, but not by a forward anchor (Fig. 5A, iv).

We began by simulating a condensing polymer containing a pair of convergent anchors 1 Mb apart. When an extrusion complex landed between the anchors, it began extruding a loop until its subunits eventually arrived at the anchor monomers. At this point, the extrusion came to a halt, yielding a “persistent loop” between the anchors (i.e., a loop that was present for a protracted period) (Fig. 5B and SI Appendix, Fig. S12C). This extrusion process did not prevent condensation and resulted in a globular state.

When we examined the resulting contact maps, we made three observations. First, a prominent peak was present between the two anchors, reflecting the formation of a persistent loop. Second, there was enhanced contact frequency between all pairs of loci lying between the two anchors, forming a contact domain. Third, the contact domains exhibited power-law scalings in contact probability with values of ɣ (0.72 ± 0.06) that match our experimental observations (0.75 ± 0.05; Fig. 5C). These findings reflect the equilibrium for a condensing polymer immersed in a solvent containing extrusion complexes and did not depend on the condensation forces (external or internal) or the initial condition (SI Appendix, Fig. S12 A and B).

Next, we examined whether the extrusion model recapitulates pairwise spatial distances observed using 3D-FISH. Repeating our previous analysis (SI Appendix, Fig. S13C), we found that the simulated distributions matched the experimental distributions almost as closely (K-S statistic = 0.16) as experimental replicates matched one another (K-S statistic = 0.18).

Thus, the extrusion model, like the tension globule model, is consistent with the contact probability scaling ɣ, the formation of contact domains between loop anchors, and the distribution of 3D distances between pairs of loci. The extrusion model explains a much wider range of observations, however. In particular, it provides a natural explanation for why loops overwhelmingly form between convergent CTCF sites. Because loops that occur in the same cell cannot overlap under the extrusion model, the model also explains why we rarely see overlapping loops in our experimental data.

Extrusion Model Can Recapitulate Hi-C Experimental Results, Given the Locations of CTCF Binding.

Next, we explored whether the extrusion model could recapitulate Hi-C experimental results in silico using CTCF ChIP-sequencing (ChIP-Seq) data alone.

We began by simulating the folding of a 2.3-Mb target region on chromosome 4 (20.3–22.6 Mb). Our algorithm created an in silico representation of the region as a uniform polymer, adding forward and reverse anchors at peaks of CTCF binding observed in experimental ChIP-Seq data for the region. The strength of each anchor (the likelihood that the corresponding subunit would halt) reflected the amplitude of the ChIP-Seq peak. Anchor orientation was assigned based on the strand of the CTCF motif associated with the peak. The inputs did not include Hi-C data.

We simulated the behavior of the model polymer in a solvent containing extrusion complexes. Strikingly, the resulting contact matrix closely resembled the contact matrix obtained using Hi-C experiments (Fig. 5D; Pearson’s r = 0.964). Peaks and contact domains were observed in the same positions, and appropriate ɣ values were obtained inside each contact domain. The results were similar for other regions (SI Appendix, Fig. S12D).

We also sought to simulate the target region using the tension globule model. As before, we identified peaks in CTCF ChIP-Seq data, and assigned each peak an orientation based on the strand of the CTCF motif associated with the peak. However, to obtain contact matrices that resembled our experimental results, we had to impose a number of ad hoc penalties that do not correspond to any natural processes in 3D diffusion: Loops were only allowed between pairs of convergent peaks, and the likelihood of such a loop depended on (i) the strength of the peaks, (ii) the distance between the peaks, and (iii) the number and strength of intervening CTCF peaks. Even so, the simulations did not provide as good a fit as the extrusion model (SI Appendix, Fig. S11E; Pearson’s r = 0.922).

Network of Loops Contains Hundreds of Isolated Cliques and Is Consistent with a Model in Which Consecutive Loops Can Form Simultaneously by Extrusion.

We then explored higher order relationships among the location of loops by constructing a “loop network” for GM12878 lymphoblastoid cells (8). The network’s nodes are genomic loci containing at least one loop anchor. Edges indicate loops.

We were particularly interested in “isolated cliques.” This network motif comprises a set of n ≥ 3 loci such that any pair in the set is connected by a loop (i.e., the set is a “clique”) but none of the loci are connected by loops with loci outside the set (i.e., the set is “isolated”) (Fig. 6).

Fig. 6.

Analysis of loop networks reveals many isolated cliques, consistent with a model in which consecutive loops can form simultaneously by extrusion. Cliques of size three (Left), four (Middle), and five (Right), shown as network representations (Above) and in the Hi-C contact map (Below). Nodes correspond to loop anchor loci; edges and open circles indicate a loop called in (8) (solid green), or using a more relaxed threshold (dashed blue). The five-clique exhibits an additional loop (gray) connecting a clique locus to a locus outside the clique. The loop anchor CTCF motifs are indicated; each middle clique locus contains a pair of CTCF motifs in the divergent orientation.

Isolated cliques were dramatically enriched in the loop network. For instance, in GM12878, we observed 69 isolated cliques with three nodes (sixfold enrichment relative to an ensemble of randomized control networks), 16 with four nodes (28-fold), and 1 with five nodes (161-fold). If we allowed for a small number of loops (≤ N − 2) between loci inside the clique and loci outside, these numbers increase: 145 cliques with three nodes (threefold enrichment), 86 with four nodes (12-fold), 5 with five nodes (14-fold), and 1 with six nodes (41-fold).

Typically, the clique loci were positioned one after another in the genome, with no other loop anchors intervening (in 64% of cases). The first clique locus (in genomic coordinates) typically contained a bound CTCF motif in the forward orientation (97%, fourfold enrichment). The last clique locus contained a bound CTCF motif in the reverse orientation (98%, fourfold enrichment). The middle clique loci typically contained CTCF motifs in both orientations (70%, 8.5-fold enrichment). These findings are consistent with the convergent rule for CTCF looping.

Isolated cliques may reflect simultaneous colocation of all clique loci at a single spatial hub within the same cells, forming a chromatin rosette (9, 27). Alternatively, it may be that some, but not all, clique loops are simultaneous. However, another possibility is that all of the loops in our isolated cliques tend to occur in distinct cells. We cannot distinguish between these alternatives using pairwise contact maps from cell ensembles because such maps do not reflect higher order colocation patterns.

However, we noticed that when a middle locus contained a unique motif in each orientation, the motifs were almost always arranged in a divergent configuration: The first motif was in the reverse orientation, pointing toward the preceding clique locus, and the second motif was in the forward orientation, pointing toward the subsequent clique locus (89% vs. 11% in the convergent orientation). Because the extrusion model predicts that the genomic intervals inside simultaneous chromatin loops cannot overlap, the overwhelming bias toward the divergent configuration would be expected only if consecutive loops in our cliques (e.g., loops A-B and B-C in a clique comprising A, B, and C) form simultaneously by extrusion.

Genome Editing of CTCF Motifs Disrupts Corresponding Loops, Consistent with the Convergent Rule.

We next sought to study the formation of loops experimentally. We used CRISPR/Cas9-based genome editing (14) to modify specific CTCF motifs and explore the effects on loop structure. To avoid allelic heterogeneity, we used HAP1, a human haploid cell line.

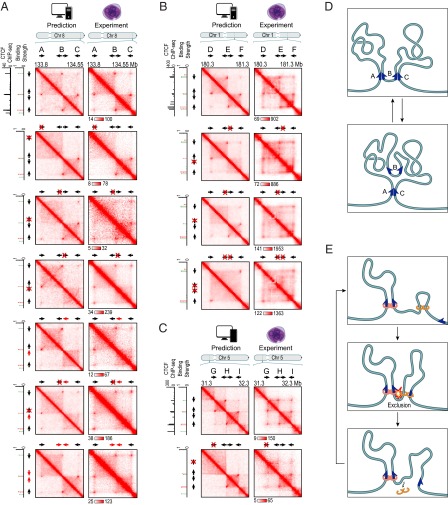
We generated an in situ Hi-C map of WT HAP1 cells, with 1.1B reads (SI Appendix, Table S6), in which we annotated 8,334 loops and 4,332 contact domains. We chose to study a target region containing three loci: A (chromosome 8: 133.9 Mb), B (134.2 Mb), and C (134.5 Mb). Each pair of these three loci forms loops with one another (A-B, B-C, and A-C). CTCF sites are present at each locus in accordance with the convergent rule: Locus A has a forward-oriented CTCF motif (dubbed A/Forward), locus B has a reverse-oriented CTCF motif (B/Reverse) followed by a forward-oriented motif (B/Forward), and locus C has a reverse-oriented motif (C/Reverse). All three loops are associated with contact domains.

If our loop anchor motif annotation is accurate, deleting the A/Forward site would disrupt the A-B and A–C loops. To test this hypothesis, we performed genome editing by using two guide RNAs designed to flank either side of the A/Forward motif (SI Appendix, Table S7). We grew a clonal population of cells carrying a 17-bp deletion spanning the A/Forward motif.

To study the effects of this and other genome editing experiments, we developed an inexpensive way to monitor Hi-C results only in the target region by performing HYbrid Capture on the in situ Hi-C library (28). We validated this method, dubbed “Hi-C²,” by applying it to WT HAP1, capturing a 2-Mb region (chromosome 8: 133–135 Mb). The results were equivalent to the results obtained using ordinary in situ Hi-C (SI Appendix, Fig. S14).

When we performed Hi-C² on our A/Forward mutant cell line, we observed that, as predicted, the A-B and A-C loops were disrupted (Fig. 7A).

Fig. 7.

Genome editing of CTCF motifs allows reengineering of loops in accordance with the convergent rule; the resulting contact maps can be predicted in silico using extrusion simulations. (A) Results of CRISPR/Cas9-based genome editing experiments at chr8:133.8–134.55 Mb in HAP1 cells. Extrusion simulations (Left) and experimental data (Right) are shown. (A, first row) Contact map for the WT locus, calculated using in silico simulations (Left), closely matches the map observed using Hi-C² experiments (Right). (A, second row) Deletion of A/Forward eliminates the A-B and A-C loops and the contact domain boundary at locus A. The predictions of our in silico simulations (Left) closely match the contact map observed using Hi-C² experiments (Right). All parameters in this and subsequent simulations of mutant regions use exactly the same parameters as the simulations of the corresponding WT contact map. The only difference in the mutant simulation is the modification of the appropriate CTCF-binding site (in this case, deletion of A/Forward). (A, third row) Deletion of B/Reverse eliminates the A-B loop. (A, fourth row) Deletion of B/Forward eliminates the B-C loop. (A, fifth row) Inversion of B/Forward eliminates the B-C loop. (A, sixth row) Simultaneous deletion of B/Reverse and inversion of B/Forward eliminates the B-C loop. (B) Similar series of results for chromosome 1 (180.3–181.3 Mb). Notably, the elimination of one loop anchor motif at the middle locus fails to eliminate either the D-E or E-F contact domain. When both loop anchor motifs are eliminated, both the D-E and E-F contact domains disappear. (C) We disrupted a forward CTCF motif by inserting a single base at chromosome 5: 31,581,788. Two loops are disrupted. The domain boundary moves to a nearby, weak CTCF site. Because the binding at this new site was weaker than the threshold value, this new boundary was not predicted by our extrusion simulations. (D) Our data suggest that the region shown in A is typically found in one of two states in wild-type cells. In the first state, both the A-B and B-C loop domains are present, but the A-C loop domain is absent. In the second, only the A-C loop domain is present. The data suggests a similar decomposition for the region in B. (E) Extrusion can explain the formation of exclusion domains. In this example, an extrusion complex forms a loop between adjacent motifs in the convergent orientation. Downstream, a second CTCF motif in the reverse orientation is unoccupied. Obstructed on both sides, extrusion complexes landing in the interval between the two reverse motifs tend to remain inside the interval. This leads to the formation of a domain.

Next, we examined the effect of disrupting the motifs at the B locus. We tested five predictions of the convergent CTCF rule: (i) Disruption of B/Forward (a 159-bp deletion) will eliminate the B-C loop alone (and not affect the loop between A and B, which, by the convergent rule, must be anchored at B/Reverse); (ii) disruption of B/Reverse (142 bp) will eliminate the A-B loop; (iii) inversion of B/Forward will eliminate the B-C loop; (iv) if B/Reverse is disrupted, inverting B/Forward will eliminate the B-C loop, but restore the A-B loop at a slightly offset anchor position (corresponding to the position of the inverted B/Forward rather than B/Reverse); and (v) inversion of both sites will not disrupt either loop, but will offset the positions of both anchors. The experimental data matched these predictions in every case (Fig. 7A and SI Appendix, Fig. S16).

We next examined a similar region on chromosome 1, spanning D (180.5 Mb), E (180.8 Mb), and F (181.1 Mb). We tested four predictions of the convergent rule: (i) Disruption of E/Reverse (a 16-bp deletion) will eliminate the D-E loop; (ii) disruption of E/Forward (10 bp) will eliminate the E-F loop; (iii) inversion of E/Forward will eliminate the E-F loop; and (iv) simultaneously disrupting E/Forward (7 bp) and E/Reverse (16 bp) will eliminate the D-E and E-F loops, leaving only the D-F loop. The experimental data matched these predictions in every case (Fig. 7B).

Finally, we targeted a similar region on chromosome 5, spanning G (31.6 Mb), H (31.8 Mb), and I (32.1 Mb). We inserted a single base pair into the G/Forward motif (chromosome 5: 31,581,788). Strikingly, both the G-H loop and the G-I loop disappeared, but the H-I loop remained (Fig. 7C).

The convergent rule, combined with our loop anchor motif annotation, correctly predicted the looping pattern in all 13 mutants (Fig. 7 and SI Appendix, Fig. S15). When we examined the effect of removing the corresponding CTCF motifs in our extrusion simulations, the contact maps predicted by the simulations closely matched those contact maps obtained experimentally (Fig. 7). These results show that it is possible to reengineer loops in a targeted fashion.

Our experiments also shed light on which loops in a clique occur in the same cells. For example, if all clique loops occurred simultaneously, then A-B would still be in close proximity even after deleting B/Reverse, because the A-C and B-C loops would sequester A and B near C/Reverse. The fact that we can disrupt the A-B loop without affecting the A-C and B-C loops suggests that the A-C and B-C loops do not occur in the same cells. Similarly, our ability to disrupt the B-C loop alone suggests that the A-C and A-B loops do not occur in the same cells. Taken together, our data are consistent with a model in which consecutive loops (i.e., A-B and B-C) tend to occur simultaneously in some cells, whereas the larger loop (A-C) tends to form in other cells (Fig. 7D).

Contact Domains Can Form Between Consecutive Loop Anchors That Do Not Loop to One Another.

Interestingly, disrupting certain anchor motifs eliminated a loop, but not the associated contact domain. For instance, deletion of the B/Forward motif disrupted the B-C loop, but not the B-C contact domain. Similar behavior was observed in all nine experiments involving the removal of a single anchor motif at a middle locus.

We found that our computational simulations produced similar results for the extrusion model (but not for the tension globule model). The reason was because even after we eliminate B/Forward, an extrusion complex landing in the B-C interval tends to remain within the B-C interval. At one end, the complex tends to halt at the C/Reverse motif; at the other end, its progress tends to be impeded by the forward subunit of the extrusion complexes positioned at B/Reverse (whenever this site is engaged in looping with A/Forward) (Fig. 7E). Because the extrusion complex is excluded from adjacent intervals, it tends to bring points within the B-C interval together, forming a contact domain. We dubbed this configuration an “exclusion domain.”

The extrusion model predicts that an exclusion domain will remain when one of the middle anchors is deleted, but not if both are deleted, as in the case of the mutant lacking both E/Forward and E/Reverse. In this case, an exclusion domain will not form between D and E because there is no E-F loop to interfere with the sliding of extrusion complexes landing in the D-E interval; similarly, an E-F exclusion domain will not form because there is no D-E loop. These predictions are precisely what is seen in our Hi-C² experiments.

The extrusion model also predicts that exclusion domains will occur in the WT genome. To identify such domains, we examined regions containing three consecutive loci, A, B, and C, such that A loops to B and to C, but B and C do not loop to one another. We found 986 such cases. An A-B contact domain was annotated in 399 cases (41%), consistent with the frequency of contact domains at loops genome-wide (38%), given the stringent threshold applied for calling domains (8). Despite the lack of an apparent loop between B and C, a B-C contact domain was seen in 158 cases (16%), a 6.3-fold enrichment (SI Appendix, Fig. S17). The reduced frequency is likely due to the fact that exclusion domains tend to be less pronounced.

Discussion

Our results illuminate the structure of chromatin at multiple scales: chromatin fibers, contact domains, and loops.

At the smallest scale, the winding of DNA around histones has long been known to form the flexible 10-nm fiber. This fiber is widely believed to coil into the larger, stiffer, 30-nm fiber, although recent studies using microscopy, electron spectroscopy, and X-ray scattering have failed to find evidence for 30-nm fibers in vivo (29, 30). Our Hi-C data allow us to measure the Kuhn length, or bendability, of chromatin fibers. We find that chromatin fibers are highly bendable, with a Kuhn length of roughly 1 kb. This value is far smaller than what would be expected for a 30-nm fiber (30–60 kb) (15), suggesting that 30-nm fibers, if they exist, are rare in intact chromatin. Our findings suggest that at the scale of the typical gene (∼15 kb), chromatin is highly flexible. This flexibility is also compatible with (and essential for) loop formation via extrusion.

In our original Hi-C study (5), we probed the physical structure of chromatin at the megabase scale by calculating the relationship between the 1D distance separating two loci, s, and the probability of physical contact between them, I(s). Because the size of our dataset was limited, our calculation was a genome-wide average. For values of s between 500 kb and 7 Mb, we found power-law behavior: specifically, I(s) ∝ s^−ɣ with ɣ = 1.08. This value of ɣ is inconsistent with an ordinary condensed polymer at equilibrium (for which ɣ = 1.5) but is consistent with a fractal globule.

In our recent Hi-C experiments at kilobase resolution (8), we observed a large number of contact domains (median length = 185 kb) that partition the genome. In the present study, we explore the structure of chromatin inside these domains by exploiting the vastly higher resolution of our new maps to calculate I(s), in a locus-specific fashion, genome-wide. The contact probability exhibits a power-law behavior at fine scale, but with a different exponent, ɣ = 0.75, than the exponent observed from our low-resolution, genome-wide average.

This value is inconsistent with an ordinary polymer at equilibrium. To determine rigorously whether such a value could be consistent with a fractal globule architecture for individual domains, we proved a novel mathematical theorem describing how the Minkowski (fractal) dimension of a set changes when the set is mapped using a fractal curve. Our result is analogous to a well-known theorem of McKean for Brownian motion. As a corollary, we find that values of ɣ inside a fractal globule must lie between 1 and 2, implying that ɣ = 0.75 is also inconsistent with a fractal globule. We illustrate our corollary by constructing a novel variant of the famous Hilbert curve: Our inside-out Hilbert curve snakes through a 2D shape with arbitrarily rough fractal boundaries, achieving ɣ close to 1. Our findings highlight the potential of genomic questions to catalyze mathematical discoveries seemingly unrelated to biology.

Another way of interpreting values of ɣ is by using physical simulations to identify polymer states with similar ɣ values. In our original Hi-C study, we showed that a polymer that was crushed by external forces naturally folds into a fractal globule with a value of ɣ = 1. In the present work, we considered the possibility that internal forces, attractions between pairs of monomers, may also play a role. We found that varying the ratio of internal and external forces results in a family of possible structures. At one extreme, when external forces dominate, the result of the condensation process is symmetrical, yielding a classic fractal globule with ɣ = 1. At the other extreme, when internal forces dominate, tension arises along the polymer chain, leading to anisotropic condensation with ɣ = 0.72. Thus, the value of ɣ observed in these tension globules closely matches the value of ɣ observed in Hi-C contact domains. The tension globule model is consistent with two other important observations: the formation of contact domains inside loops and the 3D distance between pairs of loci as measured by 3D-FISH.

However, the tension globule model does not explain many aspects of our data. These limitations emerge from the putative model of loop formation in a tension globule, in which diffusion brings loop anchors together. Such a model makes it difficult to understand why loops tend not to overlap or why CTCF motifs at pairs of loop anchors must lie in the convergent orientation.

To overcome these limitations, we explored a different model of loop formation based on a proposal by Nasmyth (25), who hypothesized that loops form during metaphase chromosome condensation through the action of an extrusion complex comprising two tethered DNA-binding subunits, each of which extrudes DNA as they slide, relative to the genome, in opposite directions. He suggested that such a process might involve cohesin proteins, which form a tripartite ring that can slide along DNA and chromatin. To date, no direct evidence has been observed in support of this model.

By means of physical simulations, we show that loop formation by extrusion results in the formation of a contact domain between the loop anchors, yields a ɣ value that closely matches the experimental data, and accurately estimates pairwise spatial distances measured using 3D-FISH. Moreover, the extrusion model can recapitulate the results of Hi-C experiments at short range (<2 Mb) in silico, including the position of peaks and contact domains, using only data about CTCF-binding sites from ChIP-Seq.

The extrusion model also explains two key features not explained by the tension globule. First, the extrusion model provides a natural explanation for why loops must lie between convergent CTCF motifs. Second, the model explains the strong tendency of loops not to overlap: Whereas simple diffusion is likely to result in substantial overlap, extruded loops cannot overlap. The extrusion model also has advantageous topological properties. Whereas simple diffusion could give rise to intrachromosomal knots and interchromosomal entanglements, extrusion would create neither intrachromosomal knots (facilitating chromatin accessibility during interphase) nor interchromosomal entanglements (facilitating chromosome condensation and segregation during metaphase) (SI Appendix, Fig. S12F).

For these reasons, we strongly favor the extrusion model.

It is interesting to consider possible structures for an extrusion complex. One such structure would comprise two cohesin rings and two CTCF proteins (Fig. 8 A and C), with the complex loaded onto DNA via loading of the cohesin rings at adjacent DNA sites and the simultaneous binding of the CTCF proteins nearby. Each CTCF/cohesin pair would then serve as a DNA-binding subunit. The subunits would engage DNA in an antisymmetrical fashion, sliding in opposing directions (one forward and one reverse) until the presence of a CTCF motif on the appropriate strand is detected. In fact, ChIP-Seq data provide evidence of antisymmetrical positioning of the CTCF and cohesin proteins with respect to chromatin loop anchors. Despite the fact that both proteins are associated with the same DNA motif, close examination of ChIP-Seq peaks at the ends of loops shows that CTCF tends to lie toward the outside of a loop, whereas RAD21 and SMC3 are positioned ∼20 bp closer to the loop interior (SI Appendix, Fig. S18). This result could indicate that the cohesin ring trails behind the CTCF protein as they slide along DNA.

Fig. 8.

We hypothesize that loops are formed during interphase by an extrusion mechanism comprising CTCF and cohesin. Here, we illustrate possible models for the extrusion complex. (A) In one model, the complex includes two DNA-binding subunits, each comprising a cohesin ring and a CTCF protein. When the complex is loaded onto DNA, a tiny loop forms. The two subunits engage the chromatin fiber in an antisymmetrical fashion, with their CTCF proteins facing the outside of the loop, scanning opposite DNA strands. The loop expands without knotting as the subunits slide in opposite directions. The interior of the loop forms a contact domain. When the CTCF proteins find a target motif on the appropriate strand, they can bind, arresting the progress of the subunit. Eventually, the extrusion complex dissociates. (B) In a second model, the sliding of cohesin alone leads to extrusion. Independently, CTCF proteins bind to their motif in an oriented fashion. When the cohesin ring encounters a CTCF protein, the extrusion process either continues or halts, depending on the orientation of CTCF. (C) Detailed view of the model in A. Other models are possible. Notably, it is unclear how many CTCF proteins and cohesin rings participate in a single extrusion complex, or whether the complex is part of a larger structure. All extrusion models predict that focal chromatin interactions mediated by CTCF must be intrachromosomal.

Other structures are possible. Extrusion complexes might contain CTCF but not cohesin, with cohesin binding only after a loop has been formed. Alternatively, extrusion complexes may include cohesin, but not CTCF. In such a model, the complex would encounter CTCF proteins bound at their target sites and would either continue or halt depending on their orientation (Fig. 8B).

We also demonstrate that it is possible to reengineer loops and domains by modifying the CTCF motifs that lie at loop anchors in accordance with the convergent rule. We show that inserting even a single base pair can eliminate multiple loops and domains, affecting genome folding at the megabase scale. Moreover, our extrusion model accurately predicts the Hi-C contact map of an engineered region, including the positions of loops and domains, using only binding sites for CTCF in WT cells as input.

In some cases, our experiments suggest that particular loops tend to occur simultaneously. Specifically, our analyses suggest that both cliques studied in detail using CRISPR appear to fold into one of two spatial states: In some cells, only the A-C loop domain is present, whereas in other cells, both the A-B and B-C loop domains are simultaneously present and the A-C loop domain is absent. These findings suggest the possibility that overlapping contact domains may reflect alternative folding states within a cell population.

Our models do not address one important feature of Hi-C data: the observation that contact domains fall into at least two compartments and six subcompartments, each comprising domains that exhibit similar chromatin modifications and long-range contact patterns. Compartmentalization, seen in humans and many other species, manifests as a plaid arrangement in Hi-C maps. Our simulations do not recapitulate this phenomenon, indicating that other mechanisms are responsible for positioning each contact domain in its nuclear neighborhood.

The ability to read out the 3D structure of a genome is improving rapidly. As shown by our genome-editing experiments, it may now be possible not only to read genome folding patterns but also to write them.