Self-assembly of smallest magnetic particles

Significance

We discovered that small magnetic nanocubes spontaneously assemble into highly ordered chains, sheets, and cuboids in solution by applying a magnetic field. We elucidate how these assemblies are formed by working out the three-dimensional equilibrium arrangement of the dipoles. This classic physics problem turned out to be amazingly complex. The discovered solution self-assembly process is of high relevance in various fields reaching from high-density data storage over magnetotactic cells to medical applications.

Abstract

The assembly of tiny magnetic particles in external magnetic fields is important for many applications ranging from data storage to medical technologies. The development of ever smaller magnetic structures is restricted by a size limit, where the particles are just barely magnetic. For such particles we report the discovery of a kind of solution assembly hitherto unobserved, to our knowledge. The fact that the assembly occurs in solution is very relevant for applications, where magnetic nanoparticles are either solution-processed or are used in liquid biological environments. Induced by an external magnetic field, nanocubes spontaneously assemble into 1D chains, 2D monolayer sheets, and large 3D cuboids with almost perfect internal ordering. The self-assembly of the nanocubes can be elucidated considering the dipole–dipole interaction of small superparamagnetic particles. Complex 3D geometrical arrangements of the nanodipoles are obtained under the assumption that the orientation of magnetization is freely adjustable within the superlattice and tends to minimize the binding energy. On that basis the magnetic moment of the cuboids can be explained.

Magnetic particles show an intriguing self-assembly behavior, due to mutual magnetic interactions or interaction with external magnetic fields. This can already be experienced by playing with toy magnets, which can assemble into strings or clusters. For much smaller magnetic particles, the knowledge about the magnetic assembly is crucial for technical applications involving magnetorheological fluids (1), high-density magnetic storage devices, hyperthermal cancer therapy, and magnetic resonance imaging (2). These applications use small magnetic particles, in the micrometer size range for magnetorheological fluids and down to 10 nm for magnetic resonance imaging or magnetothermal cancer therapy. Decreasing the size of the particles further decreases their magnetic moment to an extent that they are not considered in those applications anymore. In consequence, the assembly of sub-15-nm magnetic nanoparticles has been scarcely explored (3). Only recently, it was reported that cube-shaped magnetic nanoparticles of 13 nm showed a surprising magnetic-field-induced assembly into helices at the air–liquid interface (4) and 9-nm magnetic nanoparticles in the presence of a magnetic field uniquely assembled into very large, nearly defect-free monolayers and 3D cubic assemblies on solid substrates (5). This triggers the question about the arrangement of the magnetic dipoles in such assemblies where an amazing answer was recently found in the case of only eight dipoles (6), and where for larger magnetic nanoparticles and their assemblies considerable complexity was observed (7, 8).

Here we report very small (sub-15-nm diameter) spherical and cube-shaped iron-oxide nanoparticles with respect to their magnetic assembly behavior. The nanoparticles are sterically stabilized by oleic acid, have very narrow size distributions, and very regular shapes (SI Appendix). The controlled synthesis of such particles has only recently become possible (9). The self-assembly behavior was investigated in solution (0.2–20 wt % in toluene) to clearly identify the role of the magnetic interactions and to rule out any interfering effects by interactions with surfaces, substrates, or by evaporation of solvent (10). Our data revealed extraordinary particle geometry discrimination: cube-shaped nanoparticles formed regular assemblies, but spherically shaped nanoparticles did not. The cubic particles assembled into structures with remarkable topology discrimination: very regular 1-, 2-, or 3D assemblies were formed, each with exceptional internal order. The measured magnetization of the assemblies is surprisingly small, given the very large number of contained nanoparticles. These features can be understood by modeling the nanocubes as freely adjustable dipoles with their dipole–dipole interaction.

Fig. 1A demonstrates that 8.2-nm cubic nanoparticles self-assemble into very regular 3D large cuboids, in line with ref. 5. This scanning electron microscopy (SEM) image is obtained by solution evaporation (3 wt % in toluene) on a solid substrate at room temperature in the presence of a magnetic field (130 mT for 4 h). Fig. 1B shows the presence of large cuboids that had been formed in solution. These have the same size, structure, and order as the cuboids formed by evaporation. Fig. 1B is obtained with the same solution after exposure to an external field (130 mT) at reduced temperature (253 K) using cryoscanning electron microscopy (cryo-SEM). This temperature is still significantly above the melting temperature of the solvent toluene (178 K) and the blocking temperature of the nanoparticles (105 K, SI Appendix, Fig. S9). More examples are presented in SI Appendix, Fig. S3. In Fig. 1C and SI Appendix, Fig. S4, cryotransmission electron microscopy (cryo-TEM) (11) is used to obtain more detailed structural information on the magnetic-field-induced assemblies in dilute solution. It predominantly reveals 1D linear chains and 2D monolayer sheets. The chains are several micrometers long, and many of them are aggregated into ribbons. Sheets have typical lateral dimensions of 100–200 nm. Within individual sheets the nanoparticles are arranged on a square lattice with a striking degree of positional and bond-orientational order. The high contrast of the individual nanocubes within the sheets suggests that the images show monolayers. Adjacent sheets often have fused together at their edges, probably by a secondary sheet–sheet aggregation at a relatively late stage in the self-assembly process. With cryo-TEM it is impossible to image the large cuboids that are observed by cryo-SEM, because they deplete from the thin, sub-100-nm liquid films formed during cryo-TEM sample preparation.

Fig. 1.

Electron microscopy images of magnetic-field-induced self-assembled structures of cubic iron-oxide nanoparticles (G25 in SI Appendix, Table S2) (A) SEM image of a 3D cuboid which consists of more than 10,000 nanocubes. (B) Cryo-SEM image of a nanoparticle solution in toluene. (C) Cryo-TEM image of cubic nanoparticles in toluene showing chains, ribbons, and sheets.

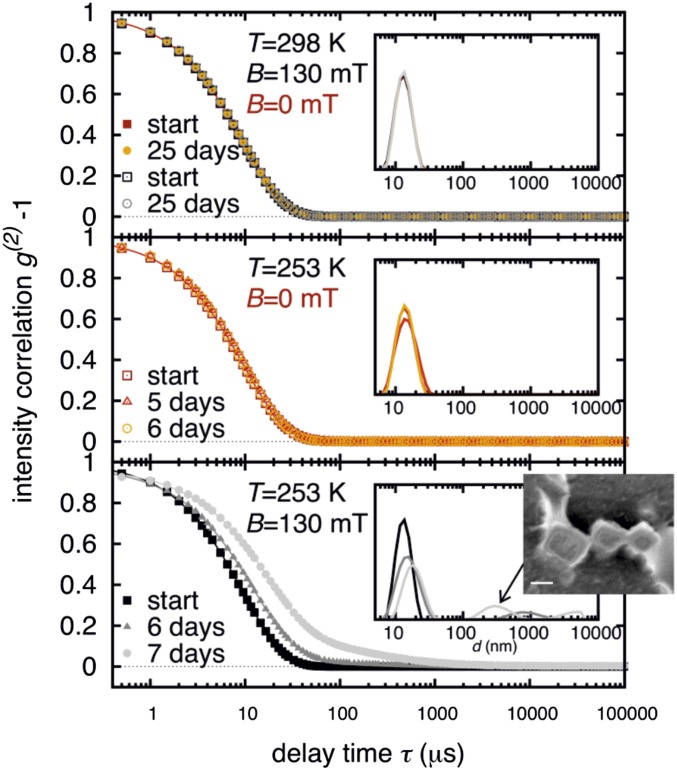
To obtain insight into the self-assembly behavior of cubic nanoparticles in solution, we measured the size distribution of the nanoparticles in dilute suspensions (0.2–3 wt %) using dynamic light scattering (DLS) (12) at different temperatures, with and without an external magnetic field. The measured intensity correlation functions and the calculated particle size distributions are shown in Fig. 2. At room temperature (298 K), both without and in the presence of an external magnetic field (130 mT), the nanoparticles are singly dispersed, even up to 25 d. For the sample shown in Fig. 2 the measured mean hydrodynamic diameter of 13 nm corresponds well to the diameter of a bare nanoparticle of about 9 nm, which is covered with an oleic acid layer of 2-nm thickness. If the particles are kept at a reduced temperature (253 K) without magnetic field (Fig. 2, Middle) we observe only tiny changes in the particle size distribution. Even after 3 wk no significant difference in the intensity correlation function was observed. However, if the samples are kept at reduced temperature (253 K) and are exposed to a magnetic field (130 mT), they start to assemble into larger aggregates. Fig. 2 (Lower) shows the ensuing slow mode in the time correlation functions and the emergence of a second peak in the particle size distribution. This corresponds to the formation of aggregates with a mean hydrodynamic diameter in the range of a few hundred nanometers.

Fig. 2.

Normalized intensity correlation functions measured by DLS from a 1-wt % solution of nanoparticles in toluene (G116 in SI Appendix, Table S2). The measurements are indicated by different symbols. (Insets) The corresponding particle distributions obtained from these data. The upper four data sets were obtained at room temperature without (red and orange) and within a magnetic field of 130 mT (black and gray). The middle three data sets were obtained at a reduced temperature of 253 K without a field. Only neglectable differences between the distributions are observed. The three consecutive measurements in the lower plot document the formation of larger aggregates, which were obtained after exposing the sample to a magnetic field of 130 mT at 253 K. The ensuing peak in the distribution at about 300 nm is presumably caused by the formation of cuboids as shown in Fig. 1 and in the overlaid image.

The DLS study demonstrates that for magnetic self-assembly of very small magnetic nanoparticles the application of an external magnetic field is necessary, and that for dilute solutions (0.2–3 wt %) temperatures need to be sufficiently low. Increasing the concentration facilitates nanoparticle assembly such that field-induced self-assembly is observed also at room temperature for concentrations of 11 wt % (SI Appendix, Fig. S10) or 18 wt % (Fig. 3) as shown by small-angle X-ray scattering (SAXS) measurements. Notably, we did not observe any magnetic-field-induced assembly for nanoparticles smaller than 7.5 nm. We attribute this fact to the existence of a size limit, under which the magnetic interaction is too small for an assembly process. Cube-shaped nanoparticles of 7–8 nm are the smallest particles that we observe to exhibit magnetic interactions.

Fig. 3.

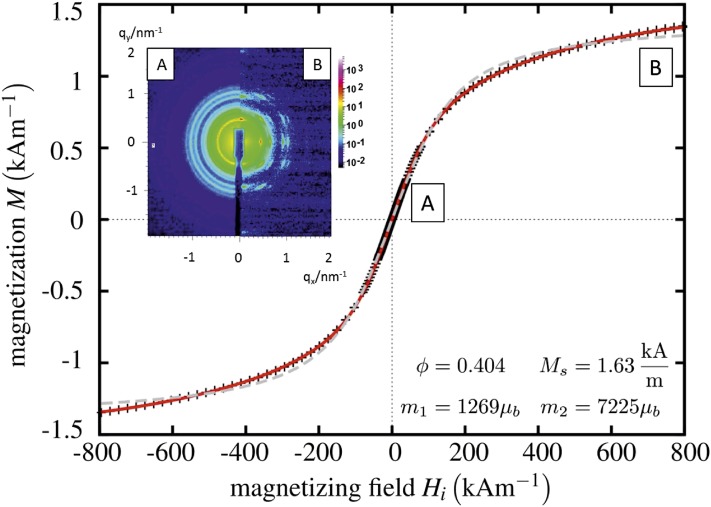
Magnetization of cubic nanoparticle solution (G25 in SI Appendix, Table S2, 18 wt % in toluene) as a function of the magnetic field strengths. The crosses represent the measured data; the gray dotted line is a fit to a Langevin function assuming monodisperse magnetic particles. The red solid line is a fit for a bidisperse solution, yielding that 40% (ϕ = 0.404) of the magnetization can be attributed to particles with magnetic moment m₁, 60% to larger ones with m₂. (Inset) Synchrotron X-ray diffraction patterns of this sample. The scattering intensity reveals isotropic orientation of cuboids at zero magnetic field (Inset, Left), and an alignment at a magnetic field at 0.98 T (Inset, Right).

The field-dependent magnetization of the solutions was measured with a commercially available vibrating sample magnetometer, as explained in detail in ref. 13, at a concentration of 18 wt %. The experimental result (symbols) and the theoretical descriptions (lines) are given in Fig. 3. A fit to a Langevin function assuming monodisperse magnetic particles (gray dashed line) fails to describe the data. By assuming a bidisperse distribution of magnetic moments the experiment can be quantitatively described (solid line). The smaller one (m₁) with about 1,300 ${\mu }_{\text{B}}$ corresponds to the nanoparticles. The self-assembled cuboids are presumably responsible for the second value (m₂), which is approximately six times larger. After Fig. 3, external magnetic fields of about 1,000 kA/m are needed to completely align the cuboids in solution. The observed saturation magnetization is ∼1.6 kA/m. This value is significantly smaller than the one expected from literature (e.g., ref. 14, figure 2.13), which is around 100 kA/m for an 18-wt % iron-oxide solution. We emphasize that according to the DLS result and the visual inspection of Fig. 1A, the cuboids are 2–3 orders of magnitude larger in volume than the nanocubes. According to the numerical evaluation of the model with freely adjustable dipoles, the magnetic moment scales approximately with the length of the cuboid, i.e., the cube root of the mass and not with the volume of the cluster (SI Appendix, Fig. S5). Hence, a solution of, say, 20 × 20 × 20 cuboids would reduce its saturation magnetization by a factor of 400 (= 8,000/20) compared with the fresh, nonaggregated solution of nanoparticles.

Fig. 3 (Inset) depicts synchrotron SAXS patterns of an 18-wt % nanoparticle solution. The left part of the pattern is obtained at zero magnetic field, whereas the right part is taken under the influence of an external magnetic field of 0.98 T perpendicular to the beam. Without field the pattern consists of Debye–Scherrer rings characteristic of an isotropic, nonoriented assembly of nanoparticles. They can be interpreted as stemming from a simple cubic lattice (space group Pn3m) formed by nanocubes within the assemblies (compare Fig. 1 and SI Appendix, Fig. S1). With increasing magnetic field the Debye–Scherrer rings develop into arcs and finally, at a magnetic field of 0.98 T, into sharp Bragg reflections. They indicate a preferred alignment of the crystalline assemblies.

Based on our observations, we propose a mechanism of the observed magnetic assembly process, and the unique magnetic properties of the ensuing cuboids. Let us assume that the individual nanoparticles carry a magnetic moment $m_0$. In consequence, their magnetic interaction potential U can then be calculated as

$$\frac{U}{U_{\text{ref}}}={\displaystyle \sum _{j>k}\frac{{\overrightarrow{e}}_j\cdot {\overrightarrow{e}}_k-3\left({\overrightarrow{e}}_j\cdot {\overrightarrow{e}}_{jk}\right)\left({\overrightarrow{e}}_k\cdot {\overrightarrow{e}}_{jk}\right)}{{\left(r_{jk}/d\right)}^3}},$$ [1]

where $U_{\text{ref}}={\mu }_0{m}_0^2/2\pi d^3$. $r_{jk}$ is the distance between two dipoles indexed by j and k, $d$ is the lattice constant of the cube superlattice, ${\overrightarrow{e}}_{jk}$ is the unit vector along the line joining the point dipoles j and k, and µ₀ is the vacuum permeability. The dipolar magnetic interaction energy for the investigated small nanoparticles is on the order of $U_{\text{ref}}\approx 0.01$ k_BT, which may be compared with other relevant interactions: (i) the van der Waals interactions with an energy of $E_{\text{vdW}}\approx 0.5$ k_BT. This magnitude indicates that the van der Waals interaction is crucial for the stabilization of the cuboids; and (ii) the interaction energy of one magnetic dipole m₀ with an external magnetic field of 0.3 T, which is $E_{\text{m}}\approx 0.9$ k_BT. This shows that an external magnetic field of less than 1 T is sufficient to align the dipoles.

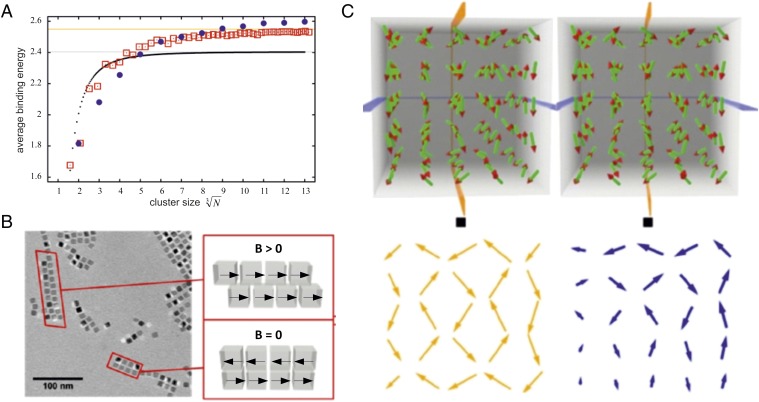
At the beginning of the magnetic assembly process in an external field the formation of 1D chains (SI Appendix, Fig. S4) is energetically favored. The calculated binding energy per nanoparticle for linear chains (1D) with head-to-tail arrangement of magnetic dipoles is shown in Fig. 4A (black dotted line) as a function of the particle number. With increasing number of particles N the binding energy per particle $U_N^{1\text{D}}/U_{\text{ref}}$ saturates and reaches an asymptotic limit, which can be calculated analytically to $U_{\infty }^{1D}=2\cdot \zeta \left(3\right)\cdot U_{\text{ref}}\approx 2.40411\cdot U_{\text{ref}}$. $\zeta \left(z\right)$ is the Riemann zeta function. The ensuing magnetized chains will have a tendency to attract each other to form ribbons and sheets, provided they are aligned antiparallel. This is the case under zero magnetic field conditions. As a result of this magnetic interaction, they will form a checkerboard arrangement as indicated in Fig. 4B in the case without a field. This arrangement is observed experimentally and indicated in the cryo-TEM picture. The sample was prepared in a magnetic field of 130 mT, which induced a second kind of arrangement, namely a brick wall texture, in parts of the sample. Hence, the magnetic chains can also attract individual nanocubes, in particular if those superparamagnetic particles have a finite averaged magnetic moment, as caused by the external magnetizing field. In that case, the magnetization within the chain and within the attached nanocube would initially be parallel to each other. The resulting spatial arrangement is illustrated in Fig. 4B in the case of magnetic field. Both 2D configurations represent local minima of the interaction energy, but the checkerboard configuration is energetically favored within our model assumption of freely adjustable magnetic dipoles, whose relative position is constrained by the geometry of the nanocubes. The fact that the cube edges are aligned parallel to each other is believed to be facilitated by the assembly of the surface-bound oleic acid into planar bilayers (15), caused by local short-range attractive interactions like van der Waals forces. Moreover, the strong short-range nature of the van der Waals force will stabilize the face-to-face self-assembled structures even after the external magnetic field is turned off.

Fig. 4.

Assembly of cubic magnetic nanoparticles with corresponding mean dipole orientations. (A) Averaged magnetic binding energy per particle as a function of the cluster size. Black dots: linear chains of particles. Red squares: planar square clusters. Blue circles: cuboids. Gray line: asymptotic limit for linear chains of dipoles with head-to-tail magnetization. Orange line: asymptotic limit for square clusters of dipoles with in-plane antiferromagnetic order. (B) Cryo-TEM image of 1D and 2D structures of cubic nanoparticles, and a sketch of the corresponding dipole orientations. (C) Stereoscopic image of the calculated arrangement of minimal energy of 5 × 5 × 5 magnetic dipoles arranged in a cubic lattice. The black squares are a guide for the eyes to help find the right observation distance to obtain the stereoscopic impression. The yellow and blue arrows indicate the orientation of the dipoles within the planes indicated in the upper part.

Under the assumption that the dipoles can be modeled as freely adjustable, the resulting dipole configuration can be obtained numerically. The red squares in Fig. 4A show the corresponding binding energy in the checkerboard arrangement. For small numbers of nanoparticles 1D chains have the highest binding energy. Beyond N ∼ 150, 2D sheets become more stable. This explains why sheets are prominent structures observed in the experiments. The binding energy saturates for large numbers of particles with an asymptotic limit, given by the checkerboard clusters of dipoles with in-plane antiferromagnetic order of $U_{\infty }^{2\text{D}}=1.06\ast 2\cdot \zeta \left(3\right)\cdot U_{\text{ref}}\approx 2.5494\cdot U_{\text{ref}}$, which is about 6% larger compared with the 1D chain. The blue points in Fig. 4A correspond to cuboids of freely adjustable dipoles. For the 3D case, the binding energy per particle outvalues the 2D case for N larger than about 1,000. This explains the existence of cuboids. We expect that at the beginning of the self-assembly process the 1D chains develop, which structurally evolve either via uptake of single nanoparticles or secondary chain–chain association into sheets. Large 3D cuboids are the result of further growth. We are unable to give an asymptotic value for the binding energy in the case of cuboids. The reason is illustrated in Fig. 4C. It presents the configuration for the 5 × 5 × 5 cuboid in a stereographic projection. Such a very specific dipole configuration for the ground state exists for each N, which was investigated up to values of 13 (2,197 particles), and there seems to be no obvious rule to guess this configuration. According to the calculated average binding energies in Fig. 4A, 2D sheets begin to have higher binding energies compared with 1D chains for a cluster size $\sqrt[3]{N}\approx 4$, and 3D cuboids start to have higher binding energies compared with 2D sheets for a cluster size $\sqrt[3]{N}\approx 8$. From this one can estimate for 8-nm cubic nanoparticles separated by a 4-nm oleic acid layer the longest 1D chains to have a length of ∼770 nm, the smallest 2D sheets of ∼100 nm, the largest 2D sheets of ∼270 nm, and the smallest 3D cuboids of ∼100 nm, which is consistent with our experimental observations (Fig. 1 and SI Appendix, Figs. S3 and S4).

Whereas dipole configurations turn out to be amazingly complicated, the overall picture concerning the magnetization of square and cuboid nanoparticle assemblies is fairly clear: the individual dipole moments tend to cancel each other. When studying cuboids of growing size, we found that the magnetic moment basically increases only proportionally to the linear dimension of a cube, i.e., with V^1/3 (SI Appendix, Fig. S5). The surprisingly low magnetization of a 3D assembly of magnetic particles has been noted previously (16).

Finally, we emphasize that we also looked for ordered structures consisting of spherical nanoparticles (SI Appendix, Table S2). In no case did we observe 1-, 2-, or 3D crystal-like ordered assemblies. This is even true in external magnetic fields of 1 T at high concentrations (18 wt %), as shown by SAXS experiments (SI Appendix, Fig. S6). This demonstrates that the nanoparticle shape is crucial for the regular self-assembly (17). In some cases irregularly shaped small clusters (n < 30) were obtained, as shown by the cryo-TEM images (SI Appendix, Fig. S7). Spherically shaped nanoparticles have a much smaller contact area compared with cube-shaped ones. Therefore, it is expected that local short-range attractive interactions are much weaker, providing no stabilization for nanoparticle assemblies. Hence larger clusters are unlikely. Our observation agrees well with a previous investigation of magnetic chain formation, which reported that in the presence of a magnetic field, spherical-shaped magnetic nanoparticles did not aggregate into 1D chains if they had diameters <10 nm, formed random clusters at ∼13 nm, and only for larger diameters assembled into chains (18).

In conclusion, we discovered an extraordinary magnetic self-assembly phenomenon of cubic nanoparticles in solution––namely, a magnetic-field-induced assembly into very regular 1-, 2-, and 3D structures such as chains, ribbons, sheets, and large cuboids. The observed assembly occurs for very small cubic nanoparticles, where the induced magnetic dipolar interaction and the interaction between the magnetic dipoles and the external field are very small, on the order of the thermal energy and van der Waals forces. The external field induces and aligns the dipole moments of the nanoparticles, leading to attractive interactions that force the particles to come into close contact such that short-range van der Waals interactions arrange the nanoparticles into regular face-to-face attachment which is stable even after the magnetic field is turned off. A model rationalizing the structural evolution from 1D and 2D into 3D structures could be developed explaining the presence of the observed assemblies as lowest magnetic energy structures. These energy states are calculated and involve unexpectedly complex configurations of the magnetic dipoles within the arrays. For small nanoparticles, the particle geometry plays a decisive role. Cubes do form ordered assemblies, but spheres do not. The discovered self-assembly phenomena are of high relevance for fundamentally science and for (bio-) medical applications involving control of superparamagnetic nanoparticles assembly in the presence of strong external magnetic fields (19). It underlines the importance of dipolar interactions in nanoparticle assemblies (7), and opens a previously unidentified pathway to controlled nanoparticle assembly in solution (20, 21).

Materials and Methods

Nanoparticle Synthesis.

Iron-oxide nanoparticles were synthesized via thermal decomposition of an iron–oleate complex according to the procedure of Park et al. (9). The iron–oleate complex was synthesized from a reaction mixture of iron(III) chloride and sodium oleate at 70 °C. The viscous and brownish iron–oleate compound (31.89 g) was dissolved in octadecene. Oleic acid (5.04 g) was added to the solution as stabilizing agent. The reaction mixture was heated under reflux at a heating rate of 2–3 K/min up to 110 °C in vacuum, and afterward in a nitrogen atmosphere with the same heating rate up to 317 °C. The reaction mixture was stirred under reflux at 317 °C for 20 min. After the solution was cooled down at room temperature (RT), 50% THF was added to the nanoparticle solution to avoid the formation of separated phases. The work-up was carried out by precipitation of the nanoparticles in acetone. The particles could be easily redispersed in toluene or THF.

DLS.

For the experiments the nanoparticles were dissolved in toluene to obtain concentrations between 0.2 and 3 wt %. If not mentioned otherwise, the samples were measured at RT and no external field was applied. For some samples 15 µL were transferred to a capillary tube (1-mm diameter), which was exposed to an external magnetic field of 130 mT at room temperature (298 K) or a reduced temperature of 253 K.

Synchrotron SAXS.

All SAXS data were measured at the beamline ID02 of the European Synchrotron Radiation Facility, Grenoble, France. The incident X-ray wavelength was 0.1 nm. SAXS intensities were recorded using a fiber-optically coupled FReLoN detector. The CCD raw data were corrected for dark current, detector response, and spatial distortion and then normalized to absolute scattering intensities as described in ref. 22. The intensities were azimuthally averaged and corrected for the scattering contribution of the solvent. The sample environment involved a variable magnetic field setup consisting of permanent magnets in a Halbach array. The magnetic field was varied from 0.0 to 1.0 T. The variation of the field was obtained by positioning the permanent magnets at different distances from the sample position. The direction of the magnetic field can be either perpendicular (standard) or parallel to the beam direction. Regularly, the exposure time was between 0.02 and 0.5 s. Further evaluation of the data was obtained using the software SCATTER (23).

Cryo-TEM.

For cryo-TEM studies, a drop of the sample was put on a lacey carbon filmed copper grid (Science Services). A sample droplet of 2 µL was put on the film and subsequently most of the liquid was removed with blotting paper, leaving a thin film stretched over the grid holes. The specimens were instantly shock-frozen by rapid immersion into liquid nitrogen in a temperature-controlled freezing unit (Zeiss Cryobox, Zeiss Microscopy GmbH). The temperature was monitored and kept constant in the chamber during all of the sample preparation steps (<90 K). After freezing, the specimen was inserted into a cryotransfer holder (CT3500, Gatan) and transferred to a Zeiss/LEO EM922Omega EFTEM (Zeiss Microscopy GmbH). Examinations were carried out at temperatures around 90 K. The TEM was operated at an acceleration voltage of 200 kV. Zero-loss filtered micrographs (ΔE = 0 eV) were taken under reduced dose conditions (100–1,000 e/nm²). All images were registered digitally by a bottom-mounted slow-scan CCD camera system (Ultrascan 1000, Gatan) combined and processed with a digital imaging processing system (Digital Micrograph GMS 1.9, Gatan).

Cryo-SEM.

Cryo-SEM was performed at a Zeiss Ultraplus field emission scanning electron microscope (FESEM) equipped with a Leica cryo unit. Solutions of nanoparticles in toluene were vitrified by plunge-freezing in liquid nitrogen. The frozen samples were freeze-fractured in a Leica MED 020, etched for 60 s at 10⁻⁶ mbar at −105 °C and subsequently sputtered. The samples were imaged with an in-lens detector at a voltage of 1 kV.

SEM.

SEM was performed at an LEO 1530 SEM equipped with energy-dispersive X-ray spectroscopy (EDX) and electron backscatter diffraction (EBSD). After drying the nanoparticle sample on the Si wafer, which was cleaned using an ultrasonic bath: 2 min in acetone, 1 min in isopropanol, 5 min in acetone/isopropanol mixed 1:1 to enhance the contrast in the SEM. Pictures were taken at 10 kV using the InLens detector. The substrate surface was not tilted in the picture shown, but for other superlattices 30° tilting was necessary to show the 3D character.

Magnetic Dipole Configurations.

The equilibrium dipole orientation distributions for 1-, 2-, and 3D assemblies were obtained by minimizing the expression for the dipolar interaction energy given in Eq. 1 using a numerical algorithm described in ref. 24.

$$\frac{U_{1\text{D}}^{\infty }}{U_{\text{ref}}}={\displaystyle \sum _{N=1}^{\infty }\frac{1}{N^3}}=2\zeta (z=3)\approx 2.40411,$$

where $\zeta \left(z\right)$ is the Riemann zeta function.