Significance
Scientists perform a tiny subset of all possible experiments. What characterizes the experiments they choose? And what are the consequences of those choices for the pace of scientific discovery? We model scientific knowledge as a network and science as a sequence of experiments designed to gradually uncover it. By analyzing millions of biomedical articles published over 30 y, we find that biomedical scientists pursue conservative research strategies exploring the local neighborhood of central, important molecules. Although such strategies probably serve scientific careers, we show that they slow scientific advance, especially in mature fields, where more risk and less redundant experimentation would accelerate discovery of the network. We also consider institutional arrangements that could help science pursue these more efficient strategies.
Keywords: complex networks, computational biology, science of science, innovation, sociology of science
Abstract
A scientist’s choice of research problem affects his or her personal career trajectory. Scientists’ combined choices affect the direction and efficiency of scientific discovery as a whole. In this paper, we infer preferences that shape problem selection from patterns of published findings and then quantify their efficiency. We represent research problems as links between scientific entities in a knowledge network. We then build a generative model of discovery informed by qualitative research on scientific problem selection. We map salient features from this literature to key network properties: an entity’s importance corresponds to its degree centrality, and a problem’s difficulty corresponds to the network distance it spans. Drawing on millions of papers and patents published over 30 years, we use this model to infer the typical research strategy used to explore chemical relationships in biomedicine. This strategy generates conservative research choices focused on building up knowledge around important molecules. These choices become more conservative over time. The observed strategy is efficient for initial exploration of the network and supports scientific careers that require steady output, but is inefficient for science as a whole. Through supercomputer experiments on a sample of the network, we study thousands of alternatives and identify strategies much more efficient at exploring mature knowledge networks. We find that increased risk-taking and the publication of experimental failures would substantially improve the speed of discovery. We consider institutional shifts in grant making, evaluation, and publication that would help realize these efficiencies.
A scientist’s choice of research problem directly affects his or her career. Indirectly, it affects the scientific community. A prescient choice can result in a high-impact study. This boosts the scientist’s reputation, but it can also create research opportunities across the field. Scientific choices are hard to quantify because of the complexity and dimensionality of the underlying problem space. In formal or computational models, problem spaces are typically encoded as simple choices between a few options (1, 2) or as highly abstract “landscapes” borrowed from evolutionary biology (3–5). The resulting insight about the relationship between research choice and collective efficiency is suggestive, but necessarily qualitative and abstract.
We obtain concrete, quantitative insight by representing the growth of knowledge as an evolving network extracted from the literature (2, 6). Nodes in the network are scientific concepts and edges are the relations between them asserted in publications. For example, molecules—a core concept in chemistry, biology, and medicine—may be linked by physical interaction (7) or shared clinical relevance (8). Variations of this network metaphor for knowledge have appeared in philosophy (9), social studies of science (10–12), artificial intelligence (13), complex systems research (14), and the natural sciences (7, 15, 16). Nevertheless, networks have rarely been used to measure scientific content (2, 11, 17, 18) and never to evaluate the efficiency of scientific problem selection.
In this paper, we build a model of scientific investigation that allows us to measure collective research behavior in a large corpus of scientific texts and then compare this inferred behavior with more and less efficient alternatives. We define an explicit objective function to quantify the efficiency of a research strategy adopted by the scientific community: the total number of experiments performed to discover a given portion of an unknown knowledge graph. Comparing the modal pattern of “real-science” investigations with hypothetical alternatives, we identify strategies that appear much more efficient for scientific discovery. We also demonstrate that the publication of experimental failures would increase the speed of discovery. In this analysis, we do not focus on which strategies tend to receive high citations or scientific prizes, although we illustrate the relationship between these accolades and research strategies (2).
Our model represents science as a growing network of scientific claims that traces the accumulation of observations and experiments (see Figs. S1–S3). Earlier scientific choices influence subsequent exploration of the network (19). The addition of one redundant link is inconsequential for the topology of science. By contrast, a well-placed new link could radically rewire this network (20). Our model incorporates two key features of problem selection, importance and difficulty, which have received repeated attention in qualitative and quantitative investigations of science. We map these features onto two network properties, degree and distance, which are central to foundational models of network formation and search (21–23). First, scientists typically select “important,” central, or well-studied topics on which to anchor their findings and signal their relevance to others’ work (10, 24). Our model uses the degree of a concept in the network of claims (i.e., the number of distinct links in which it participates) as a measure of its importance (see Figs. S4–S6). In assuming that scientists’ research choices are influenced by concept degree, we posit that scientists are influenced by the choices of others, a well-attested choice heuristic (25, 26). Second, scientists introduce novelty into their work by studying understudied topics and by combining ideas and technologies that others are unlikely to connect (17, 20). Henri Poincaré (27) and many since (28) have observed that the most generative combinations are “drawn from domains that are far apart” (ref. 27, p. 24). When the concepts under study are more distant, more effort is required to imagine and coordinate their combinations (29). More risk is involved in testing distant claims, because no similar claims have been successful (30).* We operationalize the “cognitive distance” between concepts using their topological distance in the knowledge network. If two concepts are not mutually reachable through the network (i.e., in two distinct components of the network), there is no way a scientist could hypothesize a connection simply by wandering through the literature; conceptual jumps must be made. If two molecules are distant in the network but can reach one another (i.e., they are in the same component), scientists would need to read a range of research articles—likely spread across several journals and subfields—to infer a possible connection (32). Drawing together these insights, we model unlikely combinations as connections between neglected (i.e., low degree), distant, or disconnected concepts within the network of scientific claims.
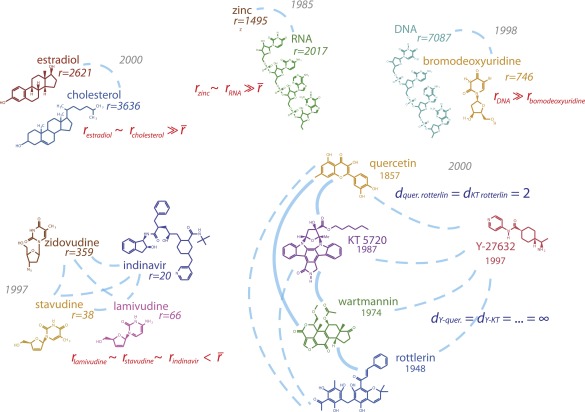
Fig. S1.
Chemical examples from the published network. Central estradiol and cholesterol molecules were linked when hormone therapies were found to have no effect on reducing heart disease (PMID 10954759 and 12904517). RNA and zinc (PMID 4040853) were recombined in the discovery of “zinc fingers” of amino acids, which are essential for gene regulation and ribosome synthesis. Bromodeoxyuridine, which replaced thymidine in DNA and so “labeled” replicated DNA, allowed scientists to discover cell division in the adult hippocampus (PMID 9809557). HIV therapeutics zidovudine, indinavir, stavidine, and lamivudine were combined in clinical trials of promising antiretroviral mixtures (PMID 9287227). Commercially available protein kinase inhibitors, including KT 5720, rottlerin, quercetin, wortmannin, and the more recently discovered Y 27632, were tested against an array of protein kinases (PMID 10998351).
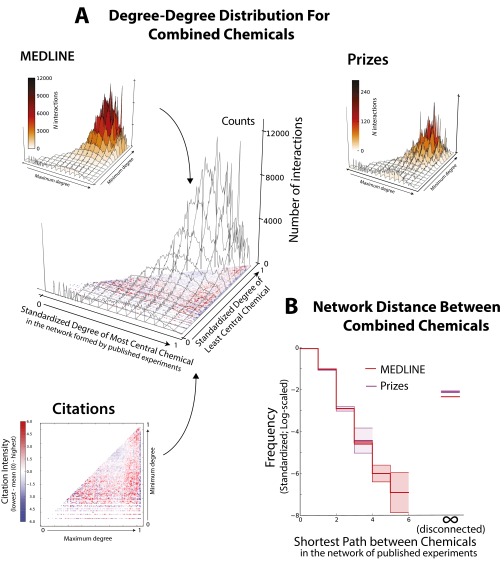
Fig. S3.
(A, Top and Middle) The distribution of node degrees for each pair of chemicals in MEDLINE abstracts and in abstracts authored by prize-winning scientists (SI Text). The (log-)degree of the most and least central chemicals of each pair is normalized to and the height of the figure represents the frequency with which each pair of chemical degrees appears in the literature. All degrees are evaluated on the full (2010) network. (A, Bottom)The “Citations” subplot shows citation counts greater and smaller than average in red and blue, respectively; the red scale has been set to the same maximum value as the blue to improve contrast. (A, Middle) The combined figure reveals how less common degree–degree combinations are more intensely cited than common degree–degree combinations. (B) Distribution of network distances between each pair of chemicals in MEDLINE abstracts and in abstracts written by prize winners. All distances were evaluated at time of linking; frequencies have been transformed to -scale. distance indicates two chemicals that are mutually unreachable—disconnected—in the current network. The red and purple bands tracing the distributions are the 95% confidence intervals, constructed by considering the actual distribution of shortest paths as a sample from an underlying multinomial distribution (SI Text). Prize winners combine disconnected molecules significantly more frequently than others.
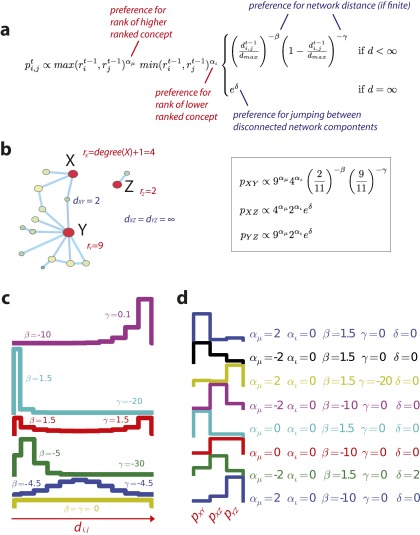
Fig. S4.
(A) Annotated version of the generative model. (B) A simple network example, which calculates the probability associated with possible node connections. (C) The probability of choosing nodes separated by distance , given different values of β and γ. (D) The probability that a scientist would investigate the relationship between X and Y, X and Z, and Y and Z in Fig. S4B, given different values of , , β, γ, and δ.
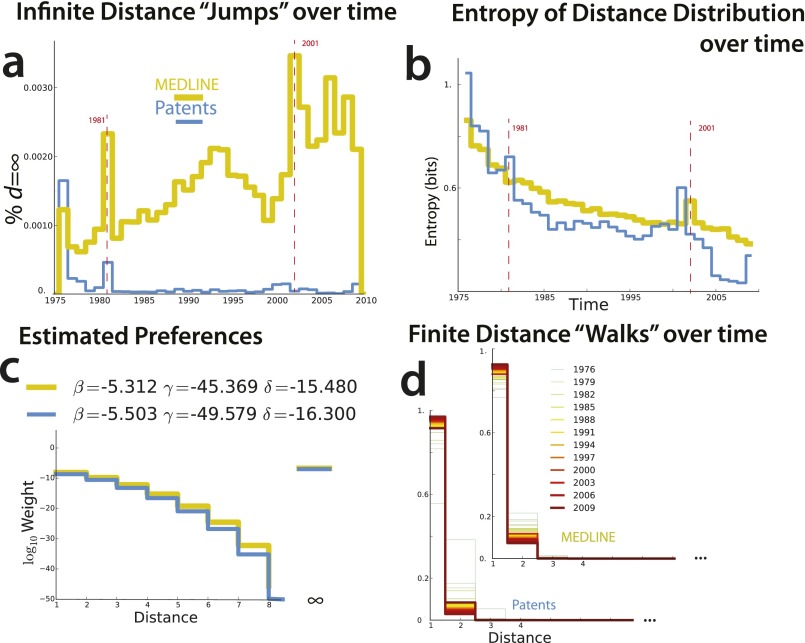
Fig. S6.
(A) Infinite distances (δ parameter, estimated separately) over time. (B) Entropy of distance distributions (bits) as a function of time. As both distance distributions become more concentrated near distance 1, entropy decreases with time. Note that there are bursts of entropy that correlate across patents and biomedical publications and correspond with the bursts of jumps pictured in A. (C) Estimated preferences for finite distances (defined by β and γ parameters) in model estimated from data. (D) Distribution of measured distances as a function of time. MEDLINE and Patents become more conservative over time, restricting distance between chemicals selected. Researchers patent pairs with shorter distances than articles (Table 1).
The Model
In our model, scientists select a pair of entities from all possible pairs and test that pair for an empirical relationship.† Problem selection is guided by a “scientific strategy,” which defines the probability of selecting a pair of entities as a function of the importance (degree) of each entity and the difficulty associated with combining them (network distance). Formalizing the studies of scientific behavior above, a strategy is determined by five parameters, which jointly define the probability of examining a relationship between entities i and j at time t:
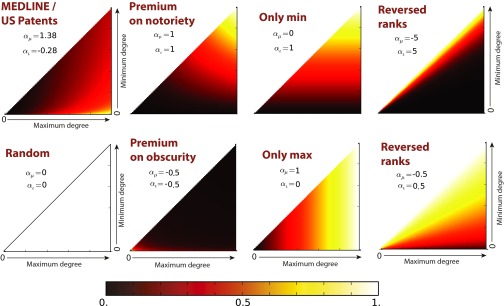
Two parameters define science’s preference for the degree centrality of each concept or entity at time t: controls the weight given to the degree of the more central node——whereas controls the weight given to the degree of the less central node.‡ Two parameters (β and γ) define the preference for short and long distance between the pair, if the entities are in the same connected component. The fifth parameter (δ) governs the preference for linking entities in distinct components of a graph (6). When all parameters are zero, the strategy is random: Each pair has a uniform and independent probability of being selected for study. Note that, depending on the parameter values, this model can describe a wide range of strategies; in fact, reducing the number of parameters would involve a priori exclusion of certain functional relationships and hence eliminate some reasonable strategies from empirical consideration. A scientist may prefer a focus on important and/or obscure concepts; short, medium, or long walks between concepts; jumps between concepts in different components; etc. (see Figs. S4 and S5 for illustrations of the model’s descriptive plasticity). This flexible framework allows us to dissect an empirical network tracing the history of published research choices. We can also test which network features are most important for scientific search.
Fig. S5.
Degree–degree preference plots: empirical and alternative preferences. The x and y axes of each subplot correspond to the maximum and the minimum degree in a degree pair. The preferences (defined only by parameters and ; Fig. S4 and Eq. S5) are normalized so that the maximum preference on the plot is equal to 1 (white) and the minimum (if distinct from the maximum) is 0 (black). The first panel corresponds to the degree–degree preferences induced from data. Other panels compare this with alternative “strategies” or preferences.
We use this model to analyze the growing network of published knowledge about chemical entities in biomedicine (hereafter “biomedical chemistry”) from 1976 until 2010. In this knowledge network, the core conceptual entity is a molecule. “Relationships” between molecules can take many forms (2). Molecules may react chemically, physically, or indirectly (the reaction byproduct of one may interact with another). Molecules may be put in relation because they are found in the same part of the body or involved in the same biological process. Or they may be chemically, structurally, or functionally similar. Knowledge about chemical relationships is central to biomedical disciplines at many scales, from organic chemistry, biochemistry, and molecular biology to microbiology, oncology, and pharmacology (Fig. S1). Of course, biomedicine studies entities besides chemicals. Specific diseases are often central to a given publication (oncology is a dramatic example), whereas papers can be further characterized by the methods used (19). Nevertheless, chemical entities can provide a reliable trace (see Fig. S2): A disease is often characterized by its molecular manifestations, and many methods are fundamentally molecular, from radiotracers to green fluorescent protein. To capture these chemical traces of biomedical knowledge, we leverage expert annotations of the MEDLINE database and match the relevant chemical terms into MEDLINE abstracts and the US Patent Database (34) (Materials and Methods and SI Text). We assume a relationship between chemicals that appear in the same article or patent abstract and infer the underlying research strategies by fitting our model to the resulting network of science.
Fig. S2.
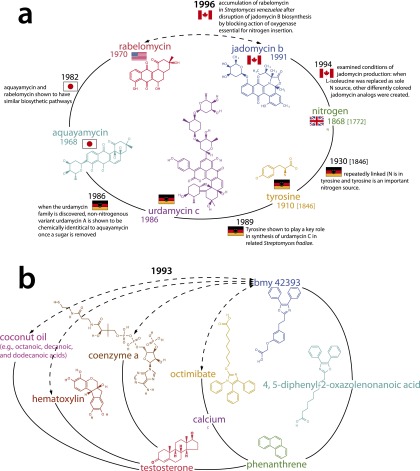
Detailed chemical examples that illustrate different dimensions of chemical distance by tracing molecules and relationships along the shortest path between discoveries. (A) The Canadian discovery (in an article with PubMed ID or PMID 8581159) of a biosynthetic connection between antibiotics jadomycin B and rabelomycin, which illustrates how chemical distances in the network can map onto underlying geographic, linguistic, or cultural distances that keep molecules studied in “distant” laboratories from being combined. (B) A Bristol-Myers Squibb investigation (PMID 8443148) that tested the ability of BMY 42393 and Octimibate to reduce cholesterol and triglyceride levels in hamsters fed with chow, cholesterol, and coconut oil. This illustrates the diversity of chemical linkages—methodological, interactional, similarity, etc.—traced by our chemical network.
Results
Before estimating our model, we explored the empirical pattern of degree and distance characterizing the chemicals combined in published articles and patents. Fig. S3 illustrates the conservative nature of most published investigations in biomedical chemistry. The vast majority of chemical relationships combine two chemicals that are moderately central by 2010; in other words, most scientists work in the “core” of various regions of biochemical knowledge (Fig. S3A). When chemicals are combined for the first time, they tend to be very close to one another in the network inscribed by prior published work (Figs. S3B and S6D and Table S1), reflecting a triadic closure mechanism (19). Most links, however, join chemicals that have already been linked before, i.e., chemicals at distance one (2). This conservatism contrasts with the strategies rewarded by high citations and prizes. Consistent with earlier work (2), we find that prize winners and highly cited scientists exhibit a more diverse range of strategies in their published research (see Table S2). Combinations of more and less central chemicals are associated with higher citations and scientific awards (Fig. S3A). Further, awards are linked with strategies more likely to bridge disconnected network components (Fig. S3B). We then use our generative model to infer the typical search strategy in biomedical chemistry. Encoding this strategy as a set of parameter values in our model allows us to evaluate its efficiency and identify more efficient alternatives by searching through the parameter space.
Table S1.
Optimal strategies for distinct levels of discovery on a representative sample of the MEDLINE graph
| % network discovered | Optimum parameter value* | Relative loss, RL† | |||||||
| β | γ | δ | |||||||
| 10 | 1.928 (1.3, 2.4) | 1.936 (0.4, 2.8) | −9.749 (−11.1, −1.2) | −168.912 (−217, 62.2) | −40.665 (−43.4, −2.5) | 47.1 ± 5.6 | 36.9 ± 11.3 | 48.3 ± 0.38 | 206.2 ± 12.6 |
| 20 | 1.712 (1.2, 2.0) | 1.185 (0.3, 2.1) | −13.310 (−13.3, −2.2) | −368.721 (−423, 51.4) | −59.600 (−59.6, −5.7) | 31.8 ± 3.2 | 21.8 ± 7.6 | 54.0 ± 0.48 | 218.4 ± 9.5 |
| 30 | 1.535 (1.2, 1.9) | 1.0764 (0.4, 1.8) | −4.774 (−5.2, −1.0) | −65.644 (−111, 56.6) | −19.438 (−21.2, −2.7) | 30.2 ± 2.6 | 16.4 ± 5.82 | 69.6 ± 0.56 | 232.7 ± 8.3 |
| 40 | 1.534 (1.2, 1.7) | 0.960 (0.4, 1.3) | −4.379 (−4.5, −0.4) | −66.852 (−96.8, 70.0) | −18.196 (−18.4, −0.7) | 30.4 ± 2.5 | 14.4 ± 4.6 | 83.5 ± 0.57 | 250 ± 7.7 |
| 50 | 1.396 (1.2, 1.6) | 0.805 (0.5, 1.3) | −3.313 (−2.9, −0.1) | −61.9 (−52.3, 67.4) | −14.196 (−9.6, 0.7) | 33.6 ± 2.4 | 13.4 ± 3.82 | 95.7 ± 0.56 | 271.4 ± 7.6 |
| 60 | 1.341 (1.1, 1.5) | 0.908 (0.5,1.2) | −4.256 (−4.3, −0.8) | −80.537 (−124, 27.4) | −17.426 (−17.9, −1.98) | 37.9 ± 2.8 | 13.4 ± 3.1 | 105.4 ± 0.55 | 298.9 ± 7.7 |
| 70 | 1.405 (1.2, 1.7) | 0.894 (0.5, 1.4) | −0.703 (−1.0, 0.5) | −62.080 (−72.6, 8.2) | −4.876 (−5.5, 1.0) | 45.2 ± 1.4 | 14.4 ± 2.5 | 125.3 ± 0.55 | 336.7 ± 8.3 |
| 80 | 1.407 (1.1, 1.6) | 0.834 (0.5, 1.4) | 0.041 (−0.1, 2.7) | −29.100 (−29.2, 78.7) | −1.410 (−1.0, 11.1) | 45.4 ± 1.4 | 15.2 ± 1.9 | 165.9 ± 0.53 | 393.7 ± 9.5 |
| 90 | 1.412 (1.2, 1.7) | 0.800 (0.3, 1.3) | −1.111 (−1.9, 0.3) | −86.890 (−128, 4.1) | −7.350 (−12.2, 0.5) | 45.3 ± 1.4 | 16.2 ± 1.3 | 254.2 ± 0.55 | 500.8 ± 12.6 |
| 100 | 1.412 (1.1, 1.7) | 0.874 (0.4, 1.4) | 0.896 (0.5, 1.9) | 10.833 (−17.3, 61.7) | 2.930 (1.6, 6.8) | 45.5 ± 1.3 | 22.3 ± 0.1 | 3253.3 ± 2.15 | 1657.3 ± 251.1 |
Parameter sets with smallest average relative loss found through simulated annealing and subsequent MCMC (parentheses contain min and max of the range containing 95% of the sample). Parameter values in lighter fonts indicate that the 95% parameter range crosses zero.
Relative loss ± sample SD.
Table S2.
Prizes
| Prize name | Field | Winners | Abstracts |
| Acharius Medal | Biomedicine | 34 | 112 |
| Albany Medical Center Prize | Biomedicine | 22 | 5,385 |
| Albert B. Sabin Gold Medal | Biomedicine | 20 | 3,546 |
| Albert Lasker Award for Basic Medical Research | Biomedicine | 290 | 13,576 |
| Albert Lasker Special Achievement Award | Biomedicine | 11 | 1,196 |
| Alexander Hollaender Award in Biophysics | Biomedicine | 5 | 602 |
| AMA Scientific Achievement Award | Biomedicine | 42 | 5,748 |
| Artois-Baillet Latour Foundation | Biomedicine | 26 | 5,128 |
| Bicentenary Medal of the Linnean Society | Biomedicine | 34 | 309 |
| C. W. Woodworth Award | Biomedicine | 40 | 444 |
| Carlos J. Finlay Prize for Microbiology | Biomedicine | 23 | 1,880 |
| Charles S. Mott Prize | Biomedicine | 36 | 5,981 |
| Colworth Medal | Biomedicine | 49 | 1,328 |
| Curt Stern Award | Biomedicine | 12 | 1,376 |
| Daniel Giraud Elliot Medal | Biomedicine | 54 | 343 |
| Darwin Medal | Biomedicine | 65 | 833 |
| Darwin–Wallace Medal | Biomedicine | 2 | 14 |
| Darwin–Wallace Medal (Gold) | Biomedicine | 1 | 3 |
| Darwin–Wallace Medal (Silver) | Biomedicine | 39 | 760 |
| Dickson Prize in Medicine | Biomedicine | 43 | 6,101 |
| Donald Reid Medal | Biomedicine | 9 | 871 |
| Dr. Paul Janssen Award for Biomedical Research | Biomedicine | 5 | 940 |
| E. B. Wilson Medal | Biomedicine | 94 | 5,573 |
| E. Mead Johnson Award | Biomedicine | 154 | 7,074 |
| E.E. Just Lecture | Biomedicine | 18 | 878 |
| Early Career Life Scientist Award | Biomedicine | 13 | 358 |
| ECI Prize | Biomedicine | 26 | 269 |
| Edwin Grant Conklin Medal | Biomedicine | 34 | 1,462 |
| Eminent Ecologist Award | Biomedicine | 61 | 322 |
| Ernst Jung Gold Medal for Medicine | Biomedicine | 22 | 5,497 |
| Ernst Jung Prize in Medicine | Biomedicine | 71 | 9,557 |
| FASEB Excellence in Science Award | Biomedicine | 25 | 3,121 |
| Gairdner Foundation International Award | Biomedicine | 624 | 31,761 |
| Gairdner Foundation International Award (Award of Merit) | Biomedicine | 4 | 387 |
| Gairdner Foundation Wightman Award | Biomedicine | 15 | 1,718 |
| Gilbert Morgan Smith Medal | Biomedicine | 11 | 349 |
| Golden Eurydice Award | Biomedicine | 5 | 728 |
| Gottschalk Medal | Biomedicine | 3 | 192 |
| Grand Prix Charles-Léopold Mayer | Biomedicine | 65 | 5,720 |
| Gruber Prize in Genetics | Biomedicine | 11 | 1,693 |
| Gruber Prize in Neuroscience | Biomedicine | 24 | 1,013 |
| Halbert L. Dunn Award | Biomedicine | 25 | 115 |
| Ho-Am Prize in Medicine | Biomedicine | 18 | 1,277 |
| International Prize for Biology | Biomedicine | 27 | 1,444 |
| Jessie Stevenson Kovalenko Medal | Biomedicine | 21 | 3,073 |
| John Howland Award | Biomedicine | 60 | 5,601 |
| John Maynard Smith Prize | Biomedicine | 8 | 53 |
| Keio Medical Science Prize | Biomedicine | 29 | 5,301 |
| Keith R. Porter Lecture | Biomedicine | 31 | 3,611 |
| Kempe Award for Distinguished Ecologists | Biomedicine | 8 | 71 |
| Kettering Prize | Biomedicine | 70 | 5,204 |
| Kistler Prize | Biomedicine | 12 | 1,262 |
| Komen Brinker Award for Scientific Distinction | Biomedicine | 84 | 7,930 |
| Larry Sandler Memorial Award | Biomedicine | 23 | 133 |
| Lasker–DeBakey Clinical Medical Research Award | Biomedicine | 264 | 10,025 |
| Leeuwenhoek Medal | Biomedicine | 13 | 465 |
| Leopold Griffuel Prize | Biomedicine | 78 | 6,242 |
| Linnean Medal | Biomedicine | 175 | 1,163 |
| Lister Medal | Biomedicine | 26 | 2,653 |
| Louis-Jeantet Prize for Medicine | Biomedicine | 73 | 9,007 |
| Louisa Gross Horwitz Prize | Biomedicine | 88 | 8,981 |
| March of Dimes Prize in Developmental Biology | Biomedicine | 54 | 4,028 |
| Marjory Stephenson Prize | Biomedicine | 11 | 1,650 |
| Marsh Ecology Award | Biomedicine | 13 | 239 |
| Max Delbruck Prize | Biomedicine | 22 | 1,237 |
| MBoC Paper of the Year | Biomedicine | 18 | 140 |
| Merton Bernfield Memorial Award | Biomedicine | 12 | 92 |
| Meyenburg Prize | Biomedicine | 60 | 3,269 |
| NAS Award in Molecular Biology | Biomedicine | 59 | 2,735 |
| NAS Award in the Neurosciences | Biomedicine | 9 | 1,541 |
| Nobel Prize in Physiology or Medicine | Biomedicine | 199 | 13,845 |
| Paul Ehrlich and Ludwig Darmstaedter Prize | Biomedicine | 115 | 11,484 |
| Pearl Meister Greengard Prize | Biomedicine | 13 | 1,826 |
| Per Brinck Oikos Award | Biomedicine | 5 | 89 |
| Pollin Prize for Pediatric Research | Biomedicine | 14 | 2,540 |
| Potamkin Prize for Research in Pick’s, Alzheimer’s, and Related Diseases | Biomedicine | 108 | 5,089 |
| Ramon Margalef Prize in Ecology | Biomedicine | 6 | 135 |
| Rema Lapouse Award | Biomedicine | 23 | 1,689 |
| Remington Medal | Biomedicine | 83 | 980 |
| Richard Lounsbery Award | Biomedicine | 84 | 4,482 |
| Robert H. MacArthur Award | Biomedicine | 15 | 203 |
| Robert Koch Medal and Award (Prize) | Biomedicine | 72 | 9,280 |
| Robert Koch Prize (Gold Medal) | Biomedicine | 49 | 6,440 |
| Robert L. Noble Prize | Biomedicine | 36 | 2,356 |
| Romer-Simpson Medal | Biomedicine | 24 | 103 |
| Royal Society Pfizer Award | Biomedicine | 6 | 122 |
| Searle Scholars Program | Biomedicine | 497 | 6,032 |
| Sedgwick Memorial Medal | Biomedicine | 81 | 2,670 |
| Selman A. Waksman Award in Microbiology | Biomedicine | 22 | 2,800 |
| Sewall Wright Award | Biomedicine | 20 | 732 |
| Shaw Prize | Biomedicine | 16 | 2,447 |
| The Llura Liggett Gund Award | Biomedicine | 5 | 592 |
| Thomas Hunt Morgan Medal | Biomedicine | 33 | 2,232 |
| UNESCO/Institut Pasteur Medal | Biomedicine | 6 | 281 |
| WICB Junior Awards | Biomedicine | 28 | 444 |
| WICB Senior Awards | Biomedicine | 26 | 2,501 |
| Wiley Prize | Biomedicine | 20 | 1,756 |
| William Allan Award | Biomedicine | 96 | 7,232 |
| William B. Coley Award for Distinguished Research | Biomedicine | 160 | 10,743 |
| William C. Rose Award | Biomedicine | 35 | 5,104 |
| Wolf Prize in Medicine | Biomedicine | 47 | 6,373 |
| Agnes Fay Morgan Research Award | Chemistry | 30 | 449 |
| American Institute of Chemists Gold Medal | Chemistry | 81 | 1,496 |
| Anselme Payen Award | Chemistry | 50 | 438 |
| Arthur C. Cope Award | Chemistry | 35 | 1,545 |
| Bunsen–Kirchoff Award for Analytical Spectroscopy | Chemistry | 19 | 84 |
| Corday–Morgan Medal | Chemistry | 153 | 1,454 |
| E. Bright Wilson Award | Chemistry | 32 | 497 |
| Earl K. Plyler Prize for Molecular Spectroscopy | Chemistry | 74 | 469 |
| Edward Harrison Memorial Prize | Chemistry | 64 | 281 |
| European Medal for Bio-Inorganic Chemistry | Chemistry | 18 | 493 |
| Faraday Lectureship | Chemistry | 34 | 204 |
| Fritz Pregl Prize | Chemistry | 112 | 308 |
| Garvan–Olin Medal | Chemistry | 69 | 1,637 |
| Glenn T. Seaborg Award for Nuclear Chemistry | Chemistry | 26 | 1,665 |
| Gregori Aminoff Prize | Chemistry | 42 | 1,571 |
| Harrison–Meldola Memorial | Chemistry | 7 | 118 |
| Heinrich Wieland Prize | Chemistry | 62 | 3,880 |
| Iota Sigma Pi National Member | Chemistry | 25 | 583 |
| Irving Langmuir Prize in Chemical Physics | Chemistry | 48 | 726 |
| Lavoisier Medal | Chemistry | 8 | 291 |
| Linus Pauling Award | Chemistry | 45 | 2,618 |
| Luigi Galvani Prize | Chemistry | 13 | 114 |
| Meldola Medal and Prize | Chemistry | 107 | 256 |
| NAS Award for Chemistry in Service to Society | Chemistry | 11 | 455 |
| NAS Award in Chemical Sciences | Chemistry | 32 | 1,893 |
| Nobel Prize in Chemistry | Chemistry | 161 | 3,939 |
| Perkin Medal | Chemistry | 105 | 827 |
| Peter Debye Award in Physical Chemistry | Chemistry | 47 | 739 |
| Priestley Medal | Chemistry | 76 | 2,126 |
| Roebling Medal | Chemistry | 72 | 419 |
| Ryoji Noyori Prize | Chemistry | 10 | 275 |
| Stokes Medal | Chemistry | 6 | 250 |
| Wayne B. Nottingham | Chemistry | 53 | 240 |
| Willard Gibbs | Chemistry | 99 | 1,993 |
| Williams–Wright Award | Chemistry | 42 | 225 |
| Wolf Prize in Chemistry | Chemistry | 44 | 1,667 |
When we estimate model parameters from the data (Table 1 and Materials and Methods), we find that typical (modal) strategies are more likely to combine a relatively “famous” chemical (one with a high degree) with a more obscure one, given the opportunity; and . This is consistent with the emergent empirical degree–degree distribution in Fig. S3A. When molecules are in the same component, biomedical scientists typically prefer to combine those close in the network (, , ). Only rarely do they study chemicals in different connected components (Figs. S3B and S6).§ In sum, the typical strategy is oriented toward exploitation, extracting further value from well-explored regions of the knowledge network (30). Strategies estimated from MEDLINE articles and US patents are very similar, with patents reflecting a slightly more conservative strategy (Fig. S6). When we estimate model parameters for 5-y windows (Fig. 1), we find that scientists have come to focus on more central chemicals (higher and ). They have become more conservative. They put increased weight on opportunities that explore slightly larger distances, e.g., preferring experiments that result in triadic closure, but these preferences interact with the space of opportunities (including the joint degree distribution) to produce a decreasing fraction of links at distances greater than 1 (Fig. S6D). The relative preference for bridging disconnected network components has increased over time, leading to a slight increase in the fraction of links that bridge disconnected components (Fig. S6A). In other words, biomedical chemistry has largely become more conservative and more reliant on the exploitation of established knowledge, although it has become slightly more adventurous in bridging disconnected components.
Table 1.
Maximum-likelihood estimates of strategies used in articles and patents, 1980–2010
| Model parameter | MEDLINE articles* | US patents* |
| Preference for degree of the more central chemical, | 1.375 (1.374, 1.377) | 1.508 (1.505, 1.512) |
| Preference for degree of the less central chemical, | −0.280 (−0.281, −0.280) | −0.172 (−0.175, −0.169) |
| Preference for network distance between chemicals, β | −5.312 (−5.328, −5.297) | −5.503 (−5.536, −5.469) |
| Preference for network distance between chemicals, γ | −45.369 (−45.470, −45.268) | −49.579 (−49.799, −49.345) |
| Preference for bridging disconnected network components, δ | −15.483 (−15.529, −15.428) | −16.303 (−16.399, −16.200) |
Modal estimates; 99% credible intervals in parentheses.
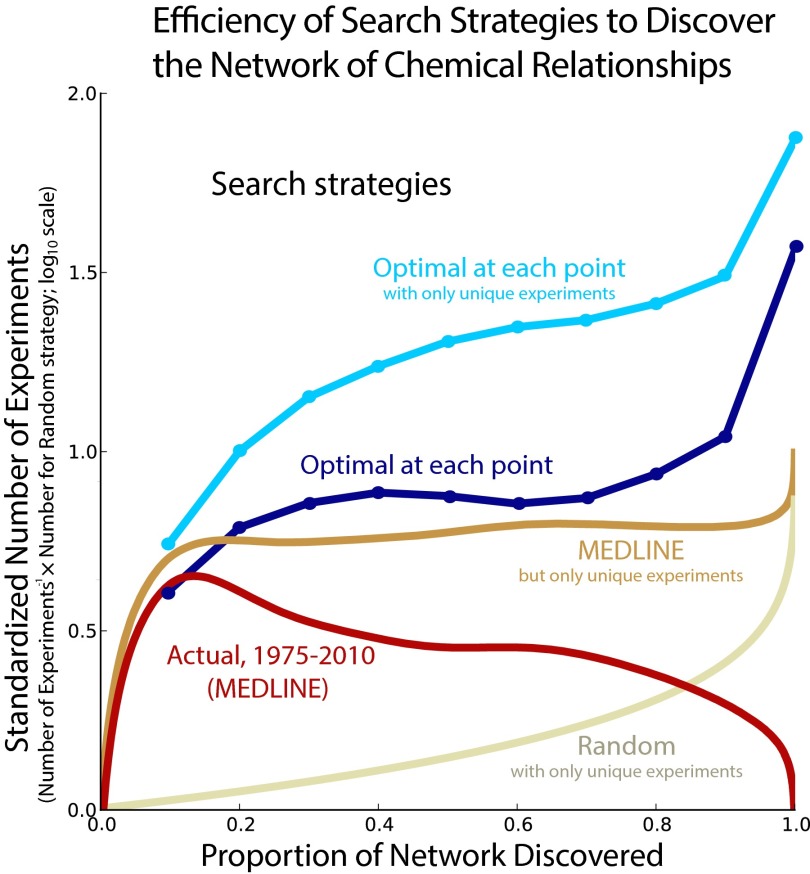
Fig. 1.
Red lines show model parameters estimated from the network of published chemical relationships over historical time, 1975–2010, every 5 y. The preference for more central chemicals (, ) increases consistently over time. The parameters controlling preference for walk length () and for jumping to disconnected network components (δ) also decrease consistently between 1975 and 2010, although the interpretation is somewhat subtle (main text). The green lines illustrate the optimal 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100% strategies against the historical trend and highlight the contrast between the trajectories.
We quantify the efficiency of a scientific strategy in terms of the total number of experiments performed, relative to the number of discoveries made, i.e., the number of new connections identified. We define X% loss as the total number of experiments performed (edges tested) before discovering X% of all edges in the target network. Relative loss is the number of experiments performed divided by the number of novel edges discovered plus one. Relative loss measures the number of experiments performed to discover one new chemical relationship (network edge). Strategies with larger relative loss continue to investigate previously explored relationships or test relationships that do not exist. This definition of efficiency implies that the objective function of science prizes the discovery of novel relationships above all else. We consider alternative objective functions in Discussion.
To estimate the efficiency of the inferred strategy and compare it with alternatives, we drew a subsample from the empirical network with a similar degree distribution (Figs. S7–S10 and SI Text) (14, 21). Then we used a supercomputer to simulate the exploration of this sample network with thousands of different strategies. Based on these simulations, we calculated the average cost (relative loss) associated with each strategy and minimize this cost with simulated annealing. By simulating the discovery process hundreds of times for each parameter setting, we identify strategies that, on average, discover a given proportion of the network with greatest efficiency. This exploration was computationally intensive and could not be conducted on the full network; in fact, our project was a use case for the development of novel parallel programming approaches (35, 36). Recall that each strategy (i.e., set of parameters) prioritizes different kinds of experiments. A given experiment “succeeds” if it proposes a relationship that is realized in the empirical (sample) network. Successful experiments are added to the network (“published”). An experiment “fails” if it proposes a relationship that is never realized in the empirical network. In the simplest scenario considered here, failures are not published. In our model, both “success” and “failure” are error free; i.e., there are no false positives or false negatives; this could be relaxed at the cost of considerable complexity and additional modeling assumptions.
Fig. S7.
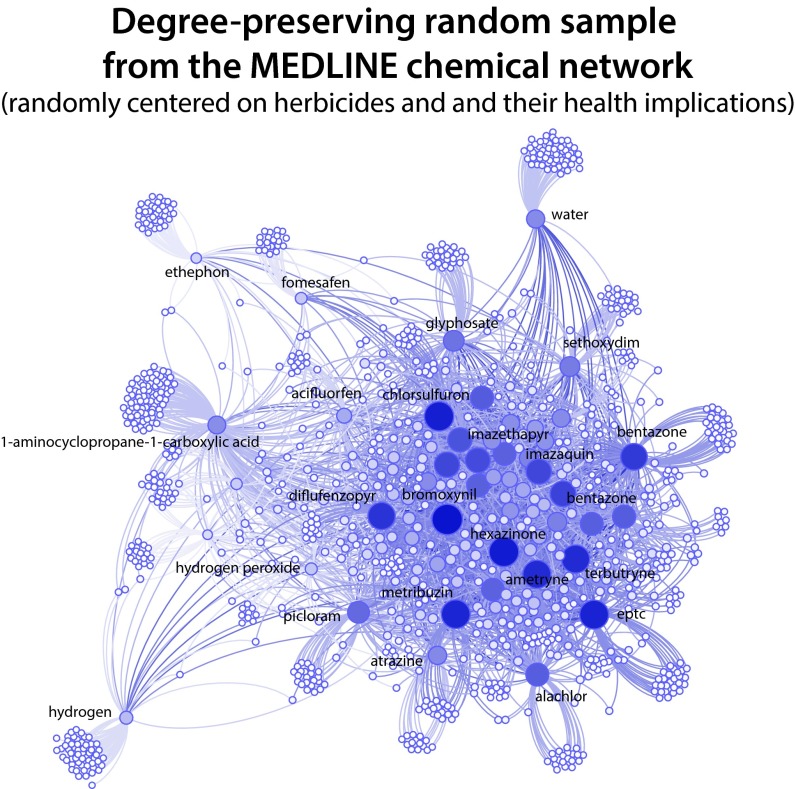
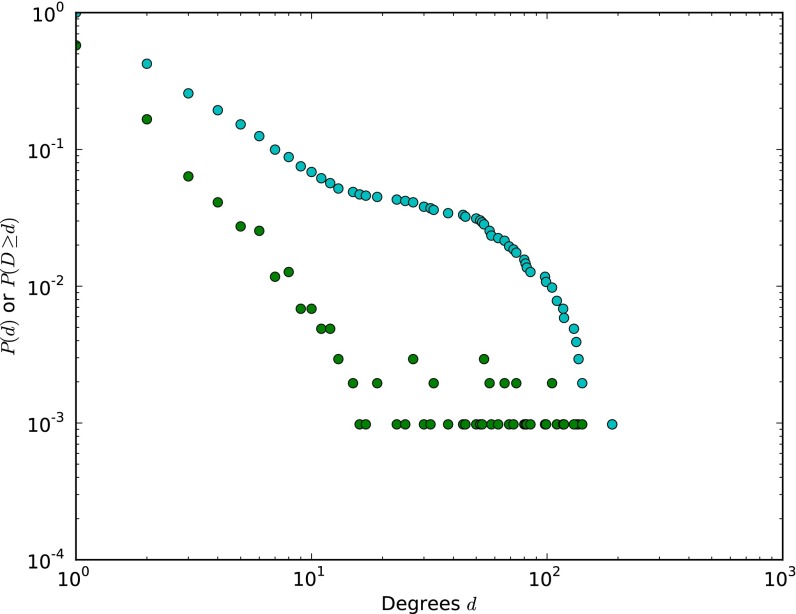
Degree-distribution-preserving random sample drawn from the complete MEDLINE network. Note that most of the chemicals in this sample happen to be herbicides; these substances are relevant to biomedicine because of their implications for human health. Also note that very high-degree network nodes (e.g., water) are at the periphery and predominantly connected to chemicals beyond the sample.
Fig. S10.
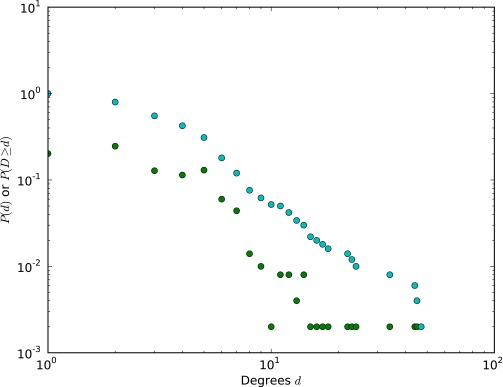
The degree distribution (green) and cumulative degree distribution (blue) for the model network used in visualizations (Fig. 2 B–D).
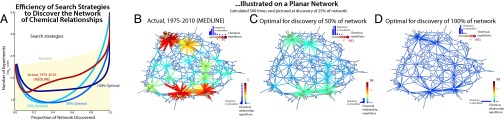
Fig. 1 and Table S1 show the optimal parameters we discovered for uncovering X% of the network (X% relative loss optimized; SI Text). We find that connecting multiple important, high-degree chemicals (positive and ) is critical for early exploration—discovering the first 10–20%—of the network. Instead of exploiting the local neighborhood of a high-profile chemical (like MEDLINE), this strategy prioritizes connections between important chemicals at either very short or infinite distance, a combinatorial exploitation strategy (driven by preferential attachment) similar to interdisciplinary approaches that mine connections between fields. By contrast, efficient discovery of 100% of the target network requires a disposition to link distant chemicals (in the same network component and disconnected components), whereas degree becomes less important. This strategy engages considerable risk, as it attempts to establish links spanning substantial cognitive distance and relies less on imitating prior scientists’ chemical choices. Fig. 1 illustrates how the history of inferred strategies for chemical discovery diverges from our estimated optimal discovery strategies. Historical strategies have become more conservative each year, as scientists focus on more central (i.e., higher-degree) chemicals. By contrast, optimal discovery strategies trend in the opposite direction. Early on they leverage existing knowledge by linking high-profile chemicals and then become riskier as they attend less to prior chemical choices and attempt more distant combinations.
Fig. 2B visualizes the strategy estimated from MEDLINE data (Table 1) on a planar network, whereas Fig. 2 C and D illustrates the 50% and 100% optimal strategies for exploring that network. Results are shown after 25% of the network has been discovered. The planar nature of the network makes the aggregate effect of these strategies apparent (see bit.ly/16QRviz for an animation of the MEDLINE strategy and SI Text for other animation URLs). In particular, Fig. 2B highlights the tendency of the MEDLINE strategy to explore the neighborhood of prominent chemicals. Fig. 2A compares the efficiency of several search strategies, quantified as the estimated number of experiments each strategy requires to discover from 1% to 100% of the network. Efficiency results use the sample network drawn from MEDLINE (Fig. S7 and SI Text). The MEDLINE strategy—which works well for generating coherent, thoroughly explored islands of knowledge in a young knowledge network—rapidly becomes inefficient, as effort is wasted by excessive focus on a few key entities and repetition of known connections. The MEDLINE strategy reaches maximum efficiency at 13% of the network discovered (Fig. 2A); it becomes increasingly inefficient at discovering larger fractions of the network. Although more efficient than the random strategy, which tests all edges with equal probability, the MEDLINE strategy is over three times more costly than the most efficient alternative when discovering the bulk of the network. By contrast, the optimal strategy for uncovering 50% of the network is nearly 10 times more efficient than the random strategy for discovering a range of network fractions (Table S1, 50% of network discovered).
Fig. 2.
(A) Comparison of the efficiency of discovery for different search strategies. Efficiency is quantified as the estimated number of experiments required to discover from 1% to 100% of a representative sample of the 2010 MEDLINE network. Compared strategies include random choice, the inferred MEDLINE strategy, and optimal strategies for discovering 20%, 50%, and 100% of the network. Results show that contemporary scientific activity (MEDLINE) may have been nearly optimal for discovering 10% of the chemical network, but becomes increasingly inefficient for discovering more than 30%. Parameters for “optimal” strategies are drawn from multistage collections of simulated annealing and subsequent MCMC search procedures. (B–D) Actual and optimal search processes illustrated on a planar network of chemical relationships. Each panel represents the average from 500 independent runs of the strategy, at the point where 25% of the possible chemical relationships have been discovered. The node and edge legends for each network strategy (Upper Right and Lower Right of each panel) are normalized to highlight differences between the strategies and are paired with histograms to illustrate the frequencies with which chemicals and chemical relationships of various degree centralities are selected for experimentation. Panels compare the strategies used by biomedical scientists publishing MEDLINE-indexed articles with alternative strategies that most efficiently discover the first 50% or 100% of the network.
Judging from the distribution of distances spanned in the empirical network (Figs. S3B and S6D), researchers rarely wander far across the knowledge network or bridge disconnected chemicals. Such behavior is critical for advance in mature areas of science (Table S1), and award-winning scientists appear to do so more frequently (“Prizes” in Fig. S3B). Scientists may hesitate to undertake a long walk or jump because of the low chance of success, even though a successful outcome could reveal the structure of the larger network and stimulate further work. In this way, individual incentives for productivity, reinforced by institutions like tenure, may be at odds with science’s collective interest in maximizing discovery.
Patterns in the parameters associated with efficient discovery reveal strategies that are consistently important. Preference for a high degree of the more central chemical is consistently associated with efficient discovery, which underscores the importance of preferential attachment as a mechanism for guiding research (21, 33). Preference for the degree of the less central chemical declines more rapidly (Fig. 1). Distinct preferences for the network distance between chemicals are rarely (clearly) implicated in optimal search (i.e., efficient discovery is robust to considerable variation in these parameters; see the ranges containing 95% of sampled parameters in Table S1).
Beyond alternative strategies, we also consider an alternative institution: “coordinated” discovery, in which scientists publish all findings, positive and negative, and do not repeat experiments. We calculate the efficiency of this regime analytically for a random strategy and numerically estimate the efficiency of coordinated MEDLINE and optimal discovery strategies on the sample network (SI Text). Coordinating research decreases the costs of discovery—the number of failed or duplicate experiments—regardless of strategy (Fig. S11).
Fig. S11.
Comparison of coordinated and uncoordinated strategies to one another. Strategy efficiencies are normalized against the efficiency of the random, uncoordinated strategy , where is the number of experiments required to discover from 1% to 100% of the network. As a result, the vertical axis shows how many times more efficient a given strategy is than the random, uncoordinated strategy.
Discussion
Our paper provides a quantitative method for inferring research strategies from data, examining their consequences, and discovering more efficient alternatives. Nevertheless, our model has several limitations. First, by modeling discovery as the exploration of a hidden network, we imply that new discoveries in biomedical chemistry always link chemicals never linked before. This is not true; a tie between two chemicals may be novel because previously linked chemicals are now linked in a new way (e.g., in the context of a new disease). Second, we evaluate efficiency only in relation to a single objective function—maximizing discovery of novel links. Many other objective functions exist, including minimizing error or increasing the robustness of discovered knowledge (37, 38). Development of useful medical and industrial technologies relies on the productive repetition of molecular relationships, which our current objective function does not reward. These alternative goals could be incorporated into the evaluation of our model—for example, by allowing repeat explorations of a known relationship to contribute to the objective function, but with diminishing marginal returns. Note that individual scientists may “locally” hold objectives that are very different from the global objective function of science. They may optimize their total number of publications or the predicted number of future citations to their work (2, 20). That said, we believe that the broader scientific community does have an implicit objective to traverse the space of possible research problems in search of novel and useful knowledge, and so we use that as a baseline here (39, 40). Third, we found that the most efficient discovery strategies are dominated by preferential attachment to the most central chemical in a problem over preferences for the degree of the less central chemical or the distance between chemicals. In the empirical network, most published links connect chemicals that have already been connected, and most novel links connect chemicals at distance two. Chemicals in disconnected components are next most frequent. All other distances are extremely rare. We could thus construct more parsimonious models that focus on preferential attachment and a few distinct categories of distance to describe the most efficient discovery strategies. Finally, our empirical network of published chemical relationships represents an imperfect sample of research effort, as effort is screened by experimental failure and the greater challenge of publishing an unconventional paper vs. an incremental one. The sample is drawn from virtually every publishing biomedical scientist, but publications overwhelmingly document successful experiments. Our data almost certainly underrepresent the risky but unsuccessful choices made by individual scientists. It nevertheless represents an informative trace of the scientific process—the very trace that scientists themselves use as they read the literature and design new experiments to build upon it. A more complete record of failures would both deepen our understanding of research behavior and improve its efficiency.¶ Future models could introduce these layers as additional features, penalties, and rewards associated with the “game” of science.
Despite these limitations, our model reveals patterns of discovery in biomedical chemistry and shows that more efficient discovery strategies would incorporate more “interdisciplinarity” and more risk, with the latter particularly important as a field matures. Efficient discovery of radically new knowledge in a mature field, including many areas of biomedicine (42), requires abandoning the current focus on important, nearby chemicals. Adopting a more efficient approach would lead to greater risk, but our findings suggest that scientists pursue progressively less risk, focusing more and more on the immediate neighborhood of high-degree chemicals, with the slight increase in bridging links as a silver lining. Successful research that goes against the crowd is more likely to garner high citations and prizes (Fig. S3), but these incentives may not be sufficient or flexible enough to motivate sustained advance in mature fields. A shift to riskier research would lead to more failures, which typically remain unpublished under current publication norms. We find that publication of failures substantially increases the speed of discovery. Thus, science policy could improve the efficiency of discovery by subsidizing more risky strategies, incentivizing strategy diversity, and encouraging the publication of failed experiments.
Policymakers could design institutions that cultivate intelligent risk-taking by shifting evaluation from the individual to the group, as was done at Bell Labs (43). They could also fund promising individuals rather than projects, like the Howard Hughes Medical Institute (44). Both approaches incentivize the spreading of risk across a portfolio of experiments that reflect multiple research strategies, instead of evaluating each experiment separately and selecting safer opportunities. Science and technology policy might also promote risky experiments with large potential benefits by lowering barriers to entry and championing radical ideas, emulating the Gates Foundation’s Grand Challenges program. Finally, new incentives to publish failures, like those mandating web publication of clinical trials at https://www.clinicaltrials.gov, should be considered if risk-taking increases. With carefully designed incentives and institutions, scientists will choose the next experiment to benefit themselves, science, and society.
Materials and Methods
Data.
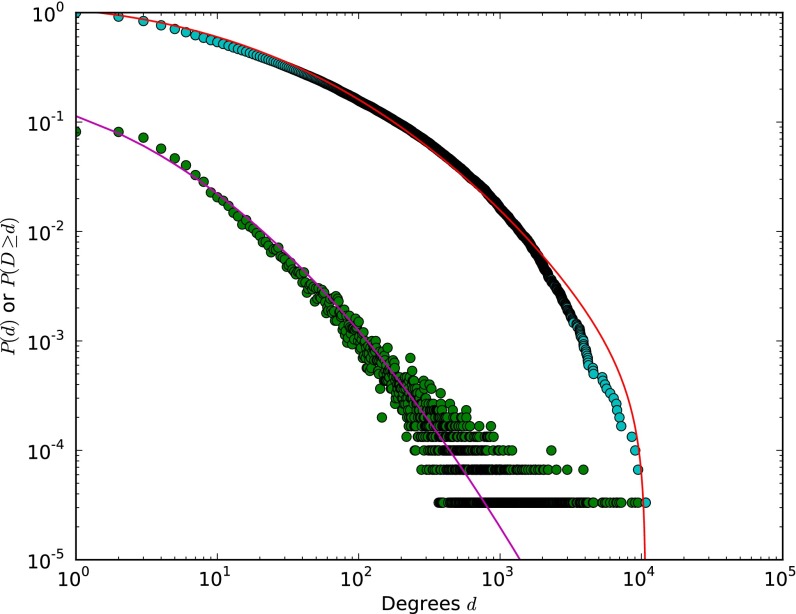
We examine scientific discovery by analyzing the growth of the knowledge network in biomedical chemistry since 1976. We constructed this network by matching a large lexicon of 52,654 distinct chemical terms extracted from MEDLINE metadata into MEDLINE from 1976 to 2010 (34) and then inferring a chemical relationship when the terms appeared in the same abstract. We used the same procedure to extract chemical relationships within US patents (SI Text). This process resulted in 30,060 unique chemicals with at least one link to others and 12,342,474 links between chemicals, corresponding to 1,338,753 unique chemical relationships. This network represents accumulated chemical knowledge within 2,363,858 articles and 295,812 patents. The combined network has a broad, approximately log-normal degree distribution (45, 46) (Fig. S8).
Fig. S8.
The degree distribution (green) and cumulative degree distribution (blue) for the MEDLINE–Patent network. Maximum-likelihood fits to a log-normal distribution are shown.
Estimating and Simulating Strategies.
In estimating parameters from the MEDLINE and US Patent networks, we considered time-dependent snapshots of the “visible” connectivity of each chemical within the growing chemical network to compute time-dependent choice probabilities. We can then compute the full likelihood of selecting a sequence of edge sets for experimentation, given model parameters. Parameter estimates are obtained by maximizing this likelihood function with respect to parameter values (SI Text). We used simulated annealing to find the maximum-likelihood estimates and Markov chain Monte Carlo (MCMC) to explore the parameter space around these estimates and assign Bayesian credible intervals (Table 1 and SI Text). We used the same approach to explore the parameter space of the model on the sample network: simulated annealing to identify an initial estimate, followed by MCMC to explore the objective function in the neighborhood of that estimate. Because of the heuristic nature of simulated annealing and MCMC, there are no formal guarantees on the global optimality of discovered strategies. Our purpose is less to establish claims of global optimality and more to demonstrate that much more efficient strategies exist and can be discovered.
Appendix
See SI Text for more details about the data, further definition and characterization of the model, analysis of the empirical network, and strategy comparisons.
SI Text
S1) Outline
The supporting information contains the following sections:
-
S2)
Overview
-
S3)
Data
-
S4)
Defining the Model
-
S5)
Analyzing the Empirical Network
-
S6)
Comparing Strategies
-
S7)
Random Discovery.
S2) Overview
Scientists, social scientists, and philosophers have long been interested in how scientists select influential but soluble research problems (47) and how their efforts should be distributed to make science most efficient (48). Research choice has been central to many classic investigations in the sociology of science (40, 49, 50) and has received sustained attention in qualitative (10, 20, 24, 51), analytical (1, 52), and simulation studies (3). Large-scale empirical investigation has been limited, however, despite the natural “self”-interest of the scientific community, profound policy implications (53), and the growing number of quantitative treatments of other topics in the “science of science” (54–58). Although science is often portrayed as highly efficient (1, 52), our results suggest that its conservative approach to discovery likely serves scientific careers better than science as a whole.
Our paper also seeks to advance a general, coarse-grained representation of scientific knowledge, provide a quantitative approach to inferring research strategies from publication data, examine their consequences for scientists and science as a whole, and discover more efficient alternatives. Our empirical findings strongly suggest that our network of chemical knowledge captures real features of scientific behavior. We discovered a wide range of more efficient strategies for discovery, as described in the main text. We posit that our approach can also be used to automatically generate “outside-the-box” hypotheses with novel strategies.
S3) Data
S3.1) Abstract Description.
We first provide an abstract description of the data, to fix notation for subsequent model description. The following subsections provide a detailed description of the text corpora studied in this paper, the annotation procedure used, the quality of annotations, and the nature of identified relationships.
is a text corpus of published science describing relationships between chemical entities. The corpus is partitioned into disjoint subcorpora that correspond to distinct consecutive time intervals,
| [S1] |
where is the oldest set of texts in the corpus, is the next, and is the set of texts most recently published. We call the subcorpus of texts appearing at time t. For simplicity, each subcorpus corresponds to 1 year.
is a set of N distinct chemical entities that occur in the corpus :
| [S2] |
is the number of undirected edges between entities that we observe in the corpus at time t. An edge represents a “relationship” between those entities. is the matrix of those edges, commonly referred to as a link list:
| [S3] |
As described below, we infer these edges from coappearance in corpus texts. Our complete data, , include the series of time-ordered matrices of chemical relationships published within the corresponding period:
| [S4] |
We assume that and are constant and known.
S3.2) Data Sources.
We describe our data sources. Our chemical substance annotations are derived from MEDLINE, a database including over 19 million biological, chemical, and biomedical journal articles. The National Library of Medicine at the National Institutes of Health began annotating entries with chemical substances in 1980. Between 1980 and 1998, a subset of these chemical substance annotations was supplemented with a Chemical Abstracts Service (CAS) registry number, meaning that the substance in question corresponded to a chemical registered by the Chemical Abstracts Service of the American Chemical Society. We pulled these 52,654 chemical names with CAS registry numbers and used them as the term list for our own annotation procedure. We annotated MEDLINE abstracts in this way, allowing us to obtain annotations for pre-1980 MEDLINE abstracts. We applied the same procedures to US Patent abstracts to facilitate comparison between these datasets—between published science and technology—and to ensure that any differences could not be attributed to differences in the annotation procedure (as would have been the case if we annotated the Patents only, but used existing MEDLINE annotations for MEDLINE abstracts). Table 1 reveals the similarity between the empirical search procedures underlying the MEDLINE and US Patent databases.
S3.3) Annotation Procedure.
We detail the procedure used to identify chemical names within the texts described above. To perform the annotations, we adapted the well-known BLAST tool for sequence alignment. BLAST is typically used to find instances of a shorter biological sequence within a longer sequence (e.g., to find a known gene in a longer strand of sequenced DNA), allowing for some noise (i.e., substitutions or gaps). The problem of finding a shorter sequence in a longer sequence is identical to the challenge we face in finding chemical names (shorter sequences) in abstracts (longer sequences). BLAST was earlier applied by one of us to annotate papers with gene and protein names (34).
We translated our initial set of chemical names harvested from the MEDLINE markup (52,654 distinct chemical entities) into the four nucleotides (A, T, C, G), using a comma-free code. All available MEDLINE abstracts and Google Patents were similarly translated. Because BLAST ranks output by statistical significance, and alignments with long sequences are scored as more statistically significant even if they contain some gaps and substitutions, we split the chemical set into three parts: short (2–6 letters), medium (7–25 letters), and long (25+ letters). This approach reduced the suppression of annotations with shorter chemical names that might otherwise occur. We compiled these three chemical subsets into three BLAST databases and split the collection of MEDLINE abstracts into sets of length 5,000 and Patent abstracts into sets of length 1,000 to optimize use of our computing resources and keep output to manageable size. These sets of abstracts were BLASTed against the chemical databases in parallel on PADS, a high-performance computing resource at the University of Chicago. BLAST uses several heuristics to perform alignments at extremely high speed, a necessity for our task, which involved more than half a trillion comparisons. Indeed, it was this speed and efficiency that motivated our use of BLAST rather than more straightforward string-matching techniques.
We further processed BLAST output as follows. Output of high quality was flagged as a potential annotation. High-quality annotations for short chemicals matched more than 99% of the chemical name and had no gaps or substitutions; for medium and long chemicals, more than 95% of the chemical name was matched, with no more than one gap or substitution. Potential annotations were searched back into the abstracts, with heuristic modifications (e.g., eliminating punctuation within names) to limit the number of false negatives due to variation in chemical terminology. Several ambiguous terms were also eliminated: apt, baseline, lead, ensure, relate, tandem, and gold when used in the phrase “gold standard.” We normalized the terms “adrenaline” and “noradrenaline” to “epinephrine” and “norepinephrine” and similarly for “estrogen” to “estradiol.”
Annotated MEDLINE and Google Patent abstracts correspond to the time-ordered sequence of subcorpora above . The chemical terms used to annotate these abstracts correspond to the entities above; in total we use 30,060 distinct chemical terms in our annotations. Finally, we infer the presence of chemical relationships through coappearance of chemical names as annotations in a document. Thus, the matrix corresponds to all coappearances of pairs of chemical names in an abstract in year t (allowing repetitions); the full graph () has 12,342,474 edges (including repetitions).
S3.4) Annotation Quality.
Although we attempted to minimize false negatives in our annotation procedure, our main goal was to minimize false positives. To check the quality of our annotations, we created two random samples of our corpus of MEDLINE abstracts: one selected from abstracts with annotations and one selected from all abstracts. We had research assistants check the list of annotations for these subsamples against the abstracts.
For the subset of 100 abstracts having at least one annotation, there were no false positives in 210 annotations (i.e., all chemical terms appeared in the abstracts), although 14 of these annotations occurred within a compound word that was not annotated (and thus might be considered a soft false positive—these compound words represented chemicals that were a variant of the annotated chemical, included the annotated chemical as a component, or primarily interacted with the annotated chemical, e.g., as a receptor, kinase, etc.). For the subset of 100 abstracts sampled without regard to annotations, there were no false positives; however, one annotation corresponded to a nonchemical use of the word (“silver,” referring to the color of a fox) and 14 were soft false positives, in which the chemical term occurred within a compound word that was not annotated.
Turning to false negatives (i.e., situations where an explicit term in the chemical annotation list appears in the abstract but is not annotated), for the subset of annotated abstracts we had only four false negatives, all corresponding to situations with confounding punctuation. Our research assistant noted an additional 204 chemical words that were not in the dictionary, including some synonyms (e.g., chemical formulas) for words in the dictionary. For the second subset (a random sample from all abstracts) we had only three false negatives, with a further 44 chemical words not in the dictionary, including synonyms for words in the dictionary. Overall, our analysis reveals a false positive rate of 0% and a per document soft false positive rate of 14%; within sample, per document false negative rate is 3.5%. The significant out of sample false negative rates point to the partial coverage of our chemical dictionary. This problem could be resolved using a larger dictionary and a synonym thesaurus for chemical terms, with corresponding (and substantial) increase in computing overhead.
Finally, we discovered after the computationally expensive parameter inference had been completed that some patents in the Google Patents dataset were replicated between formats. These duplicated data affected a very small fraction of Patents (11,635 or 5%) and duplicate edges (0.5% of all network edges and 3.7% of Patent edges). Because the key network measures used in our generative model (degree and distance) are insensitive to edge repetitions, these duplicate edges contribute to parameter inference only for the Patents (representing a very small fraction of the data used to do so) (Table 1) and for the degree–degree plots (see Fig. S3, in which duplicates represent an even smaller fraction of the data). We were unable to redo the parameter inference with these duplicates removed, but they had no influence on the MEDLINE estimates and only minimal influence on the Patent estimates.
S3.5) The Nature of Empirical Chemical Relationships.
Molecules in our inferred network are linked in many ways, including physical interaction, structural similarity, and shared clinical relevance. Fig. S1 provides several important examples. It does not, however, fully illustrate the nature of long-distance connections between molecules or the diversity of ways in which they are combined.
Fig. S2A illustrates different dimensions of chemical distance in our networks by tracing molecules and relationships along the shortest path between discoveries. In 1991, a group based in Halifax, Nova Scotia discovered a novel family of polyketide antibiotics called jadomycins. These antibiotics are produced by the bacterium Streptomyces venezuelae under heat-shock conditions. In a 1996 publication [indexed by MEDLINE PubMed IDentifier (PMID) 8581159], a group including one of these scientists (S. W. Ayer) showed that the gene cluster controlling jadomycin B synthesis contained ORFs resembling oxygenases, which were thought to play a crucial role in jadomycin B biosynthesis. These scientists blocked the action of one of the oxygenases and disrupted jadomycin B biosynthesis. The transformed bacteria produced another antibiotic, however: a polyketide-derived antibiotic called rabelomycin, which had been identified in a related bacterium (Streptomyces olivaceus) by a research group based at Bristol-Myers Squibb in 1970. Unlike jadomycin B, rabelomycin does not contain nitrogen.
The discovery that rabelomycin and jadomycin shared a synthetic pathway was likely surprising, because they are so distant—five links apart—in the chemical network. A plausible cognitive path might look something like this: The same group that discovered jadomycin B noted in 1994 (PMID 7764672) that changing the nitrogen source in the growth medium from l-isoleucine to another amino acid produced differently colored jadomycin analogs. Following the key role of nitrogen in jadomycin synthesis, we step to another amino acid and potential nitrogen source: tyrosine (the first instance of nitrogen appearing with tyrosine is in 1930, PMID 16744509). Tyrosine plays a key role in the synthesis of another antibiotic, urdamycin C, produced by yet another Streptomyces bacterium, Streptomyces fradiae. Like the jadomycins, urdamycins are polyketide antibiotics; urdamycin C synthesis relies on tyrosine as a nitrogen source, as discovered in 1989 (PMID 2753820) by German research groups from Tübingen and Göttingen. Another (nonnitrogenous) member of the urdamycin family, urdamycin A, was noted upon discovery in 1986 (PMID 3818439) to be chemically identical to a related antibiotic aquayamycin once a sugar is removed, all such antibiotics being members of the larger “angucycline” family. It is here that we shift from nitrogenous to nonnitrogenous antibiotics. (Note that there is an earlier connection between aquayamycin and tyrosine in 1968, as aquayamycin inhibits tyrosine hydroxylase, which we could not discover because no abstract is available; however, the synthetic role of tyrosine captured here is more relevant). Finally, the connection between aquayamycin and rabelomycin was noted in 1982 by a Japanese group (PMID 7107524), whose work suggested that rabelomycin, aquayamycin, and several other antibiotics possessed similar biosynthetic pathways. Thus, in principle, the biosynthetic similarity between rabelomycin and aquayamycin (1982) would suggest a biosynthetic similarity between rabelomycin and urdamycin A. Because the biosynthetic pathway generating urdamycin A (a nonnitrogenous antibiotic) also generated urdamycin C (a nitrogenous antibiotic) through a synthesis step involving tyrosine, it is not unreasonable to expect that rabelomycin might also be the nonnitrogenous analog of a nitrogenous antibiotic produced by a similar biosynthetic pathway. This antibiotic turned out to be jadomycin B. The geographical distances that this chain crosses—and the nations in which stretches of it cluster—suggest that even though much of the work is published in a central journal, The Journal of Antibiotics, the bridging of both conceptual and spatial distance is likely associated with its difficulty and surprise. In short, chemical distances in the network can map onto forms of underlying distance—like geographical, cultural, or linguistic distance—that may keep molecules studied in distant laboratories from being combined. Future work may seek to measure and model these different types of distance explicitly and independently.
Fig. S2B suggests the diversity of link combinations involved in a particular article—methodological, scientific, etc. In 1993, a research group from Bristol-Myers Squibb Pharmaceutical Company’s research institute tested BMY 42393 and Octimibate on hamsters to evaluate their effectiveness in reducing cholesterol and triglicerides (PMID 8443148). The hamsters were fed with chow, cholesterol, and coconut oil, and Octimibate was shown in vivo to reduce both cholesterol and triglicerides. Because Octimibate had previously been implicated as a CoA inhibitor, the group also tested the influence of the two compounds on the presence of macrophages and concluded that they both likely suppress monocyte–macrophage atherogenic activity and inhibit early atherosclerosis. This final series of tests was performed in vitro, using hematoxylin-stained tissues. In 1992, BMY 42393 was established as structurally similar to 4,5-diphenyl-2-oxazolenonanoic acid and functionally similar in that both inhibited ADP-induced aggregation of human platelets. The second of these chemicals had itself been deemed functionally similar to 2-[3-[2-(4,5-diphenyl-2-oxazolyl)ethyl]phenoxy]acetic acid, which became less effective in its inhibition under several conditions, including when the molecule was constrained in a planar phenanthrene system. The simple molecule phenanthrene was associated in previous research with testosterone and calcium, which themselves were linked to other research tools like hematoxylin for tissue staining, coconut oil for mammalian cholesterol studies, and CoA, all of which came together in the two-stage analyses in 1993. This example highlights the diversity of chemical linkages—methodological, interactional, similarity, etc.—that are traced by our chemical network. Future research may measure and model these linkages specifically to more precisely account for distinct research strategies.
We illustrate the empirical distribution of chemical degree–degree and distance relationships for all MEDLINE papers and those associated with prizes in Fig. S3. In Fig. S3A, note that the “Prize” distribution is much flatter than “MEDLINE,” suggesting that prize-winning authors are more likely to combine chemicals with higher or lower degrees than those most commonly combined, which are typically both of high degree. Moreover, the “citation” and combined plots in Fig. S3A, Bottom show how less common degree–degree combinations are much more intensely cited than common degree–degree combinations. In Fig. S3B, we see that prize winners combine disconnected molecules significantly more frequently than those who do not. Supporting this, qualitative and quantitative results from the sociology of science and innovation suggest that scientists who are highly successful tend to pursue atypical strategies (2, 17, 59).
S4) Defining the Model
Here we begin to build toward a full description of the generative model, in the simplest case of no missing data (all experiments are successful).
S4.1) Edge Probabilities.
We first provide a detailed description of the functions that go into the probability of exploring a relationship between chemicals i and j.
Let be the rank of the ith entity at the time t; this quantity corresponds simply to the degree of entity i, i.e., the number of distinct edges connected to it at time t, plus 1.†† For any time t the set of ranks is .
Then for an edge we introduce the following function that distinctively weights the maximum and minimum rank of the two nodes. Define
| [S5] |
In other words, the parameter controls the weight given to the degree of the higher-degree entity/node, whereas controls the weight given to the degree of the lower-degree entity. When , all entities (nodes) are treated identically regardless of their rank. When , we have . Large positive values of and represent a preference for selecting nodes with larger degree. Negative values of or represent a preference for nodes with smaller degree. Note, however, that the two are somewhat interdependent. Because determines the preference for the degree of the higher-degree node in the pair under consideration, a negative value (preferring nodes of small degree) will also drive down the preferred degree of the lower-degree node in the pair, which must by necessity be smaller than the degree of the former node. Similarly, because determines the preference for the degree of the lower-degree node in the pair, a high positive value (preferring nodes with large degree) will also drive up the preferred degree of the higher-rank node. This allows us to define not only a preference for the rank of each node, but also (indirectly) a preference for how close those ranks should be: When and , scientists prefer them to be as close as possible; when and , pairs with greater difference in rank are more probable.
Let be the shortest distance between and in the network at time t (i.e., the topological distance). If and are disconnected, we set . Having in mind, define the function
| [S6] |
where is the largest diameter (i.e., the longest path among all shortest paths connecting vertices in our network) observed in the empirical history of the network. In generative model instances (SI Text, sections S4.2 and S6.2), we assume that the true underlying network is predefined and immutable, so is known in advance and does not change during graph growth.
In the finite-distance case, this function (when properly normalized) becomes a discrete equivalent of the beta distribution [although note that the parameterization is slightly different here; in the beta distribution, the exponents would be rewritten as and ]. This distribution can take a number of shapes, depending on the parameter values, including L shapes and reversed L shapes, U shapes, and bell shapes (Fig. S4C). Heuristically, the parameters β and γ measure researchers’ propensity for “adventure” or their willingness to shoulder uncertainty. When β and γ are both negative, the distribution is single peaked and the ratio controls the expected value (60). When the ratio is greater than 1 (, e.g., and ), scientists prefer to “travel” longer distances (on average) between chemical entities to select their next experiment. When the ratio is less than 1 (, e.g., and ), scientists prefer relatively short distances (and this is what we see in the MEDLINE strategy, with and ). Note that, when , we have a perfect uniform distribution over all path lengths (as seen in the last example in Fig. S4C). When β and γ are both positive, the distribution is U shaped; when β is positive and γ is negative, the distribution is L shaped; and when β is negative and γ is positive, the distribution is a reversed L shape. See Fig. S4C for examples.
The parameter δ reflects the probability of testing a connection between chemical entities in two different connected components of the graph (including a connection to a chemical entity that has yet to “enter” the network, which can be formally represented as an isolated node in its own disconnected component). δ can range from to like all other parameters. When , the model becomes completely blind to differences in length of the shortest path between nodes; all lengths (including ) receive the same probability weight.
Combining these two functions, we can define the probability that scientists will explore a relationship between chemical entities i and j at time t,
| [S7] |
where the ranks and distances from the previous time period (i.e., the ranks and distances observable to scientists at time t) are used to compute the probability.
Our model could include structural features or nodal attributes as covariates, as in the fruitful exponential random graph approach (61). As far as we know, our complete network is too large for Exponential Random Graph Models (ERGM) methods, although we look forward to future applications of such models. Including additional features or attributes would make exploration of the parameter space much more expensive.
S4.2) Generative Model: All Experiments Succeed.
In the simplest case—in which all experiments succeed—we describe how the functions defined above can be used to generate a network.
Given.
-
i)
A network at , defined by the set of possible nodes (corresponding to the set of all chemical entities) and the initial set of edges, . This network can be either completely disconnected or partially connected.
-
ii)
The time-ordered set of numbers of added edges . Note that is a scalar quantity, counting only the number of edges to be introduced at each time step.
We can now define a generative step for a network described by parameters , and γ. An instance of the network is generated by iterating this recipe until the time-ordered set is exhausted.
Generative step for time .
-
i)
Update the set of degrees for all nodes, , and the shortest distances, , for every pair of nodes.
-
ii)
Independently choose pairs of nodes to be connected (but do not connect them); select a pair of vertices with probability .
-
iii)
After all new edges are identified, simultaneously add all new edges to the network (modeling the situation in which scientists choose their targets of analysis independently and cannot see the global picture until interactions are published).
-
iv)
Update the time from t to .
This simple generative model motivates the construction of a likelihood function that can be used to infer the most likely model parameters from the real history of the network extracted from our corpus. We also deploy a variant of this generative model in which some experiments fail—see below to compare the efficiency of different strategies.
S5) Analyzing the Empirical Network
Here we detail the likelihood function, the procedures used to estimate model parameters from data, and the methods used to analyze the empirical network.
S5.1) Likelihood Function: No Missing Data; Estimating the Model Parameters from Data.
For brevity, we package all parameters of the generative model into a parameter vector . We now describe the construction of a likelihood function over the parameter space. We seek the parameter values that maximize the likelihood for the observed data, in other words, the parameter values given which the observed data are most probable. Recall that is the list of all edges observed in year t; these edges provide the observed data for the likelihood function.
In this likelihood function, we do not take account of the possibility that experiments fail. Although this possibility could be treated (at substantial computational expense) by assuming knowledge of the “correct” network, estimating the missing data (failed experiments), and using an expectation-maximization algorithm to find the parameters that maximize this expanded likelihood function, we believe the approximation taken here—using only the observed edges to infer strategy parameters—provides a reasonable first view of the strategic preferences of biomedical scientists and avoids the strong assumption that the most recent network represents the “true” network. Furthermore, we believe the missing data problem will typically be mild for data drawn from early stages of network evolution (as in the network of biomedical knowledge). Finally, we also assume an uninformative prior over the model parameters, i.e., that is uniform.
We thus have the following relations,
| [S8] |
| [S9] |
| [S10] |
| [S11] |
where the product is taken first over all years and then over all edges observed in a given year. The probability of observing each edge is computed according to the functions described above, with parameter values taken from the vector .
The inferred parameter values are found by maximizing the likelihood function:
| [S12] |
For the inference of MEDLINE and Patent parameters, the same underlying network is used; at a given time t the ranks and distances used to compute the probability of a particular link being chosen () will be the same. The parameter inference differs for the two cases only in the explicit edge data that are used to compute the likelihood function; for MEDLINE parameters, only edges occurring in MEDLINE abstracts in period t contribute to the likelihood function for period t, whereas for Patent parameters, only edges occurring in the Google Patent dataset in period t contribute to the likelihood function for period t. Nonetheless, in the subsequent period , the network used to compute the ranks and distances (used in turn to compute the probability of a particular link being chosen ) is the full network, incorporating edges from MEDLINE and Google Patents. This assumes that both scientific authors and inventors are aware of the entire public record of chemical relationships, but that the placement of links in the different domains reveals differing strategies. We used simulated annealing (62) to find the maximum-likelihood estimates (C++ implementation) and subsequently used MCMC to assign Bayesian credible intervals (Table 1). Computation took nearly 2 wk on a 24-core Unix workstation.
Estimated model parameters are shown in Table 1 and illustrated in Figs. 1 and 2 in the text. Fig. S5 graphically compares the degree–degree preferences inferred from MEDLINE and Patent data with seven alternative preference structures. Fig. S6 supplements the empirical network distances measured from the network (shown in Fig. S3B) by illustrating the entropy of the interchemical distance distribution as a function of time. The estimated model parameters we infer from the graph suggest that investigators engage in conservative, short walks; this graph highlights that they become more conservative over time.
Rewriting the degree dependence of the model clarifies the relationship between this strategy and preferential attachment. Let be the larger degree and be the smaller. Now write ; is the ratio of degrees. Then and imply . The typical strategy shows linear preferential attachment in the larger degree and gives more weight to linking chemicals with a large difference in degree, i.e., close to 0. This strategy exploits the neighborhood of high-degree chemicals. Because of the broad degree distribution, most potential links between chemicals in disconnected components would connect low-degree nodes. The preference for high degree balances the preference for connecting distinct components, contributing to the small absolute number of such links.
S5.2) Comparing All Scientists with Prize Winners.
In Fig. S3, we compare the behavior of our entire population of scientists to the behavior of high-achieving scientists (2). We define high-achieving scientists as those who won an international award or prize. We identified the winners of 137 different prizes and awards from biology, medicine, and chemistry. To create a large list of prizes, we drew from the category pages for biology awards, medicine awards, and chemistry awards in Wikipedia and then validated them with several biomedical scientists:
en.wikipedia.org/wiki/Category:Biology_awards
en.wikipedia.org/wiki/Category:Medicine_awards
en.wikipedia.org/wiki/Category:Chemistry_awards.
Note that more and less prestigious prizes are gathered on these category pages, with the vast majority of prestigious prizes being captured (Nobel Prizes in Physiology or Medicine or Chemistry, a range of prizes considered “pre-Nobel”, etc.). To eliminate prize winners who were not necessarily high-achieving scientists, we deleted those prizes whose selection criteria were not research related (e.g., prizes awarded for teaching) as well as prizes targeted at students. For each research-related prize, we searched for the names of prize winners in PubMed and if at all possible identified three articles written by each winner. Those awards that center on biomedical contributions (e.g., the Nobel Prize in Physiology or Medicine) have deep coverage in MEDLINE articles and so necessarily represent more data points in our analysis than awards peripheral to biomedicine (e.g., The Kempe Award for Distinguished Ecologists). With this expectation, we also devoted more time to thoroughly completing our coverage of articles associated with major or broad awards, which we believed should be well represented in MEDLINE. Hence, these major and broad awards are necessarily more complete (i.e., more prize winners have associated articles) than narrower awards or those that only partially overlap the biomedical focus of PubMed (e.g., entomology). Due to one data entry error, the C. W. Woodworth award (a prize in entomology) was not entered into the prize-winner database completely. As this corresponds to an insignificant number of publications, we do not believe our results are affected in any way.
This collection of articles provided the seed for a broader search. We identified the name of the prize winner in the MEDLINE entry for each of the one to three seed articles. Using the Author-ity tool (63), this focal name can be mapped to a cluster of names with partial disambiguation. We searched MEDLINE for the names in each of the author clusters that map to the prize winner’s name in the one to three hand-assigned articles. We then assigned all papers retrieved in this way to the prize winner, if they were written from 0 year to 30 years before the award was granted; see Table S2 for a list of prizes, number of prize winners analyzed, and number of papers discovered. If we or our research assistants misassigned any of the one to three seed articles, this process could introduce false positives for common names (the Author-ity author clustering is quite conservative and is unlikely to contribute to this error). As these false positives are “typical” rather than award-winning scientists, however, they likely behave like the majority and dilute the effect we report. Authors with non-English characters in their names are also underrepresented. For example, the Nobel Prize winner Sune Bergström is not well unified by an Author-ity author disambiguation cluster and so some of his articles are not represented in our figures. These false negatives similarly dilute our estimate of the distinctiveness of award-winning scientists’ strategies. The results in Fig. S3 should therefore be viewed as a conservative estimate of the difference between prize winners and the pool of all scientists. Note that prize winners are significantly more likely to link chemicals in disconnected components of the network than the typical scientist.
S5.3) Citations.
We analyze the relationship between strategies and citations in Fig. S3. We study only citations for MEDLINE articles. The reported citations are computed as follows. For each abstract, we link it to the Thomson Reuters citation database, which lists citations between pairs of articles. We were able to link Thomson Reuters records to more than two-thirds of the MEDLINE articles; most of the remaining, unlinked articles are from journals not represented in the Thomson Reuters database. We include all citations up to 3 y after publication of the focal article, as 3 y is the typical half-life for the citation distribution of an individual article, and plot citations for papers written between 1983 and 2003 (our citation coverage begins to be less complete in 2006). Note that highly cited research neglects the low-risk chemical combinations favored by the majority, instead examining pairs with more diverse levels of importance.
S5.4) Confidence Intervals for Distance Distribution.
To assign confidence intervals to the distance distribution in Fig. S3B, we treat the distribution as a sample from an underlying multinomial distribution. We then use the Goodman-corrected confidence interval (64) for a multinomial with k types,
| [S13] |
where is the number of observations of type i, N is the total number of observations, and for the 95% confidence interval is the upper th percentile of the -distribution with 1 df.
S6 Comparing Strategies
S6.1) Permitting Failure.
Up to this point, we have assumed that every pair of chemicals chosen for an experiment culminates in a scholarly publication and thus becomes visible to other scientists at the next time period. This is clearly a strong assumption. In this section, we discuss how we relaxed this assumption to evaluate the relative efficiency of various strategies.
Assume that we know the chemical network underlying the collection of chemicals. A connection in this network is a “real” connection, and only experiments over pairs with a real connection result in publication. Testing a pair of chemicals without connection in the underlying network results in a failed experiment and is not published.
All published relationships added to the network in time slice t thus correspond to edges in the underlying network. These relationships can be partitioned into two classes: those that duplicate a relationship that was already known and visible (published earlier) and those that reveal a relationship that was previously unknown and invisible (i.e., unpublished or novel). We denote the sets of known and novel edges added in step r as and , respectively. The total number of edges published in time slice t is the sum of the two numbers: . We allow the model to generate repetitions of a known and visible relationship/edge because this is actually observed in the literature; for example, estradiol and cholesterol have been studied together in many papers.
Only true chemical associations enter the literature at each time slice t. But there are presumably also a nonnegative number, , of pairs of chemical entities that were tried experimentally, but did not produce a meaningful association (because this association does not exist in the underlying network). These experiments are not recorded in publications [corresponding to the well-known file drawer problem (37)]. We can then construct a generative model in which some experiments fail; this model can be used to define the efficiency of a given set of parameters (a “strategy”). Note two simplifying assumptions that remain in the model: We currently assume that (i) experiments fail only if the tested edge does not exist in the underlying network and (ii) experiments succeed only if the tested edge does exist in the underlying network. We know that false and fraudulent links do find their way into the published record and that experiments sometimes fail for technical reasons independent of the claim under consideration. Still, we believe that this model represents a reasonable, if simplified, first approximation and that these assumptions could be profitably relaxed in future work.
S6.2) Generative Model Where Experiments Can Fail.
We now describe a generative model in which experiments are allowed to fail. A given run of the generative model describes a history in which scientists gradually reveal the underlying network of true chemical relationships, while incurring a cost for each experiment attempted.
Given.
-
i)
Complete underlying network defined over all entities. We assume that experiments for entities and succeed if the underlying network has edge and fail otherwise.
-
ii)
Network at , defined by the set of possible nodes (corresponding to the set of all chemical entities) and the initial set of edges, . This network can be either completely disconnected or partially connected.
-
iii)
The time-ordered set of numbers of added edges .
We now define a generative step for a network described by parameters , and γ. An instance of the network is generated by iterating this recipe until the time-ordered set is exhausted.
Generative step for time .
-
i)
Update the degrees for all nodes, and the shortest distances, , for every pair of nodes.
-
ii)
Independently choose pairs of nodes to be connected (but do not connect them), until exactly edges are successfully discovered:
-
a)Select nodes and with probability .
-
b)If the edge is present in the underlying network, save the pair in the list of successful experiments. If the edge is not present, increment the count of unsuccessful experiments by 1.
-
a)
-
iii)
After edges have been successfully created, simultaneously add these edges to the network (modeling the situation in which scientists choose their targets of analysis independently and cannot see the global picture until interactions are published). Record the number of failed experiments in the set . Also record the number of novel (previously unknown) findings in the set .
-
iv)
Update the time from t to .
In the present formulation the success schedule is given as a predefined input to this process. Although we did not implement it here, we could easily add a stochastic component that generates this list. For example, we could assume that the number of published articles or positive experiments in a given time slice is distributed according to a Poisson distribution.
The output of interest here is the number of failed experiments generated in each time step, . From (given) and (computed) we can assign a total cost to the scientific history of that particular world up to time t:
| [S14] |
S6.3) Generating a Representative Subsample of the Empirical Network for Comparing Strategies.
To explore the behavior of the MEDLINE–Patent strategy and of optimal strategies in a realistic setting, we developed a two-step process for creating representative subsamples of a large empirical network. It is computationally prohibitive to thoroughly evaluate a broad sample of strategies on the entire empirical network. Likewise, visualization of strategy behavior on this large network would be hard to interpret, if not totally meaningless. Smaller networks are necessary to facilitate visualization and to rapidly search the parameter space for efficient strategies. Our sampling approach is based on the so-called “Forest Fire” method of Leskovec and Faloutsos (65); it is essentially a probabilistic snowball sample. We use this method to generate many () candidate samples and then select from these candidates a network with the desired characteristics (in this case, a degree sequence close to the empirical network and a size permitting optimal strategy search).
We first describe our sampling approach. It is a simple iterative procedure, in which the neighbors of an active vertex themselves become active (join the sample) with some probability:
-
i)
Choose a node at random from the empirical network.
-
ii)
Choose a number K from the geometric distribution . If K is greater than the degree of , set K to be the degree of . Now choose K edges of and add those edges to the sample network. Put the nodes at the end of those K edges into the “sampling front” .
-
iii)
For each node in the sampling front , choose a number K from the geometric distribution . If is greater than the degree of , set to be the degree of . Now choose edges of and add all new edges to the sample network. If the nodes at the end of those edges have not been visited before by the sampling process (“burned”), put them into the sampling front for the next iteration, . Nodes that have been burned once cannot “reignite” and add new neighbors to the sample.
-
iv)
If the sample network has less than the target number of nodes and the sampling front for the next iteration is nonempty, go back to the previous step.
-
v)
If the sampling front for the next iteration is empty, go back to step one.
Note that we choose edges in the third step so that the sampling process can, in principle, terminate in some subregions of the network. Note also that, although we do not allow nodes that have already been visited to join the sampling front again, we do permit new edges pointing “back” to those nodes to enter the sample network. This allows our sampling process to capture triangles and higher-order cliques. By construction, this process captures much of the rich local structure of empirical networks.
Using this procedure, we generated candidate samples. We targeted 1,000 nodes in our sampling process (because of the probabilistic nature of the sampling scheme, sometimes larger sample networks were generated) and used a geometric distribution with success probability (note here that success means the sampling process stops spreading at a given node). This probability was chosen such that the expected value of matched the average degree of the empirical network.
Of the candidate sample networks, we estimated their scaling behavior using the maximum-likelihood procedure of ref. 45 as implemented in ref. 46, starting the fit at degree 2. We then selected for further consideration those networks with scaling exponents α close to the target exponent (see below). Of these, we selected a network with a manageable number of nodes (1,023) and a plausible number of distinct degrees (51). This network had ; the smallest exponent observed in our sample was . See Fig. S7 for a visualization of this sample network.
Note that this procedure could be substantially extended so that the objective function of sample selection includes more than just the scaling exponent. In principle, candidate samples could be chosen on clustering, modularity, assortativity, average distance, and other standard network metrics.
We again use simulated annealing to find strategies that minimize percentage of relative loss—the objective function against which strategies/parameters are optimized. We then used MCMC (setting T = 1) to explore the parameter space around these initial parameter values. In some cases, we found that the objective function was relatively “flat” to variations in some parameters, which substantively means that these parameters are unimportant to efficiency. In fact, we occasionally discovered more efficient strategies in this exploration. This is unsurprising, as we had to run the simulated annealing for relatively few updates due to the computational cost of each step. Hence it is unlikely that our simulated annealing parameter search would converge on the global optimum. We also note that we are more confident regarding the optimality of the model fit against the complete network: Tight credible intervals suggest a well-behaved likelihood function, and we were able to run simulated annealing for longer than we did in our evaluation of thousands of strategies to minimize relative loss. As mentioned in the main text, the heuristic nature of simulated annealing and MCMC does not guarantee the global optimality of our discovery strategies (Table S1 and Figs. 1 and 2A). What is critical for our argument, however, is that much more efficient strategies can be readily discovered.
S6.4) Generating a Planar Network for Visualizing Strategies.
To visualize the behavior of different strategies and their comparative efficiencies, we need to create smaller networks that are broadly similar to the empirical (and sampled) network. We construct this model network using a variant of the Barabási–Albert model of networks with a broad degree distribution, called the Chinese Restaurant Process (CRP). We first describe the CRP and then explain how to interpret it along the lines of the Barabási–Albert model. At each step of the CRP, a new customer arrives. Assume that the “restaurant” already has K other tables and i customers. This new customer chooses to sit at a table with probability proportional to the number of customers at the table. The customer may also “request a new table” with probability proportional to a parameter ξ.
This can be directly mapped to a network growth process very similar to the Barabási–Albert model. Each node is both a customer and a table, so . Assume that when a new node arrives (a “customer” in the CRP), the network already has K other nodes (i.e., tables) and therefore also K other customers. The node chooses to connect to an existing node (i.e., sit at that table) with probability proportional to the observed degree of that node, plus one (i.e., the number of customers at the table; each node contains at least one customer at the table). When the customer (the new node) is assigned to the table, it corresponds to a link between nodes and . If the node requests a new table, with probability proportional to parameter ξ, it does not connect to any existing node but creates a disconnected component occupied by it alone.
In other words, the newly arriving node makes connection with node with probability
| [S15] |
where is the degree of the node plus one and
| [S16] |
always equals 1 (the first node is in its own component); afterward, the CRP displays path dependence, and the customer is assigned to table k given a parameter value and the previous assignment of customers:
| [S17] |
This model generates several disjoint connected components. We randomly connect these components to generate a giant component and choose to connect components using low-degree nodes to avoid skewing the degree distribution. Through this procedure we generated a model network with 500 nodes and 1,008 edges that is broadly similar to the topology of the empirical network of published chemical relationships, although not as close as the sampled network described in the previous section (see below).
Finally, to facilitate visualization, we rewired the network to make it as planar as possible. We initialize the algorithm by applying a force-directed layout algorithm to the network. We then iterate the following steps:
-
i)
Calculate the number of crossings between edges in the network.
-
ii)
Select an edge at random.
-
iii)
Make a degree-preserving rewiring by choosing another nearby edge and swapping endpoints to produce either edges and or and .
-
iv)
Apply the force-directed layout algorithm and check the number of crossings.
-
v)
If the number of crossings decreases, accept the rewiring and go to step i.
-
vi)
If the number of crossings stays the same or increases, accept the state with probability , where and are the new and the old numbers of edge intersections, respectively, and T is the simulated (strictly positive) temperature that decreases with iterations [i.e., simulated annealing (62)].
We iterated this procedure until the number of crossings was as small as possible (the network was as planar as it could be). In addition to making the histories of particular strategies much easier to visualize, this rewiring procedure had the pleasant side effect of generating realistic network features like triangles and other loops not generated by the Chinese Restaurant Process.
We note, however, that our generative model of discovery can be applied to any underlying network. This model network was created for illustrative purposes, to allow us to efficiently visualize the behavior of various strategies, discover optimized strategies for this network, and illustrate those optimal strategies (Fig. 2 B–D).
S6.5) Comparison of Empirical, Sample, and Model Networks.
To demonstrate that the forest fire sample and the planar CRP networks have broad degree distributions comparable to that found in the empirical network, we plot the degree and cumulative degree distributions for the three networks in Figs. S8–S10. Recall that the cumulative degree distribution shows the probability for each degree d that a randomly chosen node has degree .
We see that the empirical network is indeed fat-tailed, with the cumulative distribution indicating a cutoff at high degrees (Fig. S8). The distribution is almost definitely not a power law; likelihood ratio tests (45, 46) indicate that a stretched exponential, a log-normal, or a truncated power law all provide significantly better models of the data when we fit the entire distribution. A log-normal distribution with and provides the highest-likelihood fit to the whole distribution (shown in Fig. S8); the fit is significantly more likely () than stretched exponential or truncated power law. Fits and tests followed the maximum-likelihood procedure developed in ref. 45 as implemented in ref. 46.
To get a sense of the scaling behavior for comparison with the model and sample networks, we also fit the distribution beginning at . Once again a stretched exponential, a log-normal, or a truncated power-law distribution provides a significantly better fit than a power law. Tests between these distributions indicate that the stretched exponential provides the best (most likely) fit in the “scaling region,” with and . Although the stretched exponential is not significantly better than the truncated power law (), it is significantly better than a log-normal that has been fitted to the scaling region (). The exponent for the best-fitting truncated power law (with relatively slow-falling exponential truncation with ) is ; this fit in turn is not significantly better than the log-normal ().
For the forest fire sample (Fig. S9), we see a clear signal of a fat tail, with the cumulative distribution showing a cutoff at high degrees. Maximum-likelihood fits with fat-tailed distributions are significantly better than exponential, whether we start the fit at a degree of 1 or a degree of 10 (except, in the latter case, a pure power law). For fits beginning at degree 2 (as in the sampling process), likelihood-ratio tests indicate that stretched exponential or truncated power-law distributions provide significantly better fits than exponential, power law, or log-normal. Although the truncated power law does provide a slightly better fit, the improvement over the stretched exponential is not significant. The exponent for the best-fitting truncated power-law is ; as before, the exponential truncation is very slow (). For fits beginning at degree 10 (as in the empirical network and where the cumulative distribution has a slight turn), likelihood-ratio tests show a truncated power law giving a significantly better fit than exponential, power law, stretched exponential, and log-normal. The exponent for the best-fitting truncated power law when the fit begins at degree 10 is remarkably close to the empirical network: , again with (very) slow truncation ().
Fig. S9.
The degree distribution (green) and cumulative degree distribution (blue) for the forest fire sample network used in searching for efficient strategies.
For the planar network (Fig. 2 B–D and Fig. S10), the small size of the network makes it difficult to see much signal of a fat tail and results are somewhat sensitive to the choice of where to begin fitting; starting values below a degree of 5 (where the distribution has a pronounced “turn”) yield maximum-likelihood fits that are not significantly better than exponential. Nevertheless, with fits beginning at degree 5, the distribution is fitted by a power law with exponent . This is a significantly better fit than either an exponential or a log-normal, but ratio tests do not reveal a significant difference from a truncated power law or a stretched exponential.
S6.6) Costs and Benefits.
To determine the efficiency of a particular strategy for choosing experiments, we need to define a loss function that trades off the cost against the benefit of performing an experiment. Recall the assumption that both successful and failed experiments have the same cost; thus the total cost of a particular strategy up to time t is given by
| [S18] |
For benefit, we focus only on “new” discoveries, i.e., on previously unknown chemical relationships, as counted in the time-ordered set :
| [S19] |
We can imagine exploring other benefits in the future, such as improvements to the search efficiency of the network or centralization of the network topology.
We can then define the relative loss at time t as the number of experiments per new discovery,
| [S20] |
where the in the denominator prevents the cost from going to infinity when .
For a given strategy, we can estimate the expected relative loss for any target benefit (i.e., number of novel relationships discovered). We run the generative model with those strategy parameters until the target benefit is reached and repeat this process a large number of times (, or ; these runs required use of the Cray supercomputer Beagle at the University of Chicago/Argonne National Laboratory). We then average the relative loss over those instances to estimate the expected relative loss,
| [S21] |
where is the relative loss in run i when the desired benefit is achieved.
S6.7) Finding Efficient Strategies.
The quantity can be used as an objective function in an optimization procedure to find highly efficient strategies. For a given novelty level/benefit—say, such that 20% of the network has been discovered—we compute the expected relative loss for a particular set of parameters ; call this . We can search for the most efficient parameters (i.e., the ones that minimize relative loss), using simulated annealing (62). For a given point in the annealing schedule, the “temperature” will be T. Given parameters we apply slight perturbations to propose a new parameter set and compute . If , we automatically accept the move. Otherwise, we accept with probability . The temperature is initially high, meaning moves that increase the relative loss can be permitted and the annealing process can escape local minima. The temperature is slowly lowered, allowing the process to “home in” on the minimum of the expected relative loss.
These optimization calculations took months of computer time, using dozens of cores on the supercomputer Beagle. Optimization calculations were implemented in a blend of C++ and the new parallel programming language Swift/Turbine. Swift/Turbine allowed us to use the Beagle resources with maximum efficiency, rapidly distributing calculations of relative loss for given parameter sets and benefit across available Beagle cores and aggregating the results into the expected value quantities that feed into the simulated annealing algorithm. Because we need to optimize over a random variable —and because the calculation of one draw of this random variable, i.e., a single simulated history of the discovery process, is itself computationally intensive (often on the order of minutes) and hard to parallelize (requiring frequent recalculation of network properties like distance)—we could perform optimizations on the sample network only through incredibly efficient allocation of compute cycles. Swift/Turbine made this efficient allocation possible.
S6.8) Putting Bounds on Efficient Strategy Parameters.
To put reasonable bounds on the optimal strategy parameters, we modified the simulated annealing algorithm (described above) so that the temperature remained at throughout the process. Effectively, we sampled from the “energy surface” defined by the objective function , using a standard Metropolis–Hastings implementation of Markov chain Monte Carlo. Concretely, we initiated a Markov chain over the parameter space for each target benefit , starting at the optimal parameter set identified by simulated annealing. We estimated the objective function with simulations of the discovery process for a given parameter set and allowed the chain to run for between 1,000 and 2,000 cycles (each cycle proposes a new value for each parameter in the parameter set). We tuned the proposal distribution for new parameters such that of proposals were rejected. We then subsampled from the resulting chain to reduce autocorrelation. In Table S1 we give a range for each parameter that contains of the parameter values observed in the sample.
We interpret these ranges as follows. When parameters have large ranges, the objective function is relatively flat along those directions; i.e., it is insensitive to large variations in the parameter. We attend particularly to cases where the parameter range crosses zero, meaning the objective function is not even sensitive to the sign of the parameter. Note that in some cases we discovered parameter sets with smaller relative loss than those identified by simulated annealing. Recall, however, that relative loss is a random variable and its expected value must be estimated by repeated sampling. These newly discovered optimal parameter sets rarely differed by more than 1 SD in expected relative loss; they typically varied in “soft” directions, i.e., those parameters with large and/or nonsignificant ranges; and when they did vary for significant parameters, never changed the sign of the parameter.
S6.9) Strategy Movies.
To convey the difference in strategy most effectively, we created several “movies” showing the average history (i.e., sequence of links discovered) when the planar model network is explored using various strategies. We give the URLs below, with the warning that some of the movie files are quite large (several gigabytes) and can take a long time to download. These movies show how each strategy tends to explore a network and reveals why they become inefficient.
Exploration according to the strategy inferred from MEDLINE data: https://www.dropbox.com/s/6snrxexkncd7s3o/medline.mov?dl=0
The strategy that explores the network at random: https://www.dropbox.com/sh/w75o0wf6r48q2gr/AABH7Yj1rf0qouEeZiUBNieCa?dl=0&preview=Random.mov.
The most efficient strategy for exploring the first 10% of the planar network: https://www.dropbox.com/sh/w75o0wf6r48q2gr/AABH7Yj1rf0qouEeZiUBNieCa?dl=0&preview=10-per-cent-optimum.mov.
The most efficient strategy for exploring the first 20% of the planar network: https://www.dropbox.com/sh/w75o0wf6r48q2gr/AABH7Yj1rf0qouEeZiUBNieCa?dl=0&preview=20-per-cent-optimum.mov.
The most efficient strategy for exploring the first 50% of the planar network: https://www.dropbox.com/sh/w75o0wf6r48q2gr/AABH7Yj1rf0qouEeZiUBNieCa?dl=0&preview=50-per-cent-optimum.mov.
The most efficient strategy for exploring the entire network: https://www.dropbox.com/sh/w75o0wf6r48q2gr/AABH7Yj1rf0qouEeZiUBNieCa?dl=0&preview=100-per-cent-optimum.mov.
A strategy that places a premium on connecting nodes with large degrees: https://www.dropbox.com/sh/w75o0wf6r48q2gr/AABH7Yj1rf0qouEeZiUBNieCa?dl=0&preview=Premium-on-notoriety.mov.
A strategy that has a preference for large degrees in the lower-degree node and small degrees in the higher-degree node, leading to an overall preference for small differences between node degrees: https://www.dropbox.com/sh/w75o0wf6r48q2gr/AABH7Yj1rf0qouEeZiUBNieCa?dl=0&preview=Reversed-ranks.mov.
S7) Random Discovery: An Analytically Tractable Special Case
S7.1) Random Discovery with No Coordination.
Consider an undirected graph, , where V is a set of vertices and E is a set of edges.
Define
| [S22] |
so that is the number of distinct unordered pairs of vertices, i.e., the number of potential edges in the full graph over V.
Let us start with disconnected vertices. Let m be the number of edges that have been discovered so far; at this point, . Then sample pairs of distinct vertices at random and uniformly until a new edge (i.e., pair of distinct vertices in the set E that has not been seen before) is discovered. When a new edge is discovered, increment m by 1. Repeat this process until the whole graph is discovered (when ).
What is the expected relative loss for such a procedure when j edges have been discovered (i.e., the average number of trials required to find a new edge)? What is its variance?
We should expect that, given the iteration of the process, the new edge of the graph should be discovered after trials, where
| [S23] |
| [S24] |
Note that the success probability for a trial is just the number of edges that remain to be discovered divided by the number of distinct vertex pairs . The distribution is just a geometric distribution, with well-known mean and variance:
| [S25] |
| [S26] |
We define loss as the number of unsuccessful trials or experiments. Relative loss is defined as the number of unsuccessful trials per discovery. Then we can calculate the relative loss to discover j edges as
| [S27] |
where the sum over gives the loss.
We can compute the expected relative loss easily, as the expectation operator distributes over addition:
| [S28] |
| [S29] |
| [S30] |
| [S31] |
Using algebra and the delta method, we can also estimate its variance. We get
| [S32] |
| [S33] |
| [S34] |
| [S35] |
Note that the covariance term vanishes as the random variables are independent. Recall also that counts the number of distinct unordered pairs of vertices, i.e., the number of potential edges.
S7.2) Random Discovery with Complete Coordination.
As before, we have a graph with vertices and edges.
In the previous case, pairs of nodes were chosen at random for testing but could be chosen repeatedly, whether the test was successful (i.e., the pair was in the graph G) or unsuccessful (i.e., the pair was not in the graph G). In a regime of complete coordination, all failed experiments (i.e., all pairs that are sampled and found not to be in the graph) as well as all successful experiments (i.e., those that are sampled and found to be in the graph) are immediately and universally visible. Scientists therefore do not repeat these experiments. We model this complete coordination regime by ordering all possible experiments in a random queue, so that every experiment is performed only once.
Imagine that we have performed i nonrepetitive experiments and discovered j new edges (). As before, we use to denote the number of distinct unordered pairs of vertices, i.e., the number of possible distinct experiments. The probability of j successes in i trials is hypergeometric,
| [S36] |
and the expected value and variance of the number of successes j after i experiments are given by
| [S37] |
| [S38] |
As before, the relative loss after i experiments is defined as
| [S39] |
Using the standard approximation , the lower bound of is
| [S40] |
A better approximation [66] is given by
| [S41] |
where
| [S42] |
| [S43] |
| [S44] |
and
| [S45] |
Using the delta method, we can also calculate the variance for relative loss:
| [S46] |
| [S47] |
| [S48] |
S7.3) The Benefit of Coordination.
We can quantify the benefit of coordination by comparing the expected relative loss in the uncoordinated and coordinated cases, i.e., measuring their relative efficiency:
| [S49] |
Recall that in the uncoordinated case,
| [S50] |
and in the coordinated case, to good approximation,
| [S51] |
It follows that the benefit of coordination is actually independent of the total size of the graph and depends only on the number of edges to be discovered:
| [S52] |
| [S53] |
| [S54] |
This has two counterintuitive implications. First, the additional efficiency gained by complete coordination can be similar for a small, dense graph and a large, sparse one, as long as the number of edges to be discovered is comparable. Second, we see that there will be little advantage to coordination for small values of j, i.e., for the initial exploration of a graph. When j is large (on the same order as ), we see substantial returns to coordination. See Fig. S11 for a visualization of this result for random discovery. Fig. S11 also shows simulations of coordinated discovery using MEDLINE and optimal strategies; here we demonstrate that coordinating research substantially decreases the costs of discovery—the number of failed or duplicate experiments—regardless of strategy.
Acknowledgments
We thank Mike Wilde and Tim Armstrong for Swift implementations of our code on the Beagle supercomputer; Mike Papka and Ti Leggett for help parallelizing our code; research assistants Mahmoud Bahrani, Simo Huang, David Kates, Val Michelman, and Nathan Worchester for help compiling prize-winner data, as well as testing our annotations; Stefano Allesina, Carl Bergstrom, and anonymous reviewers for comments on the manuscript; the Computation Institute at University of Chicago for access to and help with the Peta-Scale Active Data Store and Beagle; Thomson Reuters for citation information; Jeff Alstott for help with his Python package powerlaw; and Enthought, Inc., for help with Python programming. This work was supported by National Science Foundation Grant SBE 0915730, National Institutes of Health Grants 1P50MH094267 and U01HL108634-01, Defense Advanced Research Projects Agency Big Mechanism contract W911NF1410333, AFOSR Grant FA9550-15-1-0162, and a John Templeton Foundation grant to the Metaknowledge Network.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
*The notion that linking distant literatures is hard but potentially fruitful underwrites Swanson’s work on literature-based discovery (31).
†Scientists often study several entities in combination. This complicates the modeling, so we approximate the discovery process with dyadic strategies.
‡Some values of and describe a mechanism analogous to preferential attachment (21, 33), in which researchers choose concepts in proportion to the product of their degrees. Our model encodes many types of preferential attachment, e.g., versions that are superlinear in the degrees. We find that such preferential attachment strategies can be much more efficient for discovery.
§Observed behavior is generated by the interaction between preferences and the evolving set of opportunities. This makes interpretation subtle. For example, when considering chemicals in different connected components, a specific opportunity to combine them would be preferred (i.e., has a higher probability than an opportunity to connect similar chemicals at finite distance). Over time, however, more nodes enter the giant component. Hence, fewer opportunities exist to connect nodes in different components, leading to their small absolute number (Figs. S3B and S6).
¶We assume that published research reflects the underlying distribution of research effort in a relatively undistorted way. Recent survey data on scientific choice are consistent with this assumption (41). Although we interpret Fig. 1 and Fig. S6D to imply that scientists pursue less risky projects over time, it is possible that scientists pursue such projects with the same intensity, but that fewer succeed and are published in later periods. We cannot tackle this issue directly, but consider how effort is screened by experimental failure, publication bias, etc., to produce the distribution of published choices. Our interpretation assumes that although a priori “risky” strategies (like combining two distant, low-degree chemicals) may fail more often than conservative alternatives, the risk is not so high that the published record no longer reflects the underlying distribution of effort. It also requires that risky strategies do not become much riskier over time. If the selection process has these plausible properties—i.e., it is well behaved and near stationary—then changes in the observed distribution and inferred parameters will track changes in the unobserved distribution of research effort and scientific choice.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1509757112/-/DCSupplemental.
††In undirected knowledge networks, degree is proportional to more sophisticated centrality measures like PageRank, but is trivially computed. We prefer degree centrality over alternatives like betweenness centrality because it is locally visible to scientists and more likely to influence their choice of chemical combinations. Alternative centrality measures could easily be incorporated, but increase computational complexity and decrease conceptual plausibility.
References
- 1.Kleinberg J, Oren S. Mechanisms for (Mis)Allocating Scientific Credit, STOC ’11. Association for Computing Machinery; New York: 2011. pp. 529–538. [Google Scholar]
- 2.Foster JG, Rzhetsky A, Evans JA. Tradition and innovation in scientists’ research strategies. Am Sociol Rev. 2015;80(5):875–908. [Google Scholar]
- 3.Weisberg M, Muldoon R. Epistemic landscapes and the division of cognitive labor. Philos Sci. 2009;76(2):225–252. [Google Scholar]
- 4.Mason W, Watts DJ. Collaborative learning in networks. Proc Natl Acad Sci USA. 2012;109(3):764–769. doi: 10.1073/pnas.1110069108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tria F, Loreto V, Servedio VDP, Strogatz SH. The dynamics of correlated novelties. Sci Rep. 2014;4:5890. doi: 10.1038/srep05890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cokol M, Iossifov I, Weinreb C, Rzhetsky A. Emergent behavior of growing knowledge about molecular interactions. Nat Biotechnol. 2005;23(10):1243–1247. doi: 10.1038/nbt1005-1243. [DOI] [PubMed] [Google Scholar]
- 7.Grzybowski BA, Bishop KJM, Kowalczyk B, Wilmer CE. The ‘wired’ universe of organic chemistry. Nat Chem. 2009;1(1):31–36. doi: 10.1038/nchem.136. [DOI] [PubMed] [Google Scholar]
- 8.Rzhetsky A, Wajngurt D, Park N, Zheng T. Probing genetic overlap among complex human phenotypes. Proc Natl Acad Sci USA. 2007;104(28):11694–11699. doi: 10.1073/pnas.0704820104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Quine WV. Main Trends in Recent Philosophy: Two Dogmas of Empiricism. The Philosophical Review. 1951;60(1):20–43. [Google Scholar]
- 10.Latour B. Science in Action: How to Follow Scientists and Engineers Through Society. Harvard Univ Press; Cambridge, MA: 1987. [Google Scholar]
- 11.Callon M, Law J, Rip A. Mapping the Dynamics of Science and Technology: Sociology of Science in the Real World. Macmillan; New York: 1986. [Google Scholar]
- 12.Evans JA. Industry collaboration, scientific sharing and the dissemination of knowledge. Soc Stud Sci. 2010;40(5):757–791. [Google Scholar]
- 13.Newell A, Simon HA. Human Problem Solving. Prentice Hall, Englewood Cliffs, NJ; 1972. [Google Scholar]
- 14.Newman M. The structure and function of complex networks. SIAM Rev. 2003;45(2):167–256. [Google Scholar]
- 15.Hewett M, et al. PharmGKB: The pharmacogenetics knowledge base. Nucleic Acids Res. 2002;30(1):163–165. doi: 10.1093/nar/30.1.163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gothard CM, et al. Rewiring chemistry: Algorithmic discovery and experimental validation of one-pot reactions in the network of organic chemistry. Angew Chem Int Ed Engl. 2012;51(32):7922–7927. doi: 10.1002/anie.201202155. [DOI] [PubMed] [Google Scholar]
- 17.Uzzi B, Mukherjee S, Stringer M, Jones B. Atypical combinations and scientific impact. Science. 2013;342(6157):468–472. doi: 10.1126/science.1240474. [DOI] [PubMed] [Google Scholar]
- 18.Beam E, Appelbaum LG, Jack J, Moody J, Huettel SA. Mapping the semantic structure of cognitive neuroscience. J Cogn Neurosci. 2014;26(9):1949–1965. doi: 10.1162/jocn_a_00604. [DOI] [PubMed] [Google Scholar]
- 19.Shi F, Foster JG, Evans JA. Weaving the fabric of science: Dynamic network models of science’s unfolding structure. Soc Networks. 2015;43:73–85. [Google Scholar]
- 20.Bourdieu P. The specificity of the scientific field and the social conditions for the progress of reason. Soc Sci Inf (Paris) 1975;14(6):19–47. [Google Scholar]
- 21.Barabasi AL, Albert R. Emergence of scaling in random networks. Science. 1999;286(5439):509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 22.Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 23.Kleinberg JM. Navigation in a small world. Nature. 2000;406(6798):845. doi: 10.1038/35022643. [DOI] [PubMed] [Google Scholar]
- 24.Latour B, Woolgar S. Laboratory Life: The Construction of Scientific Facts. Princeton Univ Press; Princeton: 1986. [Google Scholar]
- 25.Easley D, Kleinberg J. Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge Univ Press; Cambridge, UK: 2010. [Google Scholar]
- 26.Salganik MJ, Dodds PS, Watts DJ. Experimental study of inequality and unpredictability in an artificial cultural market. Science. 2006;311(5762):854–856. doi: 10.1126/science.1121066. [DOI] [PubMed] [Google Scholar]
- 27.Poincaré H. In: The Creative Process: A Symposium. Ghiselin B, editor. Univ of California Press; Berkeley, CA: 1952. [Google Scholar]
- 28.Carnabuci G, Bruggeman J. Knowledge specialization, knowledge brokerage and the uneven growth of technology domains. Soc Forces. 2009;88(2):607–641. [Google Scholar]
- 29.Leahey E, Beckman C, Stanko T. 2013. Prominent but Less Productive: The Impact of Interdisciplinarity on Scientists' Research. arXiv:1510.06802.
- 30.March JG. Exploration and exploitation in organizational learning. Organ Sci. 1991;2(1):71–87. [Google Scholar]
- 31.Swanson DR. Medical literature as a potential source of new knowledge. Bull Med Libr Assoc. 1990;78(1):29–37. [PMC free article] [PubMed] [Google Scholar]
- 32.Burt RS. Structural holes and good ideas. Am J Sociol. 2004;110(2):349–399. [Google Scholar]
- 33.Barabasi AL, et al. Evolution of the social network of scientific collaborations. Physica A Stat Mech Appl. 2002;311(3-4):590–614. [Google Scholar]
- 34.Krauthammer M, Rzhetsky A, Morozov P, Friedman C. Using BLAST for identifying gene and protein names in journal articles. Gene. 2000;259(1-2):245–252. doi: 10.1016/s0378-1119(00)00431-5. [DOI] [PubMed] [Google Scholar]
- 35.Wozniak J, et al. 2013. Swift/T: Large-scale application composition via distributed-memory dataflow processing. 95–102. 13th International Symposium on Cluster, Cloud and Grid Computing (Institute for Electrical and Electronics Engineers, New York), pp 95–102.
- 36.Wozniak JM, et al. 2012. Turbine: A distributed-memory dataflow engine for extreme-scale many-task applications. Proceedings of the 1st ACM SIGMOD Workshop on Scalable Workflow Execution Engines and Technologies. (Association for Computing Machinery, New York), pp 5:1–5:12.
- 37.Ioannidis JP. Why most published research findings are false. PLoS Med. 2005;2(8):e124. doi: 10.1371/journal.pmed.0020124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ioannidis JPA. How to make more published research true. PLoS Med. 2014;11(10):e1001747. doi: 10.1371/journal.pmed.1001747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Merton RK. Priorities in scientific discovery: A chapter in the sociology of science. Am Sociol Rev. 1957;22:635–659. [Google Scholar]
- 40.Gieryn TF. Problem retention and problem change in science. Sociol Inq. 1978;48(3–4):96–115. [Google Scholar]
- 41.Bateman TS, Hess AM. Different personal propensities among scientists relate to deeper vs. broader knowledge contributions. Proc Natl Acad Sci USA. 2015;112(12):3653–3658. doi: 10.1073/pnas.1421286112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jones BF. The burden of knowledge and the “death of the renaissance man”: Is innovation getting harder? Rev Econ Stud. 2009;76(1):283–317. [Google Scholar]
- 43.Gernter J. The Idea Factory: Bell Labs and the Great Age of American Innovation. Penguin; New York: 2012. [Google Scholar]
- 44.Azoulay P, Stuart T, Wang Y. Matthew: Effect or Fable? Management Science. 2014;60(1):92–109. [Google Scholar]
- 45.Clauset A, Shalizi C, Newman M. Power-law distributions in empirical data. SIAM Rev. 2009;51(4):661–703. [Google Scholar]
- 46.Alstott J, Bullmore E, Plenz D. Powerlaw: A Python package for analysis of heavy-tailed distributions. PLoS One. 2014;9(1):e85777. doi: 10.1371/journal.pone.0085777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Medawar PB. The Art of the Soluble. Methuen; London: 1967. [Google Scholar]
- 48.Peirce CS. The probability of induction. Popular Science Monthly. 1878;12:705–718. [Google Scholar]
- 49.Busch L, Lacy W, Sachs C. Perceived criteria for research problem choice in the agricultural sciences-A research note. Soc Forces. 1983;62(1):190–200. [Google Scholar]
- 50.Zuckerman H. Theory choice and problem choice in science. Sociol Inq. 1978;48(3–4):65–95. [Google Scholar]
- 51.Knorr KD. 1981. The Social Process of Scientific Investigation, Sociology of the Sciences A Yearbook, eds Knorr KD, Krohn R, Whitley R (Springer, Dordrecht, The Netherlands) Vol 4, pp 25–52.
- 52.Kitcher P. The division of cognitive labor. J Philos. 1990;87(1):5–22. [Google Scholar]
- 53.Payette N. 2012. Models of Science Dynamics, Understanding Complex Systems, eds Scharnhorst A, Brner K, Besselaar Pvd (Springer, Berlin), pp 127–157.
- 54.Ding WW, Murray F, Stuart TE. Gender differences in patenting in the academic life sciences. Science. 2006;313(5787):665–667. doi: 10.1126/science.1124832. [DOI] [PubMed] [Google Scholar]
- 55.Guimerà R, Uzzi B, Spiro J, Amaral LAN. Team assembly mechanisms determine collaboration network structure and team performance. Science. 2005;308(5722):697–702. doi: 10.1126/science.1106340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Shwed U, Bearman PS. The temporal structure of scientific consensus formation. Am Soc Rev. 2010;75(6):817–840. doi: 10.1177/0003122410388488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wuchty S, Jones BF, Uzzi B. The increasing dominance of teams in production of knowledge. Science. 2007;316(5827):1036–1039. doi: 10.1126/science.1136099. [DOI] [PubMed] [Google Scholar]
- 58.Petersen AM, et al. Reputation and impact in academic careers. Proc Natl Acad Sci USA. 2014;111(43):15316–15321. doi: 10.1073/pnas.1323111111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kuhn T. The Structure of Scientific Revolutions. Univ of Chicago Press; Chicago: 1962. [Google Scholar]
- 60.Johnson NL, Kotz S, Balakrishnan N. Continuous Univariate Distributions. Wiley; New York: 1995. [Google Scholar]
- 61.Snijders TA. Markov chain Monte Carlo estimation of exponential random graph models. J Soc Struct 3. 2002;3(2):1–40. [Google Scholar]
- 62.Kirkpatrick S, Gelatt CD, Jr, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 63.Torvik VI, Weeber M, Swanson DR, Smalheiser NR. A probabilistic similarity metric for medline records: A model for author name disambiguation. J Am Soc Inf Sci Technol. 2005;56(2):140–158. [PMC free article] [PubMed] [Google Scholar]
- 64.Goodman LA. On simultaneous confidence intervals for multinomial proportions. Technometrics. 1965;7(2):247–254. [Google Scholar]
- 65.Leskovec J, Faloutsos C. Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Association for Computing Machinery; New York: 2006. Sampling from large graphs; pp. 631–636. [Google Scholar]
- 66.Hidiroglou MA. An approximation of the inverse moments of the positive hypergeometric distribution. Communications in Statistics-Theory and Methods. 1978;7(15):1475–1487. [Google Scholar]