Intracellular Scaling Mechanisms

Abstract

Organelle function is often directly related to organelle size. However, it is not necessarily absolute size but the organelle-to-cell-size ratio that is critical. Larger cells generally have increased metabolic demands, must segregate DNA over larger distances, and require larger cytokinetic rings to divide. Thus, organelles often must scale to the size of the cell. The need for scaling is particularly acute during early development during which cell size can change rapidly. Here, we highlight scaling mechanisms for cellular structures as diverse as centrosomes, nuclei, and the mitotic spindle, and distinguish them from more general mechanisms of size control. In some cases, scaling is a consequence of the underlying mechanism of organelle size control. In others, size-control mechanisms are not obviously related to cell size, implying that scaling results indirectly from cell-size-dependent regulation of size-control mechanisms.

Cells grow, shrink, and change shape over time. Subcellular components use dynamic and robust mechanisms—from "molecular rulers" to limiting pools of cytoplasmic components—to regulate their size accordingly.

A cell is a highly organized unit in which functions are compartmentalized into specific organelles. Each cellular organelle carries out a distinct function, which is not only related to its molecular composition but, in many cases, also to its size. The energetic capacity of the mitochondria and the biosynthetic capacity of endoplasmic reticulum (ER) and Golgi networks depend on their surface area. The mitotic spindle must be large enough to span sufficient distance to physically separate chromosomes into two opposite halves of the cell. The contractile ring must be able to span the cell diameter and generate sufficient force to drive ingression. Clearly, size matters. However, in each of these cases, it is not absolute size, but the ratio of organelle to cell size that is critical.

We also know that cell size can vary dramatically even within one organism. Xenopus laevis is an extreme example. The smallest somatic cells are only a few micrometers in diameter, whereas the oocyte and one-cell embryo span over a millimeter. In addition, in many animals, including X. laevis, early cell divisions are rapid with little cell growth, leading to rapidly changing cell size that is often characteristic for early embryogenesis. Thus, this transition from very large to very small cells occurs on the order of hours. Cellular organelles must, therefore, possess dynamic and robust mechanisms to regulate their size, or scale, with the size of the cell.

Strictly speaking, the term scaling describes a mathematical relationship between measured quantities of a system, for example, length, volume, or area. Scaling relations typically take the form of a power law y = x^a, with a being the scaling exponent of the law. For example, the circumference of a sphere scales with its radius, its surface with radius squared, and its volume with radius cubed.

In cell biology, the term “scaling” is often used more loosely to describe the change in organelle size or functional capacity in response to changes in cell size. Simply speaking, larger cells typically have proportionally larger or more organelles (see also Marshall 2015). The key parameter of organelle functional capacity may vary depending on the organelle. Typically, this parameter is volume, surface area, or length, which, for example, are important for centrosome, ER, and mitotic spindle function, respectively. In other cases, the key parameter could be force generation or a biochemical rate. Importantly, in many biological systems, scaling often is imperfect, obscuring the precise scaling relation.

For the purposes of this review, for a system to show scaling, there should be a clear, albeit potentially imperfect, relation between some parameter of cell size and the relevant parameter describing organelle size or functional capacity. Thus, we define scaling mechanisms as those that directly regulate organelle size (or capacity) in response to changes in cell size and distinguish these from size-control mechanisms, which are the subject of reviews elsewhere in this collection (see also Amodeo and Skotheim 2015; Levy and Heald 2015; Marshall 2015; Mitchison et al. 2015). Although scaling and size-control mechanisms are distinct, they are often linked. We will highlight several cases where organelle size-control pathways either inherently show organelle scaling or can be modified to achieve it.

INTRACELLULAR SCALING MECHANISMS

Molecular Rulers

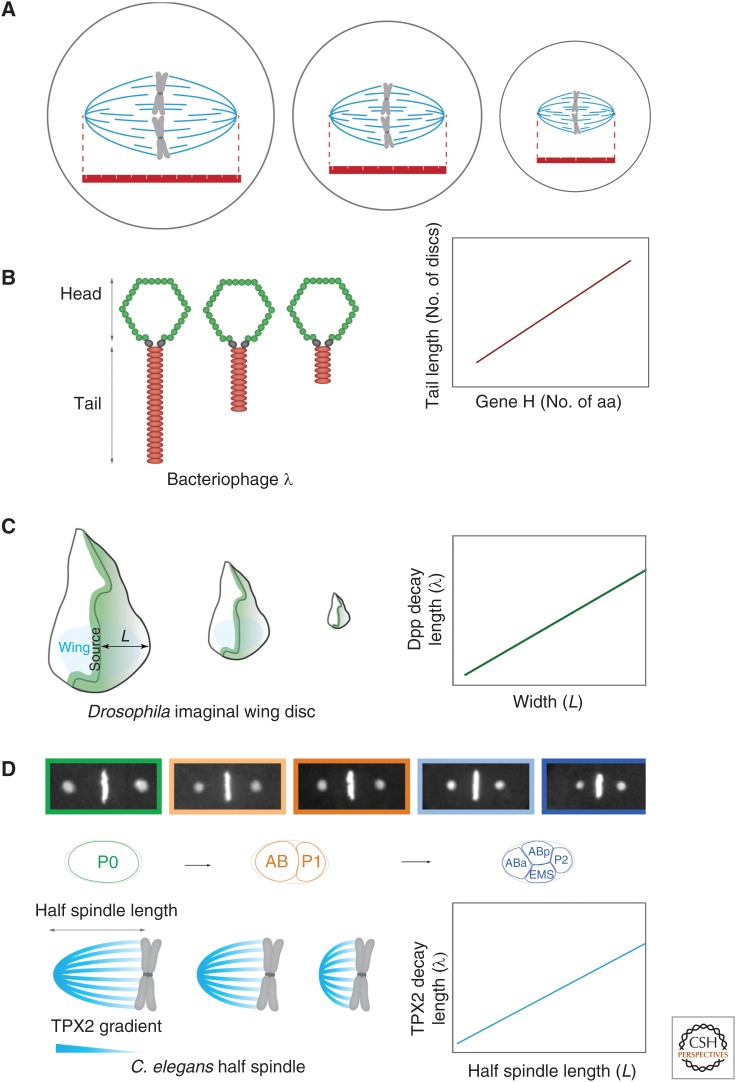
Molecular rulers provide an intuitively simple method for size control. In its simplest form, a molecular ruler provides a structural scaffold with a fixed length and shape, thereby templating the size of the target organelle (Fig. 1A). An example is the product of gene H in the bacteriophage λ, which sets phage tail length (Fig. 1B). Here, tail length is proportional to gene H protein length, with smaller gene H protein products resulting in correspondingly shorter-tailed phage particles (Katsura 1987). YscP plays a similar role in regulating the length of the injectisome needle used by pathogenic bacteria to introduce factors into host cells (Journet et al. 2003; Wagner et al. 2010). The giant protein, nebulin, may have a similar molecular ruler function in actin filament length control in myofibrils, although this remains somewhat controversial (Castillo et al. 2009; Pappas et al. 2010).

Figure 1.

Molecular rulers. (A) In its simplest form, a molecular ruler provides a structural scaffold templating the size of the target organelle. (B) Bacteriophage λ tail length is set by the product of gene H. Tail length correlates with protein length (i.e., number of amino acids). (C) Decapentaplegic (Dpp) gradients scale with tissue size of imaginal discs during Drosophila development. (Adapted from data in Wartlick et al. 2011.) (D) Centrosome size sets mitotic spindle length by controlling the length scale of a TPX2 gradient along spindle microtubules (Greenan et al. 2010).

Although perfectly good size-control mechanisms, these simple molecular rulers have obvious limitations, most significant of which is that protein size must equal organelle size. There are few, if any, proteins that are large enough to account for the majority of cellular structures, and, at least in the context of this review, it is very difficult to see how such a protein ruler could allow the size of an organelle to scale with cell size, or even to be adjusted by the cell without inducing changes in protein sequence.

Other types of “molecular rulers” that are more dynamically specified are potentially better suited to achieve scaling. Such molecular rulers could include structures, such as the putative spindle matrix (Schweizer et al. 2014) and Golgi matrix (Xiang and Wang 2011), which have been proposed to be composed of complex molecular networks. Although these structures are presumably subject to size control and, at least in the case of the spindle matrix, also subject to cell-size-dependent scaling, we know little about how their size is controlled and even less about how their size is scaled appropriately to the size of the cell.

Molecular gradients can also act as rulers, the clearest examples of which can be found during animal development where gradients of morphogens are established across tissues. Cells then read out their position in the gradient from local morphogen concentration. The simplest examples of these gradients are formed by diffusion of morphogen away from a point source. Diffusion of locally produced morphogen coupled to degradation or internalization of the morphogen within the tissue gives rise to an exponentially decaying gradient away from the source. In this case, the length scale of the gradient, λ, is specified by 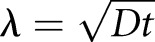, where D is the diffusion coefficient and t is the molecular lifetime. Gradient scaling occurs if D or t varies appropriately with cell size. For example, in the Drosophila wing disc, the degradation of the morphogen decapentaplegic (Dpp) is inversely proportional to and, thus, its lifetime is proportional to wing disc area (L²) (Fig. 1C) (Wartlick et al. 2011). Setting t = L², we find that λ/L is constant. Thus, the gradient length scale is proportional to system length. Scaling of the morphogen bicoid in Drosophila melanogaster embryos is achieved differently. Bicoid is synthesized from an anteriorly enriched local source of mRNA, leading to an exponential gradient extending to the posterior (Grimm et al. 2010). Instead of scaling the gradient length scale as above, differently sized embryos show scaled gradient amplitude (He et al. 2008; Cheung et al. 2013). Consequently, in terms of absolute concentration, the gradient extends further from the anterior in large embryos.

Do gradients play a role in scaling intracellular structures? Many examples of intracellular gradients exist, including the Pom1 gradient (see below); although, in most of these cases, scaling has either not been seen or not been examined. However, one exception is the spindle assembly pathway in the Caenorhabditis elegans embryo. Here, spindle length decreases during development and is set by the length scale of a TPX2 gradient along spindle microtubules (Fig. 1D) (Greenan et al. 2010). TPX2 is the first identified direct effector of RanGTP in spindle assembly (Gruss et al. 2001, 2002). It is a microtubule-associated protein and an activator of the mitotic kinase Aurora A (Tsai et al. 2003), and has been shown to affect spindle length in a number of systems (Bird and Hyman 2008). In C. elegans, the TPX2 gradient and, thus, spindle length correlates with centrosome size (Greenan et al. 2010). The centrosome itself scales with cell size via a limiting pool mechanism (discussed below), meaning that cell, centrosome, and spindle size are all coupled in this system. The Ran gradient and its effectors centered on chromatin appear to play a similar role in regulating spindle length in other systems (Kalab et al. 2002, 2006; Bird and Hyman 2008). Whether the steepness of the Ran gradient or of its effectors actively determines spindle size in these systems is still an open question. Moreover, what specifies the length scale of the Ran gradient and how this would scale with cell size are not known.

Direct Cell-Boundary Sensing

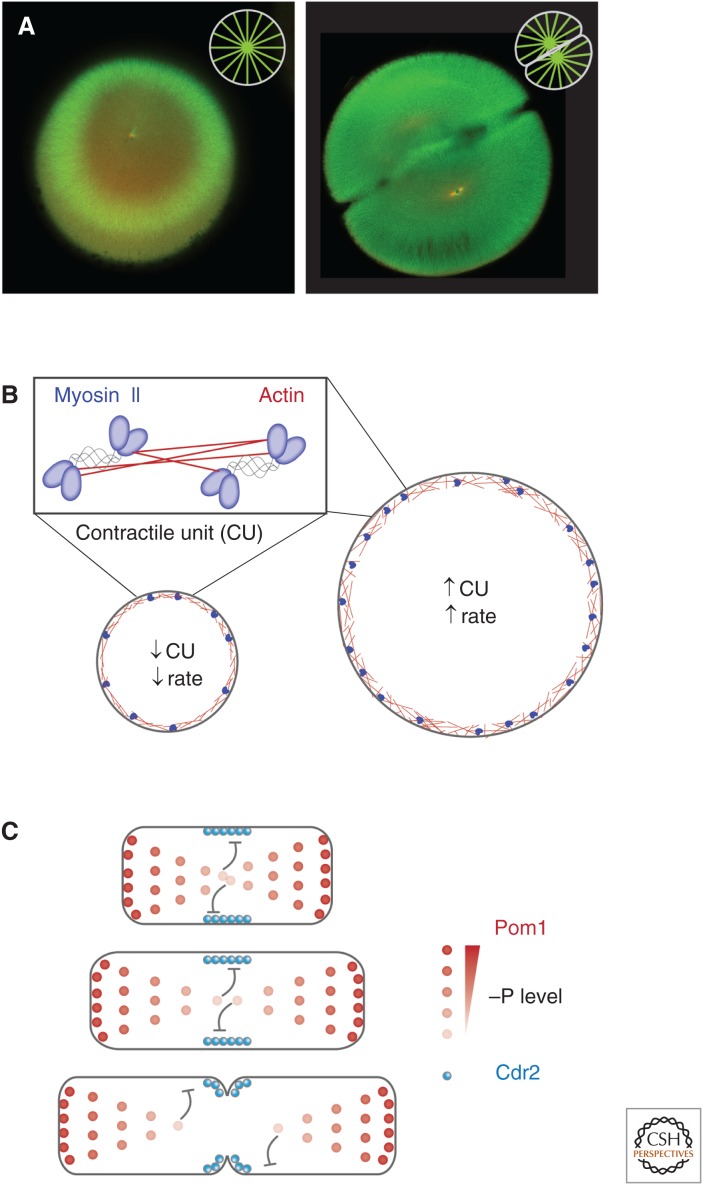
Another quite intuitive mechanism for scaling cellular structures is to simply use the cell itself as a ruler to specify size. Here, the cell boundaries (e.g., the plasma membrane or another component of the cell envelope) provide for size control by directly interacting with the assembling structure, either as an assembly template or by limiting growth (Fig. 2A).

Figure 2.

Direct cell-boundary sensing. (A) Fertilized one- and two-cell stage embryos of Xenopus laevis with microtubules labeled in green and DNA in red. (Image courtesy of Martin Wühr, Harvard Medical School.) Microtubules nucleated from centrosomes expand until they reach the cell boundary, completely filling the cell (insets show schematic representation of astral microtubules). (B) The structural components of the contractile ring, actin, and myosin II assemble directly on the plasma membrane. Thus, the initial size of the ring exactly matches cell diameter. In Caenorhabditis elegans, the number of actomyosin “contractile units” (CU) is dependent on initial ring size and is maintained throughout the constriction process. Constriction rate is set by CU number, ensuring constriction rate scales with initial ring size, and, thus, cytokinesis completes in the same amount of time regardless of initial cell size (Carvalho et al. 2009). (C) In the fission yeast Schizosaccharomyces pombe, a gradient of the cell polarity protein kinase Pom1 directs the positioning of contractile-ring assembly and subsequent cell division. Pom1 inhibits the kinase Cdr2 in a dose-dependent manner. Because of a constant gradient length, as cells elongate, Pom1 levels decrease at the cell middle, eventually allowing cytokinesis to proceed (Moseley et al. 2009).

Possibly the simplest manifestation of such phenomena is for a structure to assemble directly on the plasma membrane. This is exactly what happens with the cytokinetic ring. During anaphase, cues from the mitotic spindle, either the spindle midzone or astral microtubules, or both, trigger the assembly of the cytokinetic ring components at the membrane along the equator of the cell (reviewed in Werner and Glotzer 2008). Once assembled, the major structural components of the contractile ring—actin filaments and the motor myosin II—drive constriction of the ring thereby promoting ingression of membrane to bisect the separating chromosome masses. As ring assembly occurs directly on the membrane, scaling is trivial—the initial size of the ring simply matches the circumference of the cell at the nascent furrow position (Fig. 2B). Intriguingly, in many developmental systems, rapid cell divisions in the absence of intervening growth lead cells to become smaller with each division. Despite this scaling of the ring, the time required for cytokinesis remains roughly constant, apparently caused by a corresponding scaling of constriction rates to cell size (Carvalho et al. 2009; Calvert et al. 2011), a topic we will return to later.

Cell geometry also provides an upper size constraint for growing cellular structures that physically probe cell boundaries. A striking example of such a phenomenon is seen in extremely large vertebrate embryo cells, such as the ∼1200 µm oocyte of the amphibian X. laevis (Fig. 2A) and the ∼600 µm oocyte of the fish Danio rerio. In these cells, interphase asters are nucleated by the centrosomes and expand until they reach the cell boundary, completely filling the cell (Wühr et al. 2010; Mitchison et al. 2012). Again, scaling is trivial—aster size equals cell size. Nonetheless, this ability of interphase asters to precisely fill the cell is critical for the centrosomes to localize to the cell center. The centrosomes are positioned and oriented by dynein pulling forces acting on astral microtubules; these pulling forces are length dependent (Wühr et al. 2010; Kimura and Kimura 2011; Minc et al. 2011). If centrosome-nucleated microtubule arrays are limited by the cell boundary, the length of microtubules and, thus, pulling forces on the centrosome will only balance when the centrosome is precisely in the cell center. Away from the center, centrosomes will experience a force imbalance because of unequal microtubule lengths, which will displace it toward the cell center. Indeed, these giant asters appear to be a mechanism for particularly large cells to find their center and even determine cleavage plane geometry (Wühr et al. 2010; and discussed in detail in Mitchison et al. 2015).

Cell-boundary sensing appears to be a widely used mechanism for center determination (as reviewed in Moseley and Nurse 2010). The fission yeast S. pombe is capable of geometrically monitoring its length and importantly changes in length. In these rod-shaped cells, gradients of the cell division inhibitor kinase Pom1 extend from the cell poles decreasing to the cell center (Martin and Berthelot-Grosjean 2009; Moseley et al. 2009). Pom1 is transported by microtubules that depolymerize on contacting the cell ends, ensuring delivery of Pom1 to the cell poles. Diffusion of Pom1 back to the center is then limited by autophosphorylation-dependent membrane dissociation, yielding a characteristic gradient length scale (Fig. 2C). These inhibitory gradients help guide accumulation of division initiators at midcell (Bhatia et al. 2014; Pan et al. 2014; Rincon et al. 2014). A somewhat similar mechanism operates in Escherichia coli, where the MinCDE system relies on an oscillatory pattern of division inhibitor localization at the two cell poles (Hu et al. 1999; Raskin and de Boer 1999). Initially, the division inhibitor complex MinCD assembles on the membrane at one cell pole. As MinCD accumulates, a MinCD inhibitor MinE is recruited, which in turn triggers dissociation of MinCD. This free MinCD then reassembles at the site furthest away from MinE enrichment, which, because of the rod shape of E. coli, is the opposite pole. Ultimately, these oscillations ensure that the time-averaged concentration of MinCD is lowest at midcell.

Assembly Rates and Dynamic Balance

So far, we have primarily discussed mechanisms that rely on an organelle or cellular structure being directly templated or limited by a pre-existing structure, which in many cases may be the cell itself. Other size-control mechanisms, however, emerge if we consider that the size of a structure often is a consequence of the underlying rates of assembly and/or disassembly.

Balance Mechanism

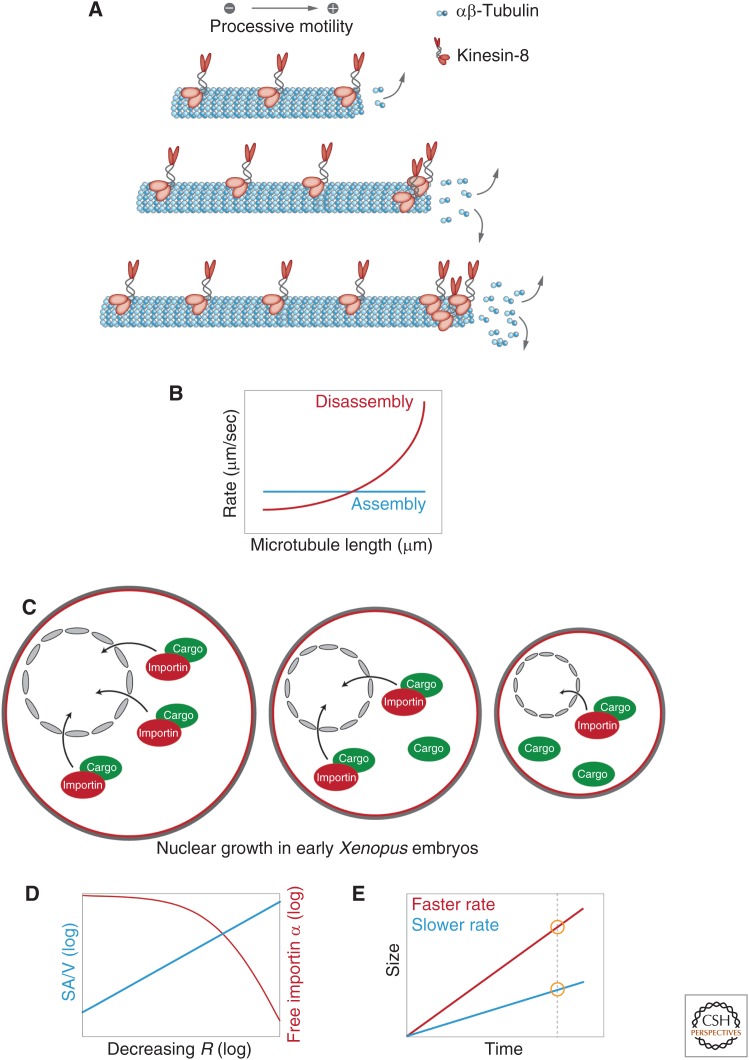
Robust size control can be achieved through so-called dynamic balance models. These models rely on either assembly or disassembly being size dependent such that they balance at one parameter-specified size or balance point. A prototypical model for such a system is flagellar length control in the green alga Chlamydomonas. Here, length-dependent assembly has been proposed to be coupled to length-independent disassembly (Marshall et al. 2005; Chan and Marshall 2012; Marshall 2015). Although the molecular details are still debated, the assembly rate appears inversely related to length, exactly balancing disassembly at only one length. The antennae model for microtubule length control by the motor protein and microtubule depolymerase kinesin-8 functions similarly (Fig. 3A) (Gupta et al. 2006; Varga et al. 2006; Leduc et al. 2012). Kinesin-8 binds uniformly to microtubules. The amount of kinesin-8 recruited to a microtubule is, therefore, proportional to its length. Because kinesin-8 is a highly processive plus-end motor, the pool of microtubule-associated kinesin-8 concentrates at the microtubule plus end where it promotes microtubule depolymerization with longer microtubules accumulating more kinesin-8. As a consequence, the microtubule disassembly rate is proportional to microtubule length, which when coupled to a length-independent polymerization rate results in microtubules of defined length (Fig. 3B). Similar models have been proposed to regulate the length of antiparallel microtubule overlaps at the spindle midzone (Bieling et al. 2010; Subramanian et al. 2013), suggesting that this may be a generic mechanism for size control of microtubule-based structures.

Figure 3.

Assembly rates and dynamic balance. (A) “Antennae model” for microtubule length control, in which accumulation of kinesin-8 leads to length dependent microtubule depolymerization (Varga et al. 2006). (B) A dynamic balance model combining length-dependent disassembly (as in A) and a length-independent assembly leading to a single stably defined steady-state microtubule length. (C) Nuclear growth in early Xenopus embryos is limited by available importin α levels, which are reduced in smaller cells (see D). (D) For spherical cells of radius, R, surface area to volume ratio (SA/V) is inversely related to cell size. In small cells, increased SA/V results in greater sequestration of importin α to the membrane from the cytoplasm, resulting in a reduction in the concentration of free importin α. (E) “Timer model”: A structure that undergoes assembly faster (red) will end up larger than a structure that assembles more slowly (blue) in a given time interval.

Although such balance point models provide an excellent framework for understanding size control, they do not in themselves account for scaling of organelle size. The mitotic spindle, for example, is known to scale with cell size in a number of systems (Wühr et al. 2008; Hara and Kimura 2009; Good et al. 2013; Hazel et al. 2013; Wilbur and Heald 2013), suggesting that if a balance point model is operating, the balance point must depend on cell size. Thus, there must be a mechanism to adjust the relevant rates (either size dependent or size independent) in relation to cell size. Only a few examples of such cell-size-dependent scaling of rates exist, several of which we will discuss here.

One way to scale rates is to render the amount of a given activity (e.g., enzyme concentration) dependent on cell size. We have already noted earlier that the constriction rate of the cytokinetic ring scales with the initial size of the ring and, hence, initial cell diameter (Fig. 2B). This has been studied in two systems to date, Neurosopora crassa (Calvert et al. 2011) and C. elegans (Carvalho et al. 2009). Although the postulated mechanistic details differ, in both cases, scaling of the constriction rate relies on larger cells assembling larger initial rings that are composed of either more myosin motors (Calvert et al. 2011) or more contractile elements (Carvalho et al. 2009). Large rings, therefore, constrict faster, allowing larger cells to divide with overall similar times compared with rings formed in smaller cells. By coupling total contractile activity in the ring to cell size, these cells achieve scaling of constriction rates to ensure total constriction time remains roughly constant across cells of varying size.

In Xenopus, importin α appears to be a key regulator of scaling through its ability to modulate the effective pools of assembly/disassembly factors. Importin α is an essential component of the nuclear import machinery that mediates the passage of proteins from the cytoplasm into the nucleus (reviewed in Görlich and Kutay 1999). Examination of nuclear size regulation in early Xenopus embryos indicated that nuclear size is limited by available importin α levels, which presumably limit import of nuclear factors important for nuclear growth (Levy and Heald 2010). A potential scaling mechanism was revealed when it was shown that reductions in nuclear size correlate with the sequestration of the nuclear transport receptor importin α into membranes (Fig. 3C) (Wilbur and Heald 2013). Importantly, because surface-to-volume ratio is inversely related to cell radius, in small cells, more importin α is sequestered. Consequently, the concentration of free importin α and, thus, nuclear import is reduced, ultimately leading to reduced nuclear growth rates (Fig. 3D).

The same mechanism of importin α sequestration has also been proposed to play a role in spindle scaling. By binding to and sequestering a microtubule destabilizer, Kif2A, cytoplasmic importin α promotes increased spindle length. As cells become smaller and importin α is increasingly bound to the membrane, Kif2A is liberated. The resulting higher levels of free Kif2 promote microtubule depolymerization, resulting in smaller steady-state spindle size (Wilbur and Heald 2013). Such a mechanism fits well with a recent mass balance model of spindle length, with the steady-state spindle size effectively set by the balance of microtubule assembly and disassembly (Reber et al. 2013). Not surprisingly, a number of factors contribute to setting spindle size, and it will be interesting to determine the relevant parameters that govern scaling in different contexts (Dumont and Mitchison 2009; Loughlin et al. 2011; Reber et al. 2013; Wilbur and Heald 2013).

Timer Mechanism

Although dynamic balance point models rely on the relationship between assembly and disassembly pathways, one can also specify size as the product of net assembly and time. In such a timer model, a structure that undergoes assembly faster or for a longer time will end up larger than a structure that assembles more slowly or for a shorter period of time (Fig. 3E). Thus, appropriate dependence of either the time interval or the assembly rate on cell size could account for scaling of organelle size. Although this timer model is appealing, we are not aware of any examples where it is used to achieve scaling. An approximation of such a mechanism can be observed during the rapid initial cleavages typical of early animal development. Here, the cell cycle places time limits on the assembly of structures, and organelles may simply not have enough time to reach their steady-state size. For example, in the one- and two-cell stages of C. elegans development, centrosomes grow exponentially until their disassembly in telophase, suggesting that centrosomes do not reach a stable steady-state size like they do in later divisions (see below) (Decker et al. 2011). Similarly, nuclei assembled in early Xenopus embryos do not reach a steady-state size (Levy and Heald 2010). In both cases, the rapid cell cycle times truncate organelle growth. Thus, one can envision a system in which the balance between net assembly and time can be used to specify the size of a structure. However, as we noted above, it is unclear whether any cells use this timer mechanism to achieve scaling. In the two cases discussed here, limiting time actually interferes with scaling mechanisms operating in these cells.

Limiting Pools

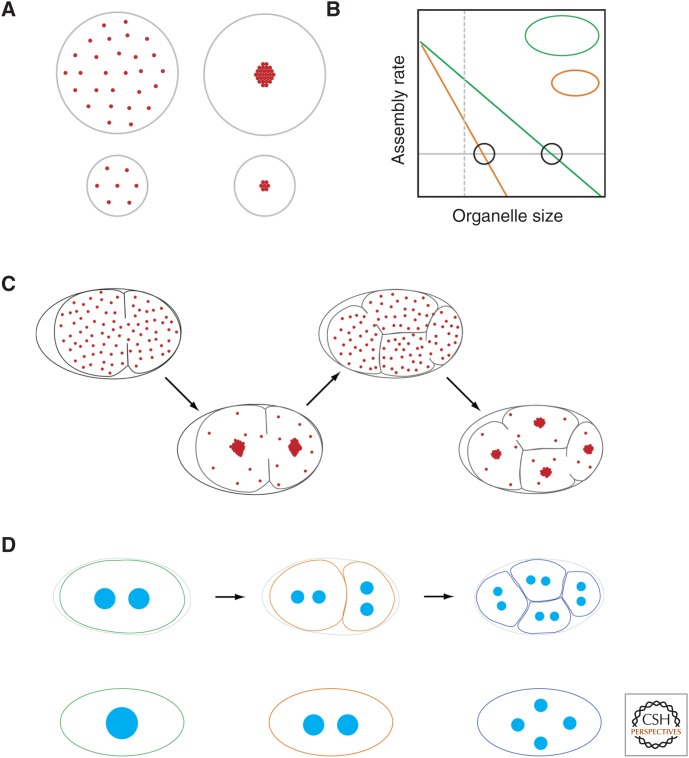
The limiting component or limiting pool hypothesis has recently received much interest as a mechanism for organelle size control (Decker et al. 2011; Chan and Marshall 2012; Goehring and Hyman 2012; Good et al. 2013; Hazel et al. 2013). In its simplest form, a cell starts with a fixed amount of an essential structural molecule, the limiting component. As the organelle is assembled, this component is used up, with final organelle size directly proportional to the starting quantity of the limiting component (Fig. 4A). One particularly attractive feature of limiting component mechanisms is that they often show natural scaling of organelle size to cell size. As long as the initial concentration of limiting component is the same in all cells regardless of size, the total amount of limiting component will be strictly proportional to cell volume. Thus, organelle and cell volume will be strictly proportional.

Figure 4.

Limiting pools. (A) In a simple limiting pool model, a cell has a fixed amount of an essential structural molecule, the limiting component. Once this component is used up, organelle growth ceases. As long as cells begin with a starting amount of the limiting component that is proportional to cell volume, organelle size will scale with cell size. (B) Limiting pools can also work with a dynamic balance model. Organelle growth depletes the cytoplasm of an essential component, thereby reducing the rate of assembly. This depletion of the component will be greater as a function of organelle size in small cells compared with large cells, which start with a larger overall pool. Thus, for a given organelle size (dashed vertical line), the assembly rate in the larger cell is higher than that for the smaller cell. Steady-state size is given by the point at which the rate of disassembly (gray line) exactly matches the assembly rate (intersections marked by circles). Note that this will occur at a larger size for larger cells. (C) A schematic of how limiting amounts of centrosome material set centrosome size in C. elegans embryos (Decker et al. 2011). The total amount of the limiting component is set by the amount of maternally provided cytoplasm in the oocyte, which is then partitioned into cells as a function of cell volume as cells divide. (D) A limiting pool model predicts that the combined total volume of all organelles should be independent of the organelle number. Consequently, for C. elegans, the total volume of the eight centrosomes in the four-cell-stage embryo is equal to the volume of the two centrosomes in the one-cell embryo. Similarly, mutants that differ in centrosome number show corresponding changes in centrosome volume, again such that total volume is constant.

In reality, limiting pool models are generally more complex because of the fact that most cellular organelles are highly dynamic, with their size reflecting a dynamic balance between assembly and disassembly processes that reflect flux of material between organelles and cellular pools of components as we highlighted in the previous section. Thus, limiting components are generally never completely used up. Rather, changes in organelle size will affect cellular pools of available limiting component. As an organelle grows larger, concentrations of the component will be reduced. As an organelle shrinks, concentrations increase. The concentration of available limiting component is, in turn, expected to affect the rate of its incorporation into the organelle and, thus, organelle growth (Fig. 4B). Organelle growth rate, therefore, is a direct function of organelle size.

In this latter, more general realization, the limiting component model behaves exactly like the dynamic balance models described in the previous section, with the limiting pool ensuring organelle size-dependent assembly rates, which when balanced with a fixed disassembly process results in an organelle of specified size. However, if the limiting pool is a function of cell volume as described above, this type of limiting pool mechanism gives rise to a natural cell-size dependence. Because larger cells start with a larger pool, the production of an organelle of a given size will have a reduced effect on the limiting component concentrations compared to the production of the same-sized organelle in a smaller cell. In other words, as an organelle grows in a small cell, the concentration of the limiting component is reduced more quickly as a function of organelle size than in a larger cell (Fig. 4C). Thus, the resulting set point—the organelle size at which assembly rates and disassembly rates balance—will be higher in larger cells and lower in smaller cells.

One prediction of the limiting component model is that the combined total volume of all organelles is independent of the organelle number, as it is the total volume of incorporated component that matters. Indeed this has been shown for C. elegans centrosomes (Fig. 4D). The total volume of all centrosomes is independent of the centrosome number, but is proportional to the cell volume (Decker et al. 2011). The idea is that when centrosomes grow in a finite volume, the cytoplasmic concentration of a limiting factor decreases as centrosomes bind and sequester material from the cytoplasm, reducing the concentration of this factor and slowing centrosome growth. In the case of the C. elegans embryo, the total amount of the limiting component is set by the amount of maternally provided cytoplasm in the oocyte.

Another prediction of the limiting component model is that organelle size is responsive to the amount of limiting component in the system. Higher starting concentrations should allow larger structures. There is evidence for this in the case of C. elegans centrosomes (Decker et al. 2011), for Lamin B as a structural limiting component of the nuclear envelope (Levy and Heald 2010), the limited availability of PAR proteins when establishing cell polarity domain size in C. elegans embryos (Goehring et al. 2011) and for tubulin as a limiting component of setting the overall spindle size in Xenopus (Good et al. 2013; Hazel et al. 2013).

Taken together, the limiting component model appears to be a general and widely prevalent mechanism for both limiting the size of intracellular organelles and achieving organelle size scaling in systems with fast cell cycles and rapidly changing cell volume (Coyne and Rosenbaum 1970; Stephens 1989; Norrander et al. 1995; Bullitt et al. 1997; Elliott et al. 1999; Brangwynne et al. 2009, 2011; Feric and Brangwynne 2013). The great advantage of the limiting component system is that it provides a robust and rapid system that takes advantage of the contribution of a defined amount of maternal cytoplasm to the embryo. Importantly, we should note that the limiting component need not strictly be a structural element.

Demand Sensing

Just as metabolic rates generally scale with the mass of an organism, reflecting the increased demand of a larger organism (although the precise scaling relation is still under debate, see Chan and Marshall 2010, and references therein), larger cells generally have increased demands on organelle function and, thus, require larger or more organelles. Rather than directly coupling organelle size to cell size, an alternative solution is to regulate organelle size in response to metabolic demands.

The regulation of organelle amounts in response to metabolic demand is well studied in the case of both mitochondria and the ER, although the following typically do not directly examine the response to changes in cell size. Muscle cells, for example, respond to increased energy demand by modifying the rates of mitochondrial biogenesis to increase mitochondrial capacity (as reviewed in Moyes 2003). B cells also undergo expansion of the ER as they differentiate into antibody-secreting plasma cells (Wiest et al. 1990). To make these adjustments, cells need to sense an imbalance between demand and capacity and actively restore homeostasis. Sensing implies the existence of a “sensor” and a “reporter” that can be measured; thus, changes can be observed and (ideally) be corrected.

ER proliferation is regulated in response to stress via the unfolded protein response (UPR) (Schuck et al. 2009). When the folding capacity of the ER is exceeded, unfolded or misfolded proteins accumulate in the lumen of the ER. The UPR machinery senses this accumulation, and then activates lipid biosynthesis to promote membrane expansion and the generation of new ER sheets. In addition, UPR triggers transcription of Golgi components needed to support protein export (Travers et al. 2000). Size regulation of the Golgi is an interesting alternative case. The Golgi is an incredibly dynamic organelle, characterized by the constant influx of cargo into the Golgi cisternae from ER exit sites and efflux out via the trans-Golgi network. Cargo influx and efflux occurs through vesicular traffic, meaning that membranes are constantly being added to and removed from the Golgi. Not surprisingly, Golgi cisternae size is dependent on this flux balance, and altering of trafficking pathways can lead to significant changes in Golgi size (Bevis et al. 2002; Bhave et al. 2014). Thus, Golgi size regulation could be considered a variant of the dynamic balance mechanisms discussed previously, only in this case with the balance point set by demand-dependent flux rates into and out of the Golgi cisternae. Because of the complex Golgi morphology and size variation of functionally distinct subcompartments, Golgi size control is likely more complex and must take into account altered transcriptional profiles of secretory cargo, the resident abundance of Golgi complex components, and direct signaling from the Golgi membrane surface (as reviewed in Sengupta and Linstedt 2011). Only recently it was shown that Golgi size and topology influence the size of its products, thereby establishing a direct link between organelle size and function (Ferraro et al. 2014). Other potential examples of demand sensing include mitochondrial networks (Rafelski et al. 2012), vacuole size scaling in yeast (Chan and Marshall 2014), and peroxisomes in the fungus Neurospora (Liu et al. 2011).

WHEN SCALING BREAKS DOWN

It is worth acknowledging that there are clear cases in which scaling fails or simply does not occur. These cases can be quite informative about the biological system. For example, they can reveal physical constraints over which scaling is achievable, limits to what scaling can actually achieve, or how aspects of organelle function (e.g., constraints on number [centrosomes] or a need to distribute organelle function throughout the cytoplasm [peroxisomes]) have necessitated deviations from isometric scaling.

We have discussed mechanisms of mitotic spindle scaling and microtubule length control in several places in this review. However, it has been noted in embryos of both C. elegans (Hara and Kimura 2009; Greenan et al. 2010) and X. laevis (Wühr et al. 2008) that scaling of the spindle breaks down in large cells. This is most clearly observable in early X. laevis embryos in which spindle scaling is only observed after the seventh mitotic division when cells become <100 μm in diameter (Wühr et al. 2008). Before this, spindles remain a fixed length of ∼60 μm, roughly matching the typical length of mitotic spindles assembled in vitro in test tubes, where cell size cannot have any influence on spindle assembly. Scaling of in vitro assembled spindles can be restored if they are assembled in defined volumes of cytoplasm rather than a test tube. In these confined droplets, spindle size is coupled to droplet diameter and scales almost linearly, provided that droplets have a diameter smaller than ∼80 μm. In droplets >80 µm, spindle length and droplet size are uncoupled (Good et al. 2013; Hazel et al. 2013), a threshold similar to what is seen in embryos. Spindle length is insensitive to droplet geometry indicating that spindles scale with cytoplasmic volume rather than droplet diameter, suggesting that a limiting component, possibly tubulin itself, may underlie scaling. However, the upper limit to spindle length is presumably because of physical constraints of microtubules, such as maximum microtubule length, which limit the functional scaling regime.

Another organelle for which scaling fails in large cells is the nucleus. Again, this is best studied in X. laevis embryos in which the maximal nuclear size fails to scale with cell size in early embryos with large cell volumes (Gerhart 1980; Levy and Heald 2010). One potential reason for this may be that the operation of a scaling mechanism is masked by the fact that, in these embryos, nuclear size is not allowed to reach steady state before mitotic entry (Goehring and Hyman 2012). Thus, in these cells, observed nuclear size is the result of a timer-like mechanism in which size is the product of assembly rate and time (as discussed earlier) (Fig. 3E). In general, scaling and size-control mechanisms require sufficient time to reach steady state, which is particularly true for limiting pool mechanisms in which the effect on assembly rates will only occur after significant depletion occurs, as well as in large cells where diffusion times of cytoplasmic substrates play a significant role. Large Xenopus cells may simply not have enough time for nuclei to reach a size where any limiting component could come into play.

A last example of the limits of a scaling mechanism is centrosome scaling, which, as we note earlier, is achieved via a limiting pool mechanism (Decker et al. 2011). This limiting pool mechanism, however, only controls for total organelle mass, which could be present altogether in one large organelle or split among many smaller copies of varying size. To properly form a functional bipolar spindle, two, and only two, mitotic centrosomes are required and these centrosomes must be of similar size. The cell’s solution to this problem appears to be to limit centrosome formation exclusively around centrioles (Zwicker et al. 2014), the number of which is highly regulated and coupled to the cell cycle (as reviewed in Nigg and Stearns 2011). Thus, cells must couple counting and scaling mechanisms to achieve precise control over organelle number and size.

CONCLUDING REMARKS

As we have tried to capture here, scaling is an essential feature of cellular systems. Cells come in different sizes and can grow, shrink, and change shape over time. Such dimensional changes require corresponding alterations of their internal structures to cope with size-dependent requirements, such as biosynthesis, transport, and force generation. Thus, the ability of cells to scale their internal components, well documented by the end of the 19th century (Conklin 1912), is essential.

As with many fundamental questions of biological organization and form, scaling processes are governed by fundamental physical laws. Galileo’s square-cubed law recognizes that an object that undergoes a uniform change in size (i.e., undergoes isometric scaling), will see its surface area increase with the square of its length but its volume with the cube. For many systems, not just living organisms, this poses a problem. Among land animals, a larger body mass requires more gas exchange to support respiration, more muscle force to move, and stronger support structures, such as bones, all of which scale with area. Consequently, as Haldane (1926) puts it, changes in size have necessitated changes in form, with larger animals possessing proportionally thicker bones and muscles and a more highly branched respiratory system. We now know the same is true for cells. Although some organelles, such as the nucleus, scale isotropically with cell size, others do not. For example, scaling of the mitochondria is manifested through changes in linear extent of a constant diameter branched network, such that surface area increases proportionally with volume rather then according to the square-cubed law expected for isometric scaling (Rafelski et al. 2012).

Uncovering new scaling relationships, unraveling the mechanisms behind them, and defining the underlying physical laws and limits that govern scaling all have the potential to provide a window into the design principles of the cell itself, ultimately helping us understand the limits of cell size and specific adaptations that have allowed extreme variations in size and shape to evolve.