Side Chain Conformational Distributions of a Small Protein Derived from Model-Free Analysis of a Large Set of Residual Dipolar Couplings

Abstract

Accurate quantitative measurement of structural dispersion in proteins remains a prime challenge to both X-ray crystallography and NMR spectroscopy. Here we use a model-free approach based on measurement of many residual dipolar couplings (RDCs) in differentially orienting aqueous liquid crystalline solutions to obtain the side chain χ₁ distribution sampled by each residue in solution. Applied to the small well-ordered model protein GB3, our approach reveals that the RDC data are compatible with a single narrow distribution of side chain χ₁ angles for only about 40% of the residues. For more than half of the residues, populations greater than 10% for a second rotamer are observed, and four residues require sampling of three rotameric states to fit the RDC data. In virtually all cases, sampled χ₁ values are found to center closely around ideal g^–, g⁺ and t rotameric angles, even though no rotamer restraint is used when deriving the sampled angles. The root-mean-square difference between experimental ³J_HαHβ couplings and those predicted by the Haasnoot-parametrized, motion-adjusted Karplus equation reduces from 2.05 to 0.75 Hz when using the new rotamer analysis instead of the 1.1-Å X-ray structure as input for the dihedral angles. A comparison between observed and predicted ³J_HαHβ values suggests that the root-mean-square amplitude of χ₁ angle fluctuations within a given rotamer well is ca. 20°. The quantitatively defined side chain rotamer equilibria obtained from our study set new benchmarks for evaluating improved molecular dynamics force fields, and also will enable further development of quantitative relations between side chain chemical shift and structure.

Introduction

It is well recognized that proteins are subject to extensive conformational fluctuations, and much research over the past two decades has focused on linking this structural and dynamic heterogeneity to function.¹⁻⁴ Recent advances in the analysis of X-ray crystallographic data now make it possible to reliably fit protein X-ray electron density maps, acquired at high resolution, to ensembles of structures that correlate with the order parameters derived from NMR relaxation data.⁵ Such analyses frequently reveal the presence of multiple different side chain conformations in any given crystal, permitting identification of distinct allosteric networks.⁶ Unfortunately, collection of high quality X-ray data often requires the use of cryogenic temperatures, which results in extensive remodeling of many of the side chains, even when samples are flash frozen,⁷ possibly providing a distorted view of the functionally relevant ensemble that exists at room temperature.

Historically, NMR spectroscopy has played a dominant role in studying internal dynamics of proteins. In particular, ¹⁵N relaxation measurements are used ubiquitously for defining the amplitudes and time scales of rapid backbone motions.⁸⁻¹¹ Side chain dynamics, in particular methyl-bearing side chains, have been extensively studied by ¹³C relaxation measurements,¹²⁻¹⁴ and ²H relaxation rates of deuterated methyl groups also have proven to be particularly robust parameters for quantifying such dynamics.^14,15 In addition, dipole–dipole cross-correlated relaxation rates were shown to be excellent reporters on methylene group motions,¹⁶ with the restriction on all of these relaxation methods being that only motions faster than the overall tumbling time of the protein can be accurately detected.¹⁷ Motions on the ms−μs time scale can be studied by NMR relaxation dispersion methods, providing access to conformational rearrangements that often are of key importance to biological function.¹⁸⁻²⁰ However, unless the chemical shift changes underlying relaxation dispersion can be interpreted in structural terms, relaxation dispersion is often limited to providing time scales and populations of the dynamic process. As a complement to these measurements, the conformational range sampled by proteins across the entire NMR time scale from ps to ms can be defined by RDCs measured under at least three linearly independent alignment conditions.^3,21−23 However, when the motional amplitudes involved are modest, as often is the case for backbone dynamics in well-ordered proteins, quantitative interpretation of the RDCs in terms of motions demands very high measurement precision, a goal that can be difficult to reach under the required three or more alignment conditions.^24,25

In the past, side chain dynamics have been studied mostly in terms of the distributions of their rotameric states, most commonly analyzed by measurement of extensive sets of ³J couplings, possibly in conjunction with ¹H–¹H nuclear Overhauser enhancements (NOEs).²⁶⁻²⁸ Interpretation of these data in terms of dynamics was shown to be rather sensitive to the distributional model underlying such analyses,²⁹ and clearly is also highly sensitive to the parametrizations of the Karplus equations used. Because energetically favorable side chain conformations typically fall close to staggered rotameric states, their dynamics in terms of changes in bond vector orientation often is of much larger amplitude than for the protein backbone, making them highly suitable for study by RDCs.³⁰ Analysis of the ¹³C^β–¹H^β RDCs measured for the B1 domain of protein L using two quite different liquid crystalline alignments yielded up to four very accurate parameters to define the χ₁ angle for side chains with C^β methylene groups, and two parameters for residues such as Val, Ile, and Thr, with only a single ¹³C^β–¹H^β RDC.³⁰ For residues with methylene groups, this permitted definition of both the populations and χ₁ values of up to two side chain rotamers that are in rapid exchange with one another or, for both residues with methylene or methine C^β carbons this could be interpreted in terms of populations of three rotamers (two independent parameters), assuming these are ideally staggered.

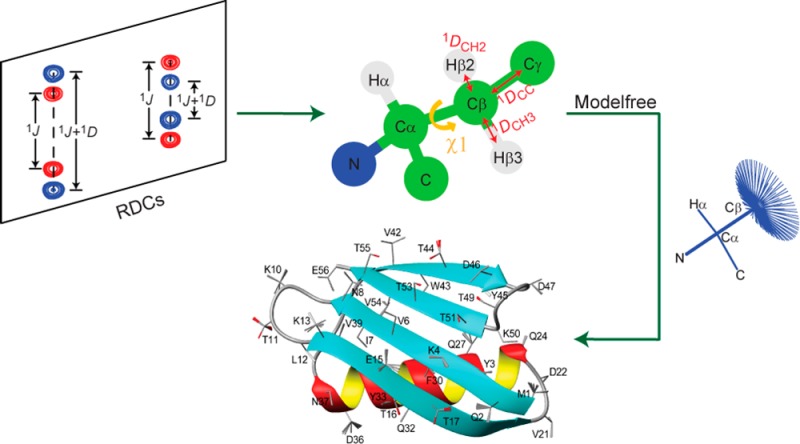
Here, we expand on the approach introduced by Mittermaier and Kay, and measure side chain RDCs for six differently oriented samples of the third Igg-binding domain of protein G (GB3 for short), and in addition to the ¹³C^β–¹H^β RDCs we also measure ¹³C^β–¹³C^γ RDCs for residues with nonprotonated C^γ (Asn, Asp, and aromatic residues) and for residues with ¹³C^γH₃ groups (Ile, Val, Thr), thereby yielding up to 18 observed parameters. Effectively, the number of independent experimental parameters is somewhat lower, however, as only five of the six protein alignments can be linearly independent of one another. Nevertheless, the now much larger set of experimental parameters allows definition of both the populations and χ₁ values of all three side chain rotamers for the vast majority of residues. In fact, for residues with a complete or nearly complete set of couplings, we show it is possible to determine a continuous distribution of χ₁ values, albeit that the latter analysis requires a “maximum entropy” term to smooth the distributions. Thus, our analysis provides a model-free evaluation of the χ₁ values sampled by each side chain, without the restriction that these cluster in two or three distinct rotameric states.

Protein alignment conditions were varied by using different liquid crystalline suspensions^30,31 as well as by introducing conservative charge mutations that alter the protein’s alignment in a medium containing a liquid crystalline suspension of the filamentous bacteriophage Pf1.³² The large amount of backbone RDC data obtained for these samples also permitted generation of an average backbone structure that predicts C^α–C^β bond vector orientations at an accuracy that is considerably increased over that of the X-ray structure, as judged by agreement between observed and predicted ¹³C^α–¹³C^β RDCs. High accuracy of these vector orientations is a prerequisite for quantitative RDC analysis of the χ₁ values sampled by the different side chains.³⁰

For nearly all solvent-exposed residues we find population of two and sometimes even three sets of χ₁ angles that typically cluster close to ideally staggered rotameric states. By contrast, the relatively small number of buried side chains in GB3 for the most part can be well fit by single, narrow clusters of χ₁ values. For the vast majority of residues, population of these clusters, as well as their centers, can be defined at high accuracy. Although the width of the clusters, i.e., the amplitude of the dynamics within a given rotameric well, is poorly defined by the RDC data, comparison between observed and predicted ³J_HαHβ values indicates that the root-mean-square amplitude of χ₁ angle fluctuations within a given rotamer well is ca. 20°.

Materials and Methods

Protein Preparation

The sequence of wild-type GB3 used in our study is MQYKLVINGK TLKGETTTKA VDAETAEKAF KQYANDNGVD GVWTYDDATK TFTVTE. Samples of the following three mutants also were generated: (1) K4A/K19E/V42E/CHis₆; (2) K19A/V42E/D47K; and (3) K4A/K19E/V42E. For mutant (1), CHis₆ refers to a set of six His residues, immediately following C-terminal residue E56. Proteins were expressed and purified as described previously,³³ and selection of the three mutants was based on those previously studied by Yao et al. in Pf1, which had shown backbone perturbations caused by the mutations to be minimal.³² Samples of uniformly 99%-enriched ¹³C/¹⁵N protein were generated by growing BL21-DE3 Escherichia coli cells in M9 medium containing 1.0 g/L ¹⁵NH₄Cl and 2.0 g/L ¹³C₆-glucose, supplemented by 0.5 g/L U–¹³C/¹⁵N Isogro rich medium (Sigma-Aldrich). Measurements were also carried out for randomly fractionally (ca. 75%) deuterated protein, obtained by growing the cells in M9 medium, including 1 g/L ¹⁵NH₄Cl and 3.0 g/L ¹³C₆/²H₇-glucose in 75% D₂O/25% H₂O, and for samples with full perdeuteration of the nonexchangeable hydrogens by growing the cells in a medium containing M9 medium, including 1 g/L ¹⁵NH₄Cl and 3.0 g/L ¹³C₆/²H₇-glucose in 99% D₂O, followed by back exchange of the labile hydrogens in H₂O for at least 24 h at 37 °C.

NMR Measurements

An extensive set of two-dimensional (2D) and three-dimensional (3D) heteronuclear NMR spectra was recorded to collect ¹⁵N–¹H, ¹³C–¹H, and ¹³C^α–¹³C^β and ¹³C^β–¹³C^γ one-bond J couplings and RDCs on isotropic and six differently aligned protein samples. A nearly complete set of ³J_HαHβ couplings was also obtained from a 3D HA[HB,HN](CACO)NH spectrum.³⁴ The different types of spectra recorded are summarized in Supporting Information (SI) Table S1, and the compositions of the different samples are summarized in Table S2. Spectra were recorded on Bruker Avance-III spectrometers operating at ¹H frequencies of 600 and 900 MHz, both equipped with triple resonance cryogenic probeheads and z-axis pulsed field gradient accessories. Details regarding the NMR measurements are presented in the SI Text Section.

All spectra were processed using the NMRPipe software system³⁵ and analyzed with the Sparky program.³⁶

Backbone Refinement of GB3

The structure of GB3 was refined starting from the coordinates of the PDB deposition 2OED,³³ against an extensive set of N–H^N, C^α–H^α, C′–C^α, C′–N, H^N–H^α, and C^α–C^β RDCs using a variable alignment tensor treatment as described previously, to reach working Q factors ranging between 0.05 and 0.11.³⁷ In addition, ³J_HNHα and ³J_C′C′ couplings reported by Li et al.³⁷ were fitted with force constants that yielded rmsd values of 0.29 and 0.1 Hz, respectively. For the PDB-deposited ensemble obtained from our study (PDB entry 2N7J), the protein structure was refined as if its backbone and C^β atomic positions are fully static, i.e., as previously done for ubiquitin,²⁵ thereby aiming to give the best representation of the time-averaged backbone structure.

Results and Discussion

Analogous to prior studies of protein backbone dynamics,^21,22,24,38 we measured RDCs for a wide range of different protein orientations. The GB3 domain, used in our study, has a quite prolate shape, making it challenging to find truly orthogonal alignment conditions.³³ Here, we rely on a combination of the two approaches previously used for this purpose. First, we collected RDC data in three liquid crystalline media that differentially align the protein relative to the magnetic field: a positively charged phospholipid bicelle suspension,^39,40 a polyethylene glycol (PEG) based liquid crystal,⁴¹ and a suspension of the negatively charged filamentous phage Pf1.⁴² Second, we used conservative mutagenesis of charged surface residues, which can be used to alter the alignment of the protein relative to the negatively charged Pf1 liquid crystal, without significantly impacting the backbone structure of the protein.³² Three such mutants were prepared and studied in Pf1. As the current study focuses on side chain conformations rather than backbone, it is important to ensure that the use of mutants does not significantly perturb the side chain conformations either. Here, we simply exclude data for residues in the mutants that have significant chemical shift differences for ¹³C^β (≥0.2 ppm) or ¹H^β (≥0.1 ppm) relative to the wild type protein. This only concerns a small number of residues (SI Tables S3 and S4; SI Figure S3), most significantly residue E15 which exhibits a >0.6 ppm ¹³C^β chemical shift change in the K4A mutants, presumably because a side chain salt bridge interaction between K4 and E15, seen in the X-ray structure of the wild type protein,⁴³ is abolished in the mutant. Although RDC data were collected under six different alignment conditions (three different media, plus three mutants in Pf1), analysis of the corresponding alignment tensors using singular value decomposition and SECONDA analysis⁴⁴ indicates that one of the five possible orthogonal alignments is only weakly sampled (SI Figure S4). However, in contrast to the study of backbone motions by RDCs, where often only a single ¹⁵N–¹H RDC is used to define the orientation of the peptide plane relative to the liquid crystal director, for our study of side chain conformations two very different orientations, ¹³C^β–¹H^β2 and ¹³C^β–¹H^β3 are sampled if their separate RDCs can be measured. For residues with methine C^β carbons, i.e., Thr, Val and Ile, ¹³C^β–¹³C^γ RDCs were measured through the ¹³C^γ methyl resonance, and for aromatic and Asp/Asn residues ¹³C^β–¹³C^γ RDCs could also readily be measured (see Materials and Methods and SI). Therefore, for each alignment condition, two or three RDCs are available for defining the χ₁ angle of most residues.

Measurement of Side Chain ¹H–¹³C RDCs

The accuracy of the experimental RDCs is paramount when using these to define a dynamic structural ensemble. Indeed, it is primarily the inconsistency between the RDCs and a single, unique χ₁ angle that necessitates their analysis in terms of an ensemble. However, random or systematic measurement errors will also result in inconsistencies, and it is therefore critical to minimize such errors.

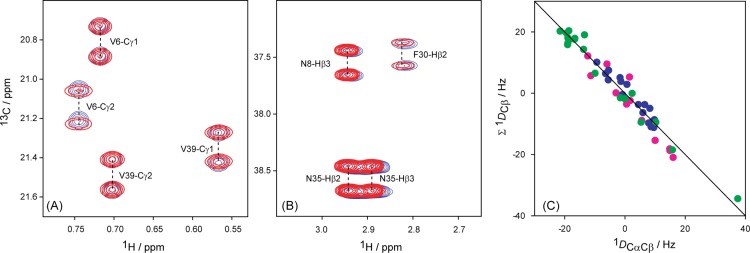
A ¹H–¹³C RDC can be derived from the change in ¹J_CH splitting observed in either the ¹H or ¹³C dimension of a multidimensional NMR spectrum. Measurement in the ¹H dimension often is adversely affected by the presence of multiple unresolved ¹H–¹H RDCs, resulting in extensive broadening of the apparent ¹H line width and thereby decreasing the accuracy of extracted couplings. For this reason, measurement of heteronuclear RDCs is usually carried out in the dimension of the low-γ nucleus, where the effect of remote ¹H nuclei is far less severe.⁴⁵ On the other hand, for methylene sites the coupled ¹³C–{¹H} spectrum yields a doublet of doublets multiplet structure, for which the center components are usually unresolvable, therefore only providing access to the sum of the two ¹J_CβHβ couplings, i.e., to the sum of the corresponding RDCs. In our study, ¹³C–¹H RDCs were measured using two independent methods. In one set of experiments, the summed ¹H^β–¹³C^β RDCs were simply measured from a 3D HN(COCA)CB spectrum, recorded without ¹H decoupling in the ¹³C^β dimension (SI Figure S5). Separate ¹³C^β–¹H^β2 and ¹³C^β–¹H^β3 RDCs were measured also in the ¹³C dimension but for a sample that had been randomly deuterated at the 75% ²H level. For this sample, ca. 38% of the ¹³C^β sites are CHD isotopomers and therefore, at least in principle, allow measurement of individual ¹³C^β–¹H^β2 and ¹³C^β–¹H^β3 RDCs from a constant-time 2D ¹H–¹³C HSQC spectrum recorded without ¹H decoupling in the ¹³C dimension, provided that ¹H^β2 and ¹H^β3 have different chemical shifts (Figure 1A). In practice, however, the ca. 3-fold smaller fraction of ¹³C^βH₂ isotopomers in such a fractionally deuterated sample gives rise to weak correlations that are partially overlapping with the ¹³C^βHD correlations. Relative to ¹³C^βH₂, ¹³C^βHD correlations are shifted upfield in both the ¹H and ¹³C dimensions by the ²H isotope effect, but insufficiently to yield well-resolved resonances (Figure 1A). Instead, we therefore developed a DEPT-filtered^46 1H–¹³C CT-HSQC pulse scheme (SI Figure S2), which actively suppresses ¹³CH₂ correlations (Figure 1B). For the vast majority of methylene sites, this experiment allows separate measurement of the ¹³C^β–¹H^β2 and ¹³C^β–¹H^β3 RDCs. To validate the accuracy of these couplings, we compare their summed values with the result measured from the 3D HN(COCA)CB spectrum. Note that the latter are measured in H₂O solution, whereas the DEPT-filtered HSQC measurement is carried out on the fractionally deuterated sample in D₂O solution, and a scaling factor is needed to account for the slightly different alignment strengths of the two samples. After scaling, the excellent agreement seen in Figure 1C (pairwise root-mean-square difference (rmsd) of 2 Hz; Pearson’s correlation coefficient, R_P = 0.99) validates the accuracy of both measurements.

Figure 1.

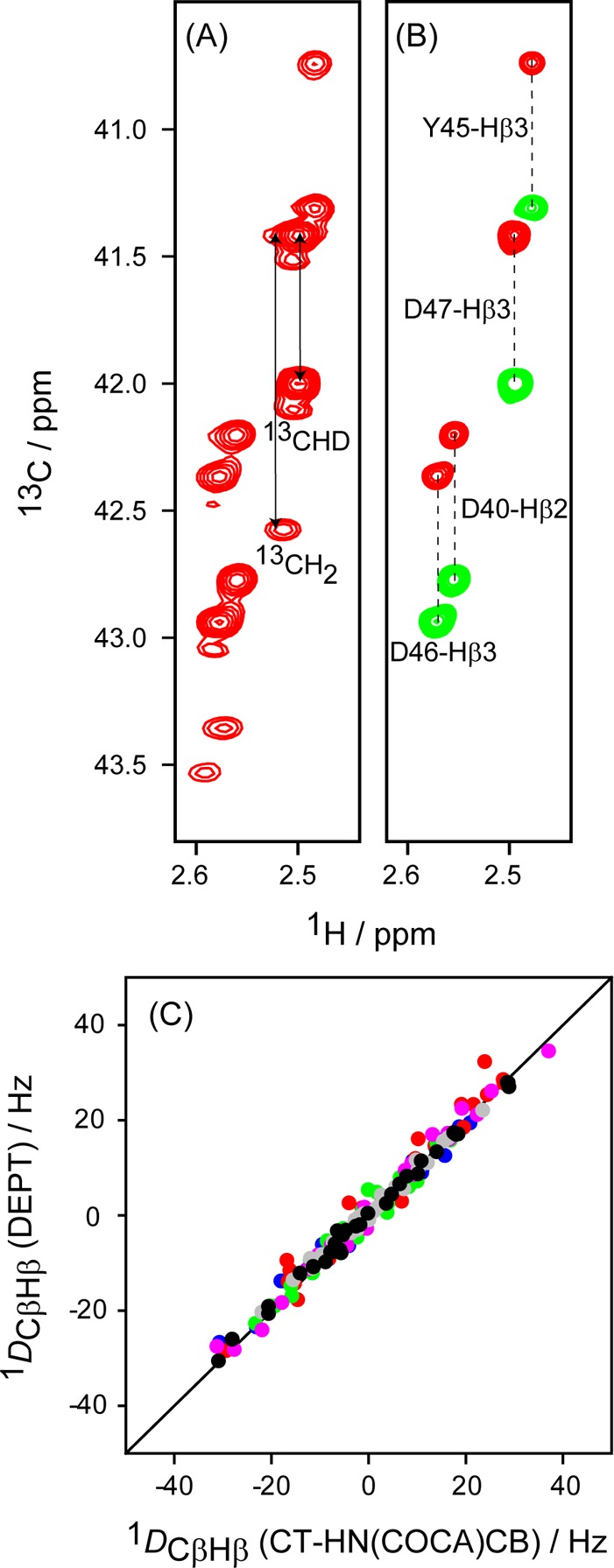
Enhanced accuracy of ¹D_CβHβ couplings through spectral editing of the ¹H–¹³C CT-HSQC spectrum of randomly fractionally (75%) deuterated GB3. (A) Small region of the regular ¹H–¹³C HSQC spectrum, ¹H-coupled in the ¹³C dimension, showing the signals of both ¹³CH₂ and ¹³CHD isotopomers, the latter upfield shifted due to the deuterium isotope effect. (B) Same spectral region, recorded with the DEPT-filtered ¹H–¹³C CT-HSQC experiment (SI Figure S2), which selects ¹³CH signals and effectively suppresses ¹³CH₂ isotopomers. (C) Comparison of the sum of ¹³C^β–¹H^β2(D^β3) and ¹³C^β–H^β3(D^β2) couplings derived from the DEPT-filtered HSQC spectra of wild-type GB3 in Pf1 and isotropic solutions, with the corresponding summed couplings derived from CT-HN(COCA)CB spectra. Blue: K4A/K19E/V42E-CHis6 in Pf1; red: K19A/V42E/D47K in Pf1; green: K4A/K19E/V42E in Pf1; pink: wild-type GB3 in bicelle; gray: wild-type GB3 in PEG; black: wild-type GB3 in Pf1. Spectra were recorded at 900 MHz ¹H frequency in 99.8% D₂O (¹H–¹³C HSQC) and at 600 MHz in 95% H₂O for the CT-HN(COCA)CB experiment.

The same set of DEPT-filtered CT-HSQC spectra used above for measurement of C^β–H^β RDCs also yielded accurate C^α–H^α couplings. A large set of these was measured previously when the structure of the protein was first refined against RDCs,³³ but values measured for the three mutants in Pf1 medium (see Materials and Methods) now add new data to this set. Moreover, with the previous and present measurements being independent of one another, contributions from small random measurement errors partially cancel when both sets are used, and the new data therefore were used jointly with the earlier data as input for all structure calculations.

Measurement of ¹³C–¹³C RDCs

As mentioned above, ¹³C^β–¹³C^γ RDCs also contain valuable information on the χ₁ angle, and are particularly useful for Val, Thr, and Ile residues for which only a single C^β–H^β RDC is available. Their values were derived from the difference in ¹J_CβCγ splitting between aligned and isotropic samples, observed in regular (non-CT) ¹H-decoupled ¹H–¹³C HSQC spectra (Figure 2A). For aromatic and Asp/Asn residues, ¹³C^β–¹³C^γ RDCs were obtained from ¹H–¹³C CT-HSQC spectra⁴⁷ in which no decoupling of the downfield ¹³C^γ nuclei was employed, and the ¹³C 180° pulse applied during the 56 ms CT-evolution period was REBURP-shaped⁴⁸ to invert only aliphatic carbon spins, thereby removing the ¹J_CαCβ splitting and leaving clean ¹J_CβCγ doublets (Figure 2B).

Figure 2.

Examples of spectral quality used for deriving ¹D_CβCγ couplings. (A) Small section of the methyl region of the ¹H–¹³C HSQC spectrum of wild-type GB3 in Pf1 medium, recorded with regular (non-CT) ¹³C evolution (red), superimposed on the corresponding spectrum recorded under isotropic conditions (blue). (B) Small region of the ¹H^β–¹³C^β region of the ¹H–¹³C CT-HSQC spectrum, recorded with a REBURP 180° pulse covering only the ¹³C aliphatic region during the CT ¹³C evolution of the aliphatic region of wild-type GB3 in Pf1 medium (red) superimposed on the corresponding spectrum recorded under isotropic conditions (blue). The spectra were recorded with a double constant-time duration (56 ms) at 900 MHz. (C) Comparison of ¹D_CαCβ and the sum of the three other C^β–related ¹D couplings, which all have been scaled to ¹D^a_CH (measurements for wild type GB3: pink, in bicelle; blue, in PEG; green, in Pf1).

In addition to the one-bond C^β–C^γ RDCs (¹D_CβCγ) that contain information on χ₁, complete sets of ¹D_CαCβ couplings (with the exception of C-terminal residue E56) were obtained from 3D HNCOCA spectra recorded on fully deuterated samples of the wild-type GB3 sample in Pf1, bicelle and PEG media. These data were used to further refine the backbone structure of the protein, and also served as a measure to evaluate the accuracy of C^α–C^β bond vector orientations in structures derived without including this data, i.e., to establish a measure for the “structural noise”.⁴⁹ Scaling factors for these values to account for the small changes in liquid crystal concentrations used in the different samples were established independently by comparing ¹D_NH values. After normalizing the alignment strengths of the different samples used for measurement of ¹D_CαCβ, ¹D_CβCγ, ¹D_CβHβ2, and ¹D_CβHβ3 values, and further accounting for the intrinsic difference between ¹D_CC and ¹D_CH couplings due to differences in bond length and gyromagnetic ratio,⁴⁵ in the absence of measurement error the sum of these four couplings must be zero under the approximation of ideal tetrahedral geometry at C^β. Indeed, for residues for which all four one-bond RDCs to C^β were measured, a very good correlation between ¹D_CαCβ and the sum of the three other, normalized couplings is observed (Figure 2C). For several residues, the residual nonzero values of these sums (SI Table S5) are somewhat larger than expected based on propagation of the estimated uncertainties in the RDC measurements, which may reflect small deviations from idealized tetrahedral geometry at C^β. Indeed, quantum calculations suggest, for example, that the H^β2–C^β–H^β3 angle can deviate by up to ∼5° from the tetrahedral 109.4° value in a χ₁-dependent manner. Deviations from ideal 109.4° values, outside of the statistical uncertainty, for the C^α–C^β–C^γ angle are also commonly seen in atomic resolution X-ray data.⁵⁰

Generation of Side Chain Ensembles

The earlier structure refinement (PDB entry 2OED) was based on an extensive set of backbone RDCs, measured in different liquid crystalline and stretched acrylamide gel media.³³ In addition to the RDC restraints used previously, the newly recorded RDC data add orientations enabled by the use of surface charge mutations while using Pf1 as the alignment medium.³² The data also include ¹³C^α–¹³C^β RDCs measured in three media for fully deuterated protein, which results in very high resolution in the ¹³C dimension, thereby increasing the accuracy of their measurements (SI Table S6). Use of perdeuterated protein also allows the use of rather strong alignment,⁵¹ which is particularly beneficial for measuring the intrinsically small ¹D_CC values. These ¹³C^α–¹³C^β RDCs directly impact the orientations of the corresponding bond vectors, whose accuracy is key when defining the distributions of χ₁ rotations around these vectors on the basis of ¹³C^β–¹H^β and ¹³C^β–¹³C^γ RDCs.

The ¹³C^α–¹³C^β RDCs also are very useful for validation purposes, establishing the accuracy of the C^α–C^β vectors in structures calculated without using any ¹D_CαCβ restraints. The averaged Q^free_Cα-Cβ factors for data measured in Pf1, bicelle and PEG media were ∼10%, corresponding to an uncertainty of 3.1 ± 0.6° (structural noise) in their time-averaged orientations.⁴⁹ The actual structures used for all χ₁ analyses and side chain ensemble generation included the ¹D_CαCβ restraints, and therefore should be of slightly higher accuracy than structures used for ¹D_CαCβ validation. Populations of the side chain conformers in the 20 structures deposited in the PDB (PDB entry 2N7J; Figure 3) then were randomly selected by sampling the distributions observed in our study (Table 1), followed by a Monte Carlo minimization of the clash score using the χ₂, χ₃, and χ₄ distributions from the backbone-independent rotameric library.⁵² During this process the backbone and the atoms defining the χ₁ torsion angles remained fixed, thus allowing rearrangement of the atoms beyond C^γ, but without consideration of side chain H-bonding or other potentially relevant physical interactions. Structural statistics are reported in SI Table S7.

Figure 3.

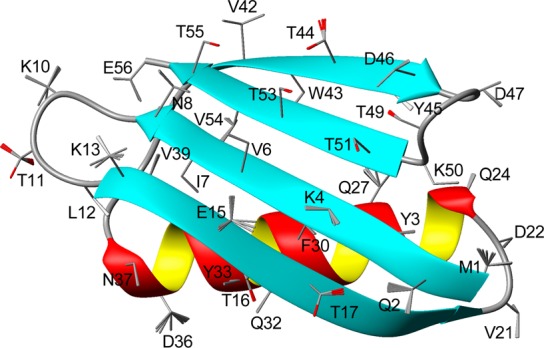
Structure of GB3, derived from NMR data. The backbone coordinates are presented as a ribbon diagram, with side chains depicted as sticks for the C^α–C^β and C^β–C^γ1 (C^β–O^γ for Thr) bonds. For residues with the RDC-derived χ₁ rotamer distributions, shown positions of the side chains (stick models) are obtained by 20 random samplings from the models reported in Table 1. Spread within each rotamer corresponds to the Monte Carlo-derived rms uncertainty of the best-fitted χ₁ values as reported in Table 1.

Table 1. Analysis of χ₁ Rotamer Distributions in GB3.

residue	NRDCa	modelb	Pc	ρ(1)d	σρ(1)e	χ̅1(1)f	σχ1(1)g	ρ(2)d	χ̅1(2)f	σχ1(2)g	ρ(3)d	χ̅1(3)f
M1	11	2	<10–4	0.53	0.04	306	12	0.47	203	15	–	–
Q2	10	2	<10–4	0.69	0.02	176	5	0.31	265	11	–	–
Y3	15	1	0.59	1.0	–	298	1	–	–	–	–	–
K4	8	2	<10–4	0.67	0.02	183	3	0.33	293	5	–	–
L5	7	1	0.98	1.0	–	173	1	–	–	–	–	–
V6	11	1	0.89	1.0	–	178	1	–	–	–	–	–
I7	10	1	0.39	1.0	–	299	1	–	–	–	–	–
N8	12	2	<10–4	0.58	0.01	190	2	0.42	296	3	–	–
K10	5	3	h	0.58	0.04	293	3	0.23	187	3	0.19	57
T11	10	3	0.09	0.63	0.03	54	3	0.28	282	7	0.09	162
K13	10	3	0.005	0.67	0.02	302	2	0.16	62	12	0.16	160
E15	8	3	0.004	0.44	0.01	285	3	0.34	40	4	0.22	163
T16	10	2	<10–4	0.74	0.01	186	2	0.26	37	8	–	–
T17	10	2	<10–4	0.76	0.01	65	1	0.24	195	7	–	–
T18	10	1	0.10	1.0	–	197	1	–	–	–	–	–
V21	13	2i	0.0002	0.60	0.05	302	3	0.40	68	4	–	–
D22	15	1	1.0	1.0	–	61	1	–	–	–	–	–
E24	10	2	<10–4	0.53	0.02	284	6	0.47	182	5	–	–
E27	10	2	0.07	0.93	0.03	185	3	0.07	286	34	–	–
K28	5	1	1.0	1.0	–	305	3	–	–	–	–	–
F30	15	1	0.35	1.0	–	289	1	–	–	–	–	–
K31	10	2	<10–4	0.84	0.01	285	2	0.16	181	9	–	–
Q32	5	2	0.05	0.72	0.04	174	6	0.28	297	15	–	–
Y33	14	1j	0.009	1.0	–	179	1	–	–	–	–	–
N35	15	2	<10–4	0.52	0.01	184	2	0.48	288	3	–	–
D36	15	2	0.04	0.95	0.11	290	4	0.05	188	40	–	–
N37	15	1	1.0	1.0	–	285	1	–	–	–	–	–
V39	15	2	<10–4	0.83	0.02	178	2	0.17	324	9	–	–
D40k	15	2	<10–4	0.69	0.13	179	11	0.31	237	15	–	–
V42	9	2	0.0005	0.83	0.02	171	1	0.17	35	6	–	–
W43	11	1	1.0	1.0	–	287	1	–	–	–	–	–
T44	10	2	0.001	0.84	0.02	48	1	0.16	270	6	–	–
Y45	15	1	1.0	1.0	–	178	2	–	–	–	–	–
D46	15	2	0.0007	0.90	0.03	179	1	0.10	30	17	–	–
D47	15	2	<10–4	0.82	0.02	189	3	0.18	98	12	–	–
T49	10	1	1.0	1.0	–	63	2	–	–	–	–	–
K50	10	1	1.0	1.0	–	299	1	–	–	–	–	–
T51	5	1	0.92	1.0	–	298	1	–	–	–	–	–
F52	15	1	1.0	1.0	–	287	1	–	–	–	–	–
T53	10	2	0.06	0.90	0.03	301	2	0.10	86	25	–	–
V54	15	2	0.0003	0.81	0.04	57	2	0.19	205	7	–	–
T55	6	1	0.06	1.0	–	303	1	–	–	–	–	–
E56	9	2	<10–4	0.56	0.02	286	7	0.44	184	8	–	–

^aN_RDC is the total number of experimental RDCs available for side chain rotamer analysis, with a maximum of 5 per bond vector, as the 6th RDC is a linear combination of the other 5.

^bModel refers to the number of discrete χ₁ rotamers required to fit the data.

^cP refers to the probability, extracted from F statistics. For cases where model 1 is selected, P refers to the probability that model 1 is more applicable than model 2; for cases where model 2 is selected, P refers to the probability that model 2 is not better than model 1; for cases where model 3 is selected, P refers to the probability that model 3 is not better than model 2.

^dFractional population of rotamer (n).

^eUncertainty in fractional population of rotamer 1.

^fχ₁ angle of rotamer (n), degrees.

^gUncertainty in χ₁ angle of rotamer (n), degrees.

^hWith H^β₂ and H^β₃ having the same chemical shifts, only 6 RDCs for the sum of the C^β–H^β couplings were available. Because these RDCs were incompatible with 1- or 2-rotamer distributions with energetically favorable χ₁ angles, a 3-rotamer fit was carried out while restricting the χ₁ angles to fall within 10° from 60, 180 and 300°.

ⁱAlthough F statistics suggests model 3, model 2 is in better agreement with ³J_HαHβ than model 3.

^jAlthough F statistics suggests the presence of a 7% populated g⁺ rotamer, g⁺ would result in severe steric clashing and is therefore excluded.

^kValues obtained for this residue may be less accurate as they were derived under the assumption of a static C^α–C^β bond orientation, whereas the backbone of this residue is known to undergo substantial dynamics.^24,53

Although it seemed likely that side chain angles of residues with fluctuating χ₁ rotamer populations will not change fully independently of one another, as some combinations of χ₁ would result in a steric clash of side chains, relatively few clear-cut examples of such concerted motions were evident in our analysis. In the deposited ensemble, structures with such clashes are simply absent due to the high energy associated with distances between atoms that are separated less than the sum of their scaled van der Waals radii during the Monte Carlo clash minimization protocol.

Evaluation of χ₁ as Continuous Distributions

The amount of RDC data available to define the χ₁ angle distribution varied strongly from residue to residue. For 33 out of 46 non-Gly/Ala residues, ten or more experimental RDCs were available to define χ₁ (Table 1). On the other hand, six or fewer couplings could be measured reliably for seven residues: For T25, which exhibits strong ¹³C^α–¹³C^β coupling due to a very small ¹³C^α–¹³C^β chemical shift difference, no reliable side chain RDCs were obtained. For K19, which has two equivalent ¹H^β chemical shifts and is the site of mutation in three of the samples studied, only three RDCs were available. Both K19 and T25 therefore were excluded, as was L12 because its high amplitude backbone dynamics^24,53 was incompatible with our analysis method. Other residues with very small numbers of RDCs included K10, K28, Q32 and T55 and T51. For K10, K28 and Q32 the equivalent chemical shifts of their H^β protons only permitted measurement of the sum of their ¹D_CβHβ. Several of the other missing RDCs result from structural perturbations caused by the mutations of K4, K19 and V42, used to alter GB3′s alignment, as judged by ¹³C^β or ¹H^β chemical shift changes >0.2 or >0.1 ppm, respectively. Moreover, the difficulty in measuring ¹³C^β–¹³C^γ RDCs at sufficient precision for several residues further decreased the number of observable parameters. Nevertheless, with the backbone and thereby C^α–C^β orientations tightly defined, at least in principle only two RDCs are needed to define χ₁ under the assumption that the side chain conformation is static. Therefore, even for residues with only very few RDCs, the lack of consistency between the RDCs and a single, static χ₁ value can reveal χ₁ dynamics.

The actual search for the ensemble of χ₁ conformers that best agrees with the experimental data is performed by means of the previously introduced variable weight fit (VW-Fit) program.²⁵ VW-Fit uses a simulated annealing protocol to select from an ensemble of conformers the population that best matches the experimental data. For the present case, a 36-member ensemble was simply generated as that of the (static) backbone structure, with the 36 ensemble members corresponding to χ₁ values ranging from 0 to 350°, regardless of steric clashing or other energetic considerations. Populations of the 36 different side chain conformers (P₀, P₁₀, ..., P₃₅₀; ∑_nP_n = 1) correspond to 35 independent variables, which in all cases exceeds the number of measured RDCs, making the solution under-determined. This problem becomes even more pronounced when dividing the conformers into narrower bins of, say, 2° each. For this case, it is readily seen that, for example, equal 33.3% populations of P₂₉₈, P₃₀₀, and P₃₀₂ give essentially indistinguishable RDCs relative to the case where only P₃₀₀ is populated. We solve this problem by adding a very weak “entropy” term, −θ ∑_n[P_n log(P_n)], to the X² penalty score that is minimized by VW-Fit:

1

Here, RDC_j^exp corresponds to one of the M experimental RDCs available to define any given χ₁ angle, σ_j is its estimated measurement uncertainty, and RDC_j(χ₁ⁿ) is the corresponding RDC value calculated for χ₁ rotamer n, using the alignment tensor obtained from the backbone ¹D_NH and ¹D_CαHα RDCs. Note that in order to avoid confusion with the χ₁ angle, we use X rather than the more common χ symbol to describe the residual in the fit. The entropy term, −θ ∑_n[P_n log(P_n)], would be at a maximum when all populations P_n are equal (i.e., 2.78% for 36 conformers), but the weight factor θ is adjusted to a very low value, such that the RDC contribution to X² increases by only 2% over the minimal value reached without inclusion of the entropy term. We find that this criterion for choosing θ is suitable for reaching convergence while only minimally broadening the distributions, which are typically centered around the staggered rotamers. Note that the entropy term aims to make the population of all χ₁ bins equal, regardless of whether or not a bin corresponds to an energetically preferred staggered rotamer, and with the very low value of θ this method essentially yields a model-free depiction of the distribution of χ₁ angles best compatible with the experimental data. Note, however, that for all residues a comparably low X² value can be reached by considering the distribution to consist of a small (≤3) number of discrete rotamers (see below).

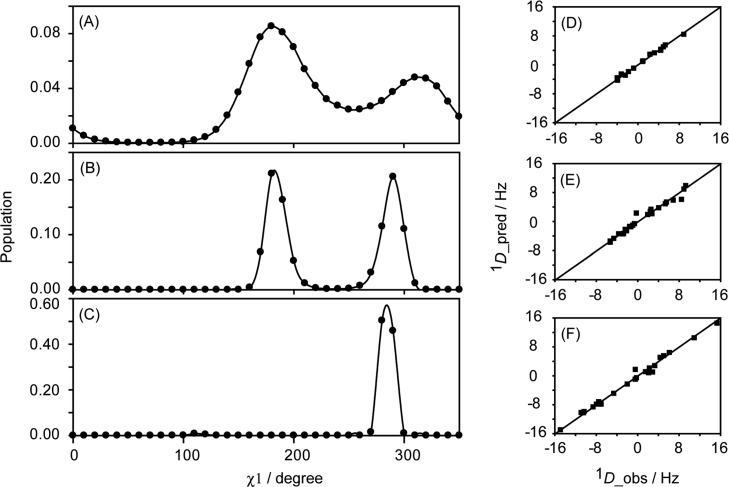
Figure 4 shows the χ₁ distributions observed for the three Asn residues, which are representative for what is observed for the full set of residues (presented in SI Figure S6 and S7). Whereas for helical C-cap residue N37 a narrow χ₁ distribution centered at 285° (i.e., equivalent to χ₁ = −75°) is observed (Figure 4C), equal populations of the t and g^– rotamers are obtained for N35, with both rotamers centered close to the ideal staggered conformations of χ₁ = 180° and χ₁ = 300° (Figure 4B). For N8, located at the end of strand β1, again population of both t and g^– rotamers is observed, but with a higher population of t (Figure 4A). The excellent correlations between observed and predicted RDCs for these residues (Figure 4D–F) highlight the close agreement between experimental data and the obtained rotamer distributions. Nevertheless, the width of the rotamer distributions is artificially increased by the maximum entropy term and, in particular for N8, results in non-negligible population of the energetically unfavorable χ₁ values near 240 and 0°. Another small problem that arises sometimes results from the degeneracy of RDCs with respect to bond vector orientation, i.e., an RDC cannot distinguish between an orientation and its inverse. Assuming tetrahedral geometry at C^β, a 180° χ₁ rotation brings the C^β–H^β and C^β–C^γ vectors close, within 39°, to their inverted orientation, sometimes creating a shallow false minimum, which then results in a false, low population at the true χ₁ plus 180° (see, e.g., the nonzero population at χ₁ = 110° in Figure 4C). Below we therefore will also analyze the best fits obtained when using a small number of discrete rotameric states.

Figure 4.

Distributions of χ₁ torsion angles for the three Asn residues in GB3, derived from RDC data, (A) Asn8, (B) Asn35, (C) Asn37 obtained with the program VW-Fit from an ensemble of 36 conformers, with identical backbone coordinates but the side chain χ₁ angles ranging from 0° to 350° in 10° increments. Corresponding distributions for all residues are presented in SI Figure S6. The positive weight of the entropy term, θ, was adjusted such as to increase the total RDC component of the error function (eq 1) by 2% over not using this term, resulting in a smoothing of the distribution profile (maximum entropy) and improved convergence of the simulated annealing protocol. The correlations between observed and predicted RDCs for these residues are shown in panel (D) Asn8, (E) Asn35, (F) Asn37.

Stereospecific H^β and C^γ Assignment

Traditionally, stereospecific assignments of H^β resonances have been made through a joint analysis of NOE and ³J_HαHβ information, which generally suffices to assign such protons for approximately half the cases.⁵⁴ Stereospecific assignment of Val C^γ methyl groups, which is needed when exploiting ¹D_CβCγ RDCs for determining Val χ₁ distributions, most commonly is accomplished by fractional ¹³C incorporation.⁵⁵ Alternatively, complete stereospecific H^β and C^γ assignments can also be obtained by using selectively deuterated amino acids in a cell-free growth medium (SAIL labeling),⁵⁶ but this approach can be technically challenging and expensive in terms of the required selectively deuterated amino acid precursors.

In our above χ₁ analysis, we followed the procedure used by Mittermaier and Kay,³⁰ and simply tried both sets of H^β (or C^γ for Val) assignments. For four residues (K10, K19, K28 and Q32) the near-identical chemical shifts of H^β2 and H^β3 obviated their stereospecific assignments. For the vast majority of the remaining residues one of the two assignments yielded a much better fit to the RDC data than the other. Moreover, we found that when using the wrong stereospecific assignment, the χ₁ populations generally no longer clustered around those of the ideally staggered rotameric states, g^–, g⁺, and t (SI Figure S8). For M1, E15, E24 and E56, the above considerations alone were insufficient for making confident stereospecific assignments. These residues showed clear indications of extensive side chain dynamics, as reflected in small ranges for the observed RDCs, small chemical shift differences (≤0.2 ppm) between H^β2 and H^β3, and broad distributions of χ₁ angles obtained with the VW-Fit program when fitting the RDC data to the ensemble of 36 χ₁ conformers (SI Figure S6). However, as described below, for all but E15 the stereospecific assignment could be completed when fitting the RDCs to a small number of discrete rotamers. Parenthetically, we note that a small chemical shift difference between H^β2 and H^β3 alone is not a sufficient indication of rotamer averaging as there are also residues in GB3 with very small |δH^β2 – δH^β3| differences (<0.1 ppm) that are well fit by single, narrow χ₁ distributions (e.g., K50, F52).

Discrete Rotamer Analysis

From the above model-free VW-Fit analysis it is clear that for the vast majority of residues χ₁ angle distributions cluster around one or two values (SI Figure S6). We therefore also carried out fits of the RDC data to models where either a single χ₁ rotamer is populated (one variable in the fit, χ₁), a fit with two χ₁ rotamers (three independent variables: two χ₁ values and one independent population), and a fit to three χ₁ rotamers (five independent variables: three χ₁ values and two independent populations). In principle, the width of the distribution around each χ₁ maximum could also be used as an adjustable parameter,³⁰ increasing the number of adjustable parameters by 1, 2, or 3 for the 1-, 2-, and 3-rotamer models. However, in relatively few of these cases a statistically meaningful improvement in the fit (P < 0.05, Student t test, see below) was obtained over the assumption of a fixed standard deviation, σ = 10°, of a Gaussian distribution centered around the optimized χ₁ value(s). The σ = 10° value was obtained from a shallow X minimum when systematically varying σ (SI Figure S12), and was therefore used in all 1-, 2-, and 3-rotamer-fit analyses.

Evaluating which of the three models is applicable was carried out by standard F statistics, where the validity of decreasing the degrees of freedom (N_A) in the fit to model A over a more complex model B (N_B) for a given number of experimental observables (N_RDC) was calculated from

2

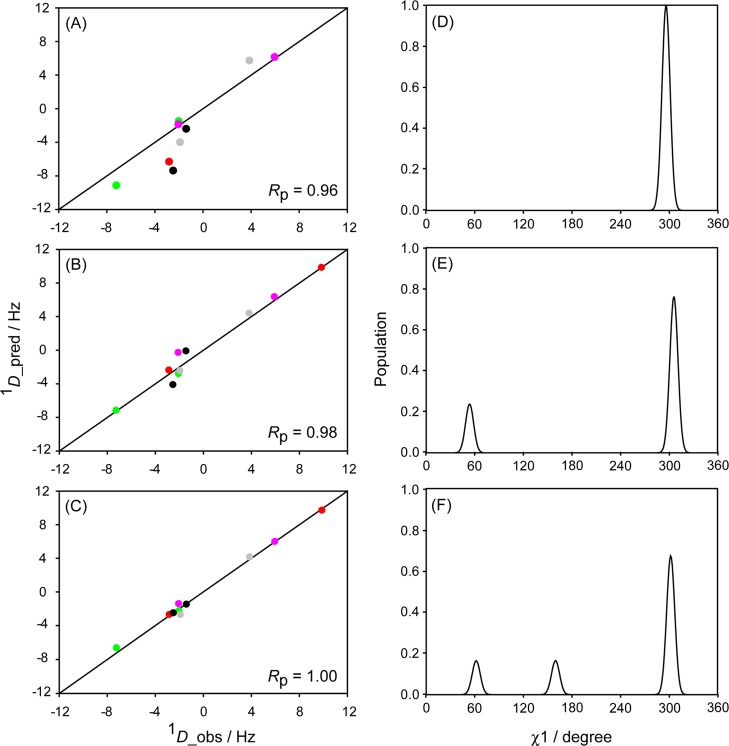
and the conditional probability that a model with N_B degrees of freedom is chosen erroneously over the simpler model is defined by P(F, N_A, N_B).⁵⁷ In our analysis we have chosen a relatively high cutoff value of P = 0.1, but it is worth noting that even if, for example, the 2-rotamer is chosen erroneously over the 1-rotamer model, the population of the second rotamer generally will be low. We also note that the most populated rotamer chosen for residues with 0.01 ≤ P ≤ 0.1 invariably moves closer to an ideally staggered conformation than when using the single rotamer model and yields better agreement with the ³J_HαHβ data (see below). Other than the experimental data there is no term driving such a selection, suggesting that the high P cutoff is physically reasonable. In practice, the presence of a second rotamer at a population higher than ca. 10% is detected quite unambiguously, in particular when 10 or more RDCs are available for such a residue (Table 1). Only four residues (K10, T11, K13, and E15), all located on the face of the protein involved in IgG-binding, show population of three rotameric states. The improvement in the RDC fit for K13, obtained when using the 1-, 2-, and 3-rotamer models is illustrated in Figure 5. The presence of three rotameric states for K10 is not mandated by F statistics, but was selected because the simpler 2-rotamer model yields highly skewed, unrealistic χ₁ angles. Because the two H^β protons are magnetically equivalent, only six RDCs are available to define the χ₁ angle of this residue, and we therefore restricted the VW-Fit search to 9 conformers, representing the ideally staggered g^–, g⁺, and t conformers, plus the 6 conformers that deviate by ±10° from these perfectly staggered conformations. For residue V21, the improvement in a 3-rotamer RDC fit over the 2-rotamer fit is acceptable based on F-statistics, but agrees less well with the experimental ³J_HαHβ = 4.1 Hz value. It also results in a minor steric clash for one of the three rotamers, and the 2-rotamer solution is therefore selected for this residue. V21 shows somewhat elevated backbone dynamics (S² = 0.74, based on RDC analysis²⁴) and it is likely that the 2-state χ₁ rotamer averaging for this loop residue is correlated with small changes in the backbone torsion angles (so-called “backrub motion”⁵⁸), which somewhat lowers the quality of the RDC fit in our 2-rotamer analysis.

Figure 5.

Best fits between measured and predicted RDCs values for K13 under six different protein orientations for (A) single-rotamer model, (B) 2-rotamer model, (C) 3-rotamer model. All RDCs are normalized relative to the ¹³C–¹H dipolar couplings, i.e., ¹D_CβCγ values are scaled up 10-fold, and all alignment strengths are scaled to D^a_NH = 10 Hz for the backbone RDCs. Colors correspond to the differently aligned samples (red: K19A/V42E/D47K GB3 in Pf1; green: K4A/K19E/V42E GB3 in Pf1; pink: wild-type GB3 in bicelles; gray: wild-type GB3 in PEG; black: wild-type GB3 in Pf1). Circles correspond to ¹D_CβHβ couplings. (D–F) The best-fitted K13 χ₁ rotamers for the 1-, 2-, and 3-rotamer models.

The continuous χ₁-population model discussed above did not allow us to make reliable stereospecific assignment for four residues: M1, E15, E24 and E56. When fitting the RDCs of these residues with the discrete rotamer model, while taking into account that significant populations of severely skewed rotamers (deviating >30° relative to the ideally staggered conformers) are unfavorable and that C^γ atoms should not make a serious steric clash with any backbone or C^β atom, this permitted additional stereospecific assignment of all but E15 (SI Table S4).

Uncertainty in ⟨χ₁⟩ and Populations of Rotamers

As mentioned above, the width of the χ₁ distribution within a given rotamer well is generally ill-defined by the RDC data. For example, assuming a Gaussian χ₁ distribution within each rotamer well of standard deviations σ yielded very similar fit qualities for any σ ≤ 15°, with a very shallow minimum for σ ≈ 10° (see SI Figure S12). The quality of the fit, however, is quite sensitive to population of the rotameric wells and to their average ⟨χ₁⟩ values. To evaluate how tightly these latter two parameters are defined by the experimental data we resorted to a Monte Carlo analysis.⁵⁹

Starting from the best-fit χ₁ result obtained from the experimental data by the multiple-rotamer fit program (Table 1), synthetic RDC values are first generated for this best-fit solution. Because the errors in the experimental RDC data were simply based on lower limit estimates, made on the basis of line width and signal-to-noise ratio,⁴⁵ Gaussian noise is added to the synthetic RDC data, with its amplitude adjusted such that the error in the best fit to these synthetic, noise-contaminated data equals that observed in the original fit of the experimental data. This level of noise is added in 1000 separate runs of the fitting program, with the distribution in the output parameters then being representative of their uncertainty. Below, we illustrate the results of this error analysis for three typical cases: K4, K13 and K50 (Figure 6). Fits to the experimental data indicate a single χ₁ = 299° rotamer for K50. For K4, a dominant (67%) population centered at χ₁ = 183 ± 3° is seen, and a minor population centered at χ₁ = 293 ± 5°. For K13, a major g^– rotamer (χ₁ = 302 ± 2°) populated at 67% is accompanied by g⁺ and t rotamers, each populated at ca. 16%. The Monte Carlo derived uncertainties in the populations of the χ₁ rotamers are quite small for most residues, but the uncertainty in the actual χ₁ values increases roughly inversely with their population (Table 1).

Figure 6.

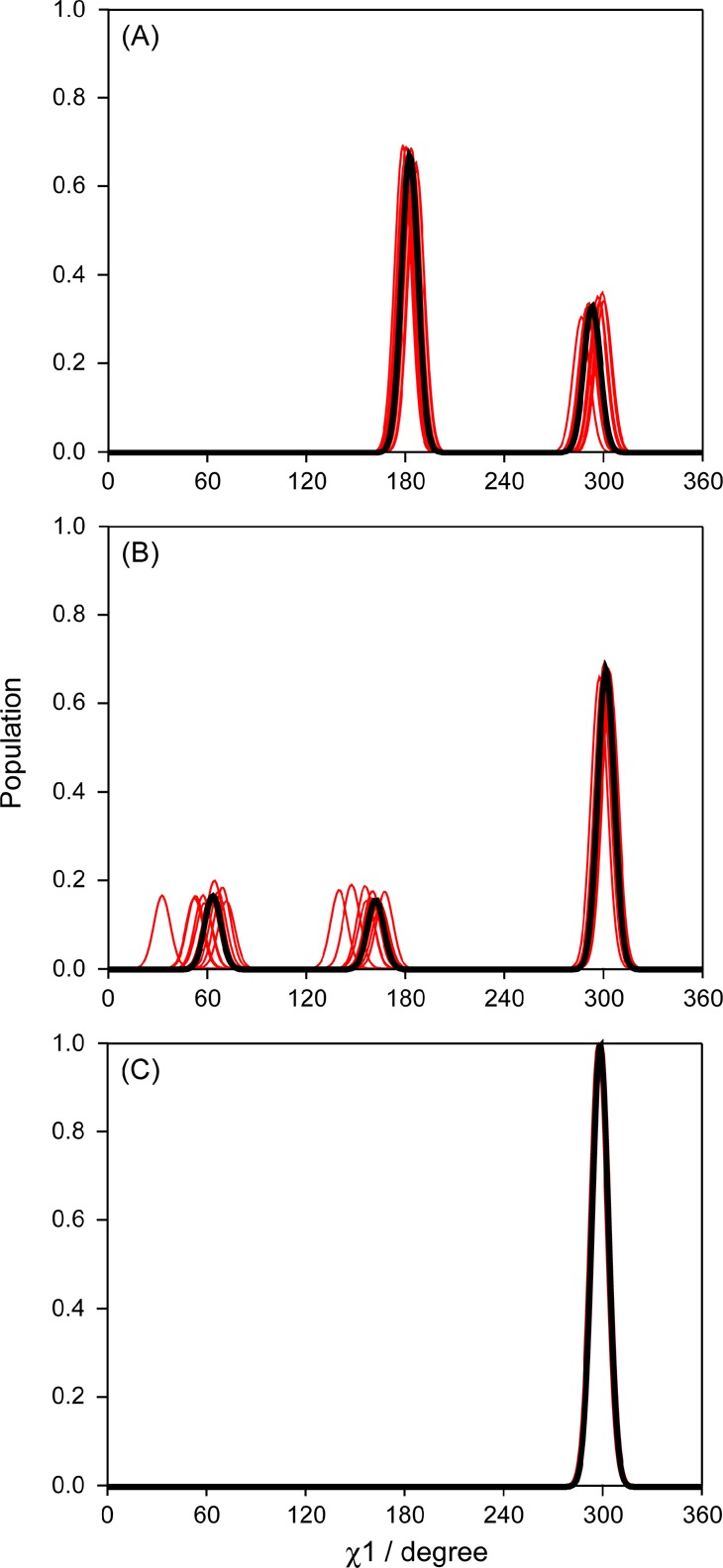
Effect of uncertainty in the structure and side chain RDC data on the χ₁ distributions, obtained by Monte Carlo rotamer analysis, of (A) K4, (B) K13 and (C) K50. The heavy line corresponds to the results of the fits to the experimental data, using the newly refined backbone structure and ¹³C^α–¹³C^β orientations. The thin lines (obscured by the black line for K50) correspond to 10 separate fits obtained when perturbing the ¹³C^α–¹³C^β orientations by 3.2° structural noise, and using the predicted RDCs of the initial fit to which Gaussian noise has been added that results in the same quality of fit as obtained for the experimental data (see text), presenting a visualization of the uncertainty in the derived rotamer populations. A full set is presented in SI Figure S9.

Comparison to X-ray Structures

Numerous high resolution X-ray structures are available for GB3 and its closely homologous first IgG binding domain, GB1, all showing very similar backbone coordinates. Below, we will focus on comparison with the X-ray structures determined by Derrick and Wigley at room temperature (PDB entry 1IGD)⁴³ and a subsequent study that used anisotropic temperature factors during refinement (PDB entry 2IGD).⁶⁰ Note that both 1IGD and 2IGD include five additional N-terminal residues, but the protein studied here by NMR is identical in sequence to these earlier structures from residue Y3 onward. Comparison to the other closely related structures is included in SI Table S8.

With backbone RDC Q-factors of ca. 18% for the N–H and C^α–H^α RDCs for both 1IGD and 2IGD, the backbone of these two X-ray structures agrees as well as, or better than, seen for any other protein for which RDCs and X-ray coordinates are available. However, as was seen previously for ubiquitin,⁶¹ side chain RDCs are predicted much less accurately by the X-ray coordinates (Q factors of 55 and 51% for 1IGD and 2IGD). To a large extent, this worse agreement for side chains is dominated by those residues that adopt multiple rotameric states in our NMR study, whereas in the X-ray study the default analysis uses a single rotameric state to fit the electron density. For example, the electron density used for generating the side chain of E24 in the 1IGD model is in good agreement with the equilibrium of g^– and t observed in our RDC study. On the other hand, the electron density of V42 is in good agreement with the g^– rotamer of its X-ray coordinates, which strongly disagrees with both the observed RDCs and the large ³J_HαHβ value, and which is considered to be energetically unfavorable in β-sheet structures.⁶² Remarkably, the predominant t rotamer seen in our NMR analysis can be accommodated in the crystal lattice without causing steric clashing. It therefore appears likely that less favorable hydration of the t rotamer within the confines of the crystalline lattice is responsible for the difference between crystal and solution states for this residue. This result highlights that even in the absence of direct crystal contacts side chain orientations may well differ between the solution and crystalline states.

Multiconformer refinement is possible for very high resolution X-ray data, and four residues in the 2IGD X-ray structure of GB3 show significantly different pairs of χ₁ values.⁶⁰ All but one of these (I7) correspond to residues for which our RDC analysis also finds multiple conformers, mostly with very similar χ₁ values and populations as the X-ray structure. For example, for V21 2IGD reports χ₁ = 295/75°, with populations of 62/38%, versus χ₁ = 302/68° and populations of 60/40% in our RDC analysis (Table 1). Similarly, for N35 2IGD shows χ₁ = 189/291°, with populations of 50/50%, versus χ₁ = 184/288°, with populations of 52/48% in our RDC analysis.

For 20 of the GB3 residues, our above RDC analysis shows a dominant (≥90%) population of a single narrow distribution of χ₁ angles. For all but one (T55) of these 20 residues, their χ₁ angle corresponds to the rotameric state observed in the X-ray structure, and for a subset of 16 the rmsd relative to the values seen in the 1.1-Å X-ray structure (PDB entry 1IGD(43)) is only 4°. For T55, 1IGD shows a t rotamer, whereas our NMR results indicate g^–, also seen in the X-ray structures of seven high resolution X-ray structures of closely related mutants (SI Table S8). For residues I7, Y33 and K50 the NMR χ₁ angle also differs substantially from 1IGD (by ca. 14°), but these residues show much above average variation in the X-ray structures too. For about half of all non-Gly, non-Ala residues we find that the side chain shows significant (≥10%) population of more than one χ₁ rotameric state. Although in most cases the most populated rotamer corresponds to the one seen in the X-ray structure, for surface-exposed residues N8 and N35 the X-ray observed χ₁ rotamer is populated just below 50% in solution.

Fitting of ³J_HαHβ to RDC-Derived χ₁ Values

The importance of ³J_HαHβ couplings for evaluating side chain conformations in peptides and proteins has long been recognized.^27,63−65 However, optimal parametrization of the corresponding Karplus equations has proven to be challenging because the assumption of static, accurately known χ₁ angles often does not apply. A number of elegant solutions have been put forward to address this problem,^28,29,66 but the challenge in empirically optimizing this relation for an intrinsically flexible system remains. On the other hand, Altona and co-workers have convincingly demonstrated for a wide range of rigid, small organic molecules that correction terms for electronegativity of substituents and their chirality can greatly improve the accuracy of the relation between ³J_HH couplings and the intervening dihedral angle.⁶⁷

Here, we compare ³J_HαHβ couplings predicted by the modified Karplus equations of Haasnoot et al.⁶⁷ for our discrete rotamer analysis (Table 1) with experimental values obtained from a 3D HA[HN,HB](CACO)NH spectrum³⁴ (SI Table S9; SI Figure S10). For peptides and proteins, six different substituent patterns apply for ³J_HαHβ, and the corresponding Karplus equations are summarized in SI Table S10. Comparison of observed with predicted ³J_HαHβ couplings shows a tight correlation (R_P = 0.96), but a slope that is distinctly smaller than 1 (Figure 7). A reduction in the slope of the correlation is consistent with the presence of fluctuations of each rotamer around its average χ₁ value.⁶⁸ The Haasnoot-modified Karplus relations are written as⁶⁷

3

with the coefficients for the different types of couplings presented in SI Table S10. In the presence of normally distributed χ₁ fluctuations with standard deviation σ, these equations can be rewritten as

4

with A′ = A exp(−2σ²); B′ = B exp(−σ²/2); C′ = C exp(−2σ²); and D′ = D + (A/2)[1 – exp(−2σ²)]. ³J_HαHβ Karplus curves, generated by eq 4 for different values of σ show the expected decrease in the amplitude of the Karplus curve.⁶⁸ Comparison of the ³J_HαHβ values predicted by eq 4 when using σ = 20° against those predicted for the corresponding static (σ = 0°) Karplus curve (SI Figure S11), yields nearly the same slope and intercept as observed experimentally, and an rmsd of 0.75 Hz. This result suggests that the smaller range of observed ³J_HαHβ couplings relative to that expected based on the static Haasnoot-modified Karplus equations is consistent with rapid χ₁ fluctuations of substantial amplitude (σ ≈ 20°). This σ amplitude is somewhat larger than the σ ≈ 10° obtained from the shallow minimum when systematically stepping σ as a global parameter (applied to all residues) in the fitting of RDCs to discrete rotamers (see SI Figure S12). However, it should be noted that the σ value obtained from RDC fitting reflects the increase in χ₁ fluctuations over the analogous fluctuations that exist in the protein backbone, whose RDCs were used to define the alignment tensor strength. By contrast, the σ value obtained from the J coupling analysis reflects the amplitude of dynamics relative to the conformationally highly restrained, and therefore quite rigid, small molecules used by Altona and co-workers to define their Karplus equations. Therefore, the larger σ value seen in the analysis of the ³J_HαHβ couplings is not surprising.

Figure 7.

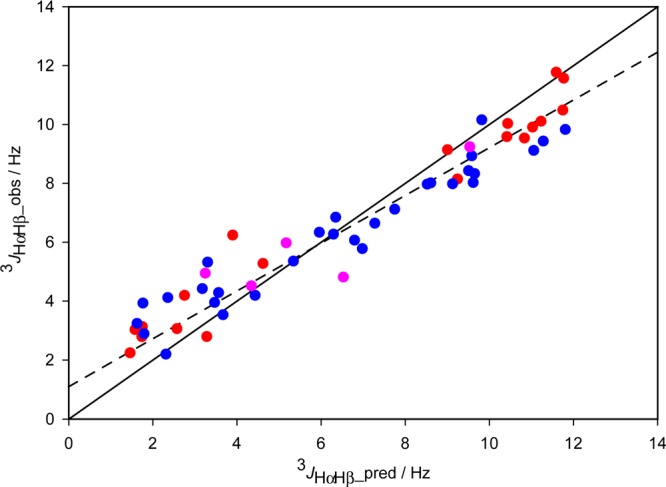
Comparison of observed ³J_HαHβ couplings with those predicted by the substituent-specific Karplus equations of Haasnoot et al.⁶⁷ The solid line corresponds to x = y; the dashed line corresponds to values predicted by these same equations after adding Gaussian fluctuations (cf. eq 4) with a standard deviation of σ = 20° to the χ₁ angles reported in Table 1. Note that to a very good approximation, the effect of σ = 20° simply scales the difference in the predicted ³J_HαHβ relative to a value of ca. 6 Hz (Figure S11). The rmsd between observed and predicted ³J_HαHβ values (using the σ = 20° motional model) is 0.75 Hz. ³J_HαHβ values (Table S16) for residues with a single χ₁ rotamer are in red, two χ₁ rotamers in blue, and three rotamers in pink.

When the Haasnoot-modified Karplus equations without any motional correction are used to predict ³J_HαHβ values for the continuous, model-free χ₁ distributions, better agreement (rmsd 0.93 Hz) is obtained than for the discrete rotamer model (1.15 Hz), presumably because the effect of the Gaussian fluctuations around the discrete rotameric states is already somewhat reflected in the model-free χ₁ distributions.

Concluding Remarks

The presence of extensive χ₁ rotamer averaging for many residues in folded proteins has long been recognized, mostly from the analysis of ³J_HH couplings^28,65 but also from analysis of NMR relaxation data of side chain ¹³C and ²H nuclei,^15,16,69 and from the observation that most side chain RDCs are smaller in solution than predicted from a static X-ray structure.^61,30 Protein X-ray structures collected at high resolution and signal-to-noise ratios also reveal the presence of extensive side chain conformational heterogeneity.^58,70,71,45 Commonly only the electron density of the most populated side chain conformers is represented in the deposited coordinates, and the presence of residual electron density reflecting alternate conformations becomes embedded in elevated temperature or B factors.^4,72 Interestingly, side chain conformational heterogeneity present at room temperature may be reduced by widely used cryo-cooling methods used for collecting X-ray diffraction data.⁷

Our study provides an exceptionally large set of precise experimental data for defining the χ₁ distribution of nearly all residues in a small protein. For slightly less than half of all non-Gly/Ala residues, we find that the χ₁ angle predominantly (≥90%) samples a single, relatively tight distribution. The width of these distributions is not very well-defined by the RDC data, but when this width is used as a global fitting parameter the RDC data suggest that the amplitude of the χ₁ fluctuations is ca. 10° larger than for the protein backbone. Comparison of the observed ³J_HαHβ couplings with those predicted on the basis of substituent-specific Karplus equations indicates χ₁ fluctuations that are ca. 20° larger than the angular fluctuations in the conformationally highly restrained small cyclic molecules, used by Altona and co-workers for parametrizing these Karplus equations.⁶⁷ We also note that the fit between experimental ³J_HαHβ and Altona-Karplus predicted values improves more than 2-fold when using our RDC analysis compared to structures obtained from the advanced eNOE analysis (PDB entry 2LUM,⁷³ averaged over its 60 ensemble members), even though these eNOE-derived structures, determined without RDCs, validate considerably better against backbone RDCs (Q_CαCβ = 28%) than those from standard NOE analysis (Q_CαCβ = 42% for PDB entry 1GB1(74)).

The majority of the residues in GB3 show significant, ≥ 10% sampling of at least two conformers (Table 1). In part, this relatively high fraction may be related to the small size of the protein, which results in a higher surface to volume ratio compared to larger proteins. Indeed, the vast majority of multiconformer side chains correspond to surface residues, whereas most interior residues predominantly sample a single χ₁ distribution. However, there are multiple exceptions to this rule: For example, solvent-exposed Asn37 shows a single, narrow χ₁ cluster, related to its side-chain being involved in a C-cap H-bond. On the other hand, Val54 which is well buried in the hydrophobic interior of the protein shows a nearly 20% population of a 25°-skewed t rotamer, in rapid exchange with its predominant nearly ideal g⁺ rotamer. Only four residues are found to sample more than two χ₁ rotamers, all of them located in the loop that connects strands β1 and β2.

As discussed above, the width of each χ₁ rotameric well is not tightly restricted by the RDC data, but the average χ₁ value of each well is sharply defined. Our analysis is completely model-free when calculating the χ₁ distributions, but inspection of the results shows exceptionally tight clustering of the center of each most populated well to the ideal staggered rotamer values of 60 + N × 120°. The center of the most populated rotamer (χ₁(1) column in Table 1) shows an rmsd of only 8° from the ideal staggered rotamer values. A previous analysis of X-ray structures indicated that the average χ₁ deviation from ideal staggered rotamers for many residue types was a function of crystallographic resolution, a finding ascribed to the electron density of minor conformers skewing the average attributed to the major conformer.⁷⁵ In the analysis of X-ray structures, the standard deviations of the rotamer distributions also were found to decrease from >20° for structures determined at a resolution >2.0 Å to ca. 15° for structures solved at higher resolution (≤2.0 Å). Our study shows a substantial further reduction in these standard deviations, at least when considering the most populated conformer for each residue (Table 1).

Many of the lowly populated side chain χ₁ conformers identified in our study deviate substantially more from ideal staggered conformations (rmsd 22°) than the major χ₁ conformer. The low values of their populations suggests that these conformers are in energetically less favorable environments, and steric clashing may cause their skewing away from perfectly staggered states. On the other hand, our error analysis also points to larger experimental uncertainty in the χ₁ angles sampled by minor conformers (σ_χ1 in Table 1). For example, when considering Monte Carlo analysis of K13 (Figure 5B), the variance in the χ₁ angle of the major g^– conformer (χ₁ = 302°) is only 2° whereas the minor t conformer (16% populated) shows a highly skewed χ₁ angle of 160° but with a standard deviation of 11°.

It can be noted that even while the values of the fitted χ₁ torsion angles as well as their total rotamer populations summed for given residue types agree well with the statistics exhibited by structural databases,^62,52 fitted site-specific χ₁ populations sampled by the individual residues differ significantly from the database-derived aggregate values. This observation indicates that selection of a given side chain rotamer is significantly influenced by its nonlocal tertiary contacts. It also is worth noting that essentially all residues located in the regions around residues L12 and G41, known to be the most dynamic based on the backbone ¹⁵N relaxation data, exhibit the sampling of more than one χ₁ rotamer, consistent with the rotameric selection being affected by tertiary contacts.

It has long been recognized that RDC data collected for a protein under multiple different alignment conditions carries valuable information on the distribution of atomic coordinates sampled.^76,77 For ordered regions in well-structured proteins, the amplitudes of angular excursions tend to be rather modest for the backbone N–H vectors, widely used for such studies, making accurate analysis of such data in terms of dynamics quite challenging.^3,25,78−80 By contrast, the changes in side chain bond vector orientations associated with χ₁ rotamer hopping are large and result in bond vector changes of ca. 110°, a value that maximizes its effect on the corresponding RDCs. Therefore, side chain RDCs are exquisitely well suited for analyzing the χ₁ rotameric averaging process. Our data show that the most populated staggered conformer χ₁ angles fall very close to those seen in atomic resolution X-ray structures of small peptides, and those of proteins when extrapolated to a resolution of 0.8 Å.⁷⁵ By contrast, the RDC data are relatively insensitive to small excursions within each rotameric well, as was highlighted by the difference in well distributions obtained when adding a small entropy term to the data analysis. This difficulty in extracting the amplitude of fluctuations within each rotameric well is akin to the above-mentioned challenges faced when quantifying from ¹⁵N–¹H RDCs the relatively small amplitudes of backbone motions typically seen in α-helices and β-sheet.

Although it may seem straightforward to extend our RDC χ₁ analysis to any other protein, we need to point out that the very detailed analysis presented here requires an extraordinary amount of data, not easily collected for many other proteins. So, most side chain analyses by RDCs likely will remain more limited in scope, and simply aim to ascertain whether a single χ₁ rotamer is populated, and which one. Our data provide strong evidence that if a single rotamer is populated, it will be very close to the ideally staggered conformation. This property allows a χ₁ rotamer estimate to be made by simply comparing the ¹D_CβHβ or ¹D_CβCγ to the backbone ¹D_CαHα and ¹D_CαC′ couplings: For example, for Thr and χ₁ = 300°, the C^β–H^β vector is antiparallel to C^α–H^α, and they will have very similar RDCs. Again for Thr, but for χ₁ = 180°, the C^β–C^γ vector is antiparallel to C^α–H^α and its normalized RDC (or the linearly related C^γH₃ methyl RDC⁸¹) will be close to ¹D_CαHα, while C^β–H^β will be antiparallel to the C^α–C′ vector, making their normalized RDCs equivalent. Similar analysis can be made for other residues, allowing straightforward evaluation of χ₁, even without recourse to a backbone structure. However, if such a cursory analysis does not point to a single rotamer, establishing the rotameric equilibrium and deviations from perfectly staggered rotameric states rapidly requires far more data.

GB3 is sufficiently small to allow generation of very long molecular dynamics trajectories and the protein has been used to evaluate the quality of computational methods by validation against experimental results.⁸²⁻⁸⁵ Our new results complement these earlier experimental data by introducing detailed side chain information, greatly extending its use for force field development. Moreover, the model-free χ₁ distributions derived in our study will enable improved parametrization of the wide range of different Karplus parametrizations that have been in common use for ³J_NHβ, ³J_C′Hβ, ³J_C′Cγ, and ³J_NCγ.^28,29,86,87 Similarly, our data will provide a new benchmark for evaluating the impact of side chain conformations on chemical shifts, an area that remains under-developed but holds strong potential for increasing the level of structural detail that can be extracted from these readily accessible parameters.⁸⁸⁻⁹¹

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.5b10072.

• Experimental procedures and additional data. (PDF)

Author Present Address

^‡ Key Laboratory of Pesticides and Chemical Biology, College of Chemistry, Central China Normal University, Wuhan, Hubei 430079, People’s Republic of China.

The authors declare no competing financial interest.