Femtosecond pulse train shaping improves two-photon excited fluorescence measurements

Abstract

Measurements of two-photon absorption (TPA) cross sections are greatly confounded by even very weak linear absorption, for example from hot bands. In this case, the experimental power dependence of fluorescence from amplified and mode-locked laser systems can differ drastically, even if the peak intensity is adjusted to be the same in both cases. A simple pulse train shaping method suppresses linear contributions and extracts the nonlinear absorption cross section, demonstrated here for a meso-to-meso ethyne-bridged bis[(porphinato)zinc(II)] fluorophore (DD) at 800 nm. This approach permits reliable TPA cross-section measurement, even with standard modelocked lasers under conditions identical to that used for multiphoton microscopy.

Two-photon excited fluorescence (TPF) microscopy has become a valuable tool to extend the utility of optical imaging, especially in biomedical applications [1,2]. However, a major challenge faced by this technique is that most natural molecules produce very little TPF [3]. This challenge motivates the development of novel chromophores with large near-IR (NIR) two-photon absorption (TPA) cross sections, typically from strong π-conjugation and enhanced transition dipole strength. Multiple examples of NIR fluorophores having TPA cross sections exceeding 10³ GM have now been reported [4,5]. Highly conjugated, meso-to-meso ethyne- and butadiyne-bridged (porphinato)zinc(II) oligomers are promising NIR two-photon imaging agents because of their outstanding chemical and photochemical stabilities, excellent biocompatibility, and high fluorescence quantum yields [6–9]. These chromophores manifest exceptional electronic structural characteristics that include low-energy π-π*-excited states that are polarized exclusively along the long molecular axis, intensely absorbing S₀ → S₁ (Q-state) and S₁ → S_n transitions that extend deep into the NIR spectral region, and unusually large polarizabilities [6–9].

While the TPA cross section can be measured directly [10,11], for applications of TPF microscopy the appropriate figure of merit is TPA times the quantum yield, which is commonly measured by direct observation of the fluorescence [12]. Spectroscopic characterization of TPA cross sections has most commonly been performed using low-repetition rate amplified laser systems (kilohertz). However, for the ultimate application (imaging), unamplified modelocked lasers with roughly 100 MHz repetition rate are preferred to scan large spatial regions in a reasonable time. Previously, a modelocked laser was used directly to evaluate the TPA cross sections of several monomeric (porphinato)zinc(II) fluorophores and multiple, oligomeric meso-to-meso ethyne- and butadiyne-bridged (porphinato)zinc(II) chromophores, but the TPA signal was overwhelmed by one-photon fluorescence [13].

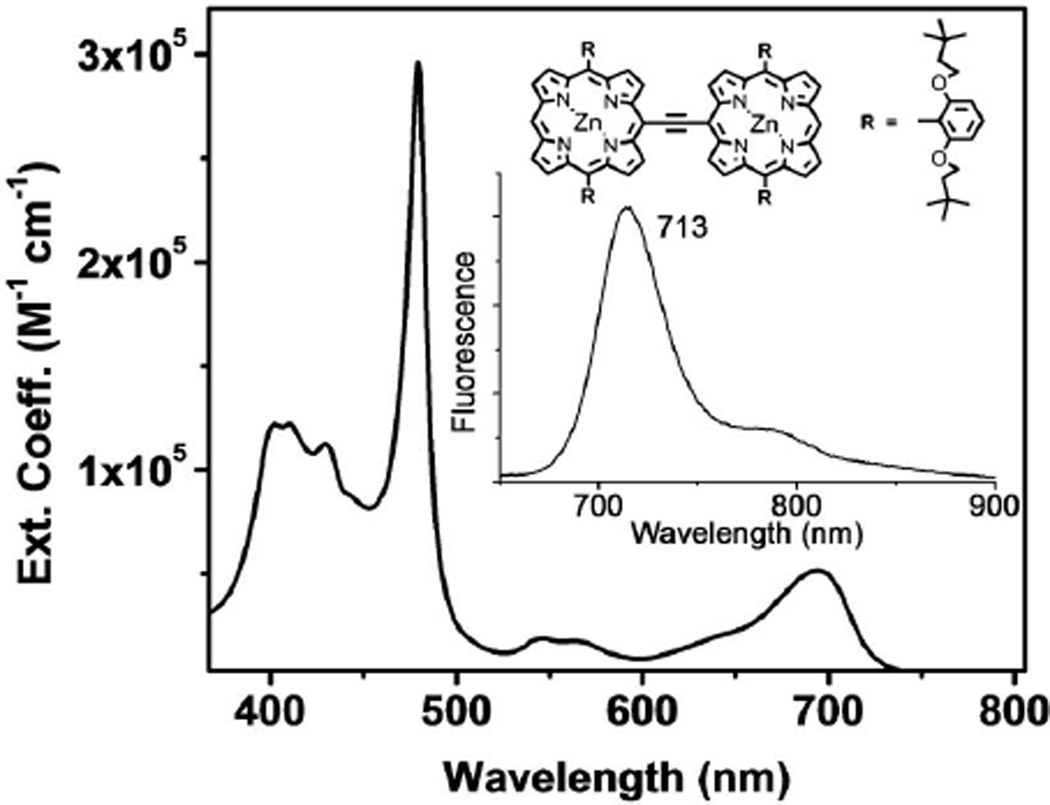
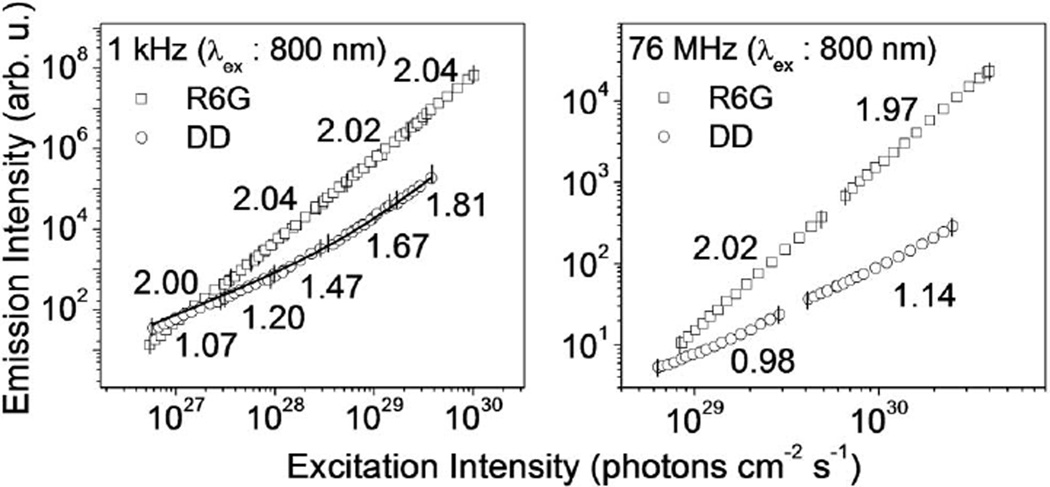
In this study, we measure the laser-induced fluorescence of a meso-to-meso ethyne-bridged (porphinato) zinc(II) dimer, bis[(5,5′-10,20-bis[2,6-bis(3,3-dimethyl-1-butyloxy)phenyl]porphinato)zinc(II)]ethyne (DD, Fig. 1), using both a regenerative amplifier (1 kHz repetition rate) and a mode-locked oscillator (76 MHz) at λ = 800 nm to compare the effect of repetition rate, excitation geometry, and excitation intensity on multiphoton fluorescence measurements. The absorption spectrum, shown in Fig. 1, suggests that one-photon absorption should be negligible at 800 nm; we estimate the extinction coefficient at this wavelength to be below 100 M⁻¹ cm⁻¹ at room temperature. Yet we find a linear contribution to DD’s fluorescence and substantial differences in the fluorescence power scaling between low- and high-repetition rate excitation (Fig. 2). For 1 kHz excitation, DD shows a linear intensity scaling (a slope of 1 in the log–log plot) for low excitation intensities (≤10²⁷ photons cm⁻² s⁻¹), increasing to 1.8 in the range of ~10²⁹ photons cm⁻² s⁻¹. For 76 MHz excitation at 800 nm, DD fluorescence emission displays an almost linear response over the entire intensity range. In contrast, Rhodamine 6G (R6G) displays only TPA at λ = 800 nm in the range of powers we studied; however, at λ = 630 nm (still far to the red of its linear absorption peak) again significant deviations from intensity-squared scaling are observed with mode-locked lasers. These data high-light that even though 76 MHz excitation better replicates the experimental conditions of the ultimate imaging application, the possibility of signal contamination because of confounding linear fluorescence contributions should always be considered when high-repetition rate lasers are utilized in TPA cross-section determinations.

Fig. 1.

Linear electronic absorption and emission (inset) spectra of DD in THF solvent.

Fig. 2.

Log–log plots of the emission intensity of DD (lower curve) and R6G (upper curve) as a function of peak excitation intensity; for comparison, 10²⁸ photons cm⁻² s⁻¹ at λ = 800 nm corresponds to 2.5 × 10⁹ W cm⁻². The numbers in the plots indicate the local power scaling within the indicated range (the slope in the log–log plot). The symbols are measured data; the solid line in the left panel is a nonlinear least-squares fit to the sum of a linear and a quadratic component.

We show that the different fluorescence power scaling of DD for 1 kHz and 76 MHz excitation arises from the significantly different focusing geometries of the two excitation laser systems: the mode-locked system employs a tight focus to achieve large enough (>10²⁵ photons cm⁻² s⁻¹) peak intensities, while the kilohertz system employs a very weak focus (70 µm beam radius at the sample position, contrasting the 1.0 µm focal point beam radius for 76 MHz excitation). We then introduce a novel pulse train shaping method which attenuates the linear fluorescence contribution. With this method, fast repetition rate laser excitation sources can be used to determine TPA cross sections under conditions identical to that used for TPF microscopy.

For a conventional 1 kHz power study, the emission intensity as a function of excitation power was acquired using a regenerative amplifier (Spectra Physics, Spitfire), producing 150 fs pulses (FWHM) at 800 nm. For excitation, a 1 cm path-length quartz cell was placed at the focal point of a weakly focused beam (producing a 70 µm beam radius at the sample position). Emission was collected at 90° with a PMT (Hamamatsu, R3896) through a set of short-pass filters (Thorlabs, FES0700 and FES0750) to reject scattered excitation light. For a conventional 76 MHz power study, a modelocked Ti:sapphire laser (Spectra Physics, Tsunami, 76 MHz) was used as the excitation source. The beam was focused in the center of a 1 cm quartz cuvette using a 10 × /NA 0.25 objective lens producing a beam radius of 1.0 µm at the focus. The mode-locked Ti:sapphire laser (76 MHz) was also used for a pulse train modulation experiment as the excitation source at 800 nm. To generate the desired intensity waveform, the beam was focused into an acousto-optic modulator whose drive signal was adjusted with an arbitrary function generator (LeCroy, LW420A). The beam was then focused in the center of a 1 cm quartz cuvette using a 10 × /NA 0.25 objective lens. The detected fluorescence was analyzed with a lock-in amplifier (Stanford Research Systems, SR830).

DD manifests a S₀ → S₁ (x-polarized Q-state) absorption maximum at 695 nm and S₀ → S₂ manifold absorption maxima at 401 and 479 nm (Fig. 1); its fluorescence emission band maximum is centered at 713 nm. Two-photon excitation at 1000 nm and one-photon excitation at 510 nm yield identical fluorescence spectra despite fundamentally different selection rules for one- and TPA, confirming that the final emissive state of DD is the low lying S₁ state regardless of excitation conditions.

The dissimilarity of the observed slopes of DD emission intensity versus excitation intensity as a function of these 1 kHz and 76 MHz excitation sources (Fig. 2) can be explained by differences in the excitation geometry. In the 1 kHz setup, the beam is loosely focused (z_R ≥ l, where z_R is the Rayleigh range and l is the optical path length of the sample; here z_R = 1.8 cm and l = 1 cm) leading to a nearly uniform (high intensity) excitation distribution along the 1 cm cuvette. On the other hand, in the 76 MHz setup the beam is tightly focused (z_R ≪ l; z_R = 4.1 µm and l = 1 cm) generating intensities high enough for nonlinear excitation only at a small focal volume (~26 µm³), while the lower intensities in the out-of-focus regions still contribute to one-photon absorption. This behavior was confirmed by a confocal-type measurement in which the fluorescence is focused through an iris placed between the sample and the detector. Partial rejection of out-of-focus light increased the power scaling from 1.18 to 1.41 in the range of ~10³⁰ photons cm⁻² s⁻¹.

With excitation at 800 nm and fluorescence shortpass filters at 700 nm, linear absorption from the electronic-vibronic ground state cannot produce a detectable emission signal. For a related conjugated multiporphyrin dimer it was noted that absorption from hot vibronic states (hot-band absorption) could contribute to linear absorption [14,15]. We confirmed this effect to be the cause of the one-photon absorptive contribution evident in Fig. 2 by cooling down our sample to 77 K (data not shown). With the low-repetition 1 kHz excitation, the linear contribution could be removed by cooling the sample to 77 K. With the high-repetition rate setup, however, cooling could not completely remove the one-photon absorptive contribution of DD emission (a slope of 1.77 in the range of ~10³⁰ photons cm⁻² s⁻¹) possibly because of light-induced local heating in the solid phase. These temperature-dependent power studies indicate that hot-band absorption adds a significant linear contribution to the fluorescence signal. This effect was also observed in previous work, e.g. [14], and is especially pronounced at room temperature for strong focusing geometries (NA 0.25 objective lens in our experiment)—conditions typically encountered in conventional multiphoton fluorescence imaging.

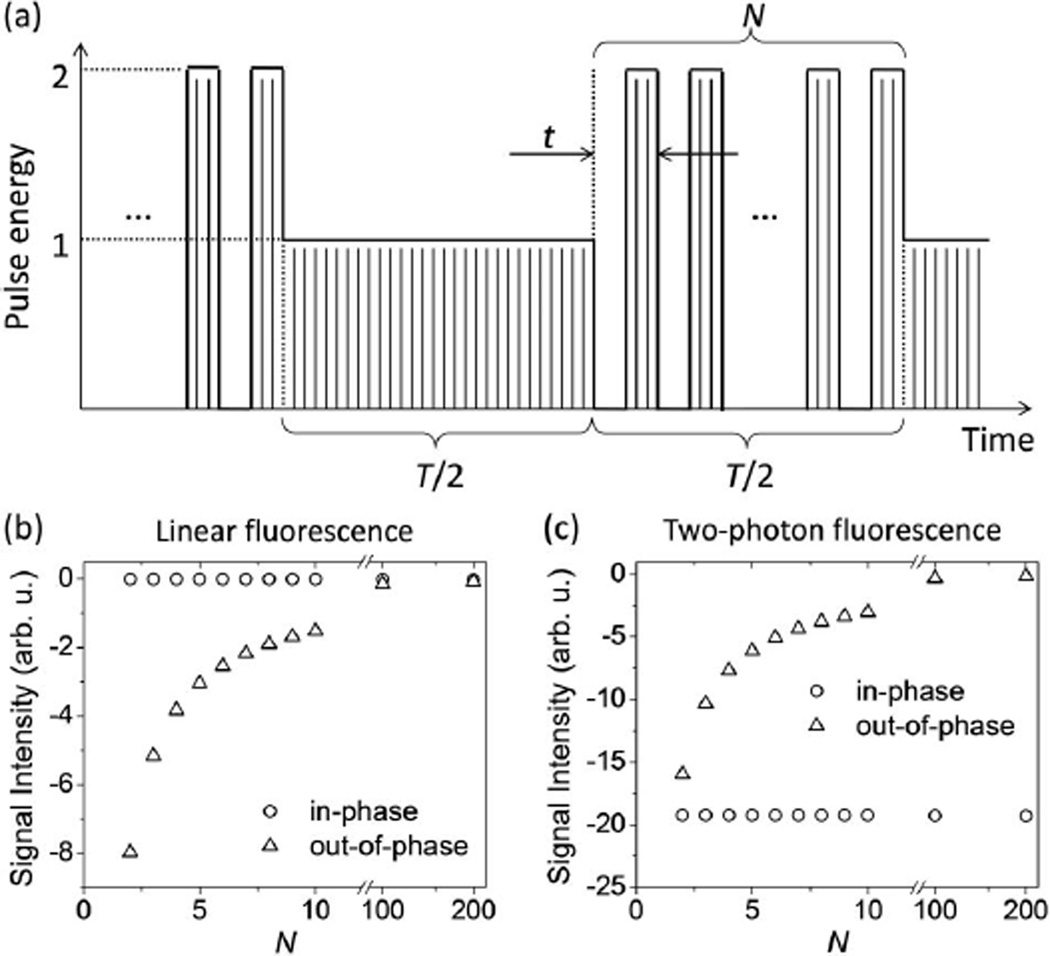
Pulse shaping (either of individual pulses [16], or of the pulse train itself [11]) offers new ways to sensitively measure nonlinear properties, such as nonlinear absorption or nonlinear refraction. For example, nonlinear absorption cross sections were measured by analyzing the electronic spectrum of an amplitude-modulated pulse train transmitted through a sample [11]. In practice, the drawback of this method is that it requires very clean sinusoidal modulation, which is difficult to achieve with high modulation depth. Here, we describe a more robust pulse train shaping method that allows for the selective recording of nonlinear fluorescence signals. The key concept of this method is illustrated in Fig. 3(a). The first half of an optical excitation pulse sequence of period T consists of a stable pulse train with pulses of fixed pulse energy, while the second half is divided up into N on–off cycles of duration t (with t ≪ T), switching between periods when the pulse energy is twice as large and when the light is off. The detected fluorescence signal is analyzed with a lock-in amplifier at the fundamental frequency f = 1/T. The resulting signal is most easily understood for a very large number of on–off cycles N (i.e., cycles shorter than the detector response time). In the case of linear fluorescence, the averaged fluorescence energy in the first half and the second half of the sequence are identical, and no signal variation at the fundamental frequency f is recorded. For two-photon fluorescence, the intensity-squared scaling leads to an average fluorescence in the second half that is twice as large as in the first half, leading to a square-wave type modulation of the fluorescence that is in phase with the imposed pulse sequence. In practice, for a finite number of cycles a lock-in amplifier separates the signal into in-phase and out-of-phase components. Figures 3(a) and 3(b) show the calculated components of the signal that are in-phase and out-of-phase with the pulse sequence as a function of N. For linear fluorescence the in-phase component is zero, while for two-photon fluorescence the in-phase component is nonzero and independent of N. Hence, recording the in-phase component in a case where both linear and nonlinear fluorescence occurs effectively suppresses the linear contribution. This pulse shaping method differs from previous methods [17] that use on–off modulation to provide time between measurement cycles for accumulated heat to dissipate; the differences in Fig. 2 are not caused by heating, but by the differences in focal geometry.

Fig. 3.

(a) Schematic of the pulse train shaping technique where T is the total period of the pulse train, t is the duration of one on–off cycle, and N is the number of on–off cycles. Thin lines represent individual pulses of a high-repetition rate laser (not to scale). Calculated “in-phase” and “out-of-phase” components of a lock-in amplifier’s signal as a function of N at frequency f = 1/T for the case of (b) linear fluorescence (c) and two-photon fluorescence.

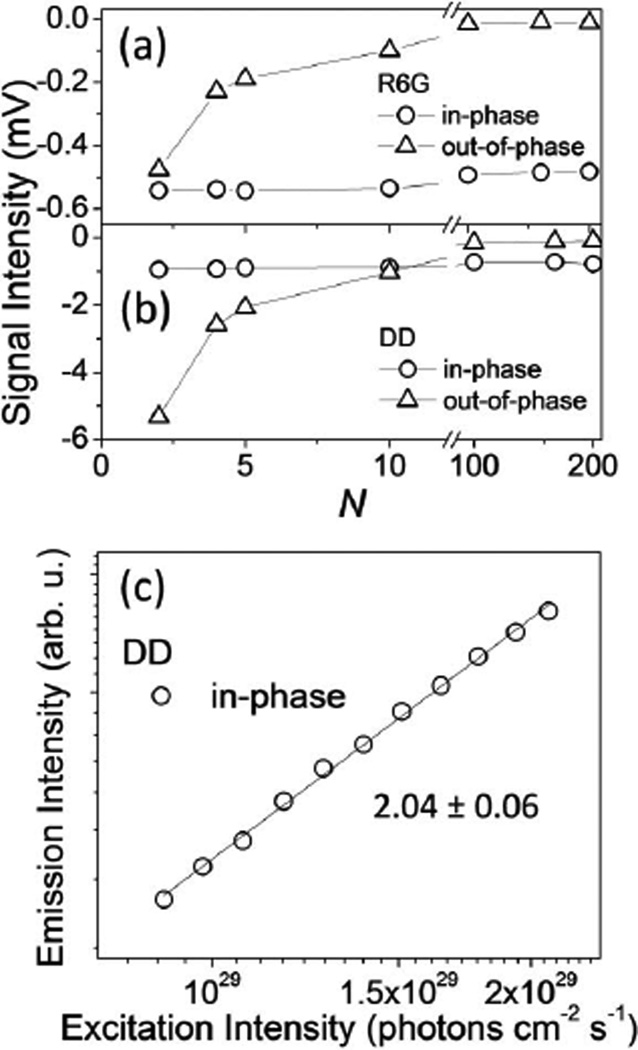
Figure 4 shows the in-phase and out-of-phase components of the measured fluorescence intensity in experiments that utilized pulse train shaping for 800 nm excitation of DD and R6G at T = 2 ms as a function of the number of on–off cycles in the waveform. Note that R6G only exhibits two-photon fluorescence; Fig. 4(a) traces reproduce the computationally predicted behavior for the in-phase and out-of-phase components of the two-photon fluorescence signal at frequency f = 1/T [Fig. 3(c)]. In contrast, the analogous experiment carried out for DD [Fig. 4(b)] reveals a mixture of linear and nonlinear fluorescence under these conditions. To demonstrate the suppression of the linear fluorescence contribution, we performed a power study using the measured in-phase fluorescence signal intensity acquired for N = 200 at excitation intensities of about 10²⁹ photons cm⁻² s⁻¹ (the lowest intensity used in Fig. 2). Whereas the conventional measurement demonstrates that the one-photon-absorptive contribution plays the dominant role in determining the magnitude of the measured fluorescence signal (Fig. 2, right panel), a similar analysis of the in-phase fluorescence component obtained in the pulse train shaping experiments demonstrates suppression of the linear contribution [evidenced by a slope of ~2.0, Fig. 4(c)].

Fig. 4.

In-phase and out-of-phase components of pulse train shaping fluorescence signals in (a) R6G and (b) DD as a function of N (the number of on–off cycles). Measurements were performed with the 76 MHz system at λ = 800 nm and T = 2 ms. (c) Logarithmic plot of the in-phase component of the emission intensity of DD as a function of excitation intensity at N = 200 and T = 2 ms; the power scaling is indicated in the graph.

Because our pulse train shaping method inherently suppresses linear contributions, we directly obtain the two-photon cross section relative to the standard R6G (taking into account the differences in the detection efficiency) using

$${\sigma }_{2,\mathrm{D}\mathrm{D}}=\frac{{[C]}_{R6G}{\eta }_{R6G}{\phi }_{R6G}{\langle F\rangle }_{\mathrm{D}\mathrm{D}}}{{[C]}_{\mathrm{D}\mathrm{D}}{\eta }_{\mathrm{D}\mathrm{D}}{\phi }_{\mathrm{D}\mathrm{D}}{\langle F\rangle }_{R6G}}{\sigma }_{2,R6G},$$ (1)

where [C] is the concentration, η the fluorescence quantum yield, φ the collection efficiency of the system, and 〈F〉 the in-phase component of the detected fluorescence. We performed measurements at 800 nm with an intensity of I = 7.2 × 10²⁷ photons cm⁻² s⁻¹ and a pulse sequence of N = 200. Using a reference value of σ_2,R6G = 65 GM [18], we obtain a TPA cross section for DD of σ_2,DD = (2300 ± 500) GM. This value is reasonably close to the value of σ_2,DD = 1100 GM obtained from the conventional 1 kHz intensity-dependent power scaling (Fig. 2, right panel) by the fit to the sum of a linear and a quadratic component. (Because of the many uncertainties in the determination of the hot-band linear cross section, no error estimate is provided.)

In summary, we have shown that for 800 nm excitation, the meso-to-meso ethyne-bridged bis[(porphinato)zinc (II)] fluorophore (DD) exhibits concomitant linear hot-band absorption, and much more substantially under high-repetition rate excitation conditions. In conventional two-photon absorptive cross-section measurements, tight focusing, typically used in high-repetition rate systems, can result in a large linear fluorescence through hot-band absorption in out-of-focus regions, which can be problematic for TPA characterization. Here we demonstrated key proof-of-principle experiments that show that appropriate pulse train shaping methods suppress linear contributions to the fluorescence and allow for extraction of pure nonlinear absorption cross sections, even in the presence of strong confounding linear fluorescence. Moreover, because this method should also be insensitive to linear fluorescence contributions in an imaging environment, it dramatically extends the excitable wavelength range of multi-photon contrast agents that can be used for tissue imaging applications.