Mathematical modeling of acid-base physiology

Abstract

pH is one of the most important parameters in life, influencing virtually every biological process at the cellular, tissue, and whole-body level. Thus, for cells, it is critical to regulate intracellular pH (pH_i) and, for multicellular organisms, to regulate extracellular pH (pH_o). pH_i regulation depends on the opposing actions of plasma-membrane transporters that tend to increase pH_i, and others that tend to decrease pH_i. In addition, passive fluxes of uncharged species (e.g., CO₂, NH₃) and charged species (e.g., HCO₃⁻ , NH₄⁺) perturb pH_i. These movements not only influence one another, but also perturb the equilibria of a multitude of intracellular and extracellular buffers. Thus, even at the level of a single cell, perturbations in acid-base reactions, diffusion, and transport are so complex that it is impossible to understand them without a quantitative model. Here we summarize some mathematical models developed to shed light onto the complex interconnected events triggered by acids-base movements. We then describe a mathematical model of a spherical cell–which to our knowledge is the first one capable of handling a multitude of buffer reaction–that our team has recently developed to simulate changes in pH_i and pH_o caused by movements of acid-base equivalents across the plasma membrane of a Xenopus oocyte. Finally, we extend our work to a consideration of the effects of simultaneous CO₂ and HCO₃⁻ influx into a cell, and envision how future models might extend to other cell types (e.g., erythrocytes) or tissues (e.g., renal proximal-tubule epithelium) important for whole-body pH homeostasis.

1. Introduction

The field of acid-base physiology has advanced significantly in recent years, thanks to the rapid accumulation of molecular biological insight–including genome-sequence data–as well as functional, biochemical, and cell biological studies. Progress with in-vitro expression systems (e.g., Xenopus oocytes, cells in culture) and genetically manipulated animals has produced a large amount of new data. In spite of significant progress, we are still far from fully understanding the mechanisms involved in acid-base homeostasis. For example, we are still unable to discern with certainty the relative contribution of the many simultaneous and interconnected processes (e.g., movements of numerous acid-base equivalents, equilibria of a multitude of buffers) that produce pH changes in a single living cell, let alone a tissue or the whole organism.

Understanding acid-base physiology is important because virtually every biological process is pH sensitive. Perturbations in pH can affect a variety of biological processes at the cellular, tissue, and whole-body level. At the cellular level, maintaining cytosolic pH (i.e., intracellular pH, pH_i) within a narrow range is essential for many processes to occur, including biochemical reactions, as well as the function of transporters, channels, receptors, structural proteins, and regulatory molecules (Ludwig et al., 2003; Roos and Boron, 1981; Waldmann et al., 1997). In addition, pH_i influences the luminal pH of membrane-bound intracellular organelles (e.g., endoplasmic reticulum, endosomes, mitochondria), and thereby has an indirect influence on the myriad events occurring inside these organelles (Igawa et al., 2010; Matsuyama and Reed, 2000; Roopenian and Akilesh, 2007). At the tissue level, local extracellular pH (pH_o) not only influences pH_i (Boron, 2012a; Roos and Boron, 1981) but also modulates the binding of extracellular ligands to cell-surface receptors (Roopenian and Akilesh, 2007), and a host of regional processes that include blood flow (Boedtkjer and Aalkjær, 2012), air flow in the lungs (Duckles et al., 1974; Kolobow et al., 1977; Winn et al., 1983), maintenance of appropriate corneal hydration and transparency (Li et al., 2005; Sun and Bonanno, 2003), epithelial transport, and the binding of ligands to extracellular receptors (Traynelis, 1998). At the whole-body level, the pH of blood plasma not only influences local tissue pH_o (which in turn affects pH_i) but also modulates interactions, in the plasma, of charged molecules (e.g., hormones and their carrier proteins). In the realm of patient care, plasma pH affects the electrical charge of therapeutic agents that are weak acids or weak bases, and how these agents interact with plasma proteins and distribute among the tissues (Rodgers and Rowland, 2006; Rodgers et al., 2005).

Because pH changes have such profound effects on biology, organisms have evolved a series of sophisticated mechanisms to achieve homeostasis of pH in the intracellular fluid, blood plasma, and other compartments in the body. The process by which cells or the whole body respond to perturbations in pH by tending to return pH to its initial value is known as “pH regulation”. Regulation of pH in the blood plasma–and, by extension, in the extracellular fluid-–is the result of the dual action of the respiratory and renal systems, which independently control the concentrations of carbon dioxide (CO₂) and bicarbonate (HCO₃⁻), the two major components of the body's most important buffering system. More specifically, the lungs regulate plasma [CO₂], whereas the kidneys, plasma [HCO₃⁻].

Cells regulate pH_i by appropriately adjusting the speeds of various transporters that move acids (including hydrogen ions or protons, H⁺) or bases (e.g., HCO₃⁻) across the plasma membrane. The movements across the membrane of uncharged weak acids or bases (e.g., butyric acid or ammonia, NH₃), or of their charged counterparts (e.g., butyrate or ammonium, NH₄⁺), can produce pH_i perturbations against which cells defend themselves using their pH_i-regulatory machinery.

Movements of acid-base equivalents across the plasma membrane–whether these movements are the insults that perturb pH_i or the regulatory response–influence one another and alter the equilibria of numerous intracellular and extracellular buffers, thereby creating complicated interdependencies among acid-base reactions, diffusion, and carrier-mediated transport. Because of the complexity of such movements, several investigators have developed mathematical models of acid-base physiology to help in data interpretation.

In this review, first we provide an overview of acid-base physiology with special emphasis to the mechanisms of pH regulation in the body and cell. Then, we summarize mathematical models of acid-base physiology by others. Finally, we summarize the most recent models from our team.

2. Overview of acid-base physiology

2.1. Acid-base chemistry

Before reviewing how the body, tissues and cells achieve pH homeostasis, it is useful to draw our attention to the most powerful buffering system¹ in the body–the CO₂/HCO₃⁻ buffer pair.

Dissolved CO₂, HCO₃⁻ , and H⁺ are related through the reactions

$${\mathrm{CO}}_2+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}_2{\mathrm{CO}}_3\rightleftharpoons {{\mathrm{HCO}}_3}^{-}+{\mathrm{H}}^{+}.$$ (1)

The first step of these reactions, the CO₂ hydration reaction, is extremely slow. To meet physiological needs, virtually all cells and tissues express a form of the enzyme carbonic anhydrase (CA), which catalyzes (or, more accurately, bypasses) this slow reaction. The second step of reactions (1), the dissociation of carbonic acid (H₂CO₃), is extremely fast. Thus, in the absence of CA, the slow CO₂ hydration reaction is the limiting step in the conversion of CO₂ into HCO₃⁻ and H⁺, and vice versa.

Ignoring the H₂CO₃ intermediate in reaction (1), we can write the thermodynamically equivalent form

$${\mathrm{CO}}_2+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {{\mathrm{HCO}}_3}^{-}+{\mathrm{H}}^{+}.$$ (2)

The equilibrium constant for this reaction is

$$K=\frac{[{{\mathrm{HCO}}_3}^{-}][{\mathrm{H}}^{+}]}{\left[{\mathrm{CO}}_2\right]},$$

which, in logarithmic form, can be written as

$$\mathrm{pH}=\mathrm{p}K+{\log }_{10}\frac{\left[{{\mathrm{HCO}}_3}^{-}\right]}{\left[{\mathrm{CO}}_2\right]}.$$ (3)

This is the Henderson–Hasselbalch (Hasselbalch, 1916; Henderson, 1908; Sendroy et al., 1934) equation which states that, in a simple CO₂/HCO₃⁻ buffer system, it is not these two individual buffer components that determine pH, but their ratio.

Recalling that, according to Henry's law, dissolved [CO₂] = s · P_CO2, where s is the solubility coefficient of CO₂ and P_CO2 is the partial pressure of CO₂, we can rewrite Equation (3) in the form

$$\mathrm{pH}=\mathrm{p}K+{\log }_{10}\frac{\left[{{\mathrm{HCO}}_3}^{-}\right]}{s\cdot {\mathrm{P}}_{{\mathrm{CO}}_2}}.$$ (4)

Substituting into Equation (4) reasonable values for the pK of the CO₂/HCO₃⁻ equilibrium (e.g., 6.1), [HCO₃⁻] (e.g., 24 mM), the solubility of CO₂ (e.g., 0.03 mM/mm Hg), and P_CO2 (e.g., 40 mm Hg), we see that the Henderson–Hasselbalch equation correctly predicts a pH of ~7.40 for normal, human arterial blood at 37 °C (Boron, 2012a).

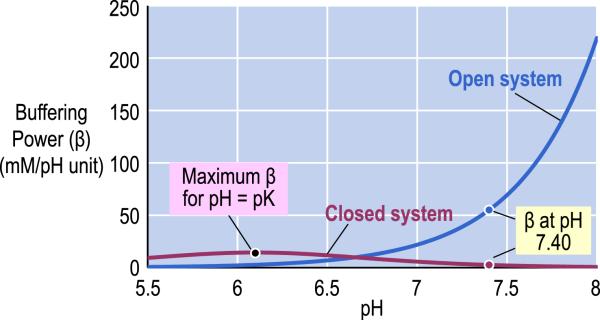
The CO₂/HCO₃⁻ buffer system is the most important buffer in the body for three reasons. First, the body independently and appropriately regulates [CO₂] and [HCO₃⁻] in response to changes in the acid-base status of the blood. Second, the sum [CO₂] + [HCO₃⁻] is higher than for any other buffer pair. And third, the body behaves as an open system for CO₂. Fig. 1 illustrates the pH dependence of buffering power (i.e., the amount of strong base per unit volume of solution necessary to produce a given increase in pH) of the CO₂/HCO₃⁻ buffer in a fluid having the composition of normal arterial blood. If the system is “closed” with respect to CO₂/HCO₃⁻ – that is, neither of its components can communicate with the environment (e.g., it is contained in a closed syringe with no gas phase)–its buffering power has a bell-shaped dependence on pH and reaches its maximum value when pH is equal to pK. If the system is “open” with respect to CO₂–that is, [CO₂] is stabilized by communication with the environment (e.g., it is contained in a beaker where the CO₂ can exchange with the overlying air)–the buffering power of the CO₂/HCO₃⁻ buffer pair rises exponentially with pH. Thus, for a closed-system buffer, buffering power (β)–a measure of the ability of the buffer to resist to changes in pH–is greatest in the pH range close to the pK, whereas for an open-system buffer, the effectiveness of the buffer increases with pH.

Fig. 1.

pH dependence of buffering power of the carbon dioxide/bicarbonate (CO₂/HCO₃⁻) buffer in a fluid having the composition of normal arterial blood. The blue line identifies the buffering power of the CO₂/HCO₃⁻ buffer in a system that is “open” with respect to CO₂ but closed to HCO₃⁻ . The purple line identifies the buffering power of the CO₂/HCO₃⁻ buffer in a system that is “closed” with respect to both CO₂ and HCO₃⁻ . For the calculations, we assumed that the pK of the CO₂/HCO₃⁻ equilibrium is 6.1, [HCO₃⁻ ] is 24 mM, the solubility of CO₂ is 0.03 mM/mm Hg, and P_CO2 is 40 mm Hg. Modified from Fig. 28–4 in Medical Physiology, 2nd Edition Updated Edition, edited by WF Boron and EL Boulpaep, Philadelphia: Elsevier, 2012.

If the system were closed for CO₂/HCO₃⁻ , the maximal CO₂/ HCO₃⁻ buffering power (i.e., at pH pK 6.1) would be modest (Fig. 1), and its buffer power at the physiological blood-plasma pH of 7.4 would be quite small (Davenport, 1974; Seldin and Giebisch, 1989). The great potency of the CO₂/HCO₃⁻ buffer in the blood derives from the system's being open for CO₂, which can continuously exit or enter the blood plasma across the alveolar blood-gas barrier, thereby achieving a near equality between the P_CO2 in alveolar air and the P_CO2 in arterial blood. Because alveolar ventilation maintains a stable P_CO2 in the alveolar air, this system maintains a stable [CO₂] in arterial blood plasma, as well. Moreover, the respiratory system can regulate ventilation to stabilize arterial [CO₂] when CO₂ production changes (e.g., during exercise), or regulate ventilation to achieve a shift in alveolar P_CO2 to compensate for an acid-base disturbances.

2.2. Whole-body pH regulation

The human body is challenged daily with a continuous production of CO₂ and far smaller amounts of strong acids (Giebisch and Windhager, 2012). An adult on a “typical Western diet” produces ~15,000 mmol/day of CO₂ via metabolism (Giebisch and Windhager, 2012). The respiratory system uses very efficient mechanisms (e.g., diffusion and convection) to remove from the blood this CO₂ that otherwise would acidify all the extra- and intracellular fluids by forming H⁺ through reaction (2). In addition to CO₂, metabolism produces ~40 mmol/day of non-volatile acids that, together with ~20 mmol/day of strong acid contained in a “typical Western diet” and the obligatory intestinal loss of ~10 mmol/day of alkali, represents a total net load of ~70 mmol/day of non-volatile acids (Giebisch and Windhager, 2012). As the 70 mmol/day of non-volatile acids appear in the extracellular fluid, extracellular HCO₃⁻ neutralizes these acids by forming CO₂ and H₂O.² 2 Thus, the appearance of ~70 mmol/day of non-volatile acids in the extracellular fluid (ECF) corresponds to the disappearance of an equal amount of HCO₃⁻ from the ECF.³ The kidneys reverse this process by excreting ~70 mmol/day of H⁺ into the urine and simultaneously transporting ~70 mmol/day of “new” HCO₃⁻ into the blood plasma, thereby regenerating the extracellular HCO₃⁻ that was consumed during the neutralization of the non-volatile acids. In so doing, the kidneys maintain blood [HCO₃⁻] constant and prevent the blood from acidifying.

In the remainder of this section, we will review how the respiratory system controls blood [CO₂] and how the renal system control blood [HCO₃⁻], thereby maintaining the blood pH in the normal physiological range.

2.2.1. The respiratory system

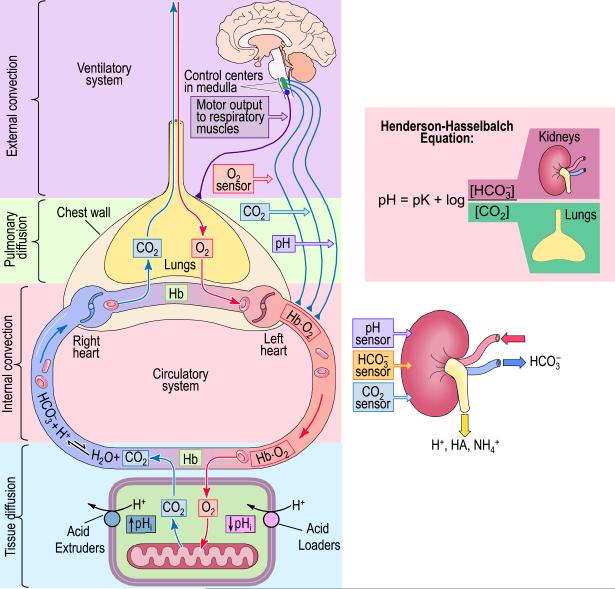
Fig. 2 provides an overview of the human respiratory system, and how it removes CO₂ from the body, using a combination of diffusion and convection (Boron, 2012b). CO₂ originates in the mitochondria as a result of aerobic metabolism. Because P_CO2 is highest in the mitochondria, CO₂ diffuses down its concentration gradient from the cell to the extracellular space, and then into the systemic capillaries. Here, ~10% of the total CO₂ remains in the blood plasma, whereas the remaining ~90% enters the red blood cells (RBCs), where most of it undergoes the reaction CO₂ + H₂O → HCO₃⁻ + H⁺, catalyzed by CA I and II. Hemoglobin (Hb) buffers the newly produced H⁺, thereby playing an important role in acid-base chemistry. Simultaneously, the Cl–HCO₃ exchanger AE1 exports the newly formed HCO₃⁻ (Jennings, 1989; Parker and Boron, 2013). Thus, RBCs are the key to CO₂ carriage in the blood. Following these diffusion and transport events, it is the internal convective system that carries the CO₂-rich blood from the systemic capillaries to the pulmonary capillaries (Boron, 2012c). Thanks to its separate right and left hearts that, respectively, drive blood through the separate pulmonary and systemic circulations, the circulatory system delivers blood with high P_CO2 to the pulmonary capillary. The result is a maximization of the CO₂ concentration gradient that now drives the diffusion of CO₂ across the capillary endothelium and alveolar epithelium into the alveolar air space in the lungs. Finally, the external convective system, the ventilatory machinery or air pump–consisting of the chest wall, the respiratory muscles and the conduits for the airflow–moves the CO₂-rich air from the alveolar space to the atmosphere, and moves O₂-rich ambient air in the opposite direction. This exchange of alveolar and ambient air, or alveolar ventilation, is under the control of the central nervous system, which sets the depth and frequency of ventilation, and appropriately modulates both in response to changes in arterial P_O2, P_CO2, and pH.

In summary, the respiratory system uses diffusion for the short-distance movements of CO₂ near the systemic and pulmonary capillaries, and convection for the long-distance movements of CO₂ from the systemic to the pulmonary capillaries and again from the alveoli to the environment.

2.2.2. The renal system

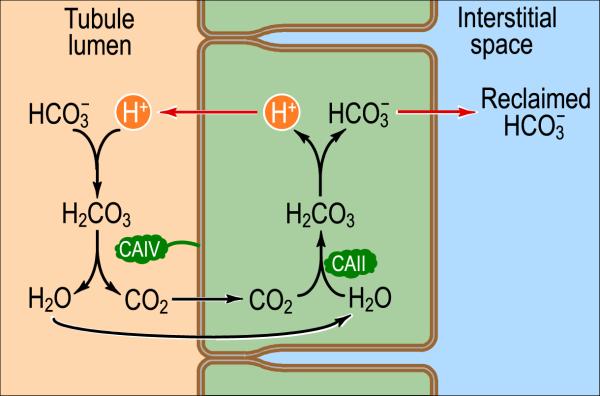
As already noted, the kidneys create and transfer to the blood an amount of new HCO₃⁻ that is equal to the sum of non-volatile acids produced by metabolism plus non-volatile acids assimilated from the diet plus base lost to the GI tract. However, before the kidneys can perform this task–known as HCO₃⁻ generation–they must retrieve from the nephron lumen all ~4500 mmol of HCO₃⁻ that the glomeruli filter each day, and that otherwise would be lost in the urine (Giebisch and Windhager, 2012; Seldin and Giebisch, 1989). Fig. 3 illustrates the basic cellular mechanism of this proces–known as HCO₃⁻ reabsorption–which occurs slightly differently at three sites along the nephron. The major site is the proximal tubule, which reclaims ~80% of the filtered HCO₃⁻ .

Fig. 3.

Basic cellular mechanism of HCO₃⁻ reabsorption in the kidneys. The basic unit of the kidney is the nephron, which is basically a tubular epithelium in which a single layer of cells separates the lumen from the interstitial space, which is in direct contact with the blood. By one of several mechanisms (indicated by the red arrow on left), tubule cells can use energy to secrete H⁺ into the tubule lumen at various sites along the nephron. One fate of this secreted H⁺ is to titrate HCO₃⁻ that had previously been filtered in the glomerulus. In parallel, the tubule cell uses one of two transport mechanisms (indicated by the red arrow on right) to move HCO₃⁻ into the interstitial space and ultimately the blood. By this general mechanism, the kidney reclaims virtually all of the filtered HCO₃⁻ . CAIV and CAII represent the enzymes carbonic anhydrase (CA) II and CA IV. Modified from Fig. 39-2A in Medical Physiology, 2nd Edition Updated Edition, edited by WF Boron and EL Boulpaep, Philadelphia: Elsevier, 2012.

As the tubule cells secrete H⁺ into the tubule lumen, the H⁺ titrates the HCO₃⁻ filtered in the glomerulus, ultimately forming CO₂ and H₂O. The newly formed CO₂ and H₂O diffuse into the tubule cell, where they regenerate intracellular H⁺ and HCO₃⁻ via the action of cytosolic CA II. This H⁺ then recycles back into the lumen, whereas the HCO₃⁻ moves out of the tubule cell across the baso-lateral membrane, and into the interstitial space and ultimately in the blood. Thus, for each H⁺ secreted in the tubule lumen, one HCO₃⁻ disappears from the lumen and one appears in the blood.

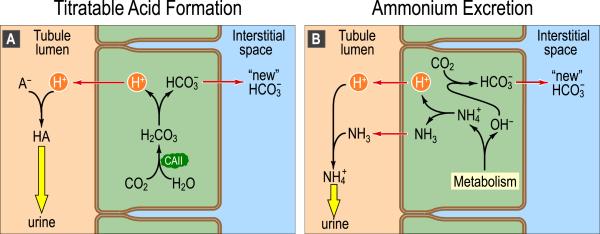
We have already mentioned that the other acid-base function of the kidney is to create the new HCO₃⁻ that replaces the HCO₃⁻ consumed by neutralizing the daily load of non-volatile acids. This creation of new HCO₃⁻ occurs when the H⁺ secreted into the tubule lumen combines with buffers other than HCO₃⁻ . When the H⁺ titrates urinary buffers other than HCO₃⁻ or NH₃, the process is known as titratable acid formation. When the H⁺ titrates NH₃ (of if the cell actually secretes NH₄⁺), the process is known as ammonium excretion.

Fig. 4A illustrates the mechanisms underlying titratable acid formation. The H⁺ secreted into the tubule lumen combines with a urinary buffer (A⁻)–such as phosphate, creatinine, or urate–and then is excreted via the urine. In parallel, one intracellular HCO₃⁻ forms and moves to the interstitial space via a transport mechanism located at the basolateral membrane of the tubule cell. Thus, for each H⁺ secreted into the tubule lumen, one “new” HCO₃⁻ appears in the blood.

Fig. 4.

Basic cellular mechanism of generation of “new” HCO₃⁻ . A: Titratable acid formation. At various sites along the nephron, the tubule cells secrete H⁺ into the lumen. One result is the titration of weak bases (A⁻), filtered from the blood in the glomerulus, to form their conjugate weak acids (HA). In parallel, a new HCO₃⁻ appears in the interstitial space and then in the blood. B: Ammonium excretion. In the proximal tubule, cells generate ammonia (NH₃) de novo from the amino acids glutamine and glutamate. In the lumen, secreted H⁺ titrates this NH₃ to form ammonium (NH₄⁺). In parallel, a new HCO₃⁻ appears in the interstitial space and then in the blood. Because the maximum free [H⁺] of the urine is only ~4 × 10⁵ M (pH ~4.4), the urinary excretion of H⁺ in the form of HA and NH₄⁺–which are typically present at mM level–allows the kidney to eliminate far more acid than it could if all of the secreted protons were excreted in the form of free H⁺. Modified from Fig. 39-2B and C in Medical Physiology, 2nd Edition Updated Edition, edited by WF Boron and EL Boulpaep, Philadelphia: Elsevier, 2012.

Fig. 4B illustrates the mechanisms underlying ammonium secretion. Metabolism of glutamine in the proximal tubule produces NH₄⁺ and OH⁻ in the cytosol (Giebisch and Windhager, 2012). NH₄⁺ dissociates into NH₃ and H⁺, which then move into the tubule lumen, where they recombine to form NH₄⁺ that is ultimately excreted in the urine. In the cytosol, CA converts the newly formed OH⁻ and CO₂ into HCO₃⁻ , which then moves into the interstitial fluid and blood.

Note that with the secretion of H⁺ into the lumen, all three processe–HCO₃⁻ reabsorption, titratable acid formation, and NH₄⁺ secretion–occur simultaneously. The extent to which each process occurs depends on the buffering power of each buffer, which in turn depends on luminal pH, the pK of each reaction, and the total concentration of each buffer species.

2.3. Intracellular pH regulation

Control of pH at the whole-body level depends on the control of pH at the level of a single cell and vice versa. Because intracellular processes (sensitive to changes in pH_i) far outnumber extracellular processes (sensitive to changes in pH_o), pH_i regulation has far more direct impact on function.

In this section, we discuss the mechanisms that influence pH_i and that cells use to maintain pH_i in the normal physiological range. For a more exhaustive overview, refer to (Bevensee and Boron, 2013).

2.3.1. Passive fluxes of uncharged weak acids and bases

Processes that can rapidly influence pH_i–though in a self-limited fashion–are the movement of an uncharged weak acid (HA)

$$\mathrm{HA}\rightleftharpoons {\mathrm{A}}^{-}+{\mathrm{H}}^{+}$$ (5)

or weak base (B)

$${\mathrm{BH}}^{+}\rightleftharpoons \mathrm{B}+{\mathrm{H}}^{+}$$ (6)

across the plasma membrane. The driving force that moves HA or B into or out of the cell is the chemical gradient (i.e., difference in [HA] or [B] between extra- and intracellular fluid).

In the case of an uncharged weak acid, suddenly increasing [HA]_o above [HA]_i would promote a net influx of HA, followed by a dissociation of intracellular HA into A⁻ and H⁺, causing pH_i to fall. The opposite would occur if [HA]_o suddenly decreased below [HA]_i (i.e., pH_i would rise). In the case of either net influx or efflux, the transmembrane movement of HA would continue until [HA]_i = [HA]_o, at which point the net flux of HA would halt–provided that HA is the only species that moves across the plasma membrane. These are examples of an acute acid load (in the case of HA influx) or an acute alkali load (in the case of HA efflux). These acid/alkali loads are “acute” in the sense that they are fundamentally limited: the production or consumption of H⁺ continues in a predictable fashion only until [HA]_i [HA]_o.

Acetic acid and CO₂ are examples of uncharged species that behaves like HA in the above examples. Note that although CO₂ is often regarded as an acid, in reality it is not. The true weak acid is H₂CO₃, the result of the interaction of CO₂ with H₂O. It is instructive to consider the consequences of suddenly increasing the rate of CO₂ production inside a cell. At first, [CO₂]_i will rise and, via the reaction CO₂ + H₂O → HCO₃⁻ + H⁺, lead to a fall in pH_i. However, the rise in [CO₂]_i will lead to a progressive increase in the passive efflux of CO₂ from the cell, so that at some point, the increment in CO₂ efflux matches the increment in production, and no further fall in pH_i occurs.

In the case of an uncharged weak base, suddenly increasing (decreasing) [B]_o above (below) [B]_i provokes the opposite series of changes that we saw in the case of increasing (decreasing) [HA]_o. Of course, the influx (efflux) of B causes an acute or self-limited alkali (acid) load.

NH₃ is an example of uncharged weak base that behaves like B in the above example. That is, transmembrane NH₃ fluxes cause pH_i to rise or fall depending on whether [NH₃]_o is higher or lower than [NH₃]_i.

The preceding discussion makes no statement about the mechanism by which HA or B passively cross the cell membrane. Although the classic view had been that CO₂ and NH₃, for example, cross all membranes by dissolving in the lipid phase of the membrane, it is now clear that some membranes are impermeable to CO₂ and NH₃ (Waisbren et al., 1994). Moreover, in many cells, dissolved CO₂ and NH₃ cross the cell membrane via “gas channels” like the aquaporins (AQPs) and Rhesus (Rhs) proteins (Boron, 2010; Cooper and Boron, 1998; Endeward et al., 2008, 2006; Geyer et al., 2013b, 2013c; Holm et al., 2005; Musa-Aziz et al., 2009; Nakhoul et al., 2001, 1998). Moreover, NH₃ can move through the urea transporter UT-B (Geyer et al., 2013a).

Although we have been discussing how transmembrane fluxes of HA and B can affect pH_i, the opposite is also true: pH_i (and pH_o) affect the transmembrane fluxes of HA and B. This principle is particularly important for biological molecules or therapeutic agents (Rodgers and Rowland, 2006; Rodgers et al., 2005) that cross the membrane as neutral weak acids or weak bases. For example, if the drug enters the cell as a weak base, a low pH_i will promote the intracellular reaction B + H⁺ → BH⁺. Thus, pH can be extremely important for pharmacokinetics and, if the drug action occurs inside the cell, pharmacodynamics.

2.3.2. Passive fluxes of charged weak acids and bases

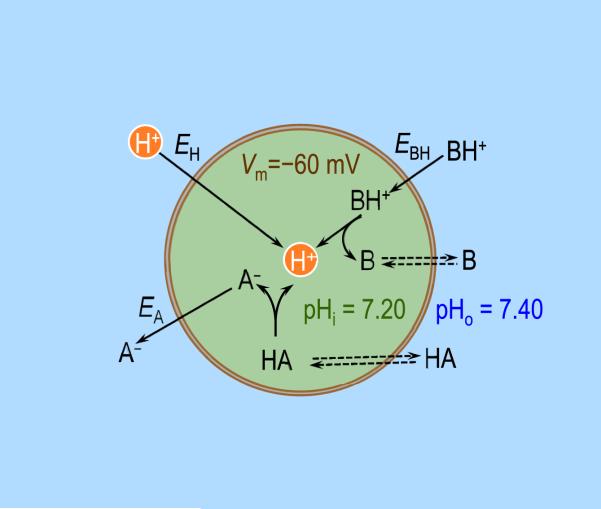
Processes that normally can slowly decrease pH_i are the passive influx of H⁺ or BH⁺, or the passive efflux of A⁻ (Fig. 5). Under conditions that might prevail in a prototypical cell–a pH_i of 7.20, a pH_o of 7.40, and a transmembrane voltage (V_m) of −60 mV (inside negative)–H⁺ would tend to passively enter the cell down its electrochemical gradient. One way of arriving at this conclusion is via the Nernst equation which predicts that the “equilibrium potential” for H⁺ is

$$\begin{array}{cc}\hfill E_{\mathrm{H}}& =\frac{2.3\mathrm{RT}}{\mathrm{F}}{\log }_{10}\left(\frac{{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{o}}}{{\left[{\mathrm{H}}^{+}\right]}_i}\right)\hfill \\ \hfill & =\frac{2.3\mathrm{RT}}{\mathrm{F}}({\mathrm{pH}}_{\mathrm{i}}-{\mathrm{pH}}_{\mathrm{o}})\cong \left(58.5\mathrm{mV}\right)(7.2-7.4)\cong -12\mathrm{mV},\hfill \end{array}$$ (7)

with R, T and F having their usual meanings. The equilibrium potential for H⁺ is the virtual value that V_m would have to be in order for H⁺ to be in electrochemical equilibrium across the membrane.

Fig. 5.

Passive fluxes of charged weak acids and bases in a prototypical cell. E_H, E_BH, and E_A are the equilibrium membrane potentials, respectively, for H⁺, cationic weak acid BH⁺, and anionic weak base A⁻ . Double arrows indicate that the neutral species is equilibrated across the plasma membrane. V_m, membrane potential (referenced to a voltage of zero in the extracellular fluid); pH_i, intracellular pH; pH_o, extracellular pH.

Because V_m is typically more negative than E_H (i.e., the trans-membrane voltage is too negative for H⁺ to be in equilibrium), protons tend to passively enter the cell. Assuming a stable V_m and no active (i.e., energy-requiring) transport of H⁺, this passive influx of H⁺ would continue until pH_i fell to ~6.37, at which point E_H V_m and no further net influx of H⁺ would occur. In this example, the influx of H⁺ is self-limited and represents an acute intracellular acid load. On the other hand, if the cell has an energy-consuming mechanism to remove H⁺ (or accumulate an alkali such as HCO₃⁻), pH_i would fall only to the point at which the passive influx of H⁺ came into balance with the active efflux of H⁺. Here, the passive influx of H⁺ represents a continuous or chronic intracellular acid load.

The same electrochemical gradient that moves H⁺ into the cell affects the movements of the cationic weak acids BH⁺ (BH⁺ ⇌ B + H⁺, e.g., NH₄⁺) and anionic weak bases A⁻ (HA ⇌ A⁻ H⁺, e.g., HCO₃⁻). Let us assume that (a) the neutral species (B or HA) is equilibrated across the plasma membrane (i.e., [B]_o = [B]_i, or [HA]_o = [HA]_i), (b) the equilibrium (BH⁺ ⇌ B + H⁺ or HA ⇌ A⁻ + H⁺) holds on both sides of the membrane, and (c) the equilibrium constant is the same on both sides of the membrane. With these three assumptions, one can show that:

For a cationic weak acid (BH⁺ ⇌ B + H⁺),

$$\frac{{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{o}}}{{\left[{\mathrm{H}}^{+}\right]}_i}=\frac{{\left[{\mathrm{BH}}^{+}\right]}_{\mathrm{o}}}{{\left[B{\mathrm{H}}^{+}\right]}_i},$$

and that the equilibrium potential for BH⁺ equals that for H⁺ (i.e., E_BH = E_H). For an anionic weak base (HA ⇌ A⁻ + H⁺),

$$\frac{{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{o}}}{{\left[{\mathrm{H}}^{+}\right]}_i}=\frac{{\left[{\mathrm{A}}^{-}\right]}_{\mathrm{i}}}{{\left[{\mathrm{A}}^{-}\right]}_{\mathrm{o}}},$$

and that the equilibrium potential for A⁻ equals that for H⁺ (i.e., E_A = E_H).

Thus, if H⁺ tends to passively enter cells, BH⁺ will tend to enter passively as well, and A⁻ will tend to exit passively. In other words, the cell is constantly challenged by intracellular acid loads due to the passive fluxes of the monovalent ionic forms of buffer pairs of the sort discussed above.

The preceding discussion makes no statement about how A⁻ or BH⁺ passively cross the cell membrane. HCO₃⁻ may move through Cl⁻ channels (Kaila and Voipio, 1987) and NH₄⁺ moves through K⁺ channels (Garvin et al., 1988; Kikeri et al., 1992). The right side of Fig. 6 suggests a mechanism for the passive fluxes of H⁺, NH₄⁺, and HCO₃⁻ –all occurring via channels.

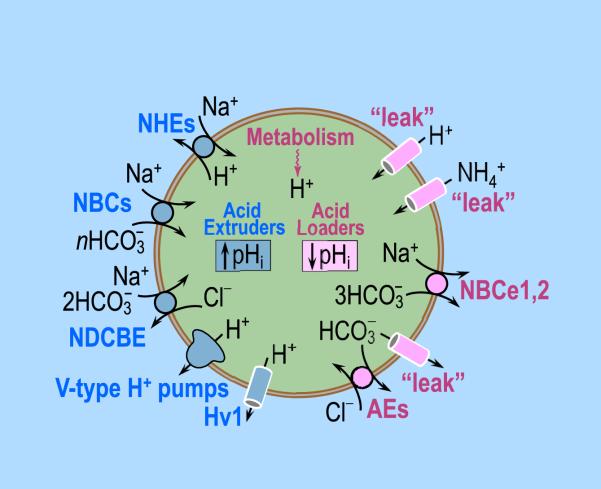
Fig. 6.

A composite of acid extruders and acid loaders in a prototypical cell. Steady-state intracellular pH (pH_i) depends on the balance between the rates of acid extruders and the rates of acid loaders. Acid extruders, listed on the left, are: (1) the Na–H exchangers (NHEs, members of the SLC9 family of solute carriers), (2) the electrogenic Na/HCO₃ cotransporters (NBCe1, NBCe2 in the SLC4 family, n = 2), (3) the electroneutral Na/HCO₃ cotransporters (NBCn1, NBCn2 in the SLC4 family, n 1), (4) the Na⁺-driven Cl–HCO₃ exchanger (NDCBE in the SLC4 family), (5) V-type H⁺ pumps (fueled by ATP hydrolysis), and (6) the voltage-gated H⁺ channel (Hv1). Acid loaders, listed on the right, are: (1) passive fluxes (“leak”) of H⁺, BH⁺ (e.g., NH₄⁺) and A⁻ (e.g., HCO₃⁻ ), (2) the electrogenic Na/HCO₃ cotransporter (NBCe1, NBCe2) operating with a 1:3 stoichiometry (i.e., n = 3), and (3) the Cl–HCO₃ (or anion) exchangers (AE1 –3 in the SLC4 family). Additional acid loaders (not listed) are the proton-driven transporters.

Here we have been discussing how transmembrane fluxes of A⁻ and BH⁺ can affect pH_i. Conversely, pH_i and pH_o can affect trans-membrane fluxes of A⁻ and BH⁺, which are of importance for biological molecules or therapeutic agents (Rodgers and Rowland, 2006; Rodgers et al., 2005) that cross the membrane as monovalent anions or cations.

2.3.3. Transporters that normally load the cell with acid

As already seen in the previous section, the passive entry of H⁺ and of cationic weak acids BH⁺ (e.g., NH₄⁺), as well as the passive exit of anionic weak bases A⁻ (e.g., HCO₃⁻) all provide a chronic intracellular acid load. The right side of Fig. 6 shows two additional chronic acid-loading mechanisms, transporters that mediate the efflux of HCO₃⁻ can load the cell with acids. The first is the sub-family of the electrogenic Na/HCO₃ cotransporters (NBCe1 and NBCe2 in the SLC4 family), operating with an apparent Na⁺:HCO₃⁻ stoichiometry of 1:3 (Boron and Boulpaep, 1983; Parker and Boron, 2013; Romero et al., 2013, 1997). The second is the subfamily of Cl–HCO₃ (or anion) exchangers (AE1–3 in the SLC4 family; Kopito et al., 1989; Romero et al., 2013; Vaughan-Jones, 1979). In addition, proton-driven transporters can move H⁺ into the cell. Examples are the high-affinity glutamate transporters (SLC1 family; Kanai et al., 2013, 1995) and the oligopeptide transporters (SLC15 family; Fei et al., 1994; Smith et al., 2013).

In these examples of carrier-mediated acid-loading mechanisms, H⁺ or protonated, cationic weak acids (e.g., BH⁺) move in the direction (generally inward) dictated by their electrochemical gradients. Similarly, the deprotonated, anionic weak bases (A⁻) move in the direction (generally outward) dictated by their electrochemical gradients. In all cases, the transport is passive from the perspective of acid-base physiology.

2.3.4. Transporters that normally extrude acid from the cell

Unlike acid loaders, acid extruders use energy to move H⁺ out of the cell or to move weak bases, such as HCO₃⁻ , into the cell against their electrochemical gradients. Thus, these transporters are active from the perspective of acid-base physiology. The left side of Fig. 6 lists transporters that normally operate as acid extruders. These include: (1) the Na–H exchanger (NHE, in the SLC9 family; Donowitz et al., 2013; Murer et al., 1976; Orlowski and Grinstein, 2004; Sardet et al., 1989), (2) the electrogenic Na/HCO₃ cotrans-porters (NBCe1, NBCe2 in the SLC4 family; Boron and Boulpaep, 1983; Romero et al., 1997; Virkki et al., 2002) operating with a Na⁺:HCO₃⁻ stoichiometry of 1:2, (3) the electroneutral Na/HCO₃ cotransporters (NBCn1, NBCn2 in the SLC4 family; Choi et al., 2000; Parker et al., 2008; Pushkin et al., 1999) operating with an apparent Na⁺:HCO₃⁻ stoichiometry of 1:1, and (4) the Na⁺-driven Cl–HCO₃ exchanger (NDCBE in the SLC4 family; Boron and De Weer, 1976a; Boron and Russell, 1983; Russell and Boron, 1976; Grichtchenko et al., 2001; Parker and Boron, 2013; Thomas, 1977). In the above four cases, the energy for exporting H⁺ or importing HCO₃⁻ is the Na⁺ electrochemical gradient, in turn established by the Na–K pump, which hydrolyses ATP (Skou, 1957). The Na–K pump is known as a “primary active transporter,” and all of the Na^+- dependent transporters are known as “secondary active transporters.” Another acid extruder is the vacuolar-type H⁺ pump; because it hydrolyzes ATP, it is a primary active transporter. The final acid extruder listed on the left side of Fig. 6 is the unusual voltage-gated H⁺ channel Hv1 (DeCoursey, 2013; Ramsey et al., 2006; Sasaki et al., 2006; Thomas and Meech, 1982) that opens only at relatively positive values of V_m, when the electrochemical H⁺ gradient is now outward (rather than the normal inward).

2.3.5. The fundamental law of pH_i regulation

We have already reviewed two general mechanisms for chronic intracellular acid loading: (1) passive fluxes of H⁺, BH⁺, and A⁻; and (2) carrier-mediated transport of BH⁺ and A⁻. To these we can add: (3) cellular metabolism, which generally results in the net production of H⁺. Together, these three mechanisms provide an indefinite or continuous acid load at the total rate J_L, tending to lower pH_i. In general, J_L is a function of pH_i and many other parameters. Opposing intracellular acidification are the chronic acid-extruding mechanism–generally working at the expense of energy–that operate at the total rate J_E (Boron, 2004). Like J_L, J_E is generally a function of pH_i and many other parameters.

The fundamental law of pH_i regulation (Bevensee and Boron, 1998; Roos and Boron, 1981) states that the rate of pH_i change is proportional to the difference (J_E–J_L), proportional to the surface to volume ratio (ρ), and inversely proportional to the total intracellular buffering power (β):

$$\frac{d{\mathrm{pH}}_{\mathrm{i}}}{dt}=\frac{\rho }{\beta }(J_E-J_L).$$ (8)

If J_E = J_L, then dpH_i/dt = 0, that is, pH_i is constant in time. If J_E > J_L, then dpH_i/dt > 0, and pH_i increases with time. Conversely, if J_E < J_L, then dpH_i/dt < 0, and pH_i decreases with time. Moreover, because dpH_i/dt is proportional to ρ, the rate of pH_i change tends to be greater in smaller cells. Finally, if β approaches zero, the rate of pH_i change approaches ±∞, regardless of the difference between J_E and J_L, as long as that difference is non-zero. On the other hand, if β approaches ∞, the rate of pH_i change approaches zero (i.e., pH_i is constant), regardless of the difference between J_E and J_L.

An important principle is that steady-state pH_i can change only if the relationship between the pH_i dependencies of J_E and J_L changes. Thus, an acute intracellular acid or alkali load can transiently shift pH_i but cannot, by itself, alter steady-state pH_i. Another corollary is that a change in buffering power cannot, by itself, alter steady-state pH_i–only the rate at which pH_i changes.

2.3.6. Intracellular buffering

In equation (8) we saw that the total intracellular buffering power affects how pH_i changes in time. The total intracellular buffering power is the sum of the buffering powers of all buffer mechanisms, of which we can describe three general types (Roos and Boron, 1981). (1) Physicochemical buffers are weak acids and bases of the form BH⁺ ⇌ B + H⁺ and HA ⇌ A⁻ + H⁺, discussed above. (2) Biochemical buffers are reactions (e.g., hydrolysis of ATP or of phosphocreatine) that can consume or produce H⁺ and are sensitive to pH_i changes in such a way as to minimize pH_i changes. And (3) organellar buffering is the transport of acid-base equivalents across organellar membranes, resulting in the stabilization of cytosolic pH at the expense of the pH within the organelle.

Chemical buffers are usually divided into two functional groups: intrinsic and extrinsic. Intrinsic buffers (e.g., inorganic phosphate) are those that behave if they are essentially in a closed system, whereas extrinsic buffers (e.g., CO₂/HCO₃⁻ , NH₃/NH₄⁺) are those for which at least one member of the buffer pair behaves as if it were in an open system. Biochemical and organellar buffers are considered intrinsic (Bevensee and Boron, 2013).

Note that buffers tend to minimize changes in pH_i. However, by definition they cannot neutralize an entire acid or alkali load. Hence the need for transporters that adjust their rate to move unbuffered acid-base equivalents across the membrane, tending to stabilize pH_i.

2.4. Interdependence between pH_i and pH_o

2.4.1. Interactions among acid-base equilibria

Regardless of mechanism, any flux of acid-base equivalent–H⁺, HA, A⁻, B, BH⁺–across the cell membrane will perturb all equilibria of intracellular and extracellular pH buffer pairs. The reason is that the reactions involving these buffer pairs all compete for H⁺, creating complex interdependencies among buffer reactions, and between pH_i and pH_o.

Imagine a simple case in which pH_i and the pH in the bulk extracellular fluid (BECF) have physiological values, and in which CO₂, a weak base B (e.g., NH₃), and a weak acid HA (e.g., lactic acid, HLac) are permeant, and all are at equilibrium across the cell membrane. If we suddenly raise [CO₂]_BECF–keeping [HCO₃⁻]_BECF and pH_BECF fixed, using out-of-equilibrium (OOE) CO₂/HCO₃⁻ technology to make and deliver the solution (Zhao et al., 1995)–the result is a net influx of CO₂ (Fig. 7, flux 1a), followed by all the reaction events (solid black arrows) and diffusion events (dashed black arrows) summarized on the left side of Fig. 7. Among these events are a transient rise in the pH near the outer surface of the cell (pH_S), and a more gradual but sustained fall in pH throughout the cell. The transient rise in pH_S will raise [B]_S (thereby promoting B influx) but will lower [HA]_S (thereby promoting HA efflux). The sustained fall in pH_i will have the opposite effects on intracellular parameters, likewise enhancing the gradient for B influx and HA efflux. Thus, a flux of CO₂ in one direction across the cell membrane will increase the flux of B in the same direction but increase the flux of HA in the opposite direction. We can make comparable statements about situations in which the primary change is a sudden increase in [B]_BECF or [HA]_BECF.

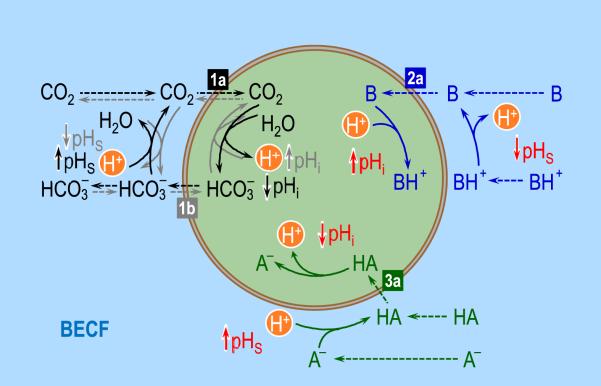
Fig. 7.

Interactions among acid-base equilibria. On the left, the black solid arrows (representing reaction) and dashed arrows (representing diffusion) show the consequences on intracellular (pH_i) and surface pH (pH_S) of the diffusion of CO₂ into the cell (label “1a”), down a CO₂ concentration gradient (i.e., [CO₂]_o > [CO₂]_i). The gray arrows show the consequences on pH_i and pH_S of the entry of HCO₃⁻ into the cell (label “1b”). At the upper right, the blue arrows show the consequences on pH_i and pH_S of the diffusion of a neutral weak base B into the cell ([B]_o > [B]_i; label “2a”). Although we do not show the consequences of the entry of BH⁺, these would be opposite to those produced by the entry of B. Finally, at the lower right, the green arrows show the consequences on pH_i and pH_S of the diffusion of a neutral weak acid HA into the cell ([HA]_o > [HA]_i; label “2a”). Although we do not show the consequences of the entry of BH⁺, these would be opposite to those produced by the entry of B. BECF, bulk extra-cellular fluid.

We can also analyze the consequences of suddenly raising [HCO₃⁻]_BECF (using OOE technology to keep [CO₂]_BECF and pH_BECF constant), which would cause a net influx of HCO₃⁻ (Fig. 7, flux 1b) and set into motion the reaction and diffusion events summarize by the gray arrows. The consequences for the other buffer pairs would qualitatively be opposite to what we discussed in the previous paragraph (where we raised [CO₂]_BECF). What would happen if we simultaneously raised [HCO₃⁻]_BECF and [CO₂]_BECF by the same fractional amount, thereby keeping pH_BECF fixed and promoting the influx of both HCO₃⁻ and CO₂? The influxes of both members of the buffer pair would set up competing tendencies between the processes represented by the black and gray arrow–producing either a rise or a fall in pH_S, depending upon whether the influx of HCO₃⁻ or CO₂ is dominant. In fact, it is possible to show that, given any fixed ratio of HCO₃⁻ and CO₂ influxes, there exists a null pH_BECF at which these parallel influxes produce no change in pH_S. Moreover, at pH_BECF values above pH_Null, the same influxes of HCO₃⁻ and CO₂ that produced a rise (or a fall) in pH_S when pH_BECF < pH_Null would have the opposite effect on pH_S.

Of course, it is possible that [HCO₃⁻]_BECF rises at a fixed [CO₂]_BECF, causing a rise in pH_BECF known as metabolic alkalosis. It is also possible that a transporter increases its rate at which it moves HCO₃⁻ into the cell at a fixed [HCO₃⁻ ]_BECF. A further complication in the case of HCO₃⁻ transport is that preliminary data from our laboratory (Lee et al., 2011) suggest that the actual substrate of the Na⁺-coupled HCO₃⁻ transporters (NCBTs) in Fig. 6 is not HCO₃⁻ but either carbonate (HCO₃⁻ ⇌ ${\mathrm{CO}}_3^{=}$ + H⁺) or the sodium carbonate ion pair (NaCO₃⁻ ⇌ ${\mathrm{CO}}_3^{=}$ + Na⁺).

In all of these examples, changes in CO₂ or HCO₃⁻ or ${\mathrm{CO}}_3^{=}$ transport will influence B/BH⁺ and A⁻/HA equilibria both inside and outside the cell. It is clear that intuition will be of limited value in understanding such systems.

2.4.2. Chronic effects of pH_o on pH_i

Disturbances in any parameter that influences processes summarized in Fig. 6–the parameters include pH_BECF, [HCO₃⁻]_BECF, and [Na⁺]_BECF–will alter one or more components of J_E or J_L. For example, a decrease in pH_BECF will directly or indirectly cause J_E to decrease and J_L to increase, thereby causing steady-state pH_i to fall. Note that this fall in pH_i occurs not simply because of an increased passive influx of H⁺ (which may have only a trivial effect because [H⁺] is so low) but because of effects on various transporters, resulting in an altered balance between J_E and J_L.

2.4.3. Effects of cellular metabolism on pH_o

Cellular metabolism, integrated over the entire body in the steady-state, produces the fixed acids that the kidney must excrete to maintain a stable blood pH (see Whole-body pH regulation). The transporters on the left side of Fig. 6 extrude this metabolically-generated acid to maintain a stable pH_i. In addition, cells produce CO₂ as the result of aerobic metabolism. In the steady state, the newly produced CO₂ merely diffuses out of the cell–in many cases through gas channel–for its journey to the alveoli for excretion via alveolar ventilation (see The respiratory system). Note that the stable CO₂ production, reflected by a stable [CO₂]_i, does not represent a chronic acid load. However, a sudden increase in cellular CO₂ production will cause [CO₂]_i to rise, eventually leading to a stable but increased rate of CO₂ diffusion from the cell. The rise in [CO₂]_i produces an acute acid load from which the cell may recover by means of the acid extruders in Fig. 6.

A final example is the cellular production of lactic acid, which occurs during anaerobic metabolism and also in cancer cells (the Warburg effect; Warburg et al., 1927). In the steady state, the cellular production of HLac is balanced by HLac efflux, mediated by a family of monocarboxylate transporters (MCTs; ref. Halestrap, 2013). This efflux of HLac is energetically downhill and, like the efflux of CO₂ in the steady state, does not represent a chronic acid load to the cell. However, a sudden increase in HLac production leads to an increase in [HLac]_i, with consequences analogous to those outlined in the previous paragraph for CO₂.

Experimental work by Pouyssegur and Swietach and their colleagues (Chiche et al., 2009; Hulikova et al., 2013; Le Floch et al., 2011; Swietach et al., 2009, 2008), and modeling work by Swietach and his colleagues (Swietach et al., 2009, 2008), has begun to elucidate how the efflux of CO₂ and HLac affect pH in the environment around cancer cells.

3. Mathematical models of acid-base physiology

3.1. A short history

We have seen that, as acid-base equivalents move across the plasma membrane, they alter the local ratios of [B]/[BH⁺], and [A⁻]/ [HA]. Thus, the transmembrane flux of any one substance, affects the transmembrane gradients of all the others, creating complicated interdependencies that cannot be understood with the use of intuition only. Moreover, each cell type, depending on its role in the tissue, has its own set of plasma-membrane transporter–each with its unique propertie–to regulate pH_i. Thus, pH_i regulation is not only complex but also diverse. Moreover, the same transporters that regulate pH_i also participate in the transport of HCO₃⁻ and other solutes across epithelia, and epithelial cells somehow coordinate the activities of these transporters to achieve both pH_i regulation and transepithelial transport.

Because of the complexity and diversity of events underling pH_i regulation, investigators have developed mathematical models to simulate cellular acid-base chemistry and help them to interpret physiological data. Here, we briefly review a few of these models.

The first to develop a mathematical model of cellular acid-base chemistry was Albert Roos in 1975. Based on an approach he introduced earlier (Roos, 1965), Roos developed a steady-state model for the passive efflux of lactate (Lac⁻)–the prime mover in his analysi–accompanied by an equal influx of lactic acid. The model guided him in postulating that the cell could achieve a steady state only if the antiparallel fluxes of Lac⁻/HLac were accompanied by the active extrusion of H⁺ at a rate equal to that of HLac influx (Roos, 1975). One year later, Boron and De Weer created the first model capable of predicting how acid-base fluxes affect the time course of pH_i (Boron and De Weer, 1976b). They proposed a single-compartment model that considered CO₂/HCO₃⁻ (or NH₃/NH₄⁺) diffusion across the cell membrane of a squid axon. This model helped guide the first clear description of active pH_i regulation and what has come to be known as the “ammonium pre-pulse.” In the steady state, this dynamic model of Boron and De Weer collapses to the model of Roos. Also in 1976, Gros et al. developed a steady-state mathematical model, based on the Nernst-Planck equation for the electrodiffusion of ions in a bulk solution, to study the role of CA in facilitating the diffusion of CO₂ in phosphate solutions (Gros et al., 1976).

Others have now developed more sophisticated models, both compartmental (Endeward and Gros, 2005) and spatially distributed (Missner et al., 2008; Swietach et al., 2003; Vaughan-Jones et al., 2002). In 2009, Endeward and Gros proposed a one-dimensional reaction-diffusion model to investigate the effects of intracellular and extracellular unstirred layers on the diffusion of CO₂, HCO₃⁻ , and H₂O across the RBC membrane (Endeward and Gros, 2009). Recently, Swietach et al. developed reaction-diffusion models of acid-base chemistry to study the role of the cancer-associated extracellular CA IX enzyme in spheroids (Swietach et al., 2009, 2008), clusters (300 μm in diameter) of thousands of cancer cells (each ~8.6 μm in diameter). Reducing the spheroid to a single homogenized cell 300 μm in diameter, and ignoring diffusion within the volume of the 300-μm spheroid, these authors conclude that CA IX facilitates CO₂ removal by spatially regulating pH_i and pH_o (Swietach et al., 2009, 2008). More recently, Hulikova and Swietach used a modified version of the above mathematical model in which they allow neutral species (e.g., CO₂, NH₃), but not their charged counterparts (e.g., HCO₃⁻ , NH₄⁺), to diffuse within the spheroid (Hulikova and Swietach, 2014).

In the following section we review the most recent mathematical models developed by our team to interpret our physiological data on Xenopus oocytes. We will discuss advantages and limitations of these models and how additional modeling needs to be performed to reproduce the details of a real biological cell in the body.

3.2. Mathematical models of a Xenopus oocyte

3.2.1. Motivation

Because of their large size (~1.3 mm in diameter) and propensity for heterologous expression, Xenopus laevis oocytes are a powerful physiological tool, widely used for functional studies of membrane proteins. In our laboratory, we use Xenopus oocytes to study several families of membrane proteins, including: (1) NCBTs, which are important for pH_i regulation and epithelial acid-base transport (Parker and Boron, 2013), as well as (2) AQPs, (3) Rh proteins, and urea transporters (UTs), which, besides conducting H₂O in the case of most AQPs (Preston et al., 1992), may also conduct CO₂ (Cooper and Boron, 1998; Endeward et al., 2008, 2006; Geyer et al., 2013b; Musa-Aziz et al., 2009; Nakhoul et al., 1998) or NH₃ (Geyer et al., 2013a, 2013b, 2013c; Holm et al., 2005; Musa-Aziz et al., 2009; Nakhoul et al., 2001; Ripoche et al., 2006).

In 2009, Musa-Aziz et al., using a polished liquid-membrane microelectrode to monitor surface pH (pH_S) in oocytes as CO₂ or NH₃ diffuses into the cell, were the first to show that different AQPs and Rh proteins have different relative permeabilities to (i.e., selectivities for) NH₃ vs. CO₂ vs. H₂O (Musa-Aziz et al., 2009). These authors used the maximal excursion in the pH_S transient (ΔpH_S) as a semi-quantitative index of CO₂ or NH₃ permeability. The principle behind their approach is the following. In the case of CO₂, exposing a cell to a solution containing equilibrated CO₂/HCO₃⁻ leads to a rapid influx of CO₂ (Fig. 8A) that causes pH_i to fall because of the intracellular reaction CO₂ + H₂O → HCO₃⁻ + H⁺ (Fig. 8B, bottom). At the extracellular side of the membrane, the CO₂ influx creates a CO₂ deficit, which can be replenished by diffusion of CO₂ from the bulk extracellular fluid and by the reaction HCO₃⁻ + H⁺ → CO₂ + H₂O, occurring near the extracellular surface (Fig. 8A). This reaction causes pH_S to rise rapidly to a peak–at a time when the CO₂ influx is maximal–and then decay as the CO₂ influx wanes (Fig. 8B, top). Thus, ΔpH_S ought to be a semi-quantitative index of maximal CO₂ influx. Indeed, expressing AQPs in oocytes causes a ΔpH_S that is larger than that measured in a control H₂O-injected oocyte (Chen et al., 2010; Endeward et al., 2006; Musa-Aziz et al., 2009; Qin and Boron, 2013).

Fig. 8.

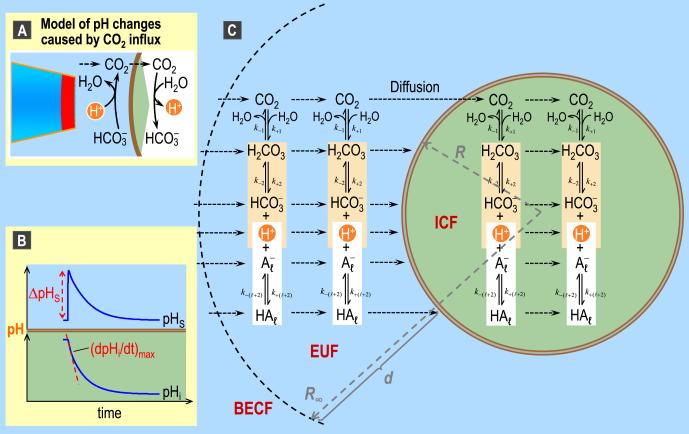
pH changes caused by CO₂ influx and major features of the mathematical model of Somersalo et al. (2012). A: Model of acid-base chemistry at the outer surface and inner surface of the plasma membrane as CO₂ enters into the cell. B: Representative intracellular (pH_i) and surface pH (pH_S) transients caused by CO₂ influx. These pH_i and pH_S trajectories are the result of a simulation, and are the same trajectories shown as the blue records in Fig. 11. C: Major components of the mathematical model for a spherical cell with radial symmetry. BECF, bulk extracellular fluid; EUF, extracellular unconvected fluid; ICF, intracellular fluid; k, a rate constant. Panel C is modified from Fig. 2 in Somersalo et al. (2012).

In the case of NH₃, exposing a cell to a solution containing equilibrated NH₃/NH₄⁺ causes a transient fall in pH_S as a result of NH₃ influx (as for “B” on the right side of Fig. 7, blue arrows) and ΔpH_S is a semi-quantitative index of NH₃ permeability.

Although the above oocyte model and experimental protocol are invaluable tools for demonstrating that CO₂ and NH₃ can move through gas channels, its power is limited by the inability to extract values of absolute permeability from pH_S measurements. In order to overcoming this obstacle, our team–through an interdisciplinary collaboration among mathematicians and physiologist–developed a theoretical model of CO₂ influx into a spherical cell (Somersalo et al., 2012) to simulate the pH_i and pH_S measurements of (Endeward et al., 2006; Musa-Aziz et al., 2009), with the ultimate goal of being able to extract absolute permeability values.

3.2.2. A first-generation theoretical model

Fig. 8 illustrates the major features of the mathematical model of (Somersalo et al., 2012). The model assumes that the oocyte is a sphere surrounded by a spherical layer of extracellular unconvected fluid (EUF), which in turn is surrounded by an infinite reservoir of BECF. Because reactions and diffusion are the two physicochemical processes occurring in the experiments of (Endeward et al., 2006; Musa-Aziz et al., 2009), Somersalo et al. designed their model to account for reactions among buffers and diffusion of solutes in both the ICF and EUF. The buffers are the CO₂/HCO₃⁻ buffer system, described by Equation (1), and an indefinitely large number ($\ell$ = 1, 2,..., N) of non-CO₂/HCO₃⁻ buffers of the form ${\mathrm{HA}}_{\ell }$ ⇌ A ${\mathrm{A}}_{\ell }^{-}$ + H⁺, each of which can be mobile or immobile. The model allows implementation of a CA enzyme in different locations, with the ability to specify the enzymatic acceleration factor A. The BECF is an infinite reservoir of pre-equilibrated solution (in which no reactions or diffusion occur) that mimics the bath solution that we continuously deliver during physiological experiments. The BECF communicates with the EUF via diffusion. The plasma membrane is assumed to be infinitely thin and permeable only to CO₂. Note that the model, as it is implemented, could in principle allow any solute to diffuse freely across the plasma membrane. However, because in the experiment of Musa-Aziz et al., CO₂ is essentially the only solute that can move through the plasma membrane, the simulations allow only CO₂ to cross the membrane.

The model assumes spherical radial symmetry, and is described by a coupled system of partial differential equations (PDEs), one for each solute s, of the form

$$\frac{\partial }{\partial t}{C}_s(t,r)=\underset{\text{Diffusion term}}{\underbrace{\frac{1}{r^2}\frac{\partial }{\partial r}\left(D_s(t\right)r^2\frac{\partial }{\partial r}{C}_s(t,r)}}+\underset{\text{Reaction term}}{\underbrace{\sum _{\ell =-3,\ell \ne 0}^3{S}_{s,\ell }{\Phi }_{\ell }}}.$$

Here, C_s is the concentration of solute s; this concentration changes in time and space (radial distance r from the center of the cell) because of diffusion (first term on the right-hand side) and of reactions (second term on the right-hand side). Diffusion events are modeled according to Fick's second law of diffusion and reactions, according to the law of mass action. D_s is the diffusion coefficient of solute s, S_s,λ are the stoichiometry coefficients and Φ_λ are the reaction fluxes.

After setting appropriate boundary conditions (Somersalo et al., 2012), we solve the PDEs numerically using the method of lines and the stiff MATLAB ode solver ode15s.

The model makes predictions that conform well to physiological observations. It can reproduce qualitatively the shape of the pH_i and pH_S trajectories as CO₂ enters the cell. Moreover, it provides interesting new insights on the dependence of (dpH_i/dt)_max–the maximal rate of intracellular acidification–as well as ΔpH_S on many parameters, including (1) the width d of the EUF⁴ and (2) the permeability of the membrane to CO₂ (P_M,CO2). In the study of gas channels, one wants to estimate the “true” membrane permeability (i.e., the permeability of the lipid phase, together with associated membrane proteins) and not the empirically measured “apparent” membrane permeability, which includes the contributions from the extra- and intracellular unconvected fluid layers that act as additional diffusion barriers in series with the plasma membrane. For example, as the width of the EUF increases, the apparent membrane resistance to CO₂ diffusion rises in parallel, so that the contribution of the membrane becomes smaller and eventually insignificant.

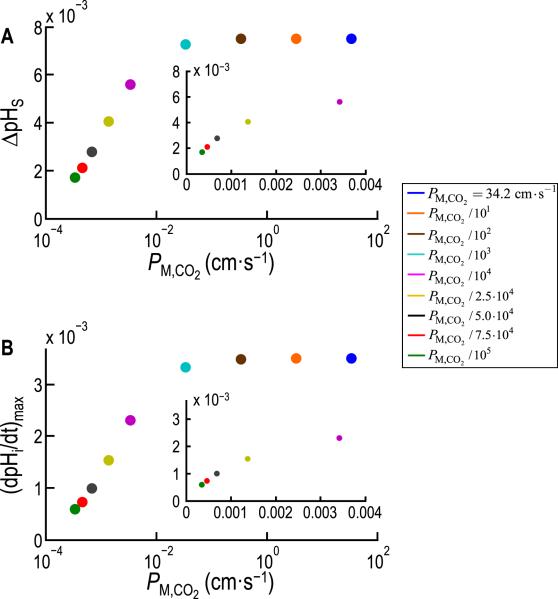
The simulations predict that as d decreases, (dpH_i/dt)_max become larger (i.e., pH_i decays faster) and ΔpH_S becomes smaller. These results reveal a competition between reaction and diffusion for the replenishment of CO₂ at the extracellular surface of the plasma membrane during CO₂ influx (Fig. 8C). In simulations, decreasing d causes the diffusive flux of CO₂ from the BECF to the membrane to increase, but reduces the contribution of the reactions HCO₃⁻ + H⁺ → H₂CO₃ → CO₂ + H₂O. As a consequence of the smaller contribution of the reaction toward CO₂ replenishment, ΔpH_S becomes smaller. As a consequence of the greater diffusive flux and thus greater overall CO₂ replenishment, the CO₂ influx increases and thus (dpH_i/dt)_max becomes larger.

Fig. 9 illustrates another interesting insight from the simulations. Starting from zero, raising P_M,CO2 causes (dpH_i/dt)_max and ΔpH_S at first to rise monotonically in parallel, and then to level off ~2 orders of magnitude before P_M,CO2 approaches the value predicted from the diffusion constant of CO₂ in water (D_M,CO2). This is an important conclusion because many investigators in the past have assumed that cell membranes offer no resistance to the diffusion of gases like CO₂. Indeed, this assumption is implicit in August Krogh's pioneering work on O₂ diffusion in tissues (Kreuzer, 1982; Krogh, 1919). However, it is now established that the expression of certain channels (Boron, 2010; Endeward et al., 2008, 2006; Geyer et al., 2013b; Musa-Aziz et al., 2009; Nakhoul et al., 1998) can increase the (dpH_i/dt)_max or ΔpH_S produced by exposing a cell to CO₂. Gas channels could not have a measureable effect on these quantities unless the basal membrane permeability to CO₂ were several orders of magnitude below the value predicted from D_M,CO2. Thus, (dpH_i/dt)_max and ΔpH_S are indices of membrane permeability.

Fig. 9.

Dependence of ΔpH_S and (dpH_i/dt)_max on the permeability of the cell membrane to CO₂ (P_M,CO2 ), predicted from the model of Somersalo et al. (2012). A: Maximal excursion in the pH_S transient, ΔpH_S (see Fig. 8B, upper), as a function of P_M,CO2 for nine simulations in which P_M,CO2 decreases from 34.20 cm s⁻¹ (value predicted from the diffusion constant of CO₂ in water) to 34.20 × 10⁻⁵ cm s⁻¹. B: Maximal rate of intracellular acidification, (dpH_i/dt)_max (see Fig. 8B, lower), as a function of P_M,CO2 for the same nine simulations reported in A. The two insets are linear re-plots for the five lowest P_M,CO2 values. Modified from Fig. 7 in Somersalo et al. (2012).

In summary, the model of Somersalo et al. makes valuable theoretical predictions and allows extracting information on quantities that one cannot directly measure in physiological experiments (e.g., time and space dependence of concentrations of solutes like CO₂). To our knowledge, none of the current mathematical models of acid-base chemistry include the biological details (competing equilibria among multiple mobile and immobile buffers) and the computational complexity of this reaction-diffusion model. However, even this model needs refinements because it cannot quantitatively reproduce some of the salient features of measured pH_i and pH_S transients. For example, the simulations produce ΔpH_S values that are too small.

3.2.3. Refinements to produce a more realistic oocyte model

Recently, Musa-Aziz et al. used simultaneous measurements of pH_i and pH_S transients to study the effects of the cytosolic enzyme CA II and of the extracellular CA IV (attached to the outer leaflet of the membrane via a GPI linkage) on enhancing transmembrane CO₂ fluxes (Musa-Aziz et al., 2014a, 2014b). They found that (1) injecting CA II into oocytes not only increases (dpH_i/dt)_max but also increases ΔpH_S and, (2) expressing CA IV in oocytes not only increases ΔpH_S but also the magnitude of (dpH_i/dt)_max.

In order to help interpret the data in the two physiological papers noted in the previous paragraph (Musa-Aziz et al., 2014a, 2014b), these authors extended and refined the model of Somersalo et al. These refinements, explained in the third paper in that series (Occhipinti et al., 2014) are the following: (1) reduced water content of cytosol, (2) reduced cytosolic diffusion to account for the viscosity and steric hindrance of the cytoplasm, (3) refined cytosolic CA (i.e., CA II) activity, (4) implementation of a layer of intracellular vesicles beneath the plasma membrane, (5) reduced membrane CO₂ permeability to account for the resistance of the membrane to the movement of CO₂, (6) implementation of folds and microvilli at the plasma membrane, (7) refined extracellular-surface CA (i.e., CA IV) activity, (8) implementation of a vitelline membrane that surrounds the oocyte, and (9) a new more realistic simulation protocol for the delivery and removal of the bulk extracellular CO₂/HCO₃⁻ solution. With these new features and the appropriate parameter values, the model can approximate the experimentally measured time required for pH_S to reach its peak, the maximal change in pH_S, the time delay (after a change in BECF) before pH_i begins to change at all, and the further lag time before pH_i achieves its maximal rate of descent/all under different sets of experimental conditions.

As noted above, the model allows access to time-dependent concentrations of solutes that cannot be measured in the laboratory. The authors used these concentrations to calculate the transmembrane CO₂ fluxes and all the diffusive and reaction fluxes near the outer and inner side of the membrane. The model predictions confirm the hypothesis that CA II and CA IV enhance transmembrane CO₂ fluxes by producing or consuming CO₂ and thereby maximizing the CO₂ gradient across the membrane.

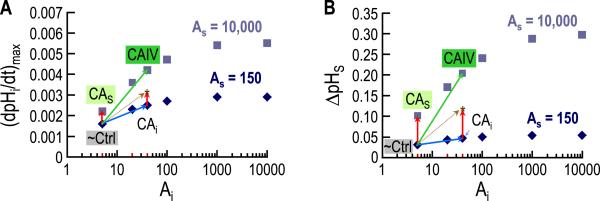
The model guided the authors in the interpretation and explanation of the data presented in the two physiological papers (Musa-Aziz et al., 2014a, 2014b). An interesting example of the power of mathematical models regards the interpretation of the experiments in which the authors expressed CA IV in oocytes and then examined the effect of intracellular or extracellular CA inhibitors. The model led to a clear understanding of data that at a first did not seem to make intuitive sense. Further simulations with many different combinations of intracellular and extracellular-surface CA activities predict that, in order to observe the full-blown up effect of extracellular-surface CA activity, a small amount cytosolic CA activity is essential. Conversely, the full effect of cytosolic CA activity requires a small amount of extracellular-surface CA activity. This analysis led to the novel and physiologically important prediction that the effects of simultaneously implementing cytosolic and extracellular-surface CA activity on (dpH_i/dt)_max and ΔpH_S are not merely additive, but supra-additive (Fig. 10).

Fig. 10.

Supra-additivity of cytosolic and extracellular-surface CA activities. A: Dependence of (dpH_i/dt)_max on the intracellular CA acceleration factor (A_i), for each of two extracellular-surface CA acceleration factors (A_S). The collection of points for each A_S value represents an isopleth, diamonds for A_S = 150 (the baseline or control value), and squares for A_S = 10,000 (expression of an extracellular CA). B: Dependence of ΔpH_S on A_i, for each of the two A_S values. The collections of points for the two isopleths have the same meaning as in panel A. In each panel we show results of 12 simulations (six for each surface CA isopleth) in which we expose a hypothetical oocyte to a BECF solution containing 1.5% CO₂/10 mM HCO₃⁻ . Each simulation differs because of the values chosen for A_i and A_S. The points labeled “~Ctrl”, corresponding to A_i = 5 and A_S = 150, identify a “control” oocyte (i.e., an oocyte not injected or expressing any heterologous protein). The points labeled “CA_S” correspond to a simulation in which we raise A_S from 150 to 10,000 but leave A_i at 5. Note that, compared to “~Ctrl”, the CA_S simulation (red vector) predicts a relatively large increase in ΔpH_S but a relatively small increase in (dpH_i/dt)_max. The points labeled “CA_i” correspond to a simulation in which we raise A_i from 5 to 40 but leave A_S at 150. Note that the CA_i simulation (blue vector) predicts a relatively large rise in (dpH_i/dt)_max but a relatively small increase in ΔpH_S. The algebraic sum of the CA_S and CA_i simulations (dashed gold arrow) predicts modest increases in both (dpH_i/dt)_max and ΔpH_S. However, the points predicted by the “CAIV” simulation–in which we simultaneously raise A_S from 150 to 10,000 and raise A_i from 5 to 40–reflect substantially larger increases in both (dpH_i/dt)_max and ΔpH_S, and mimic the actual physiological data. Thus, the effects of intracellular and surface CA are not merely additive, but supra-additive. Independent evidence indicates that the expression of CA IV in oocytes leads to increases in both surface and intracellular CA IV (Nakhoul et al., 1996; Schneider et al., 2013). Modified from Fig. 13 in (Occhipinti et al., 2014).

3.2.4. Use of the refined model to study influxes of CO₂ and HCO₃⁻, alone or in combination

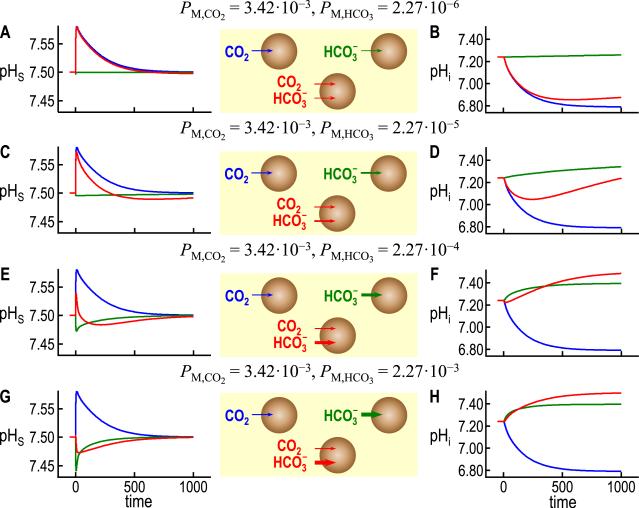
Here, we exploit our latest version of the oocyte model (Occhipinti et al., 2014) to investigate how the simultaneous in-fluxes of CO₂ and HCO₃⁻ , as might occur in a physiological experiment, would affect pH_i and pH_S. The blue curves in Fig. 11A, C, E, and G are identical and are the same pH_S waveform that we saw in the top of Fig. 8B. It is the result of a simulation for a control oocyte (i.e., not injected with or expressing any heterologous protein) exposed to 5% CO₂/33 mM HCO₃⁻ (pH_BECF = 7.50), and assumed to be permeable only to CO₂ (P_M,CO2 = 3.42 × 10⁻³ cm s⁻¹). Similarly, the blue curves in Fig. 11B, D, F, and H are identical and are the same pH_i waveform that we saw in the bottom of Fig. 8B. Thus, the blue curve in Fig. 11B is the intracellular counterpart to the blue pH_S record in Fig. 11A.

Fig. 11.

Simulations of pH_i and pH_S transients produced by influxes of CO₂ and HCO₃⁻ alone or in combination. The blue trajectories, which are identical for ΔpH_S in panels A, C, E, and G, and for pH_i in panels B, D, F, and H, are simulations that mimic the exposure of an oocyte to 5% CO₂/33 mM HCO₃⁻ (pH_o 7.50) when P_M,CO2 = 3.42 × 10⁻ cm s⁻¹ (the control value from (Occhipinti et al., 2014)) but P_M,HCO3 = 0. The green trajectories in panels A and B are simulations that mimic the exposure of an oocyte to the same CO₂/HCO₃⁻ solution, but with P_M,CO2 = 0 but P_M,HCO3 = 2.27 × 10⁻ cm s⁻¹ (estimated from known values of the NBCe1-A current (Lee et al., 2011)). Note that because P_M,CO2 = 0 in these green simulations, the influx of HCO₃⁻ leads to the formation of intracellular CO₂ that cannot escape from the cell; hence, the relatively small increases in pH_i upon HCO₃⁻ equilibration across the membrane. In panels C and D, the P_M,HCO3 values are 10 × greater than in A and B, and the P_M,HCO3 likewise increase 10 × in E and F, and again in G and H. In each panel, the red trajectories are the predictions for exposing the hypothetical oocyte to CO₂/HCO₃⁻, but with P_M,CO2 = 3.42 × 10⁻³ cm s⁻¹ and P_M,HCO3 having the same value as the corresponding green trajectory. It is clear that the red trajectories are not merely the algebraic sums of the blue and green trajectories. The red curves in B, D, F, and H all asymptote at pH_i = 7.50, reflecting the equilibration of both CO₂ and HCO₃⁻ across the cell membrane.

The green curves in Fig. 11A and B are the result of a simulation identical to the one that produced the blue curves, except that here we assume that the oocyte membrane is permeable only to HCO₃⁻ (P_M,HCO3 = 2.27 × 10⁶⁻ cm s⁻¹; P_M,CO2 0). The result is a transient but miniscule fall in pH_S (Fig. 11A) and a slow rise in pH_i (Fig. 11B), reflecting the reactions summarized by the gray arrows and the label “1b” in Fig. 7.

The red curves in Fig. 11A and B are the result of a simulation identical to those that produced the blue and green curves, except that here we assume that the oocyte membrane is permeable both to CO₂ (P_M,CO = 3.42 × 10⁻³ cm s⁻¹) and HCO₃⁻ (PM,HCO = 2.27 × 10⁻⁶ cm s⁻¹). For pH_S, the resulting red curve is hardly different from the blue curve (permeability to CO₂ only). However, for pH_i, we now see that the rapid fall in pH_i (caused by the influx of CO₂) is now followed by a slower rise that mimics the pH_i recovery seen in oocytes expressing an NBC with modest activity. The red curve is also similar to the first simulation of pH_i recovery, produced by the two-compartment model of Boron and De Weer (Boron and De Weer, 1976b).

The remaining six panels of Fig. 11 summarize three additional sets of three simulations. In each set, we hold P_M,CO2 fixed at 3.42 × 10⁻³ cm s⁻¹ but increase P_M,HCO3 by a factor of 10 compared to the row above it. For the cases in which the membrane is permeable only to HCO₃⁻ (green lines), we see that increasing P_M,HCO3 causes the initial decrease in pH_S to become progressively of greater magnitude, with progressively more rapid relaxations (Fig. 11C, E, G). Regarding pH_i, we see that increasing P_M,HCO3 causes pH_i to rise more rapidly (green lines in Fig. 11D, F, H).

For the cases in which the membrane is permeable both to CO₂ and HCO₃⁻ (red curves), we see that increasing P_M,HCO3 causes the pH_S trajectory to have a less positive ΔpH_S (eventually negative) and a faster decay with an undershoot (Fig. 11C, E, G). These trends reflect the increasing dominance of HCO₃⁻ entry vs. CO₂ entry. Regarding pH_i, we see that increasing P_M,HCO3 causes the initial rate of pH_i change to become less negative (eventually positive), the pH_i nadir to become increasingly alkaline (eventually absent), and the rate of the late alkalinization to become greater. Again, these trends reflect the increasing dominance of HCO₃⁻ entry.

Without the mathematical model, one might use intuition to predict the general shapes of the green and blue curves but, of course, not the detailed trajectories. However, even if one were given the green and blue trajectories, intuition would be of limited value in predicting even the general waveforms of the red curves.

4. Future directions

As we have seen, the reaction, diffusion, and transport events underlying pH physiology at the cell, tissue and whole-body levels are complex and diverse, depending on the cell type or tissue. At this stage, although various groups have made significant progress in modeling acid-base events at the cell and multicellular/tissue levels, we are still far away from a comprehensive, time-dependent model of pH physiology, even at the single-cell level. We now have, for a spherical cell, the beginnings of a model (Occhipinti et al., 2014; Somersalo et al., 2012) that can handle a large number of buffer reactions (necessary for handling a large number of transport events). However, this model is clearly incomplete because it lacks some components that are peculiar to the way physiologists perform experiments, and many other components that are intrinsic to the cell.

4.1. The experiment

Being able to model the cell in the context of real–and imperfect–physiological experiments is important because it is only through experiments that we can gather the data that we need to inform and validate our models. In the case of modeling our oocyte experiments, we must still consider the special environment between the pH_S electrode and the oocyte membrane, and the convective flow around the oocyte, both of which will be important for quantitatively reproducing some features of our oocyte pH_i and pH_S physiological data. Modeling these experimental features may also be valuable in providing insights to real-life problems, such as reaction-diffusion events in the small spaces between cells, or convection of blood around a protrusion in a blood-vessel lumen.

4.2. The cell

In order to model pH_i regulation in a living spherical cell, we will need to introduce the movements of acid-base equivalents like those illustrated in Fig. 6. Specifically, we will need to introduce: (1) electrodiffusion for the passive fluxes of charged weak acids and bases (e.g., H⁺ or NH₄⁺ leaks), (2) simple (e.g., constant fluxes) or sophisticated kinetics for carrier-mediated transporters (e.g., NBCs), and (3) metabolism as a source of acids (e.g., H⁺, HLac, CO₂). Additional physiological details include osmosis, cell-volume regulation, other solute-transport mechanisms (e.g., Na–K pump), and consideration of electrophysiological principles, including the generation of V_m and macroscopic electroneutrality.

4.3. The geometry

Until now, we have considered only a spherical cell. However, cells can have different and complex geometries. For example, RBCs are biconcave disks, and RBC shape can change as the cells move through the capillaries. For RBCs, others have developed model–both compartmental models (Bidani, 1991; Bidani et al., 1978; Cardenas et al., 1998; Endeward and Gros, 2005) and reaction-diffusion models (Coin and Olson, 1979; Endeward and Gros, 2009; Huang and Hellums, 1994; Moll, 1968; Vandegriff and Olson, 1984a, 1984b)–that address gas exchange across the membrane, carriage (i.e., movement of gases along the blood vessel), and acid-base chemistry. Although it is outside the scope of this paper to discuss these models in depth, we note that none of these reaction-diffusion models describe RBCs as biconcave disks in three-dimensional space. They assume that the RBC is a one-dimensional plane sheet, a sphere with radial symmetry, or a cylindrical disk. They often address only steady-state conditions, and are described by only few partial differential equations (PDEs); when more than two, the number of equations is reduced (by making additional assumptions) to make the model mathematically treatable. Kim-Shapiro's group has proposed reaction-diffusion models of RBCs to study NO permeability, and uses finite element methods (FEM) to model the RBC as a biconcave disk. However, these authors include only two PDEs, for NO and Hb (Huang et al., 2007; Jeffers et al., 2005).

Besides spheres (e.g., lymphocytes, soma of neurons) and biconcave discs (RBCs), other cellular geometries that would be of interest would be cuboids (e.g., epithelia, endothelia), cylinders (e.g., rod-shaped bacteria), and spindles (e.g., skeletal and smooth muscle).

In the case of the renal proximal tubule (a cylindrical epithelium, 1 cell thick), we briefly mention the model of a rat proximal tubule developed by Weinstein (Weinstein, 1986) and later refined (Weinstein et al., 2007). This is a four-compartment (i.e., with instantaneous mixing of solutes within each compartment), steady-state model. The four compartments are (1) the cylindrical lumen, (2) the proximal-tubule cells that form the boundary of most of the lumen, (3) the interspace between proximal-tubule cells (and which forms a small part of the boundary of the lumen), and (4) the space around the outside of the tubule (which anatomically would be in indirect contact with the blood). The model assumes that the proximal tubule is a cylinder with axial flow, where the quantities of interest depend on the position along the axis. The model takes into account the fluxes of many solutes across the boundaries of adjacent compartments. Finally, it considers the equilibria (1) H₂PO₄⁻ ⇌ H⁺ + ${\mathrm{HPO}}_4^{=}$, (2) H₂CO₂ ⇌ H⁺ + ${\mathrm{HCO}}_2^{-}$ (formic acid/formate), (3) NH₄⁺ ⇌ H⁺ + NH₃, and (4) CO₂ + H₂O ⇌ H₂CO₃ ⇌ H⁺ + HCO₃⁻ (with the last reaction being catalyzed by carbonic anhydrases).

Finally, we note the necessity of modeling the spatial inhomogeneity of enzymes, such as the carbonic anhydrases.

4.4. The algorithm

More advanced versions of detailed reaction-diffusion models in different geometries would revolutionize the field acid-base physiological chemistry. However, the inclusion of additional features in a model–even one with simple geometry–will make the model more complex mathematically. For example, in our model, the addition of each new solute requires one new reaction-diffusion equation. Moreover, various reaction and diffusion events can have very different temporal and spatial scales, which also contribute to the challenge of solving the problem numerically. Thus, progress in the field will require more advanced and computationally efficient algorithms.

Perhaps these algorithms will need to be created de novo by mathematicians. Or perhaps the approaches already exist in other disciplines, such as mathematics, chemistry, physics, astronomy, meteorology, or economics. How would we know? A problem is that we have a difficulty in communicating among disciplines because we speak different disciplinary languages, attend different meetings, and publish in different journals. The 2013 inter-union meeting on Multi-Scale Systems Biology, sponsored in part by ICSU (the International Council on Science), was a first step in bringing together representatives of at least the various biological disciplines. And this special issue of the journal, of course, is a first step in publishing together.

What further steps could we take to enhance the exchange of ideas across disciplines, and perhaps help each other to solve problems? It would be helpful to promote better interdisciplinary education among scientists, so that we could better speak one another's languages. It would also be desirable to hold additional inter-union systems biology meetings, but in the future to include modelers from disciplines outside biology. The operant term seems to be interdisciplinarity. On the other hand, it is important to build the strength of individual disciplines, because one cannot have strong interdisciplinary research without strong disciplines.

Fig. 2.

The human respiratory and urinary systems and their role in regulating extracellular pH. The respiratory system (main panel) is responsible for removing CO₂ (produced as the result of metabolism) from the body, and in the process controls [CO₂] in the arterial blood. The urinary system (lower right) excretes H⁺, acidic buffers (HA ⇌ A⁻ + H⁺), and ammonium (NH₄⁺), and thereby controls [HCO₃⁻] in the arterial blood. Together, the kidney (by controlling [HCO₃⁻]) and the lungs (by controlling [CO₂]) control pH, as described by the Henderson-Hasselbalch equation (upper right). Modified from Fig. 26–4 and Fig. 33–7 in Medical Physiology, 2nd Edition Updated Edition, edited by WF Boron and EL Boulpaep, Philadelphia: Elsevier, 2012.