An independent filter for gene set testing based on spectral enrichment

Abstract

Gene set testing has become an indispensable tool for the analysis of high-dimensional genomic data. An important motivation for testing gene sets, rather than individual genomic variables, is to improve statistical power by reducing the number of tested hypotheses. Given the dramatic growth in common gene set collections, however, testing is often performed with nearly as many gene sets as underlying genomic variables. To address the challenge to statistical power posed by large gene set collections, we have developed spectral gene set filtering (SGSF), a novel technique for independent filtering of gene set collections prior to gene set testing. The SGSF method uses as a filter statistic the p-value measuring the statistical significance of the association between each gene set and the sample principal components (PCs), taking into account the significance of the associated eigenvalues. Because this filter statistic is independent of standard gene set test statistics under the null hypothesis but dependent under the alternative, the proportion of enriched gene sets is increased without impacting the type I error rate. As shown using simulated and real gene expression data, the SGSF algorithm accurately filters gene sets unrelated to the experimental outcome resulting in significantly increased gene set testing power.

1 Introduction

Gene set testing has become a critical component in the pipeline used to analyze and interpret high-dimensional genomic data [1], [2]. Gene set testing enables researchers to step back from the single gene level and explore associations between biologically meaningful groups of genes and clinically relevant variables. A test based on the aggregate effect of a set of functionally related genomic variables offers a number of important benefits relative to individual gene tests including improved statistical power, more intuitive biological interpretation and decreased variability across distinct experimental datasets. The genomic variables of interest typically represent the abundance or variation of nucleic acid molecules associated with specific genes, e.g. expression levels of mRNA molecules, and the variable sets are defined on the basis of common biological function, e.g., all genes whose protein products are active in a specific pathway. Over the past decade, significant progress has been made building and extending gene set collections [3], [4], [5] and developing, testing and refining statistical gene set testing methods [6], [7], [8].

One of the primary motivations for gene set testing is to improve statistical power via a reduction in the number of tested hypotheses relative to single gene analysis. The significant growth in gene set collections, however, can often result in gene set testing being performed with nearly as many (and sometimes even more) gene sets than original genomic variables. For example, a version of the Gene Ontology (GO) [3] loaded on September 16, 2014 into the AmiGO browser [9] has 39,908 non-obsolete terms in the biological process, cellular component and molecular function ontologies with the biological process ontology alone containing 26,501 terms, numbers of gene sets that exceed the number of genes in any relevant experimental organism. Even the much more aggressively filtered Molecular Signatures Database (MSigDB) [5] has grown in size by an order of magnitude between 2005 to 2014 from approximately 1,000 gene sets to over 10,000 with the 4.0 release. The growth in the number of gene sets in these collections is also frequently at the expense of gene set quality with an increasing level of overlap between gene sets and a large proportion of new annotations generated via fully automated methods without any curatorial review or experimental validation. For example, well over 90% of all GO annotations have the evidence code IEA (inferred from electronic annotation), meaning the annotation was generated by a computational method such as sequence similarity and has not been reviewed by a human curator [10]. Therefore, not only does gene set testing with large collections fail to deliver an improvement in statistical power, but the decline in annotation quality and higher gene set interdependency can also compromise the biological relevance and interpretability of any associations that are discovered.

The typical approach for addressing the problem of gene set collection size is either to use pre-existing collection subsets, e.g., standard GO Slims [11] or the MSigDB C5 collection that filters out GO terms with IEA evidence codes [5], or to create custom collection subsets that match a specific use case, e.g., custom GO Slim generation [9]. Although the use of data-independent subsets addresses the issue of collection size and the subsets may closely align with the domain of investigation, the process of selecting a subset is inherently subjective and thus susceptible to researcher bias. Gene sets not believed to be relevant will not be tested with the result that novel associations may never be found. For hierarchical gene set collections such as GO, methods have also been developed that reduce the number of tested gene sets by using information theoretic measures [12], [13] or by computing the association for gene sets higher in the hierarchy conditional on the results for child gene sets [14], [15], [16], [17]. Although such GO-specific methods are effective at addressing the significant overlap between GO term annotations, they are specific to hierarchical gene set collections and, for those based on a specific data set, use a criteria for filtering is not independent of the statistic used to test gene set enrichment.

Ideally, the members of a gene set collection subset should be selected based on characteristics of the empirical data under investigation. Such data-driven filtering of hypotheses has been successfully practiced in the context of genomic data analysis at the single gene level [18], [19], [20]. In this type of application, a two-stage procedure is followed where, in the first stage, a filter statistic is computed for each genomic variable, e.g., overall variance, and then, in the second stage, the desired statistical analysis is performed on just the set of dependent variables whose filtering statistic passes a given threshold. As detailed by Bourgon et al., such filtering methods can only be successful at improving power in the second stage if the filter statistic is both independent of the second stage test statistic under the null hypothesis (H₀) and dependent under the alternative hypothesis (H_A). In other words, if the test statistics follow the null hypothesis distribution, they must be statistically independent of the filter statistics and, if the test statistics follow the alternative hypothesis distribution, the test and filter statistics must be associated. Bourgon et al. refer to filtering methods that meet these requirements as independent filters and the filter statistics as marginally independent filter statistics.

Although data-driven filtering of individual genomic variables has been advocated for gene set testing [21] and empirical methods have been developed to filter out specific annotations [22], effective independent filters are not currently available that operate on entire gene sets prior to gene set testing. To address both this shortcoming and the challenge posed by large, interdependent and low quality gene set collections, we have developed spectral gene set filtering (SGSF), a novel technique for independent filtering of gene set collections prior to standard gene set testing. The SGSF method uses as a filter statistic the p-value measuring the statistical significance of the association between each gene set and the principal components (PCs) of an empirical data set, taking into account the significance of the eigenvalue associated with each PC. Because this filter statistic is independent of standard gene set enrichment test statistics under H₀, which we prove in the Appendix, but dependent under H_A, the proportion of significantly enriched gene sets is increased without impacting the type I error rate. Using simulated gene sets with simulated data and MSigDB collections with microarray gene expression data from leukemia and heart failure studies, we show that the SGSF algorithm can significantly increase gene set enrichment power by accurately filtering gene sets unrelated to the experimental outcome.

2 Methods

2.1 SGSF inputs

The SGSF method operates over the following three data structures:

1. An n × p data matrix X quantifying p genomic variables under n experimental conditions. The genomic data held in X, e.g., mRNA expression levels, will be modeled as a sample of n independent observations from a p-dimensional random vector x. It is assumed that any desired transformations on X have been performed and that missing values have been imputed or removed. For the purpose of proving the marginal independence of the spectral gene set enrichment filter (see the Appendix), it is assumed that the distribution of x can be approximated by a multivariate normal distribution (MVN (μ, Σ) with correlation matrix P). This distributional assumption is often well justified since sources of genomic data, especially gene expression data, typically follow a multivariate normal distribution after appropriate transformations. A generalization to the exponential family of distributions is planned for future work.

2. An n × 1 vector y of clinical phenotype values measured at each of the n experimental conditions. The phenotype values held in y, e.g., binary case/control status, will be modeled as known constants. The term ”phenotype” should be interpreted quite broadly in this context and simply refers to a experimental variable that is treated as an independent variable in statistical models (see Section 2.2.3). If multiple phenotype variables exist, it is possible to use a matrix Y along with the specification of appropriate parameter contrasts (see, for example, Wu et al. [8]).

3. An f × p binary annotation matrix A that specifies the annotation of the p genomic variables to f functional categories. The rows of A represent f biological categories, e.g., Kyoto Encyclopedia of Genes and Genomes (KEGG) [4] pathways or GO categories, and the elements a_i,j hold indicator variables whose value depends on whether an annotation exists between the function i and genomic variable j.

2.2 SGSF algorithm

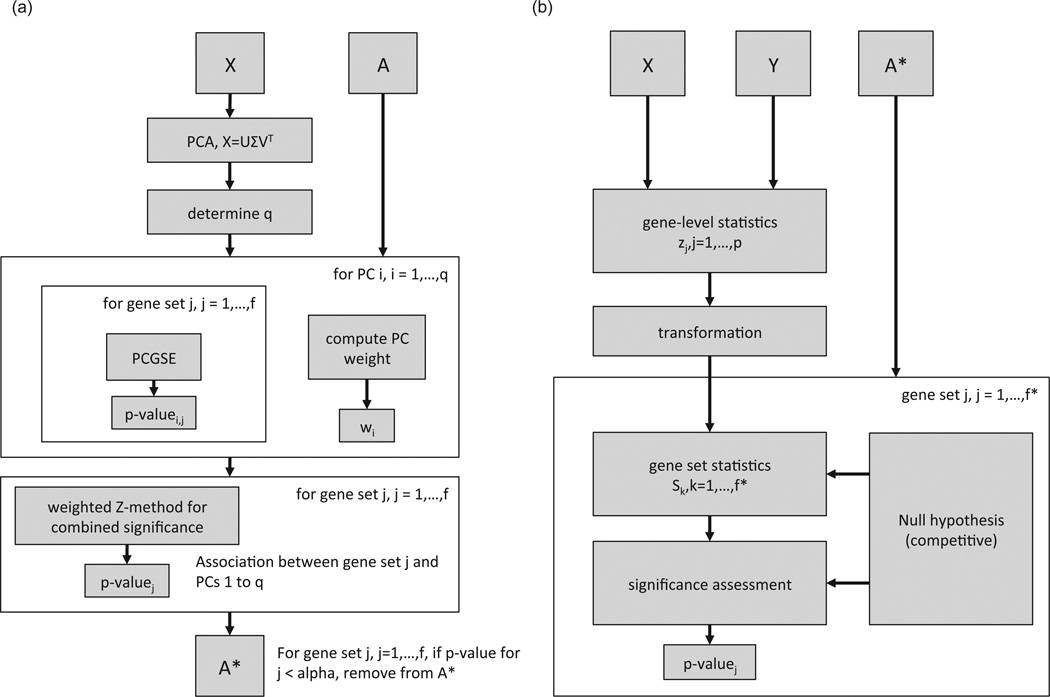
The SGSF method identifies a subset of the gene sets defined by A using a non-specific and independent filter based on the statistical significance of the association between each gene set and the spectra of X. Application of the SGSF method in the context of gene set enrichment relative to the variable y involves the following steps, which are illustrated schematically in Figure explained in greater detail in sections 2.2.1 thru 2.2.3 below.

1. Use the spectral gene set enrichment (SGSE) method [23] to compute filter statistics, F_i, i = 1, …f, for each of the f gene sets defined by A.

2. Use the filter statistics to subset the f gene sets.

3. Test the association between the gene sets that pass the filter and y.

2.2.1 Computation of filter statistics using SGSE

The SGSE method [23] is used to compute the filter statistics, F_i, for the gene sets defined by A. Specifically, F_i is set to the p-value generated by SGSE for gene set i according to the statistical significance of the association between gene set i and the PCs of X under a competitive null hypothesis. Computation of spectral enrichment p-values by the SGSE method is realized by the following steps as illustrated in Figure 1 (a) (see Frost et al. [23] for complete details on the SGSE method):

1. Perform PCA on a mean centered and standardized version of X, X̃.

2. Determine q, the number of PCs used to represent the spectra of X. This can be all PCs with non-zero variance, all PCs that are statistically significant according to the Tracy-Widom test [25] at a specific α level or a fixed number of PCs. For SGSF, the default configuration uses all PCs with non-zero variance. Although computational more expensive, this option avoids dependence on a subjectively selected α level or specific q value.

3. For all q PCs, use the principal component gene set enrichment (PCGSE) method [26] to compute the statistical significance of the association between each PC and each of the f gene sets defined by A. The PCGSE method computes a p-value for each gene set via two-stage competitive gene set testing in which the correlation between each gene and each PC is used as a gene-level statistic with flexible choice of both the gene set test statistic and the method used to compute the null distribution of the gene set statistic. For SGSF, the default configuration uses the Fisher-transformed Pearson correlation coefficient between each gene and each PC as the gene-level test statistic and computes the statistical significance of the association between a gene set and a PC using a correlation-adjusted two-sided, two-sample t-test between the gene-level test statistics for genes in the set and the test statistics for genes not in the set. See Frost et al. [26] for complete details on the PCGSE method.

4. Compute the statistical significance of the association between each of the f gene sets and the spectra of X using the weighted Z-method [27], [28] on the q PCGSE p-values with weights based on the PC variances scaled according to PC statistical significance as quantified by the lower-tailed p-value from the Tracy-Widom test [25]. An important result from the field of random matrix theory (RMT), the Tracy-Widom law of order 1 distribution describes the variation of a scaled and centered version of the largest eigenvalue of the sample covariance matrix for multivariate normal data under the null model of an identity population covariance matrix (a so-called white Wishart distribution). Using the lower-tailed p-value from the Tracy-Widom test as a weight therefore in the weighted Z-method thus discounts the contribution from all PCs whose eigenvalues are not significantly different from what would be expected under a null model of an identity population covariance matrix. Please see Frost et al. [23] for a more detailed background on the Tracy-Widom distribution and its use in the SGSE method.

Fig. 1.

SGSF workflow. (a) Screening portion of the SGSF workflow. Takes the data matrix X and gene set annotation matrix A as inputs, computes filter statistics, F_i, using the SGSE method and then filters A to generate A^*. (b) Testing portion of the SGSF workflow. Based on the gene set testing workflow in Ackermann and Strimmer [24]. Takes the phenotype values y, data matrix X and filtered gene set annotation matrix A^* as inputs and computes the association between each gene set in the filtered collection and the phenotype using a competitive gene set testing method where the gene set test statistics, S_k, have a t-distribution under H₀.

2.2.2 Gene set collection filtering

Given filter statistics, F_i, i = 1, …, f, a subset of the gene sets defined by the matrix A of size f^* < f can be identified using the following steps as illustrated in Figure 1 (a):

1. Order the filter statistics from smallest to largest.

2. Select the f* gene sets corresponding to the first f* filter statistics in the ordered list. The number f* can be either a fixed number, e.g., f* = .1f, or can be set according to a specified filter statistic threshold α, i.e., $f*={\sum }_{i=1}^{f}1(F_i<\alpha )$.

3. Generate a matrix A^* that contains just the rows of A corresponding to the f^* gene sets that pass the filter.

2.2.3 Gene set testing using filtered gene sets

It is assumed that testing of the association between each of the f* gene sets and the phenotype variable y is performed using a two-stage, competitive gene set testing method, e.g., CAMERA [8], using the following steps as illustrated in Figure 1 (b):

1. Model the relationship between the genomic variables in x and the phenotype y using a series of p univariate linear models of the form x_i ~ β₀ + β₁y + ε. If multiple phenotype variables exist, a contrast of model coefficients must also be specified. Note: if a non-Gaussian exponential family distribution is assumed for x, then a set of generalized linear models would be used instead, however, the current paper considers only the Gaussian case and linear models.

2. Compute gene-level test statistics, z_j, j = 1, …, p, from each of the p univariate models. The t-statistic associated with β̂₁ is a typical choice. CAMERA uses a normalized t-statistic.

3. Use the gene-level test statistics to generate gene set test statistics, S_i, for each of the f* gene sets. The mean difference test statistic, which follows a t-distribution under H₀, is a common choice: $S_i=({\overline{z}}_i-{\overline{z}}_{i^c})/({\sigma }_p\sqrt{\frac{1}{m_i}-\frac{1}{p-m_i}})$, wherem_i is the number of genomic variables in set i, z̄_i is the mean of the z_j for members of gene set i, z̄_i^c is the mean of the z_j for genes not in set i and σ_p is the pooled standard deviation of the z_j. CAMERA uses a correlation-adjusted version of the mean difference statistic.

4. Determine the statistical significance of the gene-level test statistics under null hypothesis that the z_j for genomic variables in the gene set are identically distributed to the z_j for genomic variables not in the gene set. CAMERA determines statistical significance using a two-sample t-test on the correlation-adjusted mean difference statistic. Many other two-stage competitive gene set testing methods use permutation of y to calculate a p-value.

2.3 SGSF evaluation

2.3.1 Alternative gene set filtering methods

To enable a comparative assessment of our SGSF method, two alternative methods for computing the filter statistics, F_i, were considered:

1. Set F_i to the p-values generated by the SGSE method when executed with weights for the PCGSE p-values in the weighted Z-method set to the PC variance.

2. Set F_i to the p-values generated according to a χ² test of independence of gene set membership relative to variable clusters. Specifically, this method generates p-values by:

   1. Clustering the p genomic variables in X̃ using k-means clustering with the Hartigan and Wong algorithm [29], 5 restarts and k set according to the global maximum of the gap statistic [30] as computed using the clusGap() function in the cluster R package [31] with the number of bootstrap resamples defaulting to 100.
   2. Computing the statistical significance of the association between each of the f gene sets defined in A and the k-means clustering using Pearson’s χ² test of independence on a 2 × k contingency table whose first row holds the counts of gene set members in each of the k clusters and whose second row holds the total size of each of the k clusters.

2.3.2 Evaluation using simulated gene sets and simulated data

The standard SGSF method described in Section 2.2 and both alternative filtering methods outlined in Section 2.3.1 were used to filter gene sets defined by a simulated annotation matrix A using 1000 simulated data sets each comprised by a matrix X and vector y generated according to the latent component model outlined in sections 4.1 and 4.2 of Paul et al. [32]. The primary simulation was performed using the following parameter settings:

• A was generated as a 60 × 2400 matrix defining 60 disjoint gene sets, each of size 40.

• X was generated as a 30 × 2400 matrix via the model $\mathbf{X}={\sum }_{i=1}^4\sqrt{{\lambda }_i}{\mathbf{v}}_i{\mathbf{u}}_i^T+{\sigma }_0\mathbf{E}$ where λ = (3, 2.5, 2, 1.5)^T, v_i ~ N₃₀(0, I), ${\mathbf{u}}_i=\sqrt{.025}{\mathbf{a}}_i$ (a_i is the i^th row of A), σ₀ = .1 and E is a 30 × 300 matrix with i.i.d N(0, 1) entries.

• y was generated as a 30 × 1 vector via the model $\mathbf{y}={\sum }_{i=1}^4\sqrt{{\beta }_i}{\mathbf{v}}_i+{\sigma }_1\mathbf{z}$ where β = (0, 1, 0, 0)^T, σ₁ = 2 and z ~ N₃₀(0, I).

To test the sensitivity of the SGSF method to changes in gene set size, error variance (i.e., σ₀) and latent factor weights (i.e., λ), simulations were also performed using the following additional six parameter settings. For each of these additional simulations, all parameters were held constant at the values listed above except the indicated parameter:

1. A was generated as a 120 × 2400 matrix defining 120 disjoint gene sets, each of size 20.

2. A was generated as a 40 × 2400 matrix defining 40 disjoint gene sets, each of size 60.

3. σ₀ = 0.05

4. σ₀ = 0.2

5. λ = (2, 1.75, 1.5, 1.25)^T

6. λ = (5, 4, 3, 2)^T

According to all simulation models, the first four simulated gene sets are associated with each of the four latent factors and, consequently, the first four PCs. Only the second latent factor, and, thus, only the second gene set, is associated with y. For the filtering method based on the χ² test on variable clusters, the number of clusters was fixed at k = 4 rather than estimated using the gap statistic, which should give this method an advantage since k-means will be executed for the exact number of latent factors used to simulated X. The CAMERA method of Wu et al. [8] was used to test the statistical association between X and y for the gene sets in A before and after filtering according to a competitive H₀. The enrichment power for each of the three filtering methods at a range of filter proportions was computed by taking the ratio of the number of truly enriched gene sets to the total number of gene sets with enrichment false discovery rate (FDR) values (as computed using the method of Benjamini and Hochberg [33]) below .2. The average enrichment power for each filter proportion was computed by simply averaging across all 1000 simulated data sets.

2.3.3 Evaluation using Armstrong et al. leukemia gene expression data and MSigDB C2 v4.0 gene sets

The standard SGSF method and both alternative filtering methods were used to filter the MSigDB C2 v4.0 gene sets for the Armstrong et al. [34] leukemia gene expression data used in the 2005 GSEA paper [6]. The MSigDB C2 v4.0 gene sets and collapsed leukemia gene expression data were both downloaded from the MSigDB repository. With a minimum gene set size of 15 and maximum gene set size of 200, 3,076 gene sets out of the original 4,722 were used in the analysis. For SGSF filtering, the SGSE method [23] was executed on the leukemia gene expression data using all PCs with nonzero eigenvalues and default settings as specified in Section 2.2.1. By filtering all gene sets with SGSE-generated p-values greater than .1, the standard SGSF method reduced the original 3,076 gene sets to 83. The two alternative filtering methods were executed using the default settings as outlined in Section 2.3.1 (k=10 was selected as optimal by the gap statistic test). To enable comparison between the three techniques, filtering via the alternative methods was configured to maintain the 83 gene sets with the best filter statistics. Enrichment of the MSigDB C2 gene sets was computed using CAMERA [8] with default settings and gene-wise test statistics calculated via the linear regression of the gene expression value on the acute myeloid leukemia (AML) versus acute lymphoblastic leukemia (ALL) phenotype. FDR values were computed using for both unfiltered and filtered subsets of p-values using the method of Benjamini and Hochberg [33].

2.3.4 Evaluation using BiKE carotid plaque gene expression data and MSigDB C2 v4.0 gene sets

The MSigDB C2 v4.0 gene sets were also filtered for the carotid plaque gene expression data used by Fokersen et al. [35]. Folkersen et al. analyzed the microarray gene expression data from 126 carotid plaque samples gathered from patients during the course of carotid endarterectomies and obtained from the Biobank of Karolinska Endarterectomies (BiKE). An ischemic event was experienced by 25 out of the 126 patients (7 myocardial infarctions and 18 ischemic strokes) during a mean follow-up period of 1,333 days. For SGSF filtering, the BiKE carotid plaque gene expression data generated using the Affymetrix Human Genome U133 Plus 2.0 Array was retrieved from the Gene Expression Omnibus (GEO) [36] as GSE21545 using a GEO2R generated script. This script created a single expression value for each gene following the procedure outlined in Folkersen et al. (i.e., the mean of the log2-transformed expression measurements for all probes associated with the same gene symbo). Using a minimum gene set size of 5 and a maximum gene set size of 200, 4,185 MSigDB C2 v4.0 gene sets out of the original 4,722 were used in the analysis. The SGSE method [23] was executed on the plaque gene expression data using all PCs with non-zero eigenvalues and default settings as specified in Section 2.2.1. By filtering all MSigDB C2 gene sets with SGSE-generated p-values greater than .1, the SGSF method reduced the original collection of 4,185 gene sets to just 14. Similar to the Armstrong et al. example, the two alternative filtering methods were also executed using the default settings as outlined in Section 2.3.1 (k=10 was selected as optimal by the gap statistic test). To enable comparison between the three techniques, filtering via the alternative methods was again configured to maintain the same number of gene sets retained by the SGSF method, i.e., the 14 gene sets with the best filter statistics. Enrichment of the MSigDB C2 gene sets was computed using CAMERA [8] with default settings and gene-wise test statistics calculated via the linear regression of the gene expression value on the binary ischemic event or no ischemic event phenotype. Alternatively, univariate Cox proportional hazard models, as employed in Folkersen et al., could be used to compute gene-wise test statistics for gene set enrichment. Linear regression against the binary ischemic event phenotype was chosen for simplicity and compatibility with CAMERA.

3 Results and Discussion

3.1 Simulation example

Figure 2 illustrates the comparative performance of SGSF filtering and the two alternative filtering methods detailed in Section 2.3.1 for the simulation example outlined in Section 2.3.2. As seen in Figure 2 (a), when no gene sets are filtered (filter proportion of 0), the behavior of all filtering methods is identical to no filtering and all techniques have an average gene set enrichment power, computed as detailed in Section 2.3.2, of approximately 0.4 across the 1000 simulated data sets. As the proportion of filtered gene sets increases, average enrichment power quickly drops to near 0 when filtering is based on the Pearson χ² p-value computed between gene set membership and k-means clusters of the variables. The poor performance of cluster enrichment in this example is due to the inability of k-means clustering to correctly recover the structure of the latent factors. Filtering according to the SGSE p-values computed using PC variance weighting also exhibits a rapid drop in average enrichment performance as the filtering proportion increases. Poor performance in this case is due to the significant impact of lower variance PCs (i.e., PCs unassociated with the four latent factors and representing only noise) on the SGSE computed p-value via the weighted Z-method, as seen in Figure 2 (b). In contrast, filtering according to the standard SGSF method (i.e., filter statistics set to SGSE p-values with weights based on the product of PC variance and the lower-tailed Tracy-Widom p-value for the PC variance) is able to achieve average enrichment power that is greater than or equal to that achieved without filtering at all filtering proportions. This is due to the fact that the Tracy-Widom p-values completely discount contributions from all PCs not associated with the four latent factors, as seen in Figure 2 (b). In this simulation example, the best average enrichment for the SGSF method is obtained when 90% of the simulated gene sets are filtered.

Fig. 2. Enrichment power for simulation example.

(a) Estimated enrichment power at different filtering proportions averaged over 1000 simulations of the model detailed in Section 2.3.2 filtering according to the chi-squared test against k-means computed variable clusters for k=4 (solid), filtering of the gene sets according to the SGSE p-values computed using PC variance weighting (dashed line) and filtering of the according to the SGSE p-value computed with the product of variance and the Tracy-Widom p-value as weighting (dotted line). Note that all methods have identical enrichment power when no filtering is performed and that, for this simulation study, filtering according to both the chi-squared p-value and SGSE-based p-value for PC variance weighting generated 0 empirical power for all other filter proportions (the lines for these two methods therefore overlap). (b) Average weights used with the SGSE method to combine PCGSE-generated p-values for the first 10 PCs of the simulation example via the weighted Z-method. Weights based on the PC variance are shown via a dashed line and weights based on the product of the PC variance and the lower-tailed Tracy-Widom p-value for the PC variance are shown via a dotted line. Grey error bars in (a) and (b) represent ±1 SE.

Results for the other six simulated parameter settings are contained in the Supplemental Material file and show a similar pattern of superior performance for the SGSF method compared to the alternative methods. These additional simulations demonstrate the robustness of the SGSF method to the tested variations in gene set size, error variance and latent factor weights.

3.2 Leukemia gene expression example

Figure 3 illustrates the significant improvement in gene set enrichment power that is possible when using variance-based filter statistics. Without any filtering, the distribution of gene set enrichment p-values computed via CAMERA relative to the AML versus ALL phenotype is consistent with the null hypothesis, i.e., the p-values are approximately U(0, 1) distributed. Although both alternative filtering methods improve enrichment power, as evidenced by the increase in the relative number of small p-values, their performance is dominated by the standard SGSF method. The specific impact of filtering on enrichment power can be seen in Table 1, which contains the gene set enrichment FDR q-values for the 25 MSigDB gene sets with the most significant enrichment p-values. Although some of these gene sets, e.g., GOLUB ALL VS AML DN, are clearly related to the phenotype, without filtering all gene sets appear to have no association after multiple hypothesis correction. The alternative filtering methods represent an improvement on the no filtering case and deliver either one or two biologically plausible gene set associations at an FDR cutoff of .2. For this example, the SGSF method is clearly the most successful at improving enrichment power with 10 out of the top 25 gene sets retained at an FDR level below .2.

Fig. 3.

MSigDB C2 filtering for Armstrong et al. leukemia gene expression data. Quantile-quantile plot of U(0, 1) versus the gene set enrichment p-values computed via CAMERA for the unfiltered and filtered MSigDB C2 v4.0 gene sets and the Armstrong et al. leukemia gene expression data using AML versus ALL status as a binary phenotype as detailed in Section 2.3.3.

Table 1.

The 25 MSigDB C2 v4.0 gene sets with the most statistically significant association with AML versus ALL status as computed via CAMERA for the Armstrong et al. leukemia gene expression data.

Gene set	Direction	GSE p-value	Unfiltered q-value	χ2 q-value	SGSE var. filtered q-value	SGSE TW-var. filtered q-value
TONG_INTERACT_WITH_PTTG1	AML	0.00117	0.914	-	0.0971	0.0576
GOLUB_ALL_VS_AML_DN	AML	0.00139	0.914	-	-	0.0576
HADDAD_B_LYMPHOCYTE_PROGENITOR	ALL	0.00141	0.914	0.117	-	-
VERRECCHIA_EARLY_RESPONSE_TO_TGFB1	AML	0.00234	0.914	-	-	-
NAKAJIMA_MAST_CELL	AML	0.00239	0.914	-	-	-
VERRECCHIA_RESPONSE_TO_TGFB1_C2	AML	0.00273	0.914	-	-	-
GUENTHER_GROWTH_SPHERICAL_VS_ADHERENT_DN	AML	0.00299	0.914	-	-	-
CHEOK_RESPONSE_TO_HD_MTX_UP	AML	0.00398	0.914	-	0.165	0.11
HUPER_BREAST_BASAL_VS_LUMINAL_UP	AML	0.004	0.914	-	-	-
ALONSO_METASTASIS_NEURAL_UP	AML	0.0042	0.914	-	-	-
GOLUB_ALL_VS_AML_UP	ALL	0.00492	0.914	-	-	-
BIOCARTA_DC_PATHWAY	AML	0.00687	0.914	-	-	-
LEE_LIVER_CANCER_E2F1_UP	AML	0.00776	0.914	-	-	0.116
KIM_ALL_DISORDERS_CALB1_CORR_DN	AML	0.009	0.914	-	-	-
TONKS_TARGETS_OF_RUNX1_RUNX1T1_FUSION_HS…	AML	0.00961	0.914	-	-	0.116
SABATES_COLORECTAL_ADENOMA_UP	AML	0.00965	0.914	-	-	-
REACTOME_CELL_SURFACE_INTERACTIONS_AT_TH…	AML	0.0102	0.914	-	-	0.116
WANG_BARRETTS_ESOPHAGUS_AND_ESOPHAGUS_CA…	AML	0.0111	0.914	-	-	0.116
HILLION_HMGA1B_TARGETS	AML	0.0112	0.914	-	0.228	0.116
MADAN_DPPA4_TARGETS	AML	0.012	0.914	-	-	-
KLEIN_PRIMARY_EFFUSION_LYMPHOMA_DN	ALL	0.0125	0.914	-	-	-
REACTOME_REGULATION_OF_INSULIN_LIKE_GROW…	AML	0.0138	0.914	-	0.228	0.116
PID_UPA_UPAR_PATHWAY	AML	0.0139	0.914	-	-	-
VERHAAK_AML_WITH_NPM1_MUTATED_UP	AML	0.014	0.914	0.422	-	0.116
YAO_HOXA10_TARGETS_VIA_PROGESTERONE_UP	AML	0.0146	0.914	-	-	-

The table columns display the gene set enrichment direction, the phenotype enrichment p-value computed via CAMERA, the FDR q-value computed using all tested MSigDB C2 v4.0 gene sets and the FDR q-value computed using each of the tested filtering methods as detailed in Section 2.3.3. If filtering according to a specific method failed to include a specific gene set, the table includes a ”-” in place of a q-value.

The SGSF method is effective in this example for two reasons: first, the SGSF filter is independent of the CAMERA gene set enrichment test statistic under H₀, as proved in Section A and, second, the SGSF filter is associated with the AML versus ALL phenotypes under H_A. Marginal independence of the filter statistic enables filtering to increase the relative proportion of significant p-values without increasing the type I error rate. The association between the SGSF filter statistic and the AML versus ALL phenotype, which is nicely illustrated in Figure 4 of Frost et al. [26], enables filtering to selectively retain significantly associated gene sets. The broader relevance of this class of gene set filters for improving gene set enrichment power in cancer gene expression studies is supported by the finding of Gorlov et al. [37] that genes with large expression variance among cancer cases are more likely to play an important role in tumorgenesis.

Fig. 4.

MSigDB C2 filtering for BiKE carotid plaque gene expression data. Quantile-quantile plot of U(0, 1) versus the gene set enrichment p-values computed via CAMERA for the unfiltered and filtered MSigDB C2 v4.0 gene sets and the BiKE carotid plaque gene expression data using ischemic event versus no ischemic event as a binary phenotype as detailed in Section 2.3.4.

3.3 Carotid plaque gene expression example

Figure 4 illustrates the impact of filtering on gene set enrichment power for the MSigDB C2 v4.0 gene sets and BiKE carotid plaque gene expression data. In this case, the distribution of gene set enrichment p-values computed by CAMERA relative to the ischemic event phenotype is approximately U(0, 1) distributed for no filtering and for each of the alternative filtering methods. Only for SGSF filtering is there a visible improvement in enrichment power. In contrast to the leukemia gene expression results shown in Table 1, it is was not feasible to show filtering results for the gene sets with the most significant phenotype enrichment p-values since none of the filtering methods retained any within the top 25. Instead, Table 2 displays the 14 MSigDB gene sets retained by the SGSF method. Although the most significant FDR q-values after SGSF filtering are only slightly below .5, these q-values are supportive of further investigation since they indicate that approximately half of the reported associations at this level are likely true. In fact, 7 of the 10 most significant gene sets in Table 2 have reported associations with atherosclerosis. Specifically, for the BHAT_ESR1_TARGETS_VIA_AKT1_DN and BHAT_ESR1_TARGETS_NOT_VIA_AKT1_DN gene sets, an association has been reported between ESR1 genetic variants and the development of atherosclerotic lesions [38]; for KEGG_ADHERENS_JUNCTION, there is evidence that junction adherens molecules are involved in atherosclerotic lesion formation through control of endothelial permeability, leukocyte recruitment and platelet deposition [39], [40]; for T_INTEGRIN_SIGNALING_PATHWAY, integrin signaling pathways have been implicated in atherosclerotic lesion development via endothelial cell activation [41]; for BIO-CARTA_TGFB_PATHWAY, TGF-β plays a key role in the development of atherosclerosis via control of the fibroproliferative response to tissue damage [42]; for PID_ALK2PATHWAY, the Alk2 signaling pathway is involved endothelial cell activation via interaction with bone morphogenic proteins [43]; for CARD_MIR302A_TARGETS, miR-302a has been implicated in lipoprotein metabolism and atherosclerosis risk [44].

Table 2.

The 14 MSigDB C2 v4.0 gene sets retained by SGSF filtering for the BiKE carotid plaque gene expression data.

Gene set	Direction	GSE p-value	Unfiltered q-value	χ2 q-value	SGSE var. filtered q-value	SGSE TW-var. filtered q-value
BHAT_ESR1_TARGETS_VIA_AKT1_DN	no event	0.115	0.958	-	-	0.488
HEDENFALK_BREAST_CANCER_BRACX_DN	no event	0.124	0.958	-	-	0.488
BHAT_ESR1_TARGETS_NOT_VIA_AKT1_DN	no event	0.135	0.958	-	-	0.488
KEGG_ADHERENS_JUNCTION	no event	0.179	0.958	-	-	0.488
ST_INTEGRIN_SIGNALING_PATHWAY	no event	0.204	0.958	-	-	0.488
STARK_PREFRONTAL_CORTEX_22Q11_DELETION_U…	no event	0.224	0.958	-	-	0.488
BIOCARTA_TGFB_PATHWAY	no event	0.244	0.958	-	-	0.488
PID_ALK2PATHWAY	no event	0.324	0.958	-	0.785	0.5
CARD_MIR302A_TARGETS	no event	0.369	0.958	-	-	0.5
IVANOVA_HEMATOPOIESIS_STEM_CELL_SHORT_TE…	no event	0.386	0.958	-	0.785	0.5
WATANABE_COLON_CANCER_MSI_VS_MSS_DN	ischemic event	0.393	0.958	-	0.785	0.5
REACTOME_CREB_PHOSPHORYLATION_THROUGH_TH…	ischemic event	0.459	0.958	-	0.788	0.535
DONATO_CELL_CYCLE_TRETINOIN	no event	0.865	0.98	-	0.932	0.932
REACTOME_NCAM1_INTERACTIONS	ischemic event	0.99	0.998	-	-	0.99

The table columns display the gene set enrichment direction, the phenotype enrichment p-value computed via CAMERA, the FDR q-value computed using all tested MSigDB C2 v4.0 gene sets and the FDR q-value computed using each of the tested filtering methods as detailed in Section 2.3.4. If filtering according to a specific method failed to include a specific gene set, the table includes a ”-” in place of a q-value.

4 Conclusion

Gene set testing is a powerful analytical tool that can improve statistical power, biological interpretation and experimental replication. Because of the significant growth in gene set collections, however, the potential gains in statistical power are lost unless some form of gene set filtering is employed. Although the use of predefined collection subsets effectively reduces the number of tested hypotheses, this approach is subjective and vulnerable to researcher bias. Ideally, gene sets collections should be filtered according to statistics of the data under investigation. For such a data-driven filter to successfully improve power, the filter statistic must be marginally independent, i.e., independent of the test statistic under H₀ and dependent under H_A. Although independent filters have been identified and successfully utilized for univariate genomic analysis, effective independent filters have not been available that operate on gene sets in the context of gene set testing.

To address this gap, we developed spectral gene set filtering (SGSF), a novel technique for independent filtering of gene set collections prior to gene set testing. The SGSF method uses as a filter statistic p-values measuring the statistical significance of the association between each gene set and the principal components (PCs) of an empirical data set, taking into account the significance of the eigenvalue associated with each PC. The SGSF method is effective in any experimental context where the variance structure of genomic variables is associated with the experimental outcome of interest under the alternative hypothesis. Because this filter statistic is independent of standard gene set enrichment test statistics under H₀, the proportion of significantly enriched gene sets is increased without impacting the type I error rate. As shown using simulated gene sets with simulated data and MSigDB collections with microarray gene expression data, the SGSF algorithm accurately filters gene sets unrelated to the experimental outcome resulting in significantly increased gene set enrichment power.

Limitations of the SGSF method include the dependence on a multivariate normal distribution for the genomic data to prove the marginal independence of the filter statistic and, importantly, the requirement for power improvement that the gene sets enriched within the variance structure of the data, as detected by the SGSE method, are also associated with the clinical outcome under the alternative hypothesis. Although this later requirement has been found to hold well for cancer gene expression data [37], further testing with different clinical endpoints and different types of genomic data will be essential to determine the generality of the SGSF approach.

Appendix A

Proof of marginal independence of SGSF filter statistic and gene set enrichment test statistic

As outlined by Bourgon et al. [19], the statistic used by a filtering method must be marginally independent of the statistic used for tests on the filtered set of hypotheses in order for filtering to increase the proportion of significant hypotheses without elevating the type I error rate. In their paper, Bourgon et al. used the notation $U_i^I$ to represent the filtering statistic for hypothesis i and the notation $U_i^{II}$ to represent the statistic employed for testing hypothesis i after filtering. The marginal independence requirement stipulates that the unconditional distribution of $U_i^{II}$ under H₀ is the same as the conditional distribution of $U_i^{II}$ given $U_i^I$ under H₀. In the context of gene set filters and our SGSF method, Bourgon et al.’s independent filtering condition is satisfied if the statistic used to filter the gene set collection, F_i, is marginally independent of the statistic used to test the association between each gene set and the phenotype. This can be proven using Basu’s theorem as follows:

1. Let $G_i^I$ be the filter statistic for gene set i. In the context of SGSF, this is the p-value computed for gene set i by the SGSE technique using the eigenvalue decomposition of the sample covariance matrix S.

2. Let $G_i^{II}$ be the enrichment statistic for gene set i. In the context of SGSF, this is a two-sample t-statistic computed using identically distributed gene-specific z-statistics for genes in gene set i and for genes not in gene set i (see Section 2.2.3).

3. Assume the genomic data held in the n × p matrix X can be modeled as n observations from a p-dimensional random vector x whose distribution is approximately multivariate normal, MVN (μ, Σ).

4. As a member of the exponential family, the multivariate normal distribution has complete minimal sufficient statistics for the population mean, μ, and population covariance, Σ, given by the vector of sample averages, x̄, and sample covariance matrix, S (Theorem 6.2.25, Casella and Berger [45]).

5. Under H₀, $G_i^{II}$ has a t-distribution. Because the t-distribution is only dependent on a degrees of freedom parameter, it is ancillary to both the vector of means, μ, and the covariance matrix, Σ. In practice, $G_i^{II}$ is a correlation-adjusted t-statistic so is only approximately t-distributed under H₀. Note: the fact that t-statistics are ancillary to the variance under H₀ was used in Bourgon et al. [19] to prove the marginal independence of an overall variance filter statistic and t-statistics via Basu’s theorem.

6. Because a complete minimal sufficient statistic is independent of an ancillary statistic according to Basu’s theorem (Theorem 6.2.24, Casella and Berger [45]), $G_i^{II}$ is independent of the sample covariance, S, and the vector of sample means, x̄, under H₀.

7. Because the gene set filtering statistic $G_i^I$ is a function of the sample covariance matrix, S, $G_i^{II}$ is also independent of $G_i^I$ under H₀.

8. $G_i^I$ and $G_i^{II}$ are therefore marginally independent and $G_i^I$ can be classified as an independent filtering statistic according to the criteria of Bourgon et al. [19].

Generalization of this proof to cases where the marginal distribution of each member of the random vector x can be modeled by a member of the exponential family will be explored in future work.