Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2014 Jul 2;23(4):507–515. doi: 10.1038/ejhg.2014.121

Pathway analysis with next-generation sequencing data

Jinying Zhao 1, Yun Zhu 1, Eric Boerwinkle 2, Momiao Xiong 2,*
PMCID: PMC4666565  PMID: 24986826

Abstract

Although pathway analysis methods have been developed and successfully applied to association studies of common variants, the statistical methods for pathway-based association analysis of rare variants have not been well developed. Many investigators observed highly inflated false-positive rates and low power in pathway-based tests of association of rare variants. The inflated false-positive rates and low true-positive rates of the current methods are mainly due to their lack of ability to account for gametic phase disequilibrium. To overcome these serious limitations, we develop a novel statistic that is based on the smoothed functional principal component analysis (SFPCA) for pathway association tests with next-generation sequencing data. The developed statistic has the ability to capture position-level variant information and account for gametic phase disequilibrium. By intensive simulations, we demonstrate that the SFPCA-based statistic for testing pathway association with either rare or common or both rare and common variants has the correct type 1 error rates. Also the power of the SFPCA-based statistic and 22 additional existing statistics are evaluated. We found that the SFPCA-based statistic has a much higher power than other existing statistics in all the scenarios considered. To further evaluate its performance, the SFPCA-based statistic is applied to pathway analysis of exome sequencing data in the early-onset myocardial infarction (EOMI) project. We identify three pathways significantly associated with EOMI after the Bonferroni correction. In addition, our preliminary results show that the SFPCA-based statistic has much smaller P-values to identify pathway association than other existing methods.

Introduction

It is increasingly realized that evolutionary forces produce substantial genetic heterogeneity in human disease.1 Different affected individuals may have a large number of different risk variants. These different risk variants may be located in the same genes or in different genes, but in the same or related pathways. Vast allelic, locus and phenotypic heterogeneity in common disease implies that identifying pathways associated with disease is a key approach to unraveling the pathogenesis of the disease.2 Pathway analysis typically tests the association of a predefined set of related genes, which are often defined by biological knowledge.3 Although pathway analysis methods have been developed and successfully applied to association studies of common variants,4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 the statistical methods for pathway-based association analysis of rare variants have not been well developed.18, 19, 20, 21 The current methods for pathway-based association analysis of rare variants are classified into two approaches. One approach is a two-step strategy, first generate gene-level statistics (combining information on all rare variants in the gene) or P-values and then aggregate the gene-level statistics or combining P-values across all genes in a pathway by gene set enrichment analysis (GSEA). An alternative approach is to aggregate all rare variants (combining all rare variants within genes in a pathway) in a pathway directly and to collectively test the association of all rare variants in the pathway by rare variant association test statistics.18 However, many investigators have observed highly inflated false-positive rates and low power in pathway-based tests of association of rare variants.22, 23 The inflated false-positive rates and low true-positive rates of the current methods are mainly due to their lack of ability to account for gametic phase disequilibrium and to reduce the high dimensionality of the data in the pathway-based association analysis.21

To overcome these limitations, we develop a novel statistical method for pathway-based association studies, which are based on the smoothed functional principal component analysis (SFPCA). The SFPCA is used to view the genotype profiles of SNPs as a function of genomic position of the SNPs and perform basis function expansion of genotype function. Therefore, the SFPCA takes information across all variants in the genomic region into account and hence, includes all individual varaint distribution. The SFPCA statistic globally compares differences in the average of functional principal component scores between cases and controls. In other words, it tests accumulation of differences in all variant variation in the genomic region between cases and controls. We extend SFPCA from a single gene to multiple genes and compare the difference in functional principal component scores that are calculated from all genes in a pathway between cases and controls. The SFPCA-based statistic for testing the association of pathway with the disease combines a measure of goodness-of-fit with a roughness penalty to retain the advantages of basis expansion and reduce the dimensionality of the data in the pathway. The SFPCA can utilize merits of both individual variant analysis and group tests. It can also efficiently use information of both risk and protective variants and allow for sign and size heterogeneity of genetic variants in the pathways. Many statistics can be used to test for association of either common variants or rare variants, but very few can test association of both common and rare variants. The SFPCA is designed to test the association of the entire allelic spectrum of genetic variation.

To evaluate the performance of the SFPCA-based statistic for pathway analysis, we will use large-scale simulations to calculate the type I error rates and systematically evaluate the power of 23 statistical methods: SFPCA, functional principal component analysis (FPCA), the weighted sum (WSS),24 variable-threshold (VT),25 combined multivariate and collapsing (CMC),26 linear combination test (LCT/LCT),13 quadratic test (QT/QT),13 de-correlation test (DT/DT),13 WSS/Sidak, WSS/Fisher combination, WSS/Fisher exact, WSS/GESA, VT/Sidak, VT/Fisher combination, VT/Fisher exact, VT/GESA, CMC/Sidak, CMC/Fisher combination, CMC/Fisher exact, CMC/GESA, PCA, SKAT27 and GESA.28

To further explore and illustrate some valuable features of the SFPCA, SFPCA and other popular statistics for pathway analysis are applied to the early-onset myocardial infarction (EOMI) exome sequence data sets, which contain individuals with European origin (EA) and African origin (AA) from the NHLBI's Exome Sequencing Project (ESP). The ESP may be the largest publically available exome sequencing data set when this paper is completed. Our results show that although sample sizes are small, we still can identify pathways significantly associated with EOMI, which can be replicated in two independent studies and confirmed in the literature.

Materials and methods

FPCA for pathway association

Let t be a genomic position in the gene. Define a genetic variant function xi(t) of the i-th individual as 1, 0, −1, if the number of major alleles at the SNP located at the genomic position t is 2, 1 and 0, respectively.

Consider k genes in a pathway. The j-th gene is located in the genomic region [aj,bj]. Let R(s,t) be a covariance function between xi(t) and xi(s), and β(t) be a functional principal component. By extension of multivariate PCA to functional PCA, the formula for the variance of stochastic integral29 and calculus of variations,30 we obtain the following k eigenequations (Supplementary Information):

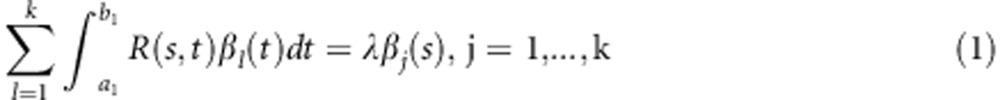graphic file with name ejhg2014121e1.jpg

Equation (1) can be solved by basis function expansion (Supplementary Information).

The observed genetic variant functions are often not smooth, which will lead to substantial variability in the estimated functional principal component curves.31, 32 To improve the smoothness of the estimated functional principal component curves, we impose the roughness penalty on the functional principal component weight functions. The smoothed functional principal components can be found by solving the following integral equations (Supplementary Information):

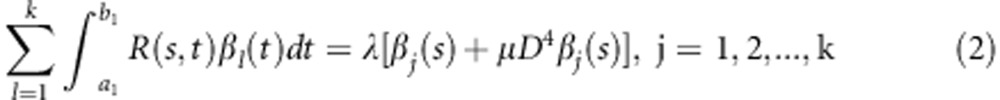graphic file with name ejhg2014121e2.jpg

Note that when μ=0 the smoothed functional principal components analysis is reduced to unsmoothed FPCA. Again, integral Equation (2) can be solved by basis function expansion, which leads to the principal component function 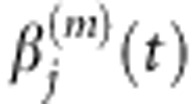Inline graphic (Supplementary Information).

Test statistic

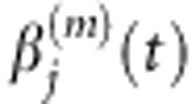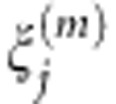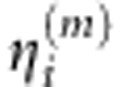We use the pooled genetic variant functions Xi(t) of cases and Yi(t) of controls to estimate the principal component function Inline graphic, j=1,...,k using the basis expansion methods (Supplementary Information). Using orthonormality of the functional principal components, we can obtain the functional principal component scores Inline graphic and Inline graphic of Xi(t) and Yi(t) (Supplementary Information). 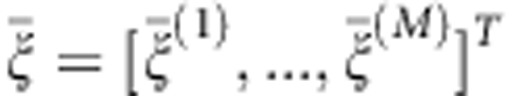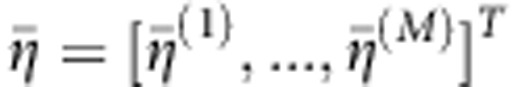Let Inline graphic and Inline graphic, where M is the number of functional principal components in the eigenfunction expansion. Define the pooled covariance matrix.

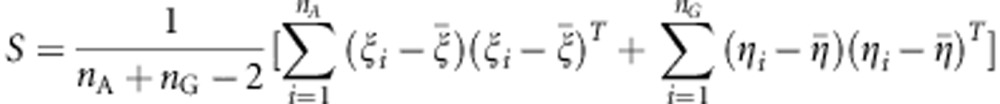graphic file with name ejhg2014121e9.jpg

where 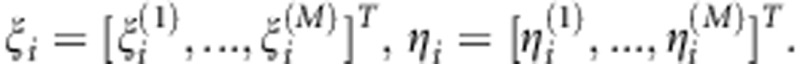Inline graphic

Define

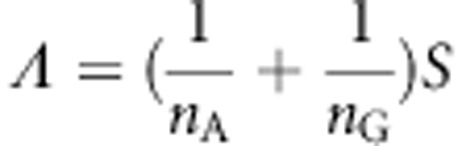graphic file with name ejhg2014121e11.jpg

Then, the statistic is defined as

graphic file with name ejhg2014121e12.jpg

Under the null hypothesis of no association of pathway with the disease, the statistic TSFPCAP is asymptotically distributed as a 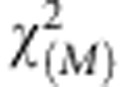Inline graphic distribution where M is the number of functional principal components in the eigenfunction expansion (Supplementary Information).

Results

Type 1 error rates

To assess the type 1 error rates of the test statistics, we performed a series of simulation studies. We randomly sampled (with replacement) from the exome sequence data in the TGF-β signaling pathway (19 genes) with 2242 European Americans in the NHLBI's ESP project to simulate 100 000 individuals. A total of 1394 SNPs with minor allele frequencies (MAFs) ranging from 4.06 × 10−4 to 0.4523 and 595 rare variants (MAF≤ 0.05) were included in the analysis. A total of 2000 individuals were randomly sampled (with replacement) and equally assigned to cases and controls. A total of 5000 simulations were repeated.

Two approaches are usually taken in pathway analysis. One approach is to first generate gene-level statistics or P-values assessed by marginal association analysis or a group test, and then aggregate the gene-level statistics or combine P-values across all genes in a pathway by GSEA. An alternative approach is to aggregate all SNPs in the pathway directly and to collectively test the association of all SNPs in the pathway by association test statistics. In this paper, the gene-based statistics that test for association of a gene with disease were the LCT, QT, DT, CMC method, WSS, VT approach and SKAT method. The statistics for aggregating the gene-level statistics in the pathway analysis in which LD information in the pathway can be explored were LCT, QT and DT. The methods for combining P-values across all genes in the pathway were GSEA with Kolmogorov-Smirnov test, Fisher's exact test and Sidak test. FPCA and SFPCA that aggregated all SNPs in the pathway were used to jointly test the association of all SNPs in the pathway. The CMC, WSS and VT were also used to serve this purpose.

Table 1 summarized type 1 error rates of 15 statistics to test pathway association including rare variants (MAF <0.05) only with disease. We observed that LCT/LCT and QT/QT tests were inflated at three significance levels, DT/DT, WSS/Fisher-exact and VT/Fisher-exact were inflated at a 0.05 significance level, but other tests were not appreciably different from the nominal levels. To examine the validity of the tests for testing the pathway association including both common and rare variants, we presented Table 2. Similar to Table 1, LCT/LCT and QT/QT tests were inflated at three significance levels. DT/DT, WSS/Fisher-exact and VT/Fisher-exact were inflated at a 0.05 significance level, and other tests were not appreciably different from the nominal levels.

Table 1. Type 1 error rates of 15 statistics for testing the association of pathway that includes only rare variants with disease.

  Nominal level
Test statistics 0.001 0.01 0.05
SFPCA 0.0012 0.0106 0.0520
FPCA 0.0012 0.0104 0.0516
Integral 0.0008 0.0084 0.0422
LCT/LCT 0.0018 0.0186 0.0742
QT/QT 0.0016 0.0017 0.0782
DT/DT 0.0014 0.0132 0.0614
WSS/Fisher exact 0.0016 0.0154 0.0682
WSS/Sidak 0.0008 0.0096 0.0504
WSS/GESA 0.0008 0.0088 0.0476
VT/Fisher exact 0.0014 0.0148 0.0596
VT/Sidak 0.0008 0.0092 0.0498
VT/GESA 0.0010 0.0096 0.0486
CMC/Fisher exact 0.0012 0.0118 0.0556
CMC/Sidak 0.0006 0.0102 0.0508
CMC/GESA 0.0008 0.0106 0.0512
Open in a new tab

Abbreviations: CMC, combined multivariate and collapsing; DT, de-correlation test; FPCA, functional principal component analysis; LCT, linear combination test; QT, quadratic test; SFPCA, smoothed functional principal component analysis; VT, variable-threshold; WSS, weighted sum.

Table 2. Type 1 error rates of 15 statistics for testing the association of pathway that includes all variants with disease.

  Nominal level
Test statistics 0.001 0.01 0.05
SFPCA 0.0010 0.0102 0.0510
FPCA 0.0012 0.0108 0.0504
Integral 0.0008 0.0082 0.0414
LCT/LCT 0.0016 0.0158 0.0638
QT/QT 0.0016 0.0172 0.0682
DT/DT 0.0014 0.0120 0.0608
WSS/Fisher exact 0.0014 0.0138 0.0622
WSS/Sidak 0.0007 0.0092 0.0456
WSS/GESA 0.0008 0.0080 0.0434
VT/Fisher exact 0.0014 0.0124 0.0556
VT/Sidak 0.0008 0.0089 0.0458
VT/GESA 0.0008 0.0085 0.0440
CMC/Fisher exact 0.0012 0.0102 0.0500
CMC/Sidak 0.0006 0.0090 0.0454
CMC/GESA 0.0008 0.0104 0.0476
Open in a new tab

Abbreviations: CMC, combined multivariate and collapsing; DT, de-correlation test; FPCA, functional principal component analysis; LCT, linear combination test; QT, quadratic test; SFPCA, smoothed functional principal component analysis; VT, variable-threshold; WSS, weighted sum.

Power evaluation

To evaluate the performance of the proposed statistics for testing the pathway association, we used simulated data to estimate their power to detect true associations. Again, we used exome sequence data in the TGF-β signaling pathway (19 genes) of 2242 European Americans in the ESP project to simulate 100 000 individuals. The number of SNPs and range of allele frequencies were the same as that described in the previous selection. We randomly selected six risk genes. In each risk gene, we selected a proportion of variants as the risk variant.

We assumed that the relative risks across all variant sites are equal and that the variants influence disease susceptibility independently (ie, no epistasis). Each individual was assigned to the group of cases or controls depending on their disease status (Supplementary Information). The process for sampling individuals from the population of 100 000 individuals was repeated until the desired samples were reached for simulations. A total of 5000 simulations were repeated.

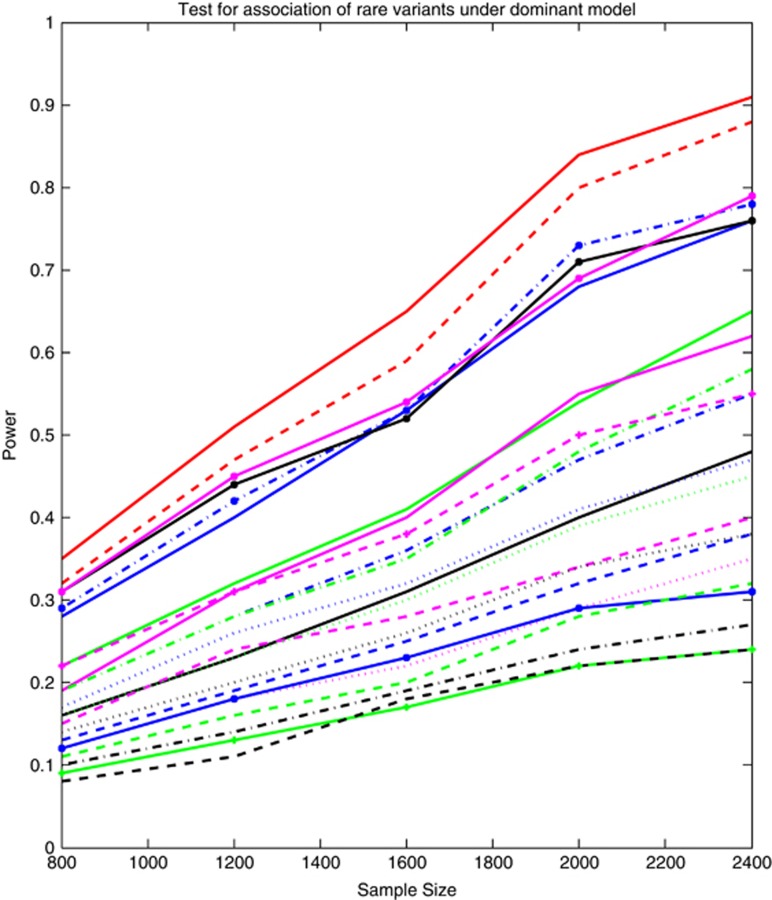
By simulations we evaluated the power of 23 statistics: SFPCA, FPCA, WSS, VT, CMC, LCT/LCT, QT/QT, DT/DT, WSS/Sidak, WSS/Fisher combination, WSS/Fisher exact, WSS/GESA,VT/Sidak, VT/Fisher combination, VT/Fisher exact, VT/GESA, CMC/Sidak, CMC/Fisher combination, CMC/Fisher exact, CMC/GESA, PCA, SKAT and GESA. Figure 1 and Supplementary Figure 1 plotted the power curves of 23 statistics for testing the pathway association harbored rare variants (MAF ≤0.05). All variants including both rare and common variants, respectively, as a function of the total number of individuals at the α=0.05 significance level, assuming that 20% of the variants in each of six genes were randomly selected as risk variants. Several remarkable features emerged from Figure 1 and Supplementary Figure 1. First, the SFPCA-based statistic had the highest power, followed by the FPCA-based statistics and other statistics. Second, the SFPCA and FPCA are designed to directly test the association of all SNPs in the pathway. We observed that SFPCA, FPCA and direct application of WSS, SKAT, PCA, VT and CMC statistics to test the pathway association had higher power than the two-stage approache. Third, the power pattern of test statistics for pathway analysis of all variants was similar to that for pathway analysis of rare variants.

Figure 1.

Figure 1

Open in a new tab

The power curves of 23 statistics for testing the association of a pathway including rare variants (MAF ≤0.05) only with disease as a function of the total number of individuals at the significance level α=0.05, where six risk genes and 20% of the risk rare variants in each gene were randomly selected. The power curves of SFPCA, FPCA, WSS, VT, CMC, LCT/LCT, QT/QT, DT/DT, WSS/Sidak, WSS/Fisher Combination, WSS/Fisher exact, WSS/GESA, VT/Sidak, VT/Fisher combination, VT/Fisher exact, VT/GESA, CMC/Sidak, CMC/Fisher Combination, CMC/Fisher exact, CMC/GESA, PCA, SKAT and GESA were denoted by red solid (-), red dashed (—), blue dashdot (-.), blue solid (-), green solid (-), black solid (-), magenta solid (-), magenta dashed (—), magenta dotted (..), blue dashed (—), blue dashdot (-.), blue dotted (..), blue solid with * marktype (-*), green dashed (—), green dashdot (-.), green dotted (..), green solid with plus marktype (-+), black dashed (—), black dashdot (-.), black dotted (..), black solid with * marktype (-*), magenta solid with * marktype (-*) and magenta dashed with plus marktype (—+), respectively.

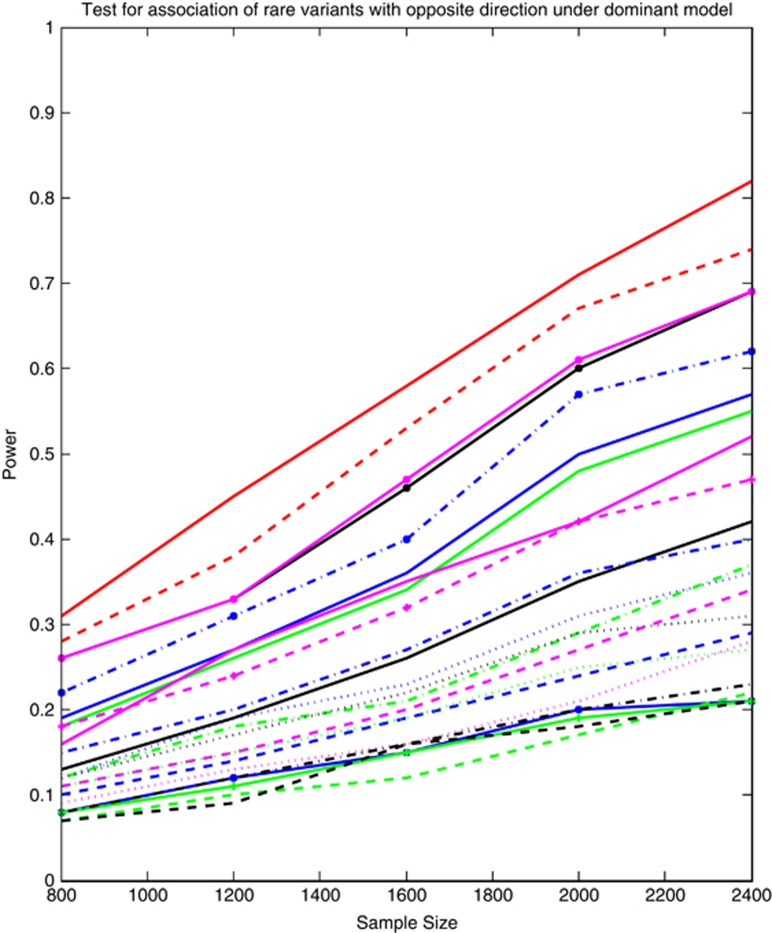
To examine the impact of the direction of association of alleles with disease risk on the power of the tests, we assume that the risk genes in the pathway include both risk and protective variants. Figure 2 and Supplementary Figure 2 plotted the power curves of 23 statistics for testing the pathway association that harbored rare variants (MAF ≤0.05), and all variants including both rare and common variants, respectively, as a function of the total number of individuals at the α=0.05 significance level. We assumed that 15% of rare (all) variants in each of six genes were randomly selected as risk variants and 15% of the rare (all) variants in each gene were protective variants. Figure 2 and Supplementary Figure 2 showed that the power pattern of the statistics for testing the association of pathway with both risk and protective variants was similar to the power patterns of the statistics for testing the pathway association with only risk variants. However, we also observed that the impact of the direction of association of alleles on the power of SFPCA and FPCA was much less than on the power of other test statistics.

Figure 2.

Figure 2

Open in a new tab

The power curves of 23 statistics for testing the association of a pathway including rare variants (MAF ≤0.05) only with disease as a function of the total number of individuals at the significance level α=0.05, where six risk genes were selected, and 15% of the rare variants in each gene were assumed to be risk variants and 15% of the rare variants in each gene were assumed to be protective variants. The power curves of SFPCA, FPCA, WSS, VT, CMC, LCT/LCT, QT/QT, DT/DT, WSS/Sidak, WSS/Fisher Combination, WSS/Fisher exact, WSS/GESA, VT/Sidak, VT/Fisher combination, VT/Fisher exact, VT/GESA, CMC/Sidak, CMC/Fisher Combination, CMC/Fisher exact, CMC/GESA, PCA, SKAT and GESA were denoted by red solid (-), red dashed (—), blue dashdot (-.), blue solid (-), green solid (-), black solid (-), magenta solid (-), magenta dashed (—), magenta dotted (..), blue dashed (—), blue dashdot (-.), blue dotted (..), blue solid with * marktype (-*), green dashed (—), green dashdot (-.), green dotted (..), green solid with plus marktype (-+), black dashed (—), black dashdot (-.), black dotted (..), black solid with * marktype (-*), magenta solid with * marktype (-*) and magenta dashed with plus marktype (—+), respectively.

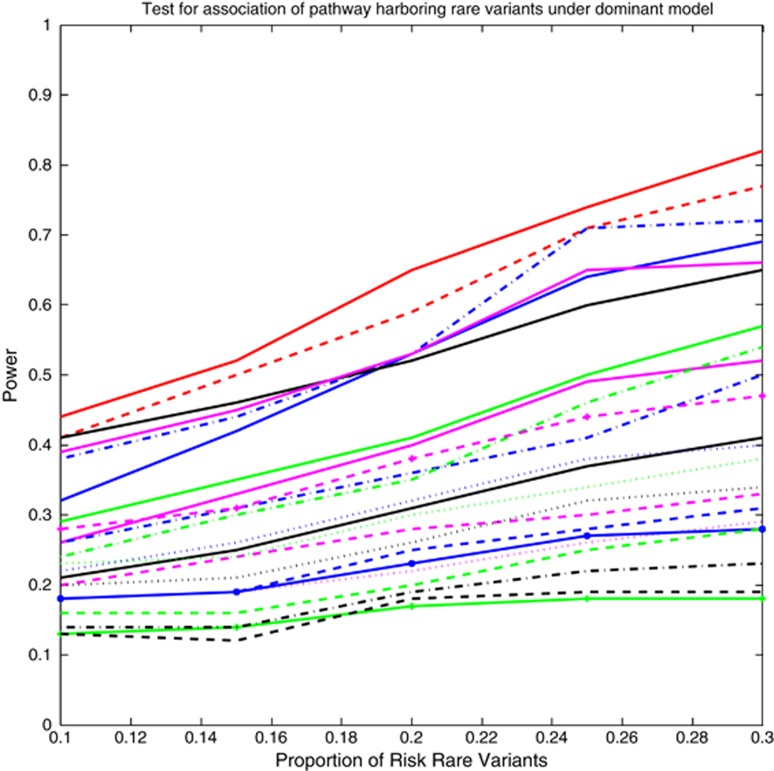
To further systematically compare the power of 23 statistics for testing the pathway association, we studied the power of the tests as a function of the ratio of risk variants. For simplicity, again we selected six genes as risk genes and assumed that the proportion of risk variants in each of the six genes was the same. Figure 3 and Supplementary Figure 3 plotted the power of 23 statistics for testing the pathway association that harbored rare variants (MAF ≤0.05), and all variants including both rare and common variants, respectively, as a function of proportion of risk variants under the dominant model at the α =0.05 significance level, assuming that 1600 cases and 1600 controls were sampled. We observed that the smoothed FPCA-based statistics had the highest power, followed by the FPCA in all settings. Varying the number of genes, or the proportion of disease variants across genes (so some genes have a higher proportion), influenced the magnitude of the power, but did not change the relative performance of methods (data not shown).

Figure 3.

Figure 3

Open in a new tab

The power curves of 23 statistics for testing the association of a pathway including rare variants (MAF ≤0.05) only with disease as a function of the proportion of risk rare variants within the six selected risk genes at the significance level α=0.05, where 1600 cases and 1600 controls were sampled. The power curves of SFPCA, FPCA, WSS, VT, CMC, LCT/LCT, QT/QT, DT/DT, WSS/Sidak, WSS/Fisher Combination, WSS/Fisher exact, WSS/GESA, VT/Sidak, VT/Fisher combination, VT/Fisher exact, VT/GESA, CMC/Sidak, CMC/Fisher Combination, CMC/Fisher exact, CMC/GESA, PCA, SKAT and GESA were denoted by red solid (-), red dashed (—), blue dashdot (-.), blue solid (-), green solid (-), black solid (-), magenta solid (-), magenta dashed (—), magenta dotted (..), blue dashed (—), blue dashdot (-.), blue dotted (..), blue solid with * marktype (-*), green dashed (—), green dashdot (-.), green dotted (..), green solid with plus marktype (-+), black dashed (—), black dashdot (-.), black dotted (..), black solid with * marktype (-*), magenta solid with * marktype (-*) and magenta dashed with plus marktype (—+), respectively.

Application to a real data example

To further evaluate their performance, 23 statistics for pathway analysis were applied to the EOMI exome sequence data from the NHLBI's ESP, where a total of 544 (188 cases and 356 controls) with EA and 312 (39 cases and 273 controls) with AA were exome sequenced. Genotype calling and quality control were described as previously.33 After quality control of the data (Supplementary Information), a total of 18 737 genes with 575 259 SNPs were included in the analysis. We assembled 249 pathways from KEGG34 and 308 pathways from Biocarta (http://www.biocarta.com). The assignment of SNPs to a gene including all SNPs within 5 kb of the gene region was obtained from the NCBI GRCh37/hg19 (ftp://ftp.ncbi.nih.gov/gene/Data/GENE_INFO). P-value for declaring significance after the Bonferroni correction is 8.98 × 10−5. We first studied pathway association including only rare variants (MAF ≤0.05). We identified two pathways: vascular endothelial growth factor (VEGF) signaling pathway and TGFβ signaling pathway that were significantly associated with EOMI in the EA population by the SFPCA-based test. Table 3 listed P-values of 11 statistics for testing the association of these two pathways with EOMI in the EA (113 201 rare variants) and AA (179 701 rare variants) populations, where P-values were calculated by permutation. Table 3 showed that the SFPCA-based statistic had the smallest P-value among 11 statistics, followed by FPCA. We also observed that the significant results by the SFPCA-based test in the EA population could not be replicated in the AA population.

Table 3. P-values of top 2 significant pathways with rare variants associated with EOMI.

Name of pathway VEGF signaling pathway TGFβ signaling pathway
Number of genes 68 17
EA
 SFPCA 7.26E-06 2.00E-05
 FPCA 4.17E-03 8.30E-04
 LCT/LCT 3.41E-01 6.93E-03
 QT/QT 6.96E-01 5.51E-02
 DT/DT 2.45E-01 3.92E-01
 WSS/Fisher exact 1.18E-02 2.87E-01
 VT/Fisher exact 2.37E-01 4.75E-02
 CMC/Fisher exact 4.81E-01 5.79E-02
 CMC 7.40E-01 8.94E-01
 SKAT 4.07E-02 2.44E-03
 GSEA 7.40E-01 7.04E-02
 PCA 4.40E-03 1.20E-03
     
AA
 SFPCA 2.85E-01 9.04E-05
 FPCA 3.32E-01 5.48E-04
 LCT/LCT 4.09E-01 4.28E-02
 QT/QT 1.11E-01 1.09E-01
 DT/DT 6.20E-01 1.91E-01
 WSS/Fisher exact 2.04E-01 2.61E-01
 VT/Fisher exact 3.98E-01 2.62E-01
 CMC/Fisher exact 5.45E-02 1.99E-02
 CMC 1.73E-01 4.68E-02
 SKAT 1.25E-01 1.72E-02
 GSEA 1.02E-01 6.06E-02
 PCA 8.70E-01 3.20E-02
Open in a new tab

Abbreviations: AA, African origin; CMC, combined multivariate and collapsing; DT, de-correlation test; EE, European origin; EOMI, early-onset myocardial infarction; FPCA, functional principal component analysis; LCT, linear combination test; QT, quadratic test; SFPCA, smoothed functional principal component analysis; VEGF, vascular endothelial growth factor; VT, variable-threshold; WSS, weighted sum.

VEGF has an important role in maintaining healthy vascular integrity and promoting homoeostasis, and is involved in atherosclerosis plaque disruption.35, 36 The VEGF signaling pathway is now used as a target pathway for treatment of ischemic cardiovascular disease.37, 38 It is reported that TGFβ signaling pathway is a risk factor for cardiovascular disease39 and has an important role in the development of myocardial infarction.40, 41

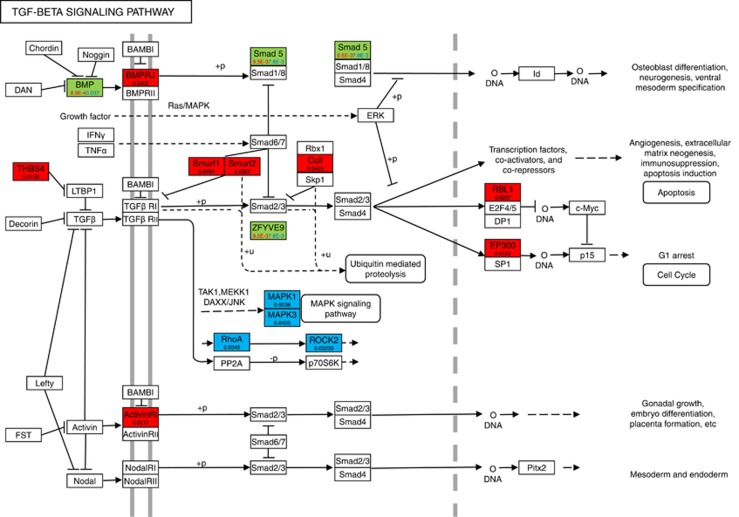
To demonstrate that replication of the results of pathways in independent samples is much easier than replication of genes, we plotted in Figure 4 where the genes with red and blue color were mildly associated with EOMI in the EA and AA populations, respectively, and the genes with green color were mildly associated with EOMI in both of the EA and AA population (see data presented in Supplementary Table 1). Figure 4 and Supplementary Table 1 showed that the EOMI studies in the EA and AA populations shared no common significantly associated genes with rare variants within the TGFβ pathway, in other words, we failed to replicate significantly associated genes within the TGFβ pathway in two independent studies. However, Table 3 showed that the TGFβ pathway in both studies was significantly associated with EOMI using the SFPCA test. This example showed that replication at the pathway level is easier than replication at the gene level. We also observed no significant genes associated with EOMI in both of the EA and AA populations. But, we observed a number of mild associations of genes within the TGFβ pathway with EOMI in the EA and AA populations. In Figure 4, there were 14 genes and 10 genes that were mildly associated with EOMI (P-value <0.05) in the EA and AA populations, respectively. Figure 4 and Supplementary Table 1 showed that each gene in the TGFβ pathway may confer a small contribution, but their joint actions may affect the function of the pathway, which in turn will cause EOMI. Other mildly associated pathways with P-values <0.0001were summarized in Supplementary Table 2.

Figure 4.

Figure 4

Open in a new tab

P-values for testing the association of genes within the TGFβ pathway with EOMI in EA and AA population by the SFPCA test, where red, blue and green colors indicate the genes associated with EOMI in EA population, AA population or both EA and AA populations, respectively.

Next we examined the association of pathways with both common and rare variants. Table 4 listed top four best pathways harboring both common and rare variants associated with EOMI. Using the SFPCA test, pyrimidine metabolism was significantly associated with EOMI in EA population, whereas association of the metabolic pathway with EOMI in the AA population quite closely reached significance level (9.40 × 10−5). Although varaint distribution association of four pathways was not significant, their P-values of association were close to significance level. It is reported that glycosaminoglycan influences the low-density lipoprotein and is involved in atherosclerosis and ischemic heart disease.42, 43, 44, 45

Table 4. P-values of top four best pathways with both common and rare variants associated with EOMI.

Name of pathway Pyrimidine metabolism Glycosaminoglycan degradation Metabolic pathway mRNA surveillance pathway
Number of genes 101 14 897 90
EA
 SFPCA 1.70E-05 1.00E-04 4.50E-04 9.00E-04
 FPCA 3.30E-04 9.10E-04 7.30E-03 8.76E-03
 LCT/LCT 4.00E-03 2.17E-01 2.60E-02 6.83E-02
 QT/QT 2.15E-02 8.80E-02 7.94E-03 5.70E-02
 DT/DT 1.95E-01 6.00E-03 1.33E-01 4.80E-02
 WSS/Fisher exact 7.40E-02 1.10E-02 5.80E-02 1.17E-01
 VT/Fisher exact 2.90E-02 5.90E-02 8.60E-02 3.45E-02
 CMC/Fisher exact 3.73E-02 7.40E-02 6.20E-02 1.06E-01
 GSEA 1.29E-02 7.30E-02 6.22E-02 5.15E-02
 SKAT 2.40E-03 1.60E-03 3.34E-02 6.33E-02
 CMC 1.30E-01 1.59E-01 1.52E-01 2.21E-02
 PCA 1.11E-02 1.30E-03 1.46E-02 1.37E-02
         
AA
 SFPCA 5.60E-04 2.80E-04 9.40E-05 5.90E-04
 FPCA 8.70E-03 7.70E-03 7.30E-02 4.20E-03
 LCT/LCT 2.61E-02 8.00E-03 2.20E-02 9.60E-03
 QT/QT 6.08E-02 6.00E-03 1.41E-01 4.02E-01
 DT/DT 1.52E-01 1.00E-03 1.07E-01 1.49E-01
 WSS/Fisher exact 8.80E-02 1.70E-02 4.60E-02 5.36E-03
 VT/Fisher exact 9.00E-03 6.00E-02 3.78E-01 1.80E-02
 CMC/Fisher exact 1.50E-02 3.25E-01 4.80E-02 3.00E-02
 GSEA 1.91E-02 4.18E-01 5.57E-01 6.65E-02
 SKAT 1.89E-02 4.91E-02 2.30E-02 8.90E-03
 CMC 3.60E-02 8.80E-02 4.19E-03 3.50E-02
 PCA 1.33E-02 1.02E-02 1.75E-01 7.00E-03
Open in a new tab

Abbreviations: AA, African origin; CMC, combined multivariate and collapsing; DT, de-correlation test; EE, European origin; EOMI, early-onset myocardial infarction; FPCA, functional principal component analysis; LCT, linear combination test; QT, quadratic test; SFPCA, smoothed functional principal component analysis; VT, variable-threshold; WSS, weighted sum.

To examine whether P-values of the pathway associations in our real data set are dependent on pathway size, we generated three types of pathway data sets. For the first type of data sets, we randomly generated a pathway with the fixed number of genes (200 genes) and fixed number of SNPs (1764). 10 000 simulations were repeated. For the second type of data sets, we randomly generated 10 000 data sets, each with 200 genes and varying number of SNPs that range from 616 to 1162, selected from different pathways of the whole EOMI data set. For the third type of data sets, we randomly selected same number of genes and SNPs as that in the four reported significant pathways identified by our method. We used three data sets to generate empirical P-values of four pathways (Supplementary Table 3). Supplementary Table 3 clearly showed that using randomly selected genes and SNPs, the observed pathway associations are no longer significant. This demonstrates that the observed pathway associations were unlikely to be caused by systematic inflation of association test statistics. Rather, our results should have some biological implication.

Discussion

We have developed a novel SFPCA-based statistic to addresses the conceptual and analytical challenges raised by pathway-based association studies for the entire spectrum of genetic variation. To our knowledge, this is among the first one to systematically evaluate the power of a large number of tests for pathway association with NGS data using large-scale simulations and real data analysis. Using simulations and real data analysis of EOMI, we have demonstrated that the SFPCA-based statistic for pathway-based association studies has broad applicability to NGS data and has several remarkable advantages over many existing methods.

First, the SFPCA-based statistic not only can jointly test association of all SNPs within a pathway, but also can capture position-level variant information. The smoothed functional principal component scores take into account information across all variants in the pathway. The SFPCA-based statistic can account for gametic phase disequilibrium. Therefore, it has a much higher power and smaller P-value than the other 22 existing statistics in all scenarios.

Second, we have developed a unified statistic that can test the association of either rare or common variants or both rare and common variants without introducing any changes in the test statistic. From large-scale simulations and real data analysis, we showed that the SFPCA-based statistic for pathway-based association studies had the correct type 1 error rate and high power.

Third, by large-scale simulations, we have shown that any GSEA that does not employ correlation information among the variants within the pathway has less power than the statistics that aggregate all genetic variants within the pathway and directly test the association of all aggregated genetic variants. The SFPCA-based statistic has the highest power to test the association of pathway among 23 statistics.

Fourth, the SFPCA-based statistic can efficiently and automatically use information of both risk and protective variants and allow for sign and size heterogeneity of genetic variants. In general, the risk and protective variants will be present in different locations in the genomic regions within the pathway. Information of risk and protective variants usually will be reflected in different eigenfunctions and hence will be included in different functional principal component scores. The SFPCA-based statistic is to summarize the square of the differences in the smoothed functional principal component scores between cases and controls. Therefore, the opposite effects of risk and protective variants on the phenotype will not compromise each other in the SFPCA-based statistics. Using simulations, we showed that the SFPCA-based statistics had substantially higher power than the existing approach in the presence of both risk and protective variants in the pathway being investigated.

Fifth, the SFPCA method can partially handle missing variant calls. By functional expansion, the SFPCA method can automatically predict genetic variation function of the missing variants from information of other known variants. We can also redefine the genetic variation function to incorporate the predicted genotypes based on its MAF, that is, the probability of carrying a rare variant.

The developed SFPCA statistic was applied to pathway analysis of EOMI with exome sequencing data. We identified the TGFβ pathway harboring rare variants significantly associated with EOMI, which were replicated in two independent EA and AA studies. We also discovered several pathways showing association, which can be confirmed in the literature. However, surprisingly, we have not observed overlap between significant pathways with common variants and significant pathways with rare variants. This may imply that genetic causes underlying diseases for common and rare variants are different. Emerging NGS technologies enable sequencing individual genomes and have the potential to discover the entire spectrum of sequence variations in a sample of well-phenotyped individuals.

The results in this paper are quite preliminary. The number of eigenfunctions in the expansion of genetic variant function and penalty parameters will influence the performance of the SFPCA for pathway-based association studies. How optimally select these parameters in pathway analysis are still open to questions in practice. Great challenges in developing innovative approaches and general framework for pathway-based association studies of NGS data need to be dealt with effectively.

Acknowledgments

We thank two anonymous reviewers for their helpful comments. The project described was supported by Grants 1R01AR057120–01 and 1R01HL106034-01 from the National Institutes of Health and the National Heart, Lung, and Blood Institute (NHLBI). We also acknowledge the support of the NHLBI and the contributions of the research institutions, study investigators, field staff and study participants in creating this resource for biomedical research. Funding for GO ESP was provided by NHLBI grants RC2 HL-103010 (HeartGO), RC2 HL-102923 (LungGO) and RC2 HL-102924 (WHISP). The exome sequencing was performed through NHLBI grants RC2 HL-102925 (BroadGO) and RC2 HL-102926 (SeattleGO). Web Resources: A program for implementing the proposed methods can be downloaded from our website http://www.sph.uth.tmc.edu/hgc/faculty/xiong/index.htm and http://www.r-project.org/.

Authors contributions

Conceived and designed the experiments: MX and ZJ. Analyzed the data: ZY. Wrote the paper: MX and EB.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

Supplementary Material

Supplementary Table S1
Click here for additional data file. (60.5KB, doc)
Supplementary Table S2
Click here for additional data file. (41.5KB, doc)
Supplementary Table S3
Click here for additional data file. (44KB, doc)
Supplementary Material
Click here for additional data file. (149.5KB, doc)
Supplementary Figures
Click here for additional data file. (38.5KB, doc)

References

  1. 1McClellan J, King MC: Genetic heterogeneity in human diseases. Cell 2010; 141: 210–216. [DOI] [PubMed] [Google Scholar]
  2. 2Ackermann M, Strimmer K: A general modular framework for gene set enrichment analysis. BMC Bioinformatics 2009; 10: 47. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. 3Wang K, Li M, Hakonarson H: Analysing biological pathways in genome-wide association studies. Nat Rev Genet 2010; 11: 843–854. [DOI] [PubMed] [Google Scholar]
  4. 4Yu K, Li Q, Bergen AW et al: Pathway analysis by adaptive combination of P-values. Genet Epidemiol 2009; 33: 700–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. 5Chen L, Zhang L, Zhao Y et al: Prioritizing risk pathways: a novel association approach to searching for disease pathways fusing SNPs and pathways. Bioinformatics 2009; 25: 237–242. [DOI] [PubMed] [Google Scholar]
  6. 6O'Dushlaine C, Kennny E, Heron EA et al: The SNP ratio test: pathway analysis of genome-wid association datasets. Bioinformatics 2009; 25: 2762–2763. [DOI] [PubMed] [Google Scholar]
  7. 7Chai HS, Sicote H, Bailey KR et al: GLOSSI: a method to assess the association of genetic loci-sets with complex diseases. BMC Bioinformatics 2009; 10: 102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. 8Chasman DI: On the utility of gene set methods in genome-wide association studies of quantitative traits. Genet Epidemiol 2008; 32: 658–668. [DOI] [PubMed] [Google Scholar]
  9. 9De la Cruz O, Wen X, Ke B, Song M, Nicolae DL: Gene, region and pathway level analyses in wholegenome studies. Genet Epidemiol 2010; 34: 222–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. 10Zhang K, Cui S, Chang S, Zhang L, Wang J: i-GSEA4GWAS: a web server for identification of pathways/gene sets associated with traits by applying an improved gene set enrichment analysis to genomewide association study. Nucleic Acids Res 2010; 38 (Suppl 2): W90–W95. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. 11Schwender H, Ruczinski I, Ickstadt K: Testing SNPs and sets of SNPs for importance in association studies. Biostatistics 2011; 12: 18–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. 12Nam D, Kim J, Kim SY, Kim S: GSA-SNP: a general approach for gene set analysis of polymorphisms. Nucleic Acids Res 2010; 38 (Suppl 2): W749–W754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. 13Luo L, Peng G, Zhu Y et al: Genome-wide gene and pathway analysis. Eur J Hum Genet 2010; 18: 1045–1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. 14Guo YF, Li J, Chen Y, Zhang LS, Deng HW: A new permutation strategy of pathway-based approach for genome-wide association. BMC Bioinformatics 2009; 10: 429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. 15Lee PH, O'Dushlaine C, Thomas B, Purcell SM: INRICH: interval-based enrichment analysis for genome-wide association studies. Bioinformatics 2012; 28: 1797–1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. 16Holmans P, Green EK, Pahwa JS et al: Gene ontology analysis of GWA study data sets provides insights into the biology of bipolar disorder. Am J Hum Genet 2009; 85: 13–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. 17Segrè AV et al DIAGRAM ConsortiumMAGIC investigators: Common inherited variation in mitochondrial genes is not enriched for associations with type 2 diabetes or related glycemic traits. PLoS Genet 2010; 6: e1001058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. 18Petersen A, Sitarik A, Luedtke A, Bekmetjev A, Tintle NL: Evaluating methods for combining rare variants data in pathway-based tests of genetic association. BMC Proc 2011; 5 (Suppl 9): S48. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. 19Yang W, Gu CC: Enrichment analysis of genetic association in genes and pathways by aggregating signals from both rare and common variants. BMC Proc 2011; 5 (Suppl 9): S52. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. 20Ngwa JS, Manning AK, Grimsby JL et al: Pathway analysis following association study. BMC Proc 2011; 5 (Suppl 9): S18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. 21Uh H-W, Tsonaka R, Houwing-Duistermaat JJ: Does pathway analysis make it easier for common variants to tag rare ones. BMC Proc 2011; 5 (Suppl 9): S90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. 22Sung YJ, Rice TK, Rao DC: Application of collapsing methods for continuous traits to the Genetic Analysis Workshop 17 exome sequence data. BMC Proc 2011; 5 (Suppl 9): S121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. 23Luedtke A, Powers S, Petersen A et al: Evaluating methods for the analysis of rare variants in sequence data. BMC Proc 2011; 5 (Suppl 9): S119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. 24Madsen BE, Browning SR: A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet 2009; 5: e1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. 25Price AL, Kryukov GV, de Bakker PI et al: Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet 2010; 86: 832–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. 26Li B, Leal SM: Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet 2008; 83: 311–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. 27Wu MC, Lee S, Cai T et al: Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet 2011; 89: 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. 28Subramanian A, Tamayo P, Mootha VK et al: Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA 2005; 102: 15545–15550. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. 29Henderson D, Plaschko P: Stochastic Differential Equations in Science and Engineering. World Scientific: New Jersey, 2006. [Google Scholar]
  30. 30Sagan H: Introduction to the Calculus of Variations. Dover Publications, Inc.: New York, 1969. [Google Scholar]
  31. 31Ramsay JO, Silverman BW: Functional Data Analysis. New York: Springer, 2005. [Google Scholar]
  32. 32Li Y, Byrnes AE, Li M: To identify associations with rare variants, Just WhaIT: weighted haplotype and imputation-based tests. Am J Hum Genet 2010; 87: 728–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. 33Fu W, O'Connor TD, Jun G et al: Analysis of 6,515 exomes reveals the recent origin of most human protein-coding variants. Nature 2013; 493: 216–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. 34Ogata H, Goto S, Sato K et al: KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res 1999; 27: 29–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. 35Zachary I, Morgan RD: Therapeutic angiogenesis for cardiovascular disease: biological context, challenges, prospects. Heart 2011; 97: 181–189. [DOI] [PubMed] [Google Scholar]
  36. 36Ropert S, Vignaux O, Mir O, Goldwasser F: VEGF pathway inhibition by anticancer agent sunitinib and susceptibility to atherosclerosis plaque distuption. Invest Drugs 2011; 29: 1497–1499. [DOI] [PubMed] [Google Scholar]
  37. 37Koransky ML, Robbins RC, Blau HM: VEGF gene delivery for treatment of ischemic caridiovascular disease. Trends Cardiovasc Med 2002; 12: 108–114. [DOI] [PubMed] [Google Scholar]
  38. 38Giacca M, Zacchigna S: VEGF gene therapy: therapeutic angiogenesis in the clinic and beyond. Gene Ther 2012; 19: 622–629. [DOI] [PubMed] [Google Scholar]
  39. 39Hilbers FS, Boekel NB, van den Broek AJ et al: Genetic variants in TGFβ-1 and PAI-1 as possible risk factors for cardiovascular disease after radiotherapy for breast cancer. Radiother Oncol 2012; 102: 115–121. [DOI] [PubMed] [Google Scholar]
  40. 40Oklu R, Hesketh R, Wicky S, Metcalfe J: TGF /activin signaling pathway activation in intimal hyperplasia and atherosclerosis. Diagn Interv Radiol 2011; 17: 290–296. [DOI] [PubMed] [Google Scholar]
  41. 41Tedgui A, Mallat Z: Cytokines in atherosclerosis: pathogenic and regulatory pathways. Physiol Rev 2006; 86: 515–581. [DOI] [PubMed] [Google Scholar]
  42. 42Hurt-Camejo E, Camejo G, Rosengren B et al: Effect of arterial proteoglycans and glycosaminoglycans on low density lipoprotein oxidation and its uptake by human macrophages and arterial smooth muscle cells. Arterioscler Thromb 1992; 12: 569–583. [DOI] [PubMed] [Google Scholar]
  43. 43Fogelstrand P, Borén J: Retention of atherogenic lipoproteins in the artery wall and its role in atherogenesis. Nutr Metab Cardiovasc Dis 2012; 22: 1–7. [DOI] [PubMed] [Google Scholar]
  44. 44Kanzler I, Liehn EA, Koenen RR, Weber C: Anti-inflammatory therapeutic approaches to reduce acute atherosclerotic complications. Curr Pharm Biotechnol 2011; 13: 37–45. [DOI] [PubMed] [Google Scholar]
  45. 45Sidhu Vaninder K., Gary D: Lopaschuk evolution of the metabolic approach to heart disease. Heart Metab 2010; 46: 5–10. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table S1
Click here for additional data file. (60.5KB, doc)
Supplementary Table S2
Click here for additional data file. (41.5KB, doc)
Supplementary Table S3
Click here for additional data file. (44KB, doc)
Supplementary Material
Click here for additional data file. (149.5KB, doc)
Supplementary Figures
Click here for additional data file. (38.5KB, doc)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES