Abstract
Accumulation of evidence models of perceptual decision making have been able to account for data from a wide range of domains at an impressive level of precision. In particular, Ratcliff’s (1978) diffusion model has been used across many different two-choice tasks in which the response is executed via a key-press. In this article we present two experiments in which we used a letter discrimination task exploring three central aspects of a two-choice task: the discriminability of the stimulus, the modality of the response execution (eye movement, key pressing, and pointing on a touchscreen), and the mapping of the response areas for the eye movement and the touch screen conditions (consistent vs. inconsistent). We fitted the diffusion model to the data from these experiments and examined the behavior of the model’s parameters. Fits of the model were consistent with the hypothesis that the same decision mechanism is used in the task with three different response methods. Drift rates are affected by the duration of the presentation of the stimulus, while the response execution time changed as a function of the response modality.
The evidence in favor of noisy accumulation of evidence as a mechanism for perceptual decision making has been growing over the last decade. In two-choice tasks, which are the most common type laboratory paradigms in psychology, diffusion models have been able to account for data from a wide range of domains at an impressive level of precision (e.g., Busemeyer & Townsend, 1993; Diederich & Busemeyer, 2003; Gold & Shadlen, 2001; Laming, 1968; Link, 1992; Link & Heath, 1975; Palmer, Huk, & Shadlen, 2005; Ratcliff, 1978, 1981, 1988; Ratcliff & Rouder, 1998, 2000; Ratcliff & Smith, 2004; Ratcliff & Tuerlinckx, 2002; Ratcliff, Van Zandt, & McKoon, 1999; Roe, Busemeyer, & Townsend, 2001; Stone, 1960; Usher & McClelland, 2001; Voss, Rothermund, & Voss, 2004). Within cognitive psychology, Ratcliff’s (1978) model (from hereon “the diffusion model”), has been one of the most widely used (see Ratcliff & McKoon, 2008, and Wagenmakers, 2009 for reviews). Most of this model’s applications have been to two-alternative forced choice tasks in which participants are instructed to classify the stimulus as a member of one of two categories (e.g., a strings of letters can be classified as a word or as a nonword), by using one key for one alternative, and a different key for the other.
Significantly, there has been evidence for the neural plausibility of evidence accumulator models from animal work. At least three linked brain areas have been shown to track decision preparation: the frontal eye field (FEF), the lateral intraparietal cortex (LIP), and the superior colliculus (SC). One of the first articles to relate accumulator models with neural recordings was by Hanes and Schall (1996), who found that the activity of single cells in the FEF can be best explained as variable evidence accumulation to a threshold. In another seminal article, Roitman and Shadlen (2002) used a motion detection task, and found that cells in the lateral intraparietal cortex LIP also exhibit behavior that is consistent with variable evidence accumulation (with the evidence being fed by extrastriate visual cortex areas MT and MST). Ratcliff, Cherian and Segraves (2003) examined Macaques’ behavioral responses with the full diffusion model and found that the pattern of activity in the SC matches the evidence accumulation process described by the model. Beyond establishing the relationship between neural activity and accumulation of evidence models, there has been considerable effort in describing the nature of the evidence accumulation process. A notable topic of discussion has been the number and location of these neural accumulators and the presence or absence of inhibition among them (see Purcell, Heitz, Cohen, Schall, Logan, & Palmeri 2010, Ratcliff, Cherian & Segraves, 2003 and Ratcliff, Hasegawa, Hasegawa, Childers, Smith, & Segraves, 2011).
Diffusion Model
The diffusion model was developed to account for fast binary decisions (i.e., those decisions that take less than a few seconds, and are between two alternative choices), like new/old recognition memory tasks (Ratcliff, 1978), perceptual tasks like discriminating between dark and light displays (Ratcliff & Rouder, 1998), or lexical decisions (Ratcliff, Gomez, & McKoon, 2004). The basic assumption of the model is that the decision-relevant information is accumulated over time, and that this accumulation of evidence is noisy. When this noisy accumulation of evidence reaches one of the two decision thresholds or decision boundaries, a response is initiated (for a more complete description of the model and its parameters see Ratcliff & McKoon, 2008).
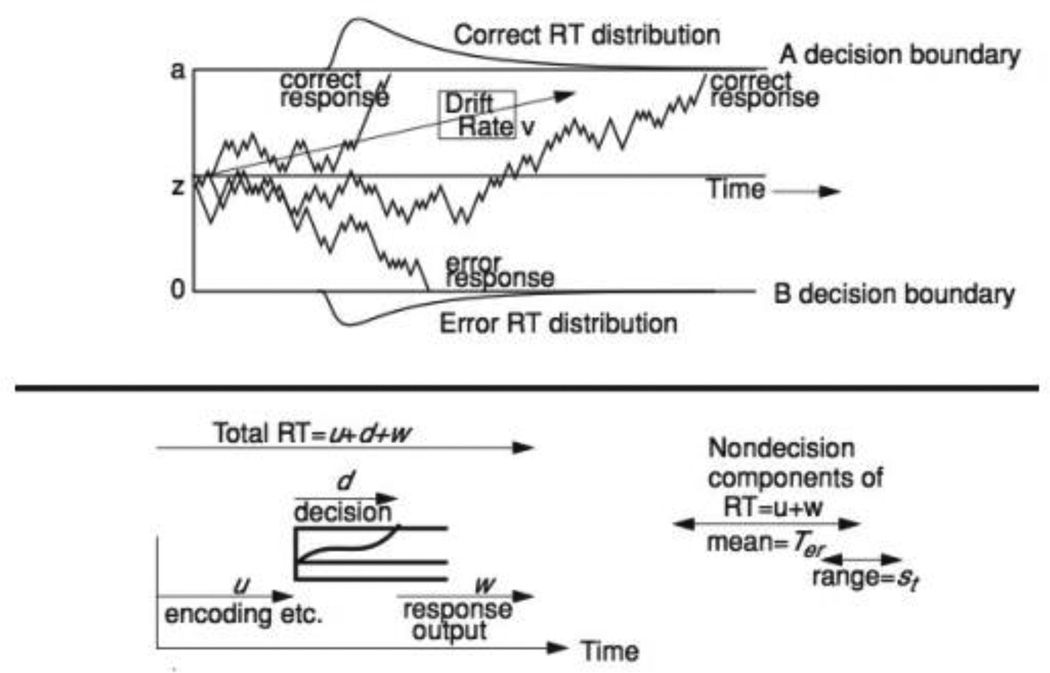
Figure 1 shows a graphical representation of a hypothetical trial according to the diffusion model. The response time in a dual-choice task is the sum of three components: (1) the time taken to extract the physical and psychological features relevant to the discrimination at hand (encoding time); (2) the time taken for the decision process (accumulation of evidence) to reach one of the two decision boundaries, and (3), the time taken for the motor components of the response execution. The sum of the encoding time and the time taken by the response execution stage are represented by the parameter Ter (the average time of encoding and response), and its uniform range st.
Figure 1.
The figure shows a representation of the diffusion model. The top panel represents simulated paths with drift rate v, boundary separation a, and starting point z. The bottom panel represents the three components of a response time: Encoding time (u), decision time (d), and response output (w) time. The non-decision component is the sum of u and w with mean = Ter and with variability represented by a uniform distribution with range st.
Drift Rate
The average rate of accumulation of evidence is termed drift rate. It can be thought of as a quality of the extraction of evidence. Difficult discriminations, such as briefly presented and masked stimuli, are associated with small drift rates (Ratcliff & Rouder, 1998), and drift rate values increase as a function of discriminability. Within a trial, the accumulation of evidence has variability that is reflected in the jagged line in Figure 1. This parameter of the model is a scaling parameter, meaning that changing this within-trial variability and scaling the other parameters could generate the same predictions. In addition to the within-trial variability, there is variability in the drift rate from trial to trial (normally distributed, SD = η); this is because trials that nominally are in the same category (e.g., the same presentation duration) cannot be expected to all have equal discriminability.
Decision boundaries
The setting of the position of the decision boundaries relates to the amount of evidence needed to make a response. The two parameters of the model that describe the boundary positions are z: the location of the starting point, and a, the distance between the decision boundaries (with the location of the negative boundary assumed to be set at 0). Biases due to instructions or base rates in favor of one choice over the other are modeled by setting the starting point (z) closer to the preferred boundary that to the other boundary. Emphasis on accuracy would separate the decision boundaries such that more evidence is needed to make a response, while emphasis on speed would reduce the amount of evidence necessary to make a decision. The starting point (z) is assumed to vary from trial to trial uniformly with range (sz).
Two recent articles (Ho, Brown & Serences, 2009; Liu & Pleskac, 2011) have explored response modality effects using random dot motion direction discrimination tasks in which participants made their responses by moving their eyes or by pressing buttons. The aim of these two articles was to find modality specific and modality independent regions consistent with accumulation of evidence. Ho et al (2009) used a four-choice task (participants chose among four movement directions), and the data was analyzed with model that is tangentially related to the diffusion model: the linear ballistic accumulator model (Brown & Heathcote, 2005). Liu & Pleskac (2011), on the other hand, used a two-choice task with 9 participants (including the two authors), and analyzed the data with a simplified diffusion model like the one used in the present work and described above. Along similar lines, an article by Palmer, Huk and Shadlen (2005) that explored the relationship between stimuli strength and the rate of accumulation of evidence in a simplified diffusion model (their model implementation did not include the variability parameters described above like the variability in starting point, across trial drift rate variability, and the vartiability in the nondecisional component). Most relevant to our work is Palmer et al’s Experiment 4, in which they used key presses and eye movements; the interpretability of their findings is limited by two factors: (1) they used a highly restricted implementation of the model, namely, a model in which not all the sources of across trial variability are included; these parameters are critical to account for features of the data such as relative speed of error and correct responses (2) they used only two response modalities. In short, a substantial body of evidence in favor of these models has been accumulated overt the last decade. Validating the detailed assumptions of these models regarding their assumptions about what parameters correspond to what components of processing becomes a central question in this line of research. Specifically, it is important to determine if the model parameters behave in the expected ways; this is, manipulations that do not affect the components of processing that a parameter supposedly relates to, should not affect the value of such parameter. Conversely, if a manipulation affects only one component of processing that the model intends to capture with one parameter, the change in the values of that parameter alone should suffice to account for the data.
Rationale
Although there are a few studies exploring the effects on response modality in accumulation of evidence models, most of the work has used random dot movement tasks in which the stimuli maps to the response in a very direct way (i.e., if the dots move to the right, press the right button). In this article we fit the model to two experiments in which we used a letter discrimination task exploring three central aspects of a two-choice task: (1) the discriminability of the stimulus (manipulated through the duration of the presentation of the stimulus), (2) the modality of the response execution (eye movement, key pressing, and pointing on a touchscreen), and (3) the mapping of the response areas for the eye movement and the touch screen conditions.
The modeling goal is twofold: First we examine if the full diffusion model adequately accounts for the data from the experimental manipulations; the description of the decision process provided by the model should not be dependent on the response modality. Second, the current interpretation of the diffusion model parameters makes some explicit predictions about the loci of the manipulations that we carried out in the present study, and such predictions need to be validated. These predictions have some important theoretical implications. The model assumes independence between the extraction of perceptual information and the response execution phase. Hence, the manipulations that affect the response only should not produce drift rate effects. In addition, our experimental manipulations naturally correspond to the response execution component of performance, and the Ter parameter; hence, these manipulations can be considered as an exploration on how the nondecision time parameter might behave across response modalities (see Voss, Rothermund, & Voss, 2004 for a study in which they included a condition in which participants had to move their finger from a central location to a key to the side of the keyboard, which affected the response execution time).
Experiment 1
Methods
Participants
Eleven paid Ohio State University students participated in this experiment ($10 per each of the four experimental sessions).
Apparatus
Stimuli were presented using a real-time computer system. For the key press condition, responses were collected using the keyboard, for the touchscreen condition responses were collected using a 17-inch CRT with serial resistive touchscreen (Footnote 1), and for the eye tracking condition data was obtained using an EyeLink 2000 system desktop mounted, and using a chin and forehead rest. The measurements were monocular (left eye) sampling at a rate of 1000 Hz.
Stimuli
For all response modalities, the stimuli were 0.85 degrees-high letters in a sans serif-bold font. There were three stimulus duration conditions (10 ms, 20 ms and 40 ms). After the stimulus presentation, a mask of random lines was shown where the stimulus was presented. The pairs of letters used as target/foil were K/W, R/G, L/P, X/T, Q/F, N/B, G/R, W/K, T/X, P/L, B/N, F/Q.
Procedure
For the eye-tracking and touchscreen conditions, there was a calibration procedure at the beginning of each block, and for all response modalities, there was an 8-trial practice phase with a long stimulus duration (60 ms). Within a block of 48 trials (16 for each stimulus duration), only one pair of target/foil letters was used and participants were told at the beginning of the block which pair was going to be used as stimuli. Although there were 24 blocks for the three response modalities, one session was used for the key press and the touchscreen conditions, but two sessions were used for the eye-tracking condition.
Key press condition: The 17-inch diagonal, 4 × 3 aspect ratio, curved CRT display was placed roughly 57 cm away the participant (chin-rests were not used for the key press or the touchscreen modalities). Stimuli were presented on the center of the screen, and articipants were asked to press the “z” or the “?” keys to make their responses.
Touchscreen condition: The display was a 17-inch diagonal, 4 × 3 aspect ratio, curved CRT, mounted on a rig roughly 57 cm away from the participant (Footnote 2), so the subject looked downward at it, allowing subjects to tap the screen in a downward motion, reducing fatigue. The response areas were centered 4.5 degrees to the left and right and 1.4 cm degrees above the center point of the stimulus. These response areas were labeled with the target and foil letters. The labels were presented at the same time as the fixation point. The screen cleared after a response was recorded. Responses were made with the index finger of whichever hand subjects preferred to use. The index finger of the response hand pressed a square “finger starting point” box below the fixation point.
Eye movement condition: A 20-inch diagonal display was placed 68 cm from the subject. The fixation point appeared in the center of the screen; simultaneously to the fixation point, the target and the lure appeared on the center of 3 × 3 degrees response boxes centered 4.5 degrees away to the right and to the left of the center of the screen where the stimulus was presented. The screen cleared after a response was recorded.
Results
Given that the focus of this article is how the diffusion model fits to the data, we present empirical results only briefly. For reference, the values of the mean latencies and the mean proportion of correct responses across subjects is shown in Table 1. Response latencies were computed as the key press, the beginning of the saccade from the fixation point, and the departure of the finger from its starting point. Responses faster than 150ms and slower than 2000ms were not used for the following analyses (less than 1% of the data).
Table 1.
Mean RTs (in ms) and accuracy results for Experiment 1
| 10ms | 20ms | 40ms | ||||
|---|---|---|---|---|---|---|
| Mean correct RT | Accuracy | Latency | Accuracy | Latency | Accuracy | |
| Eye movement | 339 | .675 | 327 | .806 | 314 | .938 |
| Touchscreen | 461 | .637 | 449 | .806 | 438 | .975 |
| Key press | 445 | .656 | 414 | .823 | 384 | .991 |
Latencies for correct responses and response proportions were submitted to separate 3 × 3 × 2 ANOVAs with response modality (eye movement, touchscreen and key press), stimulus duration (10ms, 20ms and 40ms), and side of correct alternative (left vs. right) as factors. For latency, there were significant (all p s < .05 unless otherwise noted) main effects of response modality F(2, 20) = 38.09, MSE = 261806; stimulus duration F(2, 20) = 12.42, MSE = 22694; and side of correct response F(2, 20) = 9.00, MSE = 2331, p = .01. There were also significant interactions between response modality and side of correct response which is probably a consequence of handedness -- F(2, 20) = 7.99, MSE = 2032. The responses to the right were faster for the key press and for the touchscreen conditions but not for the eye movement condition – and between response modality and duration F(4, 40) = 9.66, MSE = 2710. The interactions between side and stimulus duration, and the three-way interaction were not significant.
For accuracy, the only significant main effect was for stimulus duration F(2, 20) = 233.48, MSE = 1.65017 (F < 1 for the other main effects), and the only significant interaction was between response modality and stimulus duration F(4, 40) = 7.05, MSE = 0.022 which likely relates to the encoding time. This null main effect of modality on accuracy is consistent with the drift rate remaining the same across response methods (which will be confirmed by the modeling described below).
Experiment 2
Methods
The apparatus and stimuli was the same as in Experiment 1.
Participants
Six of the eleven participants from Experiment 1 also took part in in Experiment 2.
Procedure
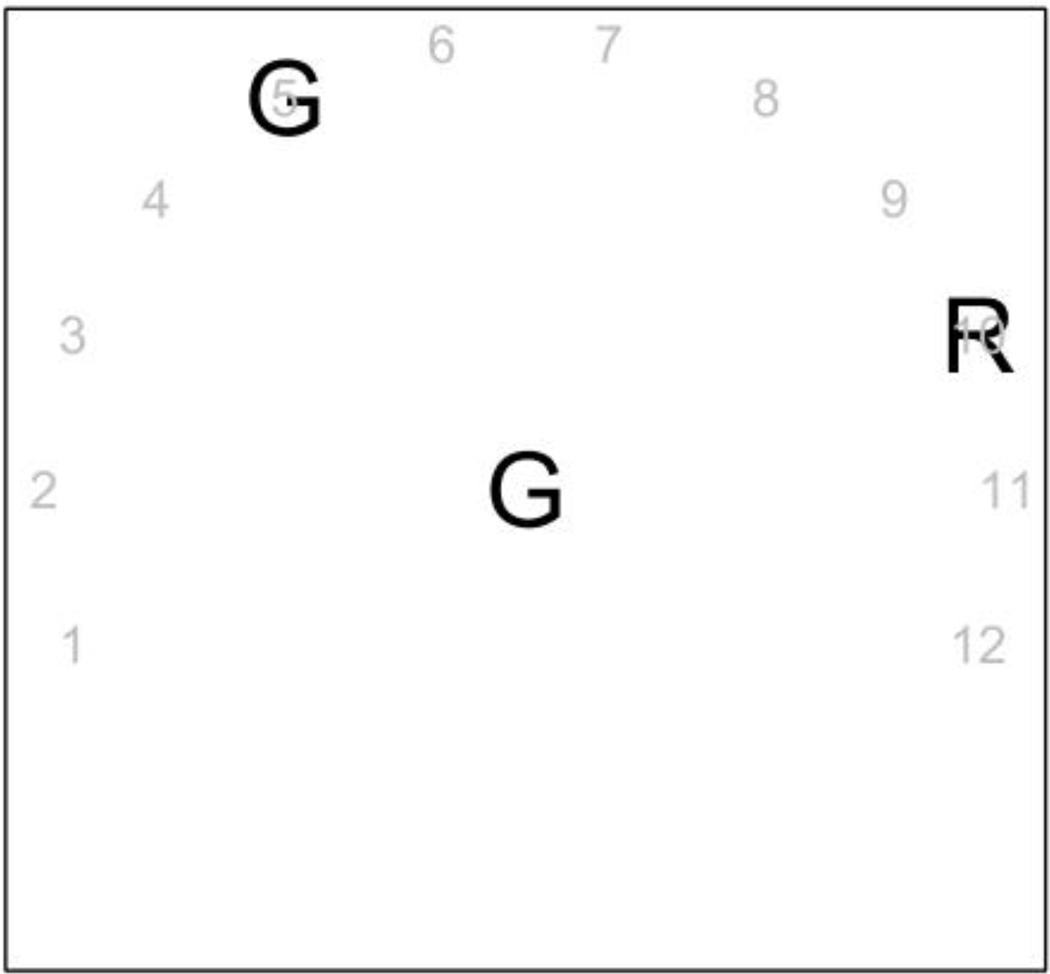
The target/foil pairs (only one pair was used in each 48 trial block) and the stimulus duration conditions (10 ms, 20 ms, and 40 ms) were the same as in Experiment 1. In Experiment 2, however, the presentation of the response areas was manipulated within subjects. There were three different types of blocks: (1) the response areas (target and lure) were fixed to the left and the right of the stimulus, and were presented 500 ms before the stimulus; (2) the response areas (target and lure) appeared randomly in 12 possible locations within a semicircle around the stimulus (see Figure 2 for an example of the target and lure presented in positions 2 & 11 respectively) and were switched on when the stimulus was presented; and (3) the response areas appeared randomly in the same possible locations as in (2), but were switched on 500 ms before the stimulus. For the conditions with the random location of response areas, the two response options were at least 40 degrees apart from each other.
Figure 2.
The figure shows a representation of the display used in Experiment 2. In this example the target was a G, and the response areas were set to the 5th and 10th locations. The gray numbers in the figure are included to show the twelve possible locations of the response areas.
Results
Latencies for correct responses and response proportions were submitted to separate 2 × 3 × 2 × 3 ANOVAs with response modality (eye movement and touchscreen), stimulus duration (10ms, 20ms and 40ms), side of correct alternative (left vs. right), and configuration of the response areas (fixed, random location uncovered 500 ms before the stimulus, and random location uncovered at the same time as the stimulus) as factors. A summary of the results can be found in Table 2.
Table 2.
Latency (in ms) and accuracy results for Experiment 2
| Random loc (0ms) | Random loc (−500ms) | Fixed | |||||||
| 10ms | 20ms | 40ms | 10ms | 20ms | 40ms | 10ms | 20ms | 40ms | |
| Eye movement | 387 | 369 | 360 | 317 | 305 | 294 | 313 | 296 | 290 |
| Touchscreen | 525 | 511 | 500 | 490 | 469 | 460 | 460 | 451 | 434 |
| Accuracy | |||||||||
| Random loc (0ms) | Random loc (−500ms) | Fixed | |||||||
| 10ms | 20ms | 40ms | 10ms | 20ms | 40ms | 10ms | 20ms | 40ms | |
| Eye movement | .579 | .661 | .809 | .616 | .785 | .848 | .702 | .845 | .930 |
| Touchscreen | .583 | .715 | .915 | .608 | .859 | .974 | .699 | .865 | .979 |
For latency, there were main effects of response modality F(1, 5) = 63.91, MSE = 1245003, stimulus duration F(2, 10) = 4.39, MSE = 12329, and configuration of response areas F(2, 10) = 41.36, MSE = 93233. None of the interactions were significant.
For accuracy, there were significant main effects of stimulus duration F(2, 10) = 102.89, MSE = 1.38, side of correct stimulus F(1, 5) = 14.15, MSE = 0.122646, and configuration of response areas F(2, 10) = 31.56, MSE = 0.295. There were significant interactions between response modality and stimulus duration F(2, 10) = 53.40, MSE = 0.043: the accuracy for the touchscreen condition has more heavily affected by the stimulus duration than the accuracy for eye movements. The other significant interaction was between stimulus duration and configuration of the response areas F(4, 20) = 7.48, MSE = 0.020, which does not have a straightforward interpretation.
Diffusion model fits
The empirical data can be easily summarized. In both experiments there is an effect of stimulus duration (latency and accuracy improve as a function of stimulus duration) and eye movement responses are faster (but not necessarily more accurate) than touchscreen and key press responses. The configuration of the response targets, on the other hand, had effects across all response procedures and all stimulus presentation times.
In order to explore how the diffusion model accounts for the data from these two experiments, we fit the model to the data using minimal assumptions about the loci of the empirical effects (i.e., which parameters should be affected by which manipulation).
The stimulus duration naturally maps into the drift rate, and hence we assumed a different drift rate for each stimulus duration. All other parameters were fixed within a response modality condition (for Experiment 1), and within a response modality and configuration of response areas (for Experiment 2). Note that we refer to these assumptions as minimal because based on the previous decade of evidence accumulation modeling, there is definite evidence for the mapping between evidence quality and drift rate.
We used the fitting procedures described by Ratcliff and Tuerlinckx (2002); we fitted the .1, .3, .5, .7 and .9 quantiles for correct and for error RTs for each subject. In Experiment 1 there were 18 conditions: three stimulus durations × three response modalities × two locations of correct alternative. In Experiment 2 there were 36 conditions: three stimulus durations × two response modalities × three configurations of response areas × two locations of correct alternative. For each condition, the quantile response times and the diffusion model were used to generate the predicted cumulative probability of a response by that quantile response time. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. These proportions are the expected values to be used in the Chi-squared calculation, while the observed values are the proportions of responses between the quantiles (i.e., the proportions between 0, 0.1, 0.3, 0.5, 0.7, 0.9, and 1.0, which are 0.1, 0.2, 0.2, 0.2, 0.2, and 0.1) multiplied by the number of observations. Summing over (Observed-Expected)2 / Expected for all conditions gives a single chi-square value to be minimized. When there were too few observations (e.g., less than 6) for the extreme low error conditions for some of the subjects to form quantiles, a single chi-square value based on the response proportion alone was added to the overall chi-square value.
In order to display the fits in Figures 3 and 4, we computed the average over subjects for the quantile RTs and the response proportions for the data and, for the model, we generated predictions from the parameter values averaged over subjects (also displayed in Table 3.) The ×’s are the data points and the ◦’s and the lines are the functions predicted from the best fitting average parameter values from the diffusion model.
Table 3.
Parameters of the Diffusion Model
| Condition | a | Ter | η | sz | p0 | st | z | v10 | v20 | v40 | vc* | χ2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Experiment 1 | ||||||||||||
| eye | 0.071 | 0.254 | 0.258 | 0.058 | .010 | 0.065 | 0.038 | 0.189 | 0.428 | 0.641 | 0.038 | 120 |
| touch | 0.067 | 0.386 | 0.211 | 0.054 | .003 | 0.147 | 0.031 | 0.147 | 0.412 | 0.755 | −0.012 | 108 |
| key | 0.085 | 0.327 | 0.237 | 0.069 | .005 | 0.110 | 0.040 | 0.108 | 0.469 | 0.761 | −0.009 | 124 |
| Experiment 2 | ||||||||||||
| eye fix | 0.061 | 0.251 | 0.180 | 0.049 | .001 | 0.047 | 0.032 | 0.217 | 0.437 | 0.712 | 0.009 | 99 |
| eye 0 | 0.074 | 0.278 | 0.187 | 0.061 | .036 | 0.115 | 0.038 | 0.022 | 0.139 | 0.343 | −0.037 | 113 |
| eye 500 | 0.061 | 0.250 | 0.232 | 0.052 | .001 | 0.046 | 0.030 | 0.143 | 0.370 | 0.511 | −0.053 | 91 |
| touch fix | 0.072 | 0.391 | 0.309 | 0.047 | .001 | 0.115 | 0.034 | 0.240 | 0.495 | 1.114 | 0.011 | 64 |
| touch 0 | 0.074 | 0.442 | 0.345 | 0.062 | .001 | 0.106 | 0.039 | 0.083 | 0.262 | 0.578 | 0.050 | 74 |
| touch 500 | 0.071 | 0.412 | 0.285 | 0.058 | .002 | 0.103 | 0.035 | 0.085 | 0.447 | 0.794 | −0.032 | 62 |
The accumulation of evidence can have some biases (i.e., all drifts can be lower or higher by a constant), this is represented in the model by the parameter vc; In all behavioral studies there is a proportion of responses that can be considered contaminants (e.g., the subject pressing a key without seeing the stimulus, this is represented in the mode by the parameter p0)
Quality of the Fits
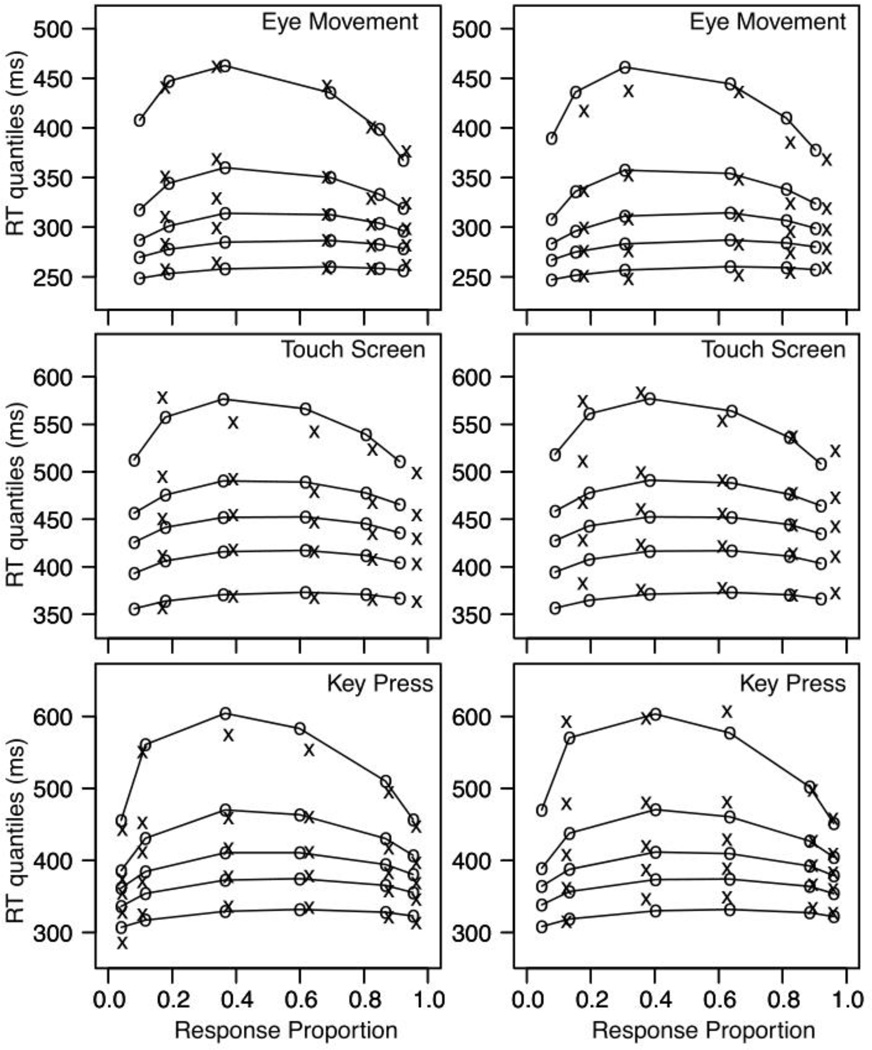
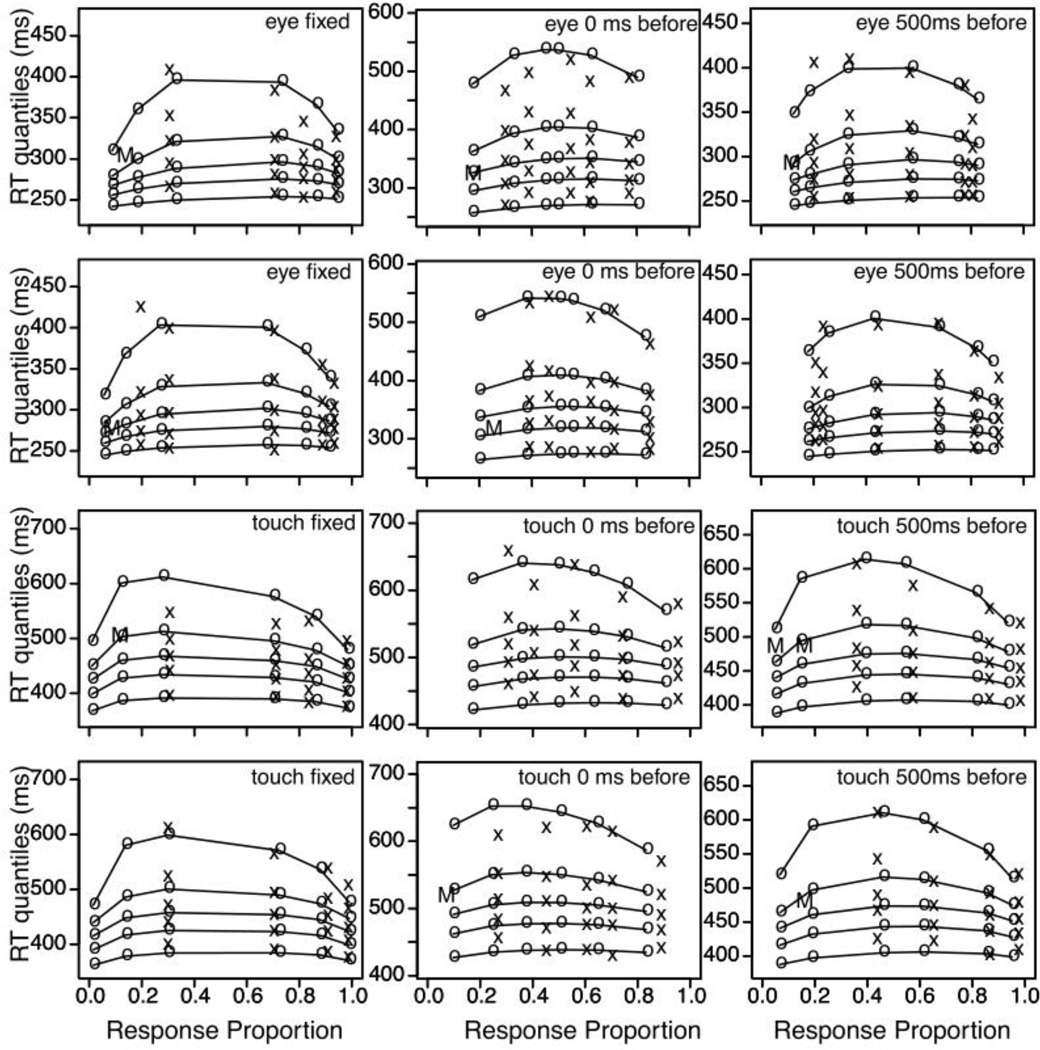
Figures 3 and 4 show the data and fits from Experiments 1 and 2. Each plot is a quantile probability function, which allows us to display the quality of the fit of the model to the latency and accuracy data simultaneously. For each plot, the 0.1, 0.3, 0.5 (median), 0.7, and 0.9 quantiles of the RT distribution for each of the experimental conditions are plotted as a function of response proportion, hence the columns of points within each plot. The columns of ×’s and ◦’s are the empirical and the predicted responses to the different levels of stimulus presentation (see the figure caption for further explanation).
Figure 3.
The different panels show the data and model fits for Experiment 1. The left hand columns show the responses for the alternative to the left for the three response modalities, and the right hand column shows the responses for the alternative to right. Within each panel, the columns of x’s and o’s are the empirical and the predicted responses to the different levels of stimulus presentation. Note that if there are too few responses in a condition to estimate the RT distributions we only display the median for the empirical values; an “M” is placed at the median when all subjects had at least one response, no symbol is showed when one or more subjects had no responses. There are six columns of data points within a panel (e.g., left side key press) because for each response there are six possible stimuli: (from left to right, i.e., from lower response proportion to higher response proportion: error responses for 40ms 20ms and 10ms stimulus duration, and correct responses for 10ms, 20ms, and 40ms stimulus duration.
Figure 4.
The different panels show the data and model fits for Experiment 2 for the different response modalities (top two rows for eye movements: within these pair of rows one for responses to the left of the stimulus, the other for responses to the right); bottom two rows for touchscreen), and for the three different conditions for the display of the response configuration (left columns for fixed location, middle column for random location shown at the same time as the stimulus, and right column for random location shown 500 ms before the stimulus presentation).
As can be appreciated from visual inspection of the figures, the quality of the fits is very good. A more formal assessment of the quality of the fits is shown in Table 4 along with the parameter values. For the fits, the number of degrees of freedom are calculated as follows: for a total of k experimental conditions and a model with m parameters, the degrees of freedom, df, are k(121) − m, where 12 is the number of bins between and outside the RT quantiles for correct and error responses for a single condition (minus 1 because the total probability mass must be 1 which reduces the number of degrees of freedom by 1). In bothe xperiments, there were 3 stimulus durations × 2 locations for the correct alternative (left vs right), for a total of 6 conditions for each response modality; there are 11 free parameters in the model, so df = 6 × 11 − 11 = 55, and the critical value of χ2(df = 55) is 77.38. The average (mean across subject) chi-square values for the fits range from below the critical value up to about 1.5 times the critical value. Note that the property that as the number of observations increases, the power of the test increases, so even the smallest deviation will lead to a significant χ2 (see Ratcliff, Thapar, Gomez & McKoon, 2004 for an explanation); the χ2 values from the two experiments in this article, are well within the range of other diffusion model applications.
Table 4.
F values from Analysis of Variablesnce for Model Parameters
| Exp. | Factor | a | Ter | η | sz | p0 | st | z | vc | Signif. F |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Response modality | 13.46* | 67.11* | 0.35 | 9.03* | 1.47 | 15.97* | 8.89* | 5.27* | 3.49 |
| 2 | Response modality | 1.16 | 169.40* | 7.83* | 0.09 | 1.13 | 6.91* | 0.53 | 2.28 | 6.61 |
| 2 | Display | 3.68 | 16.19* | 0.14 | 2.99 | 1.14 | 2.37 | 2.52 | 0.76 | 4.10 |
| 2 | Interaction | 3.32 | 1.82 | 0.58 | 0.26 | 1.19 | 6.02* | 0.42 | 1.15 | 4.10 |
Degrees of freedom and critical values: F(2, 20) = 3.49, F(2, 10) = 4.10, F(1, 5) = 6.61.
For drift rates:
Experiment 1: presentation duration (10, 20, or 40 ms), F(2, 20) = 135.82*, response type (eye movement, touch screen, or key press) F(2, 20) = 0.16, interaction F(4, 40) = 4.92*.
Experiment 2: presentation duration (10, 20, or 40 ms), F(2, 10) = 48.73*, response type (eye movement, or touch screen) F(1, 5) = 6.47, display (fixed, targets presented 0 ms before the stimulus, targets presented 500 ms before the stimulus) F(2, 10) = 21.12*.(One interaction is significant, response modality × presentation duration, F(2, 10) = 14.71).
Analysis of the behavior of the parameters of the model
The best-fitting parameters for each condition and for each subject were submitted to ANOVA’s. For all parameters except for drift rate the factors in the ANOVA were the same as in the empirical ANOVA’s except for stimulus duration. For the drift rate, the ANOVA included stimulus duration as a factor. Table 4 shows the F values along with the critical values.
Drift rates
As expected, the effect of presentation duration was significant in both experiments, with larger drift rates for longer presentations. The response modality, however, did not yield significant differences in drift rate in either experiment, although there were significant interactions in both experiments for task and duration; this might have been because of the ballistic nature of saccades, while on the other hand, during the pointing behavior the motion is not ballistic. The across trial variability in the drift rate (η) was significantly affected by the response modality only in Experiment 2. In Experiment 2, the display of the response areas did affect the drift rate. When the response areas were fixed drift rates were the highest, followed by random locations uncovered 500 ms before the stimulus, while providing the response locations at the same time as the stimulus yielded the lowest drift rates.
Encoding a response execution time (Ter)
The nondecision components of the RT were significantly affected not only in their mean duration (Ter parameter), but also in their variability (the range st) by the response modality. The display of the response options only affected the Ter parameter, but not its range.
Decision thresholds
There were some biases in the responses that tended to favor the right-side alternative, especially in Experiment 1. These are reflected in significant differences in starting point z and its variability (sz). In terms of the boundary separation (a), there were significant effects of response modality. In Experiment 1, participants set their decision criteria wider in the key press condition than in the other two modalities; while in Experiment 2, they set their decision criteria wider in the touchscreen than the eye movement condition.
Discussion
We explored the effect of manipulations of response modality. In addition, we also manipulated stimulus duration to provide a wide range of accuracy and RT values. Presentation duration had a facilitatory effect performance as measured by latency and accuracy. Furthermore, eye movement responses produced the shortest latencies in Experiment 1, and although key press responses were not as fast as eye movements, they were faster than pointing (touchscreen) responses. It is worth noting that the fits for the touchscreen conditions are not as precise as for the other modalities or for other implementations of the diffusion model. Keep in mind that the response execution in this condition might be significantly noisier (indeed the st parameter for this condition is three times the size than for eye movements).
Two important conclusions emerge from fitting the diffusion model to the data from the present experiments. First, the high quality of the fits provides strong support for the assumption that the decisional mechanism in two-choice tasks should be the same regardless of the response modality (see Gomez, Ratcliff & Perea, 2007 for a similar argument), and such mechanism seems to be very well described by the diffusion model.
Second, the parameter values across the different tasks behaved in predicted ways. Notably, the drift rates are consistently affected by the duration of the presentation of the stimulus, but not by the response modality (a main effect only for Experiment 1); the response modality affects the Ter parameter and its variability st. There are interesting interactions in the model’s parameters: namely, the drift rates seem differentially affected by stimulus duration in the pointing and the eye movement conditions. We hypothesize that it might be related to the ballistic nature of eye movements, which cannot be modified once they have been initiated. On the other hand, pointing is not by definition a ballistic motion. The overall pattern of results is similar to the one reported by Ho, et al (2009), and Liu and Pleskac (2011) in their fits to random dot moving tasks; both of these studies also found that the activation of the right insula is consistent with an accumulation of evidence process independent of response modality.
In Experiment 2, the manipulation involving the location of the response areas did interact with the extraction of perceptual information (i.e., the drift rate). In particular, when participants needed to detect the location of the response areas at the same time as they were being exposed to the stimulus, this interfered with the accumulation of evidence process and yielded lower drift rates.
From a theoretical standpoint, the findings from Experiment 1 are of particular importance. The independence between the drift rate and the Ter parameter is an important assumption that was validated by our findings: the drift rates and the Ter parameters can be differentially affected by distinct experiment manipulations.
The three most important methodologies in cognitive neuroscience (single cell recording of primate subjects, fMRI studies and behavioral experiments with human participants) point to accumulation of evidence as a mechanism for perceptual decision making. The present article suggests that the differences in the response requirements affect only the response execution stage, as predicted, and do not fundamentally change the quality of the extraction of information in the perceptual decision making process. Interestingly, the response execution and encoding times represent a large proportion of the total RT, while the evidence accumulation process can happen well within 100 ms. This is consistent with the single cell recording literature (see for example Figure 3 in Hanes & Schall, 1996), and highlights the impact of the ancillary processes in the latency measurements used in cognitive psychology.
Acknowledgments
This aricle was supported by grant NIA R01-AG17083 and AFOSR grant FA9550-11-1-0130 to Roger Ratcliff.
Footnotes
The resistive touchscreen technology consists of a glass panel with a resistive coating and a coversheet with conductive coating. When the screen is touched the flexscreen makes contact with the glass’ coating (we used an Elo-Touchsystems screen, model ET1725C-4CWE-3-G)
At 57 cm of distance, 1cm corresponds to 1 visual degree.
References
- Brown S, Heathcote A. A ballistic model of choice response time. Psychological Review. 2005;112:117–128. doi: 10.1037/0033-295X.112.1.117. [DOI] [PubMed] [Google Scholar]
- Busemeyer JR, Townsend JT. Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment. Psychological Review. 1993;100:432–459. doi: 10.1037/0033-295x.100.3.432. [DOI] [PubMed] [Google Scholar]
- Diederich A, Busemeyer J. Simple matrix methods for analyzing diffusion models of choice probability, choice response time, and simple response time. Journal of Mathematical Psychology. 2003;47(3):304–322. [Google Scholar]
- Gold J, Shadlen M. Neural computations that underlie decisions about sensory stimuli. Trends in Cognitive Sciences. 2001;5(1):10–16. doi: 10.1016/s1364-6613(00)01567-9. [DOI] [PubMed] [Google Scholar]
- Gomez P, Ratcliff R, Perea M. Diffusion model of the go/no-go task. Journal of Experimental Psychology: General. 2007;136:389–413. doi: 10.1037/0096-3445.136.3.389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanes D, Schall J. Neural control of voluntary movement initiation. Science. 1996;274(5286):5427. doi: 10.1126/science.274.5286.427. [DOI] [PubMed] [Google Scholar]
- Ho T, Brown S, Serences J. Domain general mechanisms of perceptual decision making in human cortex. The Journal of Neuroscience. 2009;29(27):8675–8687. doi: 10.1523/JNEUROSCI.5984-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laming DRJ. Information theory of choice-reaction times. London: Academic Press; 1968. [Google Scholar]
- Link SW. The relative judgement theory of two choice response time. Journal of Mathematical Psychology. 1975;12:114–135. [Google Scholar]
- Link SW, Heath RA. A sequential theory of psychological discrimination. Psychometrika. 1975;40:77–105. [Google Scholar]
- Liu T, Pleskac T. Neural correlates of evidence accumulation in a perceptual decision task. Journal of Neurophysiology. 2011;106:2383–2398. doi: 10.1152/jn.00413.2011. [DOI] [PubMed] [Google Scholar]
- Palmer J, Huk A, Shadlen M. The effect of stimulus strength on the speed and accuracy of a perceptual decision. Journal of Vision. 2005;5:376–404. doi: 10.1167/5.5.1. [DOI] [PubMed] [Google Scholar]
- Purcell B, Heitz R, Cohen J, Schall J, Logan G, Palmeri T. Neurally constrained modeling of perceptual decision making. Psychological Review. 2010;117:1113–1143. doi: 10.1037/a0020311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Ratcliff R. A theory of order relations in perceptual matching. Psychological Review. 1981;88:552–572. [Google Scholar]
- Ratcliff R. Continuous vs. discrete information processing: Modeling accumulation of partial information. Psychological Review. 1988;95:238–255. doi: 10.1037/0033-295x.95.2.238. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Hasegawa Y, Hasegawa R, Childers R, Smith P, Segraves M. Inhibition in superior colliculus neurons in a brightness discrimination task? Neural Computation. 2011;23:1–31. doi: 10.1162/NECO_a_00135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: Theory and data for two-choice decision tasks. Neural computation. 2008;20:873–922. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for decisions between two choices. Psychological Science. 1998;9:347–356. [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychological Review. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, Gomez P, McKoon G. A diffusion model analysis of the effects of aging in the lexical-decision task. Psychology and Aging. 2004;19(2):278–289. doi: 10.1037/0882-7974.19.2.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating parameters of the diffusion model: Approaching to dealing with contaminant reaction and parameter variability. Psychonomic Bulletin and Review. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. Comparing connectionist and diffusion models of reaction time. Psychological Review. 1999;106:261–300. doi: 10.1037/0033-295x.106.2.261. [DOI] [PubMed] [Google Scholar]
- Roe R, Busemeyer J, Townsend J. Multialternative decision field theory: A dynamic connectionst model of decision making. Psychological Review. 2001;108:370. doi: 10.1037/0033-295x.108.2.370. [DOI] [PubMed] [Google Scholar]
- Roitman JD, Shadlen MN. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. Journal of Neuroscience. 2002;22:9475–9489. doi: 10.1523/JNEUROSCI.22-21-09475.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone M. Models for choice-reation time. Psychometrika. 1960;25:251–260. [Google Scholar]
- Usher M, McClelland JL. On the time course of perceptual choice: The leaky competing accumulator model. Psychological Review. 2001;108:550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- Voss A, Rothermund K, Voss J. Interpreting the parameters of the diffusion model: An empirical validation. Memory & Cognition. 2004;32:206–220. doi: 10.3758/bf03196893. [DOI] [PubMed] [Google Scholar]
- Wagenmakers EJ. Methodological and empirical developments for the Ratcliff diffusion model of response times and accuracy. European Journal of Cognitive Psychology. 2009;21:641–671. [Google Scholar]