Offspring of Primiparous Mothers Do Not Experience Greater Mortality or Poorer Growth: Revisiting the Conventional Wisdom with Archival Records of Rhesus Macaques

Abstract

Female mammals often begin to reproduce before achieving somatic maturity and therefore face tradeoffs between allocating energy to reproduction or their own continued development. Constraints on primiparous females are associated with greater reproductive failure, and first-born infants often have slower growth and greater mortality and morbidity than infants born to multiparous females. Effects of early life investment may persist even after weaning when juveniles are no longer dependent on maternal care and mother’s milk. We investigated the long-term consequences of birth order in a large sample of rhesus macaques, Macaca mulatta, assigned to the outdoor breeding colony at the California National Primate Research Center (N=2724). A joint model for growth and mortality over the first three years of life allowed us to explicitly connect growth rates to survival. As expected, males are born heavier and grow faster relative to females. However, contrary to expectations, later-born males face substantially lower survival probability during their first three years, whereas first-born males survive at greater rates similar to both first-born and later-born females. Primiparous mothers are less likely to conceive during the subsequent breeding season, suggesting that their reproductive costs are greater than those of multiparous mothers. We speculate that compensatory tactics, both behavioral and physiological, of first-born offspring and their mothers, as well as the novel ecology of the captive environment, underlie these findings. The results presented here provide new insights into how maternal and infant life history tradeoffs may influence developmental trajectories even after the period of maternal dependence.

INTRODUCTION

Among mammals, females often begin their reproductive careers before attaining adult stature and consequently face tradeoffs between allocating energy to reproduction or their own continued development [Stearns, 1989]. Related to this, primiparous females often have fewer bodily resources available for mobilization during pregnancy and lactation [Dufour and Sauther, 2002; Wathes et al., 2007; Hinde and Milligan, 2011]. Perhaps as a consequence of these constraints, offspring of primiparous mothers have been shown to experience poorer growth [Small, 1981; Setchell et al., 2001] and greater mortality [Alouatta palliate: Glander, 1980; Macaca radiata: Silk, 1988; Elephas maximus, Mar et al. 2012], particularly within the first year of life [Cercopithecus aethiops: Fairbanks and McGuire, 1985; Papio anubis: Smuts and Nicolson, 1989]. From the perspective of life history evolution, limiting the costs of the current reproductive effort in favor of future reproduction as a function of residual reproductive value may improve lifetime reproductive success [Williams, 1966; Magnus et al., 1985; Seidman et al., 1988; Fairbanks and McGuire, 1995; Ong et al., 2002; Tardif et al., 2013].

Additionally, the relative costs, risks, and potential reproductive value of sons and daughters may differ, with implications for allocation of maternal reproductive effort. Greater infant mortality is experienced by males [Kohler et al., 2006], especially first born sons [Bercovitch et al., 1998; Hinde, 2007]. Males are also more likely to die once they are no longer dependent on maternal support, and appear to be more sensitive than females to fluctuations in resource availability [Clutton-Brock et al., 1981; Meikle et al., 1984; Clutton-Brock et al., 1985]. As such, constrained maternal investment is expected to have disproportionately greater consequences for male survival [Rickard et al., 2007]. The reproductive potential of males in polygynous groups is particularly variable, with a limited number of individuals gaining the majority of the matings [Wade, 1979; Le Boeuf and Reiter, 1988; Arnold and Duvall, 1994; Dubuc et al., 2014]. Balanced against the offspring’s reproductive potential and vulnerability, the costs of rearing a successful son may be proportionally greater than those of rearing a successful daughter [Trivers and Willard, 1973; Clark, 1978; Smith, 1980; Silk, 1983; Emlen et al., 1986; Leimar, 1996; Rickard et al., 2007; Silk and Brown, 2008; Shibata and Kawamichi, 2009].

Despite predictions, sex-biases in behavioral care have been somewhat equivocal among primates. Behavioral biases favoring sons (such as physical contact, carrying, nipple access, or grooming) have been documented in a diversity of primates [Ateles paniscus: Symington, 1987; Papio anubis: Bentley-Condit, 2003; Macaca silenus: Krishna et al., 2008; Trachypithecus phayrei crepusculus: Borries et al., 2014], as have biases in favor of daughters [Macaca mulatta: Mitchell, 1968; Cercopithecus aethiops sabaeus: Fairbanks and McGuire, 1985; Macaca fuscata: Nakamichi, 1989; Macaca fascicularis: Nakamichi et al., 1990; Cercopithecus mitis stuhlmanni: Förster and Cords, 2002; Papio hamadryas: Hernández-Lloreda and Colmenares, 2005]. Sometimes no biases in behavioral care are evident [Macaca fuscata: Tanaka, 1989, Schino et al., 1995; Macaca mulatta: Brown and Dixson, 2000]. Integrating maternal parity with infant sex adds to the complexity. In rhesus macaques, primiparous mothers have been shown to “protect” and spend more time in physical and nipple contact with daughters, whereas multiparous mothers demonstrate more protective behaviors towards sons [Holley and Simpson 1981]. In blue monkeys, both multiparous and primiparous mothers begin to block nipple access by daughters earlier than multiparous mothers begin to reject sons [Förster and Cords 2002].

Physiological investment in the form of milk synthesis, although less studied than behavioral care, also varies in relation to maternal parity and infant sex. Primiparous mothers are handicapped in milk synthesis [Homo sapiens: Motil et al., 1997; Oryctolagus cuniculus: Maertens et al., 2006; Macaca mulatta: Hinde 2007; Bos taurus: Wathes et al., 2007; Halichoerus grypus: Lang et al., 2011] in part as a function of mammary gland architecture [reviewed in Hinde et al., 2015]. Among rhesus macaques (Macaca mulatta), mothers of daughters produce more milk with greater concentrations of calcium compared to mothers of sons [Hinde et al. 2013], whereas primiparous mothers of sons produce milk with higher levels of fat, protein, and overall energy density [Hinde, 2007; Hinde, 2009]. However, because mothers of daughters have a greater milk yield than mothers of sons, the available milk energy for sons and daughters is seemingly comparable at peak lactation [Hinde 2009].

Birth timing within the birth season may also be an important feature for maternal tradeoffs and infant growth and survival. First-time mothers who conceive later than those in their birth cohort have more time to grow before incurring the costs of reproduction, and therefore may be better able to sustain pregnancy and lactation later [Silk 1989]. Additionally, by conceiving asynchronously, young females of some taxa may avoid giving birth during the peak birthing season when infants may endure more hazardous social environments and face greater competition for resources and caretakers compared to infants born outside of peak season [Silk, 1989; Clarke et al., 1992; Radespiel and Zimmermann, 2001]. Deviation of birth timing relative to the population mean, however, may also pose risks to infant survival [Macaca mulatta: Drickamer, 1974, Small and Smith 1986; Eulemur rubriventer: Tecot, 2010]. Infants born early in the season may attract risky social attention [Kavanagh, 1983; Shapiro, 1985; Silk, 1989; Clarke et al., 1992], whereas infants born late in the season may have difficulty foraging depending on seasonal food availability [van Schaik and van Noordwijk, 1985].

Although offspring growth and survival are relatively well studied during the period of dependence on the mother, early life input from the mother may continue to influence offspring post-weaning [Oreamnos americanus: Côté and Festa-Bianchet, 2001; Papio cynocephalus: Altmann and Alberts, 2005; Crocuta crocuta: Watts et al., 2009; Pan troglodytes: Stanton et al., 2014]. Body mass, growth, and mortality of juveniles are likely to be importantly interconnected, but are rarely investigated in concert [Guo and Carlin, 2004]. To better understand the long-term consequences of early life experience, we investigated the effects of infant sex and maternal primiparity, accounting for birth timing, on growth and survival up to three years of age in a large archival sample of rhesus macaques. We hypothesized that juvenile growth and survival would be sensitive to the quality of maternal investment received during infancy, using birth order as a proxy for maternal capacity and the relative costs of rearing infants. We specifically predicted that the impaired investment of primiparous mothers would negatively influence the growth of both sexes, with lower survival rates among males.

METHODS

Sample

We analyzed archival records from the California National Primate Research Center animal colony from 1978–2012. The animals were housed in large social groups in outdoor 0.2 ha enclosures, provisioned twice daily with commercial monkey chow, semi-weekly with fruits and vegetables, and water ad libitum. We restricted our sample to animals of known age and birth order that were born and reared in the conventional outdoor breeding colony by their biological mothers. Additionally, our sample excluded animals assigned to experimental studies that could have plausibly influenced body mass or survival. Social groups were composed of close kin, distant kin, and unrelated individuals of all age and sex classes approximating wild-living rhesus macaques. Animals were weighed at 3–5 month intervals as part of routine colony health exams (mean ± SD number of weights = 7.8 ± 5.8). We used 21212 growth records from 2,724 individuals. We selected N=1256 infants of primiparous mothers on their first parity and N=1468 infants of multiparous mothers, adult females of prime reproductive condition on their 4^th, 5^th, or 6^th parity. A total of 1726 mothers are represented in the sample, of which 917 (53%) produced infants in both primiparous and multiparous conditions. This research adheres to the American Society of Primatologists principles for the ethical treatment of primates.

Data Analysis

Joint Model for Growth and Survival

We jointly modeled juvenile growth and survival to assess the potential role of maternal investment on early life physical condition. We considered separate analyses - linear or logistic mixed models for growth, and Weibull or Cox Proportional Hazards for survival - but this strategy may not fully capture the interrelated nature of growth and survival [Guo and Carlin, 2004]. Indeed, Hackman et al. found mass and growth to be strongly influential in infant survival [Hackman, 1983].

We used a Bayesian method based on Guo and Carlin [2004] in which growth and survival models are joined via shared juvenile- and mother-specific random effects. The dependent variable in the growth model is Y_jd(t), the mass at time t of juvenile j from mother d. Assuming growth in these macaques is linear to age three, the model takes the following form:

$$Y_{jd}(t)={\mathrm{\beta }}_0+{\mathrm{\beta }}_1*{\mathit{\text{sex}}}_{\mathrm{j}}+{\mathrm{\beta }}_2*{\mathit{\text{parity}}}_{\mathrm{j}}+{\mathrm{\beta }}_3*{\mathit{\text{sex}}}_{\mathrm{j}}*{\mathit{\text{parity}}}_{\mathrm{j}}+({\mathrm{\gamma }}_0+{\mathrm{\gamma }}_1*{\mathit{\text{sex}}}_{\mathrm{j}}+{\mathrm{\gamma }}_2*{\mathit{\text{parity}}}_{\mathrm{j}}+{\mathrm{\gamma }}_3*{\mathit{\text{sex}}}_{\mathrm{j}}*{\mathit{\text{parity}}}_{\mathrm{j}})*\mathrm{t}+\mathrm{\delta }*{\mathit{\text{annual sine}}}_{\mathrm{j}}+\mathrm{\lambda }*{\mathit{\text{annual cosine}}}_{\mathrm{j}}+{\mathrm{U}}_{\mathrm{j},1}+{\mathrm{V}}_{\mathrm{d},1}+({\mathrm{U}}_{\mathrm{j},2}+{\mathrm{V}}_{\mathrm{d},2})*\mathrm{t}+{\mathrm{E}}_{\mathrm{j}\mathrm{d}}(\mathrm{t}).$$

Sex is an indicator variable for males, and parity is an indicator for first-born offspring (compared to later-born offspring). The coefficients β and γ describe estimated birth mass and growth rates, respectively, of each of the four sex-by-parity classes (with later-born females as the reference class). Annual sine, annual cosine and the coefficients δ and λ describe annual cyclical variation in estimated birth mass due to the birth timing of juvenile j. Birth mass estimates reported in the text assume a birth date of April first – near the peak of the birth season. U_j,1 and U_j,2 are juvenile-specific random effects for birth mass and growth rate, respectively capturing how heavy juvenile j is at birth, and how quickly juvenile j grows, compared to typical members of his or her sex-by-parity class. V_d,1 and V_d,2 are analogous mother-specific effects capturing how heavy juveniles of mother d are at birth, and how quickly juveniles of mother d grow, compared to typical members of their sex-by-parity classes. (U_j,1, U_j,2) and (V_d,1, V_d,2) each have mean-zero bivariate Gaussian distributions and E_jd(t) is a mean-zero Gaussian error term. We also investigated a three-parameter logistic growth model [e.g.,Aggrey 2009] but the fit of the linear model was better, based on a comparison of residual plots.

Survival is modeled as the log of the hazard H_jd as follows:

$$\mathit{\text{log}}{H}_{jd}={\mathrm{\theta }}_0+{\mathrm{\theta }}_1*{\mathit{\text{sex}}}_{\mathrm{j}}+{\mathrm{\theta }}_2*{\mathit{\text{parity}}}_{\mathrm{j}}+{\mathrm{\theta }}_3*{\mathit{\text{sex}}}_{\mathrm{j}}*{\mathit{\text{parity}}}_{\mathrm{j}}+\mathrm{\tau }*{\mathit{\text{annual sine}}}_{\mathrm{j}}+\mathrm{\varphi }*{\mathit{\text{annual cosine}}}_{\mathrm{j}}+{\mathrm{r}}_1*{\mathrm{U}}_{\mathrm{j},1}+{\mathrm{r}}_2*{\mathrm{U}}_{\mathrm{j},2}+{\mathrm{s}}_1*{\mathrm{V}}_{\mathrm{d},1}+{\mathrm{s}}_2*{\mathrm{V}}_{\mathrm{d},2}.$$

Here, the coefficients θ describe survival to age three of the sex-by-parity classes; τ and ϕ describe annual cyclical variation in survival due to the birth timing of juvenile j. The random effects U and V for estimated birth mass and growth rate appear in both the growth and survival models; in the latter they are scaled by parameters r and s. A juvenile with an estimated birth mass typical for its sex-by-parity class - and therefore with U₁ close to zero - would, for example, have a relatively small contribution r₁U₁ to its hazard. On the other hand, if r₁ < 0, a juvenile with atypically low estimated birth mass (U₁ < 0) would have a relatively large and positive contribution r₁U₁ to its hazard and consequently lower survival. Contributions from the remaining juvenile- and mother-specific effects can be interpreted similarly.

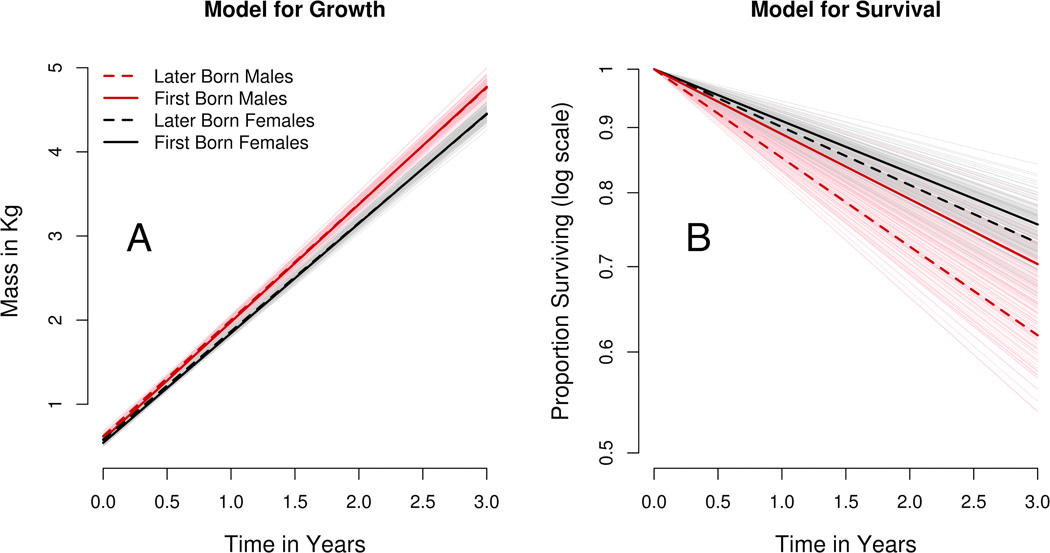
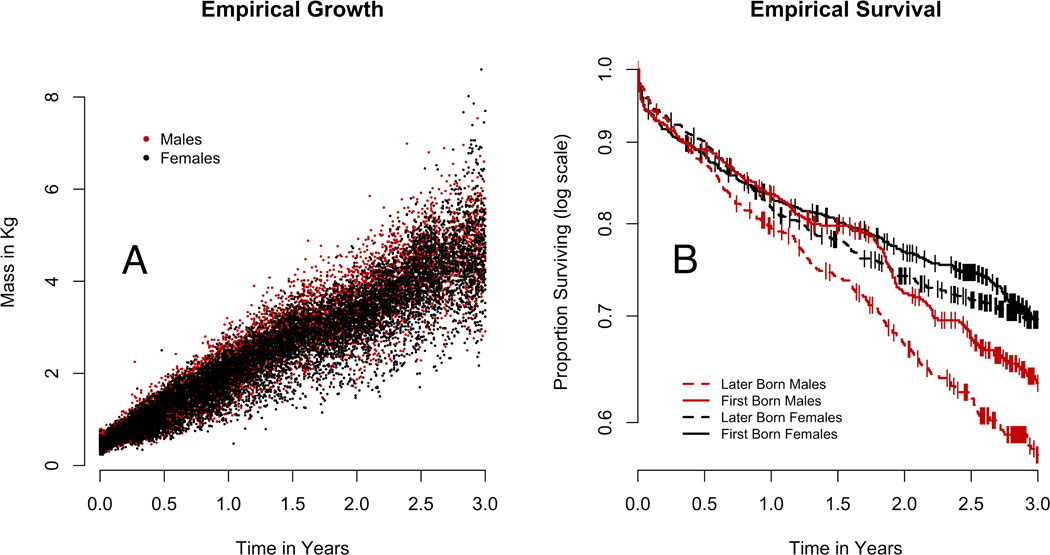
A Weibull distribution is a common choice for H_jd, but separate identification of the Weibull shape parameter and the intercept θ₀ is unfeasible for the macaque data, as it was in the case study of Guo and Carlin [2004]. As in Guo and Carlin, we fixed the Weibull shape parameter at the value one; H_jd then has an exponential distribution, for which the probability of survival beyond t years is exp(−H_jd * t) and the natural logarithm of the survivor function is −H_jd * t. The empirical survival curves for sons shown in Figure 1 are roughly linear on the log scale, suggesting that an exponential model is adequate for male lifetimes. Female survival departs from this trend, perhaps calling for a model with sex-specific hazard distributions. Although the present model limits our choices for lifetime distribution, on balance the gain in information produced by joint modeling appears to outweigh the loss of flexibility.

Figure 1.

We adapted the preferred model in Guo & Carlin [2004] (WinBUGS model code available at http://www.biostat.umn.edu/~brad/software/ModelXInew.bug) to fit the joint model to the macaque data, making modifications as necessary for implementation in JAGS (http://mcmc-jags.sourceforge.net/), a general-purpose Gibbs Sampler linked to the statistical computing language R (http://www.r-project.org/) via the library rjags (http://sourceforge.net/projects/mcmc-jags/files/rjags/). We used diffuse, mean-zero Gaussian priors for all model coefficients, inverse-Wishart priors with 23 degrees of freedom for all variance-covariance matrices, and an inverse-gamma (0.1, 0.1) prior for the error variance of the growth model.

Model estimates are based on a total of 2000 posterior realizations generated by two independent Gibbs Sampler chains. We burned-in 50000 iterations for each chain, and thinned the next 100000 iterations at a rate of 100 to obtain the posterior realizations. Trace plots of model parameters suggested that the two chains had converged on the same posterior region and that mixing was adequate. Model estimates reported in the text are posterior means and 95% credibility intervals obtained by post-processing Gibbs Sampler realizations. For example, the expected birth mass of a later-born son is estimated as β₀ + β₁, along with annual sine and cosine terms for his birthdate.

Mothers’ Conceptions in the Subsequent Breeding Season

We investigated the timing of mothers' conceptions subsequent to the births represented in the growth and survival dataset. From CNPRC archives, we extracted whether or not mothers remained in the breeding colony and were pregnant during the breeding season following the births of N=2509/2724 (92%) of the offspring in our sample. For the remaining 215 births, no information about the mother's pregnancy during the subsequent or any breeding season was available. Our interest, prompted by a reviewer's feedback, lies in whether or not subsequent pregnancies were delayed in primiparous mothers compared to multiparous mothers.

We estimated the odds that primiparous mothers failed to become pregnant, relative to the odds for multiparous mothers, during the breeding season following each birth in our sample. Whereas the binary variable subsequent pregnancy, indicating the mother's pregnancy status in the next breeding season, is unknown for 215 births, offspring sex and parity are known for all of the N=2724 births in our sample. The 2 × 2 × 2 table of sex by parity by subsequent pregnancy therefore has a monotone missing pattern (Little and Rubin, 2002; section 1.2). We assume here that missingness is independent of the variable subsequent pregnancy, and is therefore ignorable (Little and Rubin, 2002; section 6.2). Ignorable and monotone missingness together imply that odds ratios calculated from complete cases are unbiased for inference (Little and Rubin, 2002; section 13.2.2).

RESULTS

Birth Mass

The estimated birth mass differs modestly across the sex-by-parity classes (Table 2). The estimated birth mass of later-born males is 0.62 kg (with 95% posterior credibility interval [0.58, 0.66]), whereas that of first-born males is 0.58 kg [0.54, 0.62]. The overlap between intervals suggests that primiparity is not a strong determinant of male estimated birth mass. The estimated birth mass of later-born females is 0.58 [0.54, 0.61], whereas that of first-born females is 0.54 [0.50, 0.58]. The overlap between intervals indicates that the effect of primiparity on estimated birth mass of females is slight. Male and female intervals overlap to such an extent that estimated birth mass seems not to be strongly differentiated by sex. The effect of birth timing on estimated birth mass is equivocal. Offspring of a given sex-by-parity class born on April first are on average 0.05 kg [-0.06, 0.17] heavier than those born on September first, after most of the year’s births have occurred. The difference is roughly 10% of a typical individual’s estimated birth mass, but the credibility interval suggests that the contrast is weakly supported.

Table 2.

Mean birth mass by sex-parity class

Sex-Parity Class	Posterior Mean (Kg)	95% Credibility Interval
later-born males	0.62	[0.58, 0.66]
First-born males	0.58	[0.54, 0.62]
later-born females	0.58	[0.54, 0.61]
First-born females	0.54	[0.50, 0.58]

Growth Rate

Sex, but not parity, influenced growth rate. The predicted growth rate of later-born males is 1.38 kg/year [1.33, 1.43], with first-born males predicted to grow an average of 1.40 kg/year [1.35, 1.44]. The high degree of overlap between the two groups suggests that parity has little effect on male growth rate. The average growth rate for later-born females is 1.29 kg/year [1.25, 1.33], and for first-born females is 1.30 kg/year [1.26, 1.35]. As with males, there is no discernible effect of primiparity on female growth rate. There is, however, a perceptible difference between male and female growth trajectories, with males growing at a rate approximately 7% faster than their female counterparts regardless of parity class (Fig 2A, Table 1).

Figure 2.

Table 1.

Parameter estimates for the joint growth and survival model

Parameter	Posterior Mean	95% Credibility Interval
Birth Mass
intercept (later-born female)	0.54	(0.47, 0.61)
sex = male	0.04	(0.00, 0.09)
parity = first-born	−0.04	(−0.08, 0.01)
sex × parity	−0.00	(−0.07, 0.07)
annual sine	0.04	(−0.03, 0.10)
annual cosine	−0.03	(−0.08, 0.02)
Growth Rate
baseline (later-born female)	1.29	(1.25, 1.33)
sex = male	0.09	(0.04, 0.14)
parity = first-born	0.01	(−0.04, 0.07)
sex × parity	0.00	(−0.08, 0.07)
Survival
baseline (later-born female)	−2.76	(−3.18, −2.40)
sex = male	0.43	(0.15, 0.70)
parity = first-born	−0.11	(−0.44, 0.18)
sex × parity	−0.20	(−0.62, 0.23)
annual sine	0.50	(0.16, 0.86)
annual cosine	−0.29	(−0.53, −0.03)
Random Effect Coefficients
r1 (Birth Weight: U1)	−3.15	(−3.88, −2.44)
r2 (Growth Rate: U2)	−3.38	(−3.91, −2.89)
s1 (Birth Weight: V1)	−2.77	(−3.52, −2.07)
s2 (Growth Rate: V2)	−3.19	(−3.77, −2.62)

Survival

Both sex and parity influence survival of offspring to age three. The relatively large hazard for later-born sons (0.16 [0.13, 0.20]) is reduced in first-born sons (0.12 [0.09, 0.15]). These hazards imply three-year survival probabilities of 0.62 [0.55, 0.69] for later-born sons, and 0.70 [0.64, 0.76] for first-born sons. An effect of primiparity is not found in daughters: later-born daughters have hazard 0.10 [0.08, 0.13], compared to 0.09 [0.07, 0.11] for first-born daughters. These imply three-year survival probabilities of 0.73 [0.68, 0.78] for later-born daughters, and 0.76 [0.70, 0.81] for first-born daughters. Three-year survival probabilities of first-born sons are comparable to those of daughters (Figure 2B, Table 1).

We find a strong effect of birth timing on hazard. For any sex-by-parity class, the hazard for an offspring born on April 1st is 2.28 [1.25, 4.06] times greater than the hazard for an offspring born on September first. Consequently the ratio of the three-year survival probability for a later-born female born on April first, compared to her counterpart born on September first, is 0.85 [0.77, 0.94]. The analogous ratio for a later-born son is 0.78 [0.67, 0.92]. Thus offspring born during peak birthing season have reduced survival through age three.

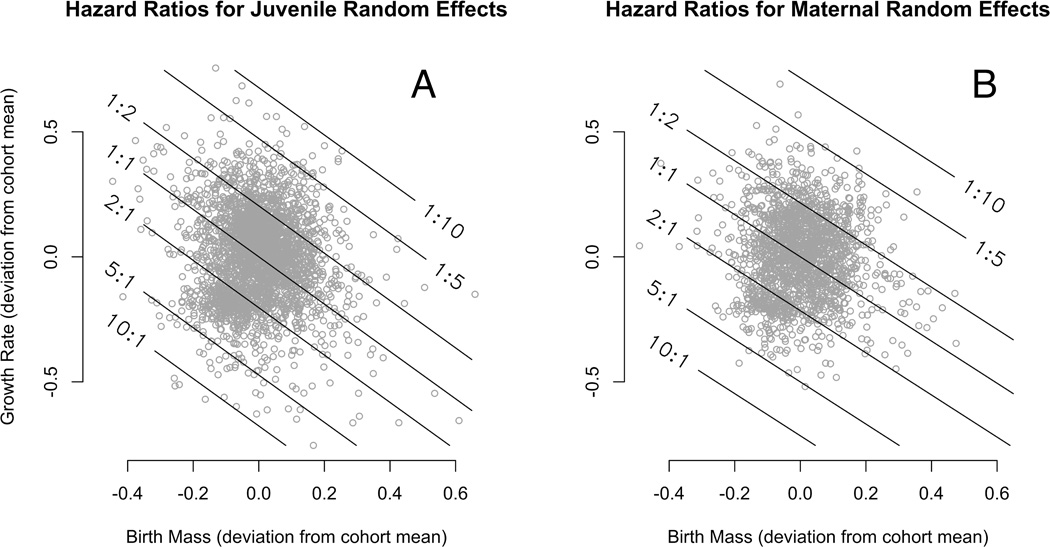
To make the connection between growth and survival more tangible, random effects for estimated birth mass and growth rate were superimposed with hazard ratios (Fig. 3). We find that individuals that are born heavier and/or grow faster than average for their sex-by-parity class have lower hazards. For the heaviest and fastest-growing juveniles, this can mean a five to ten-fold decrease in hazard. On the other hand, individuals with the lowest estimated birth mass and growth rates may have a five to ten-fold increase in hazard. Analogous hazards were found to be associated with mother-specific random effects (figure 3B).

Figure 3.

At the suggestion of a reviewer, we investigated a joint growth and survival model that included additional pairwise interactions: sex by annual sine and cosine; parity by annual sine and cosine; and the three-way interactions sex by parity by annual sine and cosine. The posterior densities of these coefficients (not shown) were all concentrated near the null value zero. Furthermore, estimates derived from the extended model, such as cohort-specific hazards, were very similar to those reported above. This suggests that little additional structure was captured by the interactions.

Mothers’ Conception in the Subsequent Breeding Season

Proportionally fewer females conceived in the breeding season immediately following the birth of a first-born offspring than did so following the birth of a later-born offspring (Table 3). Multiparous births dominate primiparous births in the complete cases (multiparous:primiparous ratios of 758:649 among female births, 602:500 among male births) and we might expect by extrapolation that multiparous births would dominate in the missing cases as well. Instead, multiparous and primiparous births are about equally represented in the missing cases. This apparent over-representation of primiparous births in the missing cases is permitted under the ignorability assumption, which requires only that missingness be independent of subsequent pregnancy.

Table 3.

Number of females who conceived in the following year by sex of offspring for all N=2724 births. Missing column counts births with information for sex and parity, but not subsequent pregnancy.

	Conceptions Following a Male Infant			Conceptions Following a Female Infant
	Yes	No	Missing	Yes	No	Missing
Primiparous	366	134	49	482	167	58
Multiparous	537	65	47	653	105	61

For female births, the odds ratio calculated from complete cases is 167 * 653 / (482 * 105) = 2.15 (with approximate 95% confidence interval 1.64, 2.83). Thus the odds of no pregnancy in the subsequent breeding season are larger by a factor of two for primiparous mothers of female offspring, compared to multiparous mothers of female offspring. For male births, the odds ratio is 3.02 (2.19, 4.19), suggesting an even longer delay for subsequent pregnancies of primiparous mothers of male offspring.

DISCUSSION

The offspring mass, growth, and survival results presented here in relation to maternal parity and infant sex represent both consistency and departure from conventional wisdom and published literature. Although estimated birth masses of males and females did not differ appreciably as they do across many primate taxa [Smith and Leigh, 1998], including rhesus macaques [Bercovitch et al. 2000], males and females do have differential growth trajectories, with divergences widening after weaning. The trajectories we observed are consistent with previous findings of the early development of sexual dimorphism in rhesus macaques [Bercovitch et al., 2000; Hopper et al., 2008], as well as other primates [Mandrillus sphinx: Setchell et al., 2001; Papio cynocephalus: Altmann and Alberts, 2005]. Additionally, maternal primiparity did not predict smaller estimated birth mass. Offspring who were born heavier, or had better growth velocity relative to the cohort mean, had better survival.

Maternal parity in combination with infant sex was predictive of juvenile survival. Using birth order as a proxy for differential capacity for maternal investment, we would expect the impaired physiological investment [Dufour and Sauther, 2002; Hinde and Milligan, 2011], and behavioral care [Fairbanks, 1996; Seay, 1966] associated with primiparity to increase infant mortality in first-born offspring [Bercovitch et al., 1998]. Instead, and counter to our predictions, first-born offspring, regardless of sex, experience mortality commensurate with later-born daughters. Later-born sons experience greater mortality during juvenility when compared to all other groups, a result inconsistent with several other studies [Alouatta palliate: Glander, 1980; Cercopithecus aethiops: Fairbanks and McGuire, 1984; Macaca radiata: Silk, 1988; Papio anubis: Smuts and Nicolson, 1989]. Although the resolution of our data does not include sources of mortality, the main causes of juvenile death in captive macaque populations are typically dehydration, electrolyte imbalance, and/or weight loss, all of which are associated with viral and bacterial diarrheal disease [Dazey and Erwin, 1976; Prongay et al., 2013].

One explanation for these findings is that first-born sons may prioritize growth, reducing behavioral activity budgets during infancy, a biobehavioral organization that may persist after the period of maternal dependence. Natural selection has likely shaped tradeoff adaptations in infants, enabling them to maximize the efficiency of the investment they receive for growth and survival during the period of maternal dependence and beyond [Moore and Haig, 1991; Wells, 2014]. Efficiency-maximizing tactics of infants may include physiological regulation, behavioral phenotype, or feeding patterns [Lummaa, 2003; Langley-Evans, 2006; Hinde and Captanio, 2010; Hinde et al., 2015]. Additionally, primiparous mothers are frequently characterized as being far more restrictive and protective of their new offspring when compared to multiparous mothers [Macaca fuscata: Seay, 1966; Mitchell and Stevens, 1968; Macaca mulatta: Holley and Simpson, 1981; Macaca fuscata: Tanaka, 1997; Macaca nemestrina: Maestripieri, 1998; Cercopithecus mitis stuhlmanni: Förster and Cords, 2002]. As a result, first-born infants may experience fewer opportunities to be behaviorally active, allowing more energy intake to be allocated to growth [Hinde, 2015]. This energy shunting may then explain why we see greater survival of first-born males relative to their later-born counterparts.

Birth timing strongly influenced infant survival. Asynchronous birth (i.e. before or after the birth peak) confers dramatic survival benefits on both first- and later-born offspring relative to their synchronously born peers. The greater mortality of later-born males does not appear to be explained by birth timing effects unique to this cohort, based on null findings for a growth and survival model with additional interactions. Asynchronous birth timing is associated with improved survival among captive macaque populations where mothers who gave birth during the peak of the birth season received greater levels of conspecific aggression [Silk, 1989; Blomquist, 2013]. However, this pattern is inconsistent across taxa [Saimiri oerstedi: Boinski, 1987; Alouatta seniculus: Crockett and Rudran, 1987; Eulemur rubriventer: Tecot 2010]. In the present case, it is possible that the social disadvantages associated with reproductive synchrony in captivity may offset the environmental benefits that synchrony is hypothesized to confer upon free-ranging primate females. This may reflect a shift in the relative cost of intragroup aggression in captivity weighed against other forms of danger found in wild populations. Another important consideration is that birth synchrony in the present study is a colony-level phenomenon, obscuring variation in birth timing at the group-enclosure level. As such, an infant may be born during the peak of the colony-wide birth season while also being born early within its own respective social group. This makes it difficult to disentangle the effects of the colony-wide physical environment, i.e. weather, from those of the social ecology within each enclosure.

The lower survival of later-born sons could also derive from the demographics of macaque mothers at the CNPRC. In natural populations, females in poor condition are less likely to achieve multiparity, and therefore later-born male (as well as female) offspring would tend to be from healthy, robust mothers. Conditions at the CNPRC relax ecological constraints on food and reproductive potential, enabling more females to reach multiparity. Our sample of later-born males contains the sons of mothers in poor condition, along with sons from robust mothers, potentially explaining their poorer survival overall. An alternative explanation for our finding is that the joint modeling strategy may have confirmed survival differences that are not as unusual as they appear. Analyses that treat growth and survival separately do not account for the endogeneity of growth to survival (and vice versa). If larger and heavier animals have better survival prospects - as it seems they do - then even the slightly greater body masses of later-born males, if not properly controlled for, could hamper accurate estimation of their survival rates. The joint growth and survival model we used incorporates this endogeneity explicitly [see Tsiatis et al. 1995; Wulfsohn and Tsiatis 1997; Guo and Carlin 2004 for biomedical applications].

How were primiparous mothers able to rear offspring who had on average similar growth and better survival relative to multiparous mothers in our study? Given that primiparous macaque mothers are constrained in their milk production during early and peak lactation [Hinde et al., 2009; Hinde et al., 2015], primiparous mothers may extend the lactation period, delaying subsequent reproduction. Follow-up analyses indicated that primiparous mothers of both males and females were less likely than multiparous mothers to conceive a detectable pregnancy during the subsequent breeding season. Primiparous mothers of males had lower odds of a subsequent pregnancy than primiparous mothers of females, suggesting that the longest delays tend to occur after the births of first-born males. As rhesus macaques are seasonal breeders, failure to conceive during the breeding season delays subsequent reproduction at least a full year. We cannot differentiate whether a delay in reproduction occurred because a primiparous mother sustained lactation and extended the period of maternal care and/or because she required a longer period of recovery before resumption of estrus. However, Stanton and colleagues [2014] recently reported that among wild-living chimpanzees, primiparous mothers engage in more suckling, grooming, and playing with their infants when compared to multiparous mothers. Because no difference in mortality between first- and later-born infants was apparent, primiparous mothers were thought to be compensating for constrained maternal capacity by investing more time with their offspring - consistent with what we know about the learned efficiency of maternal care over time [Fairbanks, 1996; Cameron et al., 2000; Nguyen et al., 2012].

The archival information used here produced a large dataset enabling estimation of survival parameters within sex-by-parity classes along with birth season effects. However, archival data also imposed some limitations. The use of birth order as a proxy for maternal investment leverages extensive previous empirical research on the differential capacity of primiparous and multiparous mothers to invest in offspring [Small, 1981; Setchell et al., 2001; Dufour and Sauther, 2002; Hinde, 2007; Wathes et al., 2007; Hinde, 2009; Hinde, 2010; Hinde and Milligan, 2011; Hinde et al., 2013]. The archival records, however, do not include information about maternal rank, previously associated with infant growth and survival in provisioned, free-ranging rhesus populations [Drickamer, 1974; Meikle et al., 1984]. Based on previous research, we would expect maternal rank to have greatest influence under natural ecological conditions where foraging success and food selection is more variable among individuals and across time [e.g. Murray et al., 2006]. However, the fact that survival disparities can be detected readily even in this well-fed captive population is encouraging, as even stronger effects may be present in populations under naturalistic conditions. The archival dataset also precluded direct measures of maternal effort in the form of behavioral care or physiological transfer of milk. Given the constraints of archival data, we hope that the phenomena described here will motivate future empirical research into the underlying processes that facilitate the increased juvenile survival of first-born offspring.

Importantly, offspring are active agents in their own development, both behaviorally and somatically [Fairbanks and Hinde, 2013; Wells, 2014]. Maternal behavioral care and physiological transfer are necessarily mediated through the offspring’s utilization of the maternal “endowment.” Detecting the signatures of such nuanced and complex dynamics - with multiple tradeoffs, strategies, and tactics shifting within and among individuals - will necessarily be challenging with archival records. However, despite its limitations, our study suggests that under some circumstances, first-born offspring may influence their own developmental trajectories in ways that enhance survival after the period of maternal dependence.