Influence of Temporal Regularization and Radial Undersampling Factor on Compressed Sensing Reconstruction in Dynamic Contrast Enhanced MRI of the Breast

Abstract

Objective

To evaluate the influence of temporal sparsity regularization and radial undersampling on compressed sensing reconstruction of dynamic contrast-enhanced (DCE) MRI, using the iterative Golden-angle RAdial Sparse Parallel (iGRASP) MRI technique in the setting of breast cancer evaluation.

Method

DCE-MRI examinations of the breast (n=7) were conducted using iGRASP at 3T. Images were reconstructed with five different radial undersampling schemes corresponding to temporal resolutions between 2 and 13.4 s/frame and with four different weights for temporal sparsity regularization (λ=0.1, 0.5, 2, and 6 times of noise level). Image similarity to time-averaged reference images was assessed by two breast radiologists and using quantitative metrics. Temporal similarity was measured in terms of wash-in slope and contrast kinetic model parameters.

Results

iGRASP images reconstructed with λ=2 and 5.1s/frame had significantly (p<0.05) higher similarity to time-averaged reference images than the images with other reconstruction parameters (mutual information (MI) >5%), in agreement with the assessment of two breast radiologists. Higher undersampling (temporal resolution < 5.1 s/frame) required stronger temporal sparsity regularization (λ≥2) to remove streaking aliasing artifacts (MI>23% between λ=2 and 0.5). The difference between the kinetic-model transfer rates of benign and malignant groups decreased as temporal resolution decreased (82% between 2 and 13.4s/frame).

Conclusion

This study demonstrates objective spatial and temporal similarity measures can be used to assess the influence of sparsity constraint and undersampling in compressed sensing DCE-MRI and also shows that the iGRASP method provides the flexibility of optimizing these reconstruction parameters in the post-processing stage using the same acquired data.

Introduction

Compressed sensing (CS) (1–3) is emerging as a powerful approach for rapid imaging that exploits image compressibility (sparsity) to reduce the number of samples required to reconstruct an image without loss of important information. Dynamic contrast enhanced (DCE)-MRI is a good candidate for the application of CS due to the presence of extensive spatiotemporal correlations in the time series of images, and the possibility to use different k-space sampling patterns for each temporal frame which introduces additional incoherence along the temporal dimension (4). However, it remains challenging to assess the influence of reconstruction parameters on temporal and spatial fidelity due to the difficulty of acquiring fully sampled conventional images at the same temporal and spatial resolutions as the images reconstructed with compressed sensing.

Similar challenges can also be found for combinations of compressed sensing and parallel imaging with golden-angle trajectories as in the iterative Golden-angle RAdial Sparse Parallel (iGRASP) MRI method that we have recently introduced (5), which exploits joint multicoil sparsity rather than in each coil separately (6–8). This approach has the advantage that data may be acquired continuously without a priori definition of particular temporal frames, and the same dataset may be used to reconstruct image series with tailored temporal resolution, by grouping different numbers of adjacent radial spokes at any time point of interest. Hence, this method provides a unique opportunity to assess how the spatial and temporal characteristics of the reconstructed dynamic images are affected by the choice of undersampling and reconstruction parameters from one acquisition data set.

The main purpose of this study is to evaluate the influence of temporal sparsity regularization and radial undersampling on compressed sensing reconstruction of dynamic contrast-enhanced (DCE) MRI, using the iGRASP MRI technique in the setting of breast cancer evaluation.

Methods

iGRASP MRI Overview

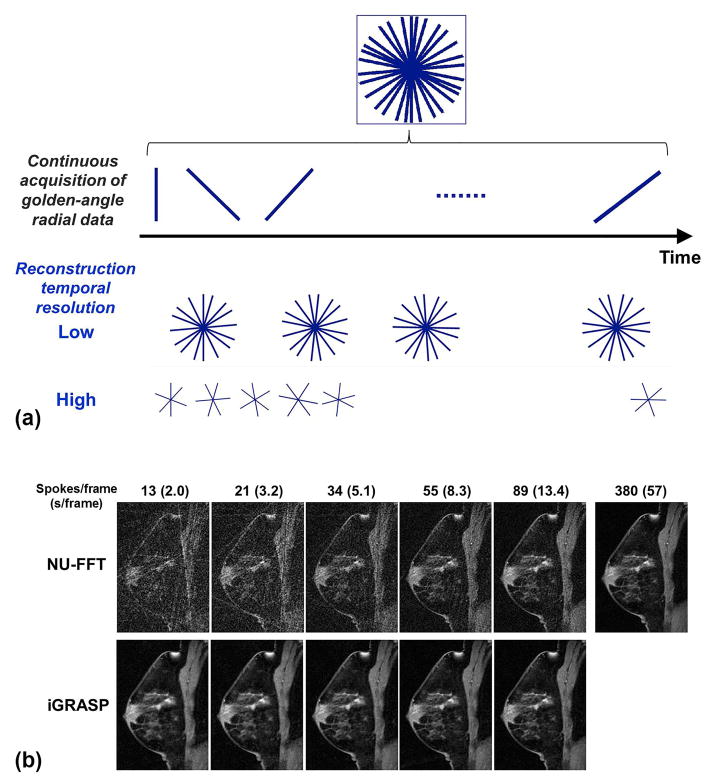
iGRASP performs continuous data acquisition using a golden-angle stack-of-stars trajectory to sample volumetric k-space information. The stack-of-stars scheme samples the k_x-k_y plane using a radial trajectory with golden-angle separation and the k_z direction on a Cartesian grid. Near-uniform coverage of the k_x-k_y plane is achieved if the number of consecutive spokes in the k_x-k_y plane is a Fibonacci number F(k+2) = F(k) + F(k+1) (e.g., 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so forth), where F(0) = 0 and F(1) = 1 (9). This type of acquisition has several advantages. First, each spoke defines a different k-space trajectory, which introduces a high degree of incoherence when the data are sorted into temporal frames. Second, arbitrary temporal frames can be created using the same raw data by grouping a different number of consecutive spokes, as shown in Figure 1(a). In this study, the iGRASP images are reconstructed using a Fibonacci number of consecutive spokes without any overlap or gap between adjacent temporal frames; hence the number of spokes per frame defines the temporal resolution. iGRASP reconstruction is formulated as a multicoil compressed sensing problem, which searches for the sparsest solution in the transform domain that is consistent with the multicoil k-space data. This is achieved by numerically solving the following optimization problem: $min{\Vert \mathbf{FSm}-\mathbf{d}\Vert }_2^2+\lambda {\Vert \mathbf{Tm}\Vert }_1$, where F is the non-uniform FFT (NU-FFT) operator defined for the radial sampling pattern, S is the multicoil sensitivity operator, m is the dynamic image series to be reconstructed, d is the undersampled k-t data, λ is the reconstruction weight that defines the tradeoff between sparsity and data consistency and T is the sparsifying transform. The reconstruction enforces joint multicoil sparsity on the image series m that represents the contribution from all coils. This approach exploits extra inter-coil correlations and yields higher performance than enforcing sparsity on each coil separately (7). Coil sensitivity maps (entries of the operator S) are estimated from the temporal average over all spokes. The undersampled k-t data is obtained by binning the continuously acquired data into time frames with the target spatial resolution, as shown in Figure 1(a).

Figure 1.

(a) Flexible image reconstruction at an arbitrary temporal resolution using golden-angle radial sampling. Different temporal resolutions can be achieved by grouping different numbers of consecutive spokes at the desired temporal positions. (b) Images reconstructed at different temporal resolutions using conventional gridding (NUFFT) and the proposed iGRASP method. Note that the spatial features of the breast parenchyma are well preserved for all images reconstructed using iGRASP.

A C++ implementation of iGRASP(5) employing the split Bregman optimization (10) was used for image reconstruction. A fixed number of 2 outer Bregman updates and 4 inner iterations was carried out, where each inner iteration computed an approximate solution to the l₂ subproblem by five iterations of non-linear conjugate gradient descent (11). In this implementation, λ was defined as a multiple of the noise level in the undersampled data, whereas it was defined relative to the maximum intensity of NUFFT images in our previous report (5). Note that the noise level is substantially lower than the maximum intensity of images; λ > 1 does not mean an emphasis on sparsity that surpasses data consistency. The sparsifying transform T was first-order temporal difference which corresponds to minimization of temporal total variation (5).

Data Acquisition

Breast DCE-MRI was performed on seven patients who underwent MRI-guided biopsy scans on a whole-body 3T scanner (MAGNETOM TimTrio, Siemens Healthcare, Erlangen, Germany) equipped with a seven element breast coil array (InVivo, FL). A prototype radial stack-of-stars 3D spoiled gradient echo pulse sequence with golden-angle spoke ordering was employed for continuous data acquisition. All partitions (i.e., phase encodes in the slice direction) corresponding to one radial angle were acquired sequentially before rotating to the next angle. Frequency-selective fat suppression was used after each partition loop and 60 initial calibration lines were acquired to estimate system-dependent gradient-delay errors (12). Relevant imaging parameters were: sagittal slab orientation, FOV=280 x 280 x 144 mm³, FA = 12 degrees, TE/TR = 1.47/3.6 ms, and BW = 710 Hz/pixel. A total of 2280 spokes were acquired for each of the 35 partitions during free breathing to cover one breast planned for biopsy. Two-fold readout oversampling (512 sample points/spoke) was used to avoid spurious aliasing along each spoke. The reconstructed image matrix size per frame is 256x256x72 with zero padding along the slice direction. The total acquisition time was 5 min 40 s. After baseline acquisition of 57 s (380 spokes), a single dose of Gd-DTPA (Magnevist, Bayer Healthcare, Leverkusen, Germany) at 0.1 mM/kg body weight was injected at 2 ml/sec into an antecubital vein while the scan continued for another 4 min 45 s (1900 spokes).

Based on the pathology evaluation of the biopsy specimens, lesions were divided into benign (n=4; 4 with fibrocystic changes; 50.3±8.9 years) and malignant (n=3; 2 with ductal carcinoma in situ and 1 with invasive ductal carcinoma; 52.0±10.1 years) categories. This retrospective study with a waiver of written informed consent was approved by our Institutional Review Board.

Image Reconstruction

Images were retrospectively reconstructed with different temporal resolutions, including 2.0, 3.2, 5.1, 8.3, 13.4 and 57 s/frame using 13, 21, 34, 55, 89 and 380 spokes/frame, respectively. For each temporal resolution, the multicoil k-space data was normalized to have unit noise intensity in each coil, which enabled to use the same range of reconstruction weights (λ). λ defines the tradeoff between sparsity and data consistency Image reconstruction was repeated with four different λ values, 0.1, 0.5, 2.0 and 6.0. Figure 1(b) shows examples of iGRASP images in comparison with corresponding non-uniform fast Fourier transform (NUFFT) images.

Assessment of Spatial Quality

Since it is nontrivial to obtain a ground-truth reference image simultaneously within a single DCE-MRI scan, spatial quality assessment of the iGRASP images was carried out using only the last 380 spokes of the dynamic data assuming that the contrast-concentration change during that time period was negligible in all voxels; the NUFFT image from the “fully-sampled” dataset with 380 spokes was used as a reference standard to assess iGRASP images reconstructed with smaller numbers of spokes and different λ values. The last 380 spokes after contrast injection were chosen, as opposed to the first 380 spokes before contrast injection, because delayed contrast enhanced images have more image contrast than the baseline images and the contrast enhanced lesions are usually of interest for the DCE-MRI exam. Mean squared difference (MSD) is a simple and widely used quality metric (13–15). However, it has been reported that MSD can be misleading in image reconstruction where images with a wide range of qualities can have a same MSD value as demonstrated by Wang et al (16) and other references therein. Hence, we included five additional image similarity measures as defined in Supplemental Table 1.

Included were two intensity-based methods, MSD and intensity cross-correlation (ICC). ICC was included in order to assess the image similarity without any bias from the image intensity scaling and/or offset, as demonstrated in various image co-registration applications (14,15,17,18). Similar types of measures based on the image gradient, gradient difference (GDF) (14,19) and gradient cross-correlation (GCC) (14,20,21), are also included as these measures give more weight to edge information than differences in low spatial frequency components. Mutual information (MI) or relative entropy is one of most commonly used measures for multimodality image registration (22–26). Although the images compared in this study were acquired using a single imaging modality, this measure has an advantage of not being sensitive to possible differences in absolute pixel intensities of the reconstructed images at different time points during the washout phase. Another type of similarity measure is mean structural similarity index (MSSIM) that has been widely used to assess the quality of JPEG (16) and MPEG4 (27) images as well as for remote sensing (28). MSSIM measures image similarity in terms of local luminance, contrast, and structure. The iGRASP images reconstructed with different reconstruction parameters were assessed using these six measures. Similarity measures with different reconstruction parameters were compared using Wilcoxon signed-rank test. A p-value of less than 0.05 was considered significant.

In addition to the quantitative assessment of image similarity with the reference standard images, the perceived image quality was evaluated by two breast radiologists with 15 (L.M.) and 9 (H.T.) years of experience, respectively. The two readers were blinded and independently evaluated the quality of images using 5 levels of quality score: 1, non-diagnostic; 2, poor; 3, adequate; 4, good; 5, excellent. The reader agreement was assessed using the weighted kappa statistics.

Assessment of Temporal Quality

Temporal quality of iGRASP images was assessed using the enhancement slope of the time-intensity curve from the aorta. The time-intensity curve of the aorta typically has the highest slope as well as the largest peak enhancement level and, thus, is most sensitive to any temporal blurring caused by different reconstruction parameters, such as the regularization factor λ and the selected temporal resolution. NUFFT images reconstructed with the same number of spokes were used as reference standards. An ROI was manually drawn in the aorta of each subject. For two given time-intensity curves, comparison of the enhancement slopes was made with the wash-in part of the data selected in the following way. For each time-intensity curve, the center of the enhancement slope was detected by finding the time point with the maximum change in the time-intensity curve. The average of the center positions found in the two curves was used as the center position for comparison, and segments of 20 s around the center from the two time-intensity curves were used to assess temporal similarity. A test curve segment, S_T(t), was transformed to S_T′(t) using the following transformation:

$$S_T^{\prime }(t)=p_1{S}_T(p_{3}t+p_4)+p_2,$$ (1)

where four parameters (p₁, p₂, p₃ and p₄) were estimated by minimizing the sum of the squared difference between S_T′(t) and a reference curve segment S_R(t). The scaling factor of the time axis, p₃, is 1 in the absence of temporal blurring, and smaller than 1 when there is temporal blurring. p₃ could be larger than 1 if the test curve has a steeper slope than the reference curve for any reason including noise effect. p₃ was used as a measure of temporal similarity.

We investigated whether p₃ is a valid indicator for temporal similarity using the time-intensity curves of the aorta from the iGRASP images reconstructed with 13 spokes/frame and λ=2.0. Temporal blurring was simulated by applying a moving-average filter with the average length up to 10 points. The simulated temporal blurring was measured using the above method; the original aorta time intensity curve was S_R(t) and the filtered curve was S_T(t). Then, we examined how the reconstruction parameters affect temporal blurring as measured by p₃. In order to assess the influence of λ on temporal quality, the NUFFT images reconstructed with the same number of spokes were used as the reference images. For assessment of the effect of the number of spokes used for each frame on temporal quality, the images reconstructed with 13 spokes/frame (the highest temporal resolution in this study) were used as the reference images and were compared with the images reconstructed using the same λ for different temporal resolutions. The one-sample t-test was used to compare the mean of the estimated p₃ values to 1.

Contrast Kinetic Model Analysis

For contrast kinetic model analysis in this study, we used the generalized kinetic model (GKM) with a plasma compartment, in which the contrast-agent concentration in a voxel (C_t(t)) is described by (29):

$$C_t(t)=v_p{C}_p(t)+K^{\mathit{trans}}{\int }_0^t{C}_p(u)exp\left(k_{ep}(u-t)\right)du,$$ (2)

where K^trans is the volume transfer constant between blood plasma and interstitial space, k_ep denotes the rate constant between interstitial space and blood plasma, v_p the volume fraction of the plasma space, and C_p the contrast agent concentration in plasma. Note that C_p was measured from the axial artery in the same reconstructed images for evaluation, as opposed to using a fixed high-temporal resolution data; hence, the estimated kinetic parameters are not direct reflection of the temporal characteristic of the lesion time-intensity curve with respect to a fixed reference input function. We assessed whether differentiation of lesion types can be affected by different reconstruction parameters. The pre-contrast T₁ relaxation value of the lesion and the contrast agent relaxivity were assumed to be 1.5 s and 4.3 mM⁻¹s⁻¹, respectively, based on literature data (30,31). Parameter estimation was performed using the Simplex algorithm (32) provided in IDL (Exelis VIS, Boulder, CO).

Results

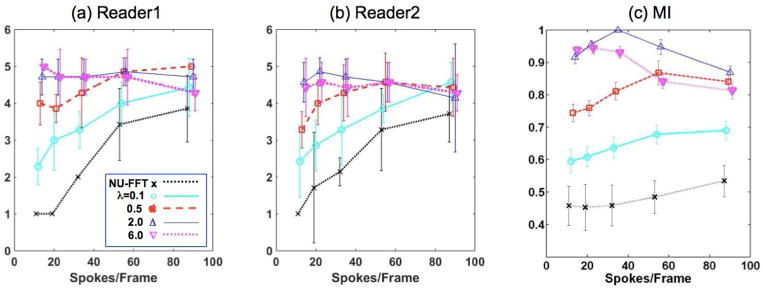
The image quality assessment scores of two readers are presented in Figure 2(a) and (b). The linear weighted kappa coefficient was 0.62 that indicates a substantial agreement between two readers. Both readers gave highest scores for images reconstructed with λ=2.0 or 6.0. For λ=0.5 or smaller, the image quality decreased noticeably when less spokes were used per frame. Among the six similarity measures used in this study, the result of MI is shown in Figure 2(c) as MI shows most separations between different reconstruction parameters. MI has trends similar to the other measures, as summarized in Supplemental Figure 1, of which iGRASP images reconstructed with λ=2.0 and 34 spokes/frame are most similar to the reference images. For λ=2.0, MI values with 34 spokes/frame are significantly (p < 0.05) higher than those with other temporal resolutions. For λ<2.0 (0.1 or 0.5), MI increases when more spokes are used per frame, except for 89 spokes/frame with λ=0.5. In contrast, when λ>2.0 (6.0), MI decreases when more spokes are used per frame, except for 13 spokes/frame. Note that the similarities of the images with λ=6.0 for 13 or 21 spokes/frames are not significantly different from those of the images with λ=2.0 for same spokes/frames; it indicates that strong regularization is helpful only when a small number of spokes are used for iGRASP. Representative examples of images reconstructed with different λ values are provided in Supplemental Figure 2.

Figure 2.

Evaluation of spatial quality by two readers (a, b) and MI (c), one of six image similarity measures used in this study. MI shows trends similar to the other measures. See Supplemental Figure 1 for all the image similarity measures. MI values are normalized by their maximum value prior to calculating the mean and standard deviation. The error bars represents +/− 1 standard deviation.

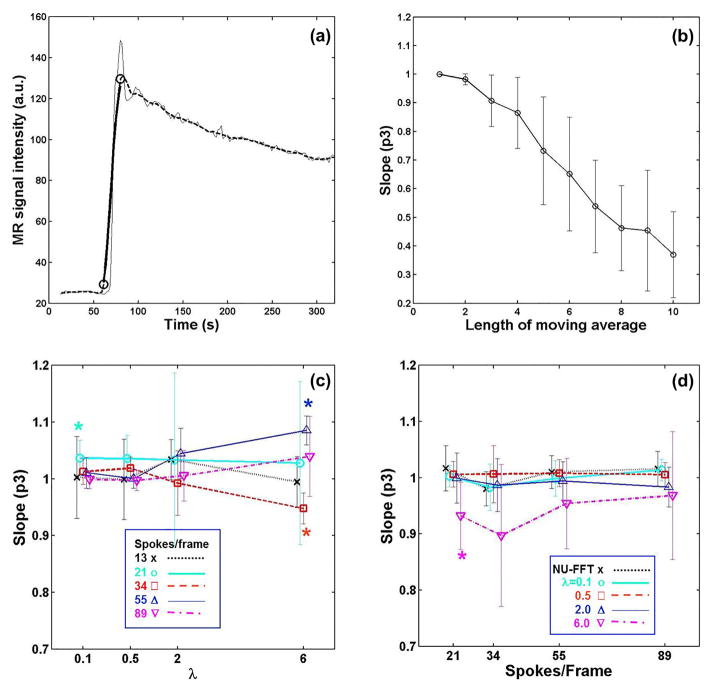
Figure 3 presents results of the temporal quality assessment. Figure 3(a) shows an example time-intensity curve from the aorta of a patient (thin line) and the same curve after filtering with a moving average of 10 points (dashed line). Figure 3b shows the time scaling factor, p₃, as a function of the moving average length, using all subject data. It shows that p₃ monotonically decreases as temporal blurring increases due to the increase of the moving average length, supporting that this parameter can be used to measure temporal blurring of an enhancing slope.

Figure 3.

Evaluation of temporal quality on the rising edge of the time-intensity curve from the aorta. (a) Example fit: the thin black line is a time intensity curve from the aorta; the dashed line is a filtered curve using a moving-average of 10 points; the thick line is the modified original curve fitted to the filtered one. (b) Time scaling parameter, p3, measured using the aorta time-intensity curves from 18 subjects decreases monotonically as the length of moving average increases. (c) Effect of regularization factor with respect to the time-intensity curve from NUFFT images. (d) Effect of temporal resolution with respect to the time-intensity curve with 13 spokes/frame. An asterisk indicates that the mean is significantly different from 1 (p < 0.05, t-test). The error bars represents +/− 1 standard deviation.

Figures 3c and 3d show comparisons of temporal quality measured by the p₃ parameter in all subjects. The results summarized in Figure 3c show the influence of λ on temporal quality; the mean p₃ values of all cases were higher than 0.9 which corresponds to the p₃ value from a moving average filter of length <= 3 as shown in Figure 3b. Figure 3d shows the effect of the number of spokes used for each frame on temporal quality; the blurring in the worst case (p₃ = 0.90±0.13 for λ = 6 and 34 spokes/frame) corresponds to a moving average filter length of 3 in Figure 3b. For the cases other than λ=6, the p₃ values were close to 1 (1.00 ±0.03 for NUFFT, 1.08±0.40 for λ = 0.1, 0.99±0.03 for λ = 0.5, and 0.99±0.04 for λ = 2.0).

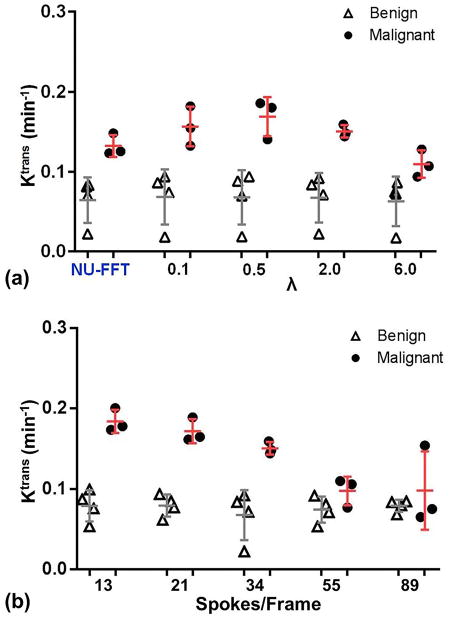
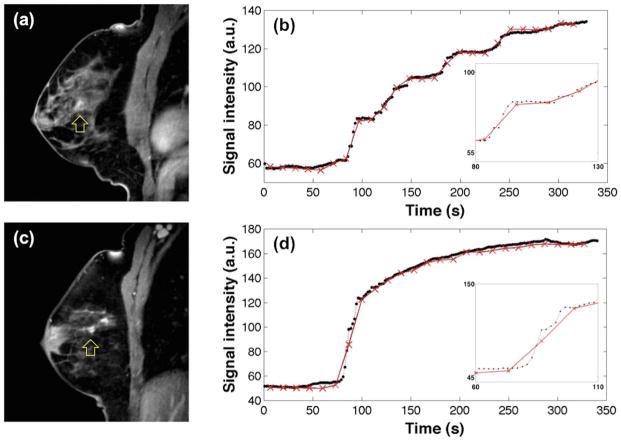
Figure 4a shows the estimated K^trans values of benign and malignant groups with different λ when the images were reconstructed with 34 spokes/frame. The difference in K^trans values between benign and malignant lesions was smallest when using NUFFT and increased with λ. K^trans values of the benign group remain the same while the K^trans of the malignant group were substantially higher with larger λ (≥ 0.5). Figure 4b shows that the K^trans values of the benign group did not change noticeably over the range of temporal resolutions used in this study, while the K^trans values of the malignant group monotonically decreased as the temporal resolution decreased. Figure 5 shows representative examples of images and lesion time-intensity curves for benign and malignant lesions.

Figure 4.

Comparison of transfer rates (K^trans) between benign and malignant lesions depending on (a) λ when temporal resolution is 34 spokes/frame and (b) temporal resolution when λ = 2.

Figure 5.

Comparison of time-intensity curves from a slowly enhancing lesion (a and b) and a fast enhancing lesion (c and d), which were proven to be a fibrocystic change and an invasive ductal carcinoma, respectively. The images in (a) and (c) were reconstructed with the last 13 spokes with λ = 2. In (b) and (d), black dots with dashed lines are the time-intensity curves for images reconstructed using 13 spokes/frame with λ = 2, whereas red crosses with solid lines are for 89 spokes/frame with λ = 2.

Discussion

With the recent rapid development of iterative image reconstruction methods in MRI, the importance of quantitative and reliable evaluation of image quality has increased. Subjective image quality assessment is a crucial part of image evaluation, since human observers, such as radiologists, are the ultimate users in most MRI applications. However, subjective assessment may not be sufficient to ensure the reliability and accuracy of iteratively reconstructed images for quantitative analysis. In this study, we used multiple spatial and temporal similarity measures to investigate how temporal sparsity constraint and radial undersampling affect iGRASP images.

The optimal reconstruction parameters can be dependent on the target application and the values reported in this study might not be appropriate for different applications. The approach demonstrated in this paper can be used to find the appropriate reconstruction parameters for other applications. The reader assessment results suggest that a wide range of λ and temporal resolutions can be used to generate a similar level of good quality images for readers. On the other hand, this may also imply that the sensitivity of reader assessment is not high enough to measure the differences among the high quality images. Future study is warranted to investigate more detailed distributions of similarity measures near the optimal values and whether maximizing the image quality based on a quantitative metric can lead to a significant improvement in clinical interpretation of the reconstructed images.

The comparison of benign and malignant lesions in this study suggests that, for the lesions with rapid enhancements during wash-in, the temporal resolution of DCE-MRI data needs to be high enough to capture the rapid initial enhancement. With a low temporal resolution, K^trans could be underestimated and also be subject to a large variability depending on the sampling position. However, a further investigation on such effect of temporal resolution on K^trans estimation and its clinical significance, combined with a high spatial resolution, needs to be conducted with a substantially large cohort to determine if this technique can improve the differentiation of benign and malignant lesions.

The iGRASP reconstruction represents a new way of performing breast DCE-MRI studies, in which data are continuously acquired for a period of time and image reconstruction is performed with flexible temporal information, such that multiple user-defined temporal resolutions with distinct numbers and positions of temporal frames can be obtained from the same dataset (5). This is a unique advantage of the iGRASP reconstruction which is difficult to achieve using other highly accelerated dynamic MRI methods with Cartesian k-space trajectories, such as in the k-t SPARSE-SENSE techniques (7,33,34). Another important advantage of using radial trajectories, as in iGRASP, is the inherent presence of incoherent aliasing in multiple dimensions (6), even with non-random under-sampling. Its robustness to motion artifact is another strength of radial trajectory based methods including iGRASP.

The iGRASP method used in this study employed the standard stack-of-stars k-space trajectory for incoherent undersampling in the k_x-k_y radial plane. This data acquisition scheme provided sufficiently high and flexible accelerations for this study as the raw data for each slice were processed in parallel after performing an FFT along the k_z dimension. However, further acceleration and image quality improvement in 3D data acquisitions can be achieved by using the shifted stack-of-stars trajectory with random shifts between the k_x-k_y radial planes (35). Although not presented in this study, our preliminary study found that the shifted stack-of-stars trajectory increased incoherence and provided a better starting point for compressed sensing reconstruction. Various other k-space trajectories, such as 3D radial spokes, can also be used to fully exploit the sparsity of the 3D DCE-MRI data.

One of the limitations of this study was the absence of ground truth DCE-MRI images for the assessment of spatial and temporal “fidelity”. Instead, we assessed the spatial and temporal similarity with the selected standard references. Currently, there is no technique available to acquire fully sampled data for DCE-MRI images of the breast at the high spatial and temporal resolutions used in this study. Even if a smaller volume is scanned for comparison, it is impractical to acquire both reference and iGRASP MRI data at the same time during a single injection of contrast agent. Due to this limitation, the present study was conducted by using the best data available for each assessment. Alternatively, numerical simulation or a standardized phantom for DCE-MRI could be used for a similar assessment of spatial and temporal fidelity. Referenceless image quality assessment (36) would also be an important subject of future studies. Other limitations include a small number of subjects as well as limited lesion types included in this study. The influence of image reconstruction parameters on the diagnostic accuracy needs to be assessed further with a larger cohort of patients which can reflect the diverse distribution of patient characteristics.

In conclusion, the spatial and temporal qualities of iGRASP breast DCE-MRI images were quantitatively assessed using objective measures for image similarity and temporal similarity. While there are a number of studies on various compressed sensing methods for DCE-MRI, a quantitative evaluation of their reconstruction parameters and temporal resolution is often not provided. Using the flexibility of iGRASP that allows image reconstructions with different temporal resolutions from a same raw data set, we demonstrated that optimization of reconstruction parameters can be an important factor in contrast kinetic model analysis and differentiation of malignant lesions from benign ones. The optimization process for image reconstruction parameters shown in this preliminary study with a small cohort can also be applied to other applications utilizing compressed sensing imaging methods similar to iGRASP.

Supplementary Material

Supp FigureS1-S2 & TableS1

Supplemental Figure 1. Evaluation of spatial quality using image similarity measures defined in Supplemental Table 1; (a) mean square difference (MSD), (b) intensity correlation coefficient (ICC), (c) gradient difference (GDF), (d) gradient correlation coefficient (GCC), (e) mutual information (MI), and (f) mean structural similarity (MSSIM). Each measure is normalized by its maximum value (minimum for MSD) prior to calculating the mean and standard deviation.

Supplemental Figure 2. Comparison of images reconstructed with different λ values. All images were reconstructed using 34 spokes/frame, except the reference image which was reconstructed using 380 spokes. The images were from a 41-year-old woman with a 1.6 cm oval mass with irregular margins. Biopsy yielded an invasive ductal carcinoma, poorly differentiated.

Supplemental Table 1. Image similarity measures used for assessment of spatial quality of iGRASP images (I_G) in comparison with the reference images (I_R).