Abstract
It is widely accepted that synaptic transmissions and gap junctions are the major governing mechanisms for signal traveling in the neural system. Yet, a group of neural waves, either physiological or pathological, share the same speed of ∼0.1 m/s without synaptic transmission or gap junctions, and this speed is not consistent with axonal conduction or ionic diffusion. The only explanation left is an electrical field effect. We tested the hypothesis that endogenous electric fields are sufficient to explain the propagation with in silico and in vitro experiments. Simulation results show that field effects alone can indeed mediate propagation across layers of neurons with speeds of 0.12 ± 0.09 m/s with pathological kinetics, and 0.11 ± 0.03 m/s with physiologic kinetics, both generating weak field amplitudes of ∼2–6 mV/mm. Further, the model predicted that propagation speed values are inversely proportional to the cell-to-cell distances, but do not significantly change with extracellular resistivity, membrane capacitance, or membrane resistance. In vitro recordings in mice hippocampi produced similar speeds (0.10 ± 0.03 m/s) and field amplitudes (2.5–5 mV/mm), and by applying a blocking field, the propagation speed was greatly reduced. Finally, osmolarity experiments confirmed the model's prediction that cell-to-cell distance inversely affects propagation speed. Together, these results show that despite their weak amplitude, electric fields can be solely responsible for spike propagation at ∼0.1 m/s. This phenomenon could be important to explain the slow propagation of epileptic activity and other normal propagations at similar speeds.
SIGNIFICANCE STATEMENT Neural activity (waves or spikes) can propagate using well documented mechanisms such as synaptic transmission, gap junctions, or diffusion. However, the purpose of this paper is to provide an explanation for experimental data showing that neural signals can propagate by means other than synaptic transmission, gap junction, or diffusion. The results indicate that electric fields (ephaptic effects) are capable of mediating propagation of self-regenerating neural waves. This novel mechanism coupling cell-by-volume conduction could be involved in other types of propagating neural signals, such as slow-wave sleep, sharp hippocampal waves, theta waves, or seizures.
Keywords: epileptical, field effect, neural propagation, osmolarity
Introduction
Electrochemical signal propagation is one of the properties that enables communication among neurons. In the hippocampus, such communication is essential for basic neural function, such as memorization or spatial navigation, but can also cause pathological conditions, such as epilepsy. Interestingly, signal propagation speeds in various conditions are similar (∼0.1 m/s). Neural spikes generated by 4-aminopyridine (4-AP) travel with a longitudinal speed of 0.09 ± 0.03 m/s along the CA3 region (Kibler and Durand, 2011), whereas in the presence of picrotoxin, synchronous firing events propagate longitudinally at 0.14 ± 0.04 m/s (Miles et al., 1988). High K+-, low Mg2+-, and zero-Ca2+-triggered spikes again exhibit speeds of 0.07-0.1 m/s, 0.1–0.15 m/s, and 0.04–0.15 m/s, respectively (Haas and Jefferys, 1984; Quilichini et al., 2002; Liu et al., 2013). In normal tissue, theta oscillations travel with a speed of 0.08–0.107 m/s in the hippocampus of living rodent rats (Lubenov and Siapas, 2009), whereas carbachol-induced theta oscillations travels with a speed of 0.119 m/s along the CA1 cell layer and a 0.141 m/s along the CA3 cell layer (Cappaert et al., 2009). Together, it is clear that 0.1 m/s is a common propagation speed regardless of experimental models, therefore a shared fundamental mechanism may underlie these neural propagations.
Despite the fact that synaptic transmission and gap junctions are generally known to be responsible for neural communication, 4-AP-induced spikes still persisted when synapses and gap junctions were blocked in vitro, essentially suggesting a non-synaptic governing mechanism. These spikes propagate at the same or even higher speed in the presence of synaptic-blockers, such as the 4-AP/low-Ca2+ aCSF condition (Haas and Jefferys, 1984; Bikson et al., 1999; Zhang et al., 2014) and gap junction blockers, such as the 4-AP/mefloquine aCSF condition (Zhang et al., 2014). Other propagation mechanisms, such as extracellular ionic transients and axonal conduction mechanisms, have very different propagation speeds (0.0004–0.008 m/s for K+ diffusion and 0.3–0.5 m/s for axonal conduction, Miles et al., 1988; Lian et al., 2001; Francis et al., 2003; Meeks and Mennerick, 2007; Jensen, 2008; Kibler et al., 2012). Thus, it is unlikely that neural propagation at ∼0.1 m/s can be explained by synaptic transmission, gap junction, diffusion, or axonal propagation.
Another mechanism is electric field effects. Experiments have shown that extracellular fields could modulate the activity of single neurons and/or network activity. In hippocampal pyramidal cells, weak electrical fields can affect the excitability of cells and the synchronization of the network (Francis et al., 2003). In cortical neurons, endogenous weak fields could entrain action leading to phase-locking of spikes to the external field to reach a “spike-field synchrony” (Fröhlich and McCormick, 2010; Anastassiou et al., 2011) and its effect is enhanced by neural packing density (Vigmond et al., 1997). Using the Wilson and Cowan (1973) model for traveling waves, the speed of propagation is determined by excitability thresholds, spatial connectivity, and the refractory time constant (Richard et al., 1995). Locally applied electrical fields can also modulate the speed of propagation (Richard et al., 1995). Thus, we tested the hypothesis that an electrical field effect could underlie the propagation of 4-AP-induced spikes at a speed of 0.1 m/s in the hippocampus using computational modeling and experimental approaches. The propagation speed and network field amplitude were measured in two simulated conditions: epileptiform and normal, and the simulated results were compared with the propagation speeds and field strengths in in vitro experiments. Further, in vitro experiments were done to study the effect of applying a blocking field on propagation. Results from the model also predict that cell-to-cell distance (extracellular space) could inversely affect speed due to field effect, and this prediction was tested in vitro with osmolarity experiments.
Materials and Methods
Computational methods
Model structure.
The compartment model was built under NEURON 7.3 simulation environment (Yale School of Medicine, New Haven, CT). A CA1 hippocampal pyramidal network was simulated because it is a typical region where 4-AP-induced spike was observed experimentally. Two simulation models were tested: 4-AP/CA2+-free condition for epileptiform propagation and normal aCSF condition for physiological propagation. In the model, each cell contains 33 compartments, with one compartment for soma, 21 compartments for the apical dendrite, and 11 compartments for the basal dendrite. The lengths of the apical and basal dendrites were 735.3 and 490.2 μm, respectively, whereas both had a diameter of 5.2 μm (Shuai et al., 2003). Similar as to previous experiments and models, the diameter of each cell body was 10 μm (Warman et al., 1994; Shuai et al., 2003; Kurt et al., 2004; Anastassiou et al., 2011). The transmembrane potential Vi for each compartment is described by the relationship known as cable equation.
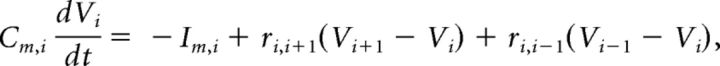 |
where Cm,i, Vi, Im,i, are the membrane capacitance, transmembrane potential, and transmembrane current of the i,th compartment respectively; ri,i+1 is the cytoplasmic (axial) conductivity between the i,th and (i +1)th compartment. To simplify the model, only the soma compartment contains active conductance; for dendritic compartments, the transmembrane current only contains leak current Im,idend = Ileak,i = gi Vi, with gi representing the passive conductance of the i,th compartment.
All passive membrane properties for each pyramidal cell were set to the following values according to patch-clamp recordings and current-clamp data in Ca2+-free conditions by Shuai et al. (2003): somatic membrane resistivity Rmsoma = 680 Ωcm2, somatic membrane capacitance Cmsoma = 1 μF/cm, dendrite membrane resistivity Rmdend = 34,200 Ωcm2, dendritic capacitance Cmdend = 1 μF/cm, and cytoplasmic (axial) resistivity Ri 530Ωcm. For each cell in the model, the transmembrane current for somatic compartments Im,isoma are given by the following:
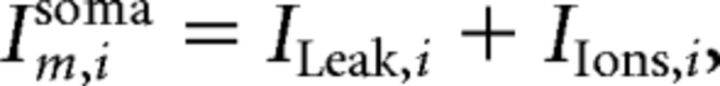 |
where ILeak,i and IIons,i are the leak current and total active ionic currents, respectively.
For 4-AP/Ca2+-free kinetics, the calcium currents and calcium-dependent potassium currents are eliminated (Shuai et al., 2003). In vitro experiments and computational models for CA1 hippocampal pyramidal cells stated that there are generally five major active ionic conductances in a Ca2+-free extracellular environment: a fast sodium current INa, a delayed rectifier current IDR, an A-type transient current IA, a muscarinic current IM, and a persistent sodium current INaP (Warman et al., 1994; Shuai et al., 2003). Thus, the total ionic current in the somatic compartment consists of five active currents:
The gating equations for each active current are implemented using the Hodgkin-Huxley formalism (Hodgkin and Huxley, 1952) as in Table 1. The maximum conductances are based on those of Shuai et al. (2003), designed to reproduce the electrophysiological behavior of CA1 pyramidal cells in low Ca2+ concentration environment. However, 4-AP is a blocker of the Kv1 voltage-activated K+ (A-type transient K) channels; thus, we greatly reduced the maximum conductance of the IA potassium channel, gA, to a near-zero value for 4-AP/Ca2+-free kinetics, Table 2 shows the maximum conductance values used in the model.
Table 1.
Gating equations for active channel current
| Channel | Gating equations |
|---|---|
| INa | gNam3h (Vm − ENa) |
| INaP | gNaPw (Vm − ENa) |
| IDR | gDRn4 (Vm − EK) |
| IA | gAab (Vm − EK) |
| IM | gMu2 (Vm − EK) |
| IL | gL (Vm − EL) |
The gating equation for each active channel's current is implemented using the Hodgkin–Huxley formulism.
Table 2.
Maximum conductance values used in the model
| Ionic channels | Maximum conductance values, S/cm2 |
|---|---|
| gNa | 0.045 |
| gNaP | 0.0003 |
| gKDR | 0.01 |
| gKA | 0.007 |
| gm | 0.059 |
| gleak,soma | 0.001 |
| gleak,dendrites | 2.922 × 10−5 |
Each gate variable x (ie, m, h, w, n, a, b, u) depends on its corresponding gate function, , where x∞ = αx/(αx + βx), and τx = 1/(αx + βx). The rate functions (αx, βx) for all currents were the same as those in Shuai et al., 2003.
To test whether field effect could mediate propagation with physiologic channel kinetics (normal aCSF), we adapted an established computational model by Wimmer et al. (2010) and Royeck et al. (2008). With these kinetics, each cell contained six different distributed Ca2+ channels, three different Na+ channels, and seven K+ channels that essentially mimicked a normal experimental condition. The morphology of the cell, the network layout, and neural activity initiation were the same as the 4-AP/Ca2+-free model.
The neural network.
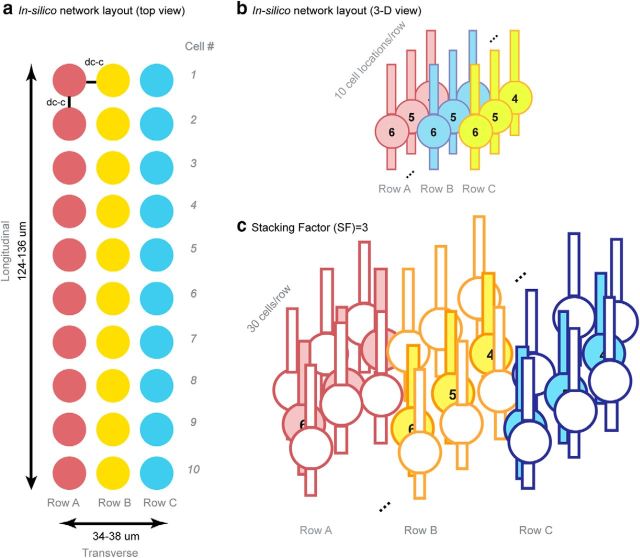
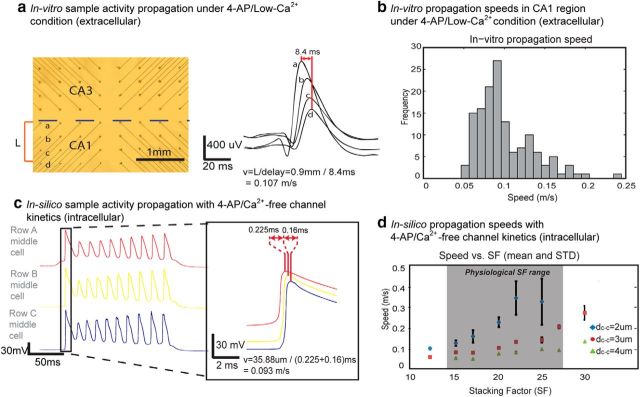
The layout of the network was designed in a way to capture the most important features of the physiological cellular layout for hippocampal activity propagation while minimizing the number of elements. The network is made up of three rows (Rows A–C) of neurons with 10 cell locations in each row (Fig. 1a,b). The distance between each two adjacent neurons (dc-c) in a physiologic pyramidal network ranges from 2 to 5 μm (Kurt et al., 2004; Anastassiou et al., 2011); in the model, we tested 10 trials for each of the mean dc-c equal to 2, 3, and 4 μm (n = 10 and variance = 0.1 μm with Gaussian distribution for each dc-c). To represent the cell stacking throughout the depth of a tissue slice, an arbitrary “stacking factor” (SF) was generated to take into account the actual number of cells around a certain location (Fig. 1c). The value of the SF was estimated from the volume cellular density reported from previous histology studies. In mice hippocampus, CA1 cellular volume density varies from ∼180,000 neurons/mm3 to 300,000 neurons/mm3 depending on specific locations in the CA1 region (Kurt et al., 2004; Jinno and Kosaka, 2010). Using a tissue thickness of ∼600 μm and the model network area equal to ∼4216–4788 μm2 (Fig. 1a; d̄ = 2 μm, area = 34 × 124 μm; d̄ = 4 μm, area = 38 × 136 μm), a SF between 15 and 28 would best represent the cellular layout in tissue. In the model, stacking factor values between 10 and 30 were tested.
Figure 1.
CA1 Pyramidal cellular network layout in the model. a, Top view of the network (solid-colored circles represent soma positions). The network contains three rows of cells with 10 cell locations in each row. The diameter of the soma is 10 μm and the soma edge-to-edge distance (dc-c) ranges from 2 to 4 μm. Thus, the dimension of the network is 34∼38 μm × 124∼136 μm. b, 3-D view of the network. c, Physical representation of the stacking factor (SF). In each row, solid-colored cells represent the actual modeled cell locations, whereas empty-colored cells represent the virtually stacked cells around the modeled cell locations. An example with SF = 3 is shown, where each cell was surrounded by two extra virtual cells at the same location and the amplitude of electrical field generated by each modeled cells was multiplied by three.
Electrical field effect calculation.
To test the hypothesis that endogenous electric field alone could induce neural propagation, the synaptic connections, gap junctions, and diffusion effects were eliminated in the network. The cells in the first row were first initiated by an experimentally determined extracellular potential (Fig. 2a). The mean values of 10 in vitro signals acquired from each of the channels located at cell layer, apical dendrites, and basal dendrites by Michigan Shank were applied extracellularly at corresponding locations in each cell of Row A in the model (Fig. 2b). The electric field effect was calculated using the quasi-static formulation of the Maxwell equations assuming homogenous and linear volume conductors (He, 2005). According to Ohm's law for conductors in Maxwell's equations, the potential ϕ at the point P at a distance r relatively to the reference electrode in a medium of conductivity σ is as follows:
 |
Using superposition, Equation 1 can be generalized to j monopolar electrodes from a total of i cells from the previous row(s) with a current Ii,j→n located at a distance ri,j→n to each target node n of the target cell. The extracellular potential inserted at a target node n is given by the following:
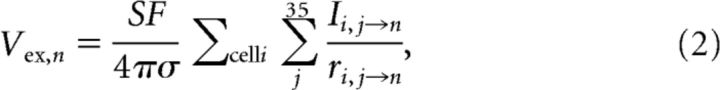 |
where Vex,n is the extracellular potential inserted at target node n in the target cell, Ii,j→n is the membrane current (assuming current going out of the cell to be positive direction) at a node j of cell i located ri,j→n distance from target node n, with a total j = 35 nodes in each cell (Fig. 2b); σ is the extracellular conductivity (typically the extracellular resistivity ρ = 1/σ is 250–380 Ωcm; 300 Ωcm was used in the model; Gold et al., 2007; Logothetis et al., 2007); SF is the stacking factor. The electric field effect could only propagate the action potential in the transverse direction to simplify the model; Row B cells were only affected by Row A cells, whereas Row C cells were affected by both Row A and Row B cells with the electric field effect.
Figure 2.
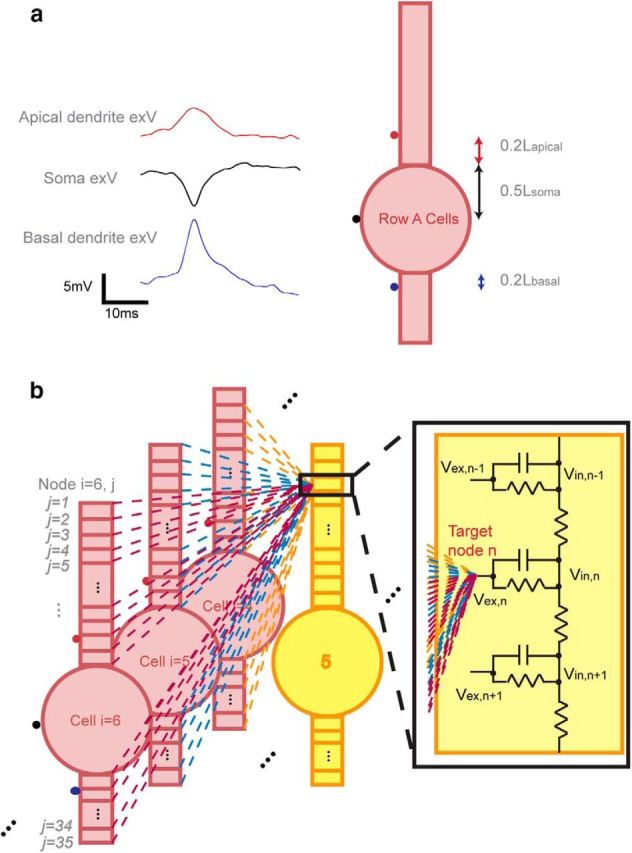
Electric field interactions within the neural network. a, Initiation of the action potential by extracellular stimulation for Row A cells using in vitro acquired signals. Each of the three signals was 10 times the average of 10 randomly selected trials from in vitro acquired signals (ie, cell layer, apical dendrites, basal dendrites). This is because physiological signals were acquired 10–30 μm away from its nearest cells due to the damage caused by the electrode insertion (estimated to be 2–3 cells layers), whereas in the model, signals were inserted directly on the cell membrane. As extracellular potential decays at a rate inversely proportional to the distance away from a point source, the potential amplitudes in the model were expected to be larger than what were seen experimentally. The signals were applied at the middle point of soma and at the dendritic compartments adjacent to the soma. b, Network field effect acting on one extracellular node of a target cell using Equation 2. The field acting on node n of cell 5 in Row B was the superposition of all fields generated by all Row A cells.
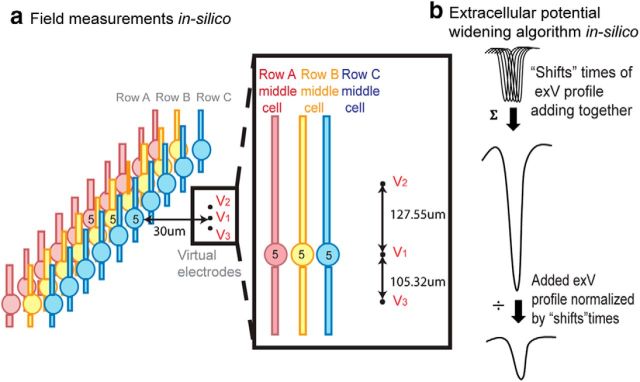
Field amplitude and speed measurement.
To measure the resulting electrical field due to the network firing activity and compare it to the experimentally recorded waveforms, we placed three virtual electrodes (v1, v2, and v3) outside of the network (Fig. 3a) vertically to test the network field amplitude, similar as to the placement of Michigan Shank electrodes into the in vitro slice. The middle electrode was placed 30 μm away from the Row C middle cell to account for approximately three rows of dead cell around the Michigan Shank electrode, a situation observed experimentally. Each row's resulting extracellular voltage at the three virtual electrodes was calculated, and the field amplitude was calculated by finding the average of the spatial derivatives (Eq. 3). The network field amplitude was the summation of the field amplitudes generated by all three Row layers (Eq. 4).
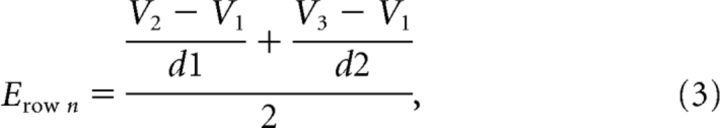 |
The propagation speed was measured based on the intracellular recording of each row's middle cell, where the first spike of the action potential peak time from each cell was recorded, and the delay from Row A to Row B and from Row B to Row C were calculated. The propagation speed was derived by taking the traveling distance divided by delay time.
Figure 3.
Speed and field measurements in the simulated network. a, Transverse action potential propagation and network extracellular field measurement. Row A affects Row B, and both Rows A and B affect Row C through electrical field effect. Three virtual electrodes were placed 30 μm away from the third row middle cell the extracellular voltages resulting from all of the cells in Row A–C were measured at v1, v2, and v3. The field amplitude was calculated as the average of the spatial difference of v1 and v2 and the spatial difference of v1 and v3 (Eq. 3). b, When measuring the field amplitude, an extracellular potential widening algorithm (“shifting algorithm”) was applied for each cell's extracellular waveform to best represent experimental recording. Each recorded extracellular voltage waveform was widened by summing “shift” times of copies (each shifted by 1 time step) and normalized to preserve the amplitude of the measured extracellular voltage signal. Among 30 randomly selected spikes from in vitro Michigan shank recording, the mean spike width was 8.57 ± 5.36 ms. The extracellular voltage from a single cell was shifted in time Nshift times and added. The resulting waveform amplitude waveform was then divided by N. With Nshift = 20, the model generated first spike width of 7.65 ms that is consistent with experimental results. This value of Nshift was used for all simulations.
Experimental methods
In vitro field amplitude measurements in unfolded hippocampus under the 4-AP/low Ca2+ condition.
In vitro measurements of extracellular activity and electric field in unfolded mice hippocampus were performed to measure the propagation speed and validate the results of the simulation. Experimental protocols were approved by the Institutional Animal Case and Usage Committee. CD1 mice from Charles River Laboratories (P10–P20; of either sex) were anesthetized and then decapitated. Subsequently, the whole hippocampus was separated from the brain and unfolded by following a previously developed protocol (Kibler and Durand, 2011). All unfolded hippocampal preparations were then transferred into a recovery solution of aCSF bubbled with 95% O2/5% CO2 and maintained at a room temperature (25°C) for at least 1 h before recording. Normal aCSF buffer consisted of the following (mm): 124 NaCl, 3.75 KCl, 1.25 KH2PO4, 2 MgSO4, 26 NaHCO2, 10 dextrose, and 2 CaCl2.
During recording, 4-AP was added into a low-calcium solution to increase the excitability of the tissue (Perreault and Avoli, 1989, 1992; Schechter, 1997) and to maximally block synapses. Low Ca2+/4-AP aCSF consisted of the following (mm): 0.1 4-AP, 124 NaCl, 5.25 KCl, 1.25 KH2PO4, 1.5 MgSO4, 26 NaHCO3, 10 dextrose, and 0.2 CaCl2. The extracellular potentials were acquired by a Michigan-type electrode array inserted into the unfolded hippocampus along the dendritic–soma axis. Electrical field amplitudes were calculated as the first difference of voltages measured by two adjacent channels on the shank, one at the depth of cell layer (200 μm from the stratum) and the other in apical dendrites. The Michigan shank was combined through a multichannel workstation with data acquisition system by Alpha ω (AlphaLab SNR).
In vitro propagation speed measurements in unfolded hippocampus under the 4-AP/low Ca2+ condition.
The propagation of the extracellular activity and its speed in the CA1 region of unfolded hippocampus was recorded by a custom-made 64-channel microelectrode array as previously described (Kibler et al., 2012; Zhang et al., 2014). The preparation for the tissue and the solution (4-AP/low-Ca2+) was the same as described above. Each microelectrode was coated with a biocompatible insulation material with only the tip being exposed. The electrodes were patterned as an 8 × 8 matrix with a 400 μm electrode-to-electrode space on the transverse direction and 300 μm space on the longitudinal direction. As the unfolded hippocampus was placed on the array, each microelectrode was inserted into the tissue and the extracellular activity at the location was recorded. The propagation speed was then calculated based on the distance between the two neighboring electrodes divided by the spike time delay recorded by the electrodes (Kibler et al., 2012; Zhang et al., 2014).
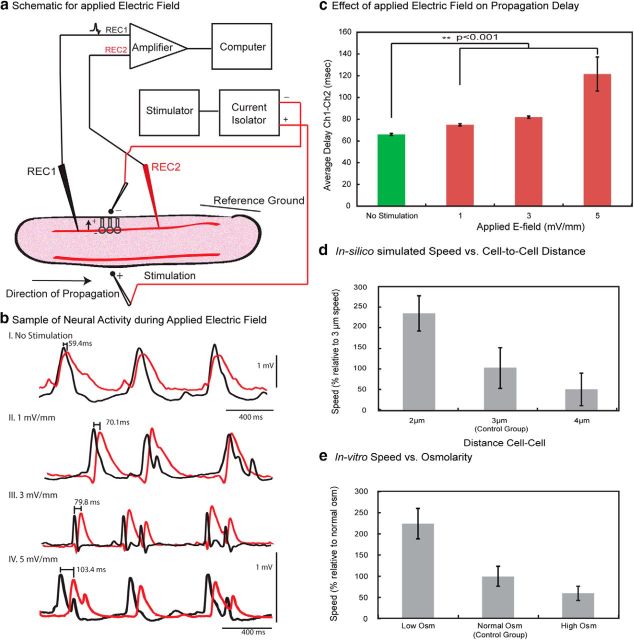
In vitro propagation speed reduction by applying a blocking field in longitudinal slices under the 4-AP condition.
Preliminary studies were conducted to observe the effect of applying an external blocking electric field on propagation of spontaneous activity in vitro. The 4-AP solution consisted of the following (mm): 0.1 4-AP, 124 NaCl, 3.75 KCl, 1.25 KH2PO4, 2 MgSO4, 26 NaHCO2, 10 dextrose, and 2.6 CaCl2. Longitudinal hippocampal slices were used to observe the effect of applying an external electric field in the opposite phase (“anti” field) to that of the propagating spike in between the two recording sites on the CA3 layer (see Fig. 6a). A stimulator and stimulus isolation unit was used to generate a field between 2 and 5 mV/mm. The electric field was generated across two 30 μm diameter tungsten-stimulating electrodes with (World Precision Instruments) that were placed across the tissue and between the two recording sites. 4-AP-induced spikes were generated when tissue was exposed to 4-AP/aCSF solution. Upon determining the propagation direction, the field strength was varied and the delay between the two recording channels was calculated.
Figure 6.
Effect of applying endogenous field in vitro and testing of the model prediction of the inverse relationship between extracellular volume and speed. a, Schematic of applied electric field between two recording sites (REC1 and REC2) on the CA3 in the longitudinal slice. An “anti” field within the physiological range (1–5 mV/mm) was generated using a stimulator and current isolator. b, An example of 4-AP-induced spikes under no stimulation followed by applied electric field of 1, 3, and 5 mV/mm. c, Effect of applied field on propagation delay between two recording channels. Observe an increase in delay with an increase in applied electric field. d, Effect of distance between cells on the speed of propagation in silico. Using dc-c = 3 μm as control group, propagation speed increased when dc-c dc-c decreased, and decreased when dc-c increased. e, Effect of osmolarity on speed of propagation in vitro. Compared with activity in normal osmolarity of the 4-AP solution, propagation speed increases at low osmolarity (cell swelling and decreased cell-to-cell distance) and decreased at high osmolarity (cell shrinking and increased cell-to-cell distance).
In vitro osmolarity test on its effect of speed in longitudinal slices under the 4-AP condition.
To determine how extracellular space (osmolarity) affects the propagation speed and thus validating the role of the electrical field effect, we performed osmolarity experiments in vitro on longitudinal slices in 4-AP solution, as the propagation is usually very robust in that direction (Zhang et al., 2014). The extracellular osmolarity was both increased and decreased relative to the normal osmolarity condition. The control 4-AP solution was the same as described above. For the low-osmolarity experiment, 150 ml of deionized water and 15 μm of 4-AP were added into the control 4-AP solution, resulting in a 15% dilution and a 10% decrease in osmolarity. For high osmolarity experiment, 30 mm d-mannitol was added to the control 4-AP solution, causing an increase in osmolarity by 10%. Each osmolarity experiment (control, low, and high) started with the tissue being exposed to the control 4-AP solution for 30 min and field potential recorded from each trial. The high- or low-osmolarity solution was then introduced, and the field potential was recorded after 15 min of osmolarity change. The traveling speed of the spontaneous activity was measured by two recording glass micropipette electrodes (1.0 mm outer diameter and 0.5 mm inner diameter borosilicate glass filled with 150 mm NaCl solution) placed on the CA3 longitudinal hippocampal slices, and the speed was determined by the transit time between the electrode pair.
Results
Neural activity can propagate non-synaptically with weak field amplitudes (pathological propagation)
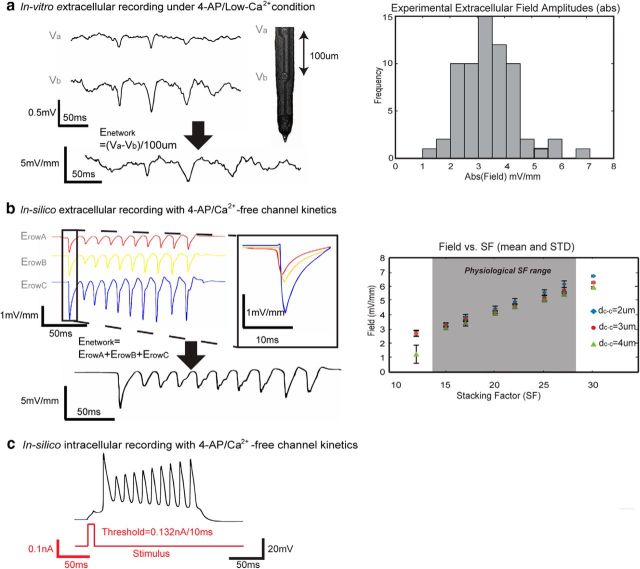
We first sought to constrain and validate the simulated pathological model by recording in vitro electric field amplitude during epileptiform activity (4-AP/low-Ca2+ solutions) in the hippocampus. Extracellular recordings obtained in the somatic layer (Va) and apical dendrites (Vb) by Michigan Shank showed trains of bursting events recorded under these conditions (Fig. 4a, Left). The electrical field amplitude near the cell layer was estimated by taking the spatial derivatives of the two voltage measurements. Among 65 spikes in five unfolded hippocampi, the field spiking amplitude was found to be between 1.60 and 7.13 mV/mm with a mean value of 3.5 ± 1.0 mV/mm; most of the amplitudes fell between 2.5 and 5 mV/mm (Fig. 4a, right). We then compared these signals with the field amplitude obtained in silico with 4-AP/Ca2+-free kinetics and observed similar characteristics (Fig. 4b, left). The median network field amplitude from the model was 4.58 mV/mm (Fig. 4b, left), and the field ranged between 3.26 and 5.80 mV/mm (Fig. 4b, right) among 180 simulated trials with randomized cell-to-cell distance dc-c (2–4 μm) and physiologically relevant SF values based on hippocampal cell density. These values fall within the known field amplitude range of ∼3–6 mV/mm (Ghai et al., 2000; Radman et al., 2007; Fröhlich and McCormick, 2010). It was also determined that the field amplitude increased with stacking factor SF (Fig. 4b, right). The extracellular activity generated in the model traveled from Row A to Row B and from Row B to Row C, showing that electrical field effect alone was responsible for action potential propagation in the CA1 hippocampal network (Fig. 4b, left, inset).
Figure 4.
Validation of the model through field amplitude and spiking characteristics. a, Left, Typical experimental recordings of extracellular potential from the somatic and dendritic layer obtained in vitro in the transverse hippocampal slice (Va and Vb, respectively); the electric field amplitude is calculated by taking the spatial derivative of the voltages. Right, A histogram of the electric field amplitude values recorded from 65 spikes from five unfolded hippocampus preparation showed that in vitro field amplitudes are between 2.5 and 5 mV/mm. b, Left, An example of simulated extracellular electric field of Row A–C layers in the model with SF = 20 and dc-c = 2.94 μm. Field amplitudes generated by Row A–C layers were 0.99, 1.14, and 2.45 mV/mm (Eq. 3), respectively, and the network electric field amplitude was 4.58 mV/mm as the sum of the field amplitude produced by the three layers (Eq. 4). Propagation of the activity between the layers is shown in the insert box. Right, For physiologically relevant values of SF, the network field amplitude ranged from 3.26 to 5.80 mV/mm (N = 180 where n = 10 trials with variance = 0.1 μm for each of the mean values of dc-c = 2, 3, and 4 μm and physiologic SF = 15, 17, 20, 22, 25, and 27; see Materials and Methods for physiologic SF range analysis), increasing with higher values of SF. c, Intracellular voltage recordings indicate that action potential had a threshold of 0.132 mA with a 10 ms pulse.
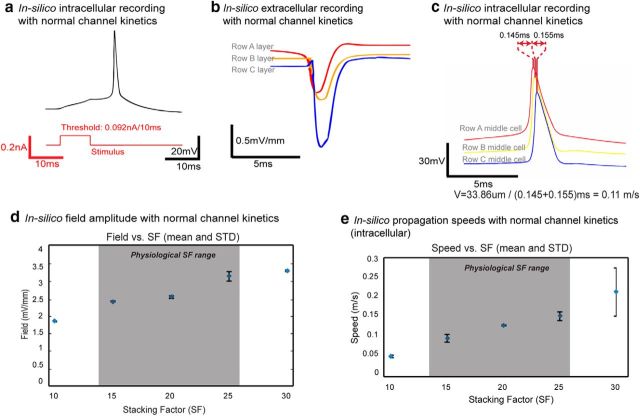
In addition, the intracellular waveform generated in silico was similar to those observed experimentally. Using the control parameters given in Table 2, the model reproduced the essential characteristics of the intracellular bursting activity seen in CA1 pyramidal cells. The resting potential, first spike amplitude, and first spike width at half-amplitude width were −61.5 mV, 93.9 mV, and 6.5 ms, respectively (Fig. 4c). These parameters fall within the experimentally measured ranges from previous CA1 pyramidal cell in vitro studies (resting potential: −75 mV∼ −52 mV; first spike amplitude: 70 ∼ 103.2 mV; and first spike width at half-amplitude: ∼1∼8 ms; Deuchars and Thomson, 1996; Su et al., 2001; Shuai et al., 2003; Golomb et al., 2006). The action potential fired at 12.09 mV above the resting potential when the stimulus was at 0.132 nA/10 ms, matching the in vivo measured threshold values (12.1 mV above the resting potential; Su et al., 2001; Fig. 4c).
Spiking events propagate by electrical field effect with speeds of ∼0.1 m/s in silico and in vitro (pathological propagation)
We then looked at the recorded epileptiform activity propagation speed in the CA1 region of unfolded hippocampus under 4-AP/low-Ca2+ environment. A high aspect ratio microelectrode array was used to record the activity and the spikes obtained in a solution containing 4-AP/low-Ca2+ at four adjacent spikes are shown in Figure 5a traveling at a speed of ∼0.1 m/s. Among 139 speed samples from the CA1 regions of six unfolded hippocampal preparations, the in vitro transverse speed ranged from 0.05 to 0.2 m/s, with a mean of 0.10 ± 0.03 m/s (Fig. 5b). These results clearly match the values obtained in the simulations, and are similar to those obtained in Zhang et al. (2014).
Figure 5.
Propagation of spiking events and their speeds in vitro and in-silico. a, Left, Picture of the array and the locations of the four recording channels (a–d) in the CA1 region of the unfolded hippocampus. Right, An example of a set of extracellular signals acquired at the four channels. With a distance of ∼0.9 mm from a to d and time delay of the peaks equal to 8.4 ms, the propagation speed is 0.107 m/s. b, A histogram of the propagation speeds acquired in vitro for 139 speed samples from 6 unfolded hippocampal preparation. c, A typical set of simulated intracellular waveforms from the middle cell in Rows A–C upon spiking initiation of the first layer. With SF = 20 and dc-c = 2.94 μm, a delay of 0.22 and 0.16 ms were recorded between the first spike peaking time of Row A and Row B middle cells and Row B and Row C middle cells. The total distance traveled is 35.88 μm, and with a total delay of 0.385 ms, the propagation speed is 0.093 m/s. d, Propagation speed at various SF (10∼30) and dc-c (2, 3, or 4 μm) with n = 10 and variance = 0.1 μm for each SF and mean dc-c (N = 180; n = 10 random trials with variance = 0.1 μm around mean values of dc-c = 2, 3, and 4 μm and physiologic SF = 15, 17, 20, 22, 25, and 27). Within the physiologic SF range (15–27), the average speed is 0.12 ± 0.097 m/s for dc-c = 2∼4 μm. Speed increases as SF increases and dc-c decreases.
The experimental propagation speed in 4-AP/low-Ca2+ was compared with the simulated propagation speeds with the 4-AP/Ca2+-free kinetics in silico. The propagation speed across the network was evaluated based on the action potential peak time delay from each row's middle cell (namely, cell 5 of each row; Fig. 1a). This is because the middle cells experience the strongest field effect compared with other cells in the row according to Equations 1 and 2. We recorded action potential waveforms and calculated the propagation speeds by taking the distance traveled from Row A to Row C divided by the total action potential delay time (Δt1 + Δt2). Figure 5c shows an example of membrane potential signals with dc-c of 2.94 μm and SF set to 20 in the middle of the physiological range. Through only the electrical field effect in the network, the activity propagated from Row A to Row C with propagation speed of 0.093 m/s. Among 180 simulated trials with random cell-to-cell distance dc-c and physiological stacking factor SF values, the field effect driven activity in the model propagated at a mean speed of 0.23 ± 0.096 m/s, 0.10 ± 0.048 m/s, and 0.05 ± 0.020 m/s for trials with mean dc-c = 2, 3, and 4 μm, respectively, with a total mean speed of 0.12 ± 0.097 m/s; the propagation speed increased with higher values of SF (Fig. 5d).
Blocking the endogenous field (in vitro) and increasing cellular distance (in silico and in vitro) both result in a decrease in speed
To determine whether electric fields directly affect the speed of propagation, two electrodes were positioned to generate a DC electric field parallel to the dendritic tree main axis thereby opposing the endogenous field (Fig. 6b). Without stimulation, the average delay between two events obtained from the two recording electrodes was 66.01 ± 1.01 ms (42 spike-pair, 3 slices). With a field of 1 mV/mm applied across the cell layer the average delay increased to 74.86 ± 0.99 ms (40 spike-pair, 2 slices), resulting in a 13% decrease of the speed (Fig. 6c). Varying the field to 3 and 5 mV/mm resulted in 81.85 ± 1.05 ms (35 spike-pair, 2 slices) and 121.58 ± 15.67 ms (34 spike-pair, 2 slices) in delay time, respectively. This corresponds to 24% (3 mV/mm) and 84% (5 mV/mm) decreases in speed. These results confirm that the propagation mechanism of spontaneous activity in the hippocampus is consistent with electric fields.
The in silico model predicted that the speed of propagation should decrease with increasing distance between neurons. When setting dc-c = 3 μm as the control group, the propagation speed increased by 130% when dc-c decreased to ∼2 μm, and decreased by 50% when mean dc-c increased to ∼4 μm (Fig. 6d). To test this prediction, we subsequently performed osmolarity experiments on longitudinal slices in 4-AP solution in vitro and found a similar relationship between the change in extracellular space volume and the resulting 4-AP-induced spike propagation speed. By decreasing the osmolarity of 4-AP aCSF (cell swelling and dc-c decreases), the time delay between signals measured along the CA3 layer decreased from 10.12 ± 3.22 ms (n = 41 spike-pairs from 2 slices in normal osmolarity) to 4.53 ± 2.59 ms (n = 73 spike-pairs from the same 2 slices in low osmolarity >10 min after dilution). With a measured distance between the two glass pipettes equal to 0.8 mm, a 125% increase in speed was obtained. Conversely, by increasing the osmolarity of 4-AP aCSF (cell shrinkage and dc-c increases), the time delay increased from 5.95 ± 1.12 ms (26 spike-pair from 2 slices in normal osmolarity) to 9.76 ± 1.78 ms (50 spike-pair from the same 2 slices in high osmolarity), corresponding to a 46.8% decrease in speed (Fig. 6e). These results confirm the predictions of the model regarding the effect of cell-to-cell distance on the speed of propagation.
Electrical field propagation of 0.1 m/s also occurs in physiological conditions in silico
Previous experimental studies suggested that physiological propagations, such as theta wave also exhibits a traveling speed of 0.1 m/s (Cappaert et al., 2009; Lubenov and Siapas, 2009). With normal aCSF kinetics, the modeled cell produced an intracellular signal that captured physiological action potential characteristics upon initial stimulation (Fig. 7a). The speed and network field amplitude were collected with random dc-c centered at 2 μm and with physiological SF range (N = 40: n = 10 trials with random cell-to-cell distance for mean dc-c = 2 μm and variance = 0.1 μm and physiological SF = 15, 20, 25, and 30). Within the physiological range of SF, the mean propagation speed was 0.11 ± 0.03 m/s (Fig. 7c,e) and the field amplitude ranged from 2.33 to ∼3.06 mV/mm (Fig. 7b,d). These results imply that electrical field effect alone can produce neural propagation not only in pathologic epileptiform-inducing environments, but also in networks with normal channel kinetics.
Figure 7.
Electrical field-induced spiking event and its propagation with physiological channel kinetics. a, Using normal channel kinetics, simulated pyramidal cells fire at an intracellular stimulation threshold of 0.092 nA/10 ms, and the action potential exhibits normal action potential characteristics. b, A sample set of extracellular field recording with SF = 20 and dc-c = 1.93 μm. The field amplitude is 0.68, 0.72, and 1.43 mV/mm for Row A, B, and C layers, resulting a total network field amplitude of 2.83 mV/mm. c, A sample set of intracellular recording from Row A, B, and C middle cells with SF = 20 and dc-c = 1.93 μm. The total propagation delay was 0.3 ms, and with a traveling distance of 33.86 μm (3 soma diameters plus 2 dc-c), the speed is 0.11 m/s. d, Network field amplitude at various SF with mean dc-c = 2 μm (n = 10 and variance = 0.1 μm for each SF). The field amplitude increases with SF, and within physiologic SF range, network field amplitude ranges from 2.33 to 3.06 mV/mm is well within the physiologic range observed in vitro. e, Propagation speed at various values of SF and dc-c varying a mean of ∼2 μm (n = 10 and variance = 0.1 μm for each SF). The speed increases with SF, and within physiologic SF range, the mean propagation speed is ∼0.1 m/s.
Parameter sensitivity analysis indicates that the model is consistent with known applied field effects and robust to changes in intrinsic parameters (pathologic condition)
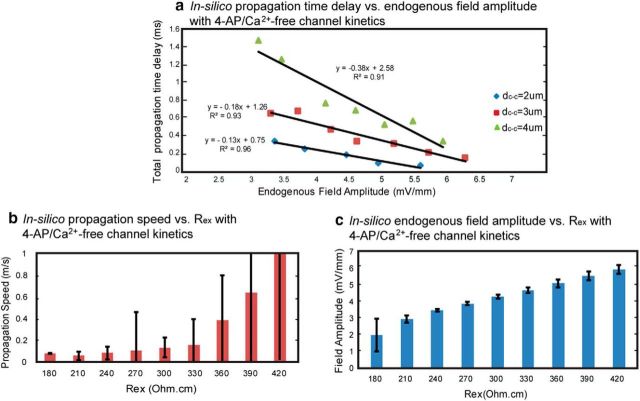
Previous studies related to the effect of an externally applied field on the speed of a traveling wave both in individual hippocampal CA1 pyramidal cells and a network of neocortical cells showed that an excitatory (or depolarizing) field can enhance the propagation speed (Richardson et al., 2005; Radman et al., 2007). Our results confirmed this relationship but with an endogenous electrical field. For both pathologic and physiologic conditions, as the field amplitude increased due to the increasing SF, the resulting speed also increased (Figs. 4b, right, 5d, for the pathologic condition; Fig. 7d,e for the physiological condition). Further, we found an inversely-linear relationship between the field amplitude and the propagation time delay for every cell-to-cell distance group (Fig. 8a), similar to the inversely-linear relationship between applied field and changes in action potential delay in a single cell shown by Radman et al. (2007). Changing the extracellular resistivity (Rex) also affected the field amplitude thus the propagation speed. We examined the effect on the propagation speed with ±40% change of the Rex value (n = 3 with dc-c = 2 μm, 3 μm, and 4 μm for each Rex). The speed increased with a larger value of Rex (Fig. 8b) because of the resulting higher field amplitude (Fig. 8c) within the physiologic range, but the effect was not significant (ANOVA one-way analysis and one-sample t test) for field amplitude or speed. These results indicate that the field effect does not depend on one important variable involving the field amplitude, namely the extracellular resistance within the physiological range of SF values. We also examined the dependence on membrane-specific resistance and capacitance (data not shown) and found that the effect is robust to changes in those variables as well.
Figure 8.
Field amplitude and extracellular resistivity effect on the propagation time delay and speed. a, Relationship between simulated action potential traveling delay time (from Row A to Row C) and endogenous field amplitude generated with various SF values in 4-AP/no Ca condition. For each dc-c group, the time delay decreases linearly as field amplitude increases. b, Propagation speed increases with extracellular resistivity (Rex; n = 3 for each Rex with dc-c = 2, 3, and 4 μm) but there is no significant differences among groups (p > 0.05 with one-way ANOVA). Within the physiologic range or Rex (250∼380 Ωcm, Anatassiou et al., 2011), the speed ranges from ∼0.1 to ∼0.4 m/s. c, Endogenous field amplitude increases with Rex (n = 3 for each value of Rex with dc-c = 2, 3, and 4 μm) but there is no significant differences among groups (p > 0.05 with one-way ANOVA). Within physiologic Rex range, field amplitude ranges from ∼4 to ∼5 mV/mm.
Discussion
The observation that neural activity can propagate at a speed of ∼0.1 m/s in both the physiologic and pathologic conditions (Haas and Jefferys, 1984; Miles et al., 1988; Quilichini et al., 2002; Cappaert et al., 2009; Lubenov and Siapas, 2009; Kibler and Durand, 2011; Liu et al., 2013) suggests that a common mechanism for neural communication is involved. Despite the fact that chemical synapses and gap junctions usually maintain propagation, 4-AP-induced spikes still persisted in the presence or absence of chemical/electrical synapses (Zhang et al., 2014), thus, the mechanism could not be synaptic or gap junction mediated. Previous studies related to such type of propagation also eliminated the possibility for axonal conductions and ionic diffusion (Miles et al., 1988; Weissinger et al., 2000; Lian et al., 2001; Meeks and Mennerick, 2007; Jensen, 2008; Kibler and Durand, 2011) as their speeds are not consistent with a speed of 0.1 m/s. The only remaining explanation for the governing mechanism is endogenous electrical field effect. The field effect is said to be endogenous when no external current or voltage source generate the field; rather, it is the electrical field generated by the cells firing themselves that in turn influence the behavior of the adjacent cells in the same network. The electrical field effect is generally thought to be too small to give rise to action potentials (Chan and Nicholson, 1986; Anastassiou et al., 2011). However, several studies have shown that electrical fields applied externally can modulate neural activity at low amplitudes or with amplitudes that match the endogenous levels (Chan and Nicholson, 1986; Radman et al., 2007; Fröhlich and McCormick, 2010; Anastassiou et al., 2011). Francis et al. (2003) demonstrated that a neural network is much more sensitive to field modulation than single neurons, and that the highly structured and dense cellular packing in hippocampus makes this region of the brain highly sensitive to field effects. Moreover, endogenous electrical fields generated by antidromic activation can trigger after-discharges in the hippocampus in the absence of synaptic transmission, indicating that transient extracellular electrical fields (filed effect interaction) could be responsible for the observed synchrony (Taylor and Dudek, 1982). However, there is little or no information in the literature concerning the ability of electric field to sustain a regenerative wave propagating in densely packed neural network. Yet, the propagation of 4-AP-induced spikes (at 0.1 m/s) recently observed in the hippocampus in the absence of synapses and gap junctions was attributed to field effects by default (Zhang et al., 2014).
In this study, we used computer simulations in silico to test the feasibility of field effect as a propagation mechanism of action potentials within a hippocampal CA1 pyramidal network and performed experiments in vitro to confirm both speed and field amplitude results. Further, by applying a blocking “anti” field into the network in vitro, we observed speed reduction. The simulation in silico also provided information on how endogenous field strength (amplitude) relates to the propagation speed, which is consistent with previous experimental studies, as well as how robust the propagation speed is in regard to internal cell and network parameters. Finally, the model made predictions that were confirmed experimentally concerning the relation between cell distance and speed, and that the speed was not related to extracellular resistivity, membrane capacitance, or membrane resistance (in silico only). Together, this study confirms that the electric field effect with amplitude within the physiologic range can be sufficient to generate propagation of neural activity. Furthermore, we provided a demonstration that the speed of propagation is determined by the amplitude of the field.
The cellular network in the simulation consists of 30 hippocampal CA1 pyramidal cell locations (10 cells/row × 3 rows; Fig. 1), where cell-to-cell distances were set between ∼2 and ∼4 μm (Kurt et al., 2004; Anastassiou et al., 2011). An arbitrary SF was used to take into account the actual number of cells around each location. Its value was constrained by the physiological cell density in hippocampal CA1 region (physiological SF range = 15∼28 based on cell density). The model was validated as the field amplitude from the simulation with pathologic kinetics (∼3 to ∼6 mV/mm; Fig. 4b) and physiologic kinetics (∼2 to ∼3 mV/mm; Fig. 7d) matched the range obtained in our experimental recordings in hippocampus (2.5–5 mV/mm; Fig. 4a) and in the literature of recorded field amplitude in hippocampal slices (Ghai et al., 2000; Radman et al., 2007; ∼5 mV/mm) and in cortex (up to 4.52 mV/mm; Fröhlich and McCormick, 2010). Finally, the model successfully reproduced physiological intracellular spike characteristics both in a 4-AP/Ca2+-free (Fig. 4c) and in normal aCSF environment (Fig. 7a). These results indicate that the model is well validated to simulate a physiological system composed of layers of neurons.
Upon initial stimulation, simulated transverse propagation of the activity was observed both with 4-AP/Ca2+-free and normal channel kinetics in the simulation at an average speed of ∼0.1 m/s (Figs. 5c,d, 7c,e), matching the 0.1 m/s speed reported for 4-AP-induced spike propagation (Miles et al., 1988; Quilichini et al., 2002; Kibler and Durand, 2011; Liu et al., 2013), low Ca2+ field-bursting (Haas and Jefferys, 1984), and physiologic theta oscillations both in vitro (Cappaert et al., 2009) and in vivo (Lubenov and Siapas, 2009). Experiments in the CA1 region of unfolded hippocampus under 4-AP/low-Ca2+ condition in vitro also showed the same speed range (Fig. 5a,b). By applying an “anti” fields of matching amplitudes as the recorded field amplitudes in real time, a reduction of speed was seen (Fig. 6c). Together, both in silico and in vitro results indicate that field effect itself can be solely responsible for neural activity propagation with a speed of 0.1 m/s in a cellular network independently of channel kinetics.
Further, the electrical field effect is consistent with the results of the experiments on the effect of osmolarity (extracellular space) on neural propagation speed. In the study, the simulation predicted that a smaller dc-c could induce a higher speed (Fig. 6d). In vitro experiments confirmed this prediction, whereby 4-AP-induced epileptiform activity in hippocampal longitudinal slices traveled faster when extracellular osmolarity was lowered (cells swelling), and vice versa (Fig. 6e). This also matches with the relationship between osmolarity and propagation speed in low Mg2+-induced seizure activity in hippocampal CA1 region (Shahar et al., 2009). These results confirmed that the strength of electrical field plays a significant role in determining the neural activity propagation speed. For instance, a smaller dc-c increases the endogenous field amplitude according to Equations 1 and 2. Experiments from Francis et al. (2003) and Vigmond et al. (1997) also confirmed that a more tightly packed network increases the electrical impedance and field sensitivity between cells, thereby strengthening the field amplitude. On the other hand, parameter sensitivity analysis showed that the propagation speed is highly influenced by change in endogenous field amplitude but not by intrinsic parameters. It has been suggested that there exists a linear relationship between externally applied field amplitude and changes in action potential timing in a single cell such that the stronger the field strength, the earlier the cell fires (Radman et al., 2007). Interestingly, we found that the endogenous field amplitude and propagation delay share a similar inverse linear relationship (Fig. 8a), where the time delay decreases (speed increases) as field amplitude increases. Parameter sensitivity analysis showed that parameters that affect minimally the field amplitude, such as extracellular resistivity (Fig. 8b,c), membrane capacitance (data not shown), and passive membrane resistance (data not shown) in turn do not affect propagation speed. These results show that network endogenous field amplitude is the key factor in determining the propagation speed induced by field effect, and the speed is robust to extracellular resistivity, membrane capacitance, and membrane resistance. Therefore, the propagating mechanism is dependent on the network properties (eg, cell density) but not individual cell properties, suggesting that this phenomenon may be more general than originally anticipated.
Thus, the hypothesis that the propagation of neural activity can be carried out solely by electric fields is consistent with experimental data as well as computer simulations. The fact that the speed of the propagation remains constant under different experimental conditions can be explained by the presence of an electric field effect associated with neural firing generated by the network configuration and not by the properties of individual cells. This electrical field effect is revealed when synaptic transmission is blocked and both pathologic and normal propagation can exist simultaneously with field effect governing short range or local propagation, where synaptic transmission may govern long-range propagation and communication.
Conclusion
This study shows that in a simulated hippocampal pyramidal cell network, an electrical field of ∼2–5 mV/mm can underlie the transverse propagation of action potentials with a speed of ∼0.1 m/s, both with pathologic (4-AP/CA2+-free) and physiologic channel kinetics. This field-effect-induced propagation speed matches with the speed of 4-AP-induced activity, as well as theta waves recorded from both in vitro and previous in vivo experiments. Parameter sensitivity analysis revealed that the endogenous field amplitude is the main factor that plays an important role in influencing the speed (there exists an inverse linear relationship between field amplitude and propagation time delay), whereas intrinsic parameters, such as passive and active membrane properties, do not significantly affect the speed. Finally, it was shown both in experiments and simulations that a tightly packed network (either in silico or induced by low osmolarity) can produce an increase in propagation speed (and vice-versa), confirming that extracellular-space induced changes in field amplitude can influence speed. Moreover, applied blocking electric fields can significantly affect the speed of propagation. Together, these results reveal a novel propagation mechanism consistent with ephaptic field effects that could lead to better understanding of neural activity propagation in both the abnormal condition, such as epilepsy, or the normal condition, such as theta waves.
Footnotes
The experimental work was funded by National Institute of Health (National Institute of Neurological Disorders and Stroke) Grant 1R01NS060757-01. We thank Drs. Kenneth Gustafson, Hillel Chiel, Thomas Ladas, and Luis Gonzalez-Reyes for valuable comments and discussions.
The authors declare no competing financial interests.
References
- Anastassiou CA, Perin R, Markram H, Koch C. Ephaptic coupling of cortical neurons. Nat Neurosci. 2011;14:217–223. doi: 10.1038/nn.2727. [DOI] [PubMed] [Google Scholar]
- Bikson M, Ghai RS, Baraban SC, Durand DM. Modulation of burst frequency, duration, and amplitude in the zero-Ca(2+) model of epileptiform activity. J Neurophysiol. 1999;82:2262–2270. doi: 10.1152/jn.1999.82.5.2262. [DOI] [PubMed] [Google Scholar]
- Cappaert NL, Lopes da Silva FH, Wadman WJ. Spatio-temporal dynamics of theta oscillations in hippocampal-entorhinal slices. Hippocampus. 2009;19:1065–1077. doi: 10.1002/hipo.20570. [DOI] [PubMed] [Google Scholar]
- Chan CY, Nicholson C. Modulation by applied electric fields of Purkinje and stellate cell activity in the isolated turtle cerebellum. J Physiol. 1986;371:89–114. doi: 10.1113/jphysiol.1986.sp015963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deuchars J, Thomson AM. CA1 pyramid-pyramid connections in rat hippocampus in vitro: dual intracellular recordings with biocytin filling. Neuroscience. 1996;74:1009–1018. doi: 10.1016/0306-4522(96)00251-5. [DOI] [PubMed] [Google Scholar]
- Francis JT, Gluckman BJ, Schiff SJ. Sensitivity of neurons to weak electric fields. J Neurosci. 2003;23:7255–7261. doi: 10.1523/JNEUROSCI.23-19-07255.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fröhlich F, McCormick DA. Endogenous electric fields may guide neocortical network activity. Neuron. 2010;67:129–143. doi: 10.1016/j.neuron.2010.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghai RS, Bikson M, Durand DM. Effects of applied electric fields on low-calcium epileptiform activity in the CA1 region of rat hippocampal slices. J Neurophysiol. 2000;84:274–280. doi: 10.1152/jn.2000.84.1.274. [DOI] [PubMed] [Google Scholar]
- Gold C, Henze DA, Koch C. Using extracellular action potential recordings to constrain compartmental models. J Comput Neurosci. 2007;23:39–58. doi: 10.1007/s10827-006-0018-2. [DOI] [PubMed] [Google Scholar]
- Golomb D, Yue C, Yaari Y. Contribution of persistent Na+ current and M-type K+ current to somatic bursting in CA1 pyramidal cells: combined experimental and modeling study. J Neurophysiol. 2006;96:1912–1926. doi: 10.1152/jn.00205.2006. [DOI] [PubMed] [Google Scholar]
- Haas HL, Jefferys JG. Low-calcium field burst discharges of CA1 pyramidal neurones in rat hippocampal slices. J Physiol. 1984;354:185–201. doi: 10.1113/jphysiol.1984.sp015371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He B. Neural Engineering: bioelectric engineering. Ed 2005. New York: Springer; 2005. Electrical stimulation of the neuromuscular system; p. 503. [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen AL. Control of axonal conduction of high frequency stimulation. PhD Dissertation. 2008:121. [Google Scholar]
- Jinno S, Kosaka T. Stereological estimation of numerical densities of glutamatergic principal neurons in the mouse hippocampus. Hippocampus. 2010;20:829–840. doi: 10.1002/hipo.20685. [DOI] [PubMed] [Google Scholar]
- Kibler AB, Durand DM. Orthogonal wave propagation of epileptiform activity in the planar mouse hippocampus in vitro. Epilepsia. 2011;52:1590–1600. doi: 10.1111/j.1528-1167.2011.03125.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kibler AB, Jamieson BG, Durand DM. A high aspect ratio microelectrode array for mapping neural activity in vitro. J Neurosci Methods. 2012;204:296–305. doi: 10.1016/j.jneumeth.2011.11.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurt MA, Kafa MI, Dierssen M, Davies DC. Deficits of neural density in CA1 and synaptic density in the dentate gyrus, CA3 and CA1, in a mouse model of Down syndrome. Brain Res. 2004;1022:101–109. doi: 10.1016/j.brainres.2004.06.075. [DOI] [PubMed] [Google Scholar]
- Lian J, Bikson M, Shuai J, Durand DM. Propagation of non-synaptic epileptiform activity across a lesion in rat hippocampal slices. J Physiol. 2001;537:191–199. doi: 10.1111/j.1469-7793.2001.0191k.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu JS, Li JB, Gong XW, Gong HQ, Zhang PM, Liang PJ, Lu QC. Spatiotemporal dynamics of high-K+-induced epileptiform discharges in hippocampal slice and the effects of valproate. Neurosci Bull. 2013;29:28–36. doi: 10.1007/s12264-013-1304-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Kayser C, Oeltermann A. In vivo measurement of cortical impedance spectrum in monkeys: implications for signal propagation. Neuron. 2007;55:809–823. doi: 10.1016/j.neuron.2007.07.027. [DOI] [PubMed] [Google Scholar]
- Lubenov EV, Siapas AG. Hippocampal theta oscillations are travelling waves. Nature. 2009;459:534–539. doi: 10.1038/nature08010. [DOI] [PubMed] [Google Scholar]
- Meeks JP, Mennerick S. Action potential initiation and propagation in CA3 pyramidal axons. J Neurophysiol. 2007;97:3460–3472. doi: 10.1152/jn.01288.2006. [DOI] [PubMed] [Google Scholar]
- Miles R, Traub RD, Wong RK. Spread of synchronous firing in longitudinal slices from the CA3 region of the hippocampus. J Neurophysiol. 1988;60:1481–1496. doi: 10.1152/jn.1988.60.4.1481. [DOI] [PubMed] [Google Scholar]
- Perreault P, Avoli M. Effects of low concentrations of 4-aminopyridine on CA1 pyramidal cells of the hippocampus. J Neurophysiol. 1989;61:953–970. doi: 10.1152/jn.1989.61.5.953. [DOI] [PubMed] [Google Scholar]
- Perreault P, Avoli M. 4-Aminopyridine-induced epileptiform activity and a GABA-mediated long-lasting depolarization in the rat hippocampus. J Neurosci. 1992;12:104–115. doi: 10.1523/JNEUROSCI.12-01-00104.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quilichini PP, Diabira D, Chiron C, Ben-Ari Y, Gozlan H. Persistent epileptiform activity induced by low Mg2+ in intact immature brain structures. Eur J Neurosci. 2002;16:850–860. doi: 10.1046/j.1460-9568.2002.02143.x. [DOI] [PubMed] [Google Scholar]
- Radman T, Su Y, An JH, Parra LC, Bikson M. Spike timing amplifies the effect of electric fields on neurons: implications for endogenous field effects. J Neurosci. 2007;27:3030–3036. doi: 10.1523/JNEUROSCI.0095-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richard V, Hogie M, Clozel M, Löffler BM, Thuillez C. In vivo evidence of an endothelin-induced vasopressor tone after inhibition of nitric oxide synthesis in rats. Circulation. 1995;91:771–775. doi: 10.1161/01.CIR.91.3.771. [DOI] [PubMed] [Google Scholar]
- Richardson KA, Schiff SJ, Gluckman BJ. Control of traveling waves in the mammalian cortex. Phys Rev Lett. 2005;94 doi: 10.1103/PhysRevLett.94.028103. 028103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Royeck M, Horstmann MT, Remy S, Reitze M, Yaari Y, Beck H. Role of axonal NaV1.6 sodium channels in action potential initiation of CA1 pyramidal neurons. J Neurophysiol. 2008;100:2361–2380. doi: 10.1152/jn.90332.2008. [DOI] [PubMed] [Google Scholar]
- Schechter LE. The potassium channel blockers 4-aminopyridine and tetraethylammonium increase the spontaneous basal release of [3H]5-hydroxytryptamine in rat hippocampal slices. J Pharmacol Exp Ther. 1997;282:262–270. [PubMed] [Google Scholar]
- Shahar E, Derchansky M, Carlen PL. The role of altered tissue osmolality on the characteristics and propagation of seizure activity in the intact isolated mouse hippocampus. Clin Neurophysiol. 2009;120:673–678. doi: 10.1016/j.clinph.2009.01.014. [DOI] [PubMed] [Google Scholar]
- Shuai J, Bikson M, Hahn PJ, Lian J, Durand DM. Ionic mechanisms underlying spontaneous CA1 neural firing in Ca2+-free solution. Biophys J. 2003;84:2099–2111. doi: 10.1016/S0006-3495(03)75017-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su H, Alroy G, Kirson ED, Yaari Y. Extracellular calcium modulates persistent sodium current-dependent burst-firing in hippocampal pyramidal neurons. J Neurosci. 2001;21:4173–4182. doi: 10.1523/JNEUROSCI.21-12-04173.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor CP, Dudek FE. Synchronous neural afterdischarges in rat hippocampal slices without active chemical synapses. Science. 1982;218:810–812. doi: 10.1126/science.7134978. [DOI] [PubMed] [Google Scholar]
- Vigmond EJ, Perez Velazquez JL, Valiante TA, Bardakjian BL, Carlen PL. Mechanisms of electrical coupling between pyramidal cells. J Neurophysiol. 1997;78:3107–3116. doi: 10.1152/jn.1997.78.6.3107. [DOI] [PubMed] [Google Scholar]
- Warman EN, Durand DM, Yuen GL. Reconstruction of hippocampal CA1 pyramidal cell electrophysiology by computer simulation. J Neurophysiol. 1994;71:2033–2045. doi: 10.1152/jn.1994.71.6.2033. [DOI] [PubMed] [Google Scholar]
- Weissinger F, Buchheim K, Siegmund H, Heinemann U, Meierkord H. Optical imaging reveals characteristic seizure onsets, spread patterns, and propagation velocities in hippocampal-entorhinal cortex slices of juvenile rats. Neurobiol Dis. 2000;7:286–298. doi: 10.1006/nbdi.2000.0298. [DOI] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik. 1973;13:55–80. doi: 10.1007/BF00288786. [DOI] [PubMed] [Google Scholar]
- Wimmer VC, Reid CA, Mitchell S, Richards KL, Scaf BB, Leaw BT, Hill EL, Royeck M, Horstmann MT, Cromer BA, Davies PJ, Xu R, Lerche H, Berkovic SF, Beck H, Petrou S. Axon initial segment dysfunction in a mouse model of genetic epilepsy with febrile seizures plus. J Clin Invest. 2010;120:2661–2671. doi: 10.1172/JCI42219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M, Ladas TP, Qiu C, Shivacharan RS, Gonzalez-Reyes LE, Durand DM. Propagation of epileptiform activity can be independent of synaptic transmission, gap junctions, or diffusion and is consistent with electrical field transmission. J Neurosci. 2014;34:1409–1419. doi: 10.1523/JNEUROSCI.3877-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]