Privacy Risks from Genomic Data-Sharing Beacons

Abstract

The human genetics community needs robust protocols that enable secure sharing of genomic data from participants in genetic research. Beacons are web servers that answer allele-presence queries—such as “Do you have a genome that has a specific nucleotide (e.g., A) at a specific genomic position (e.g., position 11,272 on chromosome 1)?”—with either “yes” or “no.” Here, we show that individuals in a beacon are susceptible to re-identification even if the only data shared include presence or absence information about alleles in a beacon. Specifically, we propose a likelihood-ratio test of whether a given individual is present in a given genetic beacon. Our test is not dependent on allele frequencies and is the most powerful test for a specified false-positive rate. Through simulations, we showed that in a beacon with 1,000 individuals, re-identification is possible with just 5,000 queries. Relatives can also be identified in the beacon. Re-identification is possible even in the presence of sequencing errors and variant-calling differences. In a beacon constructed with 65 European individuals from the 1000 Genomes Project, we demonstrated that it is possible to detect membership in the beacon with just 250 SNPs. With just 1,000 SNP queries, we were able to detect the presence of an individual genome from the Personal Genome Project in an existing beacon. Our results show that beacons can disclose membership and implied phenotypic information about participants and do not protect privacy a priori. We discuss risk mitigation through policies and standards such as not allowing anonymous pings of genetic beacons and requiring minimum beacon sizes.

Introduction

In the coming decade, a great deal of human genomic data, along with linked phenotypes in electronic health records, will be collected in the context of health care. A major goal of the human genomics community is to enable efficient sharing, aggregation, and analysis of these data in order to understand the genetic contributors of health and disease. Previous large-scale data-sharing approaches have had limited success because of the potential for privacy breaches and risks of participant re-identification. Homer et al.¹ and others^{2, 3, 4, 5} showed that subjects in a genome-wide association study could be re-identified with the use of allele frequencies, resulting in the removal of publicly available allele-frequency data.⁶

The Beacon Project by the Global Alliance for Genomics & Health (GA4GH) aims to simplify data sharing through a web service (“beacon”) that provides only allele-presence information. Users can query institutional beacons for information about genomic data available at the institution. Queries are of the form “Do you have a genome that has a specific nucleotide (e.g., A) at a specific genomic position (e.g., position 11,272 on chromosome 1)?” and the beacon server can answer “yes” or “no.” Beacons are intended to be easily set up and to allow data sharing while protecting participant privacy. By providing only allele-presence information, beacons are safe from attacks that require allele frequencies.^{1, 2, 3, 4, 5} However, a privacy breach from a beacon would be troubling given that beacons often summarize data with a particular disease of interest. For instance, identifying that a given genome is part of the SFARI beacon, which contains genomic data from families with a child affected by autism spectrum disorder, means that the individual belongs to a family where some member has autism spectrum disorder. Thus, beacons could leak not only membership information but also phenotype information. Although genetic privacy is protected to some extent by the Genetic Information Nondiscrimination Act (GINA), the offered protections are limited, and GINA does not apply to long-term care insurance, life insurance, disability insurance, or other special cases.⁷ Therefore, all data-sharing mechanisms, including beacons, must protect participant privacy.

To examine the question of re-identification in a beacon, we have developed a likelihood-ratio test (LRT) that uses allele presence or absence responses from a beacon to predict whether a given individual genome is present in the beacon database. Our approach is independent of allele frequencies. The statistical properties of the LRT guarantee that it is the most powerful test for this problem. A variation of our LRT can detect relatives of the query individual in the beacon. Our results suggest that anonymous-access beacons do not protect individual privacy and are open to re-identification attacks. As a result, they can also disclose phenotype information about individuals whose genomes are present in the beacon.

Material and Methods

We assume a beacon composed of unrelated individuals from a single population. Given query q = {C, P, A}, the beacon answers “yes” (represented as 1) if allele A is an alternate allele at position P on chromosome C and has a non-zero frequency in the sample used for constructing the beacon, and it answers “no” (represented as 0) otherwise. We consider only bi-allelic SNPs for our analysis.

Thus, given a set of n queries Q = {q₁, …, q_n}, the beacon returns a set of responses R = {x₁, …, x_n}. For our scenario, we assume that the attacker has access to more information—the number of individuals (N) in the beacon database and the site frequency spectrum (SFS) of the population in the beacon—parameterized as a beta distribution with shape parameters (a′, b′). Thus, we assume that alternate allele frequencies f for all SNPs observed in the population are distributed as f ∼ beta(a′, b′).

For our attack scenario, we assume a setting identical to that used by Homer et al.¹ and others. In this setting, the attacker receives a VCF file listing all the SNP positions at which the query individual has an alternate allele and the genotype calls at the corresponding positions. The attacker then queries the beacon for all heterozygous positions by using the alternate allele listed in the VCF and obtains the set of responses R from the beacon. We develop a LRT that can use the responses R to decide whether the query genome is in the beacon.

If the query individual is present in the beacon, then every allele in the query genome must be present in the beacon. Thus, the beacon will return a “yes” (1) response to every query. If a query individual is not present in the beacon, then the beacon response will be “yes” (1) if some individual in the beacon has the allele and “no” (0) otherwise. By calculating the likelihood of the responses, we can differentiate query individuals in the beacon from those not in the beacon. Our approach for re-identifying individuals within a beacon is based on a LRT that uses this information. For each query genome, we calculate the likelihood of the beacon responses to n allele-presence queries under the null hypothesis that a given individual is not in the beacon and the alternative hypothesis that the given individual is in the beacon. We then calculate the test statistic as the ratio of the two likelihoods.

To make our LRT generalizable across populations, we will remove direct dependence on allele frequencies given that frequencies can vary considerably for a given allele across populations. Instead, we will allow our test to depend on the shape of the SFS, which is described by (a′, b′), the parameters of the beta distribution. Although allele frequencies for a given allele can vary considerably across populations, the SFS parameters for most populations are similar to each other (Modeling SFSs by Beta Distributions in Appendix A). Therefore, the results from a test that depends on the shape of the SFS but is independent of the actual allele frequencies can be generalized to many populations (Figure S1).

Our LRT evaluates the likelihood of the beacon response under two possible hypotheses.

• •Null hypothesis H₀: query genome is not in the beacon database.
• •Alternative hypothesis H₁: query genome is in the beacon database.

LRT

In an ideal setting, we would expect x₁ = x₂ … = x_n = 1 if a query genome g is in the beacon B. In practice, because of sequencing errors and differences in variant-calling pipelines, we might have some mismatches between the query copy of a genome and its copy in the beacon. We assume that this happens with probability δ.

Let the alternate allele frequency at the SNP corresponding to query q_i be f_i. Because the beacon is only queried at the positions where the query genome is heterozygous, f_i is not distributed as beta(a′, b′) but shows an ascertainment bias. We can show that f_i ∼ beta(a, b), where a = a′ + 1 and b = b′ + 1 in theory (Posterior Distribution of Allele Frequencies in Appendix A).

The log-likelihood of a response set R = {x₁, …, x_n} can be written as

$$L\left(R\right)=\sum _{i=1}^N{x}_i\text{log}P\left(x_i=1\right)+\left(1-x_i\right)\text{log}P\left(x_i=0\right).$$ (Equation 1)

For the LRT, we need to evaluate this log-likelihood under the null hypothesis and the alternative hypothesis. The null hypothesis is that the query genome is not present in the beacon, and the alternative hypothesis is that the query genome is present in the beacon.

We can show that under the alternative hypothesis, the log-likelihood can be calculated as

$$L_{H_1}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}\left(1-\delta D_{N-1}\right)+\left(1-x_i\right)\text{log}\left(\delta D_{N-1}\right),$$ (Equation 2)

where D_{N − 1} is the probability that none of N − 1 genomes has an alternate allele at a given position (see Likelihood under the Alternative Hypothesis in Appendix A).

Similarly, the log-likelihood under the null hypothesis is

$$L_{H_0}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}\left(1-D_N\right)+\left(1-x_i\right)\text{log}\left(D_N\right)$$ (Equation 3)

(see Likelihood under the Null Hypothesis in Appendix A).

The log of the likelihood-ratio statistic can then be written as

$$\begin{array}{c}\text{Λ}=L_{H_0}\left(R\right)-L_{H_1}\left(R\right)\\ =n\text{log}\left(\frac{D_N}{\delta D_{N-1}}\right)+\text{log}\left(\frac{\delta D_{N-1}\left(1-D_N\right)}{D_N\left(1-\delta D_{N-1}\right)}\right)\sum _{i=1}^n{x}_i\\ =nB+C\sum _{i=1}^n{x}_i,\end{array}$$

where we have defined $B=\text{log}\left(D_N/\delta D_{N-1}\right)$ and $C=\text{log}\left(\delta D_{N-1}\left(1-D_N\right)/D_N\left(1-\delta D_{N-1}\right)\right)$ (see LRT Statistic in Appendix A). For $\delta <\left(D_N/D_{N-1}\right)$, we have C < 0. In practice, because $N\gg 1$, $D_N\approx D_{N-1}$, and mismatch rate $\delta \ll 1$, this will always be true.

Therefore, the LRT statistic can be stated as

$$\text{Λ}=nB+C\sum _{i=1}^n{x}_i.$$ (Equation 4)

The LRT stated above can be understood to be a test for a simple null hypothesis H₀: θ = 1 − D_N against a simple alternative hypothesis H₁: θ = 1 − δD_N when we are given {x₁, …, x_n} sampled as x_i ∼ Bernoulli(θ). By the Neyman-Pearson lemma, the LRT is the most powerful test for a given test size α.

Binomial Test

The null hypothesis is rejected if Λ < t for some threshold t. Let t_α be such that P(Λ < t_α | H₀) = α. This is equivalent to rejecting the null hypothesis if ${\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }$, where $t_{\alpha }^{\prime }=\left(t_{\alpha }-nB/C\right)$.

Because the x_i are independent and identically distributed (i.i.d.) under both hypotheses, ${\sum }_{i=1}^n{x}_i|H_0\sim \text{binomial}\left(n,1-D_N\right)$ and ${\sum }_{i=1}^n{x}_i|H_1\sim \text{binomial}\left(n,1-\delta D_{N-1}\right)$. Therefore, the power of the exact test can be calculated as $1-\beta =P\left({\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_1\right)$, where $t_{\alpha }^{\prime }$ is chosen such that $P\left({\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_0\right)=\alpha$.

A sufficient statistic for the LRT is the number of “yes” responses from the beacon.

Relationship between the Number of Queries Required and Beacon Size

In the null and alternative hypotheses, x_i is a Bernoulli random variable. Therefore, by the central limit theorem, the LRT statistic has a Gaussian distribution. We can therefore use the parameters of the Gaussian distribution to obtain a relationship between the number of queries (required for achieving a desired power and false-positive rate) and the number of individuals in the beacon.

Let μ₀ and σ₀ be the mean and SD, respectively, of the LRT statistic under the null hypothesis, and let μ₁ and σ₁ be the corresponding values under the alternative hypothesis.

For an LRT statistic with false-positive rate α, power 1 − β, and a normal distribution, we have that

$${\mu }_0+{\sigma }_0{z}_{\alpha }={\mu }_1+{\sigma }_1{z}_{1-\beta },$$ (Equation 5)

where z_y is the y quantile of the standard normal distribution.

For the LRT we describe, this relationship is equivalent to

$$\frac{n}{N^{a^{\prime }+1}}=\frac{{\left(z_{\alpha }-z_{1-\beta }\sqrt{\delta }\right)}^2\text{Γ}\left(b^{\prime }+1\right)2^{a^{\prime }+1}}{\text{Γ}\left(a^{\prime }+b^{\prime }+2\right)}$$ (Equation 6)

(see Gaussian LRT Power Approximation in Appendix A). The right-hand side of the equation is independent of both n and N for a specified false-positive rate α and power 1 − β. Thus, we have that $n\propto N^{a^{\prime }+1}$.

LRT for Detecting Relatives

The relatedness of two individuals can be parameterized with a single parameter ϕ, which is the probability that the two individuals share an allele at a single SNP. Thus, identical twins have ϕ = 1, parent-offspring and sibling pairs have ϕ = 0.5, first cousins have ϕ = 0.25, and so on.

The likelihood for the null hypothesis remains the same as before. Under the alternate hypothesis (a relative of the query genome g with relatedness ϕ is present in beacon B), the log-likelihood is given by

$$L_{H_1}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}\left(1-\delta D_{N-1}-\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N-\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-\frac{1}{2}}\right)+\left(1-x_i\right)\text{log}\left(\delta D_{N-1}+\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N+\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-\frac{1}{2}}\right)$$ (Equation 7)

(see Likelihood under the Alternate Hypothesis in Appendix B).

We can use this form to calculate the LRT statistic for this setting. Here, the exact test uses ${\sum }_{i=1}^n{x}_i$ as the sufficient statistic (as before), and the sufficient statistic is binomially distributed under both hypotheses. The distributions are given by ${\sum }_{i=1}^n{x}_i|H_0\sim \text{binomial}\left(n,1-D_N\right)$ and ${\sum }_{i=1}^n{x}_i|H_1\sim \text{binomial}\left(n,1-\delta D_{N-1}-\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N-\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-(1/2)}\right)$.

Therefore, the power of the exact test can be calculated as $\beta =P\left({\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_1\right)$, where $t_{\alpha }^{\prime }$ is chosen such that $P\left({\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_0\right)=\alpha$.

Simulation Experiments

We simulated 500,000 SNPs in a sample of 1,000 diploid individuals. Alternate allele frequencies were sampled from a multinomial distribution with probabilities obtained from the expected allele-frequency distribution for a standard neutral model under the assumption of a population size of 10,000 individuals.

We constructed a beacon by using the 1,000 simulated individuals. The query set of individuals consisted of

• •200 diploid individuals from the beacon
• •200 diploid individuals not in the beacon and whose genotypes were simulated according to the generated allele frequencies at all SNPs.

For initial experiments, the mismatch rate between the beacon and query copies of the same genomes was set to 10⁻⁶ to simulate near-ideal data.

The null distribution of the LRT statistic was obtained with the exact-test calculation for the 200 individuals not in the beacon. Power was calculated as the proportion of successfully rejected tests (out of 200) for the query genomes in the beacon.

Detecting Relatives

To examine whether relatives could be identified from the beacon, we used 200 individuals from the beacon to generate query genomes with varying degrees of relatedness to the original individual.

Effect of Noise

Genome sequencing is more error prone than array genotyping. Even with high-coverage data, biological replicates of the same individual could have 1%–5% SNPs unique to each replicate. On the same sequenced sample, different variant-calling pipelines can produce SNP calls at positions that might differ from each other. We model this in our simulation by allowing for a mismatch probability (δ) that for a query individual who is in the beacon and is heterozygous at the query SNP, the copy in the beacon is a homozygous reference, i.e., the beacon will (erroneously) return 0 as the response to the query. Table S2 shows the levels of mismatch modeled in our experiments.

Experiments with Real Data

1000 Genomes Phase 1 CEU Beacon

We created a beacon by using the CEU population (Utah residents with ancestry from northern and western Europe from the CEPH collection) from phase 1 of the 1000 Genomes Project.⁸ Of the 85 CEU samples present in phase 1, 65 were used in the beacon. 20 samples from the beacon and the remaining 20 samples were used as query genomes. Figure S4 shows the setup of the 1000 Genomes phase 1 CEU beacon.

To test the effect of censoring on power, we constructed a beacon by using the same data as above, except that the beacon always responded “no” to queries for singletons. We then used whole genomes to query the beacon, as before.

To test whether sharing SNP array data was more secure than sharing whole genomes, we repeated the setup of Figure S4 with Affymetrix array data for the CEU samples. We then used SNP array data to query the beacon.

Combining Multiple Datasets

We used the scheme of Figure S5 to create beacons that contained either a single population (65 CEU individuals) or multiple populations (a CEU + YRI [Yoruba in Ibadan, Nigeria] beacon with 32 CEU and 33 YRI individuals and a CEU + JPT [Japanese in Tokyo, Japan] beacon with 32 CEU and 33 JPT individuals). We used 40 CEU individuals as query individuals, 20 of whom belonged to all beacons and 20 of whom belonged to none of the beacons.

Re-identifying a Personal Genome Project Individual

To test our method on existing beacons, we selected from the Personal Genome Project (PGP)⁹ a single genome (ID hu48C4EB or PGP 183). We chose 1,000 heterozygous SNPs from the selected individual’s genome and used the GA4GH Beacon Network query interface to query all existing beacons for the alternate allele at the chosen SNPs. If a beacon of size N produced k “yes” responses to n queries, the p value was calculated under the null hypothesis as $P\left(x\ge k;x\sim \text{binomial}\left(n,1-D_N\right)\right)$.

Through metadata (see Web Resources), we were able to ascertain that the selected individual was present in the PGP beacon and the Kaviar¹⁰ beacon.

Results

Re-identification in a Simulated Beacon

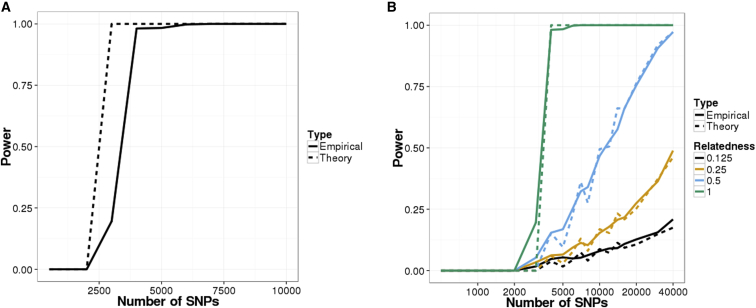
We validated our LRT framework by simulating a beacon with 1,000 individuals and 500,000 total SNPs. From the power curve (Figure 1A), we can see that the LRT had more than 95% power to detect whether an individual was in the beacon with just 5,000 SNP queries. We also see that our theoretical analysis matches the empirical results. For the same number of SNPs queried, the power for detecting relatives was reduced but still considerable (Figure 1B; Figure S2). Sequencing errors and variant-calling differences reduced the power of the test (Figure S3).

Figure 1.

Power of Re-identification Attacks on Beacons Constructed with Simulated Data

Power curves for the likelihood-ratio test (LRT) on (A) a simulated beacon with 1,000 individuals and (B) detecting relatives in the simulated beacon. The false-positive rate was set to 0.05 for all scenarios.

Re-identification in Phase 1 CEU Beacon

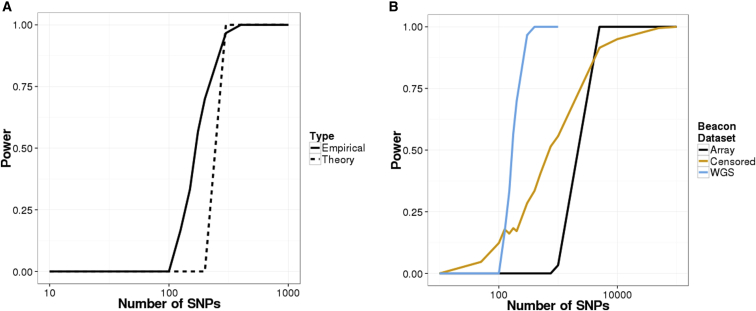
For evaluation with real data, we set up a beacon by using 65 CEU individuals from phase 1 of the 1000 Genomes Project⁸ (Figure S4). With just 250 SNPs, beacon membership could be detected with 95% power and a 5% false-positive rate (Figure 2A). A beacon constructed with the same individuals but with SNP array data showed a reduction in power, as did a beacon that used sequence data but censored responses by always replying “no” to queries for singletons (Figure 2B). Even in these scenarios, the LRT had greater than 90% power if 10,000 or more queries were permitted.

Figure 2.

Power of Re-identification Attacks on Beacons Constructed with Real Data

Power curves for the LRT on (A) a beacon constructed from 65 CEU individuals from 1000 Genomes phase 1 and (B) CEU beacons of size 65 and constructed with array data, censored WGS data (without singletons), and WGS data. The false-positive rate was set to 0.05 for all scenarios.

Re-identification in Multi-population Beacon

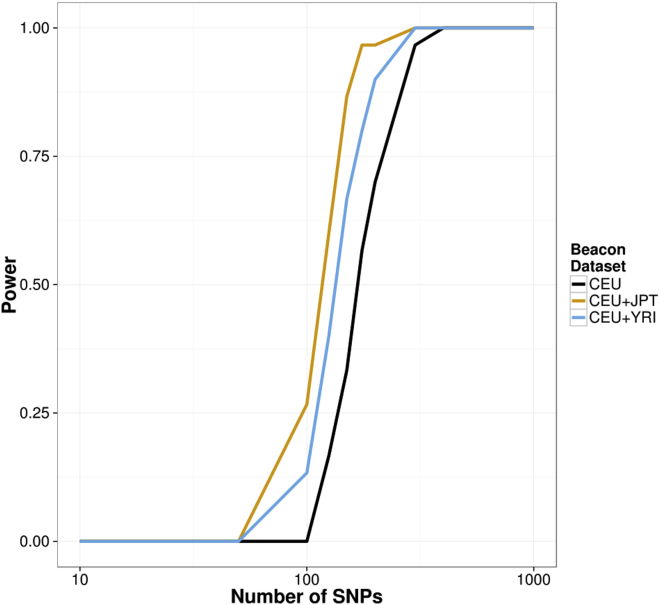
From our theoretical analysis, we can see that increasing beacon size increases the number of SNPs required for achieving a given power level at a specified threshold for the false-positive rate. Combining multiple datasets can make detection more difficult in the same way. A question of interest is whether combining multiple datasets can also make detection more difficult by affecting the SFS of the samples in the beacon.

Figure 3 shows the power curves for beacons containing multiple populations. The results show that for a fixed number of SNPs to query, the power for the multi-population beacons is higher than that for the CEU-only beacon. A single-population beacon is therefore more secure than a multi-population beacon of the same size. Because the protective effect of extra samples in the beacon against re-identification depends on their allele sharing with the query genome, including other populations in a beacon is less effective than including the same number of individuals from the population of the query genome.

Figure 3.

Power of the LRT for Multi-population Datasets

Power is larger for multi-population beacons than for the CEU-only beacon.

Re-identification in Existing Beacons

We used our theoretical analysis to estimate the number of queries our framework would require to re-identify individuals and relatives from existing beacons. We used publicly available beacon metadata to infer the number of individuals present in the beacon. Where this was not possible (the AMPlab, ICGC, and NCBI beacons), we used conservative estimates based on the size of the underlying datasets. For SFS parameters, we used the estimates we obtained for our simulation data. The Kaviar beacon contains 63,500 exomes and 8,400 whole genomes. Because exomes are only 1% of entire genomes in length, this beacon can be assumed to consist of two beacons—an exome beacon with 72,000 exomes and a genome beacon with 8,400 whole genomes. Re-identification is possible in the genome beacon if queries for SNPs in the coding regions are avoided. From Table 1, we see that only the Cafe CardioKit gene-panel beacon, the Broad Institute exome beacon, and the Kaviar beacon are safe from our re-identification attack, given that the gene panels and exomes have much fewer SNPs than genomes. For all other beacons, re-identification is possible with 95% power and fewer than 50,000 allele queries. Thus, our approach is computationally feasible with existing beacons.

Table 1.

Estimated Number of SNP Queries Required for Re-identification in Real Beacons with a 5% False-Positive Rate and 95% Power

Beacon Name	Number of Samples	SNPs Required for Re-identification
Identical Genomes	First-Degree Relatives	Second-Degree Relatives
1000 Genomes Project	1,092	3,649	34,467	157,861
1000 Genomes Project phase 3	2,535	8,469	79,976	366,276
AMPLab	2,535	8,469	79,976	366,276
Broad Institute	60,706	202,770	1,914,581	8,768,007
Cafe CardioKit	1,070	3,575	33,773	154,684
ICGC	12,807	42,779	403,936	1,849,878
Known VARiants	72,000	240,494	2,270,772	10,399,218
Known VARiants (genomes only)	8,400	28,059	264,947	1,213,368
NCBI	14,466	48,320	456,258	2,089,490
PGP	174	582	5,515	25,273
IBD	5,070	16,936	159,926	732,410
Native American + Egyptian	100	335	3,181	14,586
UK10K	6,322	21,118	199,411	913,239
SFARI	10,400	34,739	328,024	1,502,231

Re-identifying a PGP Individual

We demonstrated the feasibility of re-identification in existing beacons by querying them 1,000 times with a single genome from the PGP.⁹ To avoid overloading the beacon servers, we inserted a delay of 5 s between queries, and all 1,000 queries were completed in 3 hr 53 min from a single computer. In beacons where the presence of the individual could be confirmed from metadata, we obtained 100% “yes” responses (Table 2). The null hypothesis (the query genome is not in the beacon) could be rejected only for the PGP beacon (p = 0.0033), but not for the larger Kaviar beacon (p = 0.98), demonstrating that re-identification is more difficult in larger beacons.

Table 2.

Theoretical p Values for 1,000 Queries for SNPs from a Genome in the Personal Genome Project

Beacon Name	Beacon Size	“Yes” Responses	p Value
Known VARiantsa	72,000	1000	0.98
Broad Institute	60,706	27	1
1000 Genomes Project	1,092	711	1
PGPa	174	1000	0.0033
Cafe CardioKit	1,070	0	1
Wellcome Trust Sanger Institute	11,492	960	1
NCBI	14,466	947	1
ICGC	12,807	134	1
AMPLab	2,535	946	1
1000 Genomes Project phase 3	2,535	946	1

^aBeacons known to contain the individual (from metadata).

Discussion

We have developed a LRT for identifying whether a given individual genome is part of a beacon. Our experiments show that in a variety of settings, detecting membership in a beacon is possible with high power for not only individuals in the beacon but also their relatives. Because beacons are often designed to share samples with a certain phenotype, this also discloses phenotype information about the individual who is detected to be part of the beacon. Although detecting membership does not breach privacy, disclosure of potentially sensitive phenotype information is a serious privacy breach. In Table 1, of the nine beacons that index non-publically available genomic data (see Table S3 for details of beacon datasets and phenotypes), four are associated with a single phenotype (Cafe CardioKit, ICGC, IBD, and SFARI beacons), four are associated with multiple phenotypes (Broad Institute, Kaviar, NCBI, and UK10K beacons), and one is not associated with any phenotype (Native American + Egyptian beacon). For instance, identifying that a given genome is part of the SFARI beacon, which contains genomic data from families with a child affected by autism spectrum disorder, means that the individual belongs to a family where some member has autism spectrum disorder. The LRT we describe can be used in a number of undesirable ways. For instance, a United States direct-to-consumer genetic-testing company that collects genome-wide data from customers could use it to infer phenotype or disease information without their customers’ knowledge by querying beacons.

Because the re-identification attack we describe requires the attacker to have access to an individual’s genome, an alternative is that the attacker can use the query genome to directly predict disease risk by using existing risk-prediction methods, such as genomic risk scores¹¹ or machine-learning methods.¹² A comparison of the performance of risk prediction and the re-identification LRT would be useful in understanding whether re-identification discloses any extra information about the query individual. However, most risk-prediction methods focus on the risk that the subject will develop the disease (in 10 years or at some future time), whereas identifying beacon membership gives a direct estimate of the probability that the queried individual currently has the disease studied in the beacon sample. A fair comparison of the two is therefore not possible. If our LRT (with false-positive rate α = 5%) identifies an individual as belonging to a case-only beacon (i.e., rejects the null hypothesis) for a disease with population prevalence (prior probability that an individual has the disease) p = 1%, the posterior probability that the individual has the disease is given by (1 − α) + αp = 0.9505 according to Bayes’ theorem. For the same result in a case-control beacon with equal numbers of case and control individuals, the probability that the individual has the disease is given by 0.5 × (1 − α) + 0.05p = 0.4755. In contrast, although genomic risk prediction has high success rates for Mendelian diseases with highly penetrant alleles and in some cancers, the success of such approaches for predicting common disease risk is modest.¹³ An upper bound on performing genomic risk prediction by using an individual’s genome can be obtained if one considers the (broad-sense) heritability of the disease being studied. Polderman et al.¹⁴ examined the heritability of 17,804 human traits. From their analysis, we can see that 26 out of 43 ICD-10 (International Classification of Diseases, Tenth Revision) and ICF (International Classification of Functioning, Disability, and Health) subchapter-level disease categories have heritability less than 50%, suggesting that the performance of genomic risk prediction for many disease categories will be limited.

Our approach makes some simplifying assumptions. We assume that the beacon samples and the query genome belong to the same population. This is a reasonable assumption given that beacons often publish the ethnicity of the datasets included, whereas the ethnicity of the query genome can be identified by comparison to reference panels such as 1000 Genomes. Genotypes are assumed to be distributed according to Hardy-Weinberg equilibrium. We also assume that allele queries are independent, which can lead to overly confident predictions for common SNPs. We expect that it will not affect our results significantly, given that most SNPs are rare (<5% frequency) in human populations. Inaccurate estimates of the shape of the SFS can affect our theoretical analysis. However, as Figure S1 shows for the theoretical power, the power of the test is similar for populations with different SFS parameters, and Figure 2A shows good agreement between theoretical and empirical power curves on the CEU beacon. In addition, the empirical power of the test does not depend on the SFS parameters (Binomial Test in Appendix A). This suggests that our test is robust to different SFS parameters. A computational limitation is that establishing high confidence might need millions of queries. In our experiments with existing beacons, we were able to make 1,000 queries to the beacon server in 3 hr 53 min, with a 5 s delay between queries.

An important caveat is that the proposed LRT is only a demonstration that individual privacy can be compromised through beacons. It aims to show that beacon membership can be identified with only the query genome, even if allele frequencies are not known. As a result, the bounds we obtain for the number of queries required for re-identification (Table 1) are conservative and should not be used directly to guide the construction of beacons. A re-identification test that uses only rare SNPs and/or incorporates the allele frequencies at SNPs will be more powerful than our method and will require fewer queries than our estimates. Because the LRT we describe requires access to genomic data, such attacks might not be frequent or imminent at this time. However, as access to genomic data becomes easier, such attacks might need to be accounted for in the design of data-sharing mechanisms.

Our results have important implications for setting up beacons to allow data sharing and protect individual privacy. Beacons are designed to help researchers find datasets relevant to their research interests (e.g., datasets containing an allele that the researchers might suspect to be associated with a rare Mendelian disorder). Access to individual-level genotype data is usually controlled,⁶ and a researcher might spend considerable time and effort applying for access only to find that the dataset is not relevant to his or her study. An advantage of a beacon is that any researcher can use it to query access-controlled data without applying for access. This will allow researchers to establish whether an access-controlled dataset might be of interest to them and apply for access only for relevant datasets. Two desirable features in beacons might therefore be that they contain a single dataset (so researchers who find a relevant dataset by querying a beacon can get data access through a single request) and that they return accurate information about the presence of rare alleles. Solutions for protecting privacy in beacons must also maintain the utility of beacons by supporting these features. We examine two ways in which security can be improved for anonymous-access beacons: (1) making detection of membership in the beacon harder and (2) reducing the leakage of phenotype information from the beacon.

A number of approaches can be used for making detection of membership in the beacon harder. Increasing beacon size can make detection harder, but protection against genome-wide re-identification attacks will require tens of thousands of individuals. Beacons sharing small genomic regions (single genes or exomes) are more secure than those sharing whole genomes. Beacons containing multiple populations are less secure than single-population beacons of the same size. Publishing metadata—such as the ethnicity of samples, beacon size, or the names of datasets included—reduces beacon security. Limiting the number and/or rate of queries per IP address can only slow down attackers and is therefore ineffective. Data-anonymization¹⁵ approaches, such as using only common variation or censoring (Figure 2B; Censoring Beacon Responses in Appendix B), make re-identification harder but not impossible. All of these methods make detection of membership in the beacon harder, but they also reduce the utility of beacons to users.

An alternative way of improving beacon security is to address the leakage of phenotype information instead of the possibility of genomic re-identification. As described earlier, the probability that a re-identified sample has the disease associated with the beacon dataset depends on the proportion of case samples in the beacon dataset. Therefore, adding a suitable number of control samples or aggregating responses from multiple beacons (implemented as an option in the Beacon Network) might reduce the probability that a re-identified sample has the disease to an acceptable level. Heritability estimates can be used for determining an acceptable probability level for a particular disease. By including non-case samples, these solutions reduce the phenotype information that can be obtained from a beacon while keeping the reduction in the utility of the beacon to a minimum.

We expect that, because of the lack of monitoring and access control, anonymous-access beacons will always be open to re-identification attempts. The most important step for improving security and reducing loss of privacy through beacons would be to prohibit anonymous access. Requiring users to authenticate their identity to access beacons will allow the research community to discourage re-identification attacks through policies outlining acceptable uses of beacons.¹⁶

Published: October 29, 2015

Appendix A: LRT

In an ideal setting, we would expect x₁ = x₂ … = x_n = 1 if a query genome g is in the beacon B. In practice, because of sequencing errors and differences in variant-calling pipelines, we might have some mismatches between the query copy of a genome and its copy in the beacon. We assume that this happens with probability δ.

Let the alternate allele frequency at the SNP corresponding to query q_i be f_i. Because the beacon is only queried at the positions where the query genome is heterozygous, f_i is not distributed as beta(a′, b′) but shows an ascertainment bias. We can show that f_i ∼ beta(a, b), where a = a′ + 1 and b = b′ + 1 in theory (see Posterior Distribution of Allele Frequencies in Appendix A for details).

The log-likelihood of a response set R = {x₁, …, x_n} can be written as

$$L\left(R\right)=\sum _{i=1}^N{x}_i\text{log}P\left(x_i=1\right)+\left(1-x_i\right)\text{log}P\left(x_i=0\right).$$ (Equation A1)

For the LRT, we need to evaluate this log-likelihood under the null hypothesis and the alternative hypothesis. The null hypothesis is that the query genome is not present in the beacon, and the alternative hypothesis is that the query genome is present in the beacon.

Likelihood under the Alternative Hypothesis

Under the alternative hypothesis (query genome g is present in beacon B, $g\in B$), the response x_i is given by

• I.
  x_i = 1 if

  • (a)
    there is no mismatch between the query genome and its copy in the beacon or
  • (b)
    there is a mismatch between the query genome and its copy in the beacon but at least one of the other N − 1 genomes in the beacon has the alternate allele.
• II.x_i = 0 if there is a mismatch between the query genome and its copy in the beacon and none of the other N − 1 genomes in the beacon has the alternate allele.

The log-likelihood under the alternative hypothesis is given by

$$L_{H_1}\left(R\right)=\sum _{i=1}^N{x}_i\text{log}P\left(x_i=1|H_1\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_1\right).$$ (Equation A2)

We first calculate $P\left(x_i=0|H_1\right)$:

$$\begin{array}{c}P\left(x_i=0|H_1\right)=P\left(x_i=0|g\in B\right)\\ =P\left(x_i=0|g\in B,\text{mismatch}\right)\times P\left(\text{mismatch}\right)\times P\left(\text{none}\text{of}\text{the}\text{other}N-1\text{genomes}\text{has}\text{the}\text{alternate}\text{allele}\right)\\ =1\times \delta \times P\left(\text{none}\text{of}\text{the}\text{other}N-1\text{genomes}\text{has}\text{the}\text{alternate}\text{allele}\right)\\ =\delta {\int }_{f_i=0}^{1}P\left(\text{none}\text{of}\text{the}\text{other}N-1\text{genomes}\text{has}\text{the}\text{alternate}\text{allele}|f_i\right)P\left(f_i\right)d{f}_i\\ =\delta {\int }_{f_i=0}^1{\left({\left(1-f_i\right)}^2\right)}^{\left(N-1\right)}P\left(f_i\right)d{f}_i\\ =\delta {\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N-2}P\left(f_i;a,b\right)d{f}_i\\ =\delta {\int }_{p_i=1}^0{p}_i^{2N-2}P\left(p_i;b,a\right)\left(-d{p}_i\right)f_i\sim \text{beta}\left(a,b\right)\iff p_i=1-f_i\sim \text{beta}\left(b,a\right)\\ =\delta \times E\left[p_i^{2N-2}\right]p_i\sim \text{beta}\left(b,a\right)\\ =\delta \stackrel{2N-2-1}{\prod _{r=0}}\frac{b+r}{b+a+r}\\ =\delta \stackrel{2N-3}{\prod _{r=0}}\frac{b+r}{b+a+r}.\end{array}$$

Let $D_{N-1}={\prod }_{r=0}^{2N-3}\left(b+r/b+a+r\right)$. $D_{N-1}$ is therefore the probability that none of N − 1 genomes has an alternate allele.

Therefore, we have that

$$P\left(x_i=0|H_1\right)=\delta D_{N-1}$$ (Equation A3)

and

$$P\left(x_i=1|H_1\right)=1-\delta D_{N-1}.$$ (Equation A4)

The log-likelihood can be calculated as

$$\begin{array}{c}{L}_{H_1}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}P\left(x_i=1|H_1\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_1\right)\\ =\sum _{i=1}^n{x}_i\text{log}\left(1-\delta D_{N-1}\right)+\left(1-x_i\right)\text{log}\left(\delta D_{N-1}\right).\end{array}$$

Likelihood under the Null Hypothesis

Under the null hypothesis (query genome g is not in beacon B, $g\notin B$), the response $x_i$ is given by

• I.x_i = 1 if at least one of the N genomes in the beacon contains the alternate allele.
• II.x_i = 0 if none of the N genomes in the beacon contains the alternate allele.

The log-likelihood under the null hypothesis is given by

$$L_{H_0}\left(R\right)=\sum _{i=1}^N{x}_i\text{log}P\left(x_i=1|H_0\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_0\right).$$ (Equation A5)

We first calculate $P\left(x_i=0|H_0\right)$:

$$\begin{array}{c}P\left(x_i=0|H_0\right)=P\left(x_i=0|g\notin B\right)\\ =P\left(\text{none}\text{of}\text{the}N\text{genomes}\text{has}\text{the}\text{alternate}\text{allele}\right)\\ =D_N,\text{from}\text{our}\text{earlier}\text{definition}\text{.}\end{array}$$

Therefore, we have that

$$P\left(x_i=0|H_0\right)=D_N$$ (Equation A6)

and

$$P\left(x_i=1|H_0\right)=1-D_N.$$ (Equation A7)

The log-likelihood can be calculated as

$$\begin{array}{c}{L}_{H_0}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}P\left(x_i=1|H_0\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_0\right)\\ =\sum _{i=1}^n{x}_i\text{log}\left(1-D_N\right)+\left(1-x_i\right)\text{log}\left(D_N\right).\end{array}$$

Thus, the log-likelihood under the null hypothesis is

$$L_{H_0}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}\left(1-D_N\right)+\left(1-x_i\right)\text{log}\left(D_N\right).$$ (Equation A8)

LRT Statistic

The log of the likelihood-ratio statistic can then be written as

$$\begin{array}{c}\text{Λ}=L_{H_0}\left(R\right)-L_{H_1}\left(R\right)\\ =\sum _{i=1}^n{x}_i\text{log}\left(1-D_N\right)+\left(1-x_i\right)\text{log}\left(D_N\right)-\left[\sum _{i=1}^n{x}_i\text{log}\left(1-\delta D_{N-1}\right)+\left(1-x_i\right)\text{log}\left(\delta D_{N-1}\right)\right]\\ =\sum _{i=1}^n{x}_i\text{log}\left(\frac{1-D_N}{1-\delta D_{N-1}}\right)+\left(1-x_i\right)\text{log}\left(\frac{D_N}{\delta D_{N-1}}\right)\\ =n\text{log}\left(\frac{D_N}{\delta D_{N-1}}\right)+\sum _{i=1}^n{x}_i\left[\text{log}\left(\frac{1-D_N}{1-\delta D_{N-1}}\right)-\text{log}\left(\frac{D_N}{\delta D_{N-1}}\right)\right]\\ =n\text{log}\left(\frac{D_N}{\delta D_{N-1}}\right)+\sum _{i=1}^n{x}_i\text{log}\left(\frac{\delta D_{N-1}\left(1-D_N\right)}{D_N\left(1-\delta D_{N-1}\right)}\right)\\ =n\text{log}\left(\frac{D_N}{\delta D_{N-1}}\right)+\text{log}\left(\frac{\delta D_{N-1}\left(1-D_N\right)}{D_N\left(1-\delta D_{N-1}\right)}\right)\sum _{i=1}^n{x}_i\\ =nB+C\sum _{i=1}^n{x}_i,\end{array}$$

where we have defined $B=\text{log}\left(D_N/\delta D_{N-1}\right)$ and $C=\text{log}\left(\delta D_{N-1}\left(1-D_N\right)/D_N\left(1-\delta D_{N-1}\right)\right)$. For $\delta <\left(D_N/D_{N-1}\right)$, we have $C<0$. In practice, because $N\gg 1$, $D_N\approx D_{N-1}$, and mismatch rate $\delta \ll 1$, this will always be true.

Therefore, the LRT statistic can be stated as

$$\text{Λ}=nB+C\sum _{i=1}^n{x}_i.$$ (Equation A9)

Neyman-Pearson Optimality of LRT

The LRT stated above can be understood to be a test for a simple null hypothesis H₀: θ = D_N against a simple alternative hypothesis H₁: θ = δD_{N − 1} when we are given {x₁, …, x_n} sampled as x_i ∼ Bernoulli(θ). By the Neyman-Pearson lemma, the LRT is the most powerful test for a given test size α.

Binomial Test

The null hypothesis is rejected if Λ < t for some threshold t. Let t_α be such that P(Λ < t_α | H₀) = α.

This is equivalent to

$$P\left(\text{Λ}<t_{\alpha }|H_0\right)=\alpha$$ (Equation A10)

$$P\left(nB+C\sum _{i=1}^n{x}_i<t_{\alpha }|H_0\right)=\alpha$$ (Equation A11)

$$P\left(C\sum _{i=1}^n{x}_i<t_{\alpha }-nB|H_0\right)=\alpha$$ (Equation A12)

$$P\left(\sum _{i=1}^n{x}_i>\frac{t_{\alpha }-nB}{C}|H_0\right)=\alpha ,\text{because}C<0$$ (Equation A13)

$$P\left(\sum _{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_0\right)=\alpha ,\text{where}{t}_{\alpha }^{\prime }=\frac{t_{\alpha }-nB}{C}.$$ (Equation A14)

Because the $x_i$ are i.i.d. under both hypotheses, ${\sum }_{i=1}^n{x}_i|H_0\sim \text{binomial}\left(n,1-D_N\right)$ and ${\sum }_{i=1}^n{x}_i|H_1\sim \text{binomial}\left(n,1-\delta D_{N-1}\right)$. Therefore, the power of the exact test can be calculated as $1-\beta =P\left({\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_1\right)$, where $t_{\alpha }^{\prime }$ is chosen such that $P\left({\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_0\right)=\alpha$.

Thus, a sufficient statistic for the LRT is the number of “yes” responses from the beacon. If a “truth set” of individuals known to be (or not be) in the beacon is available, the critical value and power of the test can be computed with only the number of “yes” responses from the beacon. Thus, the empirical power is not dependent on the SFS parameters, which suggests that the test is robust to SFS parameters.

Gaussian LRT Power Approximation

In the null and alternative hypotheses, $x_i$ is a Bernoulli random variable. Therefore, by the central limit theorem, the LRT statistic has a Gaussian distribution. We can therefore use the parameters of the Gaussian distribution to obtain a relationship between the false-positive rate and power of the test.

Let μ₀ and σ₀ be the mean and SD, respectively, of the LRT statistic under the null hypothesis, and let μ₁ and σ₁ be the corresponding values under the alternative hypothesis.

From earlier results, we have that

$${\mu }_0=E\left[\text{Λ}|H_0\right]$$ (Equation A15)

$$=nB+C\sum _{i=1}^{n}E\left[x_i|H_0\right]$$ (Equation A16)

$$=nB+C\sum _{i=1}^{n}P\left(x_i=1|H_0\right)$$ (Equation A17)

$$=nB+C\sum _{i=1}^n\left(1-D_N\right)$$ (Equation A18)

$$=nB+nC\left(1-D_N\right)$$ (Equation A19)

and

$${\sigma }_0^2=\text{Var}\left[\text{Λ}|H_0\right]$$ (Equation A20)

$$=C^2\sum _{i=1}^n\text{Var}\left[x_i|H_0\right]$$ (Equation A21)

$$=C^2\sum _{i=1}^n{D}_N\left(1-D_N\right)$$ (Equation A22)

$$=C^{2}n{D}_N\left(1-D_N\right)$$ (Equation A23)

$${\sigma }_0=-C\sqrt{n{D}_N\left(1-D_N\right)},$$ (Equation A24)

where we have chosen the square root of C², which is larger than 0 (because C < 0).

Similarly, we can show that

$${\mu }_1=nB+nC\left(1-\delta D_{N-1}\right)$$ (Equation A25)

and

$${\sigma }_1=-C\sqrt{n\delta D_{N-1}\left(1-\delta D_{N-1}\right)}.$$ (Equation A26)

For an LRT statistic with false-positive rate α, power 1 − β, and a normal distribution, we have that

$${\mu }_0+{\sigma }_0{z}_{\alpha }={\mu }_1+{\sigma }_1{z}_{1-\beta },$$ (Equation A27)

where z_y is the y quantile of the standard normal distribution.

Substituting from above, we get

$${\mu }_0+{\sigma }_0{z}_{\alpha }={\mu }_1+{\sigma }_1{z}_{1-\beta }$$ (Equation A28)

$${\mu }_0-{\mu }_1={\sigma }_1{z}_{1-\beta }-{\sigma }_0{z}_{\alpha }.$$ (Equation A29)

We have

$${\mu }_0-{\mu }_1=nB+nC\left(1-D_N\right)-\left[nB+nC\left(1-\delta D_{N-1}\right)\right]$$ (Equation A30)

$$=nC\left(\delta D_{N-1}-D_N\right).$$ (Equation A31)

Also,

$$\begin{array}{c}{\sigma }_1{z}_{1-\beta }-{\sigma }_0{z}_{\alpha }=-z_{1-\beta }C\sqrt{n\delta D_{N-1}\left(1-\delta D_{N-1}\right)}+z_{\alpha }C\sqrt{n{D}_N\left(1-D_N\right)}\\ =C\sqrt{n}\left(z_{\alpha }\sqrt{D_N\left(1-D_N\right)}-z_{1-\beta }\sqrt{\delta D_{N-1}\left(1-\delta D_{N-1}\right)}\right).\end{array}$$

Therefore, we get

$${\mu }_0-{\mu }_1={\sigma }_1{z}_{1-\beta }-{\sigma }_0{z}_{\alpha }$$ (Equation A32)

$$nC\left(\delta D_{N-1}-D_N\right)=C\sqrt{n}\left(z_{\alpha }\sqrt{D_N\left(1-D_N\right)}-z_{1-\beta }\sqrt{\delta D_{N-1}\left(1-\delta D_{N-1}\right)}\right)$$ (Equation A33)

$$\sqrt{n}\left(\delta D_{N-1}-D_N\right)=z_{\alpha }\sqrt{D_N\left(1-D_N\right)}-z_{1-\beta }\sqrt{\delta D_{N-1}\left(1-\delta D_{N-1}\right)}.$$ (Equation A34)

Thus, for a given false-positive rate α, the number of SNPs that must be queried for obtaining power 1 − β is given as

$$n={\left(\frac{z_{\alpha }\sqrt{D_N\left(1-D_N\right)}-z_{1-\beta }\sqrt{\delta D_{N-1}\left(1-\delta D_{N-1}\right)}}{\delta D_{N-1}-D_N}\right)}^2.$$ (Equation A35)

Also, given a number of SNPs n and a false-positive rate α, the power that will be achieved is

$$1-\beta ={\text{Φ}}^{-1}\left(\frac{z_{\alpha }\sqrt{D_N\left(1-D_N\right)}-\sqrt{n}\left(\delta D_{N-1}-D_N\right)}{\sqrt{\delta D_{N-1}\left(1-\delta D_{N-1}\right)}}\right),$$ (Equation A36)

where Φ is the cumulative distribution function of the standard normal distribution $\mathcal{N}\left(\mathrm{0,1}\right)$.

We can show that D_N can be approximated as

$$D=D_N\approx D_{N-1}\approx \frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right){\left(2N+a+b\right)}^a}$$ (Equation A37)

(see Approximating Probability of No Alternate Alleles in Appendix A).

For $N\gg 1$, given that $D<1$ and $\delta \ll 1$, we assume $1-D\approx 1$, $1-\delta D\approx 1$, and $1-\delta \approx 1$. Also, because $N\gg a,b$, we assume $2N+a+b\approx 2N$. Then, we can write

$$\begin{array}{c}n\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right){\left(2N\right)}^a}\approx {\left(z_{\alpha }-z_{1-\beta }\sqrt{\delta }\right)}^2\\ \frac{n}{N^a}=\frac{{\left(z_{\alpha }-z_{1-\beta }\sqrt{\delta }\right)}^2\text{Γ}\left(b\right)2^a}{\text{Γ}\left(a+b\right)}.\end{array}$$

In terms of the SFS of the entire population, we can write this as

$$\frac{n}{N^{a^{\prime }+1}}=\frac{{\left(z_{\alpha }-z_{1-\beta }\sqrt{\delta }\right)}^2\text{Γ}\left(b^{\prime }+1\right)2^{a^{\prime }+1}}{\text{Γ}\left(a^{\prime }+b^{\prime }+2\right)}.$$ (Equation A38)

The right-hand side of the equation is independent of both n and N for a specified false-positive rate α and power 1 − β. Thus, we have that $n\propto N^{a^{\prime }+1}$.

Modeling SFSs by Beta Distributions

We model alternate allele frequencies for populations by beta distributions similarly to the approaches used by Sankararaman et al.² and Clayton.⁵ If $\left\{f_1,\cdots ,f_n\right\}$ are distributed as $\text{beta}\left(a^{\prime },b^{\prime }\right)$, then the sample mean and variance, respectively, are given by

$$\overline{f}=\frac{{\sum }_{i=1}^n{f}_i}{n}$$ (Equation A39)

and

$$\overline{v}=\frac{{\sum }_{i=1}^n{\left(f_i-\overline{f}\right)}^2}{n-1}.$$ (Equation A40)

The method-of-moments estimators for the parameters of the beta distribution are

$$a^{\prime }=\overline{f}\left(\frac{\overline{f}\left(1-\overline{f}\right)}{\overline{v}}-1\right)$$ (Equation A41)

and

$$b^{\prime }=\left(1-\overline{f}\right)\left(\frac{\overline{f}\left(1-\overline{f}\right)}{\overline{v}}-1\right)$$ (Equation A42)

provided that $\overline{v}<\overline{f}\left(1-\overline{f}\right)$.

Table S1 shows that the estimates of the SFS parameters for simulated data and some public datasets (1000 Genomes, SSMP,¹⁷ and GoNL¹⁸) are similar to each other. Figure S1 shows the effect of different estimates of SFS parameters for the populations in Table S1 on the theoretical power of the LRT. We see that estimates of SFS parameters affect the theoretical predictions, although results remain qualitatively similar. The test has the least power for SNP array data given that it has relatively less rare variation.

Posterior Distribution of Allele Frequencies

According to the SFS of the population, the alternate allele frequency f at a SNP is distributed as $f\sim \text{beta}\left(a^{\prime },b^{\prime }\right)$. If we assume Hardy-Weinberg equilibrium and f is the frequency observed at a SNP where the query genome is heterozygous (gt = 1), the posterior distribution of f at the SNP is given by Bayes’ rule as

$$P\left(f|gt=1\right)=\frac{P\left(gt=1|f\right)P\left(f\right)}{{\int }_{f\prime =0}^{1}P\left(gt=1|f^{\prime }\right)P\left(f\right)d{f}^{\prime }}$$ (Equation A43)

$$=\frac{2f\left(1-f\right)\frac{\text{Γ}\left(a^{\prime }+b^{\prime }\right)}{\text{Γ}\left(a^{\prime }\right)\text{Γ}\left(b^{\prime }\right)}{f}^{a^{\prime }-1}{\left(1-f\right)}^{b^{\prime }-1}}{{\int }_{f\prime =0}^{1}2f^{\prime }\left(1-f^{\prime }\right)\frac{\text{Γ}\left(a^{\prime }+b^{\prime }\right)}{\text{Γ}\left(a^{\prime }\right)\text{Γ}\left(b^{\prime }\right)}{f}^{\prime a\prime -1}{\left(1-f^{\prime }\right)}^{b^{\prime }-1}d{f}^{\prime }}$$ (Equation A44)

$$=\frac{f^{a^{\prime }+1-1}{\left(1-f\right)}^{b^{\prime }+1-1}}{{\int }_{f\prime =0}^1{f}^{\prime a\prime +1-1}{(1-f^{\prime })}^{b^{\prime }+1-1}d{f}^{\prime }}$$ (Equation A45)

$$=\frac{\text{Γ}\left(a^{\prime }+b^{\prime }+2\right)}{\text{Γ}\left(a^{\prime }+1\right)\text{Γ}\left(b^{\prime }+1\right)}{f}^{a^{\prime }+1-1}{\left(1-f\right)}^{b^{\prime }+1-1}$$ (Equation A46)

$$=\text{beta}\left(a^{\prime }+1,b^{\prime }+1\right).$$ (Equation A47)

Therefore, the posterior distribution of the alternate allele frequency f at heterozygous sites is given as f ∼ beta(a, b), where a = a′ + 1 and b = b′ + 1. In practice, for both simulated and real genomic data, the observed values of the parameters of the posterior distribution are slightly different from their expectations. In the theoretical power curves for our analyses, we use the correct estimated values of the parameters for the simulated data rather than the theoretical expectation or estimates from real data.

Approximating Probability of No Alternate Alleles

We have defined $D_N={\prod }_{r=0}^{2N-1}\left(\left(b+r\right)/\left(b+a+r\right)\right)$ as the probability that none of N individuals has an alternate allele. Here, we show that

$$D=D_N\approx \frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right){\left(2N+a+b\right)}^a}.$$ (Equation A48)

For this result, we use Stirling’s approximation to the Gamma function, given by

$$\text{Γ}\left(x\right)\approx \sqrt{\frac{2\pi }{x}}{\left(\frac{x}{e}\right)}^x.$$ (Equation A49)

We use the result that for $y\to \infty$,

$${\left(1-1/y\right)}^y\approx \frac{1}{e}.$$ (Equation A50)

We also assume that $N\gg a,b$ and $N\gg 1$.

We have

$$D_N={\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N}P\left(f_i;a,b\right)d{f}_i$$ (Equation A51)

$$={\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N}\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(a\right)\text{Γ}\left(b\right)}{f}_i^{a-1}{\left(1-f_i\right)}^{b-1}d{f}_i$$ (Equation A52)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(a\right)\text{Γ}\left(b\right)}{\int }_{f_i=0}^1{f}_i^{a-1}{\left(1-f_i\right)}^{2N+b-1}d{f}_i$$ (Equation A53)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(a\right)\text{Γ}\left(b\right)}\times \frac{\text{Γ}\left(a\right)\text{Γ}\left(b+2N\right)}{\text{Γ}\left(a+b+2N\right)}$$ (Equation A54)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}\times \frac{\text{Γ}\left(b+2N\right)}{\text{Γ}\left(a+b+2N\right)}$$ (Equation A55)

$$\approx \frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}\sqrt{\frac{2\pi }{b+2N}}{\left(\frac{b+2N}{e}\right)}^{b+2N}\sqrt{\frac{a+b+2N}{2\pi }}{\left(\frac{e}{a+b+2N}\right)}^{a+b+2N}$$ (Equation A56)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}\sqrt{\frac{a+b+2N}{b+2N}}{e}^a{\left(\frac{b+2N}{a+b+2N}\right)}^{b+2N}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A57)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}{\left(1+\frac{a}{b+2N}\right)}^{0.5}{e}^a{\left(\frac{b+2N}{a+b+2N}\right)}^{b+2N}{\left(\frac{1}{a+b+2N}\right)}^a.$$ (Equation A58)

Given that $a/\left(b+2N\right)\ll 1$, we can simplify this expression further as

$$D_N=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}{\left(1+\frac{a}{b+2N}\right)}^{0.5}{e}^a{\left(\frac{b+2N}{a+b+2N}\right)}^{b+2N}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A59)

$$\approx \frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}\left(1+\frac{a}{2\left(b+2N\right)}\right)e^a{\left(\frac{b+2N}{a+b+2N}\right)}^{b+2N}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A60)

$$\approx \frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}\times 1\times e^a{\left(\frac{b+2N}{a+b+2N}\right)}^{b+2N}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A61)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}{e}^a{\left(1-\frac{a}{a+b+2N}\right)}^{b+2N}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A62)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}{e}^a{\left[{\left(1-\frac{a}{a+b+2N}\right)}^{\frac{a+b+2N}{a}}\right]}^{\frac{a\left(b+2N\right)}{a+b+2N}}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A63)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}{e}^a{\left[\frac{1}{e}\right]}^{\frac{a\left(b+2N\right)}{a+b+2N}}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A64)

$$\approx \frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}{e}^{a-\frac{a\left(b+2N\right)}{a+b+2N}}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A65)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}{e}^{a\left(1-\frac{b+2N}{a+b+2N}\right)}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A66)

$$\approx \frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}{e}^{a\left(1-1\right)}{\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A67)

$$=\frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right)}\times 1\times {\left(\frac{1}{a+b+2N}\right)}^a$$ (Equation A68)

$$\approx \frac{\text{Γ}\left(a+b\right)}{\text{Γ}\left(b\right){\left(a+b+2N\right)}^a}$$ (Equation A69)

Appendix B: LRT Variations

We consider variations of the likelihood test to detect relatives and to examine the effect of censoring the SFS on the power of the test.

LRT for Detecting Relatives

The relatedness of two individuals can be parameterized with a single parameter ϕ, which is the probability that the two individuals share an allele at a single SNP. Thus, identical twins have ϕ = 1, parent-offspring and sibling pairs have ϕ = 0.5, first cousins have ϕ = 0.25 and so on.

The likelihood for the null hypothesis remains the same as before. Below, we show the likelihood computation for the alternate hypothesis

Likelihood under the Alternate Hypothesis

Under the alternate hypothesis (a relative of the query genome g with relatedness ϕ is present in beacon B), the response x_i is given by

• I.
  x_i = 0 if none of the other N − 1 genomes in the beacon has the alternate allele and

  • (a)
    there is no mismatch between the query genome and its copy in the beacon and the relative is a homozygous reference at the SNP or
  • (b)
    there is a mismatch between the query genome and its copy in the beacon and the relative is not a homozygous reference at the SNP.
• II.x_i = 1 otherwise.

For an individual who is heterozygous at a SNP with alternate allele frequency f, the genotype probabilities for a relative with relatedness ϕ can be shown to be

$$\begin{array}{c}P\left(g{t}_{\text{relative}}=0|gt=1;f\right)={\left(1-\varphi \right)}^2{\left(1-f\right)}^2+\varphi \left(1-\varphi \right)\left(1-f\right),\\ P\left(g{t}_{\text{relative}}=1|gt=1;f\right)=2{\left(1-\varphi \right)}^{2}f\left(1-f\right)+\varphi \left(1-\varphi \right)+{\varphi }^2,\text{and}\\ P\left(g{t}_{\text{relative}}=2|gt=1;f\right)={\left(1-\varphi \right)}^2{f}^2+\varphi \left(1-\varphi \right)f,\end{array}$$ (Equation B1)

where gt and gt_relative are the genotypes of the individual and the relative, respectively, at the SNP.

The log-likelihood under the alternate hypothesis is given by

$$L_{H_1}\left(R\right)=\sum _{i=1}^N{x}_i\text{log}P\left(x_i=1|H_1\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_1\right).$$ (Equation B2)

We first calculate $P\left(x_i=0|H_1\right)$:

$$P\left(x_i=0|H_1\right)=P\left(x_i=0|\text{relative}\in B\right)=P\left(\text{none}\text{of}\text{the}\text{other}N-1\text{genomes}\text{has}\text{the}\text{alternate}\text{allele}\right)\times \left[\delta P\left(g{t}_{\text{relative}}>0|gt=1\right)+\left(1-\delta \right)P\left(g{t}_{\text{relative}}=0|gt=1\right)\right]={\int }_{f_i=0}^{1}P\left(\text{none}\text{of}\text{the}\text{other}N-1\text{genomes}\text{has}\text{the}\text{alternate}\text{allele}|f_i\right)\times \left[\delta P\left(g{t}_{\text{relative}}>0|gt=1;f_i\right)+\left(1-\delta \right)P\left(g{t}_{\text{relative}}=0|gt=1;f_i\right)\right]P\left(f_i\right)d{f}_i={\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N-1}\left[\delta P\left(g{t}_{\text{relative}}>0|gt=1;f_i\right)+\left(1-\delta \right)P\left(g{t}_{\text{relative}}=0|gt=1;f_i\right)\right]P\left(f_i\right)d{f}_i={\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N-2}[\delta \left(1-{\left(1-\varphi \right)}^2{\left(1-f\right)}^2-\varphi \left(1-\varphi \right)\left(1-f\right)\right)+\left(1-\delta \right)\left({\left(1-\varphi \right)}^2{\left(1-f\right)}^2+\varphi \left(1-\varphi \right)\left(1-f\right)\right)]P\left(f_i\right)d{f}_i={\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N-2}\left[\delta +\left(1-2\delta \right)\left({\left(1-\varphi \right)}^2{\left(1-f_i\right)}^2+\varphi \left(1-\varphi \right)\left(1-f_i\right)\right)\right]P\left(f_i\right)d{f}_i={\int }_{f_i=0}^1\delta {\left(1-f_i\right)}^{2N-2}P\left(f_i\right)d{f}_i+{\int }_{f_i=0}^1\left(1-2\delta \right){\left(1-\varphi \right)}^2{\left(1-f_i\right)}^{2N}P\left(f_i\right)d{f}_i+{\int }_{f_i=0}^1\left(1-2\delta \right)\varphi \left(1-\varphi \right){\left(1-f_i\right)}^{2N-1}P\left(f_i\right)d{f}_i=\delta {\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N-2}P\left(f_i\right)d{f}_i+\left(1-2\delta \right){\left(1-\varphi \right)}^2{\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N}P\left(f_i\right)d{f}_i+\left(1-2\delta \right)\varphi \left(1-\varphi \right){\int }_{f_i=0}^1{\left(1-f_i\right)}^{2N-1}P\left(f_i\right)d{f}_i=\delta D_{N-1}+\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N+\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-\frac{1}{2}}=\delta D_{N-1}+(1-2\delta ){(1-\varphi )}^2{D}_N+(1-2\delta )\varphi (1-\varphi )D_{N-\frac{1}{2}}.$$

For ϕ = 1, this expression collapses to the form of Equation A3.

Therefore, we have that

$$P\left(x_i=0|H_1\right)=\delta D_{N-1}+\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N+\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-\frac{1}{2}}$$ (Equation B3)

and

$$P\left(x_i=1|H_1\right)=1-\delta D_{N-1}-\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N-\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-\frac{1}{2}}.$$ (Equation B4)

Thus, the log-likelihood under the alternate hypothesis is

$$L_{H_1}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}\left(1-\delta D_{N-1}-\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N-\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-\frac{1}{2}}\right)+\left(1-x_i\right)\text{log}\left(\delta D_{N-1}+\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N+\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-\frac{1}{2}}\right).$$ (Equation B5)

We can use this form to calculate the LRT statistic. Here, the exact test uses ${\sum }_{i=1}^n{x}_i$ as the sufficient statistic (as before), and the sufficient statistic is binomially distributed under both hypotheses. The distributions are given by ${\sum }_{i=1}^n{x}_i|H_0\sim \text{binomial}\left(n,1-D_N\right)$ and ${\sum }_{i=1}^n{x}_i|H_1\sim \text{binomial}\left(n,1-\delta D_{N-1}-\left(1-2\delta \right){\left(1-\varphi \right)}^2{D}_N-\left(1-2\delta \right)\varphi \left(1-\varphi \right)D_{N-\left(1/2\right)}\right)$.

Therefore, the power of the exact test can be calculated as $\beta =P\left({\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_1\right)$, where $t_{\alpha }^{\prime }$ is chosen such that $P\left({\sum }_{i=1}^n{x}_i>t_{\alpha }^{\prime }|H_0\right)=\alpha$.

Censoring Beacon Responses

One solution to the re-identification problem is to return accurate responses only for common variants. We consider a setting where the beacon chooses a threshold frequency f^∗ and returns “no” responses to queries for alleles that have frequency less than or equal to f^∗ in the population (not necessarily in the beacon samples). For alleles at frequency larger than f^∗, the beacon will return the true answer.

Likelihood under the Alternative Hypothesis

Under the alternative hypothesis (query genome g is present in beacon B, $g\in B$), the response x_i is given by

• I.
  x_i = 0 if

  • (a)
    the frequency of the allele f_i ≤ f^∗or
  • (b)
    the frequency of the allele f_i > f^∗ and there is a mismatch between the query genome and its copy in the beacon and none of the other N − 1 genomes in the beacon has the alternate allele.
• II.x_i = 1 otherwise.

The log-likelihood under the alternative hypothesis is given by

$$L_{H_1}\left(R\right)=\sum _{i=1}^N{x}_i\text{log}P\left(x_i=1|H_1\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_1\right).$$ (Equation B6)

We first calculate $P\left(x_i=0|H_1\right)$:

$$P\left(x_i=0|H_1\right)={\int }_{f_i=0}^{f^{\ast }}P\left(f_i\right)d{f}_i+{\int }_{f_i=f^{\ast }}^1\delta P\left(\text{none}\text{of}\text{the}\text{other}N-1\text{genomes}\text{has}\text{the}\text{alternate}\text{allele}|f_i\right)P\left(f_i\right)d{f}_i=I_{f^{\ast }}\left(a,b\right)+\delta {\int }_{f_i=f^{\ast }}^1{\left({\left(1-f_i\right)}^2\right)}^{\left(N-1\right)}P\left(f_i\right)d{f}_i=I_{f^{\ast }}\left(a,b\right)+\delta {\int }_{f_i=f^{\ast }}^1{\left(1-f_i\right)}^{2N-2}P\left(f_i;a,b\right)d{f}_i=I_{f^{\ast }}\left(a,b\right)+\delta D_{N-1}\left(1-I_{f^{\ast }}\left(a,b+2N-2\right)\right)=E_{N-1},$$

where $E_{N-1}=I_{f^{\ast }}\left(a,b\right)+\delta D_{N-1}\left(1-I_{f^{\ast }}\left(a,b+2N-2\right)\right)$.

Here, I_x(a, b) is the cumulative distribution function for a beta distribution with shape parameters a and b, evaluated at value x.

Therefore, we have that

$$P\left(x_i=0|H_1\right)=E_{N-1}$$ (Equation B7)

and

$$P\left(x_i=1|H_1\right)=1-E_{N-1}.$$ (Equation B8)

The log-likelihood can be calculated as

$$\begin{array}{c}{L}_{H_1}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}P\left(x_i=1|H_1\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_1\right)\\ =\sum _{i=1}^n{x}_i\text{log}\left(1-E_{N-1}\right)+\left(1-x_i\right)\text{log}\left(E_{N-1}\right).\end{array}$$

Likelihood under the Null Hypothesis

Under the null hypothesis (query genome g is not in beacon B, $g\notin B$), the response x_i is given by

• I.
  x_i = 0 if

  • (a)
    the frequency of the allele f_i ≤ f^∗or
  • (b)
    the frequency of the allele f_i > f^∗ and none of the other N genomes in the beacon has the alternate allele.
• II.x_i = 1 otherwise.

The log-likelihood under the null hypothesis is given by

$$L_{H_0}\left(R\right)=\sum _{i=1}^N{x}_i\text{log}P\left(x_i=1|H_0\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_0\right).$$ (Equation B9)

We first calculate $P\left(x_i=0|H_0\right)$:

$$P\left(x_i=0|H_0\right)={\int }_{f_i=0}^{f^{\ast }}P\left(f_i\right)d{f}_i+{\int }_{f_i=f^{\ast }}^{1}P\left(\text{none}\text{of}\text{the}\text{other}N\text{genomes}\text{has}\text{the}\text{alternate}\text{allele}|f_i\right)P\left(f_i\right)d{f}_i=I_{f^{\ast }}\left(a,b\right)+{\int }_{f_i=f^{\ast }}^1{\left({\left(1-f_i\right)}^2\right)}^{N}P\left(f_i\right)d{f}_i=I_{f^{\ast }}\left(a,b\right)+{\int }_{f_i=f^{\ast }}^1{\left(1-f_i\right)}^{2N}P\left(f_i;a,b\right)d{f}_i=I_{f^{\ast }}\left(a,b\right)+D_N\left(1-I_{f^{\ast }}\left(a,b+2N\right)\right)=F_N,$$

where $F_N=I_{f^{\ast }}\left(a,b\right)+D_N\left(1-I_{f^{\ast }}\left(a,b+2N\right)\right)$.

Therefore, we have that

$$P\left(x_i=0|H_0\right)=F_N$$ (Equation B10)

and

$$P\left(x_i=1|H_0\right)=1-F_N.$$ (Equation B11)

The log-likelihood can be calculated as

$$\begin{array}{c}{L}_{H_0}\left(R\right)=\sum _{i=1}^n{x}_i\text{log}P\left(x_i=1|H_0\right)+\left(1-x_i\right)\text{log}P\left(x_i=0|H_0\right)\\ =\sum _{i=1}^n{x}_i\text{log}\left(1-F_N\right)+\left(1-x_i\right)\text{log}\left(F_N\right).\end{array}$$

Finding the Optimal Censoring Threshold f^∗

We use the Gaussian approximation described earlier to obtain an estimate of the optimal censoring threshold frequency f^∗. We have that

$${\mu }_1=nB+nC\left(1-E_{N-1}\right),$$ (Equation B12)

$${\sigma }_1=-C\sqrt{n{E}_{N-1}\left(1-E_{N-1}\right)},$$ (Equation B13)

$${\mu }_0=nB+nC\left(1-F_N\right),$$ (Equation B14)

and

$${\sigma }_0=-C\sqrt{n{F}_N\left(1-F_N\right)}.$$ (Equation B15)

We have

$${\mu }_0-{\mu }_1=nB+nC\left(1-F_N\right)-\left[nB+nC\left(1-E_{N-1}\right)\right]$$ (Equation B16)

$$=nC\left(E_{N-1}-F_N\right).$$ (Equation B17)

Also,

$${\sigma }_1{z}_{1-\beta }-{\sigma }_0{z}_{\alpha }=-z_{1-\beta }C\sqrt{n{E}_{N-1}\left(1-E_{N-1}\right)}+z_{\alpha }C\sqrt{n{F}_N\left(1-F_N\right)}=C\sqrt{n}\left(z_{\alpha }\sqrt{F_N\left(1-F_N\right)}-z_{1-\beta }\sqrt{E_{N-1}\left(1-E_{N-1}\right)}\right).$$

Therefore, we get

$${\mu }_0-{\mu }_1={\sigma }_1{z}_{1-\beta }-{\sigma }_0{z}_{\alpha }$$ (Equation B18)

$$nC\left(E_{N-1}-F_N\right)=C\sqrt{n}\left(z_{\alpha }\sqrt{F_N\left(1-F_N\right)}-z_{1-\beta }\sqrt{E_{N-1}\left(1-E_{N-1}\right)}\right)$$ (Equation B19)

$$\sqrt{n}\left(E_{N-1}-F_N\right)=z_{\alpha }\sqrt{F_N\left(1-F_N\right)}-z_{1-\beta }\sqrt{E_{N-1}\left(1-E_{N-1}\right)}$$ (Equation B20)

$$1-\beta ={\text{Φ}}^{-1}\left(\frac{z_{\alpha }\sqrt{F_N\left(1-F_N\right)}-\sqrt{n}\left(E_{N-1}-F_N\right)}{\sqrt{E_{N-1}\left(1-E_{N-1}\right)}}\right).$$ (Equation B21)

All terms in this equation depend on f^∗, n, N, a, b, α, and β. Thus, while allowing n queries given a desired false-positive rate α and maximum allowable power 1 − β in a beacon with N individuals from a population with SFS parametrized by $\text{beta}\left(a-1,b-1\right)$, we can find the censoring threshold f^∗. An analytical solution cannot be obtained for f^∗ because of the form of the cumulative distribution function. However, a grid search over f^∗ can be used for finding the optimal value for the censoring threshold.

Web Resources

The URLs for data presented herein are as follows:

• GA4GH Beacon Project, http://ga4gh.org/#/beacon

• GA4GH Beacon Network, https://beacon-network.org//#/beacons/search

• Kaviar (Known Variants) beacon metadata, http://db.systemsbiology.net/kaviar/KaviarSourceDetails.html

• PGP beacon metadata, http://lightning-dev4.curoverse.com/people.html

• SFARI Beacon, http://beacon.sfari.org/