Tractography-driven Groupwise Multi-Scale Parcellation of the Cortex

Abstract

The analysis of the connectome of the human brain provides key insight into the brain’s organisation and function, and its evolution in disease or ageing. Parcellation of the cortical surface into distinct regions in terms of structural connectivity is an essential step that can enable such analysis. The estimation of a stable connectome across a population of healthy subjects requires the estimation of a groupwise parcellation that can capture the variability of the connectome across the population. This problem has solely been addressed in the literature via averaging of connectivity profiles or finding correspondences between individual parcellations a posteriori. In this paper, we propose a groupwise parcellation method of the cortex based on diffusion MR images (dMRI). We borrow ideas from the area of cosegmentation in computer vision and directly estimate a consistent parcellation across different subjects and scales through a spectral clustering approach. The parcellation is driven by the tractography connectivity profiles, and information between subjects and across scales. Promising qualitative and quantitative results on a sizeable data-set demonstrate the strong potential of the method.

1 Introduction

Understanding the brain’s organisation and function remains an elusive goal and a very active research subject. There seems to be an agreement amongst scientists that the brain’s cortical surface can be separated or parcellated into functionally and structurally distinct regions. Many approaches have sought to identify those regions over the years, principally relying on anatomical properties. Nonetheless, while some anatomical parcellations are widely known and relied upon [8, 18], they do not properly reflect the brain’s structural connectivity which is key to understanding its function and the impact of neurological diseases. Structural brain connectivity or connectome studies typically rely on anatomical or random parcellations to build connectivity graphs from diffusion MRI (dMRI) and tractography. However, such parcellations introduce a bias in the way the network is constructed and can lead to erroneous connections and conclusions [17]. This issue can be addressed via the construction of tractography driven parcellations that will identify distinct regions in terms of connectivity, and enable more meaningful connectome analysis.

A significant amount of effort has been focused on the complementary task of resting state functional MRI (fMRI) driven parcellation [4, 7]. Recently, dMRI-driven parcellation has gained interest as well. Several methods have focused on parcellation of brain substructures [2, 10], modelling the task as a clustering problem driven by the correlation between connectivity profiles. Aiming at whole brain parcellation makes the task harder, since the high dimensionality of the data prevents the direct use of common clustering techniques.

Clarkson et al. [5] proposed to refine an anatomical parcellation by introducing information from dMRI and iteratively updating labels. The method is also extended to groupwise parcellation through averaging of the connectivity profiles. Its main drawback is the strong bias introduced by the initial anatomical parcellation. Roca et al. [15] proposed an iterative approach that aims to reduce the dimensionality of the data. In each iteration, the cortical surface is divided into a set of Voronoi cells on which k-medoids clustering is performed. Parcels that respect certain size and boundary constraints are excluded from the domain for the subsequent iterations. Only a subset of the cortical surface (regions that are strongly connected) is parcellated. The method was later extended to a group parcellation [16] through averaging of the different subjects’ connectivity profiles. A hierarchical clustering based parcellation method was presented in [13]. Despite the appeal of obtaining consistent parcellations across resolutions (i.e. number of parcels), hierarchical clustering is at risk of propagating errors from low resolution clusterings and does not circumvent the need of selecting a number of parcels for further analysis.

While individual parcellations are the most faithful to a given subject’s connectivity, they can be sensitive to noise and unreliable. Furthermore, they make group studies difficult as there are no direct correspondences across subjects. Such studies are however essential if one seeks to identify a common connectome across healthy subjects (a connectome “backbone”), which could later enable to evaluate the impact of a disease on the brain’s organisation. Both issues can be overcome through a groupwise parcellation approach. Existing groupwise methods either seek a matching across subjects after independent parcellations [13] relying on possible noisy results, or perform a groupwise parcellation after constructing an average connectivity profile [5, 16] which prevents from obtaining single subject parcellations. In this paper, we propose a whole brain groupwise parcellation method that directly estimates matching parcels across subjects without the need for averaging. We borrow ideas from the concept of cosegmentation [12] and design a multi-scale and multi-subjects spectral clustering method driven by correlation between connectivity profiles. Here, consistency across scales (so-called supervertex parcellations of the cortical surface) and subjects is enforced via a set of links embedded in a constraint matrix. We tackle the challenge of evaluating brain parcellations by computing group consistency and information loss based measures, which provide sensible quantitative comparisons across methods and distinct groups. Qualitative evaluation shows how correspondences between subject-dependent parcels are obtained within a group, as well as achieving strong consistency across different groups.

2 Groupwise Multi-Scale Parcellation

In this section, we describe the method for obtaining a group parcellation of the cortical surface of a set of N different subjects into K parcels. We represent these surfaces as a triangular mesh made of N_υ vertices, and assume all surfaces to be registered to the same reference [9]. As a result, all surface vertices have direct correspondence across all subjects. Furthermore, we consider that a N_υ × N_υ tractography matrix χ_Si has been computed from diffusion data for each subject S_i. Each row of this matrix χ_Si (v) describes how a vertex v is connected to the rest of the cortical surface.

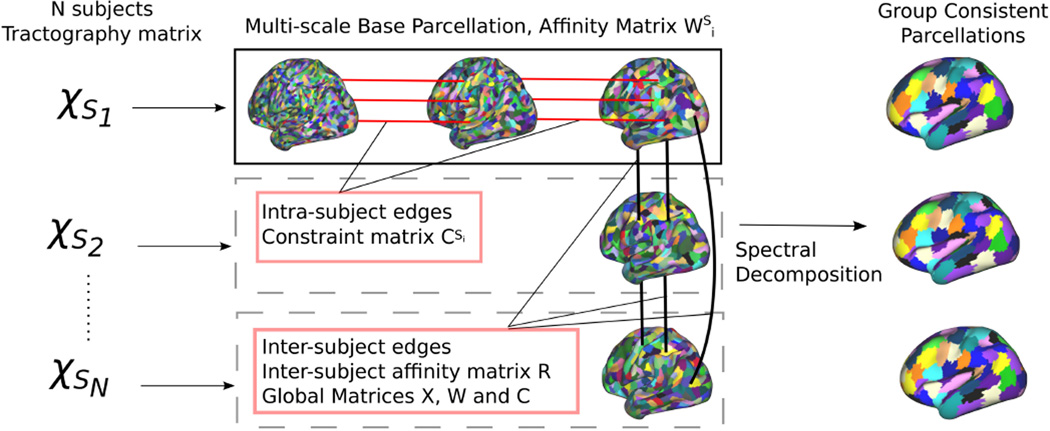
The proposed method is illustrated in Fig.1. For each subject, a set of high resolution parcellations is constructed for L different resolution layers (base parcellation). These parcellation layers then serve as the basis of a multi-scale groupwise spectral clustering problem, where the affinity between vertices is described by the tractography matrix, and edges across resolutions and subjects force the parcellations to be consistent.

Fig. 1.

Illustration of the proposed method. Each subject S_i is associated with a connectivity matrix χ_Si that drives the construction of a multi-scale base parcellation. Intra-subject edges (between base parcellation resolutions) and intersubject edges (between all pairs of subjects at the coarsest parcellation resolution) are built to allow a common spectral decomposition of the affinity matrix (connectivity profiles correlation).

2.1 Base Parcellation

The first step towards building our groupwise parcellation is to capture structural connectivity information at multiple scales through the construction of supervertices at different resolutions. Similarly to superpixels [1], supervertices can be seen as an initial over-segmentation of the cortical surface based on connectivity information such that vertices within a supervertex have very similar connectivity profiles. We rely on the geodesic distance between vertices to obtain spatially contiguous supervertices, while the correlation between their connectivity profiles enforces homogeneous connectivity.

We are inspired by the method proposed in [14] that relies on Fast Marching to compute geodesic distances for surface segmentation. In this setting, the computation of the geodesic distance d(v₀, v) = U(v) from vertex v₀ can be reformulated as a front propagation problem, where U follows the Eikonal equation ‖∇U‖F = 1 which can be solved using the Fast Marching algorithm. F is the speed function characterising the front propagation. We can compute a correlation dependent geodesic distance by defining a correlation weighted speed function: F(v) = exp(μρ(χ_Si (v₀), χ_Si (v))). Here, ρ(․, ․) is the Pearson’s correlation coefficient between the vertices’ connectivity profiles χ_Si (v) and μ is a weighting parameter. In this setting, the front will propagate faster towards vertices that have a high correlation (i.e. similar connectivity profiles) with the source vertex v₀.

Each supervertex resolution is computed through an iterative approach. Given a specified number of N_l supervertices, we initialise by uniformly sampling N_l seeds across the brain’s cortical surface. At each iteration, we first compute the correlation weighted geodesic distance from each seed to the rest of the surface, and build supervertices by assigning a vertex to its closest seed. We then reevaluate the seeds by selecting, for each supervertex, the vertex that has the highest correlation with the rest of the cluster. This process is iterated until convergence for the L different levels.

Each base parcellation level is associated to a N_l × N_l merged connectivity matrix, constructed by adding the fibre counts across vertices. The level’s affinity matrix W_l is defined as the Pearson’s correlation coefficient between those merged connectivity profiles. In order to obtain spatially contiguous parcels, correlation weighted edges are only constructed between supervertices that are adjacent.

Our next step is to build connections between the different base parcellation levels, so as to recover a common partition of the cortical surface across resolutions.

2.2 Intra-Subject Connections Between Resolutions

We seek coherence across resolutions by enforcing supervertices that are in similar locations on the cortical surface to be assigned to the same parcels through the construction of inter-resolutions edges.

For a given resolution level l, each supervertex is connected to a supervertex at the finer level l − 1 if they share vertices on the original cortical surface. The strength of the edge is defined by the amount of overlapping vertices, so that the same parcellation result is imposed on supervertices that are the most similar. The intra-subject, inter-resolutions links can be written as:

$$C_{l-1,l}(j,k)=\frac{|s_l^j\cap s_{l-1}^k|}{|s_l^j|}$$ (1)

where $s_l^j$ is the set of vertices at the original resolution that belong to the j-th supervertex at resolution level l and $|s_l^j|$ is the number of vertices in $s_l^j$.

In this setting, we can estimate a parcellation for a single subject S_i that is consistent across resolutions using the multi-scale normalised cut approach [19]. For each level l, we aim at finding a K-way parcellation matrix X_l ∈ {0, 1}^{N_υ × K} defined as:

$$X_l(i,j)=\{\begin{array}{cc}1\hfill & \text{if}{s}_l^i\in \text{parcel}\mathrm{j}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (2)

The multi-scale parcellation and affinity matrices can then be constructed as follows:

$$X^{S_i}=\left(\begin{array}{c}\hfill X_1\hfill \\ \hfill ⋮\hfill \\ \hfill X_L\hfill \end{array}\right),W^{S_i}=\left(\begin{array}{ccc}\hfill W_1\hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill W_L\hfill \end{array}\right)$$ (3)

Finally, we build a constraint matrix that encodes the inter-resolution links and ensures consistency of the recovered parcellation across resolutions:

$$C^{S_i}=\left(\begin{array}{cccc}\hfill C_{1,2}\hfill & \hfill -I_{N_2}\hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill C_{L-1,L}\hfill & \hfill -I_{N_L}\hfill \end{array}\right)$$ (4)

Here, I_Nl is the N_l × N_l identity matrix and N_l is the number of supervertices at scale l. This matrix forces the obtained parcellation to be consistent across scales through the following constraint equation:

$$CX=0$$ (5)

Optimisation of the multi-scale normalised cut criterion, subject to the inter-resolution constraint [19], yields a single subject parcellation that captures local connectivity information at different scales. Comparing the obtained parcellations within a group is however a very challenging task as there are no direct matches between parcels, and anatomical variability (as well as registration errors) can cause different subjects to have very different parcel boundaries. This issue can be addressed by performing a concurrent parcellation of all the subjects within the group to directly obtain correspondences between parcels.

2.3 Inter-Subject Connections

Spectral clustering offers the possibility to integrate different subjects in the same framework in a very natural manner. A group consistent parcellation can be obtained through a joint estimation of the parcellation matrix X across subjects. The groupwise parcellation, affinity and constraint matrices are defined as:

$$X=\left(\begin{array}{c}\hfill X^{S_1}\hfill \\ \hfill ⋮\hfill \\ \hfill X^{S_N}\hfill \end{array}\right),W=\left(\begin{array}{ccc}\hfill W^{S_1}\hfill & \hfill \hfill & \hfill R\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill R^T\hfill & \hfill \hfill & \hfill W^{S_N}\hfill \end{array}\right),C=\left(\begin{array}{ccc}\hfill C^{S_1}\hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill C^{S_N}\hfill \end{array}\right)$$ (6)

Matching parcellations are enforced by adding inter-subject connections encoded in the matrix R. Following [12], we only connect the coarsest resolution layers. This step is essential in our case as it relaxes the need for a precise registration in addition to allowing individual differences at the highest resolution.

Let us consider that all subjects have been registered to a common surface mesh. Similarly to the multi-scale parcellation approach, we seek a common parcellation across subjects by forcing supervertices in similar locations to belong to the same parcel. To this end, a supervertex from subject i is connected to a supervertex from subject j if they share the highest amount of overlapping surface vertices and have the strongest correlated connectivity profiles. We define the inter-subject edges between matching supervertices as follows:

$$R(s^i(S_1),s^j(S_2))=\alpha \rho (s^i(S_1),s^j(S_2))$$ (7)

where ρ(sⁱ(S₁), s^j(S₂)) is the correlation between the connectivity profiles of the two different subjects’ supervertices and α is a weighting parameter. Correlation weighted edges enable accounting for differences in anatomy and possible errors in registration by decreasing the strength of the edges in non matching regions.

2.4 Optimisation

The joint parcellation is eventually recovered by optimising the multi-scale normalised cut objective criterion [6] :

$$\text{maximise}E(X)=\frac{1}{K}\sum _{l=1}^K\frac{X_l^{T}W{X}_l}{X_l^{T}D{X}_l}$$

$$\text{subject to}X\in {\{0,1\}}^{N\times K},$$ (8)

$$X{1}_k=1_N,$$

$$CX=0$$

A near global-optimal solution to this NP-complete problem can be estimated in a two-step approach. First by finding the global optimum of the relaxed continuous problem Z*, and second by solving a discretisation problem to project this continuous optimum to the discrete space.

We define the normalised affinity matrix $P=D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}}$, and the projector matrix Q that integrates the constraint matrix:

$$Q=I-D^{-\frac{1}{2}}{C}^T{(C{D}^{-1}{C}^T)}^{-1}C{D}^{-\frac{1}{2}}$$ (9)

We solve the continuous problem following the Rayleigh Ritz theorem [20], through computation and normalisation of the K largest eigenvectors of the matrix QPQ. This solution is then discretised through an iterative process [19] by seeking the closest solution to Z* that satisfies the constraints of the discrete problem.

3 Experimental Evaluation

Evaluation of cortical parcellations remains a very challenging task due to the lack of a ground truth parcellation. In this section, we evaluate the quality of our parcellations based on two main ideas: group consistency and fidelity to each individual’s connectivity matrix. We are seeking to observe similarities in connectivity within and across groups, while preserving individual variability.

3.1 Data Acquisition and Preprocessing

We evaluated our method on 100 different subjects (age range 22–35 years old) from the latest release of the Human Connectome Project (HCP)³. The HCP dMRI have been acquired using a multi-shell approach, with three shells at b-values 1000, 2000, and 3000 s/mm² and 90 gradient directions per shell. The structural and diffusion data of all subjects have been preprocessed following the HCP’s minimum processing pipeline [9]. The cortical surfaces of all subjects are registered and represented as a triangular mesh of 32k vertices per hemisphere. Vertices corresponding to the medial wall are excluded from parcellations. The tractography matrix is obtained on the native mesh representing the gray-white matter interface using FSL’s bedpostX and probtrackX methods [3, 11] which estimate the fibres orientation at each voxel with a ball and stick model, and perform probabilistic tractography respectively. Following [11], we fitted three fibre compartments per voxel. 5000 streamlines were sampled from each of the mesh vertices. Each entry χ(v, q) counts the number of streamlines sampled from the surface vertex v that reach vertex q. The groupwise parcellation was performed on the left hemisphere of two disjoint groups of 50 randomly selected subjects with a base parcellation of 3 levels of 2000, 1000 and 500 supervertices and parameter μ heuristically set to 3.

3.2 Parameter Selection

The weighting parameter α has a large influence on the obtained parcellation and its consistency across subjects. We evaluate the quality of our parcellations and the impact of this parameter via an intra-subject information loss measure and a group consistency measure. Both measures are estimated on the connectivity graph rather than the parcellation itself. This is particularly relevant for group consistency, where the parcellations are expected to have different boundaries, but the merged connectivity graphs should be similar.

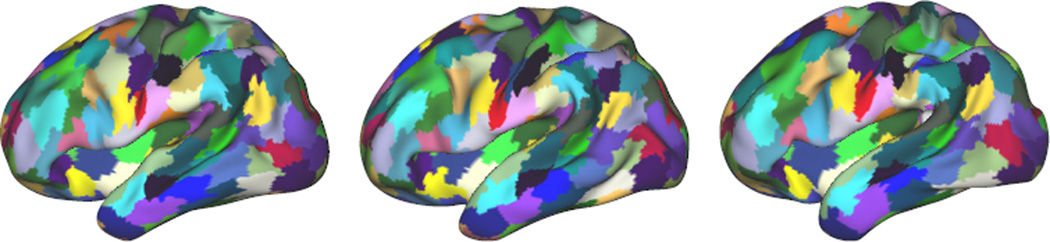
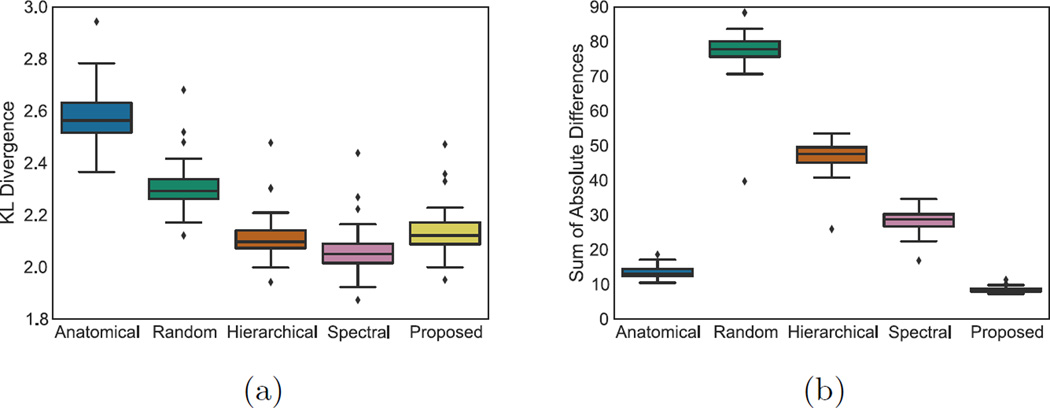
Our main objective is to obtain parcellations that summarise the structural connectivity maps faithfully. In other words, we seek to lose as little information as possible when merging the connectivity profiles of several vertices into one entity. The first measure we are computing aims to evaluate this information loss through the Kullback Leibler (KL) divergence. Each subject’s K × K merged connectivity matrix is converted into a N_υ × N_υ matrix ${\chi }_{S_i}^{\mathit{\text{clus}}}$ that should be as similar as possible to the N_υ × N_υ matrix χ_Si prior to clustering. The matrix ${\chi }_{S_i}^{\mathit{\text{clus}}}$ is constructed by assigning the same connectivity profile to all the vertices that belong to the same cluster. The KL divergence is then computed between the matrices χ_Si and ${\chi }_{S_i}^{\mathit{\text{clus}}}$, that are normalised to be probability mass functions. The idea is to evaluate how much information is lost when ${\chi }_{S_i}^{\mathit{\text{clus}}}$ is used to approximate χ_Si. Second, we evaluate group consistency using the sum of absolute differences (SAD). After parcellation, an average K × K connectivity matrix is constructed from all the subjects’ merged connectivity matrices. The deviation of each subject from the average is then evaluated by computing the SAD between the average matrix and the subject’s matrix. We compute those measures for a range of 50 to 250 parcels and the weighting parameter α ranging from 0.1 to 3. The obtained results are shown in Fig.2. Intuitively, the KL divergence should decrease when the number of parcels increases, as the averaging of connectivity profiles is reduced. Conversely, the SAD is expected to increase with the number of parcels, as more individual information is maintained. Both measures show a rapid decrease, then stabilise when α is increased. This can be explained by the fact that when α is low enough, the parcellations are not constrained to be in accordance. Hence, the K clusters will be spread across subjects, leading to different parcellations and different numbers of parcels. However, both SAD and KL tend to increase slowly after reaching a minimum as constraints that are too strong can force identical parcellations, while isolated supervertices start to appear. Our main goal is to obtain parcellations that are as faithful as possible to the subjects connectivity profiles, we therefore select the value of α that minimises the KL divergence. The two groups we tested our method on show the same behaviour, and require α to be increased with the number of parcels (from 0.1 to 0.5 in our setting). Fig.4 shows examples of parcellations obtained with the optimal value of α for 160 parcels. We can observe a strong consistency, but also the different shapes and boundaries of the parcels across subjects.

Fig. 2.

Evolution of the average KL divergence (a) and the SAD (b) across subjects depending on the value of the parameter α and the number of parcels.

Fig. 4.

Example parcellations (160 parcels) of subjects within the same group.

3.3 Method Evaluation

We have compared the proposed groupwise parcellation method to (a) multi-scale individual spectral clustering (described in sec.2.2), (b) hierarchical clustering of the finest supervertex resolution level, (c) anatomical parcellations from the Destrieux atlas [8], and (d) Poisson disk sampling random parcellations. We computed the KL divergence and SAD for the five different methods for 75 parcels (anatomical parcellation granularity). In the absence of existing matching across the subject’s clusterings, the clusters that had the highest overlap were matched. This matching is not optimal, but highlights one of the main drawbacks of individual parcellations. Results are shown in Fig.3. While it is expected that a groupwise parcellation would not perform as well as individual parcellations in terms of information loss, the increase in KL remains very limited and faithful to the data in comparison with random or anatomical parcellation. The SAD score is significantly ouperforming all methods.

Fig. 3.

Boxplot comparison of the proposed method to anatomical, random, hierarchical and spectral parcellations for the KL divergence (a) and SAD (b).

3.4 Group Comparisons

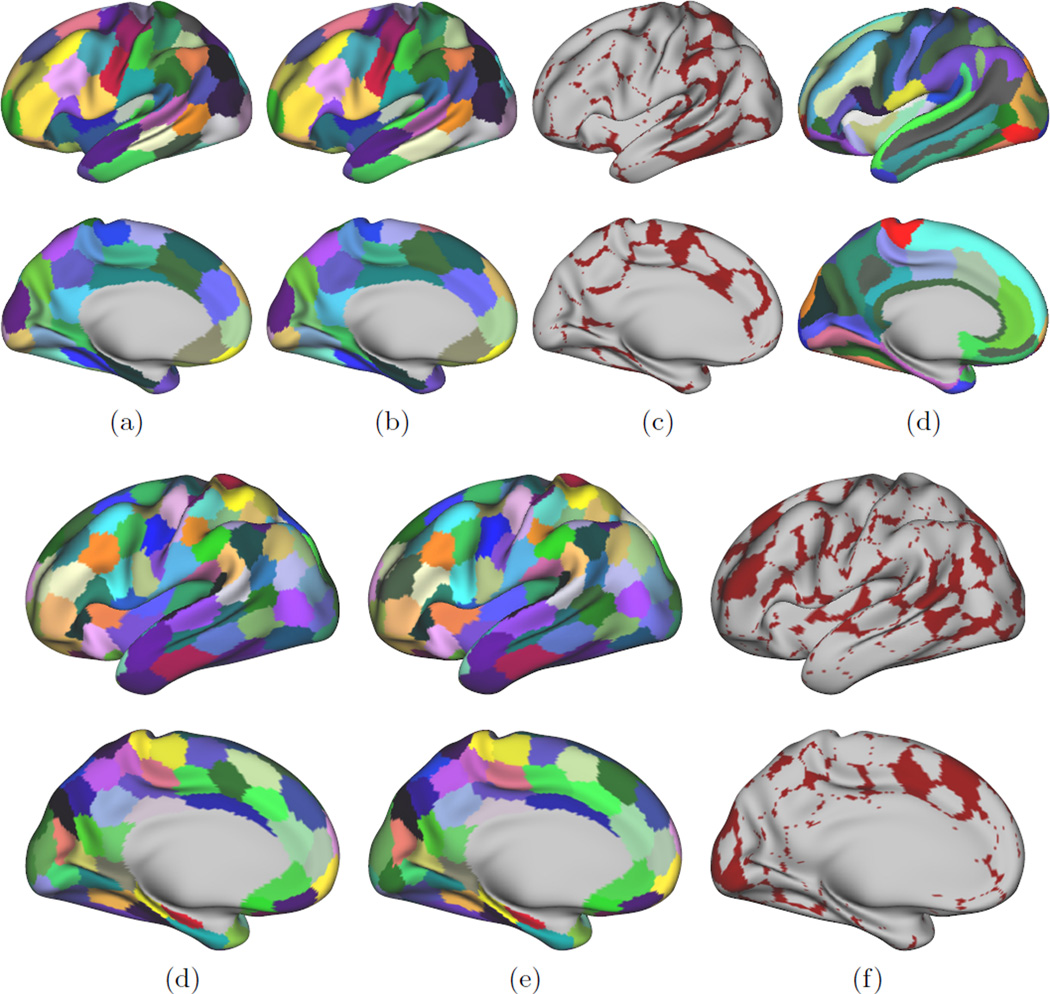
Finally, we compared the consistency across our two groups’ parcellations. Given the sizeable data-set, both groups should reflect common connectivity properties and be essentially free of inter-subject variability. The average parcellations obtained through majority voting are compared by computing the Dice score between all highest matching parcels. We obtain a mean Dice score of 72 ± 5 % across all numbers of parcels. It is as expected lower than the average intra group pairwise dice score of 79 ± 7% but significantly outperforms the average pairwise dice scores between independent parcellations (57 ± 3%). The strong similarity between the two groups’ parcellations is shown in Fig.5. We also computed the SAD score between average connectivity profiles after matching the parcels. Its mean value of 0.20 ± 0.05 is on par with intra group SAD scores (individual vs. average connectivity matrices, mean value 0.16 ± 0.07) and outperforms the SAD scores between individual parcellations (mean 0.48 ± 0.1). Inter-group comparisons for other methods are not performed here as the high within group variability does not allow the construction of a meaningful average parcellation.

Fig. 5.

Average parcellations for 70 (a,b,c) and 130 parcels (e,f,g). (a,e) and (b,f) show parcellations from two different groups of normal subjects, while (c,g) shows the disagreement between both groups. Each group contains 50 subjects. The average 75 clusters anatomical parcellation (d) is shown as comparison to our proposed 70 clusters parcellation.

4 Discussion

We presented a groupwise multi-scale parcellation method of the brain’s cortical surface that is driven by structural connectivity. Our proposed spectral clustering approach allows the recovery of consistent parcellations across subjects and scales without averaging raw connectivity profiles. It shows great consistency across and within groups as well as limited information loss with respect to the raw connectivity matrix. The proposed method paves the way for groupwise connectome analysis. First and foremost, this could enable idenfication of a connectome backbone, i.e. connections that are present across populations. Specific groups studies could consequently be considered (healthy vs. disease, young vs. ageing for instance) in order to identify possible connectivity disruptions or global differences. The obtained parcellations and networks could also be compared to fMRI based parcellations, or correlated with activation regions from fMRI to study the relationship between structure and function. Several extensions and improvements of the method could be considered. Incorporating a different base parcellation in our framework is easy, since no assumption is made on the method adopted. The consistency across scales would be more natural through a hierarchical approach where the different scales have matching boundaries. Despite correlation weighted inter-subject links, the method relies strongly on the registration across subjects that can be imperfect. Another interesting extension of the method would be to incorporate a diffusion driven registration task in an iterative fashion, where registration and parcellation alternate.