Assessing Interactions for Fixed-Dose Drug Combinations in Tumor Xenograft Studies

Abstract

Statistical methods for assessing the joint action of compounds administered in combination have been established for many years. However, there is little literature available on assessing the joint action of fixed-dose drug combinations in tumor xenograft experiments. Here an interaction index for fixed-dose two-drug combinations is proposed. Furthermore, a regression analysis is also discussed. Actual tumor xenograft data were analyzed to illustrate the proposed methods.

1. INTRODUCTION

The study of joint actions of drugs administered in combination is an important topic in cancer treatment development. The joint action of drug combinations is usually divided into three types: additive, synergistic, or antagonistic. Statistical methods to assess the joint action of drug combinations have been established for many years. For studies using multiple doses of a two-drug combination, a dose-response surface model is often used to assess the interaction by applying Loewe’s simple similar joint action principle (Loewe and Muischnek, 1926). Such methods have been extensively studied by Hewlett (1969), Finney (1971), Chou and Talalay (1984), Giltinan et al. (1988), Machado and Robinson (1994), Greco et al. (1995), Plummer (1998), and more recently by Tan et al. (2003), Straetemans et al. (2005), Kong and Lee (2006, 2008), and others. However, a response-surface model is not applicable for a fixed-dose drug combination study. Therefore, testing the superiority of the combination over its components is conducted for a fixed-dose combination study with a normally distributed response. Examples include Snapinn (1987), Laska and Meisner (1989), Hung (1993, 1996), Hung et al. (1993), and others. In cancer treatment development, drug combinations are first tested in preclinical animal models to determine whether the combination therapy should be further investigated in a clinical trial. Drug combinations are often tested in tumor xenograft studies with fixed doses to minimize the number of animals required per drug combination. There is little literature available on assessing the joint action of drug combinations in such experiments. Here we define an interaction index that quantifies the interaction of fixed-dose two-drug combinations in tumor xenograft experiments. Confidence intervals for the interaction index are derived. The joint action can be assessed based on confidence limits of the interaction index. Furthermore, a regression analysis is discussed. Tumor xenograft data from an actual two-drug combination study are analyzed to illustrate the proposed method.

2. INTERACTION INDEX

In a fixed-dose two-drug combination tumor xenograft experiment, human cancer cells are engrafted into mice to produce a xenograft model. Tumor-bearing mice are randomized into a common control group represented by C, two single-drug groups represented by A and B, and the two-drug combination group represented by AB. Tumor volumes are observed for each mouse at the initiation and end of study. The goal of the study is to assess the joint action of drug combination. Let μ_g be the mean response of group g = A, B, AB, and C. The response variable could be the tumor volume or the relative tumor volume (tumor volume divided by its initial volume) at the end of the study. The relative effect of treatment group g to control C is measured by the ratio of means θ_g = μ_g/μ_C, g = A, B, AB. The joint action is additive only if the relative effect of the drug combination equals the multiplicative of the relative effects of the two single drugs, that is, θ_AB = θ_A × θ_B. Otherwise, the interaction is either supra-additive or sub-additive, summarized as follows:

Supra-additive:

$${\theta }_{AB}<{\theta }_A\times {\theta }_B$$

Additive:

$${\theta }_{AB}<{\theta }_A\times {\theta }_B$$

Sub-additive:

$${\theta }_{AB}<{\theta }_A\times {\theta }_B$$

This is called a relative-effect multiplicative model or Bliss independent model (Bliss, 1939). Based on this multiplicative model, an interaction index can be defined on the logarithm scale as

$$\gamma =\mathit{log}\left({\theta }_{AB}\right)-\mathit{log}\left({\theta }_A\right)-\mathit{log}\left({\theta }_B\right)$$

Therefore, γ < 0, γ = 0, or γ > 0 indicates a supra-additive, additive, or sub-additive joint action of the two-drug combination, respectively. Because the joint action for fixed-dose drug combinations is only defined locally, the terms supra-additive and sub-additive are used rather than synergistic and antagonistic, respectively, to distinguish the global joint action definition.

Now let X_ig be the observed tumor volume or relative tumor volume of the ith mouse in group g at the end of the study, i = 1,…, n_g, and let ${\widehat{\theta }}_A={\overline{X}}_A/{\overline{X}}_C,{\widehat{\theta }}_B={\overline{X}}_B/{\overline{X}}_C$, and ${\widehat{\theta }}_{\mathit{AB}}={\overline{X}}_{\mathit{AB}}/{\overline{X}}_C$ be the estimate of θ_A, θ_B, and θ_AB, respectively, where ${\overline{X}}_g={\sum }_{i=1}^{n_g}{X}_{\mathit{ig}}/n_g$ is the sample mean of group g. Then an estimate of the interaction index γ is given by:

$$\begin{array}{l}\widehat{\gamma }=\mathit{log}\left({\widehat{\theta }}_{\mathit{AB}}\right)-\mathit{log}\left({\widehat{\theta }}_A\right)-\mathit{log}\left({\widehat{\theta }}_B\right)\\ =\mathit{log}\left({\overline{X}}_{\mathit{AB}}\right)-\mathit{log}\left({\overline{X}}_A\right)-\mathit{log}\left({\overline{X}}_B\right)+\mathit{log}({\overline{X}}_C)\end{array}$$ (1)

The standard error estimate of $\widehat{\gamma }$ can be obtained by the delta method as

$$\widehat{se}\left(\widehat{\gamma }\right)\simeq {\left(\frac{1}{{\overline{X}}_{AB}^2}\frac{{\widehat{\sigma }}_{AB}^2}{n_{AB}}+\frac{1}{{\overline{X}}_A^2}\frac{{\widehat{\sigma }}_A^2}{n_A}+\frac{1}{{\overline{X}}_B^2}\frac{{\widehat{\sigma }}_B^2}{n_B}+\frac{1}{{\overline{X}}_C^2}\frac{{\widehat{\sigma }}_C^2}{n_C}\right)}^{1/2}$$ (2)

where ${\widehat{\sigma }}_g^2={\sum }_{i=1}^{n_g}{(X_{\mathit{ig}}-{\overline{X}}_{\mathit{ig}})}^2/(n_g-1)$ is the sample variance of the group g. A 100(1 − α)% delta method interval of γ is given by

$[\widehat{\gamma }-z_{1-\alpha /2}\widehat{\mathit{se}}(\widehat{\gamma }),\widehat{\gamma }+z_{1-\alpha /2}\widehat{\mathit{se}}(\widehat{\gamma })]$

where z_1−α/2 is the 100(1 − α/2)th percentile of the standard normal distribution.

The sample size used in tumor xenograft studies is often small, typically 10 mice per group. Therefore, a small sample confidence interval of γ is preferred. A nonparametric bootstrap t-interval (Efron and Tibshirani, 1993) for small sample inference is described as follows:

• 1. Generate S independent bootstrap samples $\{{\mathbf{X}}_g^{\ast b}=(X_{1g}^{\ast b},\dots ,X_{n_g,g}^{\ast b}),b=1,\dots ,S\}$ from tumor volume samples $(X_{1g},\dots ,X_{n_g,g})$ of group g, where g = A, B, AB, and C.

• 2. Compute the bootstrap replication ${\widehat{\gamma }}^{\ast b}=\mathit{log}({\widehat{\gamma }}_{\mathit{AB}}^{\ast b})-\mathit{log}({\widehat{\gamma }}_A^{\ast b})-\mathit{log}({\widehat{\gamma }}_B^{\ast b})$, where ${\widehat{\gamma }}_A^{\ast b}={\overline{X}}_A^{\ast b}/{\overline{X}}_C^{\ast b},{\widehat{\gamma }}_B^{\ast b}={\overline{X}}_B^{\ast b}/{\overline{X}}_C^{\ast b}$, and ${\widehat{\gamma }}_{\mathit{AB}}^{\ast b}={\overline{X}}_{\mathit{AB}}^{\ast b}/{\overline{X}}_C^{\ast b}$ for b = 1,…, S.

• 3. A 100(1 − α)% bootstrap t-interval can be obtained directly from the bootstrap sample

  $$t^{\ast b}=\frac{{\widehat{\gamma }}^{\ast b}-\widehat{\gamma }}{{\widehat{se}}^{\ast b}},b=1,\dots ,S$$

  where ${\widehat{\mathit{se}}}^{\ast b}$ is calculated using (2) for the bootstrap sample $\{{\mathbf{X}}_{\mathit{AB}}^{\ast b},{\mathbf{X}}_A^{\ast b},{\mathbf{X}}_B^{\ast b},{\mathbf{X}}_C^{\ast b}\}$. Let the αth percentile of $\{t^{\ast b},b=1,\dots ,S\}$ be estimated by the value of ${\widehat{t}}_{\alpha }$ such that $\#\{t^{\ast b}<{\widehat{t}}_{\alpha }\}/S=\alpha$. Then the bootstrap t-interval is given by

  $$[\widehat{\gamma }-{\widehat{t}}_{1-\alpha /2}\widehat{se}\left(\widehat{\gamma }\right),\widehat{\gamma }-{\widehat{t}}_{\alpha /2}\widehat{se}\left(\widehat{\gamma }\right)]$$

To assess the joint action using a confidence interval approach, if the interval of γ contains zero, then the drug combination is additive; if the upper limit of the confidence interval is less than zero, then the drug combination is supra-additive; otherwise, the drug combination is sub-additive.

3. SIMULATION STUDY

It is important to know whether the proposed intervals for the interaction index γ are appropriate for practical use for small-sample tumor xenograft studies. In this section, we conducted simulation studies to investigate the coverage probability of proposed intervals. The coverage probability is the probability that a confidence interval captures the true parameter, and it is estimated here as the proportion of cases in a simulation in which the calculated interval includes the true value.

The parameter configurations were chosen to represent various degrees of the interaction. The sample size considered in the simulation was n = 10 for each group, which is a typical sample size for tumor xenograft studies. The mean parameters for the simulation studies are given in Table 1. The standard deviations (σ_C, σ_A, σ_B, σ_AB) used were (0.1, 0.1, 0.1, 0.1), (0.4, 0.4, 0.4, 0.4), (0.1, 0.1, 0.2, 0.2), and (0.1, 0.2, 0.3, 0.4). For each parameter configuration, we generated 5,000 random samples from a normal distribution $N({\mu }_g,{\sigma }_g^2)$ or a log-normal distribution $LN({\mu }_g,{\sigma }_g^2)$, where g = C, A, B, and AB, and used 2,000 bootstrap samples.

Table 1.

Parameter configurations for the simulation study

Mean	Normal					Log-normal
	I	II	III	IV	V	I	II	III	IV	V
μC	10	10	10	10	10	2	2	2	2	2
μA	8	8	4	4	2	1.9	1.8	1.5	1.3	0.6
μB	8	7	4	4	2	1.9	1.5	1.5	1.2	0.5
μAB	1	3	2	4	1	0.2	0.8	1.0	1.0	0.5
γ	−1.86	−0.62	0	0.92	1.61	γ range from −1.6 to 1.42

The simulated 95% coverage probabilities of interval γ are presented in Table 2. The results showed that both intervals were slightly liberal. However, the coverage probability of the bootstrap t-interval was better than that of the delta-method interval and was closer to the nominal level of 0.95.

Table 2.

Empirical coverage probabilities of 95% bootstrap t-interval of interaction index γ based on 5,000 simulations and 2,000 bootstrap samples

Distribution	(σC, σA, σB, σAB)	Interval	Design
			I	II	III	IV	V
Normal	(0.1, 0.1, 0.1, 0.1)	Delta	0.920	0.930	0.933	0.939	0.932
		Bootstrap	0.946	0.945	0.947	0.947	0.945
	(0.4, 0.4, 0.4, 0.4)	Delta	0.921	0.931	0.934	0.940	0.935
		Bootstrap	0.941	0.945	0.944	0.947	0.943
	(0.1, 0.1, 0.2, 0.2)	Delta	0.919	0.929	0.932	0.935	0.932
		Bootstrap	0.945	0.947	0.946	0.948	0.945
	(0.1, 0.2, 0.3, 0.4)	Delta	0.913	0.925	0.930	0.934	0.921
		Bootstrap	0.931	0.945	0.944	0.947	0.932
Log-normal	(0.1, 0.1, 0.1, 0.1)	Delta	0.938	0.938	0.938	0.938	0.938
		Bootstrap	0.948	0.948	0.948	0.948	0.948
	(0.4, 0.4, 0.4, 0.4)	Delta	0.935	0.935	0.935	0.935	0.935
		Bootstrap	0.943	0.943	0.943	0.943	0.943
	(0.1, 0.1, 0.2, 0.2)	Delta	0.937	0.937	0.937	0.937	0.937
		Bootstrap	0.949	0.949	0.949	0.949	0.949
	(0.1, 0.2, 0.3, 0.4)	Delta	0.931	0.931	0.931	0.931	0.931
		Bootstrap	0.942	0.942	0.942	0.942	0.942

4. REGRESSION ANALYSIS

The joint action of drug combinations can also be assessed using a regression model if the response variable follows a certain distribution. Let y_i = log(X_i) be a log-transformed response variable of the ith subject, i = 1,…, n, where X_i is the tumor volume or the relative tumor volume of the ith subject at the end of the study. The interaction of the two-drug combination can be assessed by following the regression model

$$y_i={\alpha }_0+{\alpha }_1{z}_{\mathit{Ai}}+{\alpha }_2{z}_{\mathit{Bi}}+ y{z}_{\mathit{ABi}}+{\epsilon }_i, i=1,\dots ,n$$ (3)

where {ε_i, i = 1,…, n} are independent and follow normal distribution N(0, σ²) and z_Ai, z_Bi, and z_ABi are defined as z_Ai = 1 if the ith subject belongs to group A or AB and z_Ai = 0 otherwise, z_Bi = 1 if the ith subject belongs to group B or AB and z_Bi = 0 otherwise, and z_ABi = z_Ai × z_Bi.

The parameter γ in the model describes the interaction of the drug combination, with γ < 0, γ = 0, and γ > 0 indicating a supra-additive, additive, and sub-additive interaction, respectively. An advantage of using a regression-model approach is that the interaction of the drug combination can be simply assessed by testing the hypothesis

$$H_0:\gamma =0 \text{vs}. H_a:\gamma \ne 0$$

Applying the linear regression model theorem (Searle, 1971), the maximum likelihood estimate of β = (α₀, α₁, α₂, γ)′ is given by $\widehat{\mathit{\beta }}={(X^{\prime }X)}^{-1}{X}^{\prime }\mathbf{y}$, where X = (1, z_A, z_B, z_AB) is an n × 4 design matrix and y = (y₁,…, y_n)′ is a n × 1 response vector. The variance-covariance matrix estimate of $\widehat{\mathit{\beta }}$ is $v\widehat{a}r(\widehat{\mathit{\beta }})={\widehat{\sigma }}^2{(X^{\prime }X)}^{-1}$ with ${\widehat{\sigma }}^2={\sum }_{i=1}^n{e}_i^2/(n-4)$, where {e_i, i = 1,…,n} is the residuals obtained by fitting model (3). Then the interaction parameter γ can be tested by the t-statistic $t=\widehat{\gamma }/\widehat{se}\left(\widehat{\gamma }\right)~t(n-4)$. A 100(1 − α)% confidence interval of γ is given by

$[\widehat{\gamma }-t_{1-\alpha /2;n-4}\widehat{se}\left(\widehat{\gamma }\right),\widehat{\gamma }+t_{1-\alpha /2;n-4}\widehat{se}\left(\widehat{\gamma }\right)]$

where t_{1−α/2;n−4} is the 100(1 − α/2)th percentile of the t-distribution with a degree of freedom of n − 4. Another advantage of using a regression-model approach is that it simultaneously gives the estimates of two single-drug effects α₁ and α₂, which allows normalization of the interaction term by the ratio of interaction term γ to the expected additive effect for the combination; that is,

$$100\frac{\gamma }{{\alpha }_1+{\alpha }_2}\%$$

This normalized interaction term can be conceptualized as the percentage gain or loss of the expected treatment effect observed for the combination under additivity.

It is easy to show that the coefficient estimate $\widehat{\gamma }$ from the regression model (3) is given by

$$\widehat{\gamma }=\mathit{log}\left({\stackrel{\sim }{X}}_{AB}\right)-\mathit{log}\left({\stackrel{\sim }{X}}_A\right)-\mathit{log}\left({\stackrel{\sim }{X}}_B\right)+\mathit{log}({\stackrel{\sim }{X}}_{\mathrm{C}})$$ (4)

where ${\stackrel{\sim }{X}}_g={(X_{1g}\cdots X_{n_g;g})}^{1/n_g}$ is a geometric mean of group g = A, B, AB, C. The arithmetic means in expression (1) were replaced by geometric means in expression (4). Therefore, the two approaches are not identical but similar. However, the regression approach has the advantage that it gives an exact statistical inference for the interaction parameter γ.

5. ACTUAL TUMOR XENOGRAFT DATA ANALYSIS

Data from a two-drug combination study generated in the Xenograft Core Facility of St. Jude Children’s Research Hospital were used. In this study, the human neuroblastoma cell line SKNAS was used to study the joint action between the proteasome inhibitor bortezomib (0.5mg/kg, 3 times per week) and the macrolide rapamycin (5mg/kg, 3 times per week). Both of these agents have documented anticancer activity and are currently being used in clinical trials. SKNAS tumor cells were implanted into male SCID mice in the retroperitoneum, an orthotopic location for neuroblastoma. After 2 weeks, tumor-bearing mice were size-matched into a control group, two single-agent treatment groups, and a two-drug combination group, with 9–10 mice per group. The bortezomib single-agent treatment group contained only 9 mice. Two mice in the combination group and one mouse in the bortezomib single-agent treatment group died during the course of the experiment. Mice were euthanized after 2 weeks of treatment, and tumors were measured. The volume was calculated by the formula (length × width²)/2, and tumor volumes were recorded in both Table 3 and Fig. 1.

Table 3.

Tumor volumes (cm³) measured at the time of euthanized after 2 weeks of treatment in SKNAS tumor xenograft models

	Mouse
Treatment	1	2	3	4	5	6	7	8	9	10
Control	7.94	12.62	9.80	5.29	3.06	2.68	7.84	3.52	6.09	6.85
Bortezomib	5.20	2.69	3.94	4.80	6.96	1.66	6.44	4.28	*
Rapamycin	3.80	4.15	3.07	2.25	3.22	1.80	2.74	1.08	2.36	1.87
Bortezomib + rapamycin	1.00	1.39	1.01	1.22	1.05	0.79	0.75	0.70	*	*

Note. Asterisk indicates the mouse died during the course of the experiment.

Figure 1.

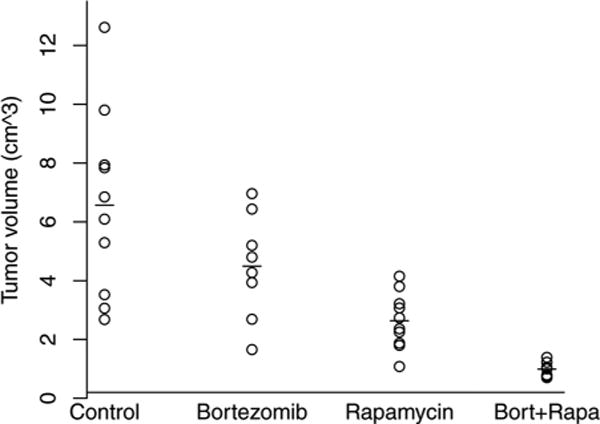
Scatter plot of tumor volume data for an SKNAS tumor xenograft model; —indicates the mean of the corresponding group.

An estimate of the interaction index (standard error) from expression (1) is $\widehat{\gamma }=-0.60\left(0.25\right)$. The 95% confidence intervals of γ were (−1.091, −0.109) and (−1.099, −0.065) for the delta method and bootstrap t-interval, respectively. Both intervals indicate a supra-additive combination. The delta-method interval was narrower than the bootstrap t-interval. To study the true coverage probabilities of both intervals at a 95% confidence level, we conducted another simulation study. In this simulation, 5,000 random samples were generated from a log-normal distribution with its mean and standard deviation parameters and sample sizes equal to the actual data recorded in Table 3, and 2,000 bootstrap samples were used for the bootstrap t-interval. The simulated empirical coverage probabilities were 0.931 and 0.942 for the delta method interval and bootstrap t-interval, respectively. The results are consistent with section 3. The lower coverage probability of the delta method interval explains its narrow interval compared with the bootstrap t-interval.

From regression analysis discussed in section 4, the fitted model was

$$y=1.77-0.35z_A-0.87z_B-0.58z_{AB}$$ (5)

with model R² = 0.73. A Q-Q plot of residuals showed an approximately normal distribution (Fig. 2). The estimated coefficient of interaction (standard error) of γ was γ = −0.58 (0.29). A p-value of 0.0488 from the t-test indicated a supra-additive combination. The 95% confidence interval of the coefficient of interaction was (−1.166, −0.003), which also indicated a supra-additive combination. The normalized coefficient of interaction was 48%, which indicated a 48% gain over the expected treatment effect for the combination under additivity.

Figure 2.

Quantile plot of residuals from fitted regression model (5).

6. CONCLUSION

Here, a nonparametric bootstrap t-interval is proposed for assessing the interaction of a fixed-dose two-drug combination. Furthermore, a regression analysis is also discussed. The regression approach has the advantage that it gives a rigorous statistical inference for the interaction parameter.