Statistical Power of Alternative Structural Models for Comparative Effectiveness Research: Advantages of Modeling Unreliability

Abstract

The advantages of modeling the unreliability of outcomes when evaluating the comparative effectiveness of health interventions is illustrated. Adding an action-research intervention component to a regular summer job program for youth was expected to help in preventing risk behaviors. A series of simple two-group alternative structural equation models are compared to test the effect of the intervention on one key attitudinal outcome in terms of model fit and statistical power with Monte Carlo simulations. Some models presuming parameters equal across the intervention and comparison groups were underpowered to detect the intervention effect, yet modeling the unreliability of the outcome measure increased their statistical power and helped in the detection of the hypothesized effect. Comparative Effectiveness Research (CER) could benefit from flexible multi-group alternative structural models organized in decision trees, and modeling unreliability of measures can be of tremendous help for both the fit of statistical models to the data and their statistical power.

Introduction

Assessing intervention effects poses some challenges to researchers, scholars, evaluators, and policy makers, especially when a quasi-experimental design is employed (Judd & Kenny, 1981; Stead, Hastings, & Eadie, 2002). When treatments and interventions move from the trial phase to being implemented on the ground, or Translating Research into Practice (TRIP, Feifer et al., 2004) the question of differential effects is of most concern to practitioners and researchers. Comparative Effectiveness Research (CER, Agency for Healthcare Research and Quality, 2007) is an emerging new approach addressing questions of comparative effects of alternative health interventions implemented in real world settings.

It is particularly difficult to decide on the best comparative results for reporting, when alternative models, accounting for various differences by condition, reach different conclusions. Evaluation challenges posed by health intervention designs in which randomization to conditions is not feasible are illustrated, by comparing alternative Structural Equation Models (SEM, Kline, 2010) testing for comparative intervention effects, in terms of both fit and statistical power. The benefits of modeling unreliability in increasing statistical power to detect true intervention effects are specifically demonstrated.

Evaluating health interventions effects on outcomes in community-based settings involves statistical modeling of non-RCT (Randomized Control Trial) designs, when different comparable groups are contrasted in terms of differential changes or responses to some program. A number of statistical approaches are commonly employed for such tests, among them regression-based linear models testing for the impact of a condition variable (the intervention of interest vs. a comparison condition) on the outcome of interest (Aiken, West, Schwalm, Carroll, & Hsiung, 1998 ; Bentler, 1991; West, Biesanz, & Pitts, 2000). In real world implementation settings however, the groups always differ in model parameters like baseline means and variances of key outcomes and covariates, as well as in terms of the outcomes change trajectories, or stability.

To accommodate such differences, structural models can be tested in several groups concurrently, like two-group models, thereby accounting for group differences that are commonly overlooked in analyses focused on whole-sample data, like paired t-tests (Macy, Chassin, & Presson, 2013) or analysis of variance (Young, Harrell, Jaganath, Cohen, & Shoptaw, 2013).

Moreover, the very assumptions about various initial and time changing group differences impact how well models fit the data and more importantly the statistical power to detect the effects of interest (Hancock, 2004). These assumptions need to be flexibly modeled for the estimates of post-test differences or differential changes to be trustworthy (Green & Thompson, 2006). A simple CER model comparison procedure for evaluating true group differences of non-RCT interventions is presented, which specifically tests both the fit to data and the statistical power of alternative SEM models and helps in sorting through competing models, using a decision tree framework. The procedure is repeated for similar models that directly include measurement errors of the measures, and the benefits of modeling unreliability are shown.

One key outcome was compared between groups of urban minority adolescents from two large cities in the USA, who were enrolled in summer job programs. One youth group was additionally engaged in a youth intervention designed to reduce drug and sexual risk behaviors (Berg, Coman, & Schensul, 2009). Low-income urban youth are often more likely to engage in risky behaviors, like substance use or unprotected sex (Farahmand, Grant, Polo, & Duffy, 2011; Simons-Morton, Crump, Haynie, & Saylor, 1999). A host of factors have been shown to be linked with behaviors that impact youth substance use initiation, like poverty, exposure to violence and drug use in their community (Caldwell, et al., 2004; DeWit, Adlaf, Offord, & Ogborne, 2000; Grant, Stinson, & Harford, 2001; Swahn, et al., 2012). On the other hand, parental support, positive peer influences and social support systems act as protective factors and are often targeted by prevention interventions (Catanzaro & Laurent, 2004; Cleveland, Gibbons, Gerrard, Pomery, & Brody, 2005). Furthermore, youth action and involvement in one’s community can reinforce group cohesion and increase individual skills and a sense of self-efficacy and control over their own behaviors (Schensul, Berg, Schensul, & Sydlo, 2004).

YARP (Youth Action Research for Prevention) was a three-year summer and after-school preventive intervention (Berg, Owens, & Schensul, 2002; Reason & Bradbury, 2007). Three youth cohorts were employed and trained over the summer and were instructed to identify a youth-related problem in their community, to develop a research model and an action plan addressing that issue, gather and interpret community data, and actively engage in social action to promote changes in their community. This intervention group was compared to a matched youth group recruited from a comparable summer-job program in a neighboring city with similar economic conditions and ethnic/racial composition.

A primary hypothesis proposed that youth-initiated research for action, along with involvement in multilevel social change activities (or activism) reinforce group cohesion and individual and collective efficacy. As a result, it was expected that among other outcomes, Internal Locus of Control (ILC) would strengthen in the intervention group compared to the matched comparison group. Figure 1 shows the pre-and post-test sample means of the ILC outcome in the intervention and comparison YARP groups. It is specifically investigated which alternative models testing for intervention effects exhibit both good fit to data and enough statistical power to detect the effects, depending on different model specifications (Hancock, Lawrence, & Nevitt, 2000). The impact of accounting for measurement unreliability in the models, thereby estimating true differences of the latent (unobserved) outcome is also explored. The models belong to the Structural Equation Modeling (SEM) framework.

Figure 1.

Outcome Means Pre- and Post-Intervention for the YARP Comparison and Intervention Groups

Methodology

Structural equation modeling for intervention effects

A major methodological tool for understanding health intervention processes and assessing comparative outcome effects is the latent linear modeling with multiple simultaneous regression equations, known as Structural Equation Modeling (SEM, Bollen, 1989; Jöreskog, 1973) or covariance structure analysis (Bentler & Dudgeon, 1996). SEM is an enormously flexible technique that can carry out virtually any analysis (Muthén, 2002; Skrondal & Rabe-Hesketh, 2004). Current extensive SEM reviews position it as an integrative general modeling framework, of which traditional analyses like the t-test, ANOVA, MANOVA, canonical correlation, or discriminant analysis are special cases (Fan, 1997; Graham, 2008; Muthén, 2008; Voelkle, 2007).

A simple SEM setup for testing intervention effects is the common one-group analysis of the effect of a dummy intervention variable on the post-intervention outcome. This approach, called ‘group code’ SEM (Hancock, 1997), tends to overlook however group differences that may need to be modeled, in other words it cannot account for a number of differences between groups, because data from both groups are combined. A more flexible tool is the testing of causal models in multiple groups, which allows for a range of tests of group differences (Bagozzi & Yi, 1989; Kühnel, 1988; Thompson & Green, 2006). Two-group models, like a two-group simple regression, provide parameter estimates for each group (Green & Thompson, 2006), and are more versatile in that they are simultaneously tested in more than one sample, with the options to hold parameters equal or allow them to vary across groups.

The general multiple-group manifest (observed) variable SEM model in multiple groups (indexed by g) is of the form:

$${\mathbf{y}}_{\mathbf{g}}={\tau }_{\mathbf{g}}+{\Gamma }_{\mathbf{g}}{\mathbf{x}}_{\mathbf{g}}+{\zeta }_{\mathbf{g}}$$ (1)

where γ is the (q × 1) vector of exogenous and x the (p × 1) vector of endogenous manifest variables, τ is the (q × 1) vector of intercepts, Γ represents the (q × p) matrix of slopes, and ζ the (q × 1) vector of residuals (or disturbances). However, when m latent variables are also modeled, the structure can be expressed separately for the latent variable relationships as:

$${\eta }_{\mathbf{g}}={\alpha }_{\mathbf{g}}+B_{\mathbf{g}}{\eta }_{\mathbf{g}}+{\Gamma }_{\mathbf{g}}{\xi }_{\mathbf{g}}+{\zeta }_{\mathbf{g}}$$ (2)

with η being the (m × 1) vector of latent endogenous variables, α the (m × 1)vector of factor score means, B the (m × m) coefficient matrix for the influence of endogenous η‘s on η‘s, Γ the (m × n) coefficient matrix of the effects of the n exogenous ξ variables on η‘s, and ζ is the (m × 1) disturbance vector assumed to have an expected value of zero and be uncorrelated with ξ and η. The model for the measurement part linking the manifest to the latent variables is (Bollen, 1989: 320):

$${\mathbf{y}}_g={\tau }_{yg}+{\Lambda }_{yg}{\eta }_{yg}+{\epsilon }_g$$ (3)

and

$${\mathbf{x}}_g={\tau }_{\mathbf{x}\mathbf{g}}+{\Lambda }_{x\mathbf{g}}{\eta }_{xg}+{\delta }_g$$ (4)

Model testing in SEM is meant to reproduce the variances, covariances and the means of the observed variables (Bentler & Yuan, 2000; Hancock, 2004). SEM testing requires first the assessment of the fit of the model to the data; the fit is simply the extent to which a model implies means and variances/covariances that are similar to the observed ones. The χ² (chi-squared) fit statistic for instance assesses the closeness between the implied covariance matrix and the sample covariance matrix (Hayduk, 1987). For a multiple-group SEM model, the χ² is obtained as (N−1) F_ML from the fit function F_ML, which is a weighted combination of the g groups fit functions (Bollen, 1989: 361):

$$F_{gML}=\mathit{\text{tr}}\left({\mathbf{S}}_g{{\sum }_g}^{-1}\right)+\mathit{\text{log}}|{\sum }_g|-\mathit{\text{log}}|{\mathbf{S}}_g|-(p+q)$$ (5)

where ∑ is the population covariance matrix and S is the sample covariance matrix.

Lack of χ² fit is generally a function of the constraints imposed on the model (Thompson & Green, 2006). A two-group SEM model fits to the extent that it closely reproduces the sample means and covariances in both groups, so model misfit can indicate misspecification at the level of both within-group means and covariances (Saris & Satorra, 1993), as well as in the assumptions about cross-group equalities or differences, like the equality of pre-intervention means or variances.

However, some specific equality constraints are supported by some data sets and rejected by others (Green & Thompson, 2003), depending on actual community initial conditions, and on differential change processes. For example, the assumption that the path (auto-regressive) coefficients from baseline to post-test outcome are equal in the intervention and comparison groups is rarely true, primarily because the intervention itself is expected to change the stability of the outcome; these assumptions are rarely tested (Bentler, 1991).

To compare groups (like gender, age, or intervention and comparison groups) on the means of the DV (dependent variable, or endogenous) in an SEM framework, researchers evaluate the fit of a structural model of no difference between the focal parameters (i.e. equality of intercepts is imposed) against another model where intercepts differ; if the models fit the data similarly, there is no difference in intercepts, whereas if the different means model fits significantly better, there is evidence for a systematic group difference.

Acceptable model fit alone however does not ensure that its conclusions are warranted, because alternative well-fitting models may lead researchers to divergent conclusions. This is partly because alternative well-fitting models can have different statistical power to detect the effects of interest (MacCallum, Lee, & Browne, 2010; Saris & Satorra, 1993), especially for small sample sizes and unequal groups (Hancock, et al., 2000). These models contain different specification errors, and therefore will vary in both fit and testing power. Researchers should then analyze the statistical power of all alternative well-fitting models that can be relied upon for testing the hypothesis of equal post-intervention means.

In summary, there always exists a range of well-fitting models that provide different model-implied estimates of between-group differences, when researchers compare effects of programs across different conditions or settings. For the sake of brevity the focus is on simple models with only one outcome variable measured twice, with the baseline measure affecting the post-test outcome, in two groups, enhanced intervention and comparison, a common quasi-experimental design (Meehl & Waller, 2002). These models can be easily expanded to include covariates and additional intervening factors.

Analytic steps

Two-group regression models were tested that gradually imposed equality constraints on model parameters across groups, in a hierarchical manner (somewhat similar the SEM decision trees, Brandmaier, von Oertzen, McArdle, et al., 2013), starting with a basic model with all parameters allowed to differ across groups. Specified models with increasingly more parameters were then constrained to be equal across the comparison and intervention groups: baseline means, then baseline variances, then the baseline to post-test regression coefficient, and combinations of them (Mplus syntax outputs are available online at http://trippcenter.uchc.edu/modeling/files/HEdRes.zip). The decisions to accept or reject models and equality-constraints are basedon chi-square (χ²) tests and Wald tests. Wald tests are asymptotically equivalent to the chi-square difference tests (Δχ²) and do not require re-specifying the model (Bollen, 1989: 295).

A simple two-group structural model with a baseline outcome causing the post-test outcome yields five model estimated parameters for each group (see for illustration the actual parameters in Figure 2). The model depicts variances as a double headed arrow, or as a covariance of the variable with itself. Such models can specify (or not) equality constraints between some of these parameters, and then test the difference between post-intervention intercepts of the outcome. The linear equations can be directly spelled out from the model in Figure 2 as:

$$IL{C}_{2g}={\tau }_g+{\beta }_g*IL{C}_{1g}+{\zeta }_g$$ (6)

where ILC_1g and ILC_2g are the baseline and post-test variables, τ_g are the intercepts (the values of ILC_2g when ILC_1g are zero), y_g are the auto-regressive coefficients, ζ_g the residual error terms, and g indexes group (intervention or treatment T, and comparison C). Organizing alternative SEM models using a decision tree that starts with an all-parameters-different model, and grows by imposing equality constraints on parameters across groups is proposed.

Figure 2.

Two group model specification for testing the equality of post-intervention difference τ_2C = τ_2T of an outcome (Note: Hexagons represent means/intercepts. T: treatment group, C: comparison.)

In addition to fit, models differ in statistical power to detect specific effects (Hancock, et al., 2000). The probability of rejecting the hypothesis of equal post-test means, when the means are different in the population, is the statistical power of the test, and should ideally be one. The power of SEM models can be obtained generally by fitting on population data an F (full) model, then an alternative R (restricted) model with an additional constraint of interest (MacCallum, et al., 2010; Satorra & Saris, 1985). Because the population F model fits perfectly, the only worsening (or ‘badness’) of fit of the reduced model R would come from the additional constraint imposed the equality of post-test means in this case. The difference between the two model X² values represents the noncentrality parameter for the noncentral distribution with one degree of freedom (Hancock, et al., 2000). Alternatively, the Wald test X² is an asymptotically equivalent method of estimating power (Buse, 1982).

The statistical power of each alternative model was assessed using Mplus 6 Monte Carlo facility (Muthén & Muthén, 2002), which generates datasets according to an F causal model assumed to be the true in the population, generates simulated sample datasets (in this study, 1,000 simulations), and then can test a constrained model R to each simulated sample dataset. The Mplus output provides descriptives of the percent of times the R replicated models rejected the (assumed false) equality of post-test means, which is the power of the model to detect the effect. Specifically, the power of the model is given by the observed proportion of replication tests for which the Wald test exceeds the critical value of 3.841 (for degree of freedom df = 1, for the equality of intercepts constraint τ_C2 = τ_T2) Unreliability was then modeled in both groups statistical power to detect intervention effects was tested for all the new models. (Muthén & Jöreskog, 1983; Thompson & Green, 2006).

Study setting and data

The research team conducted and evaluated the multi-year YARP project (2002–2005), a youth intervention implemented in Hartford, Connecticut (CT). The Institute for Community Research Institutional Review Board ensured that proper human subjects protocols were followed. The intervention group had N_T = 90 participants who completed all four surveys, recruited from Hartford, CT, of whom 56% were females, 48% Blacks, 37% Latinos, mean age M_T = 15.1 years, while the comparison group had N_C =167 from a similar inner-city youth in a summer job program in Massachusetts, U.S., with 58% females, 45% Blacks, 44% Latinos, and mean age M_C = 15.5.

Measures were taken at baseline, 2 month, 6 months, and 1 year in both groups. Internal locus of control was measured with 4 indicators (i.e., ‘I am responsible for accomplishing goals’, ‘Life offers me many choices’, ‘I can do things I set out to do’, and ‘I enjoy having control over own destiny’) from among the Internal subscale items of the Levenson Locus of Control scale (Levenson, 1973) modified for younger ages. For simplicity and because interest lies in long-term and potentially sustainable effects, the focus here is on the difference in changes from baseline to the final fourth measurement time point. A composite of the average items was calculated (rated from strongly disagree = 1, to strongly agree = 4, 4 being greater internality). Basic descriptive, reliabilities, correlations and covariances are shown in Table 1, for each group, and the entire sample. The pre-and post-test ILC measures had acceptable reliabilities, Cronbach’s alphas between .725 and .871.

Table 1.

Covariances, correlations, means and Cronbach’s α of the pre- and post-test Internal Locus of Control (ILC) outcome for the two YARP groups and for the whole sample

	Comparison NC = 167		Intervention NT = 90		Whole sample N = 257
	ILC1	ILC2	ILC1	ILC2	ILC1	ILC2	Group
ILC1	0.264	0.475*	0.174	0.448*	0.235	0.445*	−0.081NS
ILC2	0.264	0.325	0.174	0.480	0.134	0.385	0.104NS
Group (C/T)	-	-	-	-	−0.019	0.031	0.228
Means μ	1.365	1.356	1.283	1.492	1.337	1.404	0.350
Cronbach’ α	0.725	0.847	0.726	0.871	.726	.859	-

Note. Covariances are shown in bold and below diagonal and correlations above diagonals, variances in italics on the diagonals.

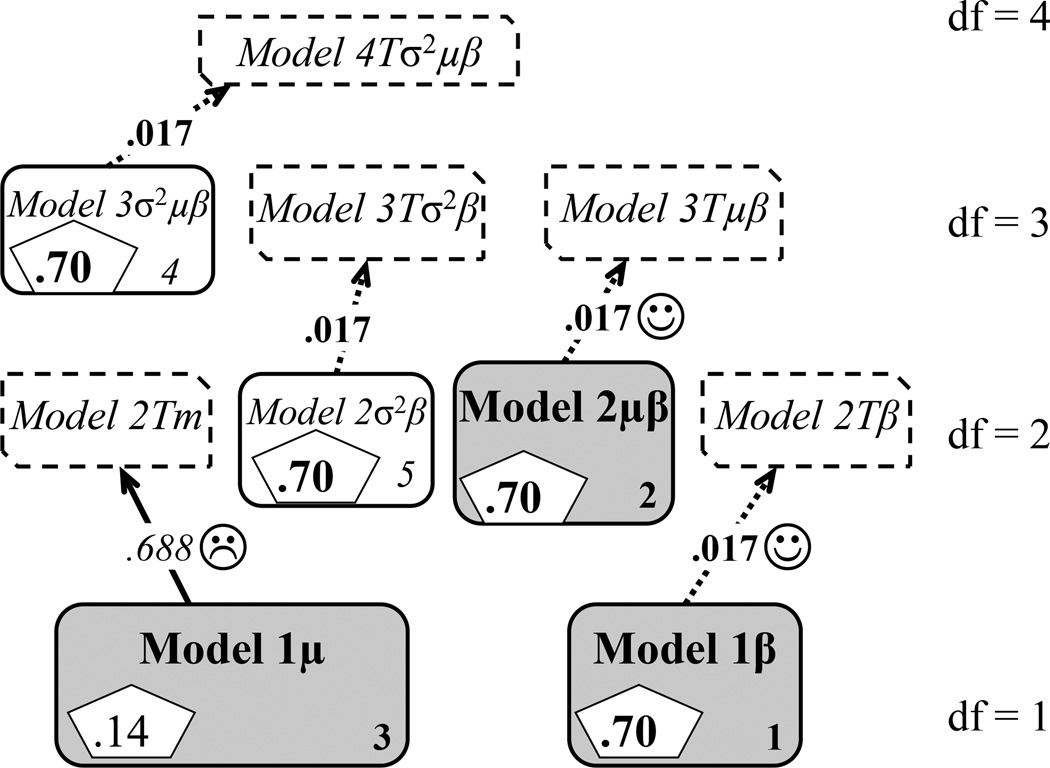
The hypothesis of equal post-intervention ILC means (technically the intercepts τ_C/T) was tested with all well-fitting models. The models are shown as a decision tree in Figure 3. The baseline model with df = 0 (the ‘root’) assumes all parameters are different across groups, and each higher layer of nodes adds one more equality constraint, hence estimating one less parameter. When adding the equality constraint between post-test intercepts (the focal parameter) led to a significant worsening of fit, or a significant Wald test statistic, it was concluded that the means were different between groups.

Figure 3.

Alternative decision-tree SEM modeling for comparing post-intervention observed outcome means in two-group causal models (Notes: Shaded models: good chi-square fit; model names indicate which equality constraints are imposed, on: σ²= variances, μ = means; β= autoregressive paths; or T= the test of equality of post-test intercepts; numbers in boxes: in pentagons –power of each model; lower right fit ordered from best fitting (1) up; arrows going up show model comparison tests, with p value for significance of Wald test, p < .05 corroborates intervention effect).

Results

The results of alternative modeling of the tests of ILC outcome differences are now reported. The three well-fitting models are shown in Table 2, which lists the common SEM measures of fit ordered by descending p values for X² larger than .05, and the Wald tests of the post-intervention differences.

Table 2.

Ordered fit indices, Wald tests, and statistical power for the well-fitting alternative causal models of the YARP intervention effect on Internal Locus of control

		Model	χ2	df	χ2 p	CFI	RMSEA	Wald	Wald p	Power
1	1β	β's equal	1.517	1	0.218	.991	.063	5.685	0.017 ☺	0.70
2	2μβ	μ's & β's equal	3.436	2	0.179	.976	.075	5.719	0.017 ☺	0.70
3	1μ	μ's equal	1.919	1	0.166	.985	.085	0.161	0.688 ☹	0.14

Note: μ = baseline means; β = auto-regressive path; italics Wald test p indicate significant intervention effect.

Two well-fitting models, 1γ, and 2μγ, indicated that there was indeed a significant intervention effect (p = .017 for the Wald statistic in both), while another well-fitting model, 1μ, reached another conclusion. Note that the baseline means cannot be deemed statistically different, because the fit of the 1μ model (baseline means set equal across groups) indicates in fact that the perfectly fitting model with all parameters different (for which df = 0) does not worsen significantly when constraining the baseline means to be equal.

The fact that only some models reject the equality of means hypothesis is an indication of differential statistical testing power (Hancock, 2006) linked to model misspecifications (Saris & Satorra, 1993). In other words, some models may have low power to reject the (false) hypothesis of equal post-test means.

In terms of statistical power, the equal baseline means model (1μ) that has initially found no effect yielded a probability to rightly reject the (assumed false) equal means hypothesis of p = .14, while the other two well-fitting models had higher sensitivities of p = .70. This indicates that for the observed sample sizes of 90 and 167, the models compared here have dramatically different sensitivities to detect the effect of interest. Examination of model fit alone, therefore, without controlling for Type II errors could lead to accepting well fitting models that are not sensitive to detect specific effects (Saris, Satorra, & van der Veld, 2009). In this particular instance, the ‘stress’ induced in this simple linear model by constraining the baseline means to be equal rendered one well-fitting model (1μ) seriously under-powered to detect the intervention effect. Next it will be shown that this particular model was underpowered because the baseline equality of means assumption was imposed on the unreliable baseline measure.

Informed knowledge of the reliability of an observed variable allows for modeling the true means of latent variables (unattenuated by measurement error). When measurement error is directly specified for composite or single-item variables, each measured variable is in fact subjected to a mini-factor analysis, in which a common factor (the true measure) is assumed to be responsible for (acting behind) the observed measure. The reliability of an observed variable is simply the proportion of the observed variance that is true variance, or the squared correlation between the true variable and the observed variable (Raykov, 1997), and a common estimate used in applied research for scale reliability is Cronbach’s alpha coefficient (Raykov & Marcoulides, 2011). Because reliability ρ is the percentage of variance that is true variance, the complement 1−ρ is the percentage that is measurement error, hence (1−ρ)*σ²ILC1 is the measurement error variance (MacKinnon, 2008: 189). The measurement error variance for the comparison group δ_1C for ILC1_1C in Figure 4, for example, whose reliability was .73 and variance .26, was fixed at (1 − .73) * .26 = .27 * .26 = .070.

Figure 4.

Illustration of two-groups model parameters with measurement errors directly modeled (Notes: Hexagons show the means/intercepts; ρ are reliabilities; σ² are observed variances; g indexes group: comparison and intervention.)

When directly modeling the unreliabilities of the baseline and post-intervention ILC outcome in both groups, the power to detect the post-intervention differences in mean ILC of the 1μ model increases to .716 (from the meager .14 of the manifest ILC model). So when assuming that the true (latent) baseline ILC means are equal, the model is better powered to detect the intervention effect unto the reliable (true) latent outcome, and the effect emerges as a significant larger increase in the true ILC in the intervention group, Wald test statistic of 6.14 (df=1), p = .012.

Conclusion

A decision-tree method of comparing alternative models of observed and true outcomes was illustrated (Kaplan, 1990), which tests for post-intervention health outcome differences between community-based groups, based on both fit to data and power to detect these effects. This procedure can assist in Comparative Effectiveness Research (CER) by providing the modeling flexibility required by actual data in terms of various group (or community) differences. It is particularly useful when trying to compare effects using summary data from separate studies, when available in the form of means, variances and covariances.

One manifest outcome well-fitting model was under-powered to detect the YARP intervention effect on Internal Locus of Control (ILC), but two other well-fitting models with better statistical power detected a positive effect on ILC in the intervention group. It was found that even small differences in parameters of the unreliable measures create ‘stress’ in the structural models which can render them underpowered to detect the effects of interest. In the illustration, the lack of power of the baseline equal means two-group structural model derived from imposing a plausible equality constraint on the unreliable observed ILC measures, rather than on the true (latent) ones.

The structural equation models tested here indicate that the lack of statistical power of the models with unreliable outcomes are due largely to modeling error in-variable measures (containing measurement errors). The example herein shows the importance of a priori specification of alternative models and the utility and relative ease of post-hoc power analysis, and also showed the benefits of directly modeling unreliabilities of outcome measures. The nuanced reporting of the alternative testing and plausibility of competing conclusions is essential for statisticians, prevention and comparative effectiveness researchers, as well as policy makers and community representatives interested in evaluating, replicating or translating successful programs.

Some limitations are worth mentioning. To the extent that one tries out repeated models on the same data, procedure called specification search and available in current SEM software like AMOS (Arbuckle, 2007), the issue of over-fitting the model to the same data (or data dredging, see Brandmaier, et al., 2013) could be a concern (Hayduk, 1987). This procedure is acceptable, if careful planning of model testing under alternative reasonable configurations is undertaken a priori (Jöreskog, Bollen, & Long, 1993), being akin to specifying equivalent models before data collection (Hershberger, 1994).

The decision tree modeling approach is useful in identifying and classifying alternative multi-group models according to differential support from multiple-group data in general. It does not of course provide criteria for deciding the true and false nature of the models, but rather their “truth-likeness” or closeness to the truth (Meehl & Waller, 2002). Quasi-experimental designs for instance require the use of covariates to control for additional baseline differences between the groups, and the modeling of selection biases (Muthén & Jöreskog, 1983); however, a basic model was chosen herein for simplicity to illustrate this method.

The method presented here becomes cumbersome when models increase in complexity, e.g. when using multiple indicator measures with numerous possible cross-group constraints, like specific loadings and intercepts (Green & Thompson, 2006). Multiple latent covariates and possibly multiple outcomes with indirect effects complicate the picture even further. Study analyses, however, make clear the benefits of directly modeling unreliability, of careful inspection of alternative models and attending to both model fit measures and statistical power of the models, when comparing the effectiveness of health interventions translated and implemented differently in separate communities.