Abstract
To predict the safety of a drug at an early stage in its development is a major challenge as there is a lack of in vitro heart models that correlate data from preclinical toxicity screening assays with clinical results. A biophysically detailed computer model of the heart, the virtual heart, provides a powerful tool for simulating drug–ion channel interactions and cardiac functions during normal and disease conditions and, therefore, provides a powerful platform for drug cardiotoxicity screening. In this article, we first review recent progress in the development of theory on drug–ion channel interactions and mathematical modelling. Then we propose a family of biomarkers that can quantitatively characterize the actions of a drug on the electrical activity of the heart at multi‐physical scales including cellular and tissue levels. We also conducted some simulations to demonstrate the application of the virtual heart to assess the pro‐arrhythmic effects of cisapride and amiodarone. Using the model we investigated the mechanisms responsible for the differences between the two drugs on pro‐arrhythmogenesis, even though both prolong the QT interval of ECGs. Several challenges for further development of a virtual heart as a platform for screening drug cardiotoxicity are discussed.
Linked Articles
This article is part of a themed section on Chinese Innovation in Cardiovascular Drug Discovery. To view the other articles in this section visit http://dx.doi.org/10.1111/bph.2015.172.issue-23
Abbreviations
- AE
allosteric effector
- APD
action potential duration
- APD90
APD at 90% repolarization
- APs
action potentials
- BCL
basic cycle length
- CV
conduction velocity
- CVR
conduction velocity restitution
- ERP
effective refractory period
- GR
guarded receptor
- HH
Hodgkin–Huxley
- ICaL
L‐type Ca2+ current
- IKr
delayed rectifier K+ channel current
- IKtof
fast component of the cardiac transient outward current
- INa
Na+ channel current
- LQTs
long QT syndrome
- MR
modulated receptor
- QTc
corrected QT interval
- VW
vulnerable window
- WL
wavelength
Tables of Links
| TARGETS | |
|---|---|
| GPCRs a | Ion channels b |
| β‐adrenoceptors | hERG (KV11.1) channels |
| L‐type Ca2+ channels | |
| Voltage‐gated K+ channels | |
| Voltage‐gated Na+ channels |
These Tables list key protein targets and ligands in this article which are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY (Pawson et al., 2014) and are permanently archived in the Concise Guide to PHARMACOLOGY 2013/14 (a,bAlexander et al., 2013a, 2013b).
Introduction
The development of a new drug from its discovery to final market approval takes, on average, about 10 years and costs over ∼$1 billion (DiMasi et al., 2003). Some drugs (e.g. cisapride) have had to be withdrawn due to their undesirable side effects, such as cardiotoxicity (Hondeghem et al., 2011). Withdrawal of a cardiotoxic drug is not just a waste of time and money for the pharmaceutical industry, but may also impose serious risks to a patient's life. Therefore, predicting the side effects of a drug at an early stage of its development is of utmost importance as regards drug safety assessments (Pollard et al., 2010).
One of the most dangerous potential side effects of a drug is pro‐arrhythmic effects arising from an interaction between drug molecules and cardiac membrane ion channels. A contemporary biomarker for predicting a drug's safety is based on its effect on the corrected QT interval (QTc) of the ECG (Friedrichs et al., 2005): a drug that prolongs the QTc is regarded as having a great potential for triggering severe pro‐arrhythmic events. As the delayed rectifier K+ channel current (I Kr) provides a major repolarizing current that determines the cellular action potential duration (APD) and, therefore, the QT interval of an ECG, testing the effects of a drug on I Kr is normally performed as a preclinical screening to predict any potential risks of the drug. However, in most cases, drug‐induced arrhythmia risk is not solely due to inhibition of I Kr, neither do all drugs that prolong the QTc interval induce arrhythmia. In fact, drug‐induced arrhythmias may result from complex interactions between a drug and cardiac electrophysiology, including tissue's excitability, refractoriness and spatial dispersion of ventricular repolarization. In some cases, where a drug acts (directly or indirectly) on multiple transmembrane ion channels simultaneously (i.e. combined actions on K+, Na+ and L‐type Ca2+channels) (Hondeghem et al., 2001; Gintant, 2012), the mechanisms involved in the pro‐arrhythmia effects of a drug are even more complex. Consequentially, the assessment of a drug's safety that is confined to preclinical screening for actions on I Kr or clinical QT interval is unlikely to be ineffective. Hence, novel methods are required to evaluate the complicated actions of a drug on cardiac activities for the assessment of drug cardiotoxicity.
In recent years, there have been rapid advances in the development of biophysically detailed computer models of the heart for simulating its electrical and mechanical dynamics (i.e. the virtual heart) (Clayton et al., 2011; Henriquez, 2014). The virtual heart has been extensively implemented as a cardiac electrophysiological platform for investigating the functions of the heart during various physiological, pathological and pharmaceutical conditions (Clayton et al., 2011; Henriquez, 2014). Recently, it has attracted attention as an appliance for quantitatively evaluating drug safety (Mirams et al., 2012).
In this review, we first present recent progress in the mathematical modelling of the drug–ion channel interactions in cardiac tissue. We then propose a family of biomarkers that can be used to quantitatively characterize the actions of a drug on cardiac electrical activities at the cellular and tissue level. To illustrate the suitability of the virtual heart as a screening strategy, we used computer models of the human ventricle to simulate and quantify the effects of cisapride and amiodarone on ventricular activities and pro‐arrhythmic substrates. Finally, we discuss several challenges that need to be considered for the future development of a whole heart model as a platform for screening drug safety.
Theory for the interaction between ion channels and drugs
Mathematical models for ion channels
Two approaches have been used for mathematical modelling of the functions of cardiac membrane ion channels. One is the Hodgkin–Huxley (HH)‐type model (Clayton et al., 2011; Henriquez, 2014), in which voltage and time‐dependent gating variables are used to describe the properties of an ion channel, with activation and inactivation processes being assumed to be independent. For instance, the fast sodium channel current can be described by (Noble, 1960; 1962; Kohl and Noble, 2009; Kharche et al., 2011):
| (1) |
where INa is the sodium channel current; gNa the maximal channel conductance; m the voltage‐ and time‐dependent activation variable; h and j the fast and slow inactivation variables, respectively; Vm the cell membrane potential; and Erev the reversal potential of the channel (for model details, please see Appendix A).
The other is the Markov chain type of ion channel model that allows for detailed descriptions of the specific channel states and the transitions between them (Iyer et al., 2004; Rudy and Silva, 2006; Clancy et al., 2007). Transitions between states can be dependent on voltage, temperature and drug concentration. So far, detailed Markov chain models have been developed for several cardiac membrane ion channels, including the transient outward K+ current I to (I Kv4.3 and I Kv1.4) (Iyer et al., 2004), I Na and I K (I Kr and I Ks) (Rudy and Silva, 2006).
Theory for a drug's interaction with ion channels
Receptor theory is an important framework for mathematical modelling of pharmacological actions of cardiac ion channels. With this theory, a receptor model is based on the known laws of physical chemistry for describing the binding of drug molecules to cellular receptors, which can be divided into three categories (Kenakin, 2004) as listed below.
Theory of simple pore block
The ‘simple pore block’ theory assumes that drug molecules continuously access the ligand‐binding site of the ion channel receptor and the affinity of the drug molecule for the receptor is independent of time and cardiac membrane voltage (Starmer et al., 1994). With this theory, the effects of a drug on blocking an ion channel can be simulated using a blocking factor k that reduces the maximum conductance of the targeted ion channel. Mathematically, k is expressed as:
| (2) |
where [D] is the drug concentration, IC50 the drug concentration at which 50% of blockade of the binding site occurs and n H the Hill coefficient.
The simple pore block theory has been widely used for simulating drug action on cardiac electrical activities. For example, Starmer et al. (1994) implemented the theory to investigate the mechanism by which a drug blocking potassium channels suppressed the responses of cardiac cells to premature stimuli. Later on, Starmer et al. (1995) also implemented the theory to investigate the anti‐arrhythmic effects of potassium channel blockade.
Theory of state‐dependent block
The ‘state‐dependent block’ theory is based on the dynamic properties of ion channels. There are two subcategories, the modulated receptor (MR) theory (Hille, 1977) and the guarded receptor (GR) theory (Starmer et al., 1984).
Both the MR and GR theories assume that the association and dissociation processes of a drug molecule are dependent on time and cellular membrane potential. However, the MR theory proposes that a drug can bind to the drug receptor regardless of the state of the targeted ion channel, and its binding affinity in each state is different. In contrast, the GR theory hypothesized that the affinity of drug binding to a particular conformation of an ion channel is constant, and the access of the drug to the binding site is limited due to alterations in the ion channel conformation.
Based on the MR theory, Hondeghem and Katzung (1977) proposed an HH type of model for simulating the action of lidocaine and quinidine on I Na. In this model, the Na+ channel model had closed (R), active (A) and inactivated (I) states, and the drug had the same affinity to block each of them, as shown in Figure 1A. Thus, a mathematical model for the I Na was represented as:
| (3) |
| (4) |
where B is the sum of the blocked Na+ channels, [D] the drug concentration, ‘i’ the fraction of channels in the three blocked states, li and ki are the dissociation and association rates of different Na+ channel states respectively (for details of the model and parameters, please see Appendix A).
Figure 1.

Schematic illustration of the modulated receptor theory and guarded receptor theory on the HH type of Na+ ion channel. Figure adapted from Comtois et al. (2008). (A) Modulated receptor model proposed by Hondeghem and Katzung (1977) with transition rates from unblocked to blocked channels (k) and from blocked to unblocked (l). (B) Guarded receptor model with affinity to the inactivated and activated states (Starmer and Grant, 1985).
With the GR theory, Starmer and Grant (1985) proposed an HH type of Na+ channel model, with the effects of a drug shown in Figure 1B. With B representing the total number of drug‐blocked channels (Starmer and Grant, 1985):
| (5) |
where kA and lA are the association and dissociation rates. For details of this model and parameters, please see Appendix A.
Theory of allosteric effect
The ‘allosteric effector’ (AE) theory differs from the ‘state‐dependent block’ theory in that the AE theory considers that drugs act as allosteric effectors to alter the transition dynamics of the targeted ion channels instead of simply blocking them. A recent study has implemented the AE theory, together with the MR and GR theories and Markov chain model of ion channel gating kinetics to illustrate how class I anti‐arrhythmic drugs, lidocaine and flecainide, affect ventricular rhythms by inducing functional changes in the dynamics of Na+ channels (Moreno et al., 2011).
Modelling the interactions between drug and ion channels
Na+ channel and drug interaction
The Na+ channel plays an important role in generating cardiac electrical action potentials (APs) (i.e. it is a major determinant of the maximal upstroke velocity of the AP and cardiac excitability) and ensuring AP conduction in the cardiac tissue. Drugs that target Na+ channels have been widely used for treating various cardiac diseases (Corrias et al., 2010).
Mathematical modelling of the interaction between the Na+ channel and drugs can be dated back to 1977 when Hondeghem and Katzung (1977) pioneered the study to investigate the anti‐arrhythmic properties of the cardiac Na+ channel blockers, lidocaine and quinidine, using the MR theory. Later on, Starmer et al. (1987; Starmer, 1987) developed a GR‐based model for simulating the actions of lidocaine on the cardiac Na+ channel and investigated the mechanisms by which the anaesthetics affect cardiac excitability (Starmer, 1987; Starmer et al., 1987). Recently, using the same GR‐based model, Starmer et al. (2003b) investigated the effects of Na+ channel blockade on the refractory period of cardiac excitations.
Models for simulating interactions between drugs and Markov chain model of Na+ channels have also been developed. In their study, Clancy et al. (2007) developed a Markov chain model for the ΔKPQ mutant Na+ channel that is associated with variant 3 of long QT syndrome (LQT3). The model presented the ΔKPQ mutant channel with drug‐binding sites for the open and inactivation states of Na+ channels for simulating the actions of mexiletine and lidocaine. Recently, Moreno et al. (2013) developed another Markov chain type of Na+ channel model, with eight states representing drug bound effects, eight discrete background states representing the non‐affected channel conformations and another four states describing Na+ channel bursting (Gima and Rudy, 2002). Modelling studies showed that acute targeting of I NaL by ranolazine effectively suppressed the triggers for bradyarrhythmias in LQT3‐linked ΔKPQ mutants or tachyarrhythmia arising from heart failure (Moreno et al., 2013). Models incorporating binding/unbinding properties between drugs and channels that are important in determining a drug's safety profile have also been developed (Cimponeriu et al., 2003).
Potassium channel and drug interaction
The I Kr activates during the plateau phase of the AP and plays an important role in AP repolarization (Sanguinetti and Tristani‐Firouzi, 2006). The KV11.1 (also known as hERG) channel is considered to be the most widely targeted potassium channel in arrhythmic pharmacological therapy.
Using a previous model of I Kr developed by Silva and Rudy (2005), Sale et al. constructed two Markov chain models for representing hERG 1a/1b and hERG 1a channels (Sanguinetti et al., 1995; Trudeau et al., 1995; Smith et al., 1996). Their modelling results showed that the time course of E‐4031 for blocking heteromeric 1a/1b channels was slower than that for blocking homomeric 1a channels (Sale et al., 2008), which suggested that specifically disrupting hERG 1b channel function was expected to reduce cardiac I Kr and enhance drug sensitivity.
Drug molecular binding to channel states with different conformations or a distinct affinity presents complex behaviours. In a recent study, Romero et al. (2014) investigated in silico the drug/channel interactions by systematically altering the transition rates in the Fink et al. (2008) Markov chain model of human hERG (KV11.1) channels. By incorporating the drug–channel model into the O'Hara et al. (2011) model of human ventricular APs, they showed that drugs with disparate affinities to conformational states of the KV11.1 channel played an important role in increasing a tissue's susceptibility to acquired LQT. Independently, Di Veroli et al. (2014) developed a mathematical model of KV11.1 channels to study drug safety with different binding configurations. Based on experimental data on the effect of the antipsychotic clozapine on hERG channel blocking and unblocking kinetics, Hill et al. (2014) proposed an hERG channel model with kinetically distinct binding states of the drug to open and inactivation states. Their modelling data effectively illustrated the interaction between clozapine and hERG channels in acquired LQT (Hill et al., 2014).
The fast component of the cardiac transient outward current, I Ktof, plays an important role in the early phase of repolarization. A Markov chain type of formulation of I Ktof with consideration of the effects of different I Ktof‐specific block states (drug bound to the three closed states and the open state of I Ktof) on mouse ventricular APD has also been developed (Zhou et al., 2014).
Calcium channel and drug interactions
L‐type Ca2+ channels constitute a main Ca2+ entry pathway into the cell and play an important role in cardiac excitation (Corrias et al., 2010). Pharmacological therapies targeting the cardiac I CaL have also been widely considered in practice.
Markov chain models for representing the I CaL have also been developed in previous studies (Hund and Rudy, 2004). These models have been implemented to investigate the effect of β‐adrenoceptor stimulation on ventricular arrhythmogenesis in association with LQT (Faber and Rudy, 2007; Faber et al., 2007).
Multichannel and drug interactions
Drugs targeting multiple membrane ion channels may be effectively anti‐arrhythmic. Computer modelling provides a tool for theoretically exploring the actions of a drug targeting multiple ion channels (Martin et al., 2004; Qu and Weiss, 2005; Bottino et al., 2006). It has been shown by a simulation study that a putative compound that blocks the three ion channels, which mediate I Kr, I Na, I CaL, had better anti‐arrhythmic effects than one that only blocks the I Kr (Mirams et al., 2011).
Some other advances in simulation of the interaction between a drug and the various ion channels are summarized in Appendix B.
Assessment flow for the action of a drug in silico
The electrical activity of the heart results from the coordinated actions of cardiac systems operating at many physiological sites, including subcellular, ion channel, cellular, tissue and organ levels. Therefore, a comprehensive assessment of drug safety has to be conducted at all of these levels. This imposes a major challenge, if not impossible, for conventional experimental preclinical drug safety screening. However, it can be achieved by computer models of the heart. In this regard, we propose an assessment flow for evaluating the actions of a drug at the cellular and tissue levels using computer models of the heart as illustrated in Figure 2.
Figure 2.
Assessment flow chart for testing drug actions using hierarchical levels of computer models including ion channel, cellular and tissue levels. The actions of a drug on cardiac electrical activity at cellular and tissue levels can be characterized by analysing their effects on a family of biomarkers.
In the following section, as illustrated, we present simulation results to demonstrate the application of computer models for evaluating the actions of cisapride and amiodarone on cardiac electrical activities at the cellular and tissue levels.
Computational evaluation of the effects of cisapride and amiodarone
Cisapride and amiodarone are both known to prolong the QT interval of the ECG, yet they have different effects on cardiac arrhythmogenesis. Cisapride, an I Kr blocker, has been withdrawn from the market due to the high risk for it to induce torsades de pointes leading to fatal cardiac arrhythmias. However, amiodarone, a multichannel blocker that simultaneously affects the channels that mediate I Kr and I CaL, has been found to be effectively safe and anti‐arrhythmic. It is unclear why the two drugs, while both increasing QT interval, have different actions on arrhythmogenesis. In this section, we used a biophysically detailed computational model of the heart to investigate the effects of the two drugs on the characteristics of cardiac electrical activities at the cellular and tissue levels.
Single‐cell simulations of cisapride and amiodarone
Choice of single‐cell AP model
The well‐established ten Tusscher and Panfilov (2006a) models of the human ventricular APs were chosen in this study as they have been well validated to simulate electrical APs of human ventricular endo‐, middle‐ and epicardial cells.
Modelling drug–channel interaction
To simulate the actions of cisapride and amiodarone, we implemented the simple pore block theory, by which the maximal channel conductance of the targeted channel(s) was reduced by various percentages according to the dose of the drug (Table 1). For cisapride, the channel conductance of I Kr was reduced to 70 and 60% of its original values in control condition for a low (150 nM) and a high dose (300 nM) respectively (Wilhelms et al., 2012). For the amiodarone case, the channel conductances of I Kr and I CaL were reduced to 43 and 85%, respectively, for a low dose (presumably 1 μM), and to 15 and 66% for a high dose (presumably 3 μM) based on experimental data (Nishimura et al., 1989; Kodama et al., 1999).
Table 1.
Scaled ion channel conductance due to actions of cisapride and amiodarone at low and high doses
| Conductivity | Cisapride | Amiodarone | ||
|---|---|---|---|---|
| Low dose (%) | High dose (%) | Low dose (%) | High dose (%) | |
| G Kr | 70 | 60 | 43 | 15 |
| G CaL | 100 | 100 | 85 | 66ss |
Effects on cellular APs
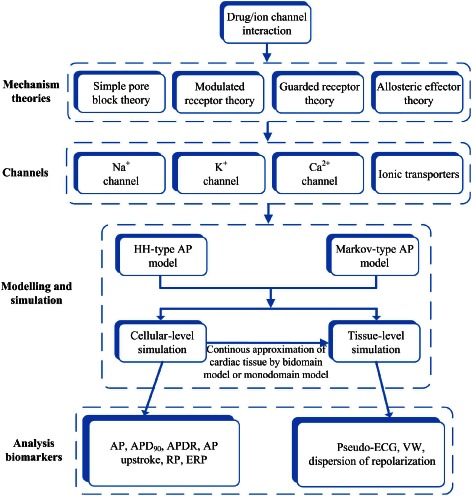
Figure 3 shows the simulated effects of cisapride (Figure 3Ai,Bi) and amiodarone (Figure 3Aii,Bii) on human epicardial ventricular APs at low (left panels) and high doses (right panels). Simulation suggested that both drugs did not markedly affect the AP amplitude, resting potential or dV/dtmax, but both prolonged the APD at 90% repolarization (APD90). This latter effect on the APD was dose‐dependent. At low doses, cisapride and amiodarone prolonged the epicardial APD90 by 12 and 13 ms, respectively, which was changed to 16 and 11 ms at high doses. Such a dose‐dependent APD prolongation is consistent with the clinically observed increase in the QT interval induced by the two drugs.
Figure 3.
Simulation of actions of cisapride and amiodarone on human epicardial ventricular APs with comparison to experimental data. Effects of a combined action of blocking of IKr by the two drugs at high and low doses together with different blocking of ICaL (from 10 to 70%) were also shown. (Ai, Aii) Actions of cisapride and amiodarone at low doses. (Bi, Bii) Actions of cisapride and amiodarone at high doses. (Ci, Cii) Comparison of simulated APD prolongation results to experimental data for cisapride (Di Diego et al., 2003) and amiodarone (Nakagawa et al., 2010).
There are no experimental data from human ventricular cells with which to compare our simulation data. However, our simulation results are qualitatively comparable with experimental data obtained from other species. For cisapride, the simulated APD prolongation was in fair agreement with experimental observations from canine (Di Diego et al., 2003) and from rabbit (Varro et al., 1996; Nakagawa et al., 2010) ventricular cells. Experimentally, it was found that 0.2 μM,cisapride prolonged the canine epicardial APD90 by 9.45 ± 6.4% at a basic cycle length (BCL) of 500 ms (Figure 3Ci). Our simulation (Figure 3Ci) showed that a low dose (0.15 μM) and a high dose (0.3 μM) prolonged the APD90 by 3.88 and 5.18%, respectively, which were close to the experimental data. Quantitative differences between the simulation and experimental data may reflect species differences between the human and canine or the rabbit hearts. The observed dose‐dependent APD prolongation is also consistent with the experimental data of Fossa et al. (2004) from the guinea pig heart.
For amiodarone, experimental data from rabbit epicardial ventricular cells showed that 5 μM amiodarone prolonged the APD by 6.63 ± 2.76% at a BCL of 400 ms (Nakagawa et al., 2010). This is also close to our simulation data of 4.20 and 3.56% for low (1 μM) and high dose (3 μM) respectively (Figure 3Cii). In simulation, we observed that the APD prolongation decreased with an increased dose of amiodarone, which is consistent with the experimental data of Wu et al. (2008) from the rabbit heart.
Simulation using the other two types of cell models (i.e. the middle and endocardial cell models) showed qualitatively similar results to the epicardial cell model. Results are summarized in Table 2.
Table 2.
Effects of cisapride and amiodarone on the cellular characteristics (i.e. biomarkers) of human ventricular endocardial, middle and epicardial cells
| Endo | M | Epi | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APA | dV/dtmax | APD90 | ΔAPD | APA | dV/dtmax | APD90 | ΔAPD | APA | dV/dtmax | APD90 | ΔAPD | |
| (mV) | (mV·ms−1) | (mV) | (ms) | (ms) | (mV·ms−1) | (ms) | (ms) | (mV) | (mV·ms−1) | (ms) | (ms) | |
| Control | 129 | 396 | 348 | – | 128 | 396 | 402 | – | 128 | 397 | 309 | – |
| Low cisapride | 129 | 396 | 363 | 15 | 128 | 396 | 425 | 23 | 128 | 396 | 321 | 12 |
| High cisapride | 129 | 396 | 369 | 21 | 128 | 397 | 433 | 31 | 128 | 396 | 325 | 16 |
| Low amiodarone | 129 | 400 | 365 | 17 | 128 | 399 | 430 | 28 | 128 | 400 | 322 | 13 |
| High amiodarone | 130 | 405 | 365 | 17 | 129 | 404 | 434 | 32 | 129 | 405 | 320 | 11 |
ΔAPD is equal to the difference between the APD90 of control condition and that of a drug dose action in the same cell type.
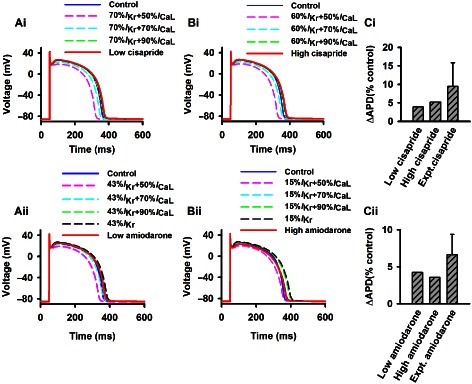
Simulation results showed that there were subtle differences between the two drugs with regard to their dose‐dependent actions on APD. For cisapride, the APD prolongation increased with an increased dose. But for the amiodarone, the APD prolongation decreased with an increased dose. Such different dose‐dependent actions of the two drugs on APD prolongation may be attributable to the different ion channels that they target: cisapride only inhibited I Kr whereas amiodarone inhibited both I Kr and I CaL. In order to test this hypothesis and investigate the functional effects of blocking I CaL, further simulations were performed with different percentages of I CaL blocking (10–70%), together with basal blocking of I Kr by cisapride at low (by 30%) and high (by 40%) doses (Figure 3Ai,Bi), and basal blocking of I Kr by amiodarone at low (by 57%) and high (by 85%) doses (Figure 3Aii,Bii). (Hereafter, simulations were also performed for characterizing the effects of the combined block of I Kr and I CaL on other characteristics of cardiac electrical activities.) It was shown that blocking I Kr alone prolonged the APD. However, when both I Kr and I CaL were blocked, the APD was prolonged when a low percentage of I CaL was blocked but shortened when a high percentage of I CaL was blocked. These simulation results explain why a high dose of amiodarone produces a smaller APD prolongation as compared with a low dose.
Effects on APD and ERP restitution curves
Measuring the action of a drug on the APD and effective refractory period (ERP) restitution curve can help to understand the rate‐dependent actions of the drug on cellular APD and ERP, which form important biomarkers for characterizing the effects of a drug. To compute the APD restitution and ERP curves, we followed the same methods as used in our previous studies (Zhang and Hancox, 2004; Zhang et al., 2013a).
Figure 4 shows APD restitution curves computed from epicardial cells at control and low and high doses of cisapride (Figure 4A,B) and amiodarone (Figure 4C,D). In comparison with the control, cisapride and amiodarone prolonged the APD90 for all the stimulus intervals tested (400–2000 ms), producing steeper APD restitution curves as shown by increased maximal slopes of the curves. This suggested an increased propensity of the two drugs for generating AP alternans leading to arrhythmogenesis (Karagueuzian et al., 2013). In comparison with amiodarone, the cisapride APD restitution curves were steeper, illustrating an even higher propensity for the induction of alternans. With regard to the combined action of I CaL blocking together with the basal blocking of I Kr by the two drugs, APD restitution curves became flatter with an increased level of I CaL block. This suggested that a drug such as amiodarone (which has a combined action on I CaL and I Kr) is superior to a drug such as cisapride that only blocks I Kr for suppressing the development of AP alternans, a predisposing factor for arrhythmogenesis.
Figure 4.
APD restitution curves computed from the epicardial cell model in the control condition and actions of low and high doses of cisapride and amiodarone. Effects of a combined block of IKr by the two drugs at high and low doses together with the different blocking of ICaL (from 10 to 70%) are also shown. (A) low dose of cisapride; (B) high dose of cisapride; (C) low dose of amiodarone; (D) high dose of amiodarone.
Simulation data also showed that both cisapride and amiodarone prolonged ERPs for all the considered range of BCL (200–2000 ms) (data not shown).
Multicellular tissue simulations of cisapride and amiodarone
Transmural ventricular tissue model
A multicellular model of transmural ventricular tissue was constructed by incorporating the ten Tusscher and Panfilov (2006a) model into a reaction diffusion partial differential equation as in our previous studies (Zhang and Hancox, 2004; Zhang et al., 2013a). The model was used to quantify the actions of cisapride and amiodarone on cardiac conduction and its vulnerability to arrhythmogenesis.
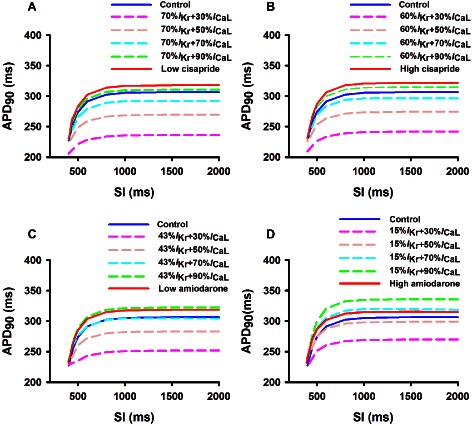
Effects on conduction velocity (CV) restitution
At the multicellular tissue level, an important biomarker for characterizing the actions of a drug on cardiac excitation wave propagation is the CV and its rate dependence, that is, the CV restitution curve (CVRC). Figure 5 show the results of the computed CVRC in control and cisapride and amiodarone conditions. It was shown that at low pacing rates with a BCL greater than 600 ms, neither cisapride (Figure 5A,B) nor amiodarone (Figure 5C,D) had any noticeable effects on the measured CV, either at low or high doses. However, at high pacing rates with a BCL smaller than 600 ms, the two drugs decreased the CV. The decreased CV at high pacing rates was attributable to reduced tissue excitability due to increased ERP.
Figure 5.
Computed effects of cisapride and amiodarone on conduction velocity restitution curves of cardiac excitation waves at low and high doses. Effects of a combined action of blocking of IKr by the two drugs at high and low doses together with different blocking of ICaL (from 10 to 70%) are also shown. (A) low dose of cisapride; (B) high dose of cisapride; (C) low dose of amiodarone; (D) high dose of amiodarone.
Blocking I CaL in addition to the basal block of I Kr by the two drugs resulted in a slight decrease in the CV at low pacing rates, but a marked increase in the CV at high pacing rates as compared with conditions when only the basal I Kr was blocked.
Effects on excitation wavelength (WL)
The excitation WL is another biomarker to characterize the action of a drug on cardiac excitation waves. A drug that increases the WL is believed to be anti‐arrhythmic, whereas a drug that shortens the WL is regarded as being pro‐arrhythmic as it allows limited cardiac tissue to accommodate multiple wavelets of excitation waves underlying fibrillations.
Figure 6 shows the computed wavelength restitution curve from the epicardial cell model in control and cisapride (Figure 6A,B) and amiodarone (Figure 6C,D) conditions at low and high doses. In contrast to the CV (Figure 5), the WL measured was always greater under cisapride and amiodarone conditions, regardless of the pacing BCL.
Figure 6.
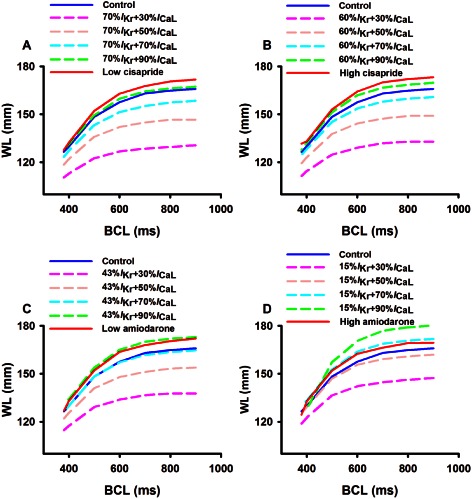
Computed wavelength restitution curves of cardiac excitation waves in control and cisapride and amiodarone conditions. Effects of a combined action of blocking of IKr by the two drugs at high and low doses together with different blocking of ICaL (from 10% to 70%) are also shown. (A) low dose of cisapride; (B) high dose of cisapride; (C) low dose of amiodarone; (D) high dose of amiodarone.
Blocking I CaL in addition to basal blocking of I Kr by the two drugs resulted in a decreased WL as compared with when only basal I Kr was blocked.
Effects on tissue vulnerability for arrhythmogenesis
Vulnerability of cardiac tissue to generate unidirectional conduction block in response to a premature stimulus provides another important biomarker to characterize the actions of a drug. In simulations, the vulnerability of cardiac tissues was quantified by the width of a time window [vulnerable window (VW)] during which a test stimulus applied to a refractory tail of a previous excitation wave to evoke unidirectional conduction. A tissue's vulnerability was measured by the same method as used in our previous studies (Zhang and Hancox, 2004; Zhang et al., 2013a). The width of the VW measures the vulnerability of the tissue for arrhythmogenesis. The greater the width of the VW, the higher the propensity for arrhythmogenesis.
Figure 7 shows th ecomputed width of the VW under control and cisapride and amiodarone conditions (Figure 7A). In the control condition, the VW was 14.3 ms. In the cisapride condition, the WL was increased to 15.2 and 15.7 ms for low and high dose respectively. For the amiodarone condition, the VW was about 15 ms for both low and high doses.
Figure 7.
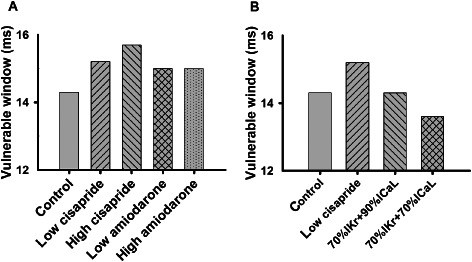
(A) Computed width of vulnerable window of cardiac tissue in control and cisapride and amiodarone conditions. (B) Comparison of vulnerable window for cisapride at a low dose, basal IKr blocking (by 30%) of cisapride together with additional blocking of ICaL by 10 and 30%.
As compared with the cisapride condition, the measured VW in the amiodarone condition was smaller, suggesting a less pro‐arrhythmic effect of amiodarone. Furthermore, the measured VW remained almost constant at low and high dose of amiodarone, rather than in the case of cisapride, where the measured VW was greater at high doses than at low doses. A smaller VW of amiodarone may be attributable to its combined action on both I Kr and I CaL. To test this hypothesis, further simulations were performed with a basal 30% block of I Kr by a low dose of cisapride, together with a 10 and 30% block of I CaL. The results are shown in Figure 7B. The combined action of blocking I Kr and I CaL reduced the measured VW (14.3 and 13.7 ms for 10 and 30% blocking I CaL, respectively), suggesting a reduced propensity of cardiac tissue for arrhythmogenesis. With 30% of both I Kr and I CaL blocked, the measured VW was smaller than that in the control condition (13.7 vs. 14.3 ms), highlighting the superiority of a drug targeting both I Kr and I CaL compared to one targeting I Kr only. These results provide insights into understanding why amiodarone is less likely to have pro‐arrhythmic effects than cisapride.
Effects on ECG
Effect of a drug on the QT interval of ECG has been used as an index to characterize the safety of the drug in practice. The effects of a drug on the characteristics of a pseudo‐ECG can also be computed in the model. In simulations, the pseudo‐ECG was computed as an integral of spatial gradient of membrane potential at all positions on the strand from a virtual electrode located in the extracellular space following the methods used by other studies (Gima and Rudy, 2002; Zhang and Hancox, 2004).
Figure 8 shows the results of simulated ECGs under control and cisapride and amiodarone conditions at low and high doses (Figure 8, left panel). It was shown that both cisapride and amiodarone prolonged the QT interval of ECG. Amiodarone increased the amplitude of the T wave at a low dose, but such an increased T‐wave amplitude became insignificant at a high dose. Cisapride did not show any noticeable effects on the T‐wave amplitude. In simulations, cisapride prolonged the QT interval by 7.50 and 8.75% for low and high dose, respectively (Figure 8, right panel), which was in fair agreement with experimental data that showed a 8.74 ± 5.28% prolongation in the QT interval by 0.2 μM cisapride in the canine heart (Di Diego et al., 2003); amiodarone at low and high doses prolonged the QT interval by 10.94 and 12.81%, respectively, which was also fairly close to the 24.63 ± 6.72% QT interval prolongation by 5 μM amiodarone in the rabbit (Varro et al., 1996).
Figure 8.
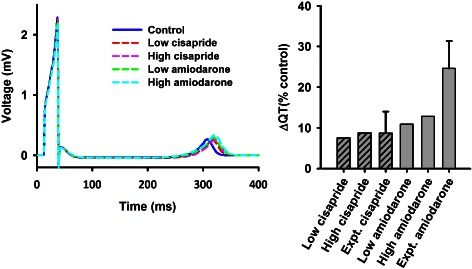
(Left panel) Computed pseudo‐ECG in control and cisapride and amiodarone conditions. Both drugs prolonged QT interval. (Right panel) Comparison of simulated QT interval prolongation to experimental data for cisapride (Di Diego et al., 2003) and amiodarone (Varro et al., 1996).
Effects on initiation and maintenance of re‐entrant excitation waves
Re‐entrant excitation waves are believed to be associated with cardiac tachycardial arrhythmias or fibrillation. Further simulations were performed to investigate the effects of cisapride and amiodarone on the initiation and maintenance of re‐entrant excitation waves in a three‐dimensional realistic model of human ventricles developed in our previous studies (Adeniran et al., 2011). In order to evaluate the effects of cisapride and amiodarone on re‐entry initiation and maintenance, the lifespan of the re‐entry and power spectrum of electrical activity recorded from a local site of the ventricle were computed.
The results are shown in Figure 9 for control (Figure 9Ai–Aiii), and high doses of cisapride (Figure 9Bi–Biii) and amiodarone (Figure 9Ci–Ciii). In the control case, re‐entry was initiated and sustained as shown by the snapshots of excitation pattern in the ventricle (Figure 9Ai). The electrical activity recorded showed rapid spontaneous ventricular excitation (Figure 9Aii) with a dominant frequency of 4.84 Hz (Figure 9Aiii). With the high dose of cisapride, re‐entry was also initiated and sustained (Figure 9Bi), with rapid spontaneous ventricular electrical activity (Figure 9Bii), but the excitation was slowed down with a dominant frequency of 4.17 Hz as compared with the control condition (Figure 9Biii). However, with the high dose of amiodarone, re‐entry was self‐terminated shortly after initiation (Figure 9Ci–Ciii). Consistent with the actions of these two drug effects on arrhythmogenic effects elucidated at the cellular and tissue levels, at the three‐dimensional organ level, cisapride increased susceptibility to initiation and maintenance of re‐entry, but amiodarone, by terminating re‐entry, was anti‐arrhythmic.
Figure 9.
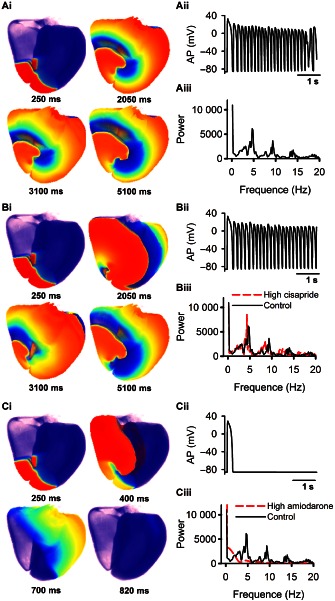
Initiation and maintenance of re‐entry in a three‐dimensional realistic model of human ventricles under control (A), high cisapride (B), amiodarone (C) conditions. (Ai, Bi, Ci) Snapshots of conduction pattern of ventricular re‐entry. (Aii, Bii, Cii) Time series of electrical activity recorded from a local site in the ventricle. (Ci, Cii, Ciii) Power spectrum of the recorded electrical activities.
Discussion
Biophysically detailed and well‐validated computer models of the heart have shown excellent promise as an alternative preclinical cardiotoxicity screening tool. Since the pioneering work of Denis Noble (1960), many complex and precise cardiac cell models have been developed in the last few decades for various species and different cell types, which form a fundamental basis for the virtual physiological heart (Kohl and Noble, 2009; Clayton et al., 2011). The virtual heart has attracted increasing attention for its application in drug development and assessment (Xie et al., 2014). With the use of the virtual heart, the effects of a drug on cardiac electrical activities can be quantitatively characterized at different levels, thus providing a better assessment of the safety profile of a drug as compared with the conventional use of QT prolongation or effects on I Kr.
Mechanistic insights into the actions of cisapride and amiodarone
Our simulation results showed that cisapride, an hERG channel blocker, prolonged cellular APD, steepened the APD and ERP restitution cures, increased a tissue's vulnerability to arrhythmogenesis and sustained but slowed down re‐entrant excitation waves. However, although amiodarone, a combined channel blocker of hERG and L‐type Ca2+ channels, also prolonged cellular APD, it steepened the APD and ERP restitution curves to a lesser degree, reduced the tissue's vulnerability to arrhythmogenesis and most importantly terminated re‐entrant excitation waves as compared with cisapride. These data explain why amiodarone is safer than cisapride as an anti‐arrhythmic treatment. Furthermore, our simulations showed that such a difference in the two drugs can be attributable to the blocking effect of amiodarone on I CaL in addition to the blocking of I Kr.
Future challenges
Although advances have been made in the last few decades in modelling drug–channel interactions and cardiac electrophysiology, there are still some challenges ahead for implementing the virtual heart model for drug safety assessment. Firstly, more studies are needed to develop biophysically accurate models for simulating the interactions between drug molecules and ion channel receptors. This requires not only further development of theories on the interaction between drug and channel(s) but also detailed experimental data on the kinetics of a drug's actions. A complete set of such experimental data will help to derive and validate mathematical equations and parameters for the drug–channel interaction model. Secondly, well‐validated models for simulating different cell types of the human heart in normal physiological and various pathological conditions are needed. A complete set of these cell models can be incorporated into the whole heart model for simulating the actions of the drug on the electrical activities of the whole heart conduction system, not just in a localized region of the heart such as the ventricle. This whole heart model can be used to answer questions such as ‘is a drug that is effective for anti‐ventricular fibrillation safe for atrioventricular node conduction?’ Thirdly, cardiac arrhythmogenesis is associated with autonomic modulations, and so are the drug‐induced cardiac arrhythmias. Therefore, it is necessary to incorporate the actions of autonomic regulations on the cardiac models for simulating the actions of drugs and their interactions with the heart during changes in autonomic systems. In addition, recently there are some new developments in structure‐based virtual drug screening (Villoutreix et al., 2008), as well as simulations of drug–ion channel interactions based on protein structures (Silva et al., 2009; Silva and Rudy, 2010; Nekouzadeh and Rudy, 2011). How to incorporate such microscale models into a large‐scale whole heart model for simulating and evaluating the actions of a drug is also a challenge.
Conclusion
A biophysically accurate, detailed and well‐validated model of the heart provides a powerful platform for quantitative assessment of a drug's safety. The platform integrates independent and distinct physical results from toxicological experiments, such as assay and patch clamp data, into a whole heart model based on detailed data from cellular electrophysiology, electro‐anatomical mapping and MRI/CT structural imaging. The whole heart model can be further integrated into a three‐dimensional human torso model, forming a multiscale physical platform allowing one to simulate the action of a drug on body surface ECGs (as shown in Figure 10). With these computational tools, the functional effects of a drug can be thoroughly analysed at the cellular, tissue and organ levels by a family of corresponding cardiac electrophysiological properties (i.e. biomarkers), from which the safety of the drug can be fully assessed.
Figure 10.
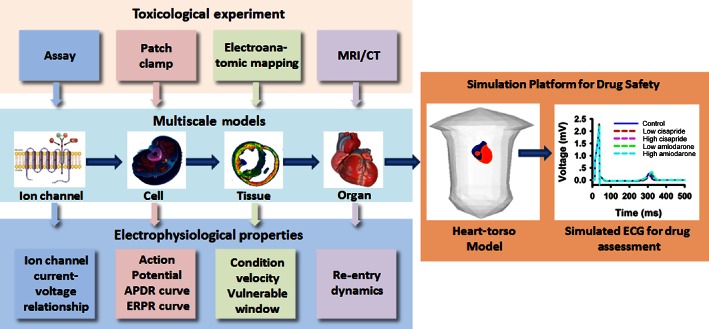
Schematic illustration of virtual heart as a platform for drug safety assessment.
Author contributions
H. Z. conceived and designed the experiments. Y. Y. and C. L. performed the experiments; Y. Y., X. B., C. L., K. W. and H. Z. wrote the manuscript.
Conflict of interest
None.
Acknowledgements
This study was supported by Natural Science Foundation of China (NSFC) grants (no. 61001167, no. 61173086, no. 61179009 and no. 61172149).
Appendix
Appendix A: Details of mathematical equation of I Na in HH and Markovian chain formats
In the HH format, I Na model is based on the Luo and Rudy (1994b) model, which is given by:
| (A1) |
| (A2) |
For V ≥ −40 mV:
| (A3) |
| (A4) |
| (A5) |
For V < −40 mV:
| (A6) |
| (A7) |
| (A8) |
| (A9) |
| (A10) |
| (A11) |
In the Markovian chain format, the Na+ channel is based on the three states of the Na+ channel: resting (R), activated (A) and inactivated (I).
MR representation of state‐dependent drug action
The sum of blocked channels (B) is given by the following:
| (A12) |
| (A13) |
| (A14) |
| (A15) |
| (A16) |
| (A17) |
| (A18) |
Guarded receptor representation of drug action
The model was proposed by Starmer et al. (1991b), with details as the following:
| (A19) |
| (A20) |
| (A21) |
| (A22) |
Simulations of lidocaine action were obtained with a binding rate kA = 1370.0 ms−1 ⋅ M−1 and an unbinding rate lA = 1.3 × 10−5 ms−1 for the open state and a binding rate kI = 60 ms−1 ⋅ M−1 and an unbinding rate lI = 2.3 × 10−4 ms−1 for the inactivated state.
Appendix B: List of some advances in simulation of ion channel–drug interactions
Table B1 Major models for simulating drug screening
| Model | Using in simulating drug screening | |
|---|---|---|
| Ion channelopathy | Reference | |
|
The Fitzhugh model (Fitzhugh, 1961) |
I
Na channel I K channel |
(Starmer et al., 1994; Starobin et al., 1996) |
|
The Beeler–Reuter model (Beeler and Reuter, 1977) |
I Na channel | (Starmer et al., 1991a, 2003a, 2003b) |
|
The Ebihara–Johnson model (Ebihara and Johnson, 1980) |
I Na channel | (Starmer et al., 2003a, 2003b) |
|
The Luo–Rudy model (Luo and Rudy, 1994a, 1994b) |
I
Na channel I K channel I Ca channel |
(Clancy and Rudy, 2002; Cimponeriu et al., 2003; Kapela et al., 2005; Terrenoire et al., 2005; Trenor et al., 2005; Clancy et al., 2007; Ahrens‐Nicklas et al., 2009; Saiz et al., 2011) |
|
The Ramirez–Nattel‐Courtemanche model (Courtemanche et al., 1998; Ramirez et al., 2000) |
I
Na channel I K channel |
(Kneller et al., 2005; Tsujimae et al., 2007; Comtois et al., 2008; Aguilar‐Shardonofsky et al., 2012; Colman et al., 2014) |
|
The Shannon–Bers model (Shannon et al., 2004) |
I Na channel | (Wu et al., 2011) |
|
The Hund–Rudy model (Hund and Rudy, 2004) |
I Na channel | (Cardona et al., 2010; Aguilar‐Shardonofsky et al., 2012) |
|
The Tusscher model (ten Tusscher et al., 2004; ten Tusscher and Panfilov, 2006a) |
I
Na channel I K channel |
(Fredj et al., 2006; Sale et al., 2008; Mirams et al., 2011) |
|
The ten Tusscher–Panfilov model (ten Tusscher and Panfilov, 2006b) |
I K channel | (Dux‐Santoy et al., 2011) |
|
The O'Hara–Rudy model (O'Hara et al., 2011) |
I
Na channel I K channel |
(Moreno et al., 2013) |
References
- Adeniran I, McPate MJ, Witchel HJ, Hancox JC, Zhang H (2011). Increased vulnerability of human ventricle to re‐entrant excitation in hERG‐linked variant 1 short QT syndrome. PLoS Comput Biol 7: e1002313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguilar‐Shardonofsky M, Vigmond EJ, Nattel S, Comtois P (2012). In silico optimization of atrial fibrillation‐selective sodium channel blocker pharmacodynamics. Biophys J 102: 951–960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahrens‐Nicklas RC, Clancy CE, Christini DJ (2009). Re‐evaluating the efficacy of beta‐adrenergic agonists and antagonists in long QT‐3 syndrome through computational modelling. Cardiovasc Res 82: 439–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander SPH, Benson HE, Faccenda E, Pawson AJ, Sharman JL, Spedding M et al (2013a). The Concise Guide to PHARMACOLOGY 2013/14: G protein‐coupled receptors. Br J Pharmacol 170: 1459–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander SPH, Benson HE, Faccenda E, Pawson AJ, Sharman JL, Spedding M et al (2013b). The Concise Guide to PHARMACOLOGY 2013/14: Ion channels. Br J Pharmacol 170: 1607–1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beeler GW, Reuter H (1977). Reconstruction of the action potential of ventricular myocardial fibres. J Physiol 268: 177–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bottino D, Penland RC, Stamps A, Traebert M, Dumotier B, Georgiva A et al (2006). Preclinical cardiac safety assessment of pharmaceutical compounds using an integrated systems‐based computer model of the heart. Prog Biophys Mol Biol 90: 414–443. [DOI] [PubMed] [Google Scholar]
- Cardona K, Trenor B, Rajamani S, Romero L, Ferrero JM, Saiz J (2010). Effects of late sodium current enhancement during LQT‐related arrhythmias. A simulation study. Conf Proc IEEE Eng Med Biol Soc 2010: 3237–3240. [DOI] [PubMed] [Google Scholar]
- Cimponeriu A, Starmer CF, Bezerianos A (2003). Ischemic modulation of vulnerable period and the effects of pharmacological treatment of ischemia‐induced arrhythmias: a simulation study. IEEE Trans Biomed Eng 50: 168–177. [DOI] [PubMed] [Google Scholar]
- Clancy CE, Rudy Y (2002). Na(+) channel mutation that causes both Brugada and long‐QT syndrome phenotypes: a simulation study of mechanism. Circulation 105: 1208–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clancy CE, Zhu ZI, Rudy Y (2007). Pharmacogenetics and anti‐arrhythmic drug therapy: a theoretical investigation. Am J Physiol Heart Circ Physiol 292: H66–H75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton RH, Bernus O, Cherry EM, Dierckx H, Fenton FH, Mirabella L et al (2011). Models of cardiac tissue electrophysiology: progress, challenges and open questions. Prog Biophys Mol Biol 104: 22–48. [DOI] [PubMed] [Google Scholar]
- Colman MA, Varela M, Hancox JC, Zhang H, Aslanidi OV (2014). Evolution and pharmacological modulation of the arrhythmogenic wave dynamics in canine pulmonary vein model. Europace 16: 416–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comtois P, Sakabe M, Vigmond EJ, Munoz M, Texier A, Shiroshita‐Takeshita A et al (2008). Mechanisms of atrial fibrillation termination by rapidly unbinding Na+ channel blockers: insights from mathematical models and experimental correlates. Am J Physiol Heart Circ Physiol 295: H1489–H1504. [DOI] [PubMed] [Google Scholar]
- Corrias A, Jie X, Romero L, Bishop MJ, Bernabeu M, Pueyo E et al (2010). Arrhythmic risk biomarkers for the assessment of drug cardiotoxicity: from experiments to computer simulations. Philos Trans A Math Phys Eng Sci 368: 3001–3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courtemanche M, Ramirez RJ, Nattel S (1998). Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am J Physiol 275 (1 Pt 2): H301–H321. [DOI] [PubMed] [Google Scholar]
- Di Diego JM, Belardinelli L, Antzelevitch C (2003). Cisapride‐induced transmural dispersion of repolarization and torsade de pointes in the canine left ventricular wedge preparation during epicardial stimulation. Circulation 108: 1027–1033. [DOI] [PubMed] [Google Scholar]
- Di Veroli GY, Davies MR, Zhang H, Abi‐Gerges N, Boyett MR (2014). hERG inhibitors with similar potency but different binding kinetics do not pose the same proarrhythmic risk: implications for drug safety assessment. J Cardiovasc Electrophysiol 25: 197–207. [DOI] [PubMed] [Google Scholar]
- DiMasi JA, Hansen RW, Grabowski HG (2003). The price of innovation: new estimates of drug development costs. J Health Econ 22: 151–185. [DOI] [PubMed] [Google Scholar]
- Dux‐Santoy L, Sebastian R, Felix‐Rodriguez J, Ferrero JM, Saiz J (2011). Interaction of specialized cardiac conduction system with antiarrhythmic drugs: a simulation study. IEEE Trans Biomed Eng 58: 3475–3478. [DOI] [PubMed] [Google Scholar]
- Ebihara L, Johnson EA (1980). Fast sodium current in cardiac muscle. A quantitative description. Biophys J 32: 779–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faber GM, Rudy Y (2007). Calsequestrin mutation and catecholaminergic polymorphic ventricular tachycardia: a simulation study of cellular mechanism. Cardiovasc Res 75: 79–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faber GM, Silva J, Livshitz L, Rudy Y (2007). Kinetic properties of the cardiac L‐type Ca2+ channel and its role in myocyte electrophysiology: a theoretical investigation. Biophys J 92: 1522–1543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fink M, Noble D, Virag L, Varro A, Giles WR (2008). Contributions of HERG K+ current to repolarization of the human ventricular action potential. Prog Biophys Mol Biol 96: 357–376. [DOI] [PubMed] [Google Scholar]
- Fitzhugh R (1961). Impulses and physiological states in theoretical models of nerve membrane. Biophys J 1: 445–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fossa AA, Wisialowski T, Wolfgang E, Wang E, Avery M, Raunig DL et al (2004). Differential effect of HERG blocking agents on cardiac electrical alternans in the guinea pig. Eur J Pharmacol 486: 209–221. [DOI] [PubMed] [Google Scholar]
- Fredj S, Sampson KJ, Liu H, Kass RS (2006). Molecular basis of ranolazine block of LQT‐3 mutant sodium channels: evidence for site of action. Br J Pharmacol 148: 16–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedrichs GS, Patmore L, Bass A (2005). Non‐clinical evaluation of ventricular repolarization (ICH S7B): results of an interim survey of international pharmaceutical companies. J Pharmacol Toxicol Methods 52: 6–11. [DOI] [PubMed] [Google Scholar]
- Gima K, Rudy Y (2002). Ionic current basis of electrocardiographic waveforms: a model study. Circ Res 90: 889–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gintant G (2012). Ions, equations and electrons: the evolving role of computer simulations in cardiac electrophysiology safety evaluations. Br J Pharmacol 167: 929–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henriquez CS (2014). A brief history of tissue models for cardiac electrophysiology. IEEE Trans Biomed Eng 61: 1457–1465. [DOI] [PubMed] [Google Scholar]
- Hill AP, Perrin MJ, Heide J, Campbell TJ, Mann SA, Vandenberg JI (2014). Kinetics of drug interaction with the Kv11.1 potassium channel. Mol Pharmacol 85: 769–776. [DOI] [PubMed] [Google Scholar]
- Hille B (1977). Local anesthetics: hydrophilic and hydrophobic pathways for the drug‐receptor reaction. J Gen Physiol 69: 497–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hondeghem LM, Katzung BG (1977). Time‐ and voltage‐dependent interactions of antiarrhythmic drugs with cardiac sodium channels. Biochim Biophys Acta 472: 373–398. [DOI] [PubMed] [Google Scholar]
- Hondeghem LM, Carlsson L, Duker G (2001). Instability and triangulation of the action potential predict serious proarrhythmia, but action potential duration prolongation is antiarrhythmic. Circulation 103: 2004–2013. [DOI] [PubMed] [Google Scholar]
- Hondeghem LM, Dujardin K, Hoffmann P, Dumotier B, De Clerck F (2011). Drug‐induced QTC prolongation dangerously underestimates proarrhythmic potential: lessons from terfenadine. J Cardiovasc Pharmacol 57: 589–597. [DOI] [PubMed] [Google Scholar]
- Hund TJ, Rudy Y (2004). Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model. Circulation 110: 3168–3174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iyer V, Mazhari R, Winslow RL (2004). A computational model of the human left‐ventricular epicardial myocyte. Biophys J 87: 1507–1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapela A, Tsoukias N, Bezerianos A (2005). New aspects of vulnerability in heterogeneous models of ventricular wall and its modulation by loss of cardiac sodium channel function. Med Biol Eng Comput 43: 387–394. [DOI] [PubMed] [Google Scholar]
- Karagueuzian HS, Stepanyan H, Mandel WJ (2013). Bifurcation theory and cardiac arrhythmias. Am J Cardiovasc Dis 3: 1–16. [PMC free article] [PubMed] [Google Scholar]
- Kenakin T (2004). Principles: receptor theory in pharmacology. Trends Pharmacol Sci 25: 186–192. [DOI] [PubMed] [Google Scholar]
- Kharche S, Yu J, Lei M, Zhang H (2011). A mathematical model of action potentials of mouse sinoatrial node cells with molecular bases. Am J Physiol Heart Circ Physiol 301: H945–H963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kneller J, Kalifa J, Zou R, Zaitsev AV, Warren M, Berenfeld O et al (2005). Mechanisms of atrial fibrillation termination by pure sodium channel blockade in an ionically‐realistic mathematical model. Circ Res 96: e35–e47. [DOI] [PubMed] [Google Scholar]
- Kodama I, Kamiya K, Toyama J (1999). Amiodarone: ionic and cellular mechanisms of action of the most promising class III agent. Am J Cardiol 84 (9A): 20R–28R. [DOI] [PubMed] [Google Scholar]
- Kohl P, Noble D (2009). Systems biology and the virtual physiological human. Mol Syst Biol 5: 292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo CH, Rudy Y (1994a). A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ Res 74: 1071–1096. [DOI] [PubMed] [Google Scholar]
- Luo CH, Rudy Y (1994b). A dynamic model of the cardiac ventricular action potential. II. After depolarizations, triggered activity, and potentiation. Circ Res 74: 1097–1113. [DOI] [PubMed] [Google Scholar]
- Martin RL, McDermott JS, Salmen HJ, Palmatier J, Cox BF, Gintant GA (2004). The utility of hERG and repolarization assays in evaluating delayed cardiac repolarization: influence of multi‐channel block. J Cardiovasc Pharmacol 43: 369–379. [DOI] [PubMed] [Google Scholar]
- Mirams GR, Cui Y, Sher A, Fink M, Cooper J, Heath BM et al (2011). Simulation of multiple ion channel block provides improved early prediction of compounds' clinical torsadogenic risk. Cardiovasc Res 91: 53–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirams GR, Davies MR, Cui Y, Kohl P, Noble D (2012). Application of cardiac electrophysiology simulations to pro‐arrhythmic safety testing. Br J Pharmacol 167: 932–945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno JD, Zhu ZI, Yang PC, Bankston JR, Jeng MT, Kang C et al (2011). A computational model to predict the effects of class I anti‐arrhythmic drugs on ventricular rhythms. Sci Transl Med 3: 98ra83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno JD, Yang PC, Bankston JR, Grandi E, Bers DM, Kass RS et al (2013). Ranolazine for congenital and acquired late INa‐linked arrhythmias: in silico pharmacological screening. Circ Res 113: e50–e61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakagawa H, Honjo H, Ishiguro YS, Yamazaki M, Okuno Y, Harada M et al (2010). Acute amiodarone promotes drift and early termination of spiral wave re‐entry. Heart Vessels 25: 338–347. [DOI] [PubMed] [Google Scholar]
- Nekouzadeh A, Rudy Y (2011). Continuum molecular simulation of large conformational changes during ion‐channel gating. PLoS ONE 6: e20186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishimura M, Follmer CH, Singer DH (1989). Amiodarone blocks calcium current in single guinea pig ventricular myocytes. J Pharmacol Exp Ther 251: 650–659. [PubMed] [Google Scholar]
- Noble D (1960). Cardiac action and pacemaker potentials based on the Hodgkin‐Huxley equations. Nature 188: 495–497. [DOI] [PubMed] [Google Scholar]
- Noble D (1962). A modification of the Hodgkin–Huxley equations applicable to Purkinje fibre action and pace‐maker potentials. J Physiol 160: 317–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Hara T, Virag L, Varro A, Rudy Y (2011). Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Comput Biol 7: e1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawson AJ, Sharman JL, Benson HE, Faccenda E, Alexander SP, Buneman OP et al; NC‐IUPHAR (2014). The IUPHAR/BPS Guide to PHARMACOLOGY: an expert‐driven knowledgebase of drug targets and their ligands. Nucl. Acids Res 42 (Database Issue): D1098–D1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard CE, Abi Gerges N, Bridgland‐Taylor MH, Easter A, Hammond TG, Valentin JP (2010). An introduction to QT interval prolongation and non‐clinical approaches to assessing and reducing risk. Br J Pharmacol 159: 12–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qu Z, Weiss JN (2005). Effects of Na(+) and K(+) channel blockade on vulnerability to and termination of fibrillation in simulated normal cardiac tissue. Am J Physiol Heart Circ Physiol 289: H1692–H1701. [DOI] [PubMed] [Google Scholar]
- Ramirez RJ, Nattel S, Courtemanche M (2000). Mathematical analysis of canine atrial action potentials: rate, regional factors, and electrical remodeling. Am J Physiol Heart Circ Physiol 279: H1767–H1785. [DOI] [PubMed] [Google Scholar]
- Romero L, Trenor B, Yang PC, Saiz J, Clancy CE (2014). In silico screening of the impact of hERG channel kinetic abnormalities on channel block and susceptibility to acquired long QT syndrome. J Mol Cell Cardiol 72: 126–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudy Y, Silva JR (2006). Computational biology in the study of cardiac ion channels and cell electrophysiology. Q Rev Biophys 39: 57–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saiz J, Gomis‐Tena J, Monserrat M, Ferrero JM Jr, Cardona K, Chorro J (2011). Effects of the antiarrhythmic drug dofetilide on transmural dispersion of repolarization in ventriculum. A computer modeling study. IEEE Trans Biomed Eng 58: 43–53. [DOI] [PubMed] [Google Scholar]
- Sale H, Wang J, O'Hara TJ, Tester DJ, Phartiyal P, He JQ et al (2008). Physiological properties of hERG 1a/1b heteromeric currents and a hERG 1b‐specific mutation associated with long‐QT syndrome. Circ Res 103: e81–e95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanguinetti MC, Tristani‐Firouzi M (2006). hERG potassium channels and cardiac arrhythmia. Nature 440: 463–469. [DOI] [PubMed] [Google Scholar]
- Sanguinetti MC, Jiang C, Curran ME, Keating MT (1995). A mechanistic link between an inherited and an acquired cardiac arrhythmia: HERG encodes the IKr potassium channel. Cell 81: 299–307. [DOI] [PubMed] [Google Scholar]
- Shannon TR, Wang F, Puglisi J, Weber C, Bers DM (2004). A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys J 87: 3351–3371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva J, Rudy Y (2005). Subunit interaction determines IKs participation in cardiac repolarization and repolarization reserve. Circulation 112: 1384–1391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva JR, Rudy Y (2010). Multi‐scale electrophysiology modeling: from atom to organ. J Gen Physiol 135: 575–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva JR, Pan H, Wu D, Nekouzadeh A, Decker KF, Cui J et al (2009). A multiscale model linking ion‐channel molecular dynamics and electrostatics to the cardiac action potential. PNAS 106: 11102–11106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith PL, Baukrowitz T, Yellen G (1996). The inward rectification mechanism of the HERG cardiac potassium channel. Nature 379: 833–836. [DOI] [PubMed] [Google Scholar]
- Starmer CF (1987). Theoretical characterization of ion channel blockade. Competitive binding to periodically accessible receptors. Biophys J 52: 405–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starmer CF, Grant AO (1985). Phasic ion channel blockade. A kinetic model and parameter estimation procedure. Mol Pharmacol 28: 348–356. [PubMed] [Google Scholar]
- Starmer CF, Grant AO, Strauss HC (1984). Mechanisms of use‐dependent block of sodium channels in excitable membranes by local anesthetics. Biophys J 46: 15–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starmer CF, Packer DL, Grant AO (1987). Ligand binding to transiently accessible sites: mechanisms for varying apparent binding rates. J Theor Biol 124: 335–341. [DOI] [PubMed] [Google Scholar]
- Starmer CF, Lastra AA, Nesterenko VV, Grant AO (1991a). Proarrhythmic response to sodium channel blockade. Theoretical model and numerical experiments. Circulation 84: 1364–1377. [DOI] [PubMed] [Google Scholar]
- Starmer CF, Nesterenko VV, Undrovinas AI, Grant AO, Rosenshtraukh LV (1991b). Lidocaine blockade of continuously and transiently accessible sites in cardiac sodium channels. J Mol Cell Cardiol 23 (Suppl. 1): 73–83. [DOI] [PubMed] [Google Scholar]
- Starmer CF, Reddy MR, Namasivayam A, Singh M (1994). Potassium channel blockade amplifies cardiac instability numerical studies of torsades de pointes. Indian J Physiol Pharmacol 38: 259–266. [PubMed] [Google Scholar]
- Starmer CF, Romashko DN, Reddy RS, Zilberter YI, Starobin J, Grant AO et al (1995). Proarrhythmic response to potassium channel blockade. Numerical studies of polymorphic tachyarrhythmias. Circulation 92: 595–605. [DOI] [PubMed] [Google Scholar]
- Starmer CF, Colatsky TJ, Grant AO (2003a). What happens when cardiac Na channels lose their function? 1. Numerical studies of the vulnerable period in tissue expressing mutant channels. Cardiovasc Res 57: 82–91. [DOI] [PubMed] [Google Scholar]
- Starmer CF, Grant AO, Colatsky TJ (2003b). What happens when cardiac Na channel function is compromised? 2. Numerical studies of the vulnerable period in tissue altered by drugs. Cardiovasc Res 57: 1062–1071. [DOI] [PubMed] [Google Scholar]
- Starobin JM, Zilberter YI, Rusnak EM, Starmer CF (1996). Wavelet formation in excitable cardiac tissue: the role of wavefront‐obstacle interactions in initiating high‐frequency fibrillatory‐like arrhythmias. Biophys J 70: 581–594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terrenoire C, Clancy CE, Cormier JW, Sampson KJ, Kass RS (2005). Autonomic control of cardiac action potentials: role of potassium channel kinetics in response to sympathetic stimulation. Circ Res 96: e25–e34. [DOI] [PubMed] [Google Scholar]
- Trenor B, Ferrero JM Jr, Rodriguez B, Montilla F (2005). Effects of pinacidil on reentrant arrhythmias generated during acute regional ischemia: a simulation study. Ann Biomed Eng 33: 897–906. [DOI] [PubMed] [Google Scholar]
- Trudeau MC, Warmke JW, Ganetzky B, Robertson GA (1995). HERG, a human inward rectifier in the voltage‐gated potassium channel family. Science 269: 92–95. [DOI] [PubMed] [Google Scholar]
- Tsujimae K, Suzuki S, Murakami S, Kurachi Y (2007). Frequency‐dependent effects of various IKr blockers on cardiac action potential duration in a human atrial model. Am J Physiol Heart Circ Physiol 293: H660–H669. [DOI] [PubMed] [Google Scholar]
- ten Tusscher KH, Panfilov AV (2006a). Alternans and spiral breakup in a human ventricular tissue model. Am J Physiol Heart Circ Physiol 291: H1088–H1100. [DOI] [PubMed] [Google Scholar]
- ten Tusscher KH, Panfilov AV (2006b). Cell model for efficient simulation of wave propagation in human ventricular tissue under normal and pathological conditions. Phys Med Biol 51: 6141–6156. [DOI] [PubMed] [Google Scholar]
- ten Tusscher KH, Noble D, Noble PJ, Panfilov AV (2004). A model for human ventricular tissue. Am J Physiol Heart Circ Physiol 286: H1573–H1589. [DOI] [PubMed] [Google Scholar]
- Varro A, Virag L, Papp JG (1996). Comparison of the chronic and acute effects of amiodarone on the calcium and potassium currents in rabbit isolated cardiac myocytes. Br J Pharmacol 117: 1181–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villoutreix BO, Bastard K, Sperandio O, Fahraeus R, Poyet JL, Calvo F et al (2008). In silico‐in vitro screening of protein‐protein interactions: towards the next generation of therapeutics. Curr Pharm Biotechnol 9: 103–122. [DOI] [PubMed] [Google Scholar]
- Wilhelms M, Rombach C, Scholz EP, Dossel O, Seemann G (2012). Impact of amiodarone and cisapride on simulated human ventricular electrophysiology and electrocardiograms. Europace 14 (Suppl. 5): v90–v96. [DOI] [PubMed] [Google Scholar]
- Wu L, Rajamani S, Shryock JC, Li H, Ruskin J, Antzelevitch C et al (2008). Augmentation of late sodium current unmasks the proarrhythmic effects of amiodarone. Cardiovasc Res 77: 481–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu L, Ma J, Li H, Wang C, Grandi E, Zhang P et al (2011). Late sodium current contributes to the reverse rate‐dependent effect of IKr inhibition on ventricular repolarization. Circulation 123: 1713–1720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie X, Zou J, Wang QY, Noble CG, Lescar J, Shi PY (2014). Generation and characterization of mouse monoclonal antibodies against NS4B protein of dengue virus. Virology 450–451: 250–257. [DOI] [PubMed] [Google Scholar]
- Zhang H, Hancox JC (2004). In silico study of action potential and QT interval shortening due to loss of inactivation of the cardiac rapid delayed rectifier potassium current. Biochem Biophys Res Commun 322: 693–699. [DOI] [PubMed] [Google Scholar]
- Zhang H, Kharche S, Holden AV, Hancox JC (2008). Repolarisation and vulnerability to re‐entry in the human heart with short QT syndrome arising from KCNQ1 mutation – a simulation study. Prog Biophys Mol Biol 96: 112–131. [DOI] [PubMed] [Google Scholar]
- Zhou Q, Bett GC, Rasmusson RL (2012). Markov models of use‐dependence and reverse use‐dependence during the mouse cardiac action potential. PLoS ONE 7: e42295. [DOI] [PMC free article] [PubMed] [Google Scholar]


