Characterizing Protein Motions from Structure

Abstract

To clarify the extent structure plays in determining protein dynamics, a comparative study is made using three models that characterize native state dynamics of single domain proteins starting from known structures taken from four distinct SCOP classifications. A geometrical simulation using the Framework Rigidity Optimized Dynamics Algorithm (FRODA) based on rigid cluster decomposition is compared to the commonly employed elastic network model (specifically the Anisotropic Network Model ANM) and molecular dynamics (MD) simulation. The essential dynamics are quantified by a mode subspace constructed from ANM and a principal component analysis (PCA) on FRODA and MD trajectories. Aggregate conformational ensembles are constructed to provide a basis for quantitative comparisons between FRODA runs using different parameter settings to critically assess how the predictions of essential dynamics depend on a priori arbitrary user-defined distance constraint rules. We established a range of physicality for these parameters. Surprisingly, FRODA maintains greater intra-consistent results than obtained from MD trajectories, comparable to ANM. Additionally, a mode subspace is constructed from PCA on an exemplar set of myoglobin structures from the Protein Data Bank. Significant overlap across the three model subspaces and the experimentally derived subspace is found. While FRODA provides the most robust sampling and characterization of the native basin, all three models give similar dynamical information of a native state, further demonstrating that structure is the key determinant of dynamics.

Graphical Abstract

Introduction

The protein data bank [1,2] (PDB) (www.pdb.org) is a repository of protein structures that continues to grow on a daily basis containing tens of thousands of structures derived from X-ray and nuclear diffraction and NMR. A key component of protein science is to generate an ensemble of conformations when provided a static structure in order to identify essential motions important to function. Molecular Dynamics (MD) [3] is a model that implements a force field to represent interactions of a protein both internally and to solvent. For an all atom force field MD provides highly detailed information about protein dynamics, with a time resolution on the order of femtoseconds, capable of investigating nanosecond time scales and beyond depending on protein size. A major disadvantage of MD has been, and continues to be, the intense computational time necessary to sample robustly the conformational space of a protein, precluding a claim of statistical relevance at longer time scales [4]. For these reasons, a coarse-grained model is often chosen to gain insight into the dynamics at long-time scales, requiring much less computational expense.

The elastic network model [5] and specifically the anisotropic network model (ANM) [6] is one such approach. In this model, the detailed atomic level force field used in MD is replaced by a simple spring model with a single spring constant [7] between a selected set of atoms, usually the carbon-alpha atoms along the backbone. This coarse-grained model enables an efficient normal mode analysis to determine the collective motions of a protein. The extracted low frequency modes have been shown to identify biologically relevant motions of the protein structure important to function [8,9]. An advantage of ANM as a result of coarse-graining is that performing an all atom energy minimization is avoided, which is not the case for traditional all atom normal mode analysis. In the procedure of constructing the spring network, by definition, the input structure represents a mechanical equilibrium point from which fluctuations within linear response (harmonic potentials) are captured. Consequently, ANM can extend to large proteins because of this coarse-graining. The major criticisms of elastic network models is that linear response may be insufficient to capture protein motions within the native basin of a protein and the amplitudes of the modes that represent the atomic fluctuations are often set larger than can be a priori justified. Much of this criticism has been dispelled by the demonstrated usefulness of ANM modes as seen through verification by complementary methods and experiment [10]. Because coarse-graining is the key feature that allows large-scale fluctuations in conformation to be quantified, the results from the elastic network model should not be sensitive to specific atomic locations of the input structure. We show in this study that the ANM modes derived from different structures selected at random from a dynamics trajectory are indeed robust.

A compromise paradigm is achieved in geometrical simulation methods, in which a single input structure is used to generate an ensemble of structures, as in MD. This method of simulation uses geometrical constraints to define the native basin, while the perturbation of those constraints (with subsequent relaxation and tolerance matching) yields conformers within the constraint space of the input structure. Floppy Inclusions and Rigid Substructure Topology (FIRST) implements a graph rigidity algorithm that identifies flexible and rigid regions of the protein given the constraints that are present in the input structure [11] through a rigid cluster decomposition (RCD). The Framework Rigidity Optimized Dynamics Algorithm (FRODA) [12,13] samples the native basin efficiently by using the RCD defined by the input structure. It has been shown through rigidity percolation analysis [14] that different choices of constraints yield different rigidity transitions in proteins. Although the constraint types used in FRODA have been selected to best match empirical characteristics of protein flexibility in the native state, there remains considerable freedom in the user-defined rules for identifying native constraints. This model parameter ambiguity is unsettling when one wants to quantitatively characterize the native state dynamics of a protein. Remarkably, as we show for the first time in this paper, the essential motions of these structures is robust in that a wide range of FIRST parameters generate quantitatively similar FRODA mode spaces. Moreover, FRODA results are in good agreement with those obtained using MD and ANM, both of which are commonly accepted methods.

In the present study, we examine how effectively the essential motions of a protein are sampled by each of the three approaches considered here, how well the identified essential motions compare across the methods, and whether there are significant differences for different structural classes of proteins. We selected four sample proteins chosen from distinct structural classes (SCOP) [15]. The proteins selected do not possess any known multiple conformational states that describe large-scale structural rearrangements within the native state basin, so that all the employed methods should be able to explore the native state basin well. To explore conformations by transitioning over energy barriers that separate different conformational states associated with large-scale structural rearrangements within the native state is a much more difficult problem. The FRODA approach has recently been modified to handle finding potential pathways between a pair of conformational states using targeting [13]. However, to our knowledge, even for single domain proteins FRODA has not been benchmarked against other commonly used methods (such as ANM and MD). Therefore, we limit our model comparisons on single domain proteins where all three methods should work well.

We identified the essential motions of the proteins by performing PCA on the trajectories obtained from MD and FRODA, and from the normal mode analysis of ANM. The top twenty modes were chosen as subspaces for model-to-model comparisons. The displacement vectors from each simulation were projected onto each of the model mode spaces to see how well each model’s collective modes capture the simulated displacements and to determine whether there is preferential clustering. Essentially, we use the collective modes defined by each of the models as a metric for all displacements generated by the other models to determine if there are regions of conformational space that are accessible to one model but not another. For a final analysis involving experimental data, atomic displacement vectors derived from many different pdb structures showing different conformational states of myoglobin are compared to the computationally generated native state conformational ensembles. We projected the displacement vectors derived experimentally onto each of the three models most relevant modes (i.e. lowest frequency from ANM or greatest variance from PCA) to determine how well a small subset of model modes capture the conformational space explored experimentally, and vice versa, we compare the experimental mode space with the mode spaces derived from the three models. Within this paper we focus primarily on the results for myoglobin (pdb code 1A6N), and corresponding results for the other three proteins in different SCOP classes are provided in Supplementary Material that lead to the same conclusions.

Our analysis reveals that ANM, MD and FRODA access similar sets of large-scale motions intrinsic to the protein, albeit each method is based on very different assumptions. For example, MD is the only method of the three considered here that allows for native contacts to break and non-native contacts to form. Nevertheless, the intra-consistency among FRODA runs, and the observed inter-consistency with ANM and MD all point to the conclusion that non-native contacts are not essential for the elucidation of the gross features of single domain protein dynamics of the native state. Ultimately, it is the latent information in the structure itself that is essential for the emergent dynamics. Each approach accesses the same structural information with its own specific assumptions, yet subjected to the same physical laws. Given this ultimate constraint, it is satisfying that significant mode space similarity is demonstrated among the three modeling paradigms.

Methods

Anisotropic Network Model (ANM)

ANM calculations were done using the Anisotropic Network Model web server:

All runs were performed online at http://ignmtest.ccbb.pitt.edu/cgi-bin/anm/

Each analysis used a distance cutoff of 15 Å and a weighted C—C distance of 2.5 Å.

Molecular Dynamics (MD)

MD trajectories were downloaded [16] from www.Dynameomics.org

The methodology used to generate the trajectories is available at the same URL.

Geometrical Simulation (FIRST/FRODA)

FRODA trajectories were created using FIRST/FRODA version 6.2:

Software downloaded [13] from http://flexweb.asu.edu/

For each protein, trajectories were created using the same command line^* for a variety of constraint assignment parameters (defined by the “x” and “y” variables within the command line^*) that modify how many of the possible constraints in the input structure are used for the RCD. Each trajectory was obtained by selecting every 50^th structure in a simulation that generated 100,000 structures, yielding 2,000 sample structures. The variations span the spectrum of rigidity from highly over constrained, with all H-bonds modeled as distance constraints, to completely flexible with no H-bonds modeled as a distance constraint. The two parameters varied were the number of H-bonds, controlled by the H-bond Ecutoff (the “x” variable), and the number of hydrophobic tethers, controlled by the hydrophobic (HP) tether cutoff (the “y” variable) using the default and recommended “H3” hydrophobic tether assignment scheme. Note that when using FIRST/FRODA it is expected that the H-bond Ecutoff will vary across proteins, but normally the hydrophobic interactions are left at the recommended default values. In this work, we also explored modifying the HP distance constraint cutoff criteria in addition to the H-bond Ecutoff. Within the H3-hydrophobic rules, distances between certain pairs of carbon atoms are restrained using inequalities that are implemented as a half harmonic potential function. That is, if the distance between a pair of carbon atoms exceeds a maximum value (an example command line specification of this value is given as –ph_tol=2.50 in angstroms), then a restoring force is applied to reduce their separation. In the FRODA setup HP tethers do not reduce the number of independent degrees of freedom (iDOF) within the network. However, in addition, if the distance between a pair of carbons atoms is less than a minimal value (an example command line specification of this minimum value is given as –c=0.50 in angstroms), two distance constraints are placed between these two carbon atoms, where each carbon atom together with their respective covalent bonded atoms are modeled as a rigid body.

Displacement Vectors (DV)

The input structure used to derive each trajectory was also used as a reference to construct a set of displacement vectors by subtracting it from each of the generated output structures.

Principal Component Analysis (PCA)

PCA was done using the covariance matrix of the alpha carbon positions from each trajectory. Since the objective was to identify global collective motions, the sensitivity cutoff for PCA was coarse-grained by using only the alpha carbons. The structures comprising each trajectory were appropriately aligned to remove overall translation and rotation from the intrinsic atomic fluctuations prior to the PCA [17]. After diagonalization of the covariance matrix, the top 20 PCA modes were selected for subspace comparisons and the projection of displacement vectors.

Overlaps between Displacement Vectors and Modes by Normalized Inner Product (NIP)

The overlap between a displacement vector and a principal mode was determined using the inner (dot) product of the two vectors, normalized by their respective magnitudes. The NIP as defined here is the same quantity as the overlap between two vectors as defined by Sanejound [18], where O_ij represents the overlap of the i^th vector u_i defined in subspace one with the j^th vector v_j defined in subspace two.

$$O_{ij}=\frac{\left|u_i\times v_j\right|}{\Vert u_i\Vert \Vert v_j\Vert }$$ Equation 1

Comparing Subspaces by Cumulative Overlap (CO)

A cumulative overlap was calculated to assess how well a given model eigenvector is represented in another model’s principal motion subspace. This value was obtained by successively determining the overlap between the given eigenvector of one model and each of the eigenvectors in the other model’s subspace [19].

$$CO(k)={\left(\sum _{j=1}^k{O}_{ij}^2\right)}^{\frac{1}{2}}$$ Equation 2

For our analysis, k was always equal to twenty and O_ij represents the overlap of the i^th vector in subspace one with the j^th vector in subspace two. Since this calculation is not symmetric, the analysis was performed twice, first for vectors in subspace one on subspace two, second for vectors in subspace two on subspace one. The average of these two values for each vector was reported as the average CO.

Comparing Subspaces by Root Mean Square Inner Product (RMSIP)

The mode subspaces were globally compared using RMSIP [20,21].

$$\mathit{RMSIP}(I,J)={\left(\frac{1}{I}\sum _{i=1}^I\sum _{j=1}^J{\left(u_i·v_j\right)}^2\right)}^{\frac{1}{2}}$$ Equation 3

In our analysis, I and J were both equal to twenty, u_i is the i^th vector in subspace one, and v_j is the j^th vector in subspace two. RMSIP scores range from zero for mutually orthogonal subspaces to one for identical subspaces. The RMSIP score is effectively the correlation between the vectors in subspace one with the vectors in subspace two. A value of 0 or 1 respectively indicates no or full correlation. A score of 0.70 is considered an excellent correspondence while a score of 0.50 is considered fair [20]. We note that the RMSIP score is dependent on the size of the subspaces compared, such that for a given RMSIP score the result is more significant for larger subspaces compared to smaller subspaces. This size dependence is not encountered when using principal angles otherwise known as canonical correlations (defined next).

Comparing Subspaces by Principal Angles (PA)

Two mode subspaces F and G with dim(F) = dim(G) = 20 were assessed using principal angle analysis, also called canonical correlations [22,23]. These angles were obtained by computing the singular value decomposition (SVD) of the matrix, M, constructed from the product of the two orthonormal bases Q_F and Q_G, where $M=Q_F^T{Q}_G$ and ${(Q_X)}_{ij}=x_j^i$ where $x_j^i$ is the j-th component of the i-th normalized eigenvector defining an orthogonal direction in subspace X. Following the process of $\mathit{SVD}(Q_F^T{Q}_G)$ produces 20 singular values {σ_k} where the k-th principal angle (PA) is given by θ_k = arcos(σ_k). PA values within the small angle approximation (< 23°) are considered excellent for similarity, while a value of 90° indicates orthogonality or complete dissimilarity. A value of 45° corresponds to about a 71% correlation. For equidimensional subspaces, the largest PA is related to the geometric notion of distance, where the “gap” between the subspaces is:

$$\mathit{gap}(F,G)=sin({\theta }_k)=\sqrt{1-{cos}^2({\theta }_k)}$$ Equation 4

In our analysis, the first principal angle θ₁ provides the most stringent measure of subspace similarity as it indicates how well the two spaces can be aligned. The value of k for which the principle angles {θ_k} surpass the small angle approximation informs as to how many principal axes the subspaces share with a high correlation. Monitoring the increase in PAs provides a quantitative way to characterize the relevant size of subspaces when intra consistency is compared.

Datasets

Data sets were constructed for each of the four proteins investigated in this paper:

• PDB ID: 1A6N [24] deoxy-myoglobin: SCOP class α, 151 residues

• PDB ID: 1WIT [25] twitchin immunoglobulin: SCOP class β, 93 residues

• PDB ID: 1UBQ [26] ubiquitin: SCOP class α+β, 76 residues

• PDB ID: 1YPI [27] triosephosphate isomerase: SCOP class α/β, 247 residues

Each data set contained the following:

1. One MD simulation trajectory obtained using explicit solvent at 298 K for at least 31 ns consisting of 2,000 structures [16].

2. 31 FRODA trajectories each consisting of 2,000 sample structures each, derived from simulation runs using a H-bond Ecutoff range of 0.0 to −10 kcal/mol and a HP tether cutoff range of 0.0 to 0.5 Å

3. PCA modes from each of the 31 FRODA trajectories.

4. One set of PCA modes derived from the combination of eight individual FRODA runs using a H-bond Ecutoff range of 0.0 to −5 kcal/mol and a HP tether cutoff of 0.5 Å. This set is referred to in the analysis as FRODA-8.

5. One set of PCA modes derived from the combination of twenty individual FRODA runs using a H-bond Ecutoff range of 0.0 to −5 kcal/mol and a HP tether cutoff range of 0.0 to 0.5 Å. This set is referred to in the analysis as FRODA-20.

6. Twenty-one sets of normal modes derived from ANM analysis on the original structure and twenty FRODA-generated structures.

7. Additionally, the 1A6N dataset contained a group of 95 structures of myoglobins with sequence identity > 98.7% and RMSDα < 1Å to 1A6N. These PDB codes are listed on the last page in the Supplementary Material.

Results and Discussion

The Dynamical Models and Essential Dynamics

FIRST uses a set of parameters that determine how constraints are identified, which is ultimately responsible for outcomes in determining the number of iDOF and the predicted rigid and flexible regions of a protein. Based on the RCD, a geometric simulation using FRODA is very efficient. The advantage of FIRST/FRODA is that the generation of output structures is by some comparisons four orders of magnitude faster than MD. However, this tremendous gain in speed comes at the price of model-dependent limitations. Only intra-molecular interactions are modeled (no solvent molecules are considered), and the set of distance constraints is chosen before the geometrical simulation begins. The geometrical simulation is an athermal simulation, where atoms are randomly moved without creating any atomic clashes while the RCD remains fixed for the entire simulation. In such a scenario, a substitute for temperature, or pseudo temperature, is based on the energy cutoff used for selecting H-bonds [28,29]. Conversely, the identified rigid and flexible regions can fluctuate between frames within a MD simulation.

Both FRODA and MD produce datasets composed of multiple structures that capture conformational changes and latent cooperativity in the high dimensional configuration space of the protein. In order to identify those conformational changes and visualize the latent cooperativity, a reduction of dimension is performed by the application of principal component analysis (PCA) [30–32] to the atomic fluctuations of the alpha carbons in the protein. The application of PCA to MD trajectories has a long history and the computation of the essential dynamics of a protein is now well-accepted [33,34]. PCA transforms a set of correlated variables in the original space to a new set of variables that are uncorrelated, similar to normal modes [19]. Furthermore, the original data may be projected onto a small set of principal components that retain a large fraction of the original information, even though the data is represented in a low dimensional subspace. The reduction in dimension can be tremendous, moving the data from a space of tens or hundreds of thousands of variables to one that typically contains less than twenty.

Conformation and Residue RMSD for MD and FRODA

Both MD and FRODA generate trajectories that sample the native basin of a protein when provided a structure. As illustrated in Fig. 1A for myoglobin, the conformational rmsd for all four proteins investigated indicate good equilibration in exploring the native state conformations in both methods. The MD run was performed at 298K, while different H-bond Ecutoff values and HP parameters were used for FRODA. As more H-bond constraints are removed in the geometrical simulation (FRODA), qualitatively similar results are obtained with progressively larger rmsd. The comparisons given in Fig. 1A show the correspondence between MD and FRODA. The amount of mobility that the residues experienced in the MD simulations is bounded by the FRODA trajectories using H-bond Ecutoffs between −1 and −3 kcal/mol. In between this range, there exist a H-bond Ecutoff that yields results with high similarity between the MD and FRODA runs, where the residue rmsd is qualitatively consistent (Fig. 1B) and robust (virtually identical) distributions in residue rmsd (Fig. 1C) are generated in both cases. It is important to note that even for the most similar case, there is not a one to one correspondence between the two methods because MD allows interactions (both native and non-native) to fluctuate while FRODA keeps the number and identity of all native interactions initially modeled as distance constraints fixed (or constant) throughout a simulation run. The similarity and differences between the residue rmsd generated by MD and FRODA is shown in Fig. 2 as cartoon representations at the special H-bond Ecutoff that yields maximum correspondence. It is evident that the overall similarity is outstanding, although some key differences within loop regions and helices are frequently detected. These differences are not surprising, as at no time during a FRODA simulation is solvent taken into account, and there is no ability to form non-native contacts.

Figure 1.

Conformational and residue RMSD from MD and FRODA runs using multiple Ecutoffs are compared for myoglobin (pdb code 1A6N). Figure 1A (Top) Conformation RMSD. Figure 1B (Middle) Residue RMSD. Figure 1C (Bottom) The distribution of residue RMSD values across the protein for MD and the most similar FRODA run using an Ecutoff of −2 kcal/mol.

Figure 2.

Cartoon representations of four proteins colored by residue RMSD using FRODA runs (right panels) with an Ecutoff to produce maximum similarity with MD simulation (left panels). Panels A1 and A2 show myoglobin (pdb code 1A6N). Panels B2 and B3 compare twitchin (pdb code 1WIT). Panels C2 and C3 compare ubiquitin (pdb code 1UBQ). Panels D1 and D2 compare triosephosphate isomerase (pdb code 1YPI). The cartoons are rendered by Pymol (the PyMOL Molecular Graphics System, Version 1.2, Schrödinger, LLC).

The level of conformational rmsd can be varied by changing temperature in MD or the H-bond Ecutoff in FRODA. As demonstrated in Fig. 1, as the H-bond Ecutoff is lowered, the effective temperature is raised and the physicality (or lack thereof) of the simulation for biological conditions must be considered. For example, using a H-bond Ecutoff of 0.0 kcal/mol predicts a globally rigid protein that is severely over-constrained while a H-bond Ecutoff lower than −5 kcal/mol erroneously predicts the protein to be extremely flexible characteristic of an unfolded state. This situation suggests that when using FRODA, there exists a range of physicality (ROP) for which the conformational ensemble that is generated can be considered valid. Although the precise range of the H-bond Ecutoff may vary between proteins, values between −1 kcal/mol and −3 kcal/mol provide a safe ROP, which was demonstrated by each of the 4 proteins studied here. While both H-bonds and HP constraints reduce the number of iDOF, the H-bond constraints are more plentiful. We find that acceptable values for the HP parameters are broad, and the FRODA default values work well in all cases. We include the results of a variety of HP parameter variation for completeness of our analysis. It is worth noting that the removal of all HP tethers is non-physical and yields overly flexible structures. Presumably a minimum number of tethers are necessary, but due to the insensitivity of this parameter range, we focused on the H-bond criteria, which is the usual way to control the degree of flexibility in the structure. These observations were shared across all proteins studied. No differences in dynamics due to tether parameter adjustments were detected because of differences in beta sheets or alpha helices.

Crosslinking patterns in the H-bonds and the spatial distribution of both HP tethers and HP constraints are dependent on secondary structure. Nevertheless, the FRODA parameters that support a ROP are found to be insensitive (if not independent) to local secondary structural motifs in all the proteins studied here. Since the HP interactions are more often modelled as distance inequalities, it is expected there will be less sensitivity in HP parameters to secondary structures than the H-bonds. As described below, the existence of this ROP was verified by analyzing the generated mode spaces using a wide range of H-bond Ecutoffs and HP parameter variation that control the assignment of constraints/tethers.

One of the most interesting results from this work is that PCA modes generated from a large range of FRODA runs (using different user-defined parameter settings) are consistent in spanning the same subspace describing low frequency and large-scale conformational changes of the protein. It seems counter-intuitive that simulations with very large differences in rmsd could yield principal motions that are quantitatively similar. That is, once the outliers were identified (H-bond Ecutoffs that are greater than −0.50 kcal/mol or less than −5 kcal/mol) all FRODA runs produced robust results using PCA. Apparently, reducing the number of native interactions modeled as distance constraints in FRODA allows exploration of conformations with larger amplitudes of atomic displacements, but the essential dynamics (described by the eigenvectors or modes, not the eigenvalues) remain markedly consistent over a large range in flexibility/rigidity. Therefore, multiple H-bond Ecutoffs within the ROP can be determined by plots like Fig. 1 to identify the FRODA runs that produce a mean value in conformational rmsd in the range of 1.25 to 2.75 Angstroms. On such a plot, a non-physical over-constrained protein shows a “flat line” in which expected backbone motions in loop regions are absent, while the non-physical under-constrained proteins show unfolding. These rmsd-based criteria for a range of physicality for FRODA simulations are supported by our subspace analysis of those simulations.

PCA for MD and FRODA

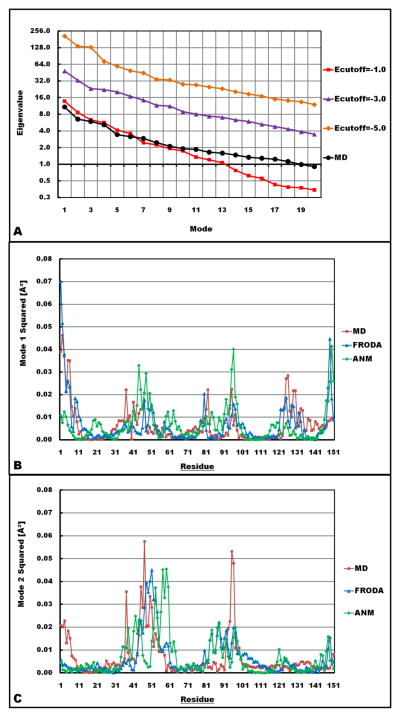
Another quantitative comparison between MD and FRODA using PCA is given in Fig. 3A. The trace of the covariance matrix, or sum of the eigenvalues of all PCA modes, quantifies the total mobility of the protein during a simulation. Sorted from largest to smallest, the scree plot shows that only a relatively small number of PCA modes capture most of the mobility. Clearly, increasing the number of iDOF by lowering the H-bond Ecutoff in FRODA leads to a dramatic increase in the mobility ascribed to each PCA mode as shown in Fig. 3A. The top two PCA modes by residue shown in Figs. 3B–C show similarities and differences in the modeling paradigms. While there are qualitative similarities, a number of regions exist where individual residue motion is differentially assigned. This comparison identifies the regions of the protein that each model addresses in distinct ways, where the key differences arise due to the context of the particular model assumptions.

Figure 3.

Comparison of eigenvalues and the top two modes. Figure 3A (Top) On a semi-log scale the rate of decay for the eigenvalues as the PCA modes increase is shown for a selection of FRODA runs and the MD run. Figure 3B (Middle) Comparing mode 1 from the PCA of FRODA and MD and from ANM. The FRODA modes are derived from the combination of eight runs using a range of Ecutoffs between 0 and −5 kcal/mol (FRODA-8). Figure 3C (Bottom) Comparing mode 2 for the same three models.

When comparing the MD run that is most similar to the FRODA run (using an Ecutoff of −1 kcal/mol) in terms of raw variance of atomic positions, it is seen that the decay of eigenvalues from the MD run is similar to the FRODA run over the first ten modes. However, as the number of modes increase beyond 10, the eigenvalues of the MD simulation rise in comparison to this FRODA run. A FRODA run performed using an Ecutoff of −2 kcal/mol gives rise to a scree plot that is slightly above the MD results, but again with an overall faster rate of decay (data not shown for clarity). This comparison indicates that for this particular MD simulation, it does not probe as much large-scale conformational change compared to the FRODA runs. On the other hand, since FRODA uses a simple force field to execute geometrical simulation, it may allow too much conformational accessibility by ignoring high-energy barriers. In an analogous way, the applied distance constraints (based on native structure) in FRODA are serving as high-energy barriers. The more constraints modeled, the less conformational space will be available. When FRODA employs large number of constraints, many protein motions get frozen out resulting in a decrease in amplitude of motion (variance), and in this case, MD simulation (at room temperature) samples more conformations.

Once a scree plot is obtained, it is desired that the mode eigenvalues decay rapidly allowing most of the motions to be reconstructed using the reduced dimensional space. Depending on FRODA parameters, the MD eigenvalues can decay faster or slower than the FRODA eigenvalues. In cases where the scree plot decays very rapidly, it may be inferred that the lowest few modes are sufficient to describe biologically relevant information. However, as in the cases shown in Fig 3A, it often happens that the scree plot decays gradually without a distinct kink (as the name scree implies). In these cases, one must make a selection based on the relative ratio of the smallest eigenvalue used compared to the largest eigenvalue. A ratio of 0.1 will usually suffice. A common approach is to look at the cumulative variance. However, in general it is not possible to set an a priori fixed number such as 85% for the cumulative variance. The reason is that a protein may intrinsically have large-scale motions contained in just a few modes making up a relatively small fraction of cumulative variance, and to reach some arbitrary predetermined value will necessarily require including many modes associated with motions that are not large-scale. In other words, the ratio of how fast the eigenvalues decrease using a scree plot serves as an appropriate guide for selecting the dimensionality to use. In this work, we selected 20 dimensions in all cases to facilitate the uniform comparative analysis across all FRODA runs, MD simulation and ANM. Based on the scree plots, the eigenvalue of the 20^th mode decreased by more than 90% in all cases. Subsequent subspace comparisons showed less than 20 dimensions (about 12 to 14) adequately describes the majority of the overlap between FRODA runs and MD simulations. If a larger dimension is used initially (say 30) for the subspace comparisons the degree of subspace overlap can only increase. However, the practical disadvantage of working with higher dimensions is that the benefit in reduction of dimensionality is not as great.

Range of Physicality (ROP) for FRODA Simulations

When FRODA is employed, a ROP must be established by adjusting the selection rules that determine which interactions are modeled as distance constraints to obtain quantitatively reasonable conformational and/or residue rmsd as Fig. 1 shows. The ROP can be further quantified by the number of independent degrees of freedom per residue (iDOF/res), as determined by FIRST. In other related work, a range of [0.5, 1.2] for iDOF/res is considered appropriate for globular proteins under biological conditions [35–37]. Our FRODA analysis indicates that this range falls safely within a parameter set that generates a robust subspace analysis (explained below). For the proteins considered here, the onset of dynamical behavior showing unphysical characteristics (as being too rigid or too flexible) is only apparent when using a H-bond Ecutoff greater than −0.5 kcal/mol or less than −5 kcal/mol. This range is based on quantitative subspace comparisons between multiple FRODA runs, and also qualitatively identified by visual inspection of protein motion animations generated by FRODA. Quantitatively, it appears that even a wide disparity in the assignment of constraints, which yields very different flexibility/rigidity profiles, behave in a coherent and consistent manner in terms of large-scale, low frequency motions as determined by PCA mode extraction. Since coherent and consistent results are reliably obtained by using H-bond Ecutoffs between [−0.5, −5] kcal/mol, a recipe for best practices involves performing a number of runs within this range of H-bond Ecutoffs using FRODA default settings for hydrophobic interactions, and then comparing the individual runs for similarities to define the ROP. After this step, all runs within the ROP are combined to improve the statistical sampling of native conformations.

Initially we expected to identify an optimal Ecutoff per protein structure. Instead, we were surprised to find that the subspaces from the PCA analyses of different FRODA runs are virtually independent of Ecutoff over a broad range, which is also insensitive to the protein structure used. Nevertheless, it is important to note that the ROP does not have absolute boundaries applicable for all proteins. Rather, the ROP can shift depending on protein, and the resolution of the input structure. This latter dependence does not pose a problem however, because as presented here, the PCA analysis of a series of FRODA runs using different parameter sets provides a protocol for determining the ROP.

Projection of the displacement vectors on model modes

An important concern is how well dynamical simulation methods such as MD sample the configuration space of a protein. One approach to address this question is to project the displacement vectors obtained from a dynamical simulation onto its principal modes [4]. This method makes no assumptions about the underlying distribution and allows one to explore how well the actual simulation events project on the top modes. Moreover, if both the eigenvectors and displacement vectors are normalized, then the projections will all be in the range [−1, 1] due to the normalized inner product (NIP), allowing for intuitive and consistent comparison.

Fig. 4 presents the results for the projection of the displacement vectors on the FRODA-8 PCA modes. All the displacement vector projections from the FRODA-8 displacement vectors cover the combined FRODA-8 mode space much better than the MD displacement vectors. For the case of 0 H-bond Ecutoff, an ellipse emerges near the origin, which shows a very different signature than any of the other runs comprising the FRODA-8 group. Interestingly, this over constrained FRODA run produces a quasi simple harmonic motion, as revealed by the hyperdimensional ellipsoidal plot. The MD run shows as a much more confined clustering on the projection plot for FRODA-8 PCA modes 1 and 2 within the 95% confidence ellipse, but it does not coincide with most of the FRODA generated displacements. As a result, MD is probing a different type of motion, in a similar way that the highly over constrained FRODA run demarked by the ellipse near the origin is atypical. We can infer that in mode 1, MD is probing much less conformational diversity than FRODA. Nonetheless, beyond mode 1, there is an increasing degree of overlap in the conformatioinal space defined by high PCA modes where the atomic displacement amplitude is rapidly decreasing.

Figure 4.

The FRODA-8 and MD displacement vectors are projected on the PCA modes derived from the combined FRODA-8 ensemble. Confidence ellipses are drawn for 95%. Projections are made on modes: 1, 2 for 4A (top left); 2, 3 for 4B (top right); 3, 4 for 4C (bottom left), and 4, 5 for 4D (bottom right). In all cases, the FRODA-8 confidence ellipse contains the MD projections. The ellipse (indicated by the arrow) seen in the top left panel is the result from a FRODA run using an Ecutoff of 0.

Comparisons within two-dimenisonal projections depend on the two modes used to define a plane. Therefore, to get a better picture of the similarities and differences between the three models, in Fig. 5 we plot the displacement projections of the MD and FRODA simulations onto PCA modes obtained from MD. The distribution of the MD displacement vectors is tri-modal in the projection on modes 1 and 2, where FRODA and MD coincide within only one of the three “lobes”. This multimodality suggests that the MD simulation spends much of the run time in a few basins, some of which are not being sampled by FRODA. The reason for this is most likely that during the MD simulation, two slight rearrangements of the residues occurred. Because MD allows native contacts to break and reform, the result of these fluctuations is that the MD run is sampling beyond the native basin defined by the input structure. The evidence for this is that there were significant changes in the number of native and non-native contacts along the MD trajectory. Variations in the number and type of contacts explain the structural rearrangement resulting in the “lobes” seen in the plots. Using the MD modes as a metric, the FRODA runs intersect with a portion of the MD displacement vectors. Interestingly, the rapid containment that was seen in Fig. 4 for projections onto the combined FRODA modes is not seen in Fig. 5, showing there is still clear cluster separation in modes 4 and 5. For the other three proteins considered (see suplemental materials) the same behavior that the projections of MD conformations onto PCA modes from MD have lobes or densely popublated skewed regions that extend beyond that derived from FRODA. However, the separation in clustering of the projections seem to disapate faster for the other proteins (mode 3 or 4). Appearently, the reason why this effect occurs is because the minimum in the energy landscape of the protein according to the MD force field differs considerably from the native-crystal structure. This could be due to crystal contacts, for which FRODA is subject too, but in principle MD is not.

Figure 5.

The FRODA-8 and MD displacement vectors are projected on the PCA modes derived from the MD ensemble. Confidence ellipses are drawn for 95%. Projections are made on modes: 1, 2 for 5A (top left); 2, 3 for 5B (top right); 3, 4 for 5C (bottom left), and 4, 5 for 5D (bottom right). Note the tri-modality of the MD series in the projection on modes 1 and 2. In all cases there is a clear separation between the FRODA-8 and MD displacement vectors, with only an interface between the two clusters that exibits an overlap.

To complete the picture of displacement projections, we also consider projecting onto ANM modes. The ANM modes serve as a metric by which the range of dynamical motion can be effectively measured and compared between the two dynamical models. As is evident in Fig. 6, the FRODA displacement vector projections cover much more of the mode space defined by the top 20 ANM modes than do the MD displacement vector projections. Once again, in mode 1, it can be seen that FRODA and MD are sampling somewhat different dynamics, but the MD projections are nearly completely contained within the FRODA runs as early as mode 1. Based on the much greater coverage, FRODA appears to be probing the same dynamics that is captured using ANM. FRODA produced trajectories that covered much more conformational space than the MD simulation. We have compared the amplitudes of conformational dynamics by projecting the model displacement vectors on the modes. The FRODA subspace is larger in that it accomodates more of the dynamical displacements generated by MD. The distinction in the projections highlights the fact that the principal motions captured in the different models have some differences.

Figure 6.

The FRODA-8 and MD displacement vectors are projected on the ANM modes. Confidence ellipses are drawn for 95%. Projections are made on modes: 1, 2 for 6A (top left); 2, 3 for 6B (top right); 3, 4 for 6C (bottom left), and 4, 5 for 6D (bottom right). The FRODA-8 confidence ellipse nearly completely contains the MD space in all cases.

Comparison of Model Mode Spaces

The question of how to compare low dimensional subspaces that are derived from PCA or ANM has been answered in a number of ways. That the overlap between two vectors can be determined by the inner product of those two vectors is generally well known, however, the overlap between subspaces of high dimensional vector spaces is less intuitive. One approach to measuring the co-incidence of two subspaces is to assess how well each vector in one subspace overlaps all the vectors in the other subspace. This cumulative overlap (CO) method quantifies how well all of a given subspace captures a given vector [19]. Another approach is to determine an average of the inner products of all the vectors in both subspaces. Such a method provides insight into how well each vector in one subspace aligns globally with the vectors in the other subspace, and it is called the root mean square inner product (RMSIP) [20,21]. A more detailed assessment of the interpenetration of two high dimensional subspaces can be made by measuring principal angles and the corresponding principal vectors that describe how one subspace can be rotated/scaled for optimal alignment with the other.

In the comparison of two subspaces, we start with a set of normalized eigenvectors (either from the covariance matrix or from the Hessian matrix) that define subspaces embedded within the high dimensional space equal to 3 times the number of residues in the protein (only alpha carbons were used in the covariance matrix). The process of finding principal angles involves computing the singular value decomposition (SVD) of a matrix of overlaps (see Methods). The SVD factorization of the matrix of overlaps (inner products) yields a matrix of vectors (left principal vectors) that describe a high dimensional rotation, a diagonal matrix of singular values that describe a scaling, and another matrix of vectors (right principal vectors) that describe another rotation. In this work, the SVD process is applied to a 20 by 20 square matrix so that the right and left vectors describe the same rotation. The singular values are the cosines of the principal angles and are ordered from largest to smallest. The whole process is an optimization that determines the best possible alignment between the two subspaces. The interpretation of a PA for two 2-dimensional subspaces within a 3-dimensional space is straightforward, because two planes with different orientations that pass through the origin always coincide or intersect along a single line. In this latter case, the first PA is zero and the second is the acute angle between the two planes. For 2-dimensional subspaces within a 4-dimensional space the situation is more complicated because the two planes may intersect only at a single point (the origin), yielding two non-zero PA. Although geometric visualization fails for 20-dimensional subspaces within a 600-dimensional space, the notion of an angle between two axes remains comprehensible. While each individual PA ranges from 0 to 90 degrees, it is often useful to compute a single value for the angle between the two subspaces, similar to the RMSIP value. The geodesic distance between the two subspaces can be determined by calculating the Euclidean norm of the vector of principal angles. This means that the largest angle between two M-dimensional subspaces derived from a N-dimensional space is not ninety degrees, but rather $\sqrt{M}·90°$ for M < N and N > 3, making the maximum possible angle between two 20-dimensional subspaces for all the proteins considered here equal to 402.5° [38,39]. The largest PA may be interpreted as the “gap” between the subspaces, so determining for which mode the angle between the two spaces leaves the small angle approximation (less than 23 degrees) indicates the number of modes that can be considered similar.

The SVD process that generates the mapping to align two subspaces always orders the set of principal angles from smallest to largest. When a PA is small in the sense that the sine of the angle is approximately equal the angle when measured in radians, this indicates that there is a high degree of overlap of the two subspaces relative to a particular rotation axis. The individual value of a PA is viewed as small or large based on the value of PA itself, independent of the dimension of the spaces being compared. In higher dimensions there are more principal angles, and typically the greatest PA will be close to 90 degrees indicating the part of the subspaces that are orthogonal. The entire set of principal angles gives a more critical assessment of how much space is in common between the two subspaces. Unlike RMSIP, which tends to increase with the size of the subspaces, the ordered list of principal angles quantifies where the increases comes from. For example, if comparing a 20 dimensional space, if the first 12 principal angles are small, and the last 8 principle angles grow rapidly, we know that the most congruent part of the two subspaces actually lives in 12 dimensions, which cannot be obtained from the RMSIP measure. Since multiple spectra of principal angles can lead to the same RMSIP, the former is a more powerful method for analyzing the similarity of subspaces. It is worth noting that the average of the cosines over all the principal angles gives a qualitatively similar measure as the RMSIP. In summary, if a single number is desired to discriminate similarity, RMSIP is a good measure. The method of PA gives a much more critical assessment, and carries with it additional information within the principal vectors that inform on how the subspaces are spatially related.

Significant similarity was seen for all three models when the subspaces were compared using the RMSIP and PA metrics. There are no significant differences related to the SCOP class of the protein (see summary results in Fig. 9). When reviewing the displacement vector projections, we found that there were substantial differences between the methods in the first few modes as indicated by distinct cluster distributions. However, for all four classes of protein, the projection space derived from FRODA was greater than the mode projection derived from MD when the ANM modes were used as a metric, suggesting that the geometrical simulation samples more of the native basin than MD does. Additionally, a clear pattern is seen as the two dimensional mode spaces are defined by higher modes with increasing interpenetration of the projection spaces. This is to be expected, as the first few modes will be rather arbitrary and model specific due to statistical sampling and the nature of PCA to maximize variance in a descending fashion. This, in conjunction with the global measure of the RMSIP, is strong evidence for homogeneity within the two dynamical models.

Figure 9.

RMSIP, average CO, and first PA scores for model-to-model comparisons for each protein. Panels A1 – A3 (top row) compare ANM and FRODA (FRODA-8). Panels B1 – B3 (middle row) compare ANM and MD. Panels C1 – C3 (bottom row) compare FRODA to MD. Although there are quantitative differences for the four classes of proteins, they are not significant, and the general trends are the same. The error bars indicate plus and minus one standard deviation unit.

While it is known that the rigidity of a protein is very sensitive to the H-bond Ecutoff that is used in FIRST [14], we conclusively show here that there is no such high sensitivity for the essential motions derived from the RCDs using a wide range of H-bond Ecutoffs. Each individual run from FRODA was comparatively assessed by the different model mode spaces as shown in Fig. 7A, B. All the subspaces derived from H-bond Ecutoffs between [−1, −5] kcal/mol are essentially the same as measured by the RMSIP (Fig. 7A) and first PA (Fig. 7B) scores. Interestingly, variations in the number of hydrophobic tethers have almost no effect on either the RMSIP or first PA within the specified range of H-bond Ecutoffs. Taken together with the earlier analysis based on conformation and residue rmsds, this is strong evidence for a ROP within the regime of the geometrical simulation. Fig. 7C shows the intra-consistency within the FRODA and MD trajectories. The MD comparison shows that parts one and two of the trajectory are quite similar for the top eight modes with a RMSIP value of 0.81 while the FRODA run was consistent for the top seventeen modes (PA < 23°) with a RMSIP value of 0.94. This substantial difference may be the result of non-equilibration of the MD trajectory and lends credence to the critics of MD for statistical under-sampling problems. Fig. 7D shows the intra-consistency results for twenty ANM analyses. These comparisons of FRODA structures to the original pdb show a remarkable amount of similarity ranging from the top 13 to 17 modes with not a single RMSIP value below 0.89. Overall, this result suggests that due to the coarse-grained nature of the ANM, small perturbations of the structure do not substantially alter the normal modes obtained. This result provides additional evidence that the distance constraint perturbations that are used by FRODA remain within the native basin of the input structure.

Figure 7.

Consistency of subspaces describing essential dynamics using RMSIP and PA. (Top 7A) RMSIP results for individual FRODA runs compared to the four model modes: FRODA-8, FRODA-20, ANM, and MD. (Upper-middle 7B) PA results for individual FRODA runs to the four model modes; the horizontal axis indicates the run parameters that were used in each case. (Lower-middle 7C) Inter-consistency is found between FRODA and MD runs using the top 20 PA, with RMSIP values parenthetically shown. (Bottom 7D) Consistency in results for 20 ANM modes derived from 20 structures produced during a default run of FRODA. In 7C and 7D, a level line is drawn for the PA value 23°.

Resolving more detail within the twenty dimensional subspace defined by the modes of different models is achieved by examining the entire set of 20 PAs and the average COs. PA values of less than 23 degrees are considered to be within the small angle approximation and suggest excellent similarity. Fig. 8 shows the comparison of the model mode subspaces using the metric of PA, with RMSIP values shown parenthetically in the legend. From Fig. 8A, it is clear that the most similar mode subspaces are those from FRODA-8 and FRODA-20 with an RMSIP score of 0.93 and PAs less than 23° for the top fifteen modes. The next most similar mode subspaces are from FRODA and ANM. These comparisons yield a RMSIP value near 0.75 and have PAs within the small angle approximation for six modes. The mode subspace comparisons between ANM and MD and MD and FRODA are very similar, each having an RMSIP value between 0.5 and 0.6 and PA values less than 45° for the top five modes. While these angle values are not within the small angle approximation, they do indicate a good amount of similarity, commensurate with the good RMSIP score.

Figure 8.

Model-to-Model Subspace Comparisons for the 4 Proteins Investigated. Figure 8A shows the results for 1A6N using the top 20 PA, with RMSIP values shown parenthetically in the legend. Figures 8B, 8C, and 8D similarly show the results for 1WIT, 1UBQ, and 1YPI respectively. The level line is drawn for PA value 23° in all four panels.

The RMSIP scores between the model mode subspaces are shown for the four proteins investigated in Fig. 9 (left column). The average cumulative overlaps (for the entire set of twenty modes) between the model mode subspaces are shown in Fig. 9 (middle column), and the first PA results are likewise shown in Fig. 9 (right column). Again, it is clear that the ANM and FRODA mode subspaces are best able to capture each other’s essential motions. This was especially evident when looking at the top ten modes where the average CO remains greater than 0.70 (not shown). Additionally, ANM to MD as well as MD to FRODA maintain an average CO greater than 0.50 for the top twelve modes (not shown). While not excellent, these values parallel the results seen in Fig. 8 and indicate a substantial amount of compatibility between the essential motions contained in these subspaces. Similar results were found for the other three SCOP classes of protein as shown in Fig. 9, with the RMSIP between FRODA and MD within the range of 0.51 to 0.63, and the RMSIP between ANM and FRODA within the range of 0.69 to 0.78 for all four SCOP classes. To put these values in perspective, the RMSIP between the FRODA-8 and FRODA-20 modes spanned the range of 0.64 to 0.93 over the four studied proteins, indicating that the inter-model comparisons were on par with the intra-model comparisons. For all four classes of proteins investigated, the ANM to MD RMSIP values were the lowest, spanning the range of (0.45 to 0.57). This result shows that ANM and MD are the most divergent of the three models investigated here. As Fig. 9 shows, there are no significant differences between the four proteins based on SCOP classification.

Projection of experimental structures on the model modes

An important consideration beyond the model-to-model comparisons that have been performed is how well are actual experimental structures accommodated by the three different models. To address this question, a 20-dimensional subspace was derived from the experimental dataset of myoglobins, and compared to those obtained from each model. We are specifically assessing how well the 3 models under investigation were able to access the set of experimental structures given only the initial structure. Figs. 10A and 10B show the projection of the experimental displacement vectors onto the model modes. In both panels, it is evident that the ANM mode space captures the experimental displacements best, with FRODA doing almost as well in terms of both the size of conformational space defined by the top three modes and the significance of the overlaps generated therein. The MD based PCA mode space does significantly worse in terms of the amount of conformational space covered and fails to yield any significant overlap to the experimental displacements. These results are echoed in Fig. 10C showing the RMSIP values of ANM and FRODA mode subspaces to the experimental mode subspace are about 0.60 while the RMSIP value of the MD mode subspace to the experimental mode subspace is only 0.44, a significantly lower result. Taken together, these results indicate that both ANM and FRODA are able to capture the majority of the displacements seen in the experimental structures, while MD captures significantly less of the displacements.

Figure 10.

Experimental and model subspace comparisons. Projection of the experimental displacement vectors on model modes 1, 2 (Top 10A) and on modes 2, 3 (middle 10B). The PA results from comparing the experimentally derived mode space to the model mode spaces, with the RMSIP values shown parenthetically in the legend (bottom 10C). The level line is drawn for PA value 23° in 10C.

Conclusions

The existence for a range of physicality using FRODA has been demonstrated in this work for the first time. For the four proteins studied here: We established that the default settings for hydrophobic tethers (rule H3) combined with a H-bond energy cutoff between −1 kcal/mol to −3 kcal/mol is robust. For much larger proteins, the H-bond energy cutoff range may shift slightly lower because the decrease in surface to volume in larger proteins gives slightly higher density of H-bonds. More importantly, the range of physicality can be established on a case-by-case basis using the protocols developed here. Namely, an all-to-all pairwise subspace comparison of multiple FRODA runs using the Root Mean Square Inner Product (RMSIP) and the Principal Angle (PA) metrics to identify the range of physicality. All FRODA runs that fall within the range of physicality should then be combined, and individual runs can be further compared with respect to a common vector space derived from PCA on the combined dataset. In particular, the PA metric provides the most mathematically precise and sensitive measure of vector subspace overlaps. Therefore, we note that the application of PA has much broader implications in the analysis of molecular dynamics, and other types of statistical data routinely encountered in bioinformatics and other fields.

We investigated three models, each based on very different assumptions concerning how to translate the latent information of a protein structure into essential motions within the native basin. Despite very different assumptions in their approach, all three models share marked consistency in the subspaces that describe the greatest fluctuations. The subspaces derived from ANM using a selection of structures obtained from a dynamical trajectory are robust as measured by RMSIP (> 0.85) and first PA (< 10°). Moreover, the subspaces derived from FRODA are robust across a broad range of H-bond energy cutoffs and hydrophobic tether definitions. MD trajectories are as much consistent to ANM and FRODA results, as it is consistent against itself with respect to using PCA on partial statistics. The subspace defined by an experimental set of mutant structures is well covered by both FRODA and ANM. Being less covered by MD clearly indicates longer simulations are required.

The structural basis for observed motions within single domain proteins or for proteins that do not exhibit large-scale structural rearrangement via conformational states separated by an energy barrier can be understood within the scope of a coarse-grained view of protein dynamics. The input structure imparts the information needed for the construction of a dynamical vision of the protein contained within a small subspace. However, there are differences regarding the resolution of the motions and comparing individual modes. Which model to employ will depend on what one wishes to optimize. MD allows the underlying structure to change and thus can sample beyond the native basin defined exclusively by the input structure. However, for this advantage to be fully realized very long simulation times are required. The time needed to run an all-atom geometric simulation (FRODA) on myoglobin that generates 100,000 output structures is a few hours on a modern desktop computer, compared to several seconds for ANM. On the other hand, FRODA allows one to break free of the required harmonic limitation imposed by ANM, while the choice of runtime parameters is non-critical. In other works [40,41], we have used FRODA to explore native state dynamics for myosin V, which is a multistate protein, because it gives the most information about the essential motions within a native basin for the least resource cost. Our experience using FRODA shows promise for extending its ability to efficiently explore conformation space for a given set of constraints. Nevertheless, without using targeting, finding large-scale motions between distinct conformational states is a much more difficult problem that needs to be solved. Looking toward future applications, we are currently working on a method that enables FRODA to break and reform constraints, including non-native constraints, in order to find the pathways between distinct conformational states without using targeting.