Abstract
Thermodynamic stability in polypeptides is described using a novel Distance Constraint Model (DCM). Here, microscopic interactions are represented as constraints. A topological arrangement of constraints define a mechanical framework. Each constraint in the framework is associated with an enthalpic and entropic contribution. All accessible topological arrangements of distance constraints form an ensemble of mechanical frameworks, each representing a microstate of the polypeptide. A partition function is calculated exactly using a transfer matrix approach, where in many respects the DCM is similar to the Lifson–Roig model. The crucial difference is that the effect of network rigidity is explicitly calculated for each mechanical framework in the ensemble. Network rigidity is a mechanical interaction that provides a mechanism for long-range molecular cooperativity and enables a proper treatment of the nonadditivity of a microscopic free energy decomposition. Accounting for (1) helix ↔ coil conformation changes along the backbone similar to the Lifson–Roig model, (2) i to i + 4 hydrogen-bond formation ↔ breaking similar to the Zimm–Bragg model, and (3) structured ↔ unstructured solvent interaction (hydration effects), a six-parameter DCM describes normal and inverted helix– coil transitions in polypeptides. Under suitable mixed solvent conditions heat and cold denaturation is predicted. Model parameters are fitted to experimental data showing different degrees of cold denaturation in monomeric polypeptides in aqueous hexafluoroisopropanol (HFIP) solution at various HFIP concentrations. By assuming a linear HFIP concentration dependence (up to 6% by mole fraction) on model parameters, all essential experimentally observed features are captured.
Keywords: network rigidity, cold denaturation, protein stability, cooperativity, helix– coil transition, free energy decomposition, mixed solvent, hydration
INTRODUCTION
Polypeptides make ideal systems of study both experimentally and theoretically. The α-helix to coil transition in polypeptides is a well-studied problem, with the thermodynamic driving forces described by Schellman1,2 almost 50 years ago. Despite the accumulated wealth of research on polypeptides, interest continues as experimental techniques become more sophisticated3–5 and computational methods6 – 8 improve, thereby providing ever increasing detailed information. Knowledge gained from these studies further scientific understanding of the general problem of protein stability.
It is well known that solvent conditions together with the polypeptide composition play an important role in the character of the transition. There are two extreme limits. First, the normal transition where an α-helix (hereafter simply referred to as a helix) at low temperature unravels into a disordered coil at high temperature. Second, the inverted transition where a disordered coil at low temperature will self-organize into a helix at high temperature.11 In mixed solvent conditions, it is at least conceivable that there can exist an experimentally accessible window of temperature in which both effects occur. That is, starting from low temperature and upon heating, the peptide will change conformation characteristics from being a disordered coil to helix, and then to disordered coil at still higher temperature.
The effect of a protein denaturing upon heating or cooling has been well established more than 30 years ago,12 where cold denaturation is more pronounced under mixed solvent conditions13 and/or high pressures.14,15 Privalov and Gill16 proposed the explanation that hydration (structured water) is the mechanism responsible for cold denaturation. At low temperatures, a high propensity for formation of structured solvent around various residues makes it favorable for the protein to open up, abandoning its native fold. The disordered coil conformations at low and high temperatures have distinctly different structural or topological characteristics. Experimental observation of cold denaturation in nonmonomeric polypeptides has been readily demonstrated,17–19 and it has also been observed in monomeric heterogeneous polypeptides in aqueous hexafluoroisopropanol (HFIP) as first reported by Andersen et al.20
Phenomenological models are often employed to describe helix– coil transitions in polypeptides.21 Most common is the Zimm and Bragg22 model (ZBM) and the Lifson and Roig23 model (LRM). Both models require a small number of parameters (typically 2 for ZBM and 3 for LRM) to describe a homogeneous polypeptide. They share two types of phenomenological parameters that are ascribed to a nucleation and propagation process. The ZBM and LRM have since been generalized to account for heterogeneous polypeptides and additional interactions.21,24 –26 In order to fit to a wide spectrum of experimental data, nucleation parameters must be chain-length dependent27 and propagation parameters temperature dependent.28 With the exception of sophisticated parameterization, to our knowledge, the underlying coarse grain statistical mechanical descriptions of the helix–coil transition have not changed since the end of the 1960s.29
In this article, a Distance Constraint Model (DCM) is introduced for homogeneous polypeptides based on a new paradigm related to the nonadditivity of free energy decomposition generally found in biopolymers.30,31 In many respects the DCM is similar to the ZBM and LRM. The principal difference is that network rigidity of the polypeptide is explicitly calculated and used in defining the free energy of a conformation. Qualitative discussion of rigidity and flexibility of polypeptides found in earlier works1 is replaced with mechanical calculations for conformational entropy. Better estimates are achieved by not over counting component entropies in rigid regions associated with redundant constraints. Mathematical details can be found in prior work.32 The main objective of this work is to show how network rigidity can be used to solve, in a computationally tractable way, problems arising from nonadditivity of component free energies.
Here, the DCM is extended further to include hydration effects in mixed solvent conditions. A minimal six-parameter DCM is constructed that is able to describe both normal and inverted helix– coil transitions in a homogeneous polypeptide chain. These parameters are physically motivated by considering a minimum set of molecular mechanisms that are invoked ubiquitously throughout the literature on protein stability. Moreover, the six parameters are taken to be independent of temperature and chain-length. It is shown that cooperativity and the nucleation process are described by the properties of network rigidity, without recourse to a chain-length dependent nucleation parameter. To demonstrate the potential usefulness of the DCM, CD measurements of Andersen et al.20 are described using two representative models (I and II) parameterized by fitting. An effective homogeneous chain is considered to keep the discussions simple, and to minimize the number of free parameters. Assuming the DCM parameters have a linear dependence on HFIP concentration within the range probed experimentally, excellent fits are obtained.
THEORY: DISTANCE CONSTRAINT MODEL
The DCM is a coarse grain statistical mechanical formalism32 that views a system as a network of constraints, and focuses on topological properties of that network. Each constraint corresponds to a type of interaction associated with a microscopic free energy. Assuming additivity in free energy components generally leads to inconsistencies in molecular systems exhibiting cooperativity. Hallerbach and Hinz33 pointed out that the second law of thermodynamics can be violated when modeling cold denaturation by simply adding positive conformational and negative hydrational entropy contributions. Errors in conformational entropy can be corrected by adding contributions only from independent entropic contributions.34 Nonadditivity of component free energies30,31 (enthalpy is additive but not entropy) is accounted for in the DCM by using network rigidity as an underlying mechanical interaction to identify the relevant independent constraints. The helix– coil transition in polypeptides is special only in that the partition function is calculated exactly using transfer matrices.
The ZBM and LRM are limited in scope to polypeptides, making theoretical generalizations to proteins difficult. Moreover, the nucleation parameter has been criticized in the literature due to misconceptions of its meaning,35 it being inherently nontransferable27 and its use in calculating partition functions yields ill-defined thermodynamic state functions.36 In the DCM, there are no nucleation or propagation parameters that are tied to a specific process. A nucleation process is an outcome of the network rigidity calculation. Chain-length dependence in the helix–coil transition is related to the correlation length of how far rigidity extends along the polypeptide. In application to other biopolymers such as proteins, a nucleation process will depend on the topology of how constraints are distributed, which includes details on the type of constraints present and how they are cross-linked. Most important, the DCM parameters should be transferable between systems modeled with the same set of constraint types.
Network Rigidity
Network rigidity37 is used here as an umbrella phrase referring to rigid clusters, overconstrained regions, flexible regions, and independent constraints within a generic mechanical bar-joint framework. The term generic38 implies that all bar-joint frameworks with the same topological distribution of constraints have the same rigidity properties independent of geometrical details. A mechanical description of this sort has been shown to predict flexible and rigid regions in proteins that correlate well with long-time biologically relevant motions.39,40 Follow-up investigations have suggested that folding pathways are related to network rigidity,41 and the folding transition is related to a rigidity transition.42 These works have been made possible because of recent developments in graph algorithms43– 48 that calculate network rigidity.
The algorithm to identify independent constraints recursively adds one constraint at a time to build a framework. A new constraint is redundant when added to an already rigid region and independent if it removes a degree of freedom. Although the numbers of independent constraints and degrees of freedom are unique, the specific assignment of which constraint is independent and where the independent degrees of freedom are located is not unique.49 The nonuniqueness of assignments is tantamount to the freedom one has in choosing generalized coordinates within a La-grange formalism. The success of a strict mechanical view of constraints is limited, however, because it is athermal (i.e., a mechanical T = 0 calculation).
The DCM32 generalizes the network rigidity calculations to finite temperatures by associating constraints with thermodynamic properties and taking into account statistical ensembles of mechanical frameworks. Constraints can be quenched or they can fluctuate. Covalent bonds are quenched, while hydrogen bonds, dihedral-angle interactions, and hydration shells are allowed to fluctuate. Each constraint corresponds to a microscopic free energy component that provides an enthalpy and maximal entropy contribution. Enthalpy and entropy estimates are made for all accessible topological constraint arrangements, each defining a subensemble of different coordinate geometries represented by a single generic framework. Total enthalpy is additive over the contributions from each constraint, but the entropy is nonadditive.30 The nonadditive property of component entropies derives from not knowing which degrees of freedom are independent or redundant. However, even if one adds entropy contributions from only the independent constraints as previously pointed out,34 this is not sufficient information because as discussed above, the identification of which constraint is independent is not unique.
Constraints are quantified as strong or weak based on their maximal entropy contribution. A (greater, lesser) entropy contribution implies a (weaker, stronger) constraint. Even feeble interactions having large component entropies are regarded as a constraint. The key aspect of the DCM is that stronger constraints are placed in the network before weaker ones. This preferential selection of independent constraints is implemented operationally as follows:
Sort all constraints based on entropy assignments in increasing order, thereby ranking them from strongest to weakest.
Add constraints recursively one at a time according to the rank ordering from strongest to weakest, identifying the independent constraints until the entire framework is completely rigid.
The condition that the framework is completely rigid after all constraints are placed ensures the set of constraint types is complete, in the sense that no internal degrees of freedom appear in any framework.
Total conformational entropy is calculated as a linear sum of component entropies associated with the preferential independent set of distance constraints. Redundant constraints do not change conformational entropy. This prescription is an approximation32 that appears adequate to accurately describe thermodynamic response functions obtained from experiments and computer simulation. Moreover, the DCM calculation is tractable and efficient. The DCM is mathematically well defined, having the property that the preferential set of independent constraints yields the minimum total conformational entropy compared to any other complete set of independent constraints (discounting ties). Physically, the essential idea is that weak constraints allow more conformational freedom than strong constraints. Stronger constraints take precedence in defining rigid structures because weaker constraints are more accommodating, thus providing a natural mechanism for enthalpy– entropy compensation. For example, if by some fluctuation a strong constraint breaks (such as a hydrogen bond or hydration shell) there will be a destabilizing gain in enthalpy, but also a compensating gain in conformational entropy as a weaker constraint substitutes.
Minimal DCM Describing Heat and Cold Denaturation
The DCM is similar to the LRM in that it uses partial configuration space integrals to define parameters. In the LRM, w is associated with three consecutive residues each in a local helical conformation defined by the backbone (ϕ, ψ) angles of a Ramachandran plot.50,51 Because a small region of configuration space is integrated, w has the same properties as a partition function, and commonly expressed as
| (1) |
where ΔH and ΔS are corresponding enthalpy and entropy contributions, and R the universal gas constant. The LRM invokes microscopic partition functions u, v, and w characterizing three successive residues along the polypeptide that are allowed to be in either an α-helical state (denoted as a) or a coil state (denoted as c). Note that the α-helical state is denoted with the letter “a,” whereas the traditional letter “h” will be used later to denote a locally hydrated state. In particular, w corresponds to a triplet of residues with conformation (aaa), v corresponds to any combination with a central helix and at least one coil (aac, caa, cac), and u corresponds to all other triplets having the center residue in a coil state (ccc, acc, cca, aca). In principle, eight such parameters could be used to account for 23 distinct states.
It is convenient to reexpress Eq. (1) in terms of a microscopic free energy function. Let –RT ln w → ΔGt to give the thermodynamic relation
| (2) |
where the subscript t labels some particular type of partial configuration space integral. Microscopic interactions are discretized and partitioned differently than that done in the LRM. Each microscopic free energy function corresponds to a particular type of interaction. Here, a free energy decomposition is made using five interaction types:
Covalent bonds (t ≡ cb).
Residue i to i + 4 backbone hydrogen bonds (t ≡ hb).
Backbone α-helical conformation in (ϕ, ψ) space (t ≡ a).
Backbone coil conformation in (ϕ, ψ) space (t ≡ c).
Hydration shell or structured solvent (t ≡ h).
Each type of microscopic free energy depends on local geometrical details. Therefore, distinction between i to i + 4 backbone hydrogen bonds will be made depending on (ϕ, ψ) conformations of three consecutive residues spanned by the hydrogen bond (H-bond). End-cap solvation, residue heterogeneity, side-chain interactions, i to i + 3 backbone H-bonding, and other (ϕ, ψ) regions can be added to the free energy decomposition. However, these details are unnecessary to capture essential features of (α)-helix–coil transitions.
Each constraint type requires two thermodynamic parameters (ΔHt, ΔSt) that in principle are functions depending on temperature, pressure, and osmolyte concentrations. At standard pressure and over the accessible experimental temperature range, these parameters are taken as temperature independent. Additionally, each constraint type may contain one or more distance (or angular) constraints. Following previous work,32 the constraint that restricts the backbone into an a-conformation involves two mechanical dihedral angle constraints (one for ϕ and one for ψ), and likewise for the c-conformation. The residue i to i + 4 H-bond is modeled as three constraints, associated with the hydrogen–acceptor distance, the donor– hydrogen–acceptor angle, and the angle between the hydrogen–acceptor– carbon atoms.39,40 Other alternatives have been explored, but three constraints have proved to be an optimal coarse grain description in the sense that (more, less) constraints (over, under) estimate the mechanical role of the H-bond.39
Manipulating the microscopic free energy given in Eq. (2), the various constraint types share the same generic form given by
| (3) |
where εt is an energy parameter, γt is a dimensionless pure entropy (i.e., entropy = Rγt) per distance constraint, and mt is the number of independent distance constraints associated with a particular constraint of type, t. When isolated, a torsion constraint in the a-, c-, or h-conformation has ma = mc = mh = 2, respectively, and a H-bond has mhb = 3. A H-bond contributes a maximum of 3Rγhb to the entropy of the polypeptide when all its distance constraints are independent—as calculated from network rigidity using the preferential selection rule. Depending on the constraint topology of the framework, the possible values for mhb are {0, 1, 2, 3}. Strong H-bonds (having relatively low εhb and γhb values) will be favored at low temperature because they substantially lower the energy of the polypeptide, despite not contributing greatly to the entropy. When many strong constraints are present, weak constraints will be redundant and provide no additional entropy contribution. As temperature is increased, it becomes more probable (and eventually advantageous) for a strong H-bond to break, giving way to weaker constraints that are not as energetically favorable, but become independent and compensate with a greater entropy contribution. Thus, enthalpy– entropy compensation is intimately connected with network rigidity, providing the basis for molecular cooperativity.
The free energy of each accessible mechanical framework, ℱ, must then be calculated. For each of these frameworks, corresponding to distinct topological arrangement of constraints, the free energy of the polypeptide (system) is given by
| (4) |
where Nt is the number of constraints of type t present, and is the number of independent constraints of type t calculated by the preferential rules [emphasized by the superscript (p)] as described above. The partition function is obtained by summing over all frameworks as
| (5) |
where in this work, Z is calculated exactly using a transfer matrix method described in, appendix A. Two observations are worth pointing out. First, the covalent bonds are assumed to be associated with the lowest component entropies and they are quenched constraints. Thus, they contribute the same amount of free energy for all the frameworks in the ensemble. Factoring out this common contribution eliminates the need to explicitly consider them, as they do not affect helix content and give a background contribution to heat capacity. Thus, only noncovalent interactions are parameterized. Second, an optimal ensemble of constraint topologies will be associated with the minimum free energy. Changes in the most probable constraint topologies manifests itself as molecular cooperativity, where network rigidity serves as the mechanism responsible for structural transitions.
In prior work32 the normal helix– coil transition was described by torsion constraints associated with a- and c-conformations, intramolecular backbone H-bonding and H-bonding to unstructured solvent. To describe the inverted transition, the “hydrated conformation” (h-conformation) is introduced. The h-conformation models structured solvent (usually water) around a residue that causes the local flexibility of the polypeptide to be greatly limited. This is the same mechanism that Privalov and Gill16 invoked to explain cold denaturation. Thus, the hydrated state, h, posits a structural cage or clathrate of solvent molecules surrounding the side chain and backbone of a residue. Clathrate formation is energetically favorable, but is a state of low entropy for the polypeptide. The introduction of this hydrated state is sufficient for the DCM to predict heat and cold denaturation in polypeptides in good, poor, and mixed solvents over a broad temperature range.
The properties of a torsion constraint are assumed to depend only on its local a-, c-, or h-conformation. The conformation of its flanking neighbors is irrelevant. This is a simplification from the LRM, in that three-body terms involving triplets of residues specified as aaa, aac, etc., have been replaced with one-body terms involving a single residue. The three body terms in the LRM gives rise to molecular cooperativity, whereas this is the role of network rigidity in the DCM. However, similar to the LRM, some local molecular cooperativity is explicitly built into the DCM by introducing some topological correlations. Out of the 33 possible triplets of residues (such as aac, aah, ach, etc.) any triplet having two neighboring residues with one in the a-conformation and the other in the h-conformation is disallowed. For example, aha, aah, cah are disallowed, while ach, hcc, hhc, hhh are allowed. Altogether, the DCM has 17 accessible types of triplets. A c-conformation just before or after a h-conformation provides the polypeptide with enough plasticity to accommodate forces from solvent. In addition, intramolecular backbone H-bonds are not allowed to span over any residue in a h-conformation.
To understand how the DCM parameters might depend on concentration of cosolvents, it is useful to compare the DCM with the Gibbs–Dimarzio model (GDM) for a helix– coil transition in solvent.52 A direct correspondence is made by recasting Eq. (2) into a microscopic partition function, Qt, given by e−βΔGt where β = 1/RT. In the GDM, Qt represents properties of solvent molecules that either H-bond to CO— group acceptors, QCO, or NH— group donors, QNH, or are free solvent molecules not interacting with the polypeptide, Qs. The latter case is important in the GDM because the system is defined as the polypeptide and solvent. However, in the end, Gibbs and Dimarzio factor out all microscopic partition functions associated with solvent degrees of freedom, and work with the partition function for the polypeptide that retains terms that relate to the transfer of a noninteracting solvent molecule to an interacting one. In the DCM, the system is defined as the polypeptide, where direct solvent interactions are accounted for by specific constraint types. All solvent degrees of freedom are always integrated out under conditions specified by the particular constraint type. In principle, the DCM goes further by integrating out all polypeptide degrees of freedom consistent with the specified constraint topology! This is the reason why the partition function given in Eq. (5) is a sum over discrete topologies. In practice, the problem is broken down into a finite number of discretized parts that define a free energy decomposition, and then these parts are pieced together while accounting for independent entropy contributions.
Differences and similarities between the minimal ZBM, LRM, GDM, and DCM are summarized in Table I. Treating all constraints in all accessible frameworks as independent, the DCM exactly maps onto the ZBM, LRM, or the GDM— depending on the choice of free energy decomposition. The GDM is particularly important because it focuses on solvent effects. It is worth noting that Gibbs and Dimarzio52 in passing (page 279, third to last paragraph) describe the possibility of having two helix– coil transitions based on an unsolvated random coil (here denoted as c). The DCM also accounts for local solvation through the hydration interaction (denoted as h). Most importantly, the DCM is fundamentally different because better estimates for total conformational entropies are calculated using network rigidity, accounting for nonadditivity in free energy decomposition.30,31 Table I shows that a small number of parameters in the ZBM and LRM result from implicitly lumping different interactions into a single phenomenological parameter. More parameters are required in the DCM by distinguishing different interaction types. For example, properties of an intramolecular backbone H-bond depends on the conformation of the three residues it spans. Moreover, H-bonding to solvent is considered to occur whenever an intramolecular backbone H-bond is broken. Within this scheme, two different H-bond models (I and II) are considered and compared.
Table I.
Four Free Energy Decomposition Schemes to Describe the α-Helix to Coil Transitiona
| Type of Interaction | ZBM | LRM | GDM | DCM | |
|---|---|---|---|---|---|
| Covalent bonds | ✓ | ✓ | ✓ | ✓ | |
| Coil conformation | No | u ≡ 1 | z | Vc, δc, 2 | |
| Helical conformation | No | v, w | 1 | Va, δa, 2 | |
| Hydration shell | No | No | No | Vh, δh, 2 | |
| Intramolecular H-bond | σ, s | No | ε | Uxyz, δxyz, 3 | |
| Solvent H-bond | No | No |
|
Uo | |
| Network rigidity | No | No | No | ✓ | |
| Electrostatics | No | No | No | No | |
| Side-chain interactions | No | No | No | No | |
| Self-avoidance | No | No | No | No |
All models implicitly account for covalent bonding. ZBM focuses on H-bonds, LRM focuses on backbone triplet conformations and GDM focuses on solvent effects. The DCM explicitly accounts for network rigidity, encompasses all three of these models, and treats solvent interactions like a two-state model of water having H-bonding to a clathrate structure or to unstructured mobile solvent. The DCM column defines respectively the energy, pure entropy and number of distance constraints associated with the particular interaction. For intramolecular H-bonding, the variables x, y, and z represent either a or c. For solvent H-bonding, only energy is specified as explained in the text.
Model I
The intramolecular i to i + 4 backbone H-bond is allowed only when it spans the aaa-triplet of residues. That is, Uxyz is effectively set to positive infinity for the other seven accessible triplets, which requires H-bonds to form between the polypeptide and solvent. Therefore, model I considers three H-bond parameters, consisting of Uaaa, γaaa for the intramolecular backbone H-bond, and Uo for solvent H-bonding. For simplicity, no entropy parameter is introduced for H-bonding to unstructured solvent because this bonding posits negligible decrease in the flexibility of the polypeptide. Flexibility can be maintained in the polypeptide because unstructured solvent mobility is considered sufficient to create the necessary bonding geometries.
Model II
The intramolecular i to i + 4 backbone H-bond is allowed to form across any triplet of residues that do not include h. For example, there can exist an intramolecular H-bond spanning a ccc-triplet. Model II is more realistic because there are many geometries associated with the ccc-triplet that are appropriate for formation of a H-bond, as confirmed by a bioinformatics study of i to i + 4 backbone H-bonds in protein structures.53 The reason is that hard cutoffs are fictitiously imagined after coarse graining, but actually there will always be some ccc-conformations having (ϕ, ψ) dihedral angles very near that of some aaa-conformations. However, mathematical simplifications are made to reduce the number of H-bond parameters. Here, aac-, aca-, and caa-triplets are treated exactly the same, and cca-, cac-, and acc-triplets are treated exactly the same. Therefore, model II requires nine H-bond parameters, associated with (Uaaa, γaaa), (Uaca, γaca), (Ucac, γcac) and (Uccc, γccc) and Uo.
As demonstrated in next section, model II is not needed to describe CD data of Andersen et al. because model I gives excellent fits. Employing model II is motivated by the tantalizing idea that DCM parameters should be transferable. Since the backbone H-bond interactions are viewed as residue-type independent, the parameterization should not depend on composition of the polypeptide. Therefore, the eight intramolecular parameters were uplifted from prior work32 that were obtained by fitting to simulation data for polyalanine in aqueous solution.54,55 The Uo parameter is free, as it is expected to depend on solvent–polypeptide interaction details. Some parameters can be arbitrarily fixed without affecting any thermodynamic response function. There is freedom to fix one of the torsion constraint energy parameters, {Vc, Va, Vh}, one of the H-bond energy parameters, {Uxyz, Uo}, and one of the pure entropy parameters {δc, δa, δh, γxyz}. In this work, the fixed parameters are Va = 0, Uaaa = −4.64 kcal/mole, and γaaa = 2, leaving the same 6 free fitting parameters for both models I and II.
The key difference between models I and II is the occurrence of entropy replacements that occur whenever there are redundant constraints. Fits to model I find γaaa > δa. As will be discussed in detail, this means that spanning H-bonds over triplets of aaa do not further constrain the helix. In this case, no entropy replacement occurs because the intramolecular H-bond constraints are always redundant. This makes model I as close to a generalized LRM as possible, but differences remain in both the free energy decomposition and not counting entropy contributions from redundant constraints.
DCM Parameter Dependence on Denaturant Concentration
Models I and II contain 6 free parameters that encompass normal and inverted transitions, and provides the possibility of both heat and cold denaturation. As solvent properties are modified by changing denaturant concentration, the model parameters must also change. The question then becomes: Is there any simple concentration dependence, at least for dilute aqueous solutions, on the model parameters?
Free energy shifts of molecules and biopolymers are generally found to be linearly dependent on the concentration of denaturant in dilute solutions, with the proportionality constant defined as an m-value. Likewise, a linear dependence should apply for microscopic free energies, ΔGt, defining model parameters. Since model parameters reside in exponents of Boltzmann factors, they will depend more weakly on cosolvent concentration than the total free energy itself. We expect this approach to be quite general —consistent with the common finding that for low mole fractions a mixed multicomponent solvent acts effectively as a one component solvent.52,56 Therefore, DCM parameters are Taylor expanded away from their aqueous values as a function of cosolvent concentration up to first order. A conversion between volume concentration and mole fraction for HFIP was done using measured molar volume data,57 which is virtually independent of temperature. Up to 30% HFIP (v/v) there is a near linear relationship to mole fraction, making the choice in linearly expanding by % volume or mole fraction to be a matter of convenience. Note that 30% (v/v) corresponds to a mole fraction of ≈6.5%. Here, percent by volume is used to directly compare with Andersen et al. raw data. Unless stated otherwise, all following discussions give HFIP concentrations as percent by volume. The linear dependence on denaturant concentration, c, requires specifying (d/dc)εt|c = 0 for all energy parameters and (d/dcγt|c = 0 for all pure entropy parameters. Using this linearity assumption, data of Andersen et al.20 will be fitted to obtain model parameters, consisting of 6 pure water and 6 slope parameters. However, HFIP is a halogen alcohol that has an unusual degree of potency for inducing helix conformation, for which the origin is unclear.58 – 65 An exotic mechanism might jeopardize the proposed generic approach.
Considering Special Properties of HFIP
The measured activity coefficient66 of HFIP in aqueous solution starts very high (≈15.3) and monotonically decreases until a minimum of ≈0.75 is reached at 80%, at which point it increases to unity at 100% HFIP. The activity of water is suppressed at low HFIP concentrations, reaching a shallow minimum near 27%, then increases to a maximum near 76%, after which it monotonically decreases until 100% HFIP is reached. Considering the entire range from 0 to 100%, there is significant variation in the nature of how HFIP interacts with itself and with water as HFIP concentration is varied. More recently, it has been shown by x-ray scattering that near 30% HFIP there is a maximum in micelle-like clustering of HFIP, but these clusters were not thought to be held together as rigidly as that found in amphiphiles such as SDS.61 Additionally, it was reported61 that helix content in melittin does not decrease for HFIP concentration above 30%, beyond which HFIP clustering decreases.
Apparently, the minimum in water activity can be associated with the maximum HFIP micelle-like clustering. The range of HFIP concentration used by Andersen et al.20 goes as high as 25%, and the most interesting features exhibiting cold and heat denaturation is around 8 –10%. Therefore, attributing the interesting signature of heat and cold denaturation to the intrinsic HFIP clustering behavior in water is not possible, unless the concentration of polypeptide has an affect. Andersen et al. showed their data to be independent of polypeptide concentration (at low dilution), so this is implausible. Moreover, the dramatic effects of activity coefficients for HFIP and water as a function of HFIP concentration is not present until 75% — considerably beyond the range of Andersen’s experiment and expected range of the proposed linear dependence on cosolvent concentration. In addition, the m-value approach has been applied in the study of induced helix transition in melittin using HFIP cosolvent up to 20% by volume.60 Despite its unusual behavior, there appears no reason to make special exceptions for HFIP in the modeling scheme of the DCM.
RESULTS
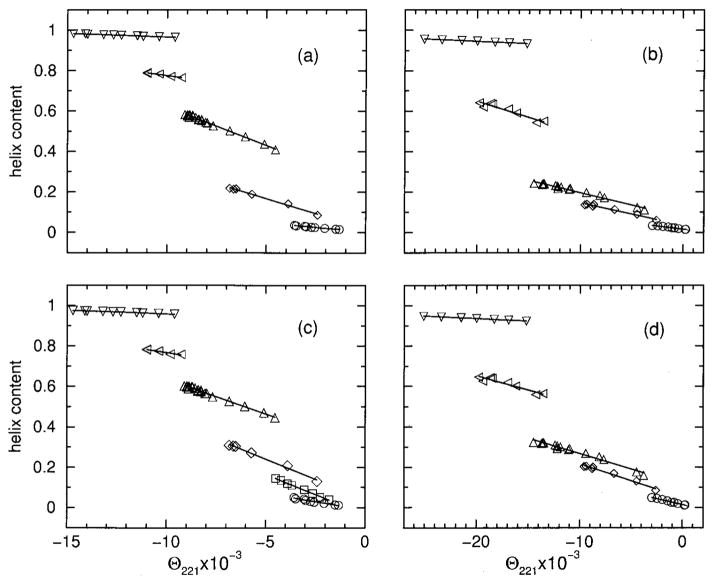
Both models I and II are compared to experimental data of Andersen et al.20 where heat and cold denaturation was observed for some HFIP concentrations in several different monomeric heterogeneous polypeptides. Raw experimental data from CD measurements over temperatures between 270 and 340 K and HFIP concentrations between 0 and 25% by volume were shown for two polypeptides labeled as sCT(8 –32) and YGG-3V. Model predictions for helix content are transformed to compare directly with CD measurements at 221 nm wavelength. Following standard practice it is assumed that a linear transformation between the calculated helix content, θa, and the measured signal, [θ]221, exists. Consequently,
| (6) |
where θa gives the fraction of helix ranging between 0 and 1. The coefficients a and b are situation-dependent transformation variables that depend on experimental setup and the precise coarse graining procedure used to define the helix conformation. Moreover, there is no reason to expect that the linear relationship given in Eq. (6) should be independent of HFIP concentration. Therefore, the two transformation parameters (a and b) are viewed as functions of HFIP concentration. A linear relationship between [θ]221 and θa is used as the fitting objective to optimize the model parameters. The slope of the transformation given by a and the y-intercept given by b are determined by least squares linear regression for each HFIP concentration separately. This method of fitting offers the advantage that neither temperature dependent baselines nor helix content saturation values in [θ]221 are a priori required. To our knowledge, fitting to experimental data in this way has not been employed before. Details of the fitting procedure are given in appendix B.
Fitting the minimal DCM predictions to data from heterogeneous polypeptides gives a set of effective parameters where differences in residues are averaged out. Consequently, the chain length of the effective homogeneous polypeptide refers to the number of residues playing an active role in the transition, which is not well defined. Therefore, different chain lengths were considered in fitting. It was found that the precise chain length was not crucial to obtain an excellent fit to the data. Nevertheless, there is a strong dependence on chain length for a fixed set of model parameters due to molecular cooperativity. The DCM parameters presented here corresponds to n = 16 for the sCT(8 –32) polypeptide and n = 18 for the YGG-3V polypeptide.
Figures 1 and 2 show the raw CD data20 and the corresponding predictions of model I and II, using best-fit parameters to the data. Table II list the best-fit DCM parameters for both models, for both polypeptides, and for 0 and 20% HFIP concentrations. Parameters for any other HFIP concentration is obtained by linear interpolation using the 0 and 20% data points. The best fits for models I and II were obtained by simulated annealing while simultaneously fitting both polypeptides consisting of 12 data curves. This dual dataset fitting involved 16 free model parameters as summarized in the caption of Table II and explained in appendix B. In spite of models I and II having considerably different H-bond parameterization, both models fit to experimental CD data equally well within experimental error bars.
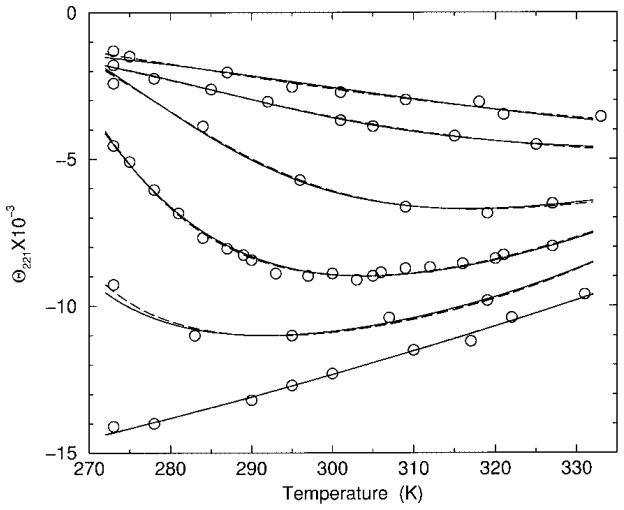
FIGURE 1.
Best fits to experimental CD data for polypeptide sCT(8 –32). Calculated results from models I and II are (inversed) transformed and shown as dashed and solid lines, respectively. From top to bottom the curves correspond to 0, 6, 8, 10, 12, and 25% HFIP concentration.
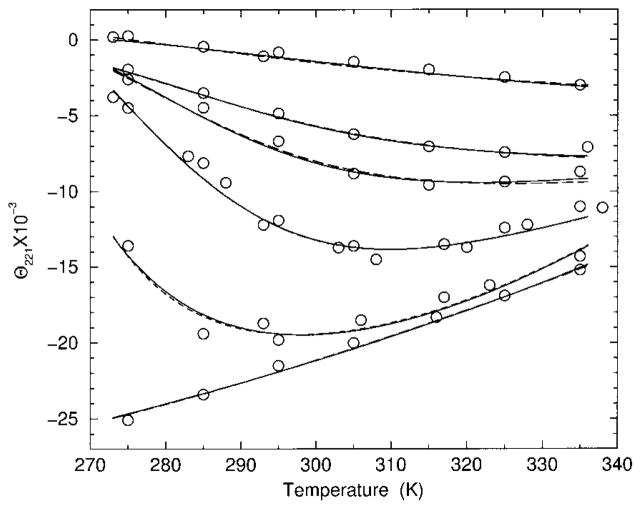
FIGURE 2.
Best fits to experimental CD data for polypeptide YGG-3V. Calculated results from models I and II are (inversed) transformed and shown as dashed and solid lines, respectively. From top to bottom the curves correspond to 0, 6, 7, 8, 10, and 20% HFIP concentration.
Table II.
A List of all Model Parametersa
| Parameter | sCT(8–32)
|
YGG-3V
|
||||||
|---|---|---|---|---|---|---|---|---|
| Model I
|
Model II
|
Model I
|
Model II
|
|||||
| 0% HIFP | 20% HIFP | 0% HIFP | 20% HIFP | 0% HIFP | 20% HIFP | 0% HIFP | 20% HIFP | |
| Vh | −2.84 | −3.16 | −2.84 | −2.20 | −3.04 | −3.37 | −2.87 | −2.24 |
| δh | −0.0212 | −1.19 | 0.763 | 0.552 | 0.0541 | −1.11 | 0.731 | 0.520 |
| Va | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| δa | 1.39 | 1.39 | 2.25 | 2.25 | 1.67 | 1.67 | 2.24 | 2.24 |
| Vc | −0.579 | 2.00 | 1.14 | 1.51 | 0.597 | 2.02 | 1.08 | 1.46 |
| δc | 3.19 | 2.69 | 4.10 | 3.08 | 3.52 | 3.01 | 4.10 | 3.07 |
| Uccc | ∞ | ∞ | 0 | 0 | ∞ | ∞ | 0 | 0 |
| γccc | — | — | 2.92 | 2.92 | — | — | 2.92 | 2.92 |
| Ucac | ∞ | ∞ | −2.34 | −2.34 | ∞ | ∞ | −2.34 | −2.34 |
| γcac | — | — | 2.76 | 2.76 | — | — | 2.76 | 2.76 |
| Uaca | ∞ | ∞ | −2.83 | −2.83 | ∞ | ∞ | −2.83 | −2.83 |
| γaca | — | — | 2.15 | 2.15 | — | — | 2.15 | 2.15 |
| Uaaa | −4.64 | −4.64 | −4.64 | −4.64 | −4.64 | −4.64 | −4.64 | −4.64 |
| γaaa | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Uo | −3.63 | −3.32 | −3.27 | −3.21 | −3.63 | −3.32 | −3.27 | −33.21 |
The parameter Va is fixed to zero as an arbitrary energy reference. The parameters δa, Uo, Uxyz, γxyz are fixed to the values given in the table, independent of HFIP concentration. The value of ∞ for Uxyz indicates that such a H-bond is not allowed to form, and dashes are used for γxyz whenever the H-bond is disallowed. In each model, all slope parameters are constrained to be the same for both polypeptides.
Helix Content
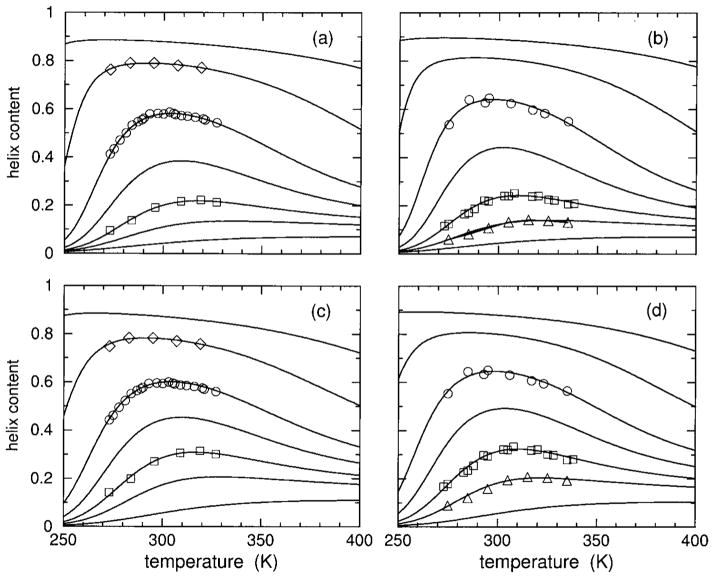
Within the measured temperature range, the DCM predicts practically 0% helix content at 0% HFIP concentration, and at 20% HFIP concentration there is nearly 100% helix content. These predicted saturation limits are in agreement with the interpretation of the raw CD measurements given by Andersen et al.20 The predicted helix content as a function of temperature over an extended temperature range is shown in Figure 3. DCM predictions show weak reentrant behavior in helix content, even at optimal HFIP concentrations, due to the mild gain in disordered coil conformations at high temperatures. Moreover, for large HFIP concentrations, the predicted helix content saturates at a high value at high temperatures. Thus, the behavior of helix content as a function of temperature closely resembles that of an inverted helix– coil transition, with only small amount of reentrant behavior for a narrow window of intermediate HFIP concentrations. According to the DCM predictions, hydration effects at low temperature are playing the dominant role in the structural transition, in agreement with the reported observation of dramatic cold denaturation,20 but heat denaturation is marginal. Although there is a decrease in helix content upon heating, a peak in the heat capacity is necessary as part of the signature for a second helix– coil transition. It will be shown in the Discussion how the sharpness of the transition(s) depend on chain length as a consequence of molecular cooperativity.
FIGURE 3.
Using parameters linearly interpolated from Table II, helix content over an extended temperature range is shown for 4, 7, 8, 9, 10, 12, and 15% HFIP concentrations, which correspond to the solid line curves ordered from bottom to top in each panel. In panels (a) and (c) results are shown for polypeptide sCT(8 –32) with an effective chain length of 16, using models I and II, respectively. Also included are the symbols square, circle, and diamond corresponding to the transformed CD data onto fractional helix content for 8, 10, and 12% HFIP concentrations. Similarly, panels (b) and (d) show results for polypeptide YGG-3V with effective chain length of 18, using models I and II respectively. The symbol up triangle, square, and circle correspond to the transformed CD data onto fractional helix content for 7, 8, and 10%) HFIP concentrations.
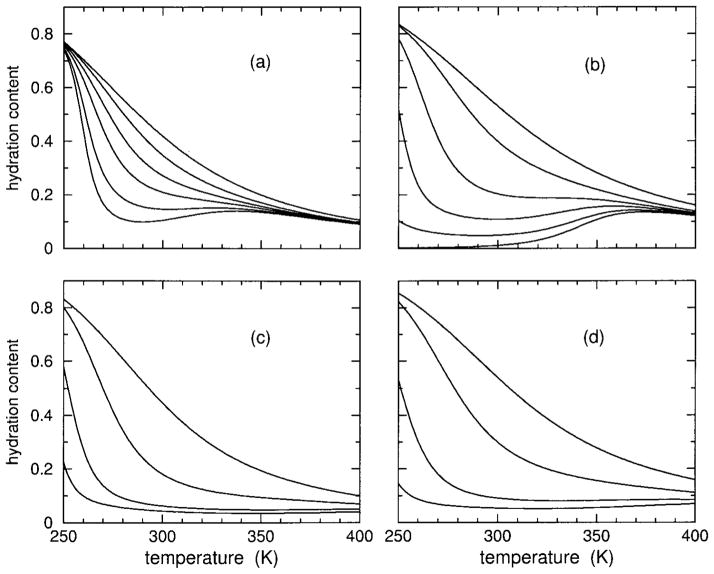
Hydration Content
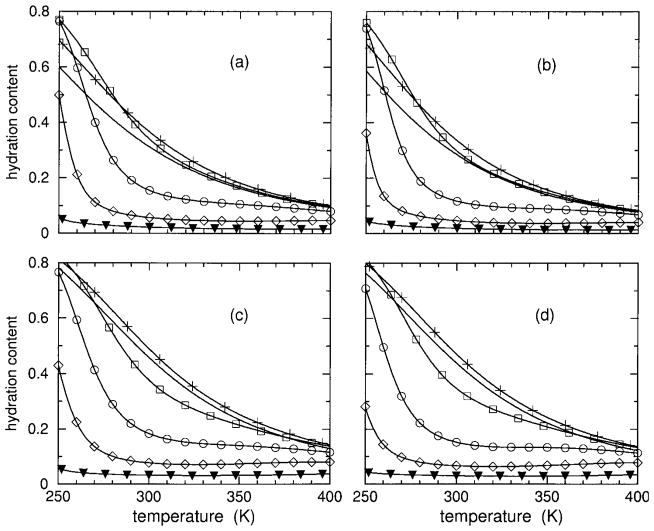
The predicted hydration content, θh, is plotted in Figure 4. Hydration content also ranges between 0 and 1 and is used as a second order parameter. Helix content, regarded as the primary order parameter, and hydration content together characterize the transition(s). It is seen that both models show that both polypeptides have very high hydration content at low temperatures, decreasing as temperature increases. As HFIP concentration increases from 0% up to about 5%, the DCM predicts hydration content will increase slightly, and then this trend reverses. In particular, at some critical HFIP concentration (near 9%) the hydration content exhibits a sharp transition. As HFIP concentration increases above this critical value, there is an increase in sharpness of hydration loss with a corresponding decrease in the (cold) transition temperature. At very high HFIP concentrations, there is virtually no hydration content. The trends predicted by the DCM above the critical HFIP concentration is indicative of molecular cooperativity found in inverted helix– coil transitions.
FIGURE 4.
Using parameters linearly interpolated from Table II, hydration content over an extended temperature range is shown for 0, 4, 8, 10, 12, and 15% HFIP concentrations. In panels (a) and (c), results are shown for polypeptide sCT(8 –32) with an effective chain length of 16, using models I and II, respectively. In panels (b) and (d) results are shown for polypeptide YGG-3V with an effective chain length of 18, using models I and II, respectively. Because hydration content curves cross, the symbols plus, square, circle, diamond, and filled down triangle) are added to identify the 4, 8, 12, and 15% HFIP concentrations. The solid line without any symbol corresponds to 0% HFIP concentration.
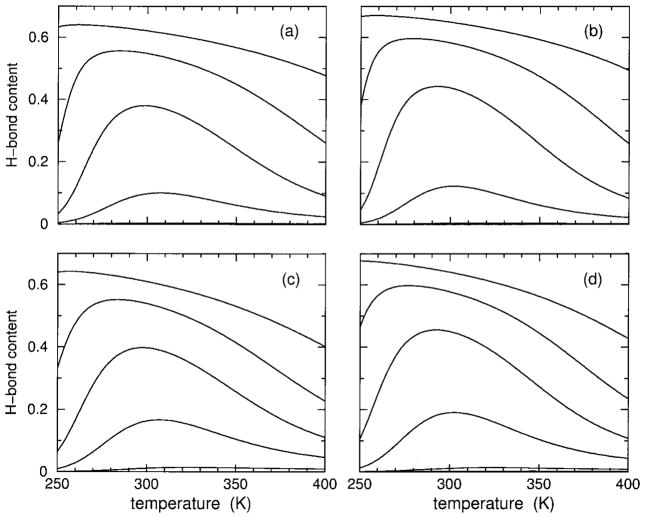
Hydrogen-Bond Content
In addition to hydration and helix content, it is also possible to track H-bond content. Both models I and II explicitly account for the possibility of having H-bonding to solvent in favor of intramolecular backbone H-bonding. The greatest difference between models I and II is in how the backbone H-bonding is modeled. Nevertheless, as Figure 5 shows, H-bond content is remarkably similar between models I and II, as well as for both polypeptides. It is seen that H-bond content has similar reentrant behavior exhibited in helix content. Comparing the results of helix and H-bond content gives no indication whether intramolecular H-bonds can be considered to be the driving mechanism for the (heat) transition or not. In the Discussion, it will be shown that models I and II give slightly different answers to this question, but in both models H-bonding plays an important role in thermodynamic stability that influences the degree of molecular cooperativity. For example, it will be seen that the hydration content is depleted because forming intramolecular H-bonds is more favorable.
FIGURE 5.
Using parameters linearly interpolated from Table II, H-bond content over an extended temperature range is shown for 15, 12, 10, 8, 4, and 0% HFIP concentrations, which correspond to the solid line curves ordered from top to bottom in each panel. In panels (a) and (c), results are shown for polypeptide sCT(8 –32) with effective chain length of 16, using models I and II respectively. Panels (b) and (d) show results for polypeptide YGG-3V with an effective chain length of 18, using models I and II, respectively. In all cases, no H-bond content is found at 0% HFIP concentration, and only a tiny amount is predicted by model II at 4% HFIP concentration.
Thermodynamic Characteristics
It is worth mentioning that a few entries in Table II have a negative best-fit hydration pure entropy parameter, δh. Although fundamentally all pure entropy parameters should be positive, it is also true that in the DCM the entire set of pure entropy parameters can be globally shifted by an arbitrary constant without affecting any order parameter, heat capacity, or differences in thermodynamic quantities. Recall that this freedom was exercised when the intramolecular backbone H-bond parameters were preset to the best-fit values obtained from prior work32 on polyalanine in aqueous solution, where γaaa = 2 is used here as the pure entropy reference for both models I and II. Thus, there is no special significance in having a positive or negative pure entropy. To reflect the intrinsic arbitrary reference, all free energies, enthalpies, and entropies per residue for the polypeptide are labeled as Δg, Δh, and Δs, respectively. These free energy differences do not refer to differences between the native and denatured (unfolded) states.
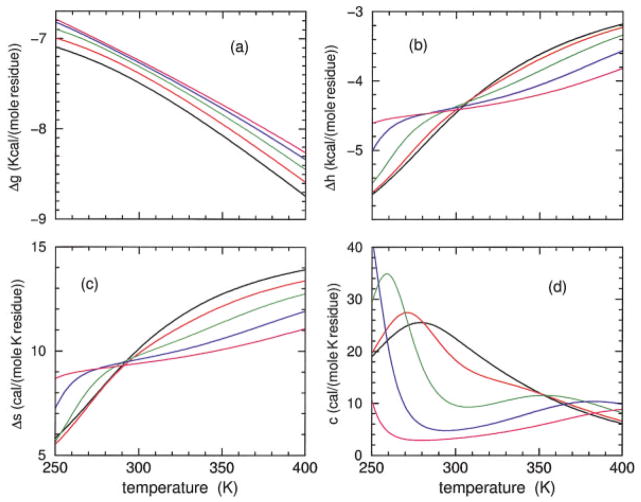
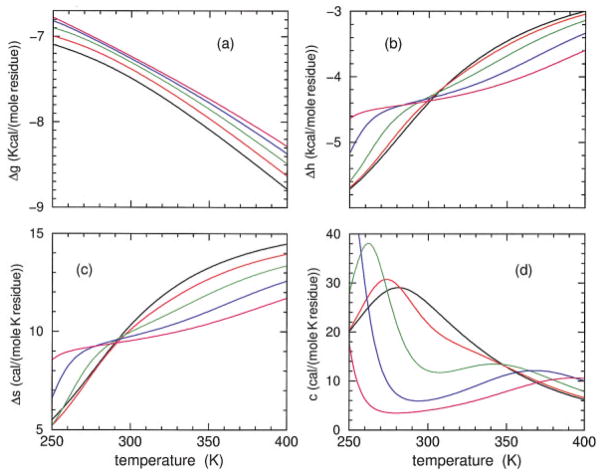
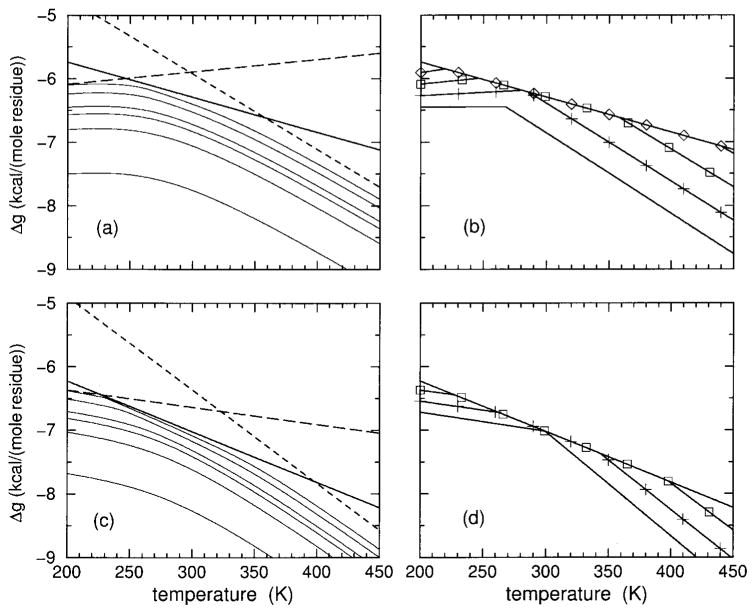
Model I predictions for the Gibbs free energy, enthalpy, entropy, and heat capacity are shown in Figure 6 for the sCT(8 –32) polypeptide, and Figure 7 shows the corresponding model II predictions. Predictions from models I and II are in qualitative agreement, having similar thermodynamic response. It is seen that the free energy increases as HFIP concentration is increased, although the rate of increase decreases. As HFIP concentration increases above 11%, the free energy curves hardly shift. For all HFIP concentrations, both the enthalpy and entropy increase with temperature, which allows for enthalpy–entropy compensation (at least in part). At low HFIP concentrations the increase in enthalpy and entropy as a function of temperature takes the form of a broad sigmoid curve requiring a temperature range from nearly 100 to 600 K to fully capture the lower and upper baselines. In Figures 6 and 7 only the top part of the sigmoid curves can be seen for 6 and 8% HFIP concentrations. Near the critical HFIP concentration of ≈9% and above, both the enthalpy and entropy increase sharply at both low and high temperatures. The dramatic change in enthalpy and entropy at low temperature is associated with the rapid decrease in hydration content as observed in Figure 4 that governs cold denaturation. After a near plateau, there is a second increase at higher temperature that reflects having helical conformations changing to disordered coil conformations and the breaking of intramolecular backbone H-bonds.
FIGURE 6.
Using model I parameters determined from Table II, predicted free energy (a), enthalpy (b), entropy (c), and heat capacity (d) are plotted over an extended temperature range for polypeptide sCT(8 –32) and effective chain length of 16. The colors black, red, green, blue, and magenta correspond to HFIP concentration of 6, 8, 10, 12, and 14%.
FIGURE 7.
Using model II parameters determined from Table II, predicted free energy (a), enthalpy (b), entropy (c), and heat capacity (d) are plotted over an extended temperature range for polypeptide sCT(8 –32) and effective chain length of 16. The colors black, red, green, blue, and magenta correspond to HFIP concentration of 6, 8, 10, 12, and 14%.
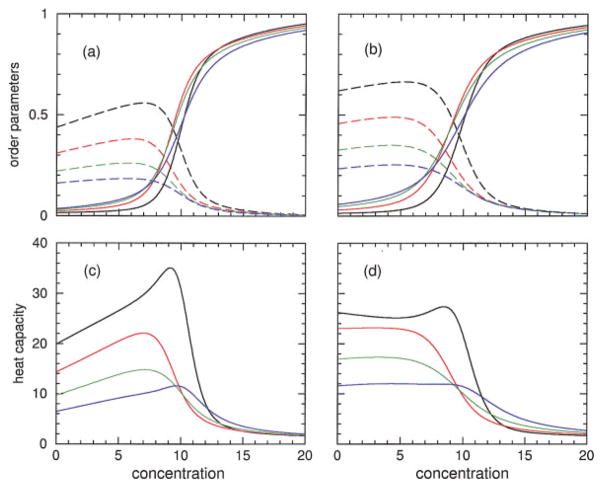
The predicted heat capacity for both models has a single broad peak at 8% HFIP concentration and below. Interestingly, the heat capacity at 8% concentration exhibits a shoulder that appears at the onset of a secondary peak. Indeed, for larger HFIP concentrations two well defined peaks in the heat capacity curves are predicted by both models. However, the low temperature peak is located below 260 K, and the high temperature peak is above 340 K. The two peaks shift further apart when HFIP concentration is increased, indicating the low and high temperature transitions are governed by an increase in molecular cooperativity. The (decrease, increase) in the transition temperature for (cold, heat) denaturation is akin to the (inverted, normal) helix–coil transitions that occurs as chain length is increased. Unfortunately, at any fixed HFIP concentration, these predicted dramatic effects as a function of temperature are not fully experimentally accessible. As a function of HFIP concentration, at fixed temperature, helix and hydration content and heat capacity give a pronounced signature for changes in molecular cooperativity, as shown in Figure 8. It is seen that models I and II are in qualitative agreement, but do have quantitative differences that can be easily discerned at low temperatures. Similar results for both models are obtained for the YGG-3V polypeptide (not shown).
FIGURE 8.
Additional predictions for the sCT(8 –32) polypeptide with effective chain length of 16. In panels (a) and (b) the hydration and helix content are plotted HFIP concentration at four different temperatures. The (dashed, solid) lines correspond to (hydration, helix) content. Panels (c) and (d) show the heat capacity in units of cal/(mole K residue) for the same set of temperatures as a function of concentration. The black, red, green, and blue curves correspond to the temperatures of 275, 300, 325, and 350 K in all panels. Panels (a) and (c) are the predictions from model I, while model II predictions are shown in panels (b) and (d).
DISCUSSION
The general formalism of the DCM is applicable to biopolymers and many other physical systems. The helix– coil transition in polypeptides serves as a well suited example for illustrating the DCM, and the important role that network rigidity plays in determining molecular cooperativity. Except for some comments on the generalization of the DCM to heterogeneous polypeptides at the end of this section, the analysis given below is restricted to a homogeneous polypeptide.
Three-State Model for an Infinite Chain
Similar to Schellman’s two-state model,1,2 the essential features of the helix– coil transition for an infinitely long polypeptide immersed in arbitrary solvent conditions can be understood using three limiting states. Employing the minimal 6-parameter DCM presented here, the free energy of five distinct frameworks are worked out, three of which govern the limiting states of interest. These free energies (per residue) denoted as Δgh, Δga, and Δgc with respect to an arbitrary reference state, correspond to a framework that is 100% hydrated, 100% helix, and 100% disordered. In terms of the DCM parameters,
| (7) |
| (8) |
| (9) |
where (Δga1, Δga0) correspond to a polypeptide that is 100% helix with all H-bonds (present, missing). Likewise, (Δgc1, Δgc0) correspond to a polypeptide that is 100% disordered coil with all H-bonds (present, missing). These latter four free energies are given by
| (10) |
| (11) |
Although near room temperature it can be expected that Δga1 < Δga0 and Δgc0 < Δgc1, these inequalities need not be the case. Therefore, five distinct frameworks must be considered to properly determine the three limiting states of interest.
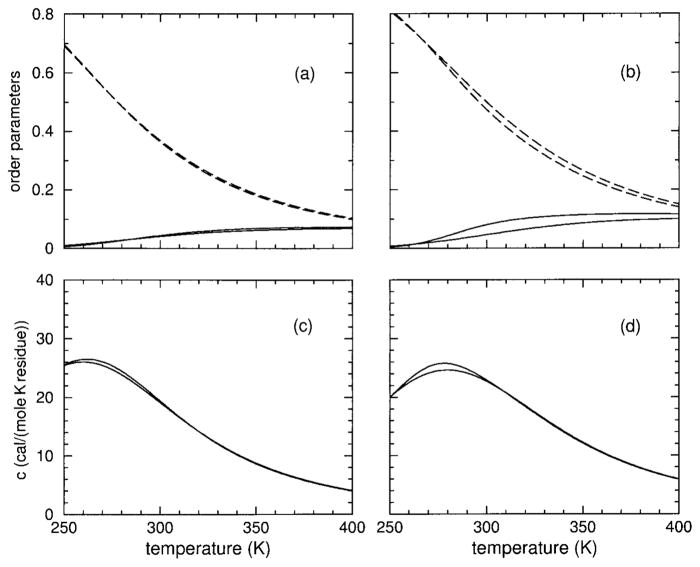
Examples of the three limiting case free energies given in Eqs. (7)–(9) are shown in the right two panels of Figure 9 for 8% HFIP concentration. Each of these free energies are linear functions of temperature with negative slope. The state with the lowest free energy at any given temperature is the most thermodynamically stable. Free energy crossings will generally occur as temperature is increased, shifting (less, more) importance to the (enthalpy, entropy) contributions. At 8% HFIP concentration, both models I and II form a triangle with a long base of lowest free energy in the helix state. The apex of the triangle corresponds to a transition directly from the disordered hydrated state to the disordered coil state. However, both these disordered states are thermodynamically unstable at the temperature where the apex forms. Instead, the polypeptide will track the state with lowest free energy, which depends on the temperature. As temperature increases starting from low temperature, the three-state model predicts the polypeptide will undergo two transitions—passing from disordered hydrated to helix to disordered coil. The introduction of a third state, representing the effects of structured solvent (hydration) allows the possibility of having cold denaturation take place, forming a limit-triangle as shown in Figure 9.
FIGURE 9.
The free energy for three limiting thermodynamic states of a hypothetical infinite homogeneous chain is shown in panels (a) and (c) using best-fit parameters of model I and II at 8% HFIP concentration for polypeptide sCT(8–32) respectively. The (hydrated, helix, coil) states are shown as (long-dashed, solid, short-dashed) straight lines. Also, from bottom to top, a series of curves show the free energy obtained from DCM calculations for chain lengths 5, 10, 15, 20, 50, and 10000, respectively. Panel (b) plots the lowest free energy among the 3 limiting states (for model I) as a function of temperature at 0, 4, 8, 12, and 16% HFIP concentrations. The plus, square, and diamond symbols identify the 4, 8, and 12% cases. The lowest two lines without symbols, which form an upward “wedge,” correspond to the 0% case. Panel (d) is the same as (b) except model II is used. Note the helix state serves as a fixed reference between panels (a and b) and between (c and d) because Va and δa are independent of HFIP concentration.
The limit-triangle continuously changes shape as a function of HFIP concentration. The lowest free energy from the three limiting states is also plotted in Figure 9 as a function of concentration. At low HFIP concentration the limit triangle is inverted, such that the helix state is always relatively unstable compared to both the hydrated and coil states for all temperatures. Thus at low enough HFIP concentration the polypeptide is exposed to a good solvent and it will not form a helical structure. As HFIP concentration increases, a limit-triangle forms and proceeds to grow in such a way that the cold-denaturation (transition) temperature, locating the crossing between the hydrated and helix states, decreases. Simultaneously, the heat-denaturation temperature, locating the crossing between helix and coil states, increases. Thus the two transition temperatures describing cold and heat denaturation move away from one another as HFIP concentration increases. When the two transition temperatures move past experimental accessibility, the polypeptide will remain a helix— characteristic of poor solvent conditions. When a single (normal, inverted) transition is observed, the (first, second) free energy crossing occurs (below, above) the experimentally accessible temperature range.
It is natural to use 6 free parameters in a minimal DCM since it takes six parameters to describe the limit-triangle (a slope and y-intercept for each of the three lines). However, with further thought it would appear that only four parameters are required to explain two distinct transitions. This is because the limit-triangle will yield the same predictions whether all slopes (representing negative entropies) and all y-intercepts (representing energy) of each of the three free energy functions are shifted by the same amount. However, this freedom of selecting an arbitrary overall energy and entropy reference has been used up already. In this work, the selection of Va = 0, Uaaa = −4.64 kcal/mole and γaaa = 2 was made. Thus, it is more appropriate to consider 6 free parameters as a minimal model (one for the H-bond to solvent and five for the residue).
Heat and Cold Denaturation in Finite Length Chains
Whether a polypeptide will actually exhibit cold and heat denaturation as predicted by the presence of the limit-triangle shown in Figure 9(a and c) depends on the length of the polypeptide and relative free energy differences between different frameworks. Note that a limit-triangle can be defined for finite length polypeptides. The existence of a limit-triangle is necessary for both cold and heat denaturation to take place, but it is possible that one or neither of the predicted two transitions is realized due to the subtle balance of many interactions. The detailed DCM computations will agree well with the three-state model predictions when (a) polypeptides are much longer than the rigidity correlation length, and (b) there is a small subset of frameworks that have free energies well below all others making up most of the ensemble. This, however, generally does not occur. In Figure 9(a and c) the exact free energy as as a function of chain length is compared with the limiting infinite chain length prediction of the three-state model. In both models I and II, exact DCM calculations for chain lengths more than 100 times longer than the rigidity correlation length have free energies (per residue) less than that predicted by the three-state model. The lower free energy can be ascribed to mixing of many frameworks having similar free energy assignments.
Molecular Cooperativity
The DCM makes a distinction between two types of mechanisms that lead to molecular cooperativity. The first type of mechanism has to do with forming a favorable geometric arrangement to lower the enthalpy, without an associated cost in conformational entropy. Cooperativity resulting from this first type of mechanism is entropically irrelevant. In the DCM, this situation arises whenever a constraint type is completely redundant. A good example of such a constraint is the aaa H-bond that is allowed in model I. Specifically, from Table II for the sCT(8 –32) polypeptide, the pure entropy for an α-helical conformation is given as δa = 1.39 compared to the pure entropy for the allowed H-bond given as γaaa = 2. With these numerical values, the H-bond constraint is always redundant thereby providing cooperativity only via lowering enthalpy when three α-helical conformations consecutively occur. The presence of these H-bonds do not reduce conformational entropy.
The second type of mechanism concerns itself with changes in conformational entropy that arise because of a particular topological arrangement of constraints. This second type of mechanism is entropically relevant, and is generally associated with an enthalpy change as well. Entropy changes are calculated in the DCM using network rigidity. This case is clearly demonstrated in model II, where from Table II using the sCT(8 –32) polypeptide, the pure entropy for an α-helical conformation and the aaa H-bond are δa = 2.25 and γaaa = 2, respectively. The presence of an aaa H-bond will lower the conformational entropy that would otherwise be present if no intramolecular H-bonds were present. As temperature is increased, the entropic cost becomes more of a burden, and a lower overall free energy can be achieved by the H-bond breaking sooner than would happen in model I if the changes in enthalpy were the same. Additionally, model II has other types of weaker H-bonds, such as one that spans a ccc conformation having pure entropy of γccc = 2.92. At 20% HFIP concentration, the pure entropy for a disordered coil conformation is given as δc = 3.08. Since many of these pure entropy contributions are similar, there are many frameworks in the ensemble that have similar free energies. Consequently, as shown in Figure 9(a and c) the free energy of the polypeptide obtained from exact DCM calculations deviate from the simple three state model predictions. More interesting is that combinations of H-bonds forming various types of H-bond networks pay different amounts of entropic penalties depending on the details of constraint arrangements. Entropy penalties paid by H-bonds (and other constraint types) strongly depend on the topology of cross-linking between constraints, which is governed by the long-range nature of network rigidity.
In the DCM, the first type of mechanism is just a special case of the second type, but has important consequences in predicting molecular cooperativity and thermodynamic stability. Model I gives an example where only entropically irrelevant H-bond constraints are accessible. In this case, the total conformational entropy of a polypeptide having Nh hydrated, Na α-helical, and Nc coil conformations is simply additive, given by ΔSc = R(Nhδh + Naδa +Ncδc). It is relatively straightforward to see how component entropies add in a transfer matrix approach. In the ZBM, LRM, DCM, or any other model using a transfer matrix, the general form of the elements will be e−βΔG → eγe−βε, where ΔG = ε − RTγ. Without explicitly accounting for network rigidity during the process of multiplying out the transfer matrix, products of various matrix elements result in an over estimate for the total conformational entropy because all entropic contributions are simply added. Specifically, an additional term of the form Naaaγaaa would be generated using model I without accounting for network rigidity — erroneously adding an aaa H-bond entropy contribution whenever it is present in the framework. Although model I is in many ways similar to a generalized LRM that includes a third state to model hydration, it is different in two respects. First, the DCM separates out free energy contributions from different types of interactions. Second, the redundant component entropies of H-bonds do not contribute to the total entropy.
At the heart of the DCM, only the preferential independent set of constraints contribute to total conformational entropy. As described in appendix A, larger transfer matrices are required to employ network rigidity as an underlying mechanical interaction to account for proper entropy replacements so as not to overestimate the total conformational entropy. The DCM transfer matrix maintains all information about the propagation of network rigidity along the polypeptide. More complex parameterizations, such as exemplified in model II, can be easily calculated, where many entropy replacements occur. Yet models I and II are described using the same mathematical formalism. It is worth noting that models I and II serve as two representative examples, as many more excellent fitted parameterizations to the raw CD data have been generated. However, for each of these good fits to the experimental data at hand, there are dramatic consequences when chain length and HFIP concentrations are varied, both of which can be used to nail down the true thermodynamic response. In prior work32 it was found that model I (with any rank ordering of pure entropies) could not fit well to the simulation data54,55 on polyalanine. Keeping transferability of parameters as a goal, we favor model II.
Chain Length Dependence
The long-range character of molecular cooperativity can be better understood by considering chain length (size) dependencies. Key to the observed response is the competition that plays out between the various types of constraints defined in the DCM. As shown in Results, changing the HFIP concentration changes the relative importance of the various constraint types, which also depends on the temperature. In Figure 10, helix content, hydration content, and heat capacity are plotted vs temperature for two extreme sizes: length 5 and 10,000 residues for both models at 4% HFIP concentration. Virtually no differences are observed as a function of size, although some difference is seen in model II due to weak backbone H-bonds (of the type aca or cac) collectively increasing helix content, at the expense of decreasing hydration content and lowing the peak in heat capacity. At this low HFIP concentration, the transition is not clear, involving a large mixture of frameworks near all three limiting states. The helix content curves resemble an inverted transition, except that at high temperatures helix content remains at a low saturation value. High temperature saturation values are always determined by the pure entropies, as β → 0.
FIGURE 10.
Panel (a) shows (hydration, helix) content as (dashed, solid) lines for model I applied to the sCT(8–32) polypeptide at 4% HFIP concentration. Panel (c) shows the corresponding heat capacity. Similarly, panels (b) and (d) show results for model II. Two curves are shown for each quantity plotted. In all cases, the (bottom, top) curve corresponds to a chain length of (5, 10,000).
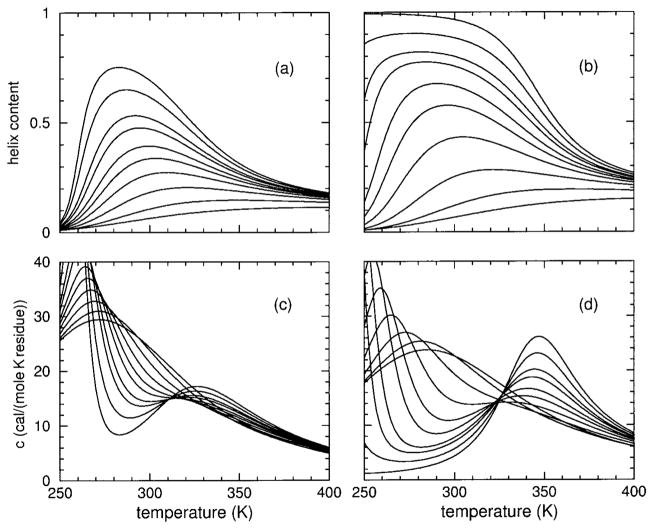
In Figure 11, helix content and heat capacity are again plotted vs temperature for models I and II for various sizes from length 5 up to 10,000, but at 8% HFIP concentration. At this concentration the limit-triangle shown in Figure 9(a and c) predicts a wide experimentally accessible temperature range for which the helical state is thermodynamically stable. For small chain lengths, the H-bonds cannot form long overlapping cooperative strings, and as a result the actual helix content is far from unity for both models. As chain length increases, however, helix content rises in both models, where two peaks in the heat capacity develop. Although the lower and upper peaks move apart as chain length increases, many of the features (if not the peaks themselves) are experimentally accessible, such as the minimum between the two peaks with sharp rise on both sides. Although models I and II give virtually equivalent predictions for the raw CD data they were fitted to, considerable differences emerge as molecular cooperativity is probed via chain length dependence.
FIGURE 11.
Panels (a) and (b) show helix content for models I and II, respectively, applied to the sCT(8–32) polypeptide at 8% HFIP concentration. From bottom to top, the curves correspond to chain lengths 5, 10, 15, 20, 25, 30, 40, 50, 100, and 10,000. Panel (c) shows the corresponding heat capacities for model I. From top to bottom at temperature 300 K the curves correspond to chain lengths 5, 10, 15, 20, 25, 30, 40, 50, 100, and 10000. In panel (d) the same ordering of chain lengths occur at 310 K for model II. Note that in pannels (c) and (d) the ordering of the curves differ at different temperatures because the heat capacity curves cross one another.
At 12% HFIP concentration, Figure 12 shows the same type of data as plotted in Figure 11 and discussed above. The results shown in Figure 11 clearly indicate model II is more cooperative than model I. Here, in contrast, less difference in chain length dependency is found between predictions from models I and II. Differences in molecular cooperativity observed between models I and II further decreases as HFIP concentration increases beyond 12%. To examine the nature of molecular cooperativity, or the lack thereof, Figure 13 plots hydration content vs temperature for various chain lengths, for both models, and at 8 and 12% HFIP concentrations. A chain length of 5 residues derives virtually no molecular cooperativity from the H-bond network. Therefore, hydration content for a 5 residue polypeptide chain reflects the natural propensity of the effective homogeneous chain under consideration to be hydrated. Not unexpectedly, hydration content is predicted to be high at low temperature and it continuously decreases as the temperature increases for any HFIP concentration. As chain length increases, hydration content is depleted due to the formation of many consecutive overlapping intramolecular H-bonds along the helix. Up to some rigidity correlation length, the longer the helix the greater molecular cooperativity will be generated by the presence of long strings of overlapping H-bonds.
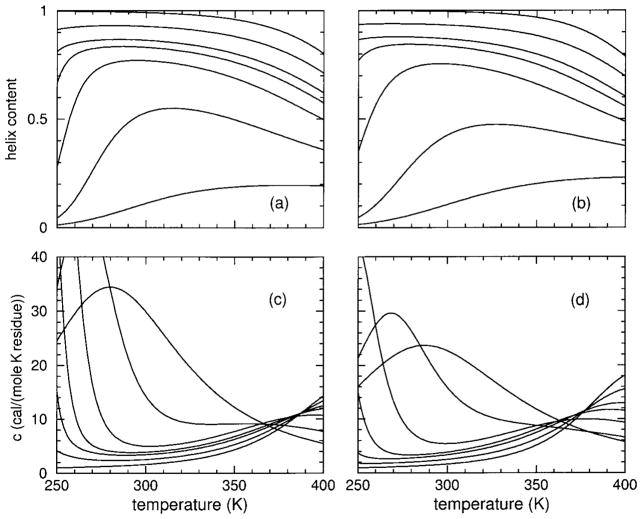
FIGURE 12.
Panels (a) and (b) show helix content for models I and II respectively applied to the sCT(8–32) polypeptide at 12% HFIP concentration. From bottom to top the curves correspond to chain lengths 5, 10, 15, 20, 25, 50, and 10,000. Panels (c) and (d) show the corresponding heat capacities for models I and II, respectively. At 300 K, from top to bottom the curves correspond to chain lengths 5, 10, 15, 20, 25, 50, and 10,000. Note that at other temperatures the ordering is different as heat capacity curves cross one another.
FIGURE 13.
Hydration content as a function of temperature for a variety of chain lengths is shown. Panels (a) and (b) respectively show the results of model I and II for the sCT(8–32) polypeptide at 8% HFIP concentration. From top to bottom the curves correspond to sizes 5, 15, 25, 40, 100, and 10000. Panels (c) and (d) show the corresponding information for models I and II at 12% HFIP concentration, where curves from top to bottom correspond to chain lengths of 5, 10, 15, and 20.
The dip and subsequent recovery of hydration content shown in Figure 13 is directly related to the cooperativity of the intramolecular H-bonds. The sharp decline in the hydrated state, with corresponding rise in the α-helical state, is a signature for structural self-organization. There is an optimal constraint topology that changes depending on the thermodynamic conditions. At 8% HFIP concentration and low temperature, a large amount of hydration is present. As the temperature is increased, hydration is disrupted due to the more stable conformations that contain many overlapping intramolecular spanning H-bonds. The longer chains have more influence in disrupting the hydration, as the H-bonds work collectively together. That is, redundant H-bonds are enthalpicly favorable, but do not add any entropic penalty. In general, regions of high density of H-bonds, will pay less entropic cost than otherwise would be expected if the same number and types of H-bonds were distributed as isolated units. However, as the temperature is further increased, the entropic penalty paid by the long strings of intact intramolecular backbone H-bonds becomes too great, resulting in the aaa H-bonds breaking, yielding to weaker intramolecular H-bonds and/or H-bonds to solvent. With this, disordered coil conformations appear as this is a strong entropic driving force. At this point, the hydration content approaches the limiting value it has when there is virtually no cooperativity from the H-bond network.
The sharpness of the transition(s) is greatly influenced by differences in slopes of the free energies of two limiting-states. The difference in pure entropies describing cold-denaturation for the sCT(8–32) polypeptide at 8% HFIP using models I and II are δa − δh = 1.88 and γaaa − δh = 1.32, respectively. The greater pure entropy difference in model I explains why it has a much sharper cold denaturation transition seen in Figure 11. Differences in pure entropies describing heat denaturation for models I and II are respectively δc − δa = 1.6 and δc − γaaa = 1.69. Model II exhibits greater heat capacity peaks than model I, although the pure entropy difference of model II is only slightly greater. Not surprisingly, the sharpness of the transition is more subtle to characterize than by a single pure entropy difference (or nucleation parameter) because of details in entropy replacements. Dependent on chain length, nonadditivity of component entropies is intimately tied to molecular cooperativity. Nevertheless, the nucleation parameter, v, in the LRM can most closely be related to differences in pure entropies, where ln(v) is given by −2(δc − δa) or −2(δc − γaaa) for models I or II—yielding estimates of 0.040 and 0.034 respectively for v. Interestingly, v = 0.0361 was used in a LRM to describe helix content for the melittin helix–coil transition in HFIP–aqueous solvent,60 where v was assumed independent of HFIP concentration. Here, differences in pure entropies linearly depend on HFIP concentration, implying cosolvents affect the ability of a polypeptide to initiate a helical structure.
Physical Significance of Parameters
The essential physics of the helix–coil transition in a polypeptide in mixed solvent has been captured using an effective one component solvent model. Excellent fits to measured CD data shown in Figures 1 and 2 were obtained using an effective homogeneous polypeptide requiring only 6 parameters that linearly depend on cosolvent concentration. With these simplifications and using 16 free parameters to fit 12 curves (6 curves per polypeptide as discussed in appendix B), an important question must be asked: How physically sound are the best-fit values listed in Table II? Since model II is more likely to have transferable H-bond parameters, and due to the similarity between the sCT(8–32) and YGG-3V polypeptides, only DCM parameters given in Table II for model II and sCT(8–32) are discussed here.
Correspondence with the LRM yields v = 0.015 in pure water and v = 0.115 at 20% HFIP, indicating the polypeptide nucleates into a helix more readily as HFIP concentration increases. This result is a consequence that δc decreases as HFIP concentration increases —physically implying proximity of HFIP restricts the polypeptide conformational space in the unsolvated coil more than mobile water. The greater steric hindrance presented by HFIP is presumably related to its mammoth size compared to water. This effect is supported by molecular dynamics simulations on melittin in HFIP–aqueous solution63,65 showing a decrease in mobility of the polypeptide via HFIP coating. There is also an increase in Vc as HFIP concentration increases — indicating HFIP–polypeptide interactions not involving H-bonding, such as van der Waals, are unfavorable compared to mobile water. These trends are also consistent with molecular dynamics simulations of Dwyer62 showing HFIP and trifluoroethanol (TFE) are superior helix initiators while retaining unfavorable interactions with the polypeptide.
Solvent H-bond interactions are characterized by the Uo parameter. Uo increases slightly with increasing HFIP concentration, but it can be regarded as approximately constant. It is worth noting that a large increase in Uo would provide a simple mechanism for HFIP induced helix formation. Early explanations along these lines were not successful, however, leading to investigations for alternative explanations.58–65 It is now well established that halogen alcohols provide (stronger, weaker) proton–(donor, acceptor) H-bonding capability than water.54,61 Unlike the GDM, the DCM presented here does not have individual terms describing CO— and NH— solvent H-bonds, but takes into account their average effect. Therefore, weak dependence on HFIP concentration for net change in energy to replace an intramolecular H-bond with two solvent H-bonds (comprising of normal-water, weak-HFIP, and strong-HFIP H-bonds) is consistent with H-bonding properties of halogen alcohols.
For infinite chain length, and as T → ∞, the ratio of helix to coil conformational entropies determine helix-saturation values. A smaller ratio of δc/γaaa implies greater steric hindrance by solvent molecules. The limiting saturation value will depend on chain length because of end-cap effects. Neglecting end-cap effects (as done here) yields a chain length independent saturation value, but the approach to this limiting value strongly depends on chain length as shown in Figures 10–12, also showing successive increase in saturation value. Helix content will be higher than the asymptotic saturation limit at accessible temperatures due to stabilizing enthalpic gain of intramolecular H-bonds and their cooperative effects. A subsequent decrease in helix content toward the saturation value will follow after an inverted transition. The shallow reduction at high HFIP concentrations seen in Figure 3 is consistent with the general arguement given by Gibbs and Dimarzio52 based on the unsolvated coil state being entropically more favorable. Thus, high concentration of HFIP destabilizes the unsolvated coil state by raising the helix content saturation value and suppressing the approach to the limiting value, eventually eliminating heat denaturation. These mechanistic explanations are consistent with the finding that TFE destabilizes the coil state.58
At low temperature and sufficiently low HFIP concentration, why is a helical structure unstable? This is where the hydrated state is invoked in the DCM. Clathrate structures (which dynamically form and break) are enthalpicaly more favorable than mobile solvent, but severely reduce conformational entropy.16,67 In mixed solvent, there will be residues with preferential hydration56,67 depending on their chemistry and whether they are buried or not. Here, all residues are treated equivalently, and preferential hydration is a statistical process driven by cosolvent concentration. Considering pure water, the best-fit parameters is Vh = −2.84 kcal/mole and δh = 0.763. The corresponding LRM nucleation parameter is v = 0.084, where in this case ln(v) is given by −2(δh − γaaa). Since v is large (for example, greater than 0.0361 used in other works60, helical conformations should initiate quite easily. However, there will be an enthalpic penalty too, and a helix cannot form until after the clathrate structures melt. Another helix initiation parameter is the z variable (see Table I) of the GDM. The closest correspondence shows z = e2(δc − γaaa) and z = e2(δh − γaaa) for helix → coil (normal) and coil → helix (inverted) transitions yielding z = 66.7 and z = 0.084 respectively. In addition, for a (normal, inverted) transition to occur, there must be a cost in energy to change from (helix → unsolvated coil, hydrated coil → helix) analogous to Table I given in the Gibbs and Dimarzio paper.52 At 20% HFIP, Vh = −2.20 and δh = 0.552, implying the addition of HFIP restricts the polypeptide more than pure water, but the clathrate structures themselves are not as enthalpically favorable. The latter trend is intuitive, as it can be expected that normal H-bond patterns are disturbed by HFIP. As Figure 9 shows, adding HFIP results in a lower melting point of clath-rate structures — in similar way the melting point of bulk water is lowered. This effect is a colligative property, also consistent with the linear-dependence assumption on free energy shifts.
The overall interpretation of the DCM parameters suggests the polypeptide prefers interacting with water, rather than HFIP. Then why doesn’t water push HFIP away from the polypeptide? The unfavorable cosolvent–polypeptide interactions are driven by experimental control, where increasing HFIP concentration increases polypeptide free energy as shown in Figure 7. The high activity of HFIP in water,66 and its micelle-like clustering behavior,61 explains why HFIP (and to a lesser extent TFE) dislikes the polypeptide less than water. Hydrophobic attributes of HFIP and TFE are found to make them good helix inducers.58,59,62,63 These bulk effects complete the big picture — showing that hydrophobic effects are driven by the bulk solvent properties.64 However, bulk solvent properties are part of a faceless thermodynamic reservoir in the DCM, reflected in the concentration dependence of parameters describing specific mechanisms actuated by an effective one-component solvent. Explicit modeling of hydration accounts for hydrophobic effects between polypeptide and solvent. The linear concentration dependence on parameters is expected to hold in the dilute limit, but is not a requirement nor expected to hold at high cosolvent concentrations. It has not escaped our attention that the enthalpy parameters could be linearly expanded as functions of pressure to addresses pressure induced cold denaturation.
The DCM provides a good interpretation for physical mechanisms responsible for cold and heat denaturation. However, the parameters in Table II should not be cast in stone, because multiple good fits are obtained with 16 parameters, implying there are physically multiple ways to achieve the same measured helix content for a polypeptide. Does this mean that the DCM is over parameterized? Absolutely not. The DCM has many parameters, but they are all physically well rooted, allowing the DCM to predict many response functions, such as heat capacity, hydration content, H-bond content, as well as absolute baselines, and changes in enthalpy, entropy and free energy. The uncertainty in the parameters given here appear because only helix content was used to determine them. It is worth mentioning that no bias was used in obtaining these parameters based on findings from literature. Knowing specific details in advance, it is possible to enforce trends, restrict parameter ranges, or fix parameter values. Most polypeptides will not show cold and heat denaturation over the accessible temperature range, simply because the limit-triangle shown in Figure 9 is difficult to achieve experimentally.20 We propose transferable parameters can be obtained by careful comparison to more experimental data using a variety of polypeptides, solutes, and most importantly different chain lengths. Undoubtedly these measurements will require using heterogeneous polypeptides.
Generalization to Heterogeneous Chains
The current source code that performs the DCM calculations is able to handle heterogeneous polypeptides, where each type of amino acid has its own set of 5 parameters given as {Vh, δh, Va ≡ 0, δa, Vc, δc}. Respecting differences between different types of residues introduces considerably more parameters. This, in turn, requires more experimental data to prevent overfitting. For example, the amount of experimental data used in this work was not sufficient to pin down 24 free parameters for two effective chains, and is far from sufficient to determine 5 parameters for each distinct residue contained within the sCT(8–32) and YGG-3V polypeptides. Only with much additional systematic experimental data that includes helix content and heat capacity for different chain lengths and different residue rearrangements, will it be possible to determine a transferable set of DCM parameters. Nevertheless, it is worth making a comparison in the nominal number of free parameters for the DCM and LRM for describing heterogeneous polypeptides in pure aqueous solvent.
Restricting the discussion only to α-helices, the number of DCM parameters for i to i + 4 backbone H-bonds as defined above is 17. This number derives from requiring an energy and pure entropy parameter for 23 types of intramolecular backbone H-bonds associated with conformations such as aaa, ccc, aca (i.e., no h-state is allowed) as well as an energy parameter to model H-bonding directly to solvent. The important point is that these parameters do not depend on the types of the three consecutive residues that the H-bond spans. Considering 20 different residues each requiring 5 parameters gives a nominal total of 117 DCM parameters. The generalized form of the LRM, which does not account for hydration effects, requires 2 parameters for each of the 23 possible conformations, such as aaa, ccc, aca. However, the LRM is based on 3-body interactions that couple different types of consecutive residues, leading to 203 different types of triplets. Thus, the nominal total parameter count tallies to 128,000. The situation is far worse than this because the so-called nucleation parameters (associated with each type of triplet) are actually functions of chain length due to their inherent nontransferability. Remarkably, with a variety of simplifications, such as using the same parameters for different types of triplet conformations and neglecting differences in residue types on the flanking ends of a triplet, many useful LRM parameterizations have been made over the years, but with noticeable problems.36 Perhaps the most sophisticated parameterization is applied in AGADIR,25 having more than 1000 parameters, but does take into account many effects not considered here. With modern computing power, applying the admittedly more mathematically complex DCM could possibly prove advantageous in self-consistently describing large amounts of experimental data on polypeptides with far fewer number of free parameters than has been accustomed.
The interesting prospect of applying the DCM to heterogeneous polypeptides is that it can be expected that some residues will have pure entropies for an α-helical conformation lower than a particular H-bond pure entropy, while other residues it will be greater. Thus, it would be very surprising if moving the different types of residues around, while maintaining the same composition, does not yield a different thermodynamic response. It is well known that residue rearrangement at fixed composition does shift transition temperatures and alters CD measurements.
CONCLUSION
A DCM has been employed to describe the helix–coil transition. Microscopic free energies are assigned to specific types of interactions, and the associated enthalpy and entropy contributions are assigned to distance constraints. Using network rigidity as a mechanical interaction, the entropic contributions are added over a preferential independent set of distance constraints. In this way, the problem of nonadditivity of entropies (or free energies) has been directly addressed, which was shown to be intimately connected to molecular cooperativity. The DCM is a general formalism that can be applied to biopolymers and other physical systems. The precise details of constructing constraint types remains unspecified, but the DCM formalism is specific in how to construct the partition function from component free energies. By focusing on the α-helix to coil transition, exact calculations were performed using a transfer matrix approach by taking advantage of the one dimensional topology of the problem. The transfer matrix is generally much larger than the transfer matrices used in other models, such as the Zimm–Bragg or Lifson–Roig models, because the DCM explicitly accounts for network rigidity, which is an inherently long-range interaction. The size of the transfer matrix depends on the details of constraint types considered in a problem.
It was demonstrated that a 6 parameter model can satisfactory describe inverted and normal transitions under poor and good solvent conditions. The essential constraint types used here model intramolecular backbone H-bonds, H-bonding to solvent, torsional forces associated with α-helical and disordered coil conformations, and a hydrated coil state that accounts for structured solvent. The hydrated state turns the usual two-state description into a three-state description, allowing the DCM to describe an inverted transition and cold denaturation. Besides the generalization of including a third type of state, the most significant aspect of the DCM is that it sums only independent entropy contributions determined by network rigidity. The nucleation process involved in a structural transition is an outcome of the rigidity properties, eliminating the inherently nontransferable nucleation parameter.
Under certain mixed solvent conditions, the DCM predicts that a polypeptide can exhibit both cold and heat denaturation. This could have been demonstrated easily by arbitrarily fixing parameters so as to emphasize the effects. Instead, parameters were used that gave excellent fits to experimental data of Andersen et al.,20 using aqueous solutions at various hexafluoroisopropanol (HFIP) concentration. The DCM parameterization assumed a linear dependence on HFIP concentration, and appears to be an adequate description at least up to 6% mole fraction. A new method was introduced for fitting to the experimental CD data that does not require a priori knowledge of temperature dependent baselines and saturation values, which is explained in detail in appendix B Two representative specialized models (I and II) were defined and parameterized. It was shown that the DCM is adequate to explain the experimental data, but there is not enough data to determine a good set of effective parameters without overfitting. In the future, better parameterizations can be obtained by fitting to measured CD and heat capacity data over systematic sets of polypeptides that include many heterogeneous polypeptides having same composition but different residue arrangements, different chain lengths, and under different mixed solvent conditions using one type of denaturant, such as HFIP. Lastly, measurements probing hydration content would also be desirable.
Acknowledgments
The authors are grateful for financial support from California State University, Northridge, the Research Corporation (CC5141), and to the NIH (GM48680-0952). We also wish to thank Dennis Livesay for many useful discussions. Our discussions on HFIP concentration dependence and physical significance of the DCM parameters was motivated by an anonymous referee, who we thank for pointing us to relevant literature.
APPENDIX A
For completeness, the rules on how to propagate rigidity along the polypeptide while at the same time determining the preferential independent set of constraints is described. This procedure gives the minimum possible total conformational entropy consistent with network rigidity. Each residue has two dihedral angles, and these are constrained to be in a particular conformational state, such as α-helical, hydrated, or disordered coil by torsion constraints. Since proline is not considered here, two distance constraints are used per torsion constraint. In addition to these three types of torsion constraints, there is also H-bond constraints that start from the ith to (i + 4)th residue. The H-bond is modeled as three distance constraints. When an intramolecular H-bond is present, it spans three consecutive residues that contain three torsional constraints involving six distance constraints. Including the three H-bond distance constraints, there are a total of 9 distance constraints 6 of which will be independent.
The procedure begins by rank ordering the pure entropy values associated with each type of constraint. Entropies for the torsional constraints that specify the conformational states along the backbone are listed in consecutive order from the N-terminus to the C-terminus. Two pure entropies (taken to be degenerate) are listed per residue to account for the ϕ and ψ dihedral angles. A H-bond has three pure entropies (taken to be degenerate). Working from the N-terminus (the rules also work starting from the C-terminus), the pure entropies of the torsional constraints can potentially be replaced by those from H-bonding whenever the pure entropy of a H-bond is lower than those of the torsion constraints it spans. The question now becomes, which pure entropies should be replaced to yield the minimum overall entropy, while remaining consistent with network rigidity. The answer to this question is explained in detail elsewhere,32 but is briefly described below with illustrative examples, not given before.
The replacement question is answered by the following algorithm: For each H-bond constraint encountered, working from the N- to C-terminus, replace the largest pure entropy available whenever the pure entropy of the H-bond is smaller. If there are multiple equal largest entropies, select the furthest back from the direction of propagation (taken as the leftmost) position. After replacement, consider all entropies to the left of the replacement. If any of these are larger than the replacement value, swap the replacement value with the largest value found to the left. Again, in the case of a tie, choose the leftmost position to swap with. Repeat looking left and continue to swap entropies with the next available largest values (if any) until no larger values exist to the left, or until all six ranks spanned by the H-bond have been checked. Swapping is necessary because H-bonds that might be encountered to the right as the right propagation continues can possibly change which value the earlier H-bonds should have replaced. This swapping procedure properly allows for any eventuality.
Computing the partition function requires summation over all accessible frameworks consisting of all possible conformations and H-bond configurations. Before working into these details, some short example conformations will be considered. A shorthand notation is employed to illustrate the algorithm. Each entropy (δ or γ) is replaced with its rank. Rank 1 corresponds to the lowest entropy and so on. For the purpose of these examples, consider a specific rank ordering:
| (12) |
Note that rank 0 is used for boundary conditions, which are not discussed here, but are detailed in previous work.32 First consider a triplet of states, aāc, that is spanned by a H-bond. The H-bond is indicated by the bar over the center residue. The rank of the aac H-bond is 3, the a-conformation has rank of 4, and the c-conformation has rank of 7. Translating this segment into 9 ranks, gives (4, 4)(4, 4)(7, 7) + (3, 3, 3). Propagating from left to right, the first entropy re placement gives (4, 4)(4, 4)(3, 7) + (3, 3), then after swapping with larger ranks to the left yields (3, 4)(4, 4)(4, 7) + (3, 3). The next replacement gives (3, 4)(4, 4)(4, 3) + (3), then after swapping with larger ranks to the left yields (3, 3)(4, 4)(4, 4) + (3). After the final replacement and swapping, the triplet has the rank ordering of (3, 3)(3, 4)(4, 4). The swapping allows a later H-bond to replace the 4’s at the end, instead of a 3 to hedge against replacing to much or too little. If a future H-bond rank replaces a 4, it can be regarded as replacing a 7, with the original H-bond rank replacing a 4.
Now consider the segment cc̄āa as a longer example. The first H-bond spanning cca has a rank of 5 and the second H-bond spanning caa has a rank of 3. Propagating from left to right, the first H-bond with three rank 5 constraints is placed first, and is compared to the ranks of the six constraints associated with the three residues it spans. Thus the first triplet, cc̄a is translated into 9 ranks given as (7, 7)(7, 7)(4, 4) + (5, 5, 5). After the first H-bond is placed, by replacing one rank at a time followed by all necessary swapping, the final ranking of the 4-residue segment is given by (5, 5)(5, 7)(4, 4)(4, 4) + (3, 3, 3), where the two leftmost ranks of 5 are out of range of the second H-bond and can no longer be replaced by anything lower. After the second H-bond placement, the final ranking of the 4-residue segment is given by (5, 5)(3, 3)(3, 4)(4, 4). Note the second H-bond replaced a constraint of the earlier (weaker) bond. No distinction is made between the origins of the rank values as propagation continues. To illustrate that the same final rank count is obtained by propagation from right to left, consider the placement of the first H-bond. The rank ordering is given by (5, 5, 5) + (7, 7)(4, 4)(4, 3)(3, 3), where after the second H-bond is placed gives a final rank ordering of (5, 5)(4, 4)(4, 3)(3, 3). Note only two of the second H-bond’s three constraints are used, since it is a weaker constraint and its third distance constraint is actually redundant. Although the order of ranks differ between the directions of propagation, the number of each rank is the same.
A much larger 16-residue example is now considered. Near the transition temperature for cold denaturation, one can imagine finding a conformation in state hhhcaaaachcchhhh. To begin, consider model I, where H-bonds can only form over aaa-triplets. There are only two locations that an intramolecular H-bond can form. The first position spans the first consecutive triplet of a-conformations, and the second position is located at the right neighboring aaa triplet. Once both conformational and H-bond configurations are specified, computation of the total enthalpy and entropy of the chain is possible. Consider a H-bond configuration where both H-bonds are present. The energy of the state is straightforward: four coil states, four α-helical states, eight hydrated states, two intramolecular H-bonds and 12 H-bonds to solvent. These enthalpies add. The total entropy is the sum over contributions only from the preferential set of independent constraints. This is trivial to evaluate when δc > γaaa > δa > δh, as there are no entropy replacements, yielding a sum of 2(8δh + 4δa + 4δc). However, if the pure entropies were ordered as δc > δa > γaaa > δh, then the total pure entropy is given by 16δh + 2δa+ 6γaaa + 8δc. Note that for a chain of length n residues, there will always be 2n entropy terms— enough to constrain (lock) all the ϕ and ψ angles. However, in general there will be more than n energy terms.
Although the above 16-residue example is rather simple, the complexity grows when model II is considered. In model II, H-bonds can span a variety of different triplet types. Moreover, H-bond pure entropy ranks cannot only replace the helix or coil states, but also can replace each other. A minimum of five consecutive H-bonds is necessary to potentially begin replacing one H-bond entropy by another. The rules described above handle all these complications.
Working with model II, five 16-residue examples are considered with the initial torsional ranks listed. The final rank ordering obtained by applying the above propagation rules from left to right, fully taking into account any intramolecular H-bonds present, is listed in Table III. The rank orderings used in these next five examples are displayed in Eq. (12), which were used in the initial short segment examples. Here, however, the rank orderings are shown in compressed notation, noting that all ranks are only single digits.
Table III.
Example A.1
| Framework 1 | hhhcācaāāc̄ccaācc |
| Initial ranks | 11111177447744444477777744447777 |
| Final ranks | 11111155445722233344557733344477 |
The framework listed in example A.1 will be taken as an initial state from which four new states will be derived by minor perturbations. Counting from the left, the next four examples are related to changes at positions in the seventh and the thirteenth residues. The initial reference framework is repeated for making easy comparisons in the differences between final and initial frameworks. To illustrate long-range effects, the next two examples A.2 and A.3—Tables IV and V respectively) add one H-bond in different locations along the chain, but are placed over identical triplets where the initial state having triplet caā changes to cāā. Changes in energy (enthalpy) and entropy are listed with respect to the initial state in example A.1.
Table IV.
Example A.2
| Framework 1 | hhhcācaāāc̄ccaācc |
| Framework 2 | hhhcācāāāc̄ccaācc |
| Initial ranks | 11111177447744444477777744447777 |
| Final ranks | 11111155443322233334557733344477 |
| ΔE = E2 − E1 | Ucaa − U0 |
| ΔS = S2 − S1 | R(3γaca − δa − γcac − δc) |
Table V.
Example A.3
| Framework 1 | hhhcācaāāc̄ccaācc |
| Framework 3 | hhhcācaāāc̄ccāācc |
| Initial ranks | 11111177447744444477777744447777 |
| Final ranks | 11111155445722233344553333334477 |
| ΔE = E3 − E1 | Ucaa − U0 |
| ΔS = S3 − S1 | R(3γaca − δa − 2δc) |
In the final ranks (Table IV) boldface numbers indicate the ranks that differ from the original final rank ordering given in example A.1. The first two rank 3’s have replaced a 5 and a 7 because of the new H-bond. The third rank replacement occurs seven dihedral angles down the chain. Consider the third example (Table V).
Examining the ΔE columns from examples A.2 and A.3, we find them identical, yet the ΔS columns differ. In A.3, a rank 7 was replaced instead of the rank 5 that occurred in example A.2. So despite having identical nearest neighbors, the difference in next-nearest neighbors effects the entropy. More exotic examples can arise in which even the next-nearest neighbors can be identical, yet differences will arise due to the long-range nature of network rigidity. A fourth and fifth example is considered in Tables VI and VII.
Table VI.
Example A.4
| Framework 1 | hhhcācaāāc̄ccaācc |
| Framework 4 | hhhcāccāāc̄ccaācc |
| Initial ranks | 11111177447744444477777744447777 |
| Final ranks | 11111155445733333344557733344477 |
| ΔE = E4 − E1 | Ucaa − Uaaa + Vc − Vh |
| ΔS = S4 − S1 | R(3γaca − 3γaaa) |
Table VII.
Example A.5
| Framework 1 | hhhcācaāāc̄ccaācc |
| Framework 5 | hhhcācaāāc̄cccācc |
| Initial ranks | 11111177447744444477777744447777 |
| Final ranks | 11111155445722233344557755445777 |
| ΔE = E5 − E1 | Ucac − Uaac + Vc − Vh |
| ΔS = S5 − S1 | R(3γcca − 3γaca − δa + δc) |
Examples A.4 and A.5 consist of changing the a-conformation to a c-conformation at the seventh and thirteenth residue respectively. The changes in energy and entropy are due to next nearest neighbor effects and the long-range nature of network rigidity.
Transfer Matrix
The transfer matrix is constructed from a direct product space formed by a triplet conformational state denoted by |λ, x,y,z〉, where λ is one when a H-bond spans the x,y,z triplet, zero otherwise, and x,y,z are either helix (a), hydrated (h), or coil (c). A triplet is completely specified as
| (13) |
where r1 and r2 are the ranks of the constraints on the ϕ and ψ backbone dihedral angles of the x state, and r3 and r4 are the corresponding ranks of the constraints on the y state. The 4 ranks on the first two amino acids, the presence or absence of a spanning H-bond, and the conformational state (hydrated, helix, or coil) of each residue together completely specify a state. Most elements of the transfer matrix, T, will be zero. The nonzero matrix elements have the form given by
| (14) |
The matrix elements will only be nonzero if the set of final ranks in the local rigidity state obeys the rigidity propagation rules. The nonzero matrix element then contributes a Boltzmann factor that accounts for both the energy and pure entropy contributions of the constraints encountered. The variables Δτp and Δεp respectively represent the change in pure entropy and energy upon propagation of one step along the chain. The contribution to Δτp at each propagation step is given by the sum of pure entropies of the two constraints that permanently lock the two degrees of freedom within the first amino acid of a triplet. Thus Δτp is determined by the rigidity state space in accordance with the rigidity propagation rules described above. In contrast, Δεp is determined by the conformational state space where it is a function of only λ[xyz] and it is found by summing the H-bond energy given by Uxyz when λ = 1 and U0 when λ = 0, and with the torsional force constraint energy given by Vx. By construction, the zeros and nonzeros of the transfer matrix accounts for the rigidity propagation rules, thereby correctly propagating rigidity. As such, the matrix size is necessarily bigger than a transfer matrix not accounting for correlations induced by network rigidity.
Exact DCM calculations describing a helix–coil transition is not difficult to perform using large transfer matrices with todays computers. The greatest difficulty is to set up the transfer matrix that accounts for the long-range nature of network rigidity. As such, the size of the transfer matrix cannot be a priori determined as it depends on the values of the model parameters.32 For example, Model I requires a 21 × 21 matrix, whereas model II requires a 305 × 305 matrix. The dimension of the matrix reported here does not include the auxiliary boundary states, as was the way matrix size was reported in earlier work.32 The same matrix sizes were required for both polypeptides because the pure entropy rankings were identical, despite differences in numerical values. The matrix size is large in order to account for correlations induced by network rigidity. A large matrix gives some indication that there is considerable amount of competition between different types of interactions and/or the transition will exhibit a high degree of cooperativity. Although these details are important, the essential features of the transition can be understood in terms of a three-state model, similar to Schellman’s two-state model.1,2
APPENDIX B
To compare directly to experimental results, it is necessary to select baselines for the CD experiments. Instead of a priori choosing arbitrary baselines, we developed a method that intrinsically computes optimal baselines for fitting the data. Finding the best fit between the theoretical prediction for fraction of helix content, θa, to CD measurement, θ221, begins by computing θa vs temperature for a given set of model parameters. Assuming a linear relationship as specified by Eq. (6), a linear least squares fit is calculated by plotting θa versus θ221 at their respective temperatures. As shown in Figure 14 for polypeptides sCT(8–32) and YGG-3V, a different linear fit is allowed for each HFIP concentration. By simulated annealing, the DCM parameters are adjusted and eventually fine-tuned to obtain the best set of linear fits. With this method, recourse to temperature-dependent baselines is not needed, leaving only the single most commonly used assumption that each experimental curve has a linear correspondence to helix content.
FIGURE 14.
For the best-fit set of DCM parameters specified in Table II, linear fits between calculated fraction of helix content vs the raw CD experimental measurement is shown. Panels (a) and (c) show the results for model I and II, respectively, for polypeptide sCT(8–32), and the symbols down triangle, left triangle, up triangle, diamond, square, and circle correspond to 25, 12, 10, 8, 7, and 0% HFIP concentration. In (a) the 7% concentration is not shown for clarity. Likewise, panels (b) and (d) show models I and II results for polypeptide YGG-3V. The symbols down triangle, left triangle, up triangle, diamond, and circle correspond to 20, 10, 8, 7, and 0% HFIP concentration, where the 6% concentration is not shown for clarity. The solid straight lines through the data points are the linear least squares fits. The slopes and y-intercepts defining the linear transformation of Eq. six are given in Tables VIII and IX for polypeptides sCT(8–32) and YGG-3V.
A set of linear transform variables is given for both model I and II in Table VIII for polypeptide sCT(8–32) and in Table IX for polypeptide YGG-3V. These tables also specify the precise sequence of the polypeptides used in the experiment. The slope and y-intercepts are not model parameters, but do depend on the model employed and the values of the DCM parameters. Note that the very small slopes corresponding to pure water and extreme high HFIP concentrations result in helix content curves that are nearly independent of temperature. Effectively, Andersen et al. achieved the same result by transforming all curves by temperature-dependent baselines that are nearly parallel to the pure water and maximum concentration curves that were measured [25 and 20% for sCT(8–32) and YGG-3V respectively]. The y-intercepts approach unity at extremely high concentration of HFIP. The y-intercepts for the pure water and high HFIP concentration curves have special meaning. In these cases, because the experimental curves are nearly straight lines, and the slopes are very small, the y-intercept roughly gives the fraction of helix content. It is found in both polypeptides (as predicted by models I and II) that fractional helix content is neither completely zero or unity in the extreme limits. As the polypeptides do not solely consist of excellent helix formers (or breakers) and are of finite length, it is not expected that they should achieve a complete saturation on either side of the transition. Andersen et al. achieved the same effect by leaving a gap between employed straight line temperature dependent baselines with respect to the data obtained at extreme limits.
Table VIII.
The HFIP Concentration-Dependent Transformations (Slopes and y-Intercepts) for Polypeptide sCT(8–32) Obtained from Least Squares Linear Regression for Models I and II
| sCT(8–32) % HFIP | VLGKLSQELHKLQTYPRTNTGSGTPNH2
|
|||
|---|---|---|---|---|
| Model I
|
Model II
|
|||
| a | b | a | b | |
| 0 | −8.66 × 10−3 | 1.86 × 10−3 | −1.79 × 10−2 | −1.49 × 10−2 |
| 6 | −2.32 × 10−2 | −1.18 × 10−2 | −4.02 × 10−2 | −3.48 × 10−2 |
| 8 | −2.89 × 10−2 | 2.53 × 10−2 | −3.92 × 10−2 | 4.74 × 10−2 |
| 10 | −3.82 × 10−2 | 0.239 | −3.48 × 10−2 | 0.284 |
| 12 | −1.60 × 10−2 | 0.614 | −2.00 × 10−2 | 0.563 |
| 25 | −3.57 × 10−3 | 0.930 | −3.71 × 10−3 | 0.920 |
Table IX.
The HFIP Concentration-Dependent Transformations (Slopes and y-Intercepts) for Polypeptide YGG-3V Obtained from Least Squares Linear Regression for Models I and II
| YGG-3V % HFIP | AcYGGKAVAAKAVAAKAVAAKNH2
|
|||
|---|---|---|---|---|
| Model I
|
Model II
|
|||
| a | b | a | b | |
| 0 | −6.17 × 10−3 | 1.61 × 10−2 | −1.21 × 10−2 | 1.32 × 10−2 |
| 6 | −1.09 × 10−2 | 1.48 × 10−2 | −1.73 × 10−2 | 1.15 × 10−2 |
| 7 | −1.15 × 10−2 | 3.10 × 10−2 | −1.70 × 10−2 | 4.50 × 10−2 |
| 8 | −1.27 × 10−2 | 6.82 × 10−2 | −1.56 × 10−2 | 0.108 |
| 10 | −1.77 × 10−2 | 0.297 | −1.56 × 10−2 | 0.342 |
| 20 | −2.33 × 10−3 | 0.898 | −2.57 × 10−3 | 0.883 |
The DCM appears to have more parameters than the commonly used LRM, because it nominally requires two parameters for each interaction that is explicitly considered. The two models introduced here require 6 parameters that are temperature and chain-length independent. Further, these parameters do depend on denaturant concentration. By assuming a linear dependence on HFIP concentration, all 6 curves obtained from experiment are described by 12 free parameters. Two free parameters per curve yields considerably fewer parameters than applying the LRM for each curve separately (as is usual practice) requiring minimally 18 model parameters in addition to two baseline parameters per curve. If there had been n curves measured, at more denaturant concentrations and perhaps different chain lengths, the number of DCM parameters remains constant, while the number of LRM parameters increase linearly with n, characterizing the size of the dataset. The dependence on dataset size is a direct result from not having model parameter transferability. The DCM has the potential to produce transferable model parameters. One step toward demonstrating transferability is to explicitly show that large datasets can be self-consistently fitted with a relatively small number of free model parameters.
In attempting to fit to the 6 curves for each polypeptide, while employing either model I or II and using 12 free model parameters with two fitted baseline parameters a and b per curve, it was found that in each case a multitude of excellent best-fit solutions can be obtained. Unfortunately, many of the parameters were not consistent in their trends between the different best-fit solutions from simulated annealing—indicating that the 12 parameters are overfitting the data. Since many different effects are competing, it is not possible with the limited data at hand to completely determine the best set of model parameters that are most physically meaningful and transferable. Instead of fitting the two datasets individually, each having 6 curves, a dual fitting to all 12 curves for both polypeptides were simultaneously fitted, nominally requiring 24 parameters. However, many of these parameters were arbitrarily taken to be polypeptide independent, with some justification offered as follows. Since both polypeptides behave similarly to one another, it is reasonable to expect their dependence on HFIP concentration to be similar. Therefore, all slope parameters for both polypeptides were constrained to be the same, reducing the nominal total number of free model parameters from 24 to 18. This restriction forces all HFIP concentration-dependent trends to be the same. The remarkable similarity between the two polypeptides could be an artifact of requiring the slope parameters to be identical. With more experimental data, this arbitrary choice will not be necessary.
Parameters associated with solvent–peptide properties, such as the coil and hydrated states, are expected to be most affected by solvent conditions, while intramolecular H-bonding and α-helical conformation parameters are expected (or at least desired) to be independent of denaturant concentration. To this end, (d/dc) Va and (d/dc) δa were set to zero. Thus, 16 parameters were used in both models I and II to fit to 12 curves simultaneously using simulated annealing.
References
- 1.Schellman JA. Compt-Rend Lab Carlsberg, Sér Chim. 1955;29(15):230–259. [PubMed] [Google Scholar]
- 2.Schellman JA. J Phys Chem. 1958;62:1485–1492. [Google Scholar]
- 3.Kishimoto A, Mutai T, Araki K. Chem Commun (Camb) 2003;21(6):742–743. doi: 10.1039/b212851a. [DOI] [PubMed] [Google Scholar]
- 4.Wallimann P, et al. J Am Chem Soc. 2003;125(5):1203–1220. doi: 10.1021/ja0275360. [DOI] [PubMed] [Google Scholar]
- 5.Lapidus LJ, Eaton WA, Hofricheter J. J Mol Biol. 2002;319(1):19–25. doi: 10.1016/S0022-2836(02)00193-6. [DOI] [PubMed] [Google Scholar]
- 6.Aremin R, Alonso DO, Daggett V. Protein Sci. 2003;12(6):1145–1157. doi: 10.1110/ps.0240103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Garcia AE, Sanbonmatsu KY. Proc Natl Acad Sci USA. 2002;99(5):2782–2787. doi: 10.1073/pnas.042496899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kise KJ, Bowler BE. Biochemistry. 2002;41(52):15826–15837. doi: 10.1021/bi026608x. [DOI] [PubMed] [Google Scholar]
- 9.Lowe SL, et al. J Pept Res. 2003;61(4):189–201. doi: 10.1034/j.1399-3011.2003.00046.x. [DOI] [PubMed] [Google Scholar]
- 10.Witter R, et al. J Biomol NMR. 2002;24(4):277–289. doi: 10.1023/a:1021625231147. [DOI] [PubMed] [Google Scholar]
- 11.Doty P, Bradbury JA, Holtzer AM. J Am Chem Soc. 1956;78:947–954. [Google Scholar]
- 12.Tong MM, Pinock RE. Biochemistry. 1969;8:908–913. doi: 10.1021/bi00831a021. [DOI] [PubMed] [Google Scholar]
- 13.Lin SH, Von Wart HE. Biochemistry. 1982;21(22):5528–5533. doi: 10.1021/bi00265a023. [DOI] [PubMed] [Google Scholar]
- 14.Foguel D, Weber G. J Biol Chem. 1995;270(48):28759–28766. doi: 10.1074/jbc.270.48.28759. [DOI] [PubMed] [Google Scholar]
- 15.Ballard JJ, Nash D. Biophys J. 1998;75(1):445–452. doi: 10.1016/S0006-3495(98)77532-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Privalov PL, Gill SJ. Adv Protein Chem. 1988;39:193–234. doi: 10.1016/s0065-3233(08)60377-0. [DOI] [PubMed] [Google Scholar]
- 17.Holtzer ME, et al. Biophys J. 2000;78(4):2037–2048. doi: 10.1016/S0006-3495(00)76751-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ooi T, Oobtake M. Proc Nat Acad Sci USA. 1991;88(7):2859–2863. doi: 10.1073/pnas.88.7.2859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Boice JA, et al. Biochemistry. 1996;35(46):14480–14485. doi: 10.1021/bi961831d. [DOI] [PubMed] [Google Scholar]
- 20.Andersen NH, et al. J Am Chem Soc. 1996;118:10309–10310. [Google Scholar]
- 21.Doig AJ. Biophys Chem. 2002;101–102:281–293. doi: 10.1016/s0301-4622(02)00170-9. [DOI] [PubMed] [Google Scholar]
- 22.Zimm BH, Bragg JK. J Chem Phys. 1958;31(2):526–535. [Google Scholar]
- 23.Lifson S, Roig A. J Chem Phys. 1961;34:1963–1974. [Google Scholar]
- 24.Gans PJ, et al. Biopolymers. 1991;31(13):1605–1614. doi: 10.1002/bip.360311315. [DOI] [PubMed] [Google Scholar]
- 25.Munoz V, Serrano L. Nature Struct Biol. 1994;1:299–409. doi: 10.1038/nsb0694-399. [DOI] [PubMed] [Google Scholar]
- 26.Muñoz V, Serrano L. J Mol Biol. 1995;245:275–296. doi: 10.1006/jmbi.1994.0023. [DOI] [PubMed] [Google Scholar]
- 27.Bierzynski A, Pawlowski K. Acta Biochim Polonica. 1997;44:423–432. [PubMed] [Google Scholar]
- 28.Scheraga HA, Vila JA, Ripoll DR. Biophys Chem. 2002;101–102:255–265. doi: 10.1016/s0301-4622(02)00175-8. [DOI] [PubMed] [Google Scholar]
- 29.Poland D, Scheraga HA. Statistical Mechanical Theory of Order–Disorder Transitions in Biological Macromolecules. Academic Press; New York: 1970. Theory of Helix-Coil Transitions in Biopolymers. [Google Scholar]
- 30.Mark AE, van Gunsteren WF. J Mol Biol. 1994;240:167–176. doi: 10.1006/jmbi.1994.1430. [DOI] [PubMed] [Google Scholar]
- 31.Dill KA. J Biol Chem. 1997;272(2):701–704. doi: 10.1074/jbc.272.2.701. [DOI] [PubMed] [Google Scholar]
- 32.Jacobs DJ, Dallakayan S, Wood GG, Heckathorne A. Phys Rev E. 2003;68:061109. doi: 10.1103/PhysRevE.68.061109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hallerbach B, Hinz HJ. Biophys Chem. 1999;76:219–227. doi: 10.1016/s0301-4622(98)00239-7. [DOI] [PubMed] [Google Scholar]
- 34.Dill KA, Stigter D. Adv Protein Chem. 1995;46:59–104. doi: 10.1016/s0065-3233(08)60332-0. [DOI] [PubMed] [Google Scholar]
- 35.Wetlaufer DB. Trends Biochem Sci. 1990;15(11):414–415. doi: 10.1016/0968-0004(90)90275-g. [DOI] [PubMed] [Google Scholar]
- 36.Bierzynski A. Comments Mol Cell Biophys. 1987;4:189–214. [Google Scholar]
- 37.Thorpe MF, Duxbury PM, editors. Rigidity Theory and Applications. Plenum; New York: 1999. pp. 357–384. [Google Scholar]
- 38.Graver J, Servatius B, Servatius H. Combinatorial rigidity; American Math Society; Providence: 1993. [Google Scholar]
- 39.Jacobs DJ, Rader A, Kuhn LA, Thorpe MF. Proteins. 2001;44:150. doi: 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
- 40.Thorpe MF, Rader A, Lei M, Jacobs DJ, Kuhn LA. J Mol Graphics Modeling. 2001;19:60–69. doi: 10.1016/s1093-3263(00)00122-4. [DOI] [PubMed] [Google Scholar]
- 41.Hespenheide BM, Rader AJ, Thorpe MF, Kuhn LA. J Mol Graphics Modeling. 2002;21:195–207. doi: 10.1016/s1093-3263(02)00146-8. [DOI] [PubMed] [Google Scholar]
- 42.Rader AJ, Hespenheide BM, Kuhn LA, Thorpe MF. Proc Natl Acad Sci USA. 2002;99:3540–3545. doi: 10.1073/pnas.062492699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jacobs DJ, Thorpe MF. Phys Rev Lett. 1995;75:4051–4055. doi: 10.1103/PhysRevLett.75.4051. [DOI] [PubMed] [Google Scholar]
- 44.Moukarzel C, Duxbury PM. Phys Rev Lett. 1995;75:4055–4058. doi: 10.1103/PhysRevLett.75.4055. [DOI] [PubMed] [Google Scholar]
- 45.Jacobs DJ, Hendrickson B. Comput Phys. 1997;137:346–365. [Google Scholar]
- 46.Jacobs DJ. J Phys A Math Gen. 1998;31:6653–6668. [Google Scholar]
- 47.Jacobs DJ, Thorpe MF. 6014449. US Pat. 1998 Feb 20;
- 48.http://firstweb.asu.edu/. Web site maintained by Thorpe, M. F.
- 49.Jacobs DJ, Kuhn LA, Thorpe MF. In: Rigidity Theory and Applications; Thorpe MF, Duxbury PM, editors. Plenum Publishing; New York: 1999. pp. 357–384. [Google Scholar]
- 50.Ramachandran GN, Ramakrishnan C, Sasisekharan V. J Mol Biol. 1963;7:95–99. doi: 10.1016/s0022-2836(63)80023-6. [DOI] [PubMed] [Google Scholar]
- 51.Lovell SC, Davis IW, Arendall WB, III, de Bakker PIW, Word JM, Prisant MG, Richardson JS, Richardson DC. Proteins. 2003;50:437–450. doi: 10.1002/prot.10286. [DOI] [PubMed] [Google Scholar]
- 52.Gibbs JH, DiMarzio EA. J Chem Phys. 1959;30:271–282. [Google Scholar]
- 53.Dallakyan S, Jacobs DJ. unpublished data. [Google Scholar]
- 54.Mitsutake A, Okamoto Y. Chem Phys Lett. 1999;309:95–100. [Google Scholar]
- 55.Peng Y, Hansmann UHE, Alves NA. J Phys Chem. 2003;118(5):2374–2380. [Google Scholar]
- 56.Timasheff SN. Adv Protein Chem. 1998;51:355–432. doi: 10.1016/s0065-3233(08)60656-7. [DOI] [PubMed] [Google Scholar]
- 57.Murto J, Kivinen A, Kivimaa S, Laakso R. Suomen Kem B. 1967;40:250–257. [Google Scholar]
- 58.Cammers-Goodwin A, Allen TJ, Oslick SL, McClure KF, Lee JH, Kemp DS. J Am Chem Soc. 1996;118:3082–3090. [Google Scholar]
- 59.Rajan R, Balaram P. Int J Peptide Protein Res. 1996;48:328–336. doi: 10.1111/j.1399-3011.1996.tb00849.x. [DOI] [PubMed] [Google Scholar]
- 60.Hirota N, Mizuno K, Goto Y. J Mol Biol. 1998;275:365–378. doi: 10.1006/jmbi.1997.1468. [DOI] [PubMed] [Google Scholar]
- 61.Hong D, Hoshino M, Kuboi R, Goto Y. J Am Chem Soc. 1999;121:8427–8433. [Google Scholar]
- 62.Dwyer DS. Biopolymers. 1999;49:635–645. doi: 10.1002/(SICI)1097-0282(199906)49:7<635::AID-BIP8>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- 63.Fioroni M, Burger K, Mark AE, Roccatano D. J Phys Chem B. 2001;105:10967–10975. [Google Scholar]
- 64.Eggers DK, Valentine JS. J Mol Biol. 2001;314:911–922. doi: 10.1006/jmbi.2001.5166. [DOI] [PubMed] [Google Scholar]
- 65.Diaz MD, Fioroni M, Burger K, Berger S. Chem Eur J. 2002;8:1663–1669. doi: 10.1002/1521-3765(20020402)8:7<1663::aid-chem1663>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- 66.Murto J, Kivinen A. Suomen Kem B. 1967;40:258–264. [Google Scholar]
- 67.Brandts JF, Hunt L. J Am Chem Soc. 1967;89:4826–4838. doi: 10.1021/ja00995a002. [DOI] [PubMed] [Google Scholar]