Critical behavior of subcellular density organization during neutrophil activation and migration

Abstract

Physical theories of active matter continue to provide a quantitative understanding of dynamic cellular phenomena, including cell locomotion. Although various investigations of the rheology of cells have identified important viscoelastic and traction force parameters for use in these theoretical approaches, a key variable has remained elusive both in theoretical and experimental approaches: the spatiotemporal behavior of the subcellular density. The evolution of the subcellular density has been qualitatively observed for decades as it provides the source of image contrast in label-free imaging modalities (e.g., differential interference contrast, phase contrast) used to investigate cellular specimens. While these modalities directly visualize cell structure, they do not provide quantitative access to the structures being visualized. We present an established quantitative imaging approach, non-interferometric quantitative phase microscopy, to elucidate the subcellular density dynamics in neutrophils undergoing chemokinesis following uniform bacterial peptide stimulation. Through this approach, we identify a power law dependence of the neutrophil mean density on time with a critical point, suggesting a critical density is required for motility on 2D substrates. Next we elucidate a continuum law relating mean cell density, area, and total mass that is conserved during neutrophil polarization and migration. Together, our approach and quantitative findings will enable investigators to define the physics coupling cytoskeletal dynamics with subcellular density dynamics during cell migration.

INTRODUCTION

Neutrophils, the most plentiful white blood cell population, are a central component of the innate immune system. These highly mobile first-responders to infection actively search out, recognize, and destroy bacteria. Neutrophil locomotion is controlled by external cues of mechanical, electrical, and chemical origin.^19,23,27 These stimuli activate molecular signaling networks that dynamically remodel the cellular cytoskeleton and its focal adhesions to the surrounding microenvironment to enable directed motility.²⁰

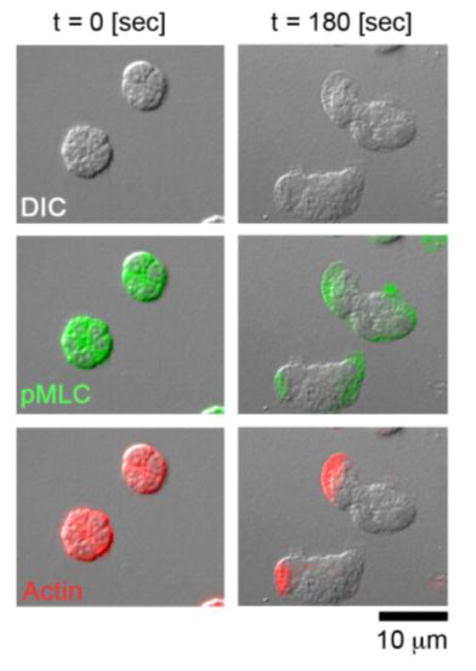
The molecular basis of neutrophil locomotion following bacterial exposure is well characterized: upon stimulation through activation of G-protein coupled receptors, neutrophils extend membrane protrusions in the direction of the attractant through Rac mediated filamentous actin assembly at the leading edge (LE) of the cell. At the trailing edge (TE), membrane contraction is regulated through RhoA stimulation of ROCK and myosin light chain II (Figure 1). Spanning the entire cell body is a microtubule network (MN) that serves as both a sink and delivery system for cytoskeletal effectors of the LE and TE of the neutrophil.¹⁵ The crosstalk among molecular components of the LE, TE, and MN are required for the coordination of cellular shape change and motility.^8,11 Pharmacologic perturbations of this circuitry have revealed that the LE recruits the SCAR/WAVE complex, which both shapes the actin architecture and provides a scaffold for inhibitors of RhoA/myosin components specific to the TE.²⁵ In tandem, the TE of the cell opposes actin-based membrane protrusion.²⁶ The MN delivers Rho family guanine nucleotide exchange factors to locally activate Rho/myosin components of the TE, while actin polymerized at the LE physically excludes the MN.^4,10 Together, these molecular events give rise to cell-wide coordination of membrane protrusions, retractions, and adhesions to bring about a polarized cell shape (Figure 1) and directed cellular motion.⁷

FIGURE 1. Cytoskeletal dynamics underlying neutrophil migration.

DIC imagery (first row), phospho-myosin light chain II (pMLC) staining (second row; shown in green), and actin staining (third row; shown in red) of neutrophils prior to fMLP stimulation (left) and 180 sec after fMLP stimulation (right).

The cell-level physics resulting from the collective molecular machinery governing cell motility continues to be established.^12–14 Studies of subcellular granule dynamics in response to physical perturbations have revealed coexisting viscoelastic states within the neutrophil: the TE of the neutrophil was found to be more solid-like with a structural-dampening rheology compared to the less stiff, less viscous, and more fluid-like LE of the neutrophil.²⁸ Further, neutrophil membrane tension has been shown to play a central role in the constraint of actin-rich pseudopod formation to the LE of motile neutrophils while extracellular matrix rigidity and concentration of available adhesive ligands alters neutrophil morphology, spreading area, and motility.^6,22,23 In concert, traction force microscopy has provided evidence that contraction forces are centered at the TE of the neutrophil and these forces squeeze intracellular material forward – causing a net flow of subcellular components towards the fluid-like LE of the neutrophil.²¹

Despite knowledge that neutrophil motility requires the redistribution of cytoskeletal and intracellular components, a quantitative understanding of the effect of these dynamics on the organization of the subcellular mass-density of neutrophils has remained elusive. Understanding the evolution of the subcellular density is of primary importance in building a deterministic model of cellular motion. Label-free imaging modalities, such as differential interference contrast (DIC) and phase contrast, have been utilized for decades to qualitatively investigate the subcellular density of biological specimens.^9,16 Although these label-free imaging techniques offer direct visualization of cell structure, they provide minimal quantitative information of the specimens. The direct measurement of the cell density within any cell type of interest through label-free means will enable investigators to uncover new physical laws describing the coupling of cytoskeletal dynamics with subcellular density dynamics during cell migration.

Here, we present measurements of the spatial organization of the subcellular neutrophil density using non-interferometric quantitative phase microscopy (NIQPM). We made use of label-free NIQPM in fixed-cell assays over 6 time points to capture the spatiotemporal dynamics of subcellular density organization in polarizing neutrophils undergoing chemokinesis following exposure to the bacterial peptide, formyl-Met-Leu-Phe (fMLP). We demonstrate that subcellular density decreases in a power-law dependent fashion as neutrophils become activated, and that a critical density is reached when neutrophils polarize and begin chemokinesis. Finally, we identify a continuum law of mass conservation that links area, mean density, and total dry mass that holds for resting, activated, and motile neutrophils. These relationships can be utilized in multi-scale theoretical approaches to link cell-wide density behaviors to the micro dynamics of cytoskeletal and membrane motion underlying locomotion.

Our quantitative findings demonstrate a new means to passively monitor the rheology of neutrophil locomotion and can serve as a means to inform physical theories of cell motion through the incorporation of mass conservation and the critical behavior of cell density required for the dynamical transition from basal to activated and motile cell states. The measurement techniques in this study are readily accessible to other researchers as the NIQPM approach and DIC rely only on a standard optical microscope.¹⁸

MATERIALS AND METHODS

Neutrophil isolation, preparation for imaging, and antibody labeling

Human venous blood was collected from healthy volunteers into citrate-phosphate-dextrose (1:7 vol/vol). Written informed consent was obtained from study participants, and the Oregon Health & Science University Institutional Review Board approved the protocol. Blood was layered over equal volume of Polymorphprep (Fisher Scientific, Pittsburgh, PA) and centrifuged at 500g for 45 min at 18°C. The lower band containing polymorphonuclear leukocytes was collected and washed with Hank’s balanced salt solution (HBSS; Life Technologies, Grand Island, NY) by centrifugation at 400g for 10 min. To remove contaminating red blood cells, the pellet was resuspended in sterile H₂O for 30 sec, followed by the immediate addition of 10× PIPES buffer (250 mM PIPES, 1.1 mM NaCl, 50 mM KCl; pH 7.4). After centrifugation at 400g for 10 min, the pellet was resuspended in HBSS containing 2 mM CaCl₂, 2 mM MgCl₂ and 1% w/v BSA.

Acid-washed 22 mm circular coverslips (# 1.5, 0.16–0.18 mm; Fisher Scientific) were coated with fibronectin (20 μg/mL; Sigma-Aldrich, St. Louis, MO) for 1 hr and blocked with heat-inactivated BSA (1% w/v, Sigma-Aldrich) for 1 hr. Purified human neutrophils were incubated at 37°C for 30 min on the coverslips. The buffer in the well was aspirated, and buffer containing 10 nM fMLP (Sigma-Aldrich) was added. Neutrophils were then fixed in 4% paraformaldehyde every 20 seconds. Coverslips were mounted on microscope slides with Fluoromount-G (SouthernBiotech, Birmingham, AL) for visualization.

For fluorescence studies, actin and phospho-myosin light chain II (pMLC) staining was carried out as previously described.⁸ Briefly, following fixation, cells were permeabilized with methanol. Cells were stained with anti-myosin light chain2 pSer19 (3675) (1:200 dilution; Cell Signaling, Boston, MA), and anti-actin (1:100 dilution; Sigma-Aldrich) in blocking buffer overnight at 4°C. Secondary antibodies conjugated with AlexaFluor 488 or TRITC (1:1000; Life Technologies) in blocking buffer were added and incubated for 2 hr in the dark.

Quantification of subcellular density: Non-interferometric quantitative phase microscopy (NIQPM)

We have previously characterized and made available the protocol and computer implementation of NIQPM to quantify cell structure using a standard transillumination microscope.¹⁸ Briefly, cellular density of neutrophils was quantified using NIQPM on an upright optical microscope (Axio Imager; Carl Zeiss, Gottingen, Germany) equipped with a ×63/1.4 numerical aperture (NA) oil immersion objective and an air-coupled condenser lens providing Köhler illumination at an NA of 0.1. Through-focus bright field imagery of the cells was acquired using an illumination wavelength of 540 ± 20 nm. Bright field images of the sample field were recorded with a charge-coupled device camera (AxioCam MRc5 12-bit camera; Carl Zeiss) under software control by Slidebook 5.5 (Intelligent Imaging Innovations, Denver, CO). Through-focus images were acquired in 0.1 μm increments over a 10 μm range along the optical axis. These images formed the input to a transport of intensity equation (TIE) solver to extract phase of transmitted waves through the sample from intensity measurements.⁵

To fix the free parameters of the TIE solver and establish the dynamic range of the method we performed measurements on polystyrene spheres whose sizes were varied from below the diffraction limit of our system, up to 9.8 microns in diameter. We then ensured agreement between our measurements of phase with those determined from the specified sphere diameters from the manufacturer (Figure S1H). We next established the noise floor of NIQPM to verify that this approach is sufficiently sensitive to quantify small features of cellular specimens ranging in size from pseudopodia to the cell body (Figure S1). We determined the noise floor through measurements on a blank substrate with our embedding media and glass coverslip overlaid. We found a full-width at half maximum (FWHM) phase fluctuations ~0.02 radian enabling a density measurement of 0.01 pg/μm² as the smallest value on our density scale, (Figure S1A–C). This noise floor is sufficient to resolve typical pseudopodia structures whose thickness ranges from 100–200 nm and possess a refractive index variation of 0.01–0.02 about the background.

Knowledge of the phase of transmitted waves through the sample enables the enumeration of the projected mass density, defined as the sum of the three-dimensional density along the optical axis of the microscope, through the following relationship,^17,18

$$\mathrm{\rho }(\mathrm{x},\mathrm{y})=\frac{\mathrm{\lambda }\mathrm{\varphi }(\mathrm{x},\mathrm{y})}{2\mathrm{\pi }\mathrm{\alpha }}[\text{pg}/\mathrm{\mu }{\mathrm{m}}^2].$$ (1)

Here ρ(x, y) denotes the projected mass density, ϕ(x, y) is the phase of the transmitted waves, λ is the illumination wavelength, and α is the specific refraction increment of the cell solids (~ 0.2 mL/g). The correct mass density map is verified by computing the digital DIC image as previously described, (Figure S2).^2,3,18

To examine cellular dry mass density parameters, histograms of the subcellular density maps were constructed with bin sizes of 0.01 over the range of 0 to 2 pg/μm² for each cell.³ For each time point we determined: total dry mass, dry mass density mean, and standard deviation of the dry mass density.

High numerical aperture (NA) 2D & 3D DIC image segmentation to quantify cell area, height, and approximate cell volume

3D Köhler illuminated DIC imaging was performed on an upright optical microscope (Axio Imager; Carl Zeiss) equipped with a ×63/1.4 NA oil immersion objective with an air-coupled NA = 0.9 condenser lens as previously described.¹⁸ DIC images of the sample field were recorded with a charge-coupled device camera (AxioCam MRc5 12-bit camera; Carl Zeiss) under software control by Slidebook 5.5. Through-focus images were acquired in 0.1 μm increments over a 20 μm range along the optical axis.

DIC images were converted to binary images through the isolation of fluctuations in the DIC signal intensity as previously described.^1,16 Briefly, DIC axial-intensity profiles were transformed according to the following procedure: letting I_DIC(x, y, z) denote the DIC image cube intensity, for a particular choice of x and y we exaggerate DIC intensity fluctuations and thus enhance background rejection through

$$\mathrm{I}(\mathrm{x},\mathrm{y},\mathrm{z})={\left[\frac{\mathrm{d}}{\text{dz}}({\overline{\mathrm{I}}}_{\text{DIC}}(\mathrm{z})-\langle {\mathrm{I}}_{\text{DIC}}\rangle )\right]}^2$$ (2)

in which Ī_DIC(z) denotes the 5-point moving average of I_DIC(x, y, z) over the axial (z) dimension. 〈I_DIC〉 is the cube-wide mean of the DIC intensity. Lastly, to construct binary cross-sectional image cubes, we define σ, the standard deviation of I(x, y, z), and μ the mean of I(x, y, z). I(x, y, z) is then thresholded such that if I(x, y, z) > (2σ − μ), I(x, y, z) is set to 1 otherwise, I(x, y, z) is set to 0 resulting in binary images, as seen in Figure 4B.

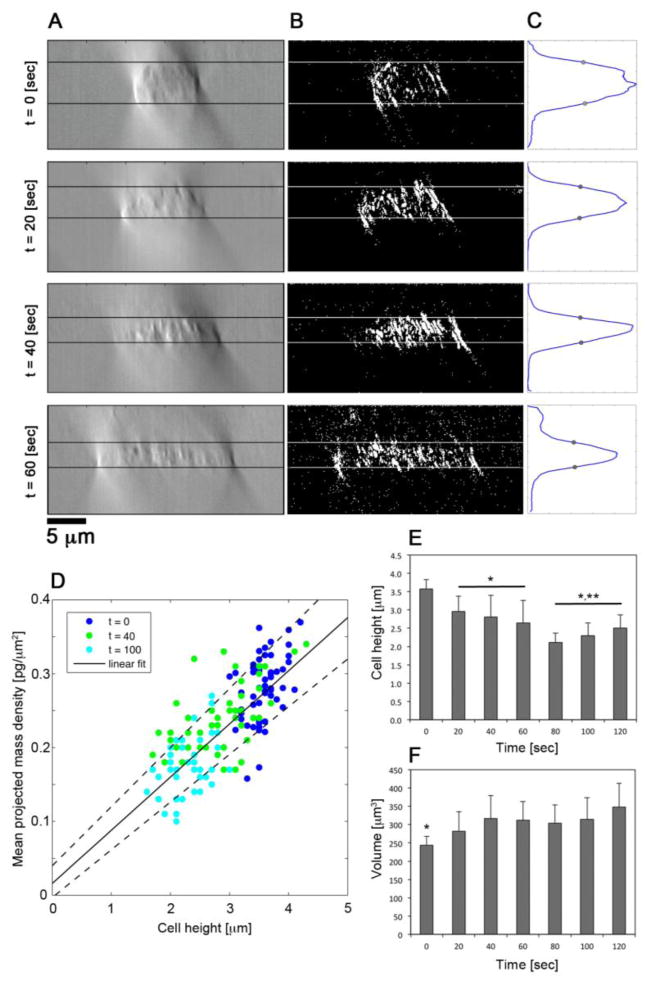
FIGURE 4. Three-dimensional analyses of neutrophil geometry.

(A) Representative cross-sectional DIC images with a Kohler illumination of NA = 0.9 of neutrophils fixed at 0, 20, 40, and 60 seconds after fMLP stimulation. (B) Binary image segmentation of cross sectional images in (A). (C) Transverse sum of binary images in (B) yielding a Gaussian-like distribution along the optical axis. The full width at half max (FWHM) is denoted by gray circles and lines in (A) and (B) correspond to the axial positions of the FWHM. (D) Scatter plot of mean projected density versus mean height of neutrophils fixed at 0 (blue), 40 (green), and 100 (cyan) seconds after fMLP stimulation. Linear fit line denotes $\langle \mathrm{\rho }(\mathrm{t})\rangle =(0.07)\left[\frac{\text{pg}}{\text{fl}}\right]\langle \mathrm{h}\rangle [\mathrm{\mu }\mathrm{m}]+0.01[\text{pg}/\mathrm{\mu }{\mathrm{m}}^2]$. (E) Quantification of mean neutrophil height at 20 second intervals after fMLP stimulation. * denotes p-value < 0.05 compared to t = 0. ** denotes p-value < 0.05 compared to 20 ≤ t ≤ 60 seconds. (F) Approximate neutrophil volume at 20 second intervals after fMLP stimulation determined from the product of mean neutrophil height and area. * denotes p-value < 0.05 in comparison to time points ≥ 20 seconds.

In the final binary images, at each x position in the image cube, cross-sectional images were summed along the y-direction to yield a Gaussian-like profile along the optical axis (Figure 4C). The FWHM of the Gaussian-like profiles was used to establish the mean cell height for each time point explored in this study (Figure 4D). Cell area was determined from outlining the cells in the central focal plane of the image cube (Figure 4E). A custom written MATLAB program was used to outline cells at each time point and align their perimeters along their major axis (Figure 2B). To approximate cell volume we multiplied cell area and mean cell height (Figure 4F). This approach was validated on (N = 50) resting neutrophils whose volumes were determined to be 244 ± 24 fL in agreement with our previous results and those obtained by other investigators using micropipette aspiration.^16,17,24

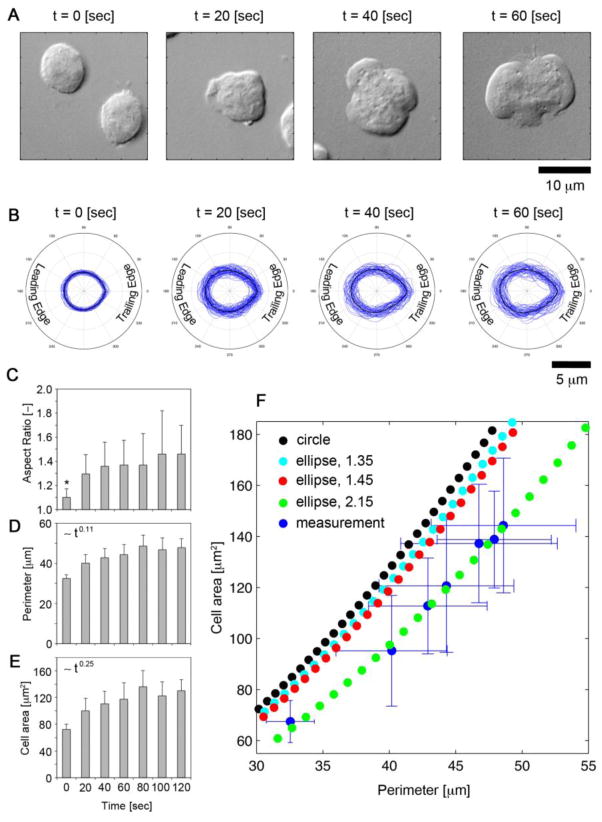
FIGURE 2. Symmetry breaking of migrating neutrophils.

(A) DIC imagery of neutrophils fixed with 4% paraformaldehyde at 0, 20, 40, and 60 seconds after fMLP stimulation. (B) Alignment of neutrophil perimeter along semi-major axis at 0, 20, 40, and 60 seconds after fMLP stimulation. (C) Quantification of neutrophil aspect ratio, (D) perimeter [μm], (E) and cell area [μm²] at 20 second intervals after fMLP stimulation. * denotes a p-value < 0.05 compared to t < 60 sec. (F) Scatter plot of area versus perimeter of measured neutrophils (blue) and profiles of a circle (black) and ellipses with aspect ratios of 1.35 (cyan), 1.45 (red), and 2.15 (green). Error bars denote standard deviation along each dimension.

We remark that these optical approaches using “off-the-shelf” instruments are suitable for fixed samples. Slow z-stack acquisition time on commercial scopes, due to translation of the entire sample stage as opposed to just the objective lens, currently limits the investigation of phenomena faster than roughly 1 frame/min. Further, diffraction effects restrict the utility of NIQPM and DIC to objects ranging in size from 0.2 up to 10 and 20 μm in diameter, respectively. Hence, the specimen and its associated time dynamics of interest must meet certain size and temporal constraints to enable the use of the methods used in this study.

Statistical analysis

The Jarque-Bera test was used to evaluate normality of all parameters. One-way analysis of variance with Bonferonni post hoc correction was used to assess statistical significance among parameters across multiple normally distributed cell parameters. The Kruskal-Wallis test was used to assess significance among non-normally distributed parameters. P-values of 0.05 or less were considered statistically significant. At each time point N = 40 cells were evaluated. All values are reported at mean ± standard deviation unless otherwise noted. Fits to the data are performed on average quantities at each time point.

RESULTS

Characterization of neutrophil morphology following bacterial peptide stimulation

Upon engagement of bacterial peptide receptors, neutrophils develop a distinct front or LE which is rich in filamentous actin, called the lamellipodium, and a back or trailing edge, called the uropod, that is rich in acto-myosin complexes. The subcellular organization of these elements into a polarized geometry enables the cell to convert cytoskeletal chemical reactions into cellular motion. To study the geometric properties of neutrophils resulting from activation in response to exposure to the bacterial peptide fMLP, we utilized a fixed cell assay in which purified neutrophils on fibronectin-coated cover glass were treated with a uniform distribution of fMLP in solution before fixation with paraformaldehyde. Neutrophils in parallel experiments were fixed in 20-second intervals over a two-minute period. We visualized neutrophils using DIC microscopy with high NA Kohler illumination.

The perimeter and area of each cell was determined by tracing DIC images of the cells at each time point. To investigate aspect ratio alterations in the cells, the extracted tracings were numerically fit to an ellipse to determine the major and minor semi-axes lengths of the cell shape (Figure 2A). Tracings were aligned to visualize the ensemble behavior of the cells at each instant with a mean cell shape computed from the ensemble measurements (Figure 2B). Symmetry was quantified through the aspect ratio, defined as the ratio of the major and minor axis lengths. As seen in Figure 2C, fMLP induced activation resulted in statistically significant increases in the aspect ratio within the first 20 seconds; however, at subsequent times following fMLP stimulation, statistically significant alterations were not observed, suggesting that symmetry breaking occurs early in the evolution of cytoskeletal remodeling following activation.

To elucidate the geometric organization of neutrophils during activation and migration, we investigated the relationship of neutrophil area and perimeter. For reference we plot the area-perimeter relationships for a circle and ellipses with aspect ratios of 1.35 and 1.45. Upon plotting neutrophil area (ordinate) against perimeter (abscissa), we found that neutrophil perimeter outpaces increases in the area, due to non-uniform membrane protrusions, and as a result, possesses an area – perimeter relationship resembling an ellipse with a higher aspect ratio, ~2.15. This feature of neutrophil geometry was conserved across the time points (Figure 2F).

Critical behavior of subcellular density organization during neutrophil activation and migration

It is known that DIC image contrast arises from the gradient of the phase of transmitted waves through the sample. As Eq. 1 relates, the phase is linearly proportional to the projected mass density, hence the DIC image contrast is linearly related to the derivative of the density along the shear direction of the Wollaston prisms utilized in the DIC optics.¹⁶ Further, the DIC imagery in Figure 2A demonstrates the evolution of the neutrophil geometry but does not provide quantitative access to density information. To address this need, and to quantify potential changes in neutrophil subcellular density, we employed NIQPM in tandem with DIC imagery to characterize both cellular density and geometric architecture following fMLP stimulation.

NIQPM is carried out through an image acquisition step and post processing procedure in which through-focus bright field imagery, under low NA Kohler illumination conditions, are inputted into a TIE solver to extract phase and then mapped through Eq. 1 to the projected mass density.⁵ The correct density map is ensured through a self-consistency procedure in which a digital DIC image is numerically determined from the recovered density map and compared to the true DIC image.³ This procedure was carried out on all cells at all time points in this study; example comparisons of digital DIC and DIC images are presented in Figure S2.

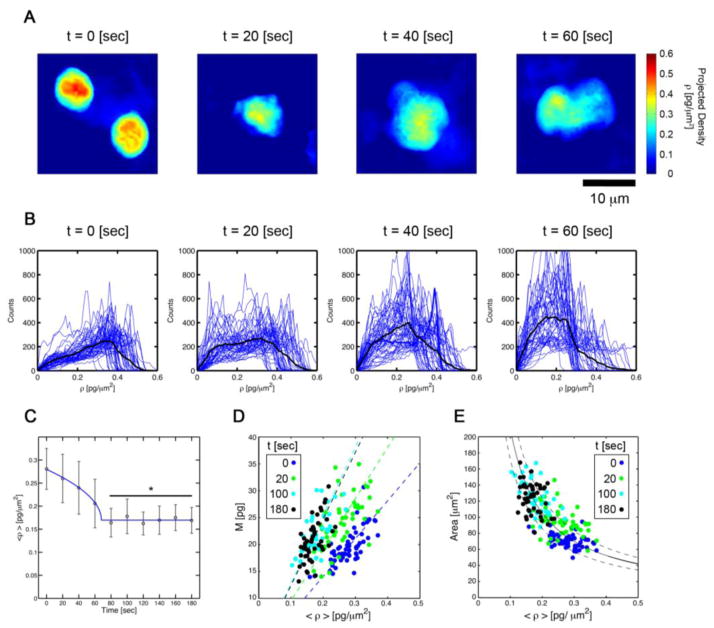
We observed a redistribution of intracellular components of the neutrophil following fMLP stimulation (Figure 3). Image segmentation and histogram analysis indicated that the sub-cellular density shifted from a skewed distribution peaked at ~0.38 pg/μm² to a more even distribution peaked about ~0.18 pg/μm². Moreover, computing the spatial mean of the projected mass density over the extent of each cell, denoted 〈ρ(t)〉, at each time point revealed a power law dynamics (r² = 0.99) given by Eq. 3:

$$\begin{array}{ll}\langle \mathrm{\rho }(\mathrm{t})\rangle =\mathrm{C}{\left[\frac{t_c-t}{t_c}\right]}^{\frac{1}{2}}+\mathrm{D},& \mathrm{t}<t_c,\\ \langle \mathrm{\rho }(\mathrm{t})\rangle =\mathrm{D},& \mathrm{t}>t_c.\end{array}$$ (3)

wherein the basal level mean density, 〈ρ(t = 0)〉 = ρ_o decreased from ρ_o = C + D = 0.28 pg/μm² to ρ_c = D = 0.17 pg/μm² over the course of t = t_c = 68 sec (Figure 2C). This decreased density persisted for t > t_c in a statistically significant way (p < 0.05) with respect to all times points t < t_c. The maintenance of this persistent critical density suggests a specific density threshold required for neutrophil chemokinesis.

FIGURE 3. Neutrophil subcellular density dynamics.

(A) Projected subcellular density map of neutrophils fixed with 4% paraformaldehyde at 0, 20, 40, and 60 seconds after fMLP stimulation. (B) Histograms of subcellular density of neutrophils fixed at 0, 20, 40, and 60 seconds after fMLP stimulation. (C) Piece-wise continuous power law fit of subcellular density organization during neutrophil activation and migration. Projected subcellular density versus (D) mass and (E) area of neutrophils fixed at 0 (blue), 20 (green), 100 (cyan), and 180 (black) seconds after fMLP stimulation.

Continuum law of mass conservation in basal, activated, and motile cell states

In the absence of staining for specific cellular components, label-free microscopy has largely been limited to the 2D measurement of cell geometry and motility. Here we sought to elucidate potential relationships between subcellular density metrics, including total mass and mean density quantified using NIQPM, and 2D geometric features of neutrophils. We investigated correlations among area, total mass, and mean density at each time point.

We observed a linear correlation (r² = 0.9) among mass, M, and mean spatial density, 〈ρ〉, whose slope was given by the average of cell area, A. Interestingly, this finding was observed at each time point (Figure 3D). This result suggests a simple linear continuum law coupling the cellular area, mean density, and total cell mass

$$\mathrm{M}=\mathrm{A}(\mathrm{t})\langle \mathrm{\rho }(\mathrm{t})\rangle ,$$ (4)

independent of activation status.

We further validated this simple law by investigating fits to the data based on the variation of Eq. 4 given by

$$\mathrm{A}(\mathrm{t})=\mathrm{M}/\langle \mathrm{\rho }(\mathrm{t})\rangle .$$ (5)

Using Eq. 5 we ascertained if we could fit scatter plots of area versus mean density for the mean neutrophil mass. The results of this fit demonstrate the inverse density dependence of area (Figure 3E) and the conservation of mass; the fit line denotes a mass of 21.0 ± 3.8 pg (r² = 0.9), over the time points of our investigation.

Characterization of cell height, area, and volume of stimulated neutrophils

To determine if three-dimensional geometric alterations accompany the redistribution of neutrophil cytoskeletal and intracellular components during polarization, we utilized high NA through-focus DIC imagery to visualize the volumetric extent of each cell. Figure 4A presents cross sectional DIC images of neutrophils with the borders identified using fluctuation-based image segmentation of the DIC signal (Figure 4B).¹⁶ Mean cell height was quantified from the numerically determined cell boundaries (Figure 4C).

Following fMLP-induced activation, cell height decreased in a power law dependent fashion, h ~ t^−0.18, from an initial cell height of 3.6 ± 0.3 μm decreasing to 2.1±0.3 μm, at t = 120 sec. In parallel, area increased in a power law dependent fashion, A ~ t^0.25, from 68.7 ± 8.2 μm² to 139.4 ± 18.9 μm² (Figure 2D). Cellular volume, approximated by taking the product of mean cell height and cell area, was found to be conserved for times t ≥ 20 sec, while a statistically significant increase in volume was observed when comparing t = 0 and t = 20 sec treatment groups (Figure 4F). We next ascertained to what degree density alterations were correlated with the three-dimensional geometry of the neutrophil. Scatter plots of mean projected dry mass density versus cell height revealed a linear relationship (Figure 4D) that enabled the quantification of the mean cell density. Letting 〈C〉 denote the spatial average of the three dimensional density with units pg/fL, and 〈h〉 denoting the mean cell height in μm, we find that the 〈ρ〉 vs. 〈h〉 is well described by the one parameter fit (r² = 0.9)

$$\langle \mathrm{\rho }\rangle =\langle \mathrm{C}\rangle \langle \mathrm{h}\rangle +\mathrm{0.02.}$$ (6)

Through this linear fit we observe that 〈C〉 = 0.07 pg/fL, independent of activation state. This value is in keeping with our previous findings.^16,17

DISCUSSION

Neutrophils serve as frontline defenders of the body and are a central component of the innate immune response. Their dynamic recruitment to sites of infection is a multistep process requiring rolling and adherence to the endothelial wall of the vasculature, followed by transmigration through the endothelial wall, and chemotaxis to the site of infection. Lastly neutrophils phagocytose bacteria or release oxidative agents to kill pathogens. Underlying these events is a host of different chemical signaling events that are altered by the physicochemical cues of the tissue microenvironment. The physics of neutrophil locomotion is still being established with efforts currently centered on the investigation of migration speed and neutrophil geometry.

Interestingly, the alteration of the neutrophil density has been observed for many years - owing to its contribution to image contrast in label-free imaging modalities such as DIC microscopy. While DIC approaches have enabled the geometric characterization of neutrophil behaviors spanning states of activation to migration, the corresponding evolution of the subcellular density has remained quantitatively out of reach. This time and space sensitive quantity is currently omitted in theories of active matter that seek to link cytoskeletal processes of actin (de)polymerization to cell motion. A more complete physical theory of neutrophil locomotion will link the molecular level function of actin/myosin, and their effectors, to downstream cell density alterations at the micron scale.

Here we present the use of NIQPM, an accessible optical technique, to measure density alterations in motile neutrophils. We quantify physical processes that occur in parallel with the crosstalk among molecular components of the LE, TE, and MN required for the coordination of cellular shape change and motility. We found that the mean subcellular density decreases in a power-law dependent fashion as neutrophils become activated, and that a critical density is reached when neutrophils polarize and undergo locomotion. Further, we identify a continuum law of mass conservation that links area, mean density, and total dry mass that holds for resting, activated, and motile neutrophils. Lastly, we connect three-dimensional alterations of cell geometry to subcellular density dynamics by demonstrating the linear relationship of mean cell density with cell height. Together these findings illustrate cell-wide laws governing neutrophil dynamics that are currently missing in theories of cellular locomotion.

Our study elucidates fundamental constraints on the collective material organization of the cell through the relationship of cell density, area, and volume. These findings provide a quantitative guide for the ensemble dynamics arising from many-body theories governing small-scale dynamics of the cytoskeleton, the cell membrane, and the other components of the cell. These relationships can be utilized in multi-scale theoretical approaches to link cell-wide density behaviors to the micro dynamics of cytoskeletal motion underlying locomotion.

Supplementary Material

12195_2015_400_MOESM1_ESM. SUPPLEMENTAL FIGURE 1. Dynamic range and noise floor of the TIE-based phase reconstruction.

(A)Bright field intensity, and (B) corresponding phase map and (C) histogram of background phase fluctuations from a bright field image. The FWHM is calculated to be 0.015 rad or 0.007 pg/μm², however, diffraction limits this to 0.3 rad or 0.14 pg/μm². Bright field image (left) and corresponding phase map (right) of a (D) 0.11 μm and (E) 9.8 μm diameter sphere. Phase recovery based on the transport intensity equation (TIE) of a (F) 0.11 μm (below the diffraction limit) and a (G) 9.8 μm (above the diffraction limit) diameter sphere and corresponding percent error of the phase recovery. (H) Measured versus theoretical TIE phase recovery of 0.11, 0.95, 3.0, 4.8, 9.8, and 20.9 μm diameter spheres, where blue dots are the measured maximum phase through the sphere and red triangles denote the theoretical phase range based on manufacturer uncertainty in sphere diameter.

12195_2015_400_MOESM2_ESM. SUPPLEMENTAL FIGURE 2. Validation of projected mass density calculation.

Bright field intensity measurements under NA = 0.1 Kohler illumination (first column), projected mass density measurements using defocus bright field imagery in a TIE solver (second column), digitally computed DIC imagery (third column), and DIC imagery at NA = 0.9 Kohler illumination (fourth column) of neutrophils fixed with 4% paraformaldehyde at 0, 20, 40, and 60 seconds after fMLP stimulation.

ABBREVIATIONS

NA

Numerical aperture

DIC

Differential interference contrast

NIQPM

Non-interferometric quantitative phase microscopy

FWHM

Full-width at half maximum

BSA

Bovine serum albumin

PBS

Phosphate buffered saline