Abstract
A statistical mechanical distance constraint model (DCM) is presented that explicitly accounts for network rigidity among constraints present within a system. Constraints are characterized by local microscopic free-energy functions. Topological rearrangements of thermally fluctuating constraints are permitted. The partition function is obtained by combining microscopic free energies of individual constraints using network rigidity as an underlying long-range mechanical interaction, giving a quantitative explanation for the nonadditivity in component entropies exhibited in molecular systems. Two exactly solved two-dimensional toy models representing flexible molecules that can undergo conformational change are presented to elucidate concepts, and to outline a DCM calculation scheme applicable to many types of physical systems. It is proposed that network rigidity plays a central role in balancing the energetic and entropic contributions to the free energy of biopolymers, such as proteins. As a demonstration, the distance constraint model is solved exactly for the α-helix to coil transition in homogeneous peptides. Temperature and size independent model parameters are fitted to Monte Carlo simulation data, which includes peptides of length 10 for gas phase, and lengths 10, 15, 20, and 30 in water. The DCM is compared to the Lifson-Roig model. It is found that network rigidity provides a mechanism for cooperativity in molecular structures including their ability to spontaneously self-organize. In particular, the formation of a characteristic topological arrangement of constraints is associated with the most probable microstates changing under different thermodynamic conditions.
I. INTRODUCTION
Network rigidity deals with a system of particles subjected to a set of constraints. Depending on the number and position of these constraints, the system will have a residual number of independent degrees of freedom. A simple way of characterizing the degree of mechanical stability of a given framework is to ignore the way constraints are positioned and to treat all constraints as independent. In this approximation, the number of independent degrees of freedom governing internal motions, F, in the framework is given by F =dN−Nc−d(d+1)/2, where d is the dimension of the system, N is the number of vertices, Nc the number of constraints, and the trivial rigid body motions of the entire framework subtracted out. The use of constraint counting to determine structural stability in macroscopic systems dates back to Maxwell [1]. Nearly 25 years ago, Philips [2] realized that constraint counting is applicable to microstructure in covalent glasses by treating central and bond-bending forces in covalent bonds as nearest and next nearest neighbor distance constraints. This simple global counting of constraints is commonly referred to as Maxwell counting, which may result in positive or negative values for F. A negative F indicates the network is overconstrained. Philips [2] qualitatively explained why covalent glass networks with low average coordination form more easily. Shortly afterward, the notion of rigidity percolation was introduced by Thorpe [3], where depending on chemical composition a network would microscopically be in a floppy or rigid state, having a well defined rigidity percolation threshold. Experiments [4,5] have shown that many physical properties in covalent glasses are related to the rigidity transition. In spite of the unique insight that the theory of network rigidity offers, it is unfortunate that it still remains a relatively obscure subject. An authoritative source on concepts of rigidity and its broad range of interdisciplinary applications can be found in Ref. [6].
Network rigidity exhibits long-range character [7] that makes calculating properties difficult using brute force methods on elastic networks [8]. However, the mathematics of first order graph rigidity [9–11] referred to in the physics literature as generic rigidity greatly simplifies calculations [12,13]. Atomic coordinates are not required in generic rigidity. Only the connectivity property of the network is important, making it possible to calculate many static mechanical properties exactly using an integer based combinatoric algorithm. In particular, the exact number of internal independent degrees of freedom can be calculated, all rigid substructures can be identified, as well as all correlated motions that couple the network of rigid clusters. One such algorithm, referred to as the pebble game, is available for general networks in two dimensions [14] and for bond-bending networks in three dimensions [15]. A bond-bending network has the property that all angles between the central-force constraints that stem outward from an atom are fixed. In addition, dihedral angles can be constrained.
Covalent glasses are ideal systems to model as a quenched bond-bending network, where there is a natural separation between hard-strong forces (central and bond-bending forces) and soft-weak forces (torsional and non-bonding forces). The large gap in force strength justifies the treatment of covalent glass networks at room temperature to be modeled as a mechanical network—essentially a T=0 calculation. Recently, constraint counting has been applied to protein structure [16] where covalent bonds, salt-bridges, hydrogen bonds and torsional forces on resonant bonds (the peptide bond, for example) were modeled as mechanical distance constraints. By treating the folded protein structure as a quenched mechanical bond-bending network, flexible and rigid regions were identified and found to correlate well with biologically relevant motions. Network rigidity in proteins has also been found to correlate with protein folding pathways [17,18]. The success of the T=0 calculations on protein structure suggest that the folded state of the protein acts very much like a mechanical machine under the conditions responsible for the native fold to be thermodynamically stable. This result is reassuring, as it has been well appreciated that protein function is very precise in its response to molecules it encounters having a high degree of specificity that makes it appear to respond like a mechanical machine. This empirical observation motivated the use of network rigidity calculations at T=0 in the first place. In spite of the success that many mechanical aspects of a protein fold can be quantitatively characterized, it is also well known [19,20] that protein stability is a result of a delicate balance between many weak noncovalent interactions. In particular, enthalpic and entropic contributions must be part of the ledger of accounts to understand protein stability.
The study of protein stability has motivated this work in generalizing the concept of network rigidity to be applicable at finite temperatures in physical systems having interactions that do not divide into strong and weak compared to kT. When viewing a protein as a mechanical network, two serious problems immediately become apparent. First, hydrogen bonds are continually breaking and forming consistent with thermal fluctuations and, second, hydrogen bonds have a wide variety of strength that is dependent on their local environment [21,22]. In prior work an energetic cutoff criterion [16,23] was introduced to determine a set of hydrogen bonds to model as a constraint. As the energy cutoff was varied, a hierarchical analysis of rigid clusters was used to characterize the protein structure. Unfortunately, the energy cutoff was not directly related to thermodynamic stability, nor the entropy from molecular flexibility was considered, which limited the range of validity of the (T=0) rigidity model to be near the native structure. These problems can be resolved by modeling microscopic interactions as distance constraints, where each distance constraint represents a free-energy component within the system. Assigning free-energy contributions to specific types of interactions is commonly done to interpret experimental measurements and used in theoretical discussions on protein stability [24,25]. However, the utility of such a decomposition is questionable because, in general, it is not possible to obtain the total free-energy by simply summing the free-energy components [26]. It will be shown that the free-energy of a system can be obtained from its free-energy components by employing network rigidity calculations at finite temperature, which combines mechanical and thermodynamic points of view.
In Sec. II a distance constraint model (DCM) is introduced that enables the partition function to be calculated in terms of an ensemble of mechanical frameworks. After the concept of a constraint is generalized to contain thermodynamic information, each mechanical framework of constraints provides an underlying interaction that couples en-thalpic and entropic terms appearing in Boltzmann factors. In Sec. III two simple two-dimensional toy models are worked out to illustrate the details involved in a calculation. As a final example, an exact solution of a distance constraint model for homogeneous peptides that undergo an α-helix to coil transition is considered in Sec. IV. In Sec. V, the results from all three models are discussed, and the standard Lifson-Roig model for a helix-coil transition is compared with the DCM. Conclusions are made in Sec. VI.
II. DISTANCE CONSTRAINT MODEL
Lord Kelvin said, “I never satisfy myself until I can make a mechanical model of a thing. If I can make a mechanical model I can understand it!” The DCM that will be introduced and carefully discussed in the following sections closely adheres to Kelvin’s belief. The objective is to use a mechanical model to understand thermal stability in biopolymers (the focus of this paper) as well as other systems such as formation of chalcogenide glasses.
The DCM begins by representing a macromolecule and interactions therein as a mechanical bar-joint framework. For a single static structure, generic network rigidity properties can be calculated exactly using a graph-algorithm that does not depend on geometrical coordinates of atoms, but only on the topological arrangement of distance constraints. Network rigidity is used here as an umbrella phrase to refer to the following mechanical properties of a bar-joint framework: (1) Identification of all rigid clusters, where each distinct cluster of atoms forms a rigid body; (2) identification of all overconstrained regions, within which elastic strain energy resides; (3) identification of all flexible regions, wherein the atomic structure can continuously deform; and (4) identification of all independent constraints and degrees of freedom.
These basic mechanical properties are quite useful in characterizing a single static structure. In this paper, we will generalize the mechanical description (at T=0) by employing an ensemble-based approach to account for thermodynamics. Thermodynamics determines the fate of a biopolymer, albeit kinetic detours and traps. For example, a protein unfolds when an increase in conformational entropy outweighs a gain in enthalpy from an associated loss of many favorable intramolecular noncovalent interactions. Furthermore, a functional protein in the native state is stable against thermal fluctuations through enthalpy-entropy compensation.
The DCM uses network rigidity as an underlying interaction. Through nonlocal mechanical interactions, network rigidity answers the question about which degrees of freedom are independent, and directly relates to the nonadditivity of measured component free energies. Although the total enthalpy is additive, the entropy is not. This nonadditive property of component entropies derives from not knowing which degrees of freedom in the system are independent or redundant. However, generic network rigidity properties can be calculated exactly with the pebble game by recursively adding one constraint at a time to build a framework. As constraints are added, some atoms will become part of a rigid cluster. A new constraint is redundant when added to an already rigid region and independent when it removes a degree of freedom. All distance constraints are treated the same in the pebble game, and there is a clear distinction between a constraint and degree of freedom.
In the DCM, interactions are represented as distance constraints, each characterized by an enthalpy and an entropy contribution assumed to depend only on local structural properties. Constraints are quantified as being strong or weak based on their entropy contribution. A greater or lesser entropy contribution implies a weaker or stronger constraint. The key aspect of the DCM is that stronger constraints must be placed in the network before weaker ones in order to generalize network rigidity to finite temperatures. This leads to a preferential ordering, which is implemented operationally as the following.
Sort all constraints based on entropy assignments in increasing order, thereby ranking them from strongest to weakest.
Add constraints recursively one at a time using the pebble game according to the rank ordering from strongest to weakest, until the entire structure is completely rigid.
The DCM is mathematically well defined and physically intuitive. The essential idea is that weak constraints allow more conformational freedom than do strong constraints. Stronger constraints take precedence in defining rigid structures because weaker constraints are more accommodating. Thus, a weak constraint acts like a degree of freedom relative to a strong constraint. Consequently, the notion of a constraint and degree of freedom cannot be distinguished clearly once entropy price tags are introduced. Rather, a quantitative measure for conformational entropy is obtained for the structure, whereas the T=0 style of constraint counting simply regards the structure as completely rigid. In this way the DCM provides a natural mechanism for enthalpy-entropy compensation. For example, if by some fluctuation a strong constraint breaks (such as a hydrogen bond), there will be a destabilizing gain in enthalpy, but also a compensating gain in conformational entropy as a weaker constraint substitutes. The technical aspects and mathematical details of the DCM are now addressed.
A. Relating thermodynamics to constraint topology
The DCM views a physical system at a coarse-grain level as defining a mechanical bar-joint framework. A framework is constructed from distance constraints that are used to represent microscopic interactions. Each distance constraint defines an equation of the form R=const, where R is the distance between a pair of atoms. A microscopic interaction involving a group of atoms (more than two) can be modeled by more than one distance constraint, where the collection of distance constraints between different pairs of atoms are simply referred to as a constraint (without the word distance as a qualifier). A hydrogen bond is an example of a many body interaction that will be modeled as a particular type of constraint consisting of three (pairwise) distance constraints. The enthalpy and entropy contributions from a specific type of interaction characterize the corresponding constraint type. Therefore, let ΔHt , (ΔS)t be the change in enthalpy (entropy) that quantifies constraint type t when it is added to a framework. Over the ensemble of all accessible atomic configurations, many different geometries between atoms will potentially result in a vast number of constraint types that must be introduced. However, as demonstrated below, a remarkably few number of constraint types will often be sufficient to quantitatively capture the essential physics.
The microstates of a system are specified in terms of mechanical frameworks ℱ where each framework uniquely defines the topology of all distance constraints. The DCM is built upon the idea that each framework ℱ having a specific topology represents a mini ensemble of bar-joint networks of strict distance constraints within the tolerance allowed by the geometrical coarse graining. One framework consists of many possible atomic-coordinate realizations of strict distance constraints. However, because generic rigidity properties are sought that do not depend on the geometrical details of atomic coordinates, each realization in this mini ensemble has exactly the same network rigidity properties. Thus, the framework label ℱ represents an ensemble of bar-joint frameworks sharing identical network rigidity properties that are calculated using strict distance constraints.
The relation to thermodynamics can be made because a framework uniquely identifies a mini ensemble having constant constraint topology, enabling a free-energy, given as G(ℱ), to be meaningfully assigned. To this end, the total enthalpy of a framework is given by
| (1) |
where Nt is the number of constraints of type t that are present. By exploring all accessible atomic configurations, an ensemble of frameworks (each representing a distinct topology) is generated. The ensemble of frameworks partitions phase space into discrete parts, each having a constant enthalpy over a limited range of conformational freedom. Therefore, the partition function is given by
| (2) |
where Ω(ℱ) is the conformational degeneracy of framework ℱ.
The novel aspect of the DCM is that the conformational entropy, given by ΔS(ℱ)=klnΩ(ℱ), is obtained by adding component entropies over independent distance constraints that are explicitly identified using generic rigidity. Simply adding component entropies over all distance constraints will generally lead to a drastic overestimate for Ω(ℱ). However, identification of whether a distance constraint is independent or redundant is not unique. The freedom in choosing which distance constraints are independent is akin to the freedom in choosing an independent basis set of vectors to span a vector space. Consequently, the addition of component entropies over independent distance constraints will lead to multiple answers for ΔS(ℱ) if based on arbitrary selections. Therefore, an auxiliary preferential selection criterion for how to choose the optimal set of independent distance constraints is required. The crucial part of the DCM is that it enforces a preferential selection criterion that corresponds to the determination of the minimum possible value of ΔS(ℱ).
The total conformational entropy for framework ℱ is given by
| (3) |
where is the number of independent distance constraints of type t present in the framework as determined by the preferential (p) selection criterion. The method for determining linearly independent constraint equations involves building a basis set by iteration, where a new constraint equation is checked for independence against the current basis set. If the new constraint equation is independent, then the basis set expands. The procedure is continued until all distance constraints in the framework are checked. The preferential selection criterion is defined as distance constraints with lower component entropies take precedence in the order that they are checked for linear independence. By applying the preferential selection criterion in conjunction with exact constraint counting for generic rigidity, the change in Gibbs free-energy for framework ℱ is given as
| (4) |
Only in the case that all distance constraints in the framework are independent will ΔG(ℱ) be equal to a straightforward sum over the component free energies ΔGt(ℱ) associated with each constraint type. The partition function is calculated as
| (5) |
in accordance to the standard form, except that each microstate corresponds to a generic mechanical framework ℱ made up of (infinitely strong) holonomic distance constraints, and the ensemble consists of all topologically distinct frameworks.
B. Generic rigidity and nonadditivity of entropy
Meaningful thermodynamic properties are directly tied to local atomic structure because of coarse graining over geometrical bins. To reflect the geometrical aspect of the DCM, the index t is represented by two indices i,q, where i now specifies the type of constraint and q labels a specific geometrical bin. For example, a hydrogen bond is a particular type of interaction, but its strength depends on its local geometry. The component free-energy of the i-th type of microscopic interaction is expressed as a free-energy function , which accounts for all atomic positions of the group of atoms under consideration within the qth geometrical bin. The process of obtaining a free-energy decomposition [26] (the set of used in the model) is not unique because different types of interactions will involve one or more overlapping atoms. Also there will be unavoidable many body effects, such as electrostatic interactions between the atoms of interest with all other atoms, including those in solvent. The nonuniqueness of a free-energy decomposition can be used as an advantage in the process of defining constituent types of constraints.
An effective strategy in employing the DCM is to define a minimum number of constraint types with a limited number of geometries that will yield a desired level of accuracy in predictions. For each i,q, the enthalpy and entropy contributions denoted as , and can, in principle, be determined self-consistently in lieu of not being unique. Self-consistency is satisfied when the free-energy assignment to small clusters of atoms used in defining constraint types locally obey the preferential selection criterion. This means that various clusters of atoms (for example, those within an amino acid or hydrogen bond) define subsystems that are treated in the same way as the full system. Knowing the thermodynamic properties of a cluster of atoms allows constraint types to be defined and characterized with a and . It is worth mentioning that, in principle, a hierarchical set of constraint types can be constructed iteratively by defining constraints with lowest component entropies first, and in succession defining constraints with the next lowest component entropy, etc.
The procedure to determine the local thermodynamic functions for all constraint types and their geometries constitutes a preliminary step in the DCM. In principle, explicit calculations for could be made using accurate physical theories (i.e., quantum mechanical calculations) involving clusters of atoms within a coherent potential approximation scheme. This type of bottom up approach should be tractable and the results would be very useful. However, these difficult calculations can be sidestepped (completely or in part) by writing down the parametric form of a microscopic free-energy function with empirically derived parameters. The important outcomes are given as follows.
-
Interactions are modeled as constraints characterized by two quantities
that can be determined by theoretical means or fitting to large sets of experimental data.
The DCM parameters can be expected to be transferable between systems that are well described by the same set of constraint types.
The DCM invokes a probabilistic interpretation that all distance constraint realizations between atoms are uniformly distributed within a geometrical bin. By allowing each atom a finite amount of freedom, it is ensured that the framework can be treated as generic. Although there will be configurations that have atypical atomic positions, these will be of zero measure. Therefore, the system is modeled as a collection of generically placed holonomic constraints, for which many mechanical properties can be calculated using exact constraint counting algorithms. The connection to thermodynamics enters into the rigidity calculation by determining the correct Boltzmann weight assignment to each mechanical framework, which is related to the nonadditivity of component entropies. The selected set of independent constraints under the preferential selection criterion does not depend on coordinates insofar that the same framework is maintained over a limited range of conformational freedom. This limited range of conformational freedom is quantified by the total entropy ΔS(ℱ) which depends strongly on the topology of distance constraints present in the system.
Calculating the exact value for ΔS(ℱ) will unfortunately not be possible in the DCM. The preferential selection criterion is enforced to obtain the best estimate for each framework. Fundamentally, overlap in phase space can occur when two constraints are independent but not orthogonal. The direct result of adding component entropies associated with only independent constraints is that less phase space will be “double counted.” Therefore, adding component entropies over independent constraints gives an upper bound for ΔS(ℱ). The preferential selection criterion ensures the lowest possible upper bound because the strongest distance constraints defined by the smallest entropies are taken as independent before weaker distance constraints having larger entropies. The utility of the DCM will depend on the degree of accuracy in estimating conformational degeneracy. Note that distance constraints not sharing atoms are orthogonal, and do not contribute in overcounting phase space. Although the distance constraints that share atoms will not generally be orthogonal, by construction of a self-consistent hierarchical series of constraints, phase space overlap between themselves locally is correctly taken into account. Therefore an accurate Ω(ℱ) can be expected by using a complete set of self-consistent constraint types. The phrase “complete set” is used to mean that for any position of atomic coordinates, a framework is always defined such that after all constraints are placed it is rigid. As more constraint types are defined, a framework becomes increasingly more overconstrained, which can only lead to a better lowest upper bound.
The preferential selection criterion has a simple physical interpretation. Each constraint that is added to a system can potentially reduce entropy. However, a redundant distance constraint does not reduce entropy [27]. This is because when a constraint is added to a rigid region that is formed by stronger constraints, the weaker constraint will accommodate the structural geometry dictated by the cohort of stronger constraints [28]. The strength of a constraint (strong or weak) is tied to phase space volume. Therefore, a clear distinction between a constraint and degree of freedom is not possible. The rigidity calculation at finite temperature treats constraints and degrees of freedom on equal footing in the sense that weaker constraints act as degrees of freedom relative to stronger constraints. The entropy loss associated with an overconstrained region is paid at a premium by the strongest member constraints. Fortunately, the pebble game algorithm [14,15] for determining distance constraint independence is based on a recursive procedure of building a framework one constraint at a time. The new implementation only requires using a presorted list of distance constraints from strongest to weakest. It is worth noting that this algorithm does not model a kinetic process as the constraints in a particular framework are present all the time. Rather, the entropy loss from a constraint is concerned with its effectiveness relative to all other constraints in the framework.
C. Quenched and fluctuating constraints
The term quenched constraint refers to a constraint type that will be present among a particular group of atoms in all frameworks of the ensemble. For example, over the temperature range of biological importance, covalent bonding between atoms within a protein is modeled as a set of quenched constraints. Furthermore, the central and bond-bending forces that make up covalent bonding are modeled by constraints having microscopic free energies associated with a single geometrical bin. The torsional force component will also be modeled by a quenched constraint (as the torsional force is always present) but will have a microscopic free-energy , with multiple geometrical bins (labeled by q) depending on the dihedral angle. A system modeled by a complete set of quenched constraints will generally be associated with an ensemble of frameworks because the enthalpic and entropic characteristics of distance constraints depend on local geometry. In the extreme case where only one framework is accessible, the DCM will not provide optimal accuracy whereas normal mode analysis is more appropriate. For example, if a fcc solid is modeled using one central-force constraint type, then the DCM is equivalent to the Einstein model.
The term fluctuating constraint refers to a constraint type that may or may not be present among a particular group of atoms having a fixed geometry. When a fluctuating constraint is present, it is associated with a microscopic free-energy in the same way as a quenched constraint. However, a fluctuating constraint is not strictly tied to geometry because it may not be present. The DCM allows for fluctuating constraints to account for degrees of freedom (dof) that are not explicitly part of a system. For example, solvent dof couple to protein atoms defining a system. The solvent-protein interactions are modeled as fluctuating constraints on the system. In this way, hydration shells around protein atoms are modeled as fluctuating constraint types characterized by enthalpy, , and entropy, , contributions that account for the many body interactions. Even more basic is the hydrogen bond. Hydrogen bonding is modeled as a fluctuating constraint because (1) the protein atom electronic dof are not explicitly described and (2) solvent dof compete with intramolecular hydrogen bonding for a given geometry. Thus, the DCM provides a real-space description involving mechanical constraints, which directly accounts for fluctuating hydrogen bonding, such as that found in proteins and water.
D. Temperature independent model parameters
The enthalpy and entropy contributions, assigned to the various constraint types are functions of temperature, pressure, and other thermodynamic conditions dealing with the chemical environment, such as pH, ionic strength, or whether the local geometry is in a hydrophobic or polar neighborhood. Therefore, caution must be exercised in the ordering of the constraints from strongest to weakest, because this ordering may change as the thermodynamic conditions change. Consequently, the environmentally induced reordering of constraint types by relative strength could potentially cause dramatic conformational change. However, the utility of the DCM can best be appreciated by using a simplified description.
Model parameters will be taken as constants. Furthermore, the entropic term will be distributed equally over all the distance constraints that model a particular constraint type. Then, all microscopic free energies will have the generic form
| (6) |
where is energy, is a dimensionless variable referred to as pure entropy, and mi is the number of distance constraints that are used to model the ith constraint type. Pure entropies are taken to be positive because they are fundamentally related to the number of accessible quantum states that are associated with a specified geometrical bin tolerance, given by . Figure 1 shows two example constraint types that will be used in Sec. IV to model an α-helix to coil transition. A constraint type is now generically characterized as ( ). These parameters can be interpreted as being derived by Taylor expanding to first order the true microscopic Gibbs free-energy about some temperature of most interest. Analogous to Eq. (1), the total energy of a framework is given as
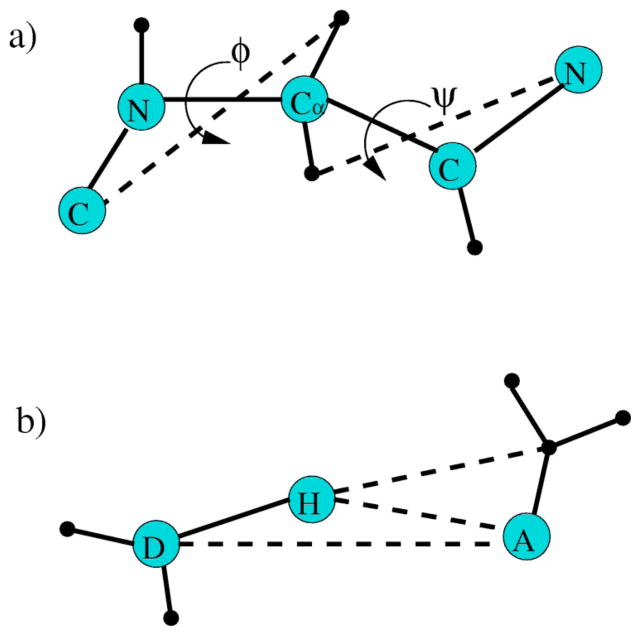
FIG. 1.
(a) The torsion interaction within the backbone of an amino acid is modeled by two distance constraints shown as dashed lines that lock two dihedral angles. Except for proline, the torsion constraint is characterized by (Vq ,2δq), where q denotes a geometrical bin within a two dimensional (ϕ,ψ) space. When the geometry is such that both angles fall within region q, the energy is Vq and each distance constraint has δq pure entropy. For the α helix to coil transition, q represents either a α helical or coil geometry. (b) The hydrogen bond interaction is modeled by three distance constraints shown as dashed lines. The hydrogen bond constraint is characterized by (Uq ,3γq), where q labels geometrical bins that can be defined in different ways. For the α helix to coil transition, q represents the geometry formed by spanning across three consecutive amino acids that can independently be in either α-helical or coil geometry.
| (7) |
where equals (1,0 when the jth constraint of the ith type is present or not present within the qth geometrical bin. Analogous to Eq. (3) the total pure entropy of a framework is given as
| (8) |
where is the number of independent distance constraints within the jth constraint of the system, in accordance with generic rigidity and the preferential selection criterion. Note that {0, 1, . . . ,mi} are the possible values that can take.
The partition function is now written as
| (9) |
where the form of Eq. (9) suggests that the energy and entropy contributions are independent. However, not only do the values of { } depend on calculations from generic rigidity, but also when then . Thus, the energy and entropy of each framework are coupled through topology via the underlying interaction of network rigidity. For example, consider the entropy loss associated with the formation of a hydrogen bond. As shown in Fig. 1b the hydrogen bond constraint is modeled as three distance constraints. For a particular geometry, the hydrogen bond contributes energy Uq and it contributes {0, γq , 2γq , 3γq} amount of pure entropy to the system, depending on whether it has {0, 1, 2, 3} independent distance constraints. If γq is comparatively small indicating a relatively strong distance constraint, then the greatest entropy loss for the system occurs when all three distance constraints are independent. In contrast, if γq is comparatively large indicating a relatively weak distance constraint, then the greatest entropy loss for the system occurs when all three distance constraints are redundant. Since the results depend on the topological arrangement of all constraints in the system, no a priori statement can be made about whether the formation of a hydrogen bond will supply a favorable or unfavorable entropic contribution.
III. TOY MODELS IN TWO DIMENSIONS
The (internal) partition function for the two-dimensional molecule shown in Fig. 2 is calculated to illustrate basic concepts. The molecule consists of four identical atoms connected together by four strong central-force bonds forming a quadrilateral. The central force (cf) bonds are modeled as quenched constraints characterized by energy Ucf and pure entropy γcf . Four torsional forces are also modeled as quenched constraints. In two dimensions (2D) the torsion force (tf) is a function of the angle between a pair of central-force bonds. It is modeled as a next nearest neighbor distance constraint characterized by energy Vtf and pure entropy δtf . The torsional free-energy surface is assumed shallow over a large range of angles. A hydrogen bond (hb) in 2D is considered a single central force, and is modeled as a fluctuating constraint characterized by energy Uhb and pure entropy γhb . Within a length tolerance, a hydrogen bond can form between a pair of atoms along either diagonal of the quadrilateral.
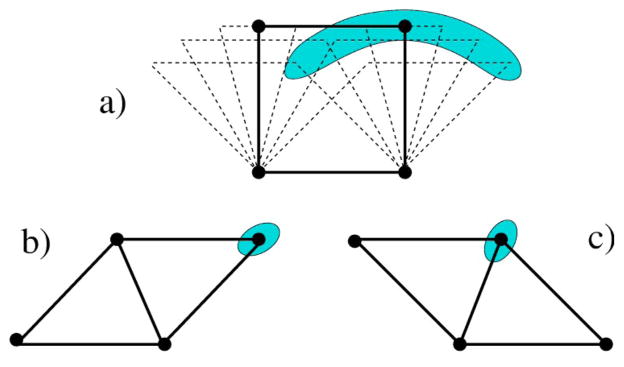
FIG. 2.
A small two-dimensional ring molecule in the shape of a quadrilateral. The shaded regions schematically show the allowed geometrical variation for fixed topology indicative of the degree of flexibility. Configuration (a) is topologically distinct from (b) and (c). For identical atoms at each corner, configurations (b) and (c) represent the same topology of constraints, but are distinct otherwise. The framework in (a) is referred to as state H; where it has greater energy and conformational entropy than (b)/(c). The [(b) and/or (c)] framework is referred to as state L; where the bond along the diagonal leads to a lower energy and conformational entropy than (a).
As Fig. 2 shows, there are only two distinct types of frameworks, labeled as L and H when the hydrogen bond is and is not present. This is a two-level system (three states are required for distinguishable atoms). Employing the DCM, the first step is to rank order the distance constraints from strongest to weakest. This ranking is based on sorting the pure entropies from lowest to highest, assumed to be given as
| (10) |
The second step requires calculating the total energy and pure entropy for each framework using the preferential selection criterion. In state H there are eight distance constraints (four cf and four tf) and in state L there are nine distance constraints (four cf, four tf, and one hb). There are eight dof, three of which involve global translations and rotations. Five distance constraints will always be independent making the framework rigid. From Eqs. (7) and (8) it follows that
| (11) |
Therefore, the (internal) partition function is given as
| (12) |
With Uhb<0, as expected for chemical bonding, the states L and H will be more probable at low and high temperatures, respectively. Since for both states, the energy and pure entropy terms associated with the cf constraints and the energy terms for the tf constraints are the same, the partition function simplifies to
| (13) |
where Z0 contains the terms common in both L and H states. This example illustrates a general result that the strongest quenched constraints play a passive role. Molecular cooperativity is controlled by competition among weaker interactions. It is worth mentioning that if the two-level approximation does not produce a sufficiently accurate temperature response, then the model parameters could be regarded as temperature dependent functions. Alternatively, the single geometrical bin for the assumed weakly varying (as a function of temperature) torsional free-energy can be further subdivided to better account for thermodynamic response by creating more terms in the partition function.
The (internal) partition function for a more interesting two-dimensional molecule shown in Fig. 3 is calculated. This molecule consists of five backbone and five side-chain atoms connected by central forces. A side-chain atom at the end of the chain can swing around the backbone atom, but it is assumed that a potential barrier must be crossed. The highest point of the energy barrier is when the side-chain atom is collinear with the backbone chain. Therefore, the molecule is regarded to have four topologically distinct conformations, each having the same characteristic energy basin. Finally, side-chain atoms that are in sufficient proximity of one another can hydrogen bond.
FIG. 3.
A small two-dimensional chain molecule. Backbone atoms are denoted by filled circles. There are only four topologically distinct conformations (a)–(d) accessible to the molecule as it deforms during the process of hydrogen bonds breaking and reforming. Dashed lines represent hydrogen bonding. Left side: All conformations have a large conformational degeneracy. Right side: When all hydrogen bonds are present the molecule has much less conformational degeneracy. In particular, for conformation (d) a rigid state is defined when all four side chain atoms form a rigid cluster from hydrogen bonding.
The central-force constraint is characterized by (Ucf , γcf ), and the hydrogen bond constraint is characterized by (U, γ). There are two types of torsion force constraints involving angles between BBB atoms, or BBS atoms, where B and S represent backbone and side-chain atoms respectively. The torsional constraint type for the BBB angle is characterized by (VBBB , δBBB) and the torsional constraint type for the BBS angle is characterized by (V, δ). The distance constraints are now ranked from strongest to weakest, assumed given as
| (14) |
Since both torsion constraint types are quenched constraints, it follows that the pure entropy parameter for the BBB type of angle is always irrelevant for all frameworks in the ensemble. This example illustrates an important point that weak forces often need not be associated with an entropy term, because they will always be redundant. Nevertheless, many weak forces can still play an important role in the energetics.
There are a total of 112 possible frameworks, corresponding to 24 different frameworks (due to fluctuating hydrogen bonds), for each of the topologically distinct conformations shown in Figs. 3(a)–(c) and 26 frameworks for the conformation shown in Fig. 3(d). Once all the central-force constraints are placed (first) there are eight internal dof remaining in the molecule. If no hydrogen bond constraints are placed, then the total pure entropy of the molecule will be 9γcf +8δ, which gives the maximum possible value. As hydrogen bond constraints are added, the total pure entropy will decrease. The best chance of finding a redundant hydrogen bond is when the maximum number is present for each distinct topology. By inspection, only one framework out of 112 has a redundant hydrogen bond constraint, corresponding to the six hydrogen bonds, all simultaneously present in the conformation shown in Fig. 3d. Recall that the parameters associated with the quenched constraints common to all frameworks can be factored out. Therefore, relative to the conformations containing no hydrogen bonds, the change in Gibbs free-energy ΔG(n) for the molecule having n hydrogen bonds is given by
The factor of (8–n) appears because each independent hydrogen bond constraint eliminates an angular dof. The remaining (weakest) torsion force constraints rigidify the molecule.
In this example many of the frameworks have degenerate Gibbs free-energy. The Gibbs free-energy already accounts for conformational degeneracy, but there is also a configurational degeneracy in the number of hydrogen bond combinations that are possible. Therefore, the partition function is written as
| (15) |
where g(n) is the number of frameworks with n hydrogen bonds. The values of g(n) for different n are tabulated in Table I, which is obtained by straightforward counting.
TABLE I.
Hydrogen bond configurational degeneracy.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| g(n) | 4 | 18 | 33 | 32 | 18 | 6 | 1 |
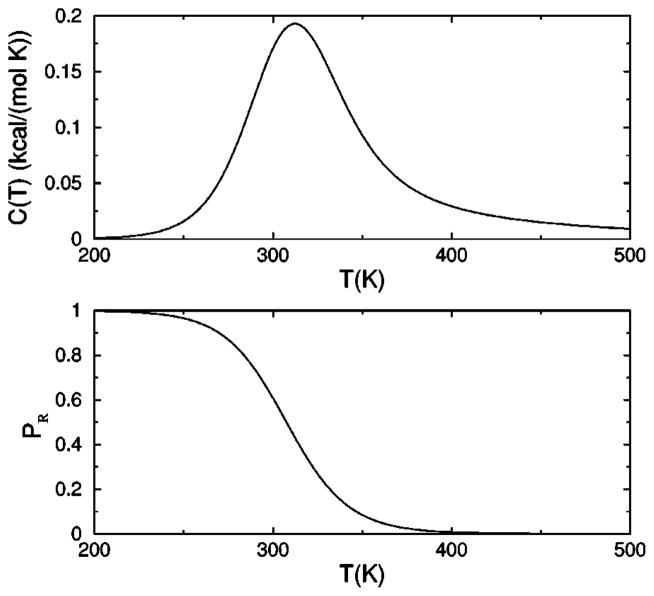
The heat capacity is plotted in Fig.4(a), showing a peak near 310 K, where the model parameters were fixed to convenient values to show interesting features. This peak is a manifestation of a structural transition from the rigid state [defined in Fig. 3(d)] at low temperature to a flexible state at high temperature. The degree of rigidity is also shown by plotting the equilibrium probability PR for the molecule to be described by a framework with five or six hydrogen bonds, where
FIG. 4.
(a) Heat capacity as a function of temperature. (b) Probability for the molecule to form a rigid structural unit. The selected parameters were obtained by choosing the marked point on the phase diagram in Fig. 5, and fixing the transition temperature to be near 310 K.
| (16) |
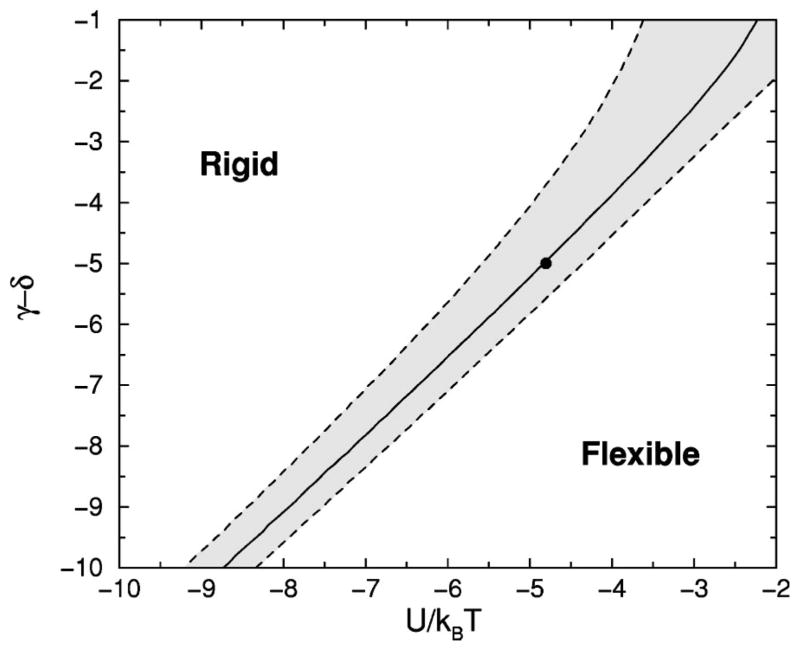
represents only the frameworks that form a rigid structural unit. The probability for being in the rigid state is used as an order parameter. A phase diagram is shown in Fig. 5, where the solid line corresponds to the maximum heat capacity used to locate the transition temperature. The shaded area defines a broad transition region defined as 0.1<PR<0.9, indicating no substantial preference for either the rigid or flexible states.
FIG. 5.
The phase diagram of the two-dimensional chain molecule. The difference in pure entropy between the hydrogen bond and torsional force constraints, and the hydrogen bond energy scaled by thermal energy are the only two relevant variables.
IV. α-HELIX TO COIL TRANSITION
The DCM is employed to describe a transition from a stable α-helix structure that is rigid at low temperature to a flexible coil involving many disordered conformations at high temperature. The backbone of a homogeneous peptide chain, as depicted in Fig. 6(a), is considered for simplicity. Compared to the Zimm-Bragg [29] or Lifson-Roig [30] models, the DCM is mathematically more complicated because network rigidity is a long-range interaction that will be explicitly quantified in terms of a direct product between a rigidity state space and a conformational state space, from which a transfer matrix is constructed.
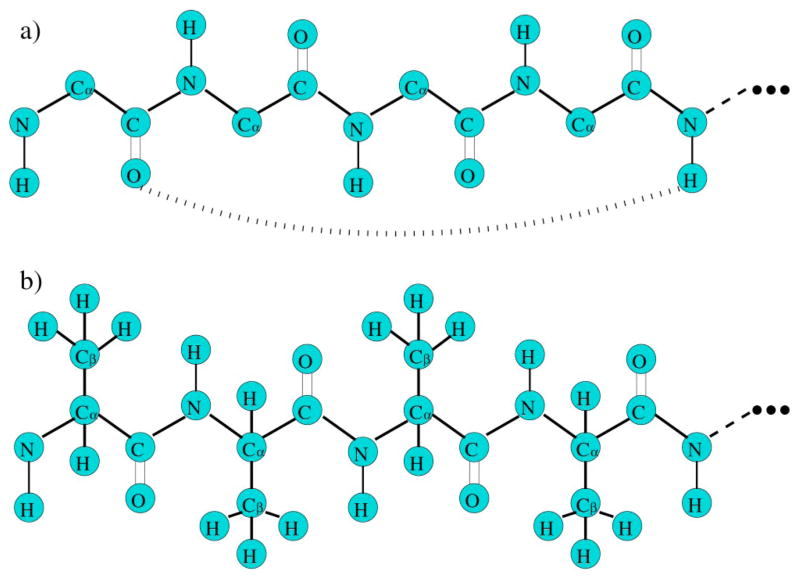
FIG. 6.
(a) The backbone of a peptide chain. The dihedral angle of the peptide bond (C-N) cannot rotate. The long curved dashed line represents a possible hydrogen bond. (b) An example of poly-alanine. The dihedral angle between Cα−Cβ can rotate.
Four constraint types are used here to model central, bond-bending, and torsional forces involved in covalent bonds as well as hydrogen bonds. The strongest two constraint types, modeling the central and bond-bending forces, are placed in the network before the weaker constraint types. Thus, a chain of n amino acids has 2n dof along the backbone because only the ϕ and ψ dihedral angles in each amino acid (proline is not considered here) are free to rotate. The energy and pure entropy parameters for the central and bond-bending constraint types are not of concern because they play a passive role in the partition function, as explained in Sec. III. The remaining two constraint types depend on the local conformation of the backbone, as determined by the ϕ and ψ dihedral angles. Explicit side-chain to side-chain and side-chain to backbone interactions are not considered in the analysis given here.
The third constraint type describes a torsion interaction. Torsion constraints along the backbone are partitioned into distinct geometrical bins depending on the ϕ and ψ angles. For example, different bins can be defined using a Ramachandran plot [31,32] for each type of amino acid. Here, the α-helical and coil geometries, labeled a and c, respectively, are considered to be the only two accessible conformational states. The coil geometry c includes all other secondary structures (non-α-helical) such as a β-strand, 3–10 helix, or left-handed α helix. The energy and pure entropy of the α-helical and coil torsion constraints are given by (Va ,2δa), and (Vc , 2δc) respectively. As shown in Fig. 1(a), the torsion constraint contains two distance constraints to lock the ϕ and ψ angles. Each distance constraint carries a pure entropy of δa or δc in the α-helix or coil geometry, respectively.
The fourth constraint type describes hydrogen bonding. For simplicity, only backbone hydrogen bonds between the carbonyl oxygen of the ith amino acid and the amine nitrogen of the (i+4)th amino acid are considered accessible. The energy and pure entropy for a hydrogen bond constraint are given by Uxyz and 3γxyz , where x, y, and z specify the local (a or c) backbone geometries of the i+1, i+2, and i+3 amino acids that are spanned. As shown in Fig. 1(b), a hydrogen bond constraint contains three distance constraints, where each distance constraint carries a pure entropy of γxyz . Noting that there are eight possible geometries, each requiring the two parameters Uxyz and γxyz , gives a tally of 16 parameters for the hydrogen bond constraint type.
The peptide chain is decomposed into triplets, denoted by [xyz]i , where x, y, and z represent a or c geometries for the {i, i+1, i+2} amino acids. To account for hydrogen bond fluctuations, a triplet may or may not have a spanning hydrogen bond. Another variable λi=(1,0) is used to specify whether a hydrogen bond constraint is present or not across the ith triplet. When present, a hydrogen bond spans the ith triplet by connecting the i–1 amino acid to the i+3 amino acid. The greatest number of hydrogen bonds that can form within an α helix of n amino acids is n–4, since the only triplets that can have a spanning hydrogen bond are (i =2,3, . . . ,n–3). Note that the variable λi corresponds to the ith amino acid in the chain, and therefore it is associated with the leading edge of a triplet. A triplet (not at the ends) will have 16 possible conformational states corresponding to eight different local geometries with or without a hydrogen bond. The complete specification of the conformation of a triplet has the general form λ[xyz]. An energy U0 is introduced for triplets of the form 0[xyz], which represents the hydrogen bond energy resulting between the peptide backbone and solvent. Therefore, U0 is an additional hydrogen bond parameter (17 total) in the DCM considered here.
A. Rigidity propagation rule
To facilitate exact constraint counting subjected to the preferential selection criterion, the degree of rigidity for a triplet is specified by a local rigidity state, denoted as |lrs〉. The local rigidity state contains the minimum amount of information about rigidity at the end of a chain such that when the next amino acid is added, the local rigidity state of the end triplet is uniquely specified. The set of all accessible local rigidity states, {|lrs〉}, will serve as a basis set for a rigidity state space. A complete basis set will be generated using the rigidity propagation rule.
Each triplet has six dof, six torsional force distance constraints, and when there is a spanning hydrogen bond three additional hydrogen bond distance constraints. The pure entropies of each type of distance constraint is rank ordered from 1 to 10 because there are eight different γxyz and two different δx assuming no degeneracies. A torsional force distance constraint (tfdc) and a hydrogen bond distance constraint (hbdc) lock dihedral angles differently. A tfdc is confined to lock a specific dihedral angle, whereas a hbdc spans all six dof within a triplet. A hbdc can be used to lock any of these six dof, and should lock the one which will minimize the total conformational entropy of the chain. In this sense, hydrogen bond distance constraints are promiscuous. Consequently, the dof that are best to lock cannot be determined solely on the local triplet conformation because network rigidity is a long-range interaction. Therefore, an algorithm for propagating the local rigidity state must be established.
A local rigidity state specifies the current rank assignment of constraints used to lock the first four dof in a triplet. The rank assignment corresponds only to independent constraints. The local rigidity state is represented as
| (17) |
where rk is the rank of the distance constraint that locks the kth dihedral angle in a triplet. The ranks of the last two dihedral angles within a triplet will become important in determining the local rigidity state of the next triplet upon propagation. The explicit form for |lrs〉 in Eq. (17) provides a bookkeeping device to calculate the preferential sum of pure entropies over independent constraints. The algorithm for propagating rigidity from left to right takes the following form.
Given |r1 ,r2 ,r3 ,r4〉: Retain the four temporary rank assignments and augment the two ranks from the torsional constraint on the third amino acid, thus forming a temporary template involving six ranks, given by {r1 ,r2 ,r3 ,r4 ,r5 ,r6}.
If no hydrogen bond is present continue to the next step. Otherwise, perform the following operations when a hydrogen bond spans the new triplet. Attempt to place one distance constraint at a time, each having a rank of rhb . Find the maximum rank, denoted as , out of the six current ranks in the template. The superscript (1) indicates that this is the maximum rank, and the index i specifies its location within the template. If , continue to the next step because this and any of the remaining hydrogen bond distance constraints are redundant. Otherwise, replace the maximum rank by rhb . Working from right to left (the direction opposite to propagation) find the next maximum rank, denoted as . If then swap ranks. That is, let . Continue the process of swapping rank rhb with the next greatest rank to its left, until it can no longer be shifted to the left. Continue to the next step when all three hydrogen bond distance constraints have been placed.
The first two degrees of freedom in the triplet are permanently locked by distance constraints that are associated with the ranks r1 and r2 in the template. The remaining four ranks in the template define the current local rigidity state of the new triplet given as . Repeat this process [back to step (1)] until the propagation through all triplets is finished.
Step (2) can be understood conceptually. Ranks within a template act as a dof relative to a hbdc rank whenever they are greater than rhb , otherwise they act as a constraint. Among the ranks acting as a dof, a lower rank acts as a constraint relative to a greater rank. Therefore, the greatest rank should be replaced by rhb . However, it could happen in a future test (as the chain is propagated from left to right) that the largest rank within the current template could be replaced by a different hbdc that spans a different triplet downstream. If this happens, it would be better to use the current hbdc to lock the second highest rank. Replacing the highest rank, or replacing the second highest rank, depends on the relative rank of a future hbdc, if any appear at all. This makes the transfer matrix approach different than the usual case, because rigidity is nonlocal where the conformations down the chain will affect the optimal rank substitution at the current triplet.
The first hbdc encountered down the line that overlaps with part of the current triplet will be effective as a constraint within the current triplet only if its rank is lower than the greatest rank r(1) found in Eq. (17). The second effective hbdc must have a rank lower than the second greatest rank r(2). If no effective hbdc is encountered, it is best to replace r(1) with rhb in step (2) of the algorithm. If one effective hbdc is encountered, it is best to replace r(2) with rhb . More generally, if n effective hbdc are encountered, it is best to replace r(n+1) with rhb if possible. All these cases are properly handled by building the definition of a local rigidity state a chain reaction that automatically swaps higher ranks into lower ranks when needed. The chain reaction is initialized in step (2) by the process of swapping ranks within a triplet from highest to lowest working in the opposite direction of propagation. The outcome of the above algorithm is that both the long-range interaction of rigidity and the global preferential selection criterion are properly described.
Figure 7 shows how the rigidity propagation rule is implemented on a short chain in a particular framework. The initial description of the chain includes the ranks of all torsion and hydrogen bond constraints that are present. This framework contains 18 redundant constraints since the chain in any conformation is always just rigid (isostatic) whenever there are no hydrogen bonds along the backbone, and here there are 3 × (six hydrogen bonds) extra distance constraints. The final description shows the ranks of only independent distance constraints that remain after being permanently assigned in step (3) of the propagation rule. The final ordering of ranks generally depends on the direction of propagation, but the final distribution of ranks (i.e., number of independent constraints having rank 1, 2, . . . ) is invariant. Moreover, the final rank distribution is identical to that of a preferential selected set of independent constraints obtained by placing the strongest distance constraints before weaker ones in otherwise arbitrary order.
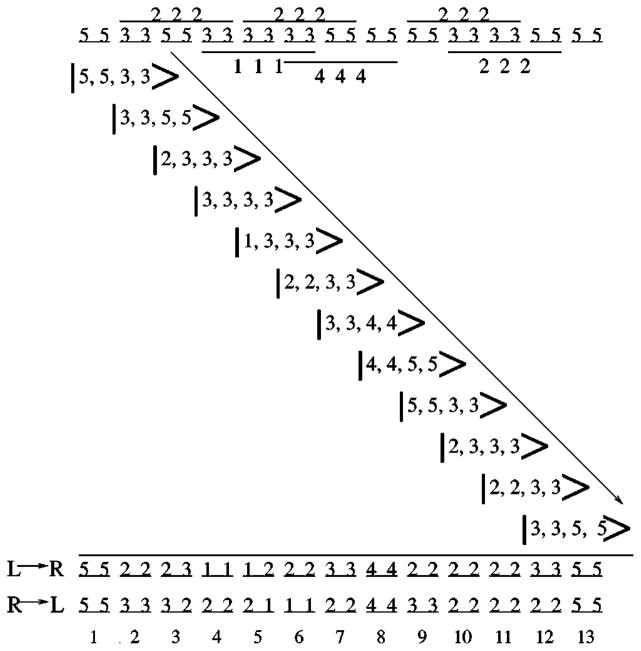
FIG. 7.
The top schematic describes the backbone of a 13-mer peptide chain in a conformation that has torsional constraints with pure entropy ranked either 3 or 5 and occasional hydrogen bond constraints (pictorially represented as bars spanning three consecutive pairs of dihedral angle dof) with pure entropy ranked either 1, 2, or 4. Each step in the propagation of the local rigidity state from left to right is shown along the diagonal. The final ranks that remain after propagating from left to right (L→R) is given on the third to last row. The final ranks obtained by propagating from right to left (R→L) are given on the second to last row. The last row labels the amino acids. Both propagation directions yield three rank-1, 12 rank-2, five rank-3, two rank-4, and four rank-5 independent distance constraints.
Referring to Fig. 7, the entire process of propagating from left to right is shown. The first triplet has a local rigidity state given by |5,5,3,3〉. This first triplet does not have a spanning hydrogen bond, therefore, the next triplet (after the first propagation) has a local rigidity state given by |3,3,5,5〉. During the first propagation step, each tfdc within the first amino acid is recorded as independent, locking the ϕ1 and ψ1 dihedral angles. The pure entropy associated with these two distance constraints is recorded in terms of the two ranks {5,5}. For the second propagation step, the spanning hydrogen bond across the second triplet changes the temporary rank assignments as follows:
| (18) |
ϕ2 and ψ2 are considered to be locked by two of the promiscuous hydrogen bond distance constraints, and recorded by the two ranks {2,2}.
The rigidity propagation rule applied to a specified framework ℱ allows the total pure entropy τ(ℱ) to be calculated as the sum over pure entropies associated with the ranks of the distance constraints used to permanently lock the ϕ and ψ dof. For a given framework, the alternative calculation for τ(ℱ) is to use the pebble game algorithm [14,15], where the distance constraints with lowest ranks are placed in the network first. The propagation algorithm was explicitly tested [33] against exact calculations using the pebble game. Although preferential constraint counting offers an exact calculation method by incorporating the rigidity propagation rule into a transfer matrix, τ(ℱ) no longer requires explicit calculation on each framework in the ensemble.
B. Transfer matrix and the partition function
The transfer matrix is constructed from a direct product space formed by a triplet conformational state denoted by |λ,x,y,z〉, where λ is one when a hydrogen bond spans the x,y,z triplet, zero otherwise and x,y,z are either α helix (a) or coil (c). A triplet is completely specified as
| (19) |
where r1 and r2 are the ranks of the constraints on the ϕ and ψ angle (backbone angles) of the x state, and r3 and r4 are the corresponding ranks of the constraints on the y state. The four ranks on the first two amino acids, the presence or absence of a spanning hydrogen bond, and the conformational state (helix or coil) of each residue together completely specify a state.
Most elements of the transfer matrix T will be zero. The nonzero matrix elements have the form given by
| (20) |
where after a propagation to the right the new first amino acid corresponds to the prior middle amino acid and the new middle amino acid corresponds to the prior right amino acid. In addition to this, the matrix element will only be nonzero if the set of final ranks in the local rigidity state obey the rigidity propagation rules. The nonzero matrix element then contributes a Boltzmann factor that accounts for both the energy and pure entropy contributions of the constraints encountered. The variables Δτ p and Δε p , respectively, represent the change in pure entropy and energy upon propagation along the chain. The contribution to Δτ p at each propagation step is given by the sum of pure entropies of the two constraints that permanently lock the two dof within the first amino acid of a triplet. Thus Δτ p is determined by the rigidity state space in accordance to step (3) of the rigidity propagation rule. In contrast, Δε p is determined by the conformational state space where it is a function of only λ[xyz] and it is found by summing the hydrogen bond energy given by Uxyz when λ=1 and U0 when λ=0, with the torsional force constraint energy given by Vx . By construction, the zeros and nonzeros of the transfer matrix account for the rigidity propagation rules, thereby correctly propagating rigidity.
Ignoring boundary conditions momentarily, the (internal) partition function could be calculated as
| (21) |
The method for constructing the transfer matrix T is explained by working through an example. Consider a chain of 13 amino acids where the framework given as
| (22) |
is one realization taken from an ensemble of 2(13+9) frameworks describing all accessible chain conformations (of a chain of length 13). The numbers of 1 or 0 on top of an a or c specify λ in a triplet, λ[xyz]. A number placed over an amino acid describes a hydrogen bond that spans it and the next two amino acids to the right. In order for a chain of length n to be represented by n triplets, two s solvent states are explicitly shown as being augmented at the right end of the chain. Effects of this state are discussed below under boundary conditions. The first and last three zeros (in bold) correspond to triplets for which an intramolecular hydrogen bond cannot form.
The dimension and form of the transfer matrix T strongly depends on the rank ordering of pure entropies. For the purpose of illustration, consider the rank ordering
| (23) |
where rank 0 is associated with the special s conformation and rank 6 is associated with a hydrogen bond that spans a local [ccc] geometry. In this case, γccc plays no role because it will always be redundant. In this example, intramolecular hydrogen bonds that span the same number of coil states within a triplet are degenerate. Thus, γcaa=γaca =γaac and Ucaa=Uaca=Uaac , etc.
The initial product vector that needs to be propagated is given as |0,c,a,c〉|5,5,3,3〉, where the symbol ⊗ will be dropped from now on. This vector is obtained below by considering the process of propagating triplet 0[ssc] to 0[sca] before arriving to the current triplet 0[cac]. Using the rigidity propagation rule, the first matrix multiplication by T propagates the initial vector into vector |1,a,c,a〉|3,3,5,5〉, while the second matrix multiplication gives |0,c,a,a〉|2,3,3,3〉. The shifts in the conformational states are obvious, and the propagation of the local rigidity states is calculated according to example (18). In fact, the initial configuration of ranks shown in Fig. 7 precisely correspond to the framework given in example (22). In the first propagation step, the contribution of pure entropies from constraints that lock the ϕ1 and ψ1 dihedral angles is given as Δτ1=2δc . The energy contribution is Δε1=Vc+U0 , which reflects the hydrogen bond energy between peptide and solvent. At each propagation step another product vector will be generated. The second step takes the vector |1,a,c,a〉|3,3,5,5〉 into vector |0,c,a,a〉|2,3,3,3〉. The energy contribution is Δε2= Va+ Uaca , which reflects the intramolecular hydrogen bond energy that depends on local geometry [aca]. The pure entropy contribution is given by Δτ2= 2γaca , resulting from two rank 2 pure entropy values. All matrix elements are determined by energy contributions from consecutive triplet conformation states described in example (22), and pure entropy contributions are determined by the final rank ordering (from left to right) listed in Fig. 7. Some matrix elements generated by the framework given in example (22) are listed in Table II.
TABLE II.
A short list of selected matrix elements that are generated from the framework given in example (22). Refer to Fig. 7 to check the correspondence between the pure entropy contribution Δτp on the p th propagation step with the final ranks listed from left to right propagation.
| Step | Transfer matrix element | Boltzmann factor |
|---|---|---|
| 1 | 〈1,a,c,a|〈3,3,5,5|T|0,c,a,c〉|5,5,3,3〉 | e2δce−β(Vc+U0) |
| 2 | 〈0,c,a,a|〈2,3,3,3|T|1,a,c,a〉|3,3,5,5〉 | e2γacae−β(Va+Uaca) |
| 3 | 〈1,a,a,a|〈3,3,3,3|T|0,c,a,a〉|2,3,3,3〉 | eγcaa+δae−β(Vc+U0) |
| 4 | 〈1,a,a,c|〈1,3,3,3|T|1,a,a,a〉|3,3,3,3〉 | e2γaaae−β(Va+Uaaa) |
| ⋮ | ⋮ | ⋮ |
| 10 | 〈0,a,c,c|〈2,2,3,3|T|1,a,a,c〉|2,3,3,3〉 | e2γcaae−β(Va+Uaac) |
| 11 | 〈0,c,c,s|〈3,3,5,5|S|0,a,c,c〉|2,2,3,3〉 | e2γaace−β(Va+U0) |
| 12 | 〈0,c,s,s|〈5,5,0,0|R|0,c,c,s〉|3,3,5,5〉 | e2δae−β(Vc+U0) |
| 13 | 〈0,s,s,s|〈0,0,0,0|Q|0,c,s,s〉|5,5,0,0〉 | e2δce−β(Vc+U0) |
1. Boundary conditions
In addition to constructing the transfer matrix T the boundary conditions on both the left and right ends of the chain must be specified. The boundary conditions are of particular importance for peptides that are experimentally studied because most often they are less than 20 amino acids long. The approach taken here is to add auxiliary triplet states before and after the chain to take into account solvation effects. A requirement that the left and right boundary conditions must satisfy is: left to right propagation and right to left must yield identical results for all observable quantities. This basic requirement is satisfied by the approach used here.
An infinite number of auxiliary s conformations are appended to the beginning and end of the chain to represent bulk solvent. A triplet of auxiliary s conformations is of the form 0[sss], and it is used as a reference state. The transfer matrix propagates the triplet 0[sss] into another 0[sss] triplet with a Boltzmann weight of 1 by definition. The auxiliary s conformations play a passive role in the calculation (as if they are not present) except in triplets at the ends of the chain where they mix with a or c conformations within the chain. Physical boundary conditions require the local rigidity state of the last 0[sss] solvent triplet just before the chain to be equal to the local rigidity state of the first 0[sss] solvent triplet at the end of the chain. Furthermore, this local rigidity state must be the same for any peptide, regardless of its length or composition. Therefore, the local rigidity state for the 0[sss] solvent triplet is defined as |rs ,rs ,rs ,rs〉, where rs≡0 to represent the lowest rank associated with a minimum pure entropy, γs≡0, which is the lowest physically realizable value. Consequently, when propagating from one solvent triplet to the next Δτ p=0, and by setting Δε p≡0, then the Boltzmann weight of 1 is ensured. With these boundary conditions no bulk properties of solvent (the reservoir) are calculated, while peptide to solvent interactions are taken into account by fluctuating constraints acting on the peptide (the system).
Consider propagating from left to right. Then the left boundary condition is most conveniently represented as a column vector in the direct product space, denoted as |i〉. The form of the initial vector is given by
| (24) |
The ranks rx and r y are, respectively, associated with the pure entropy of a tfdc in conformation state (x of the first amino acid) and (y of the second amino acid). No entropic contributions arise in propagating from the 0[sss] triplet to the 0[xyz] triplet because of the rigidity propagation rule when no hydrogen bonds are present and the definition of the special s conformation. However, Δε0ssx and Δε0sxy account for solvation energy between the peptide and solvent. Here a triplet with no spanning hydrogen bond is taken to contribute U0 energy. Therefore, the initial state vector simplifies to
| (25) |
The right-end boundary condition is implemented using three special transfer matrices that involve the s conformation. Starting from the λ[xyz]n−3 triplet, transfer matrices S, R, and Q are defined to, respectively, propagate from λ[xyz]n−3 to 0[yzs] to 0[zss] and finally to the 0[sss] triplet. These three matrices in succession channel all possible local rigidity states accessible at triplet λ[xyz]n−3 to |rs ,rs ,rs ,rs〉 when the 0[sss] solvent triplet is reached. Therefore, the only nonzero component in the direct product space after matrix Q is applied is given by the vector |0,s,s,s〉 ⊗ |rs ,rs ,rs ,rs〉, which is denoted as | f 〉. By construction, the final vector does not change upon further propagation from 0[sss] to all remaining 0[sss] solvent triplets [34].
Including boundary conditions, the (internal) partition function is calculated as
| (26) |
for homogeneous peptide chains with n amino acids, and it involves n matrix multiplications over n triplets. The form of Eq. (26) is independent of the direction used to propagate rigidity. By inspection the partition function for a tripeptide (n=3) reduces to
| (27) |
The expression for Z3 highlights two subtleties about the simplifying assumptions invoked here that are worth mentioning.
Unlike the intramolecular hydrogen bonds, the energy U0 for hydrogen bonding between the peptide and solvent is not considered to depend on the local peptide geometry (specified by [xyz].)
No pure entropy parameter (given by γ0) is associated with the peptide-solvent hydrogen bonds because it has been assumed to be larger than all other pure entropies that characterize the four constraint types introduced above. As illustrated by the second toy model in Sec. III, constraints having a pure entropy greater than all others that are always redundant do not contribute entropically. Not allowing for entropic contributions from peptide-solvent hydrogen bonds implies the solvent molecules (aqueous solution being of primary interest) are unstructured around the peptide. In other work, hydration effects due to structured water around the peptide is explicitly modeled [35] as an additional constraint type.
2. Generating the complete basis set
With Eq. (26) at hand, what remains is to generate the complete basis set of vectors in the product space. This is done during the process of constructing the transfer matrices. The procedure for generating the transfer matrices, T, S, R, and Q begins by considering all eight possibilities for the starting product space vector. Then propagation to all possible next triplets is performed. Each distinct vector that is created defines another basis vector. For each basis vector that was not previously generated, it is propagated to all possible next triplets. Eventually the same vectors continue to be generated by recursively considering all vectors—indicating a complete basis set is formed. It is worth mentioning that the product space is ergodic, in the sense that starting from any vector representing a triplet state of the peptide chain, any other vector can be reached by some number of transfer matrix multiplications. In some cases, this number can be quite long, depending on the size of the transfer matrix. A priori, the number of distinct product space vectors is not known because the number of local rigidity states must be calculated using the rigidity propagation rule. In Table III the dimension M of the product vector space is listed for several choices of rank orderings. A large matrix size is an indication of the long-range nature of rigidity that manifests itself as molecular cooperativity.
TABLE III.
Some examples of possible results that can be obtained after sorting the set of DCM pure entropies from lowest to highest, and then assigned ranks of 1 and greater, respectively. Pure entropy values listed on the leftmost column are rank ordered in the various columns. The letter R indicates that the constraint is always redundant, and therefore is always ineffective in reducing conformational entropy. The last row gives the dimension [34] of the transfer matrix T for the particular rank ordering. Column h corresponds to the rank ordering used in example (23). Column l is similar to column h except that degeneracy is lifted from all the γxyz pure entropies.
| a | b | c | d | e | f | g | h | i | j | k | l | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| δa | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| δc | 2 | 3 | 3 | 3 | 4 | 5 | 6 | 5 | 6 | 5 | 6 | 9 |
| γaaa | R | 1 or 2 | 1 or 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| γcaa | R | R | 2 | 2 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 |
| γaca | R | R | 2 | 2 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 3 |
| γaac | R | R | 2 | 2 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 4 |
| γcca | R | R | R | R | R | 4 | 4 | 4 | 4 | 3 | 3 | 6 |
| γcac | R | R | R | R | R | 4 | 4 | 4 | 4 | 3 | 3 | 7 |
| γacc | R | R | R | R | R | 4 | 4 | 4 | 4 | 3 | 3 | 8 |
| γccc | R | R | R | R | R | R | 5 | R | 5 | R | 5 | R |
| dim(T) | 16 | 16 | 28 | 60 | 60 | 96 | 140 | 200 | 244 | 376 | 436 | 444 |
C. DCM results compared to Monte Carlo simulation
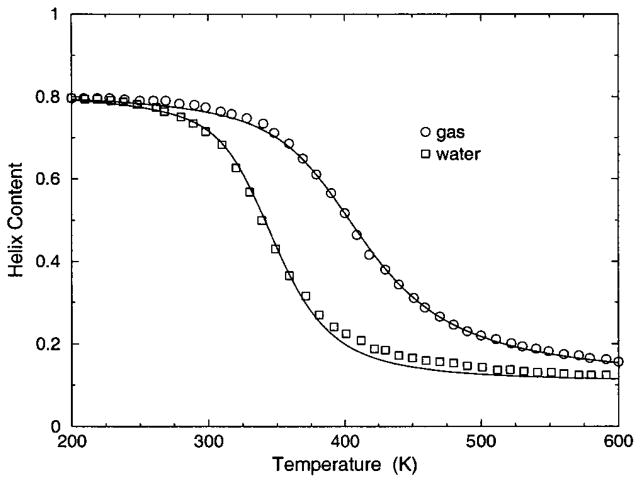
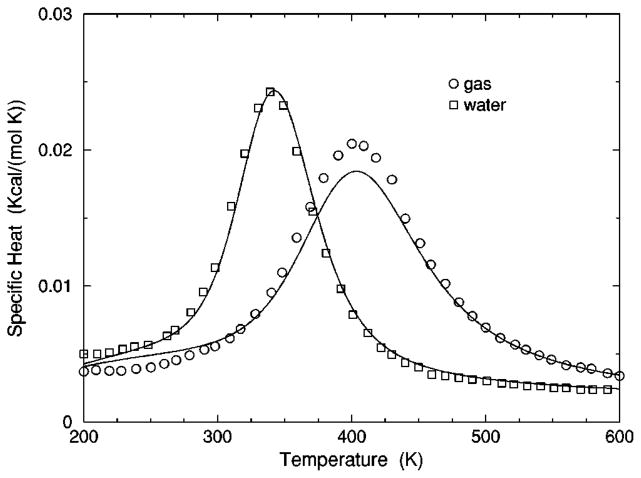
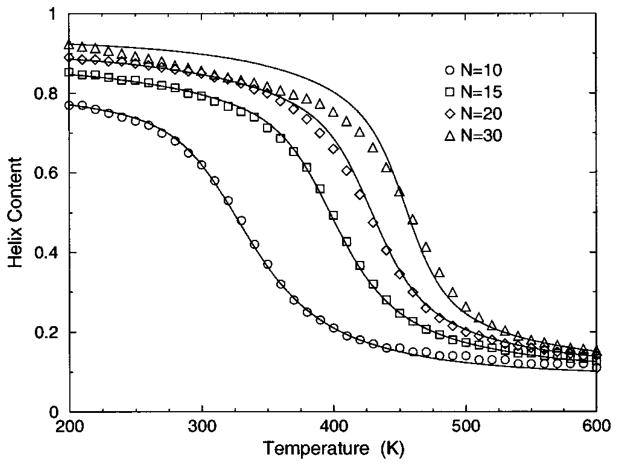
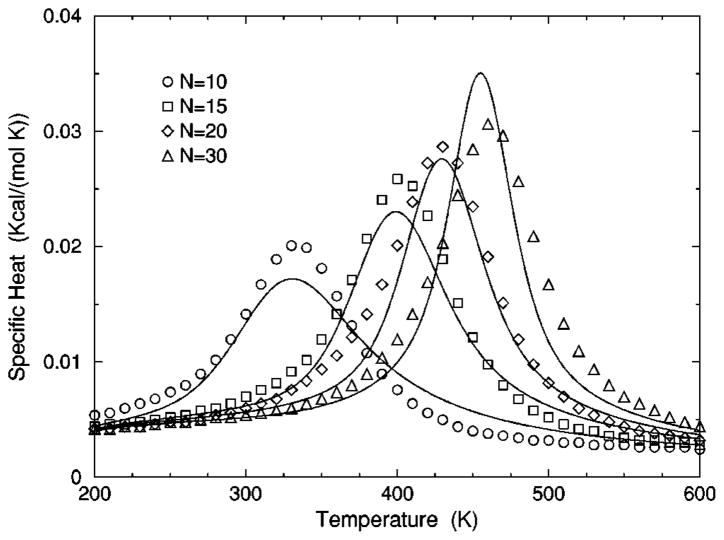
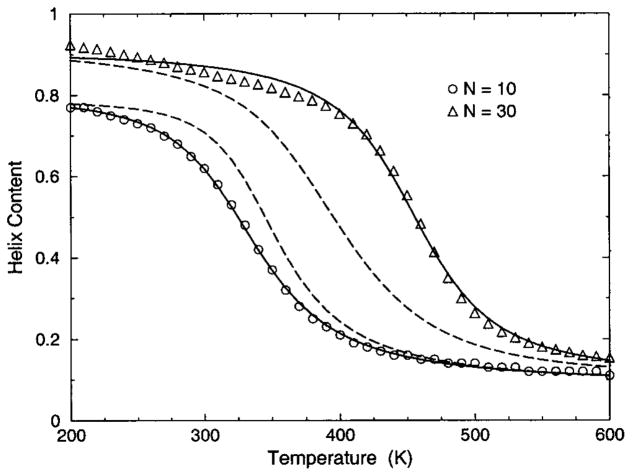
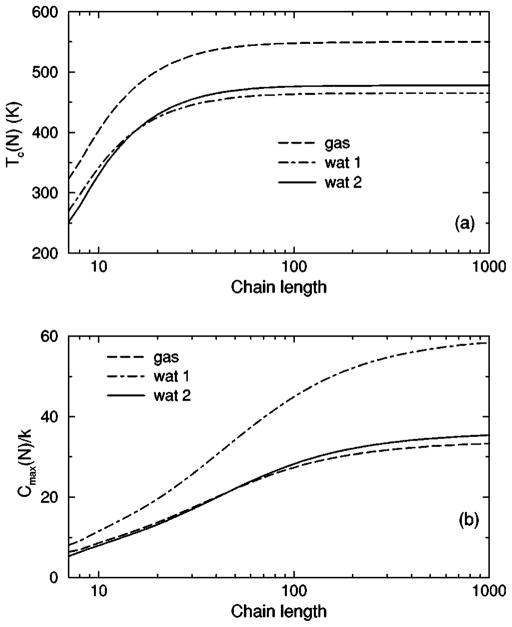
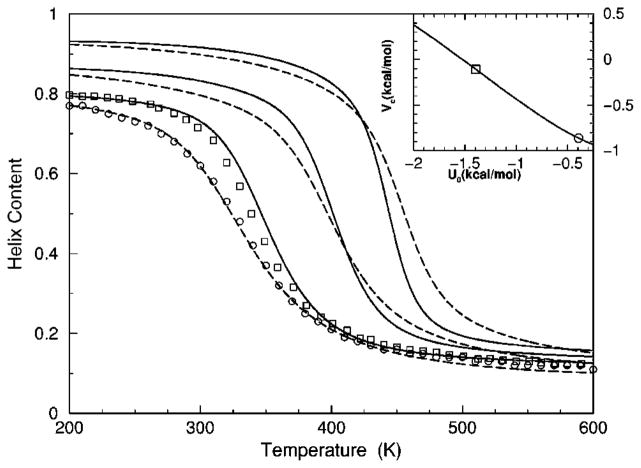
The transition from a rigid α-helical state to a flexible coil state is characterized by helix content, which serves as an order parameter. The helix content is defined as the average fraction of amino acids in the chain having ϕ and ψ dihedral angles of α-helix geometry. The conformational state of the first and last amino acids is explicitly taken into account. Helix content is given by the number of amino acids in the α-helical conformation divided by the number of amino acids in the chain. Applying standard transfer matrix methods, helix content and specific heat are numerically calculated for any specified set of model parameters. Using simulated annealing methods, the DCM parameters were optimized to fit to Monte Carlo (MC) simulation data [36] for polyalanine of length 10 in both gas phase (no solvent) and model-water solvent 1, as well as MC simulation data [37] for chain lengths of 10, 15, 20, and 30 in model-water solvent 2.
The DCM parameters describing the backbone dof for a homogeneous peptide in solvent include {Va , δa , Vc , δc }. Since the amino acids located at the N and C termini are exposed to solvent differently, it is expected that the backbone parameters for the first and last amino acids should be modified. To keep the number of model parameters to a minimum, the set of parameters given by { } are Va δa Vc δc used for both the N and C termini. Besides these eight parameters describing dihedral angle characteristics along the backbone, 17 parameters describe hydrogen bonding. To obtain a more manageable number of model parameters, many hydrogen bond parameters are considered to be degenerate, where it is assumed that (1) Ucca=Ucac=Uacc , (2) Ucaa = Uaca=Uaac , (3) γcca=γcac=γacc , (4) γcaa=γaca =γaac . This simplification reduces the number of hydrogen bond parameters to nine. Taking advantage of the arbitrariness in absolute energies and entropies, the parameters γaaa , U0 , Va , and can be preset without affecting the helix content or the specific heat. Therefore, all backbone dof are fully described by 13 (8+9−4) DCM parameters.
Fitting the DCM to MC simulation of polyalanine requires additional parameters to account for the flexibility in the alanine side chain. The side chain of alanine consists of one dihedral angle between the C α and C β atoms as shown in Fig. 6(b). An additional torsion constraint type was applied to this single side chain dihedral angle. The side chain torsion constraint is partitioned into two geometrical bins. Only differences in energy and pure entropy between the two states are required, which are characterized by (Vs , δs). Since no interactions are considered between an alanine side chain with the backbone or other side chains, the values of (Vs , δs) have no affect on helix content, but do affect specific heat. Another fitting variable cb (not a model parameter) is introduced to represent a constant base line for the specific heat. The variable cb is required because the DCM is defined at a coarse-grained level, and as such it cannot account for residual energy fluctuations.
In total, 16 variables are to be determined by fitting to helix content and specific heat data generated by MC simulation [36,37]. Although each DCM parameter has a physical basis, 16 variables create the unfortunate problem that helix content and specific heat can be simultaneously fitted with a multitude of excellent best-fit solutions. This over parametrization can be quickly avoided, however. An important aspect of the DCM is that although many parameters have been initially generated when the set of constraint types were defined for the helix-coil system; there is no size dependence. Furthermore, the number of parameters grow slowly when fitting to different solvents because no solvent dependence is assumed for (1) intramolecular hydrogen bond parameters, (2) backbone dihedral angle parameters not depending on coil conformations, (3) side chain dihedral angle parameters and (4) the specific heat base line.
The cohort of MC data allows 12 curves to be fitted simultaneously. Superscripts g, 1, and 2 are used to, respectively, refer to gas phase and model-water solvents 1 and 2. Both model-water solvent 1 and 2 refer to the MC data generated using the ECEPP/2 force field [38]. Initially, it was assumed that the model-water solvent of both simulations could be treated identically, since both groups used the same force field. However, as shown in Fig. 8 there are sufficient differences between the chain length ten data to warrant treating them as different model-water solvents. Between the two model-water solvents, 10 solvent independent parameters are in common and (5+5) solvent dependent parameters are required. Including the gas phase data requires 5 more solvent dependent parameters. In total, 25 fitting parameters to 12 distinct curves eliminates overfitting.
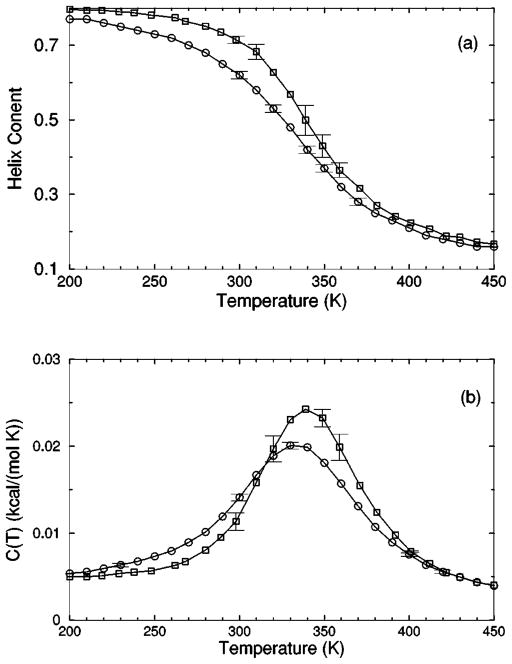
FIG. 8.
The (a) helix content and (b) specific heat from two Monte Carlo simulations are shown. The deviation between the two simulation data for chains of length 10 creates an intrinsic error that prevents us finding a ‘‘good’’ fit when both results are treated as a single solvent type. Ignoring these deviations makes the meaning of goodness not sufficiently restrictive, which allows too many ‘‘good’’ parameter solutions. Instead, these data are treated as two different solvents, where squares and circles represent model-water solvents 1 and 2, respectively.
Interestingly, it was found (from several good best fits) that some parameters are consistently in close proximity to one another. A greater fitting error was exchanged for a maximum reduction of free parameters [39]. Specifically, it was possible to obtain good fits when forcing different parameters that were found in close proximity to be equal. This results in demanding (1) , (2) , (3) , (4) and (5) —as suggested by the unconstrained fits. With this reduction, 19 free parameters were used to fit 12 distinct curves simultaneously.
The results of the simulated annealed best fits are given in Table IV for solvent independent DCM parameters, and Table V for solvent dependent DCM parameters. Figures 9 and 10 respectively, show the fit of helix content and specific heat for both gas phase and model-water solvent 1. Figures 11 and 12, respectively show the fit of helix content and specific heat for all chain lengths in model-water solvent 2. Good fits to helix content were achieved for all six datasets, with the chain length of 30 in model-water solvent 2 showing greatest deviations in the helical phase. Likewise, the fits to specific heat were in remarkably good quantitative agreement, considering that the DCM parameters are taken as temperature independent over a 400 K temperature range. Moreover, employing temperature dependent parameters appears unnecessary for removing systemic error, because it can be attributed to the oversimplified model of representing the peptide-solvent hydrogen bonding as a single state. Overall, the minimalist network rigidity model has successfully captured the essential physics that the MC simulation does.
TABLE IV.
Listing nine solvent independent parameters. Units of energy is in kcal/mol, and pure entropies are dimensionless. The numbers with three digits represent a typical best-fit solution, which were used to generate Figs. 9–12 and 14. The numbers directly below these are the averages obtained over eight typical simulated annealed fitting solutions, including standard deviations for statistical errors. In addition to these DCM parameters, the specific heat base line was considered solvent independent and was given as: 0.001 33 kcal/(mol K) with average and standard deviation given as 0.0014±0.0001 kcal/(mol K).
| aaa | aca | cac | ccc | ||||
|---|---|---|---|---|---|---|---|
| Uxyz | −4.637 | −2.827 | −2.339 | 0.000 a | |||
| −4.95±0.39 | −3.11±0.32 | −2.56±0.33 | 0.000 a | ||||
| γxyz | 2.000 a | 2.149 | 2.760 | 2.917 | |||
| 2.000 a | 2.19±0.07 | 2.81±0.04 | 2.99±0.12 | ||||
| Va | δa |
|
|
Vs | δs | ||
| 0.000 a | 2.656 | 0.000 a | 2.000 a | 1.590 | 3.614 | ||
| 0.000 a | 2.56±0.24 | 0.000 a | 2.000 a | 1.57±0.13 | 3.38±0.15 | ||
Arbitrarily fixed parameters.
TABLE V.
List of five solvent dependent DCM parameters per solvent type. The same units and notation are used as in Table IV.
| U0 | Vc | δc |
|
|
|||
|---|---|---|---|---|---|---|---|
| Gas | −0.399 | −0.321 | 3.603 | −1.344 | 4.034 | ||
| −0.67±0.34 | −0.35±0.08 | 3.58±0.09 | −1.18±0.22 | 3.62±0.25 | |||
| Solvent 1 | −1.154 | −0.321 | 3.603 | −3.095 | 3.523 | ||
| −1.40±0.33 | −0.35±0.08 | 3.58±0.09 | −2.73±0.18 | 3.55±0.14 | |||
| Solvent 2 | −0.399 | −0.857 | 3.603 | −3.095 | 3.523 | ||
| −0.67±0.34 | −0.87±0.09 | 3.58±0.09 | −2.73±0.18 | 3.55±0.14 |
FIG. 9.
Best fit to helix content for gas and model-water solvent 1, obtained by simultaneous fitting 19 parameters to the cohort of MC data.
FIG. 10.
Best fit to specific heat for gas and model-water solvent 1, obtained by simultaneous fitting 19 parameters to the cohort of MC data.
FIG. 11.
Best fit to helix content for model-water solvent 2, obtained by simultaneous fitting 19 parameters to the cohort of MC data. The large deviation seen in the chain of length 30 is at an acceptable level when the trustworthiness of the MC data in the helical phase itself is factored in.
FIG. 12.
Best fit to specific heat for model-water solvent 2, obtained by simultaneous fitting 19 parameters to the cohort of MC data. A systematic fitting error can be seen, where the DCM (as presented here) predicts too fast an increase in the maximum peak as a function of chain length.
V. DISCUSSION
The toy models in Sec. III and the helix-coil transition in Sec. IV demonstrate how generic rigidity calculations are used to construct a partition function at finite temperatures. Each framework in the ensemble is weighted by a conformational degeneracy eτ that depends on the type of constraints present and their specific placement relative to one another. Effectively, the conformational degeneracy represents the free volume available to a particular framework. It has long been recognized [40] that free volume plays an important role in both phase change and relaxation in structural glasses. In the DCM, free volume is quantified by τ(ℱ), which depends on the strongest independent constraints that limit motion. A direct connection between free volume and the degree of mechanical flexibility is established through network rigidity—an inherently long-range cooperative interaction. Although the importance of rigidity in the conceptual understanding of structural transitions is not new, the DCM allows the role of network rigidity at finite temperatures to be calculated quantitatively.
In some respects the DCM is similar to a normal mode analysis in that entropies are additive over independent degrees of freedom. If the system of interest can be well approximated as a network of coupled harmonic oscillators, then the normal modes define an appropriate set of independent coordinates. However, normal mode analysis applied to the soft condensed phase is subject to difficulties because of anharmonic potentials [41] that limit the range of validity over the assumed harmonic motions. In the DCM, the ‘‘strength’’ of a constraint is inversely proportional to its free volume quantified by a pure entropy. An extremely weak constraint having a large free volume will pose no effective restrictions on conformational freedom. Although normal mode analysis is not intrinsically suited to deal with bonds breaking and forming via thermal fluctuations, a self-consistent phonon theory [42] has been used to account for breaking and forming of hydrogen bonds in protein structure. Both the DCM and normal mode analysis offer approximation schemes, but from opposite directions. For example, soft anharmonic (or flat) potentials are easier to deal with in the DCM because they require less geometrical partitioning.
The DCM explicitly accounts for fluctuating topological constraints, allowing a global picture to emerge in understanding structural self-organization. From the three worked examples presented, we observe the following.
The effectiveness of a constraint in changing the free-energy of the system depends on temperature and its location in relation to all other constraints.
Molecular cooperativity derives from competition between frameworks having different energetic and entropic contributions. More generally, a change in thermodynamic conditions (temperature, pressure, pH, etc.) can lead to a global rearrangement of optimally well placed constraints.
The most probable microstates will often correspond to a characteristic pattern of constraints, manifesting itself as structural self-organization. For example, in the helix-coil transition, mechanical frameworks switch character as some constraint types tend to break (α-helical torsion constraints and backbone hydrogen bond constraints) while others tend to form (coil torsion constraints). This type of structural self-organization has been produced in athermal network rigidity models [43] applied to covalent glass networks, where redundant constraints were suppressed to avoid strain energy. In other work to be published elsewhere [35], hydration effects are included in the DCM. Structured water around a hydration site is considered to impose another type of constraint on the peptide, where it is enthalpically favorable and entropically unfavorable. Under certain thermodynamic conditions, cold denaturation occurs as the character of constraint type and pattern changes.
A. The helix-coil transition
The helix-coil transition has been studied for nearly 50 years [44,45]. For a simple statistical mechanical approach, the Zimm and Bragg (ZB) [29] and Lifson and Roig (LR) [30] models are commonly used. The ZB and LR models share two types of parameters—referred to as nucleation and propagation parameters. Only two- and three-dimensional transfer matrices are required for the ZB and LR models, respectively [46]. Without a doubt, the application of the LR model to explain experimental data has been very fruitful over the years. The question then arises, why use the more complicated DCM when the traditional LR model will do?
The DCM clearly makes a distinction between a cooperative process governing a structural transition to that of a non-cooperative process that happens to have a sharp transition. A true signature for the degree of cooperativity is in how the transition temperature depends on chain length. The MC simulation data from Y. Peng et al. [37] shows a large degree of cooperativity, as the transition temperature dramatically increases by 130 K when increasing chain length from 10 to 30. The DCM is able to capture this degree of cooperativity without requiring temperature or size dependent model parameters.
For comparison, the LR model was also fitted to model-water solvent 2 MC data [37]. LR relates the so called nucleation parameter v and the propagation parameter w to partial configurational integrals defined by coarse-grain sections of dihedral angle space (helical or coil conformations) along the backbone. These dimensionless parameters are expected to be functions of temperature, where −kTlnv and −kTlnw represent microscopic component free energies, and are treated phenomenologically [47]. The LR parameters can be written in a form similar to the DCM, where v=e2δv and w=e2δwe−βVw. Here the parameters {δv , δw , and Vw} are taken as temperature independent, and fitted to the four helix content curves. Note that the v parameter is assumed here to be temperature independent, following common practice. Since the LR model as commonly invoked does not explicitly account for end effects, two additional parameters (not model parameters) are required to account for helix content base lines.
Helix content for chain lengths 10, 15, 20, and 30 were individually fitted with the LR-model, each with five fitting parameters, requiring a total of 20 parameters. Figure 13 shows the simulation data for chain lengths 10 and 30, as well as the best fit for each size. In addition, the prediction for helix content for chain lengths 30 and 10 using the fitted parameters from chain lengths 10 and 30, respectively, are shown. The LR model in its three parameter form does a very good job in fitting to each helix content curve. However, as Fig. 13 clearly shows, the fitted parameters obtained for one size cannot be used to predict helix content of a different size. The LR parameters are inherently nontransferable because they depend on the size of the system. Although the sharpness of the helix content curve is accounted for in the so called nucleation parameter, the mechanism creating the cooperativity is completely missed in this simplest three-parameter form. To be fair, a simultaneous fit to all four helix content curves was attempted using 12 parameters (four model parameters and eight base line parameters). The extra LR-model parameter was introduced by letting v =e2δve−βVv. Not surprising, no good simultaneous fit solutions were possible.
FIG. 13.
The solid lines through the MC data for model-water solvent 2 show the best five parameter fit for each size chain separately using the standard LR model. The dashed line on the (left, right) corresponds to the LR prediction of helix content for a chain of lengths 30 and 10 using the best-fit parameters obtained from chain lengths 10 and 30.
Bierzynski and Pawlowski (BP) [48] show that the nucleation parameter is required to be a function of chain length due to the long-range character of helix formation. It seems unsporting to us to predict a helix with parameters that vary with chain length. Furthermore, BP demonstrate that a common implementation of the LR model predicts thermodynamic state functions that are erroneously path dependent: giving slightly different results depending on which end of the peptide the computation begins at, and wrong predictions when prenucleated peptides are considered. Fundamentally, the so called nucleation parameter is ill defined for use in calculating a partition function [48], and its widespread use has created misconceptions [49]. The DCM avoids these issues. The DCM has long-range character through network rigidity, thus recourse to length dependent parameters is unnecessary.
The DCM is actually very similar to the LR model. Both models are based on parameters that can be derived from local microscopic free energies. The difference is that the DCM attempts to include nonlocal cooperative interactions explicitly by using generic rigidity calculations to account for the nonadditivity of entropy. Yet it is possible to construct a DCM where there is very little entropic competition between constraint types, such as given in column a in Table III. In this case, the DCM for a helix-coil transition is identical to the general form of the LR model. It is worth noting that the two commonly used LR parameters [47] (v,w) are only a subset of 16 parameters that must be defined for each possible type of propagation (i.e., aac → aca, and 15 more). Lifson and Roig simplified the model considerably to solve it analytically. Unfortunately, the advantages of simplifying the mathematical form of the model has lead to non-transferability of parameters that have created many inconsistencies in the literature [50]. With modern computers it is no longer necessary to invoke the two-parameter form of the LR model. The disadvantage of retaining the two-parameter form is that the parameters become strongly dependent functions of temperature [36,37,51] and chain length [36,37,48].
B. Solvent effects on the helix-coil transition
The DCM parameters naturally divide into two categories that are expected to be either weakly or strongly dependent on solvent conditions. Moreover, the results obtained by fitting the DCM to MC simulation data indicate the essential physics of the helix-coil transition for polyalanine is well described by the ten solvent independent parameters in Table IV and 5 solvent dependent parameters given in Table V. For these DCM parameters Fig. 14 shows the affect of solvent on the helix-coil transition. Comparing gas phase and model-water solvents 1 and 2 with each other, we see that the transition temperature and the sharpness of the transition can be substantially modified. Not surprising, the gas phase transition temperature is elevated with respect to model-water solvent, because alternate hydrogen bonds from backbone to solvent cannot replace intrahydrogen bonds as they break. The greater energy cost to unravel the rigid helical structure requires a higher transition temperature where gains in conformational entropy can begin to compensate. It is also seen that the transition temperature as a function of chain length for model-water solvents 1 and 2 are very similar, as one might expect if the differences shown in Fig. 8 are viewed as systematic uncertainties, rather than two different solvents.
FIG. 14.
The (a) transition temperature and (b) maximum value of the specific heat as a function of chain length for gas phase and model-water solvents 1 and 2. The parameters used in generating these curves are given in Tables IV and V.
The sharpness of the transition, as characterized by the maximum in specific heat, is found to depend on the particular combination of solvent dependent parameters. With respect to the gas phase, from Fig. 14 it is seen that the transition sharpens considerably for model-water solvent 1, but remains virtually the same for model-water solvent 2. These results correctly reproduce the observations of the authors that generated the original MC simulation data [36,37]. Of course, model-water solvents 1 and 2 are actually the same, albeit systematic uncertainties shown in Fig. 8. This uncertainty and the differences seen in Fig. 14 are the result of differences found in parameters (U0 and Vc), listed in Table V. Therefore, it is easy to interpolate between the two different MC results within a two-dimensional parameter space. The interpolation was done by fitting only to model-water solvent 2 data. Letting U0 range between −1.4 and −0.4 kcal/mol, a one-parameter fit to obtain the optimal Vc was performed, while holding U0 and all other 17 parameters given in Tables IV and V fixed. It was found that the DCM model predictions smoothly change as a function of U0 . In Fig. 15, the helix content is shown for model-water solvent, but now the uncertainties in the parameters U0 and Vc encompass both MC simulation results for the chain length of 10. Chain lengths of 10, 15, and 30 are shown in Fig. 15, which gives some indication of the true uncertainties in helix content for model-water solvent (using the ECEPP/2 force field).
FIG. 15.
Large graph: The dashed and solid curves show predictions for chain lengths 10, 15, and 30 that are obtained in a one-parameter best fit for Vc when setting U0=−0.4 and U0 =−1.4 respectively. The circles and squares show the results of MC simulation from Peng et al. [37] and Okamoto [36], respectively. Inset: The solid line shows the best-fit value of Vc along the ordinate as a function of U0 along the abscissa. The circle and square indicates the Vc and U0 values used to generate the dashed and solid lines in the large graph. Due to the intrinsic uncertainty in the MC data, perhaps the best DCM parameter estimates are U0 =−0.900 kcal/mol and Vc=−0.485 kcal/mol, which split the differences roughly in to half.
In the DCM presented here, solvent effects on the helix-coil transition were described well using just five parameters. A better description is possible by including more states representing the peptide to solvent interactions. In other work [35] hydration constraints are included, for example. Furthermore, inverted transitions from coil to helix as temperature increases from low to high can be described.
C. Molecular cooperativity
Admittedly, the DCM requires more effort than the LR model to describe the helix-coil transition. The benefit of this additional labor is that the final parametrization for understanding the nature of competing microscopic interactions becomes considerably less complicated in the end. In particular, the DCM offers the potential of having transferability of parameters. Parameter transferability is intimately tied to the proper summation of component entropies, which is quantified in the DCM via the long-range underlying mechanical interaction between constraints. From the fitted model parameters (given in Tables IV and V) it is seen from column i in Table III that a 244×244 transfer matrix was necessary to describe the MC simulation results. The large size of the transfer matrix is an indication of a high degree of cooperativity among the hydrogen bonding along the backbone.
In exchange for the nontransferable nucleation parameter to characterize the degree of cooperativity, it is characterized by a rigidity correlation length in the DCM. The rigidity correlation length gives an indication of how far away from a point of interest that perturbations in constraints will lead to little affect at the point of interest. It can be roughly estimated at the helix-coil transition by locating the crossover point where the shift in transition temperature becomes small as chain length increases. From Fig. 14, the rigidity correlation length is estimated to be ≈40 amino acids for both gas and model-water solvents, also corresponding to the inflection point on the curves for maximum specific heat. The correlation length is quite long considering that in one-dimension thermal fluctuations severely reduce the effectiveness of the long-range nature of network rigidity.
The primary motivation for introducing the DCM is to study flexibility and stability in proteins [53]. The concept of a rigidity correlation length applies to any topology of constraints, such as found in globular proteins. The DCM can be used to directly study the affect of hydrogen bonds on protein stability, which has been difficult to ascertain experimentally and theoretically. Not only does the answer depend on the specific thermodynamic conditions, but also on the particular hydrogen bond in question. Stability questions are particularly difficult to answer when there is a high degree of cooperativity in a molecular system. Proteins are particularly interesting, where it has been suggested that the folding pathway is encoded in the hydrogen bond network [17,18]. In addition, mechanical stability probed by single-molecule force spectroscopy appears to depend on the kinetic stability of the hydrogen bond network [52]—also a cooperative process that can be addressed within a DCM. More generally, the DCM describes protein folding as a manifestation of a structural self-organization caused by the topological optimization of constraint placement. Indeed, all model calculations presented here suggest that the most probable frameworks correspond to well defined structural units (such as secondary structure, protein domains, etc.) that change character under different thermodynamic conditions.
VI. CONCLUSION
The DCM generalizes the T=0 generic rigidity calculation to finite temperatures by quantifying constraints with energetic and entropic characteristics. The effectiveness of a constraint strongly depends on its type and where it is placed in the network in relation to all other constraints. Generic rigidity is then used as an underlying long-range mechanical interaction between constraints, providing the mechanism for the nonadditive property of component entropies. The DCM accounts for fluctuating topological patterns of constraint placements. From a computational point of view, the network rigidity calculations are easy to implement by invoking fast graph algorithms that are available in two dimensions [12,14] for general networks and in three dimensions [16] for bond-bending networks.
In this paper, a DCM applied to the helix-coil transition was considered in detail and compared to the Lifson-Roig model. Thermodynamic state functions are calculated exactly, without recourse in using a nucleation parameter. The helix-coil transition in peptides is special only in that it can be exactly solved as a one-dimensional system using a transfer matrix method. Our use of the DCM has been to coarse grain into the smallest number of states necessary to describe the physics at hand. For example, α helix and coil backbone states are used in modeling the helix-coil transition. In this work, 12 different thermodynamic response functions were described well by the DCM using 20 parameters that are independent of temperature and chain length. The entropic parameters indicate that the degree of cooperativity extends over ≈40 amino acids.
As a practical application, the DCM may be able to predict helix formation in proteins with parameters derived from helix-coil transition studies. The DCM is readily scalable to include more types of interactions, where far more backbone states could have been introduced such as 3–10 helix, β sheet, β turn, hydrated or not hydrated, buried or surface exposed. If the DCM parameters are found to be transferable (as we expect) flexibility and stability studies on proteins will be far more feasible, because the DCM gets more physics out with fewer parameters. The DCM has the potential to gain a better understanding of these issues from a mechanical point of view. More generally, the DCM gives a description of a coarse-graining procedure to describe physical systems. Its applicability goes beyond biopolymers, offering a new paradigm not previously available.
Acknowledgments
The authors are grateful for financial support from California State University, Northridge, the Research Corporation (Grant No. CC5141), and to the NIH (Grant No. GM48680-0952). We thank Dennis Livesay for many useful discussions. We also thank Professor Hansmann for sharing his raw MC simulation data with us.
References
- 1.Maxwell JC. Philos Mag. 1864;27:294. [Google Scholar]
- 2.Phillips JC. J Non-Cryst Solids. 1979;34:153. [Google Scholar]
- 3.Thorpe MF. J Non-Cryst Solids. 1983;57:355. [Google Scholar]
- 4.Tatsumisago M, Halfpap BL, Green JL, Lindsay SM, Angell CA. Phys Rev Lett. 1990;64:1549. doi: 10.1103/PhysRevLett.64.1549. [DOI] [PubMed] [Google Scholar]
- 5.Feng XW, Bresser WJ, Boolchand P. Phys Rev Lett. 1997;78:4422. [Google Scholar]
- 6.Thorpe MF, Duxbury PM, editors. Rigidity Theory and Applications. Plenum; New York: 1999. [Google Scholar]
- 7.Guyon E, Roux S, Hansen A, Bideau D, Troadec JP, Crapo H. Rep Prog Phys. 1990;53:373. [Google Scholar]
- 8.Feng S, Sen P. Phys Rev Lett. 1984;52:216. [Google Scholar]
- 9.Crapo H. Structural Topology. 1979;1:26. [Google Scholar]
- 10.Tay TS, Whiteley W. Structural Topology. 1985;11:21. [Google Scholar]
- 11.Graver J, Servatius B, Servatius H. Graduate Studies in Mathematics. Vol. 2. American Mathematical Society; Providence, RI: 1993. Combinatorial Rigidity. [Google Scholar]
- 12.Jacobs DJ, Thorpe MF. Phys Rev Lett. 1995;75:4051. doi: 10.1103/PhysRevLett.75.4051. [DOI] [PubMed] [Google Scholar]
- 13.Moukarzel C, Duxbury PM. Phys Rev Lett. 1995;75:4055. doi: 10.1103/PhysRevLett.75.4055. [DOI] [PubMed] [Google Scholar]
- 14.Jacobs DJ, Hendrickson B. Comput Phys. 1997;137:346. [Google Scholar]
- 15.Jacobs DJ. J Phys A. 1998;31:6653. [Google Scholar]
- 16.Jacobs DJ, Rader A, Kuhn LA, Thorpe MF. Proteins. 2001;44:150. doi: 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
- 17.Rader AJ, Hespenheide BM, Kuhn LA, Thorpe MF. Proc Natl Acad Sci USA. 2002;99:3540. doi: 10.1073/pnas.062492699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hespenheide BM, Rader AJ, Thorpe MF, Kuhn LA. J Mol Graphics Modell. 2002;21:195. doi: 10.1016/s1093-3263(02)00146-8. [DOI] [PubMed] [Google Scholar]
- 19.Dill KA. Biochemistry. 1990;29:7133. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- 20.Rose GD, Wolfenden R. Annu Rev Biophys Biomol Struct. 1993;22:381. doi: 10.1146/annurev.bb.22.060193.002121. [DOI] [PubMed] [Google Scholar]
- 21.Habermann SM, Murphy KP. Protein Sci. 1996;5:1229. doi: 10.1002/pro.5560050702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.The Weak Hydrogen Bond in Structural Chemistry and Biology. Chap 1 Oxford University Press; Oxford: 2000. [Google Scholar]
- 23.Jacobs DJ, Kuhn LA, Thorpe MF. In: Rigidity Theory and Applications. Thorpe MF, Duxbury PM, editors. Plenum; New York: 1999. pp. 357–384. [Google Scholar]
- 24.Hedwig GR, Hinz HJ. Biophys Chem. 2003;100:239. doi: 10.1016/s0301-4622(02)00284-3. [DOI] [PubMed] [Google Scholar]
- 25.Gao J, Kuczera K, Tidor B, Karplus M. Science. 1989;244:1069. doi: 10.1126/science.2727695. [DOI] [PubMed] [Google Scholar]
- 26.Mark AE, van Gunsteren WF. J Mol Biol. 1994;240:167. doi: 10.1006/jmbi.1994.1430. [DOI] [PubMed] [Google Scholar]
- 27.The entropy loss from a redundant constraint is expected to be a small fraction of what would occur if the constraint was independent. Accounting for this second-order effect is possible at the expense of losing simplicity.
- 28.The DCM explicitly neglects relaxation within constraints. Relaxation in structure can be described by incorporating more geometrical bins at the expense of losing simplicity.
- 29.Zimm BH, Bragg JK. J Chem Phys. 1958;28:1247. [Google Scholar]
- 30.Lifson S, Roig A. J Chem Phys. 1961;34:1963. [Google Scholar]
- 31.Ramachandran GN, Ramakrishnan C, Sasisekharan V. J Mol Biol. 1963;7:95. doi: 10.1016/s0022-2836(63)80023-6. [DOI] [PubMed] [Google Scholar]
- 32.Lovell SC, Davis IW, Arendall WB, III, de Bakker PIW, Word JM, Prisant MG, Richardson JS, Richardson DC. Proteins. 2003;50:437. doi: 10.1002/prot.10286. [DOI] [PubMed] [Google Scholar]
- 33.The propagation rule was applied from left to right and right to left on 200 000 chains with length of 100 000 as well as millions of chains of lengths ranging from 10 to 1000 all having random conformations. These results were compared to exact calculation using the pebble game per framework. Agreement between all three results was always obtained.
- 34.Technically adding the s conformations, rank rs and the special matrices {S, R, Q} required expanding the dimension of the direct product space. The dim(T) referes to the subspace that excludes the s state.
- 35.Jacobs Donald J, Wood GG. unpublished. [Google Scholar]
- 36.Mitsutake A, Okamoto Y. Chem Phys Lett. 1999;309:95. [Google Scholar]
- 37.Peng Y, Hansmann UHE, Alves NA. J Phys Chem. 2003;118:2374. [Google Scholar]
- 38.Sippl MJ, Némethy G, Scheraga HA. J Phys Chem. 1984;88:6231. [Google Scholar]
- 39.The objective of finding an optimal set of parameters with available data in the literature is outside the scope of this work. The subject of obtaining an accurate DCM parametrization is deferred to future work.
- 40.Grest GS, Cohen MH. Adv Chem Phys. 1981;48:455. [Google Scholar]
- 41.Hayward S, Kitao A, Go N. Proteins. 1995;23:177. doi: 10.1002/prot.340230207. [DOI] [PubMed] [Google Scholar]
- 42.Cao ZW, Chen YZ. Biopolymers. 2001;58:319. doi: 10.1002/1097-0282(200103)58:3<319::AID-BIP1008>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
- 43.Thorpe MF, Jacobs DJ, Chubynsky MV, Phillips JC. J Non-Cryst Solids. 2000;266–269:859. [Google Scholar]
- 44.Schellman JA. J Phys Chem. 1958;62:1485. [Google Scholar]
- 45.Doig AJ. Biophys Chem. 2002;101–102:281. doi: 10.1016/s0301-4622(02)00170-9. [DOI] [PubMed] [Google Scholar]
- 46.Poland D, Scheraga HA. Theory of Helix-Coil Transitions in Biopolymer. Academic Press; New York: 1970. [Google Scholar]
- 47.A third parameter called u in the LR model is arbitrarily set to unity, which is analogous to the arbitrary choices made in fixing some DCM parameters.
- 48.Bierzynski A, Pawlowski K. Acta Biochim Pol. 1997;44:423. [PubMed] [Google Scholar]
- 49.Wetlaufer DB. Trends Biochem Sci. 1990;15:414. doi: 10.1016/0968-0004(90)90275-g. [DOI] [PubMed] [Google Scholar]
- 50.Bierzynski A. Comments Mol Cell Biophys. 1987;4:189. [Google Scholar]
- 51.Scheraga HA, Vila JA, Ripoll DR. Biophys Chem. 2002;101–102:255. doi: 10.1016/s0301-4622(02)00175-8. [DOI] [PubMed] [Google Scholar]
- 52.Carrion-Vazquez M, Oberhauser AF, Fisher TE, Marszalek PE, Li H, Fernandez JM. Prog Biophys Mol Biol. 2000;74:63. doi: 10.1016/s0079-6107(00)00017-1. [DOI] [PubMed] [Google Scholar]
- 53.Huynh D, Dallakyan S, Jacobs DJ. unpublished. [Google Scholar]