A Sequential Algorithm for Multiblock Orthogonal Projections to Latent Structures

Abstract

Methods of multiblock bilinear factorizations have increased in popularity in chemistry and biology as recent increases in the availability of information-rich spectroscopic platforms has made collecting multiple spectroscopic observations per sample a practicable possibility. Of the existing multiblock methods, consensus PCA (CPCA-W) and multiblock PLS (MB-PLS) have been shown to bear desirable qualities for multivariate modeling, most notably their computability from single-block PCA and PLS factorizations. While MB-PLS is a powerful extension to the nonlinear iterative partial least squares (NIPALS) framework, it still spreads predictive information across multiple components when response-uncorrelated variation exists in the data. The OnPLS extension to O2PLS provides a means of simultaneously extracting predictive and uncorrelated variation from a set of matrices, but is more suited to unsupervised data discovery than regression. We describe the union of NIPALS MB-PLS with an orthogonal signal correction (OSC) filter, called MB-OPLS, and illustrate its equivalence to single-block OPLS for regression and discriminant analysis.

1. Introduction

The method of nonlinear iterative partial least squares (NIPALS) has firmly entrenched itself in the field of chemometrics. Implementations of principal component analysis (PCA) and projections to latent structures (PLS) that utilize NIPALS-type algorithms benefit from its numerical stability, as well as its flexibility and simplicity [1-3]. Only a few subroutines from level 2 of the basic linear algebra subprograms (BLAS) specification are required to construct a complete NIPALS-type algorithm [4, 5], making it an attractive means of constructing PCA and PLS models of high-dimensional spectroscopic datasets.

One particularly recent addition to the NIPALS family of algorithms, called orthogonal projections to latent structures (OPLS), integrates an orthogonal signal correction (OSC) filter into NIPALS PLS [6, 7]. By extracting variation from its computed PLS components that is uncorrelated (orthogonal) to the responses, OPLS produces a more interpretable regression model compared to PLS. In fact, when trained on the same data and responses, an OPLS model and a PLS model with the same total number of components will show no difference in predictive ability [8]. Despite its relative novelty to the field, the enhanced interpretability of OPLS over PLS has made it a popular method in exploratory studies of spectroscopic datasets of complex chemical mixtures (e.g., metabolomics [9], food and soil science [10], and chemical process control [11]).

Extensions of NIPALS PCA and PLS to incorporate blocking information that partitions the set of measured variables into multiple ‘blocks’ of data have recently gained attention in the field as more experimental designs involve the collection of data from multiple analytical platforms per sample. In such experiments, referred to as ‘class II’ multiblock schemes by Smilde et al. [12], correlated consensus directions are sought from the blocks that maximally capture block variation and (optionally) maximally predict a set of responses. Of the available extensions of NIPALS to multiblock modeling, a class of methods exists that bears attractive computational qualities, namely computability from single-block bilinear factorizations. When both super weights and block loadings are normalized in consensus PCA (i.e. CPCA-W), the obtained super scores are equivalent to those obtained from PCA of the concatenated matrix of blocks [13]. Likewise, scores obtained from PLS of the concatenated matrix are equivalent to super scores from multiblock PLS (MB-PLS) when super scores are used in the deflation step [13, 14]. As a result, these multiblock bilinear factorizations inherit many of the useful properties of their single-block equivalents.

A second class of multiblock methods exists in which every block is predicted in a regression model by every other block. In the first of such methods, known as nPLS, the MAXDIFF criterion [15] is optimized one component at a time (i.e. sequentially) to yield a set of predictive weight vectors for each block [16]. The recently described OnPLS algorithm also falls within this class [16]. OnPLS extends O2PLS to three or more matrices and may be considered a prefixing of nPLS with an OSC filtering step. OnPLS deflates non-globally predictive variation that may or may not be orthogonal to all blocks from each matrix, and then computes an nPLS model from the filtered result [16]. While fully symmetric OnPLS is a powerful and general addition to the existing set of multiblock modeling frameworks, it is arguably an over-complication when the regression of a single response matrix on multiple data blocks (i.e. MB-PLS) is sought. For such situations, a novel algorithm termed MB-OPLS for multiblock orthogonal projections to latent structures is introduced that embeds an OSC filter within NIPALS MB-PLS, thus solving an inherently different problem from OnPLS. It will be shown that MB-OPLS, in analogy to CPCA-W and MB-PLS, is computable from a single-block OPLS model of the matrix of concatenated data blocks. Thus, MB-OPLS forms a bridge between this special class of consensus component methods and the highly general symmetric regression framework of OnPLS.

2. Theory

MB-OPLS belongs to a set of multiblock methods that exhibit an equivalence to their single-block equivalents. A short discussion on these methods follows, in which the optimization criterion of each method is shown to belong to the MAXBET family of objective functions. This is contrasted to nPLS and OnPLS, which have been shown to optimize a MAXDIFF objective. The principal difference between MAXBET and MAXDIFF is one of explained variation: while MAXBET captures between-matrix covariances and within-matrix variances, MAXDIFF only captures the former [15, 17]. Finally, the equivalence of MB-OPLS and OPLS is demonstrated, which highlights its differences from OnPLS.

In all following discussions, it will be understood that there exist n data matrices X₁ to X_n, each having N rows (observations) and K_i columns (variables). The matrix X = [X₁] … [X_n] of all concatenated blocks will be used in cases of single-block modeling. Finally, a response matrix Y having N rows and M columns will be assumed to exist for the purposes of regression (i.e. PLS-R, MB-PLS-R, etc.) or discriminant analysis (i.e. PLS-DA, MB-PLS-DA, etc.).

2.1. nPLS and OnPLS

In their initial description of the OnPLS modeling framework [16], Löfstedt and Trygg introduced nPLS as a generalization of PLS regression to cases where n > 2, and a model is sought in which each matrix X_i is predicted by all other matrices X_j≠i. The nPLS solution involves identifying a set of weight vectors W_i that simultaneously maximize covariances between each pair of resulting scores t_i = X_iw_i via the following objective function:

$$\underset{i\ne j}{{\sum }_{i,j=1}^n}{{\mathit{t}}_i}^T{\mathit{t}}_j=\underset{i\ne j}{{\sum }_{i,j=1}^n}{{\mathit{w}}_i}^T{{\mathit{X}}_i}^T{\mathit{X}}_j{\mathit{w}}_j$$ (1)

subject to the constraints ‖w_i‖ = 1. This objective was subsequently recognized to be a member of the MAXDIFF family of functions, whose solution is obtainable using a general algorithm from Hanafi and Kiers [17]. After the identification of a set of weight vectors, the scores

$${\mathit{t}}_i={\mathit{X}}_i{\mathit{w}}_i$$

and loadings

$${\mathit{p}}_i=\frac{{{\mathit{X}}_i}^T{\mathit{t}}_i}{{{\mathit{t}}_i}^T{\mathit{t}}_i}$$

may be computed for each matrix, which is then deflated prior to the computation of subsequent component weights:

$${\mathit{X}}_i\leftarrow {\mathit{X}}_i-{\mathit{t}}_i{{\mathit{p}}_i}^T=(\mathit{I}-\frac{{\mathit{t}}_i{{\mathit{t}}_i}^T}{{{\mathit{t}}_i}^T{\mathit{t}}_i}){\mathit{X}}_i$$ (2)

This deflation scheme follows the precedent set by two-block PLS regression. Because their described approach used a distinct deflation scheme from single-component (sequential) MAXDIFF, it was given the name “nPLS” by the authors to distinguish it from MAXDIFF [16, 18].

OnPLS extends nPLS by decomposing each matrix into a globally predictive part and a non-globally predictive (orthogonal) part using an orthogonal projection. By removing orthogonal variation from each block prior to constructing an nPLS model, OnPLS optimizes the following MAXDIFF-type objective function:

$$\underset{i\ne j}{{\sum }_{i,j=1}^n}{{\mathit{t}}_i}^T{\mathit{t}}_j=\underset{i\ne j}{{\sum }_{i,j=1}^n}{{\mathit{w}}_i}^T{{\mathit{X}}_i}^T{\mathit{Z}}_i{\mathit{Z}}_j{\mathit{X}}_j{\mathit{w}}_j$$ (3)

where Z_i represents the orthogonal projector identified by OnPLS for matrix i:

$${\mathit{Z}}_i=\mathit{I}-{\mathit{T}}_{\mathit{o},i}{\left({{\mathit{T}}_{\mathit{o},i}}^{\mathit{T}}{\mathit{T}}_{\mathit{o},i}\right)}^{-1}{{\mathit{T}}_{\mathit{o},i}}^T$$

where T_o,i = [t_o,i,1| … |t_o,i,Ao], the concatenation of all orthogonal score vectors for the block, and t_o,i,a = X_iw_o,i,a. In OnPLS, each orthogonal weight w_o,i,a is chosen such that its score t_o,i,a contains maximal covariance with the variation in X_j≠i that is not jointly predictive of X_i. The OnPLS framework provides a powerful set of methods for unsupervised data mining and path modeling [16, 19-21].

2.2. CPCA-W and MB-PLS

The consensus PCA method, introduced by Wold et al. as CPCA and modified by Westerhuis et al. as CPCA-W, identifies a set of weights p_i that maximally capture the within-block variances and between-block covariances of a set of n matrices [13]. It was further proven by Westerhuis, Kourti and MacGregor that the results of CPCA-W computed on matrices X₁ to X_n are identical to those from PCA of the concatenated matrix X = [X₁] … [X_n]. It immediately follows from this equivalence that the CPCA-W algorithm optimizes the following objective function:

$${\mathit{t}}^T\mathit{t}={\mathit{p}}^T{\mathit{X}}^T\mathit{X}\mathit{p}={\sum }_{i,j=1}^n{{\mathit{t}}_i}^T{\mathit{t}}_j={\sum }_{i,j=1}^n{{\mathit{p}}_i}^T{{\mathit{X}}_i}^T{\mathit{X}}_j{\mathit{p}}_j$$ (4)

subject to the constraint ‖p‖ = 1, where p^T = [P₁^T| … |P_n^T]. Maximizing the above function yields a set of super scores t that relate the N observations in X to each other based on the extracted consensus directions in p, as well as block scores t_i and loadings p_i that describe each block. This objective function is of the MAXBET variety, in contrast to the MAXDIFF objective of nPLS and OnPLS. As a result, the CPCA-W NIPALS algorithm may be considered a special case of the general algorithm from Hanafi and Kiers [17].

The multiblock PLS (MB-PLS) method, when deflation is performed using super scores [14], shares an equivalence with single-block PLS as proven by Westerhuis et al. [13]. Therefore, the MB-PLS objective takes on a similar form as in CPCA-W, with the addition of a weighting matrix:

$${\mathit{t}}^T{\mathit{\text{YY}}}^T\mathit{t}={\mathit{w}}^T{\mathit{X}}^T{\mathit{\text{YY}}}^T\mathit{X}\mathit{w}={\sum }_{i,j=1}^n{{\mathit{t}}_i}^T{\mathit{\text{YY}}}^T{\mathit{t}}_j={\sum }_{i,j=1}^n{{\mathit{w}}_i}^T{{\mathit{X}}_i}^T{\mathit{\text{YY}}}^T{\mathit{X}}_j{\mathit{w}}_j$$ (5)

where once again ‖w‖ is constrained to unity. In analogy to Höskuldsson's interpretation of PLS as a regression on orthogonal components, where YY^T is used to weight the covariance matrix, the above function corresponds to a MAXBET objective with an inner weighting of YY^T [2]. Alternatively, equation (5) could be interpreted as a MAXBET computed on the n cross- covariance matrices Y^TX₁ to Y^TX_n.

2.3. MB-OPLS

Extension of prior multiblock NIPALS algorithms to incorporate an OSC filter rests on the observation that, in both the case of CPCA-W and MB-PLS, deflation of each computed component is accomplished using super scores. For any super score deflation method, a loading vector is computed for each block:

$${\mathit{p}}_i=\frac{{{\mathit{X}}_i}^T\mathit{t}}{{\mathit{t}}^T\mathit{t}}$$

and the super scores t and block loadings are then used to deflate their respective block:

$${\mathit{X}}_i\leftarrow {\mathit{X}}_i-\mathit{t}{{\mathit{p}}_i}^T=(\mathit{I}-\frac{\mathit{t}{\mathit{t}}^T}{{\mathit{t}}^T\mathit{t}}){\mathit{X}}_i$$ (6)

Equation (6) differs from equation (2) used in nPLS and OnPLS, which uses block-specific scores and loadings during deflation. This method of super score deflation ensures that the super scores are an orthogonal basis, while allowing scores and loadings to become slightly correlated at the block level, and is a necessary condition for the equivalences between CPCA-W and MB-PLS and their single-block counterparts [13]. We shall employ this condition in MB-OPLS by deflating each matrix by a set of orthogonal super scores T_o, which shall be shown to be equal to the orthogonal scores obtained from single-block OPLS. By constructing an MB-PLS model on the set of matrices after deflation by T_o, we effectively arrive at another MAXBET objective:

$${\mathit{t}}^T{\mathit{\text{YY}}}^T\mathit{t}={\mathit{w}}^T{\mathit{X}}^T\mathit{Z}{\mathit{\text{YY}}}^T\mathit{Z}\mathit{X}\mathit{w}={\sum }_{i,j=1}^n{{\mathit{t}}_i}^T{\mathit{\text{YY}}}^T{\mathit{t}}_j={\sum }_{i,j=1}^n{{\mathit{w}}_i}^T{{\mathit{X}}_i}^T\mathit{Z}{\mathit{\text{YY}}}^T\mathit{Z}{\mathit{X}}_j{\mathit{w}}_j$$ (7)

where w is constrained to unit norm and Z is the orthogonal projector for the super scores T_o:

$$\mathit{Z}=\mathit{I}-{\mathit{T}}_{\mathit{o}}{\left({{\mathit{T}}_{\mathit{o}}}^{\mathit{T}}{\mathit{T}}_{\mathit{o}}\right)}^{-1}{{\mathit{T}}_{\mathit{o}}}^T$$

2.3.1. The MB-OPLS Model

MB-OPLS constructs an OPLS model for each matrix X_i, where the predictive and orthogonal loadings for each matrix are interrelated by a set of predictive and orthogonal super scores, respectively:

$${\mathit{X}}_{\mathit{i}}=\underset{{\mathit{X}}_{\mathit{p},i}}{\underbrace{\mathit{T}{{\mathit{P}}_{\mathit{i}}}^{\mathit{T}}}}+\underset{{\mathit{X}}_{\mathit{o},i}}{\underbrace{{\mathit{T}}_{\mathit{o}}{{\mathit{P}}_{\mathit{o},i}}^T}}+{\mathit{E}}_i$$ (8)

where each E_i is a data residual matrix that holds all variation in X_i not explained by the model. Concatenation of all block-level matrices together in equation (8) results in a top-level consensus model, which is in fact equivalent to an OPLS model trained on the partitioned data matrix X:

$$\mathit{X}=[{\mathit{X}}_1|\dots |{\mathit{X}}_n]=\underset{{\mathit{X}}_{\mathit{p}}}{\underbrace{\mathit{T}[{{\mathit{P}}_1}^{\mathit{T}}|\dots |{{\mathit{P}}_n}^T]}}+\underset{{\mathit{X}}_{\mathit{o}}}{\underbrace{{\mathit{T}}_{\mathit{o}}[{{\mathit{P}}_{\mathit{o},1}}^T|\dots |{{\mathit{P}}_{\mathit{o},n}}^T]}}+\underset{\mathit{E}}{\underbrace{[{\mathit{E}}_1|\dots |{\mathit{E}}_n]}}$$ (9)

Like PLS and MB-PLS, an MB-OPLS model contains a second equation that relates the predictive super scores and responses:

$$\mathit{Y}=\mathit{T}{\mathit{C}}^T+\mathit{F}$$ (10)

where C is the response loadings matrix that relates the super scores to the responses, and F is the response residual matrix that holds Y-variation not captured by the model.

2.3.2. The MB-OPLS Algorithm

The proposed MB-OPLS algorithm described herein admits a matrix of responses Y, but also supports vector-y cases. Direct and normed assignment will be indicated by “←” and “∝”, respectively. All assignments to block-specific structures (e.g. w_i) that are to be performed over all values of i from 1 to n are suffixed with “∀i ∈ {1, …, n}”.

1. For each m ∈ {1, …, M} do

   1. v_i,m ← X_i^Ty_m · (y_m^Ty_m)⁻¹ ∀i ∈ {1, …, n}

   2. V_i ← [V_i|v_i,m] ∀i ∈ {1, …, n}

2. Initialize u to a column of Y

3. w_i ∝ X_i^Tu ∀i ∈ {1, …, n}

4. t_i ← X_iw_i ∀i ∈ {1, …, n}

5. R ← [t₁| … |t_n]

6. w_T ∝ R^Tu

7. t ← Rw_T

8. c ← (Y^Tt) · (t^Tt)⁻¹

9. u ← (Yc) · (c^Tc)⁻¹

10. If ‖u – u_old‖/‖u_old‖ > ∈, return to step (3).

    Otherwise, continue to step (11).

11. p_i ← (X_i^Tt) · (t^Tt)^–1 ∀i ∈ {1, …, n}

12. To compute an orthogonal component, continue to step (13).

    Otherwise, proceed to step (21).

13. w_o,i ← p_i ∀i ∈ {1, …, n}

14. For each m ∈ {1, …, M} do

    1. $\phi \leftarrow \left({\sum }_{i=1}^n{{\mathit{v}}_{i,m}}^T{\mathit{w}}_{\mathit{o},i}\right)·{\left({\sum }_{i=1}^n{{\mathit{v}}_{i,m}}^T{\mathit{v}}_{i,m}\right)}^{-1}$

    2. w_o,i ← w_o,i – φv_i,m ∀i ∈ {1, …, n}

15. ${\mathit{w}}_{\mathit{o},\mathit{i}}\leftarrow {\mathit{w}}_{\mathit{o},i}·{\left({\sum }_{i=1}^n{{\mathit{w}}_{\mathit{o},i}}^T{\mathit{w}}_{\mathit{o},i}\right)}^{-1\backslash 2}\forall i\varepsilon \{1,\dots ,n\}$

16. t_o,i ← X_iw_o,i ∀i ∈ {1, …, n}

17. ${\mathit{t}}_{\mathit{o}}\leftarrow {\sum }_{\mathit{i}=1}^n{\mathit{t}}_{\mathit{o},i}$

18. p_o,i ← (X_i^T t_o) · (t_o^T t_o)⁻¹ ∀i ∈ {1, …, n}

19. X_i ← X− t_op_o,i^T ∀i ∈ {1, …, n}

20. Return to step (2).

21. X_i ← X_i− tp_i^T ∀i ∈ {1, …, n}

22. To compute another component, return to step (2).

    Otherwise, end.

In the above algorithm, the value of ∈ is set to a very small number, e.g. 10⁻⁹. For each predictive component in the model, a set of orthogonal components is extracted. After the computation of a new orthogonal component, the current predictive component is updated to reflect the removal of orthogonal variation from the matrices X_i. The MB-OPLS algorithm closely follows the matrix-Y OPLS algorithm presented by Trygg and Wold [6], but replaces the standard PLS computation (steps 4-10 in OPLS) with an MB-PLS computation (steps 2-11 above). However, as described below, the mechanism by which orthogonal variation is removed (steps 13-19 above) is identical to that of OPLS.

2.3.3. Equivalence to OPLS

In both the vector-y and matrix-Y OPLS algorithms proposed by Trygg and Wold [6], a basis V for the response-correlated variation in X is constructed by regressing the data onto each column of responses:

$${\mathit{v}}_m\leftarrow \frac{{\mathit{X}}^T{\mathit{y}}_m}{{{\mathit{y}}_m}^T{\mathit{y}}_m}\forall m\in \{1,\dots ,M\}$$ (11)

where y_m and v_m denote the m-th columns of Y and V, respectively. When X is partitioned into multiple blocks, the computed basis also bears the same partitioning, i.e. V^T = [V₁^T| … |V_n^T], where each of the n submatrices corresponds to the regression of its respective block X_i onto the responses:

$${\mathit{v}}_{i,m}\leftarrow \frac{{{\mathit{X}}_i}^T{\mathit{y}}_m}{{{\mathit{y}}_m}^T{\mathit{y}}_m}\forall m\in \{1,\dots ,M\}$$ (12)

where v_i,m is the m-th column of V_i. Given a single-block PLS loading vector p, the OPLS algorithm computes an orthogonal weight w_o by orthogonalizing p to the columns of V:

$${\mathit{w}}_{\mathit{o}}\leftarrow {\mathit{w}}_{\mathit{o}}-\left(\frac{{{\mathit{v}}_m}^T{\mathit{w}}_{\mathit{o}}}{{{\mathit{v}}_m}^T{\mathit{v}}_m}\right){\mathit{v}}_m\forall m\in \{1,\dots ,M\}$$ (13)

after w_o has been initialized to p. From the proof of Westerhuis et al. [13], it is known that the single-block PLS loading p equals the concatenation of all block loadings from MB-PLS, i.e. that p^T = [p₁^T| … |p_n^T]. Expansion of all vector terms in the above equation into their partitioned forms results in the following new assignment rule:

$${\mathit{w}}_{\mathit{o},i}\leftarrow {\mathit{w}}_{\mathit{o},i}-\left(\frac{{\sum }_{i=1}^n{{\mathit{v}}_{i,m}}^T{\mathit{w}}_{\mathit{o},i}}{{\sum }_{i=1}^n{{\mathit{v}}_{i,m}}^T{\mathit{v}}_{i,m}}\right){\mathit{v}}_{i,m}\forall m\in \{1,\dots ,M\}$$ (14)

The scalar term in equation (14) should be recognized as φ in the MB-OPLS algorithm. By the same reasoning, step (15) in the algorithm is equivalent to scaling w_o to unit norm. In effect, by computing φ as the fraction of orthogonal variation to remove from its loadings, MB-OPLS yields the same orthogonal weights (w_o) as OPLS of the concatenated matrix. Therefore, because w_o equals the column-wise concatenation of all weights w_o,i, it is then apparent that the orthogonal super scores extracted by MB-OPLS are identical to those from OPLS of the concatenated matrix X, as illustrated in the following equation:

$${\mathit{t}}_{\mathit{o}}=\mathit{E}{\mathit{w}}_{\mathit{o}}=[{\mathit{E}}_1|\dots |{\mathit{E}}_n][\begin{array}{c}{\mathit{w}}_{\mathit{o},1}\\ ⋮\\ {\mathit{w}}_{\mathit{o},n}\end{array}\rceil ={\sum }_{i=1}^n{\mathit{E}}_i{\mathit{w}}_{\mathit{o},i}={\sum }_{i=1}^n{\mathit{t}}_{\mathit{o},i}$$ (15)

From this equivalence, and the fact that steps (2-11) and (21) in MB-OPLS constitute an MB-PLS iteration, we arrive at the equivalence between MB-OPLS and OPLS. Thus, orthogonality between the responses and orthogonal super scores t_o computed by MB-OPLS is also ensured. However, because the computation of orthogonal weights involves all blocks, the resulting orthogonal block scores t_o,i are not guaranteed to be orthogonal to the responses.

2.3.4. Computation from an OPLS Model

The equivalence between MB-OPLS super scores and OPLS scores may be leveraged to generate an MB-OPLS model from an existing OPLS model of a partitioned data matrix, saving computation time during cross-validated model training. The following algorithm details the extraction of MB-OPLS block scores and loadings from an OPLS model:

1. Initialize a = 1, b = 1

2. t_o ← [T_o]_a

3. w_o,i ← [W_o]_i ∀i ∈ {1, …, n}

4. t_o,i ← X_iw_o,i ∀i ∈ {1, …, n}

5. p_o,i ← (X_i^T t_o) · (t_o^T t_o)^–1 ∀i ∈ {1, …, n}

6. T_o,i ← [T_o,i|t_o,i] ∀i ∈ {1, …, n}

7. P_o,i ← [P_o,i|P_o,i] ∀i ∈ {1, …, n}

8. W_o,i ← [W_o,i|W_o,i] ∀i ∈ {1, …, n}

9. If another orthogonal component exists, increment a and return to step (2). Otherwise, continue to step (10).

10. X_i ← X_i− T_oP_o,i^T ∀i ∈ {1, …, n}

11. u ← [U]_b

12. t ← [T]_b

13. w_i ∝ X_i^T u ∀i ∈ {1, …, n}

14. t_i ← X_iw_i ∀i ∈ {1, …, n}

15. p_i ← (X_i^T t) · (t^T t)⁻¹ ∀i ∈ {1, …, n}

16. T_i ← [T_i|t_i] ∀i ∈ {1, …, n}

17. P_i ← [P_i|P_i] ∀i ∈ {1, …, n}

18. W_i ← [W_i|w_i] ∀i ∈ {1, …, n}

19. X_i ← X_i − tp_i^T ∀i ∈ {1, …, n}

20. If another predictive component exists, increment and return to step (1). Otherwise, end.

The keen observer will recognize the equivalence between steps (10-19) above and the procedure outlined by Westerhuis et al. for extracting MB-PLS block components from a PLS model [13]. By using the above algorithm to compute MB-OPLS models, the analyst avoids the unnecessary computation of block components during cross-validated model training. For example, a G-fold Monte Carlo cross-validation having R iterations requires the construction of RG models in order to yield R cross-validated response matrix estimates. In each of these RG models, MB-PLS requires 2Nn additional floating-point multiplications (per power iteration) over PLS. In addition, computation of multiblock components from single-block models ensures greater stability of super scores and loadings, especially in cases of missing data [13].

3. Datasets

Two datasets will be described to illustrate how MB-OPLS effectively integrates an OSC filter into an MB-PLS decomposition of a set of n matrices. The first synthetic dataset contrasts the mixing of predictive information in MB-PLS with its separation in MB-OPLS using a contrived three-block regression example similar to that introduced by Löfstedt and Trygg [16]. The second dataset, a joint set of nuclear magnetic resonance (NMR) and mass spectrometry (MS) observations [22, 23], is used to demonstrate the enhanced interpretability of MB-OPLS models over MB-PLS in a real example of discriminant analysis. All modeling and validation wereperformed using routines available in the MVAPACK chemometrics toolbox (http://bionmr.unl.edu/mvapack.php) [24].

3.1. Synthetic Example

In the first dataset, three matrices (all having 100 rows and 200 columns) were constructed to hold one y-predictive component (tp_i^T) and one y-orthogonal component (t_op_o,i^T). The score vectors were non-overlapping (orthogonal) Gaussian density functions, and all block loading vectors were mutually overlapping Gaussian density or square step functions. The true synthetic block loadings are illustrated in Figure 1A. A two-component MB-PLS-R regression model was trained on the synthetic three-block example dataset, as well as a 1+1 (one predictive, one orthogonal) component MB-OPLS-R regression model. Block loadings extracted by MB-PLS-R and MB-OPLS-R are shown in Figures 1B and 1C, respectively.

Figure 1.

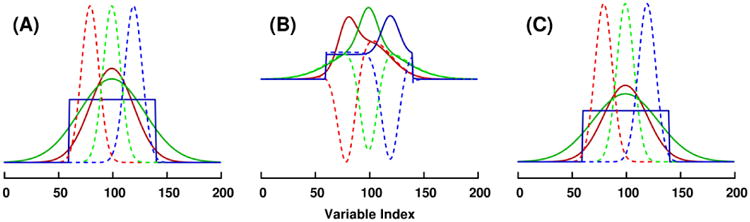
Block loadings in the synthetic multiblock example dataset. (A) True predictive loadings (solid) and orthogonal loadings (dashed) used to construct the three-block dataset. First, second and third block loadings are colored in red, green and blue, respectively. (B) First component (solid) and second component (dashed) loadings identified by MB-PLS modeling of the three data blocks. (C) Predictive (solid) and orthogonal (dashed) block loadings identified by MB-OPLS, illustrating the separation of y-uncorrelated variation accomplished by the integrated OSC filter.

3.2. Joint ¹H NMR and DI-ESI-MS Datasets

The second dataset is a pair of processed and treated data matrices, collected on 29 samples of metabolite extracts from human dopaminergic neuroblastoma cells treated with various neurotoxic agents [23]. The first matrix, collected using ¹H NMR spectroscopy, contains 16,138 columns and the second, collected using direct injection electrospray ionization mass spectrometry (DI-ESI-MS), contains 2,095 columns. Prior to all modeling, block weighting was applied after Pareto scaling to ensure equal contribution of each block to the models (fairness) [12].

In previously performed work, a two-component, two-class (vector-y) multiblock discriminant analysis (MB-PLS-DA) model was trained on the dataset in order to discriminate between untreated and neurotoxin-treated cell samples. To highlight the improved interpretability of MB-OPLS over MB-PLS, a 1+1 MB-OPLS-DA model was trained on the data using an identical vector of class labels. Block components were extracted from an OPLS-DA model of the concatenated matrix X = [X_NMR|X_MS] using the above algorithm. For both models, fifty rounds of Monte Carlo seven-fold cross-validation [25, 26] were performed to compute per-component Q² statistics [3], in addition to the R² statistics available from model training. CV-ANOVA significance testing was also applied to further assess model reliability [27].

4. Results and Discussion

In both the contrived dataset and the real spectroscopic dataset, the interpretative advantage offered by MB-OPLS over MB-PLS is strikingly apparent. In the synthetic example, MB-OPLS capably identifies the true predictive and orthogonal loadings in the presence of y-orthogonal variation that clouds the interpretation of MB-PLS loadings (Figure 1). By design, this comparison between MB-OPLS and MB-PLS is highly similar to the first example presented by Löfstedt and Trygg to compare nPLS and OnPLS for general data discovery [16]. However, as is evidenced by the differences between equations (3) and (7) above, MB-OPLS solves an inherently distinct problem from OnPLS: the identification of consensus variation in multiple blocks of data that predicts a single set of responses.

The ability of MB-OPLS to separate predictive and orthogonal variation from multiple data matrices is further exemplified in the discriminant analysis of the real spectroscopic dataset. From the rotated discrimination axis in the MB-PLS-DA scores (Figure 2A), it is clear that predictive and orthogonal variation have become mixed in the corresponding block loadings (Figure 3). Integration of an OSC filter into the multiblock model in the form of MB-OPLS-DA achieves the expected rotation of super scores to place more predictive variation into the first component (Figure 2B). As a consequence of this rotation, spectral information that separates paraquat treatment from other neurotoxin treatments is also moved into the orthogonal component. For example, strong loadings from citrate in the ¹H NMR MB-PLS block loadings (Figure 3A, 2.6 ppm) are substantially diminished in the predictive block loadings from MB-OPLS (Figure 4), as separation between paraquat and other treatments has been isolated along the orthogonal component in super scores. Inspection of the orthogonal block loadings from MB-OPLS (Supplementary Figure S-4) will reveal, as expected, that citrate contributes more to separation between neurotoxin treatments than to separation between treatments and controls. Similar patterns were observed in the DI-ESI-MS block loadings at m/z 203.058 and 233.067, which were assigned via accurate mass and tandem MS measurements as sodium adducts of hexose and heptose, respectively [23]. These results agree with detailed prior analyses of pairwise MB-PLS-DA models between each drug treatment and untreated cells, which indicate that paraquat treatment uniquely alters metabolic flux through glycolysis and the pentose phosphate pathway [22]. In contrast to the multiple MB-PLS-DA models employed by Lei et al. to arrive at this conclusion [22], the MB-OPLS-DA model has provided the same set of core results in a single, substantially more interpretable model.

Figure 2.

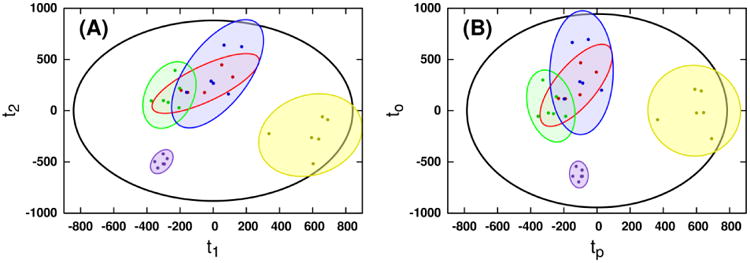
Super scores identified by (A) MB-PLS and (B) MB-OPLS modeling of the joint ¹H NMR and DI-ESI-MS data matrices. Extraction of y-orthogonal variation from the first PLS component is clear in the MB-OPLS scores. Ellipses represent the 95% confidence regions for each sub-class of observations, assuming normal distributions. Colors indicate membership to the untreated (yellow), 6-hydroxydopamine (red), 1-methyl-4-phenylpyridinium (green) and paraquat (violet) sub-classes. Cross-validated super scores for each model are shown in Supplementary Figure S-1. Block scores for each model are shown in Supplementary Figures S-2 and S-3.

Figure 3.

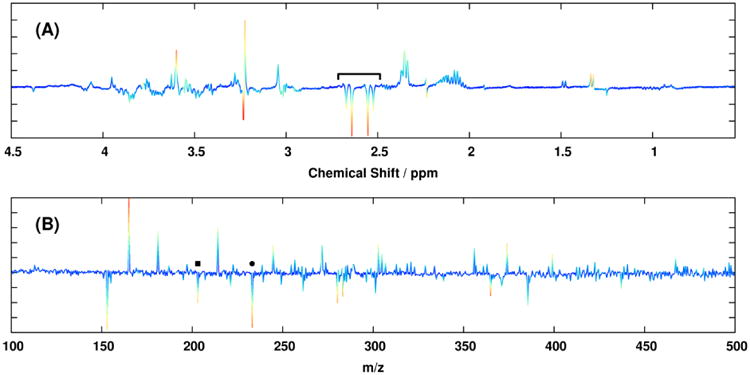
Backscaled first-component block loadings from the MB-PLS model of the (A) ¹H NMR and (B) DI-ESI-MS data matrices. Coloring of each loading vector ranges from blue to red based on the amount of point-wise weighting applied during Pareto scaling. It is important to note that a second PLS component exists in the MB-PLS model that is not shown. Spectral contributions from citrate in the ¹H NMR MB-PLS block loadings (2.6 ppm) are indicated by a bracket, and contributions from hexose and heptose in the DI-ESI-MS loadings are indicated by black squares and circles, respectively.

Figure 4.

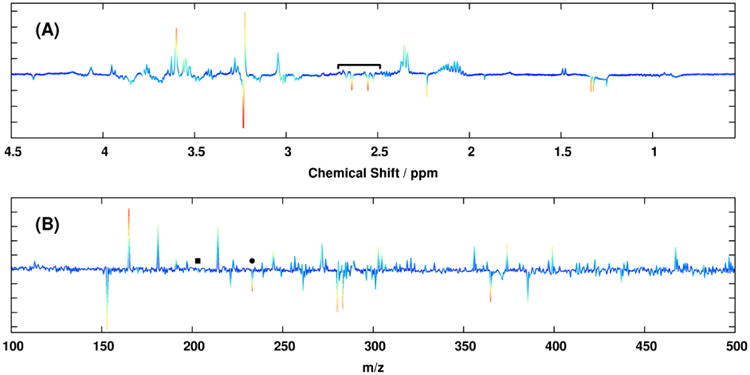
Backscaled first-component block loadings from the MB-OPLS model of the (A) ¹H NMR and (B) DI-ESI-MS data matrices. Coloring of each loading vector is identical to that of Figure 3. Spectral contributions from citrate in the ¹H NMR MB-OPLS block loadings (2.6 ppm) are indicated by a bracket, and contributions from hexose and heptose in the DI-ESI-MS loadings are indicated by black squares and circles, respectively. Unlike the two-component MB-PLS model, the single predictive MB-OPLS component here fully separates observations between the classes under discrimination. Backscaled orthogonal block loadings from the same model are shown in Supplementary Figure S-4.

The partial correlation of both predictive and orthogonal block scores in MB-OPLS is readily observed in the comparison of block scores from MB-PLS and MB-OPLS (Supplementary Figures S-2 and S-3). While the super scores in Figure 2B are rotated to separate predictive and orthogonal variation, block scores in Figures S-2B and S-3B have rotated back into alignment with the MB-PLS block scores. This partial correlation and re-mixing of predictive and orthogonal variation in MB-OPLS block scores is a consequence of the use of super score deflation in the proposed algorithm. When all matrices contain similar patterns of orthogonal variation, their MB-OPLS block scores will reflect this by retaining the OSC-induced rotation captured at the consensus level by the super scores. However, because the interpretative advantage of MB-OPLS over MB-PLS lies in the relationship between super scores and block loadings, the fact that orthogonal block scores have partial y-correlation is relatively benign.

Because the MB-OPLS-DA model of the real spectral data matrices was trained using the single-block OPLS routine already present in MVAPACK, all readily available cross-validation metrics were available in the model without further computational expenditure. Monte Carlo cross-validation of the MB-PLS model produced cumulative R²_Y and Q² statistics of 0.903 and 0.819±0.024, respectively, and validation of the MB-OPLS model resulted in statistics of 0.903 and 0.736±0.021, respectively. As expected, the MB-OPLS model captured the same fraction of response variation (R²_Y) as MB-PLS, reaffirming the fact that the two methods have the same predictive ability. In addition, MB-OPLS modeling yielded R²_Xp and R²_Xo statistics of 0.378 and 0.245 for the first block, and 0.236 and 0.083 for the second block. Monte Carlo cross-validated super scores from MB-PLS and MB-OPLS are depicted in Supplementary Figure S-1. Compared to MB-PLS scores in Figure S-1A, MB-OPLS scores (Figure S-1B) exhibit an increased uncertainty during cross-validation due to the coupled nature of predictive and orthogonal components in OPLS models. Further validation of the MB-OPLS-DA model via CV-ANOVA produced a p value equal to 2.88×10^-6, indicating a sufficiently reliable model.

It is worthy of final mention that the objective solved by MB-OPLS is but a single member of a superfamily of multiblock methods introduced in detail by Hanafi and Kiers [17]. In the first family, nPLS and OnPLS maximally capture the between-matrix covariances before and after orthogonal signal correction, respectively, and thus serve to regress a set of matrices against each other. Methods in the second family capture both within-matrix variances and between-matrix covariances of a set of matrices (CPCA-W), a set of response-weighted matrices (MB-PLS), and a set of response-weighted OSC-filtered matrices (MB-OPLS). By casting these methods in the light of MAXDIFF and MAXBET, we obtain an informative picture of their characteristics, commonalities, and differences. For example, nPLS and OnPLS force an equal contribution of each matrix to the solution through the constraint ‖w_i‖ = 1, while CPCA-W, MB-PLS and MB-OPLS allow contributions to float based on the “importance” of each matrix to the modeling problem at hand. This super weight approach necessitates a block scaling procedure to avoid highly weighting any given matrix due to size alone [12, 13].

5. Conclusions

The MB-OPLS method proposed here is a versatile extension of MB-PLS to include an OSC filter, and belongs to a family of MAXBET optimizers that share an equivalence with their single-block factorizations (Supplementary Figure S-5). By removing consensus response-uncorrelated variation from a set of n data matrices, MB-OPLS expands the scope and benefits of OPLS to cases where blocking information is available. The ability of MB-OPLS to separate predictive and orthogonal variation from multiple blocks of data has been demonstrated on both synthetic and real spectral data, both in cases of vector-y regression and discriminant analysis. Of course, while both examples were interpreted in the light of spectroscopic datasets like those used in metabolomics [22, 23], MB-OPLS is a fully general algorithm that admits any multiblock dataset for the purposes of regression or discriminant analysis. For example, recent applications of MB-PLS for investigating food spoilage [28], iron-ore content [29], chemical toxicity [30], the evolution of human anatomy [31], and the assessment of cortical and muscle activity in Parkinson's disease patients [32] would benefit from our MB-OPLS algorithm. The presented algorithm admits either a vector or a matrix as responses, and is implemented in the latest version of the open-source MVAPACK chemometrics toolbox [24].

Highlights.

• Extension of OPLS to multiblock modeling situations

• Relationships established to other multiblock model objectives

• Use of NIPALS admits simple implementation of MB-OPLS