Abstract
Motivation: Model organisms play critical roles in biomedical research of human diseases and drug development. An imperative task is to translate information/knowledge acquired from model organisms to humans. In this study, we address a trans-species learning problem: predicting human cell responses to diverse stimuli, based on the responses of rat cells treated with the same stimuli.
Results: We hypothesized that rat and human cells share a common signal-encoding mechanism but employ different proteins to transmit signals, and we developed a bimodal deep belief network and a semi-restricted bimodal deep belief network to represent the common encoding mechanism and perform trans-species learning. These ‘deep learning’ models include hierarchically organized latent variables capable of capturing the statistical structures in the observed proteomic data in a distributed fashion. The results show that the models significantly outperform two current state-of-the-art classification algorithms. Our study demonstrated the potential of using deep hierarchical models to simulate cellular signaling systems.
Availability and implementation: The software is available at the following URL: http://pubreview.dbmi.pitt.edu/TransSpeciesDeepLearning/. The data are available through SBV IMPROVER website, https://www.sbvimprover.com/challenge-2/overview, upon publication of the report by the organizers.
Contact: xinghua@pitt.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Due to ethical issues, modal organisms such as rat and mouse have been widely used as disease models in studying disease mechanisms and drug actions (Brown, 2011; McGonigle and Ruggeri, 2014). For example, mouse models have been used to study the disease mechanisms and treatment of type-2 diabetes (Omar et al., 2013). Since significant differences exist between species in terms of genome, cellular systems and physiology, the success of using model organisms in biomedical research is hinged on the capability to translate/transfer the knowledge learned from model organisms to humans. For example, when using a rat disease model to screen drugs and investigate the action of drugs, rat cells inevitably exhibit different molecular phenotypes, such as proteomic or transcriptomic responses, when compared with corresponding human cells. Thus, in order to investigate how the drugs act in human cells, it is critical to translate the molecular phenotypes observed in rat cells into corresponding human responses.
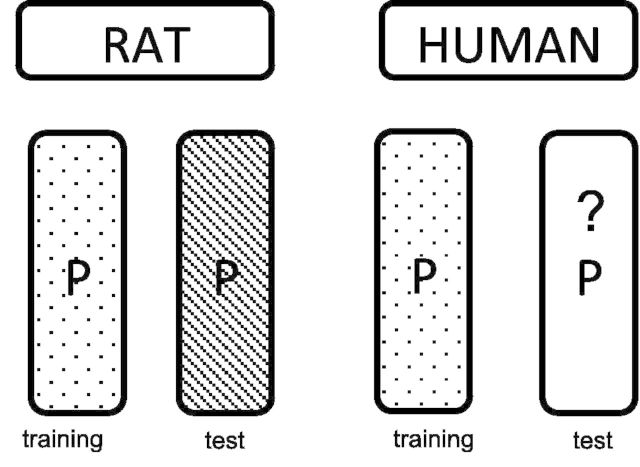
Recent species-translation challenges organized by the Systems Biology Verification combined with Industrial Methodology for Process Verification in Research (SBV IMPROVER, 2013) provided an opportunity for the research community to assess the methods for trans-species learning in systems biology settings (Rhrissorrakrai et al., 2015). One challenge task was to predict human cells’ proteomic responses to distinct stimuli based on the observed proteomic response to the same stimuli in rat cells. More specifically, during the training phase, participants were provided with data that measured the phosphorylation states of a common set of signaling proteins in primary cultured bronchial cells collected from rats and humans treated with distinct stimuli (Poussin, 2014). In the testing phase, the proteomic data of rat cells treated with unknown stimuli were provided, and the task is to predict the proteomic responses of human cells treated with the same stimuli (Fig. 1).
Fig. 1.
Trans-species learning task specification. The objective of the SBV challenge was to predict the phosphorylation states of a set of proteins in human cells treated with different stimuli, based on the observed phosphorylation states of the same set of proteins in rat cells treated with the same stimuli. The blocks labled as “training” are matrices representing the observed phosphorylation states of proteins under different treatment conditions in human and rat cells. In test phase, the phosphorylation states of the proteins in rat cells treated with a set of unknown stimuli are provided, and the task is to predict the phosphorylation states of the human cells treated with the same stimuli
To address the trans-species learning task, a simplistic approach is to train regression/classification models that use the phosphorylation data from rat cells as input features and treat the phosphorylation status of an individual protein from human cells (treated with the same stimulus) as a target class. In this way, predicting the proteomic profile of human cells can be addressed as a series of independent classification tasks or within a multi-label classification framework (Jin et al., 2008; Tsoumakas and Katakis, 2007). However, most contemporary multi-label classification methods treat the target classes as independent or are incapable of learning the covariance structure of classes, which apparently does not reflect biological reality. In cellular signaling systems, signaling proteins often form pathways in which the phosphorylation of one protein will affect the phosphorylation state of others in a signaling cascade, and cross-talk between pathways can also lead to coordinated phosphorylation of proteins in distinct pathways (Alberts et al., 2008). Another shortcoming of formulating trans-species learning as a conventional classification problem is that contemporary classifiers, such as the support vector machine (Bishop, 2006) or regularized regression/classification (Friedman et al., 2010), concentrate on deriving mathematical representations that separate the cases, whereas the real goal of trans-species learning is to capture the common signaling mechanisms employed by cells from both model organisms and humans in response to a common stimuli. Indeed, the cornerstone hypothesis underpinning trans-species learning is that there is a common encoding mechanism shared by cells from different species, but distinct signaling molecules are employed by different species to transmit the signals responding to the same environmental stimuli. Therefore, it is important to explore models that are compatible to the above hypothesis.
Recent advances in deep hierarchical models, commonly referred to as ‘deep learning’ models (Bengio et al., 2012; Hinton et al., 2006; Hinton and Salakhutdinov, 2006), provide an intriguing opportunity to model the common encoding mechanism of cellular signaling systems. These models represent the signals embedded in observed data using multiple layers of hierarchically organized hidden variables, which can be used to simulate a cellular signaling system because the latter is also organized as a hierarchical network such that signaling proteins at different levels compositionally encode signals with different degrees of complexity. For example, activation of the epidermal growth factor receptor (EGFR) will lead to a broad change of cellular functions including the activation of multiple signaling molecules such as Ras and MAP kinases (Alberts et al., 2008), which in turn will activate different transcription factors, e.g. Erk-1 and c-Jun/c-Fos complex, with each responsible for the transcription of a subset of genes responding to EGFR treatment. The signals encoded by signaling molecules become increasingly more specific, and they share compositional relationships. Therefore, deep hierarchical models, e.g. the deep belief network (DBN) (Hinton et al., 2006), are particularly suitable for modeling cellular signaling systems.
In this paper, we present novel deep hierarchical models based on the DBN model to represent a common encoding system that encodes the cellular response to different stimuli, which was developed after the competition in order to overcome the shortcomings of the conventional classification approaches we employed during competition. We applied the model to the data provided by the SBV IMPROVER challenge and systematically investigated the performance. Our results indicate that, by learning better representations of cellular signaling systems, deep hierarchical models perform significantly better on the task of trans-species learning. More importantly, this study leads to a new direction of using deep networks to model large ‘omics’ data to gain in depth knowledge of cellular signaling systems under physiological and pathological conditions, such as cancer.
2 Methods
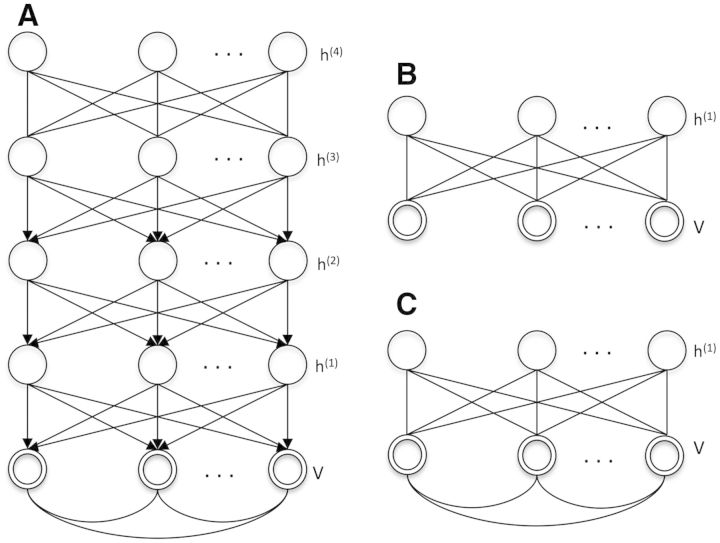
In this study, we investigated using the DBN model (Hinton et al., 2006) to represent the common encoding system of the signal transduction systems of human and rat bronchial cells. A DBN contains one visible layer and multiple hidden layers (Fig. 2A). An efficient training algorithm was introduced by (Hinton et al., 2006; Hinton and Salakhutdinov, 2006), which treats a DBN as a series of restricted Boltzmann machines (RBM; Fig. 2B) stacked on top of each other. For example, the visible layer v and the first hidden layer, h(1), can be treated as a RBM, and the first and second hidden layers, h (1) and h (2), form another RBM with h (1) as the ‘visible’ layer. The inference of the hidden node states and learning of model parameters are first performed by learning the RBM stacks bottom-up, which is followed by a global optimization of generative parameters using the back-propagation algorithm. In certain cases, edges between visible variables can be added in a RBM to capture the relationship of the visible variables, which leads to a semi-restricted RBM (Fig. 2C). In the following sub-sections, we will first introduce the models and their inference algorithms.
Fig. 2.
Graph representation of the Deep Belief Network and related models. (A) The graph representation of a 4-layered deep belief network. The double circles represent visible variables, and the single circles represent hidden variables. (B) The graph representation of a restricted Boltzmann machine. (C) The graph representation of a semi-restricted Boltzmann machine in which visible variables are connected
2.1 Restricted Boltzmann Machines (RBMs)
A RBM is an undirected probabilistic graphical model consisting of a layer of stochastic visible binary variables (represented as nodes in the graph) and a layer of stochastic hidden binary variables . A RBM is a bipartite graph in which each visible node is connected to every hidden node (Fig. 2B) and vice versa. The statistical structure embedded in the visible variables can be captured by the hidden variables. The RBM model defines the joint distribution of hidden and visible variables using a Boltzmann distribution as follows:
| (1) |
The energy function E of the state of the RBM is defined as follows:
| (2) |
where is the binary state of visible variable i; is the binary state of hidden variable j; are the model parameters. represents the bias for visible variable i and represents the bias for hidden variable j. represents the weight between visible variable i and hidden variable j.
The ‘partition function’, , is derived by summing over all possible states of visible and hidden variables:
| (3) |
The marginal distribution of visible variables is
| (4) |
2.2 Learning parameters of the RBM model
Learning parameters of a RBM model can be achieved by updating the weight matrix and biases using a gradient descend algorithm (delta methods; Hinton and Salakhutdinov, 2006).
| (5) |
| (6) |
where is the learning rate; is the expected product of the observed data and inferred hidden variables conditioning on observed variables; is the expected product of the model-predicted v and . One approach to derive is to obtain samples of v and h from a model-defined distribution using Markov chain Monte Carlo (MCMC) methods and then average the product of the samples, which may take a long time to converge. Representing the derived MCMC chain after convergence as , one updates the model parameter as follows:
| (7) |
To calculate , one can alternatively sample the states of hidden variables given visible variables and then sample the states of visible variables given hidden variables (Salakhutdinov et al., 2007) based on the following equations.
| (8) |
| (9) |
where is the logistic function .
The convergence of a MCMC chain may take a long time. Thus, to make RBM learning more efficient, we adopted a learning algorithm called contrastive divergence (CD) (Welling and Hinton, 2002). Instead of running a MCMC chain for a very large number of steps, CD learning just runs the chain for a small number n of steps and minimizes the divergence between Kullback–Leibler divergence and to approximate (Carreira-Perpinan and Hinton, 2005).
Therefore, the updating algorithm for a parameter of a RBM can be rewritten as follows:
| (10) |
| (11) |
| (12) |
The pseudocode for training a RBM is as follows:
Repeat for t iterations:
- 1) Infer state of hidden units given visible units
2) Gibbs Sampling binary matrix
- 3) Infer state of visible units given hidden units
- 4) Infer state of hidden units given visible units
- 5) Update parameters (weight between visible i and hidden j, bias of visible and bias of hidden)
2.3 Learning a Deep Belief Network
Unlike a RBM, which captures the statistical structure of data using a single layer of hidden nodes, a DBN strives to capture the statistical structure using multiple layers in a distributed manner, such that each layer captures the structure of different degrees of abstraction. Training a DBN involves learning two sets of parameters: (i) a set of recognition weight parameters for the upward propagation of information from the visible layer to the hidden layers, and (ii) a set of generative weight parameters that can be used to generate data corresponding to the visible layer. The learning of recognition weights can be achieved by treating a DBN as a stack of RBMs and progressively performing training in a bottom-up fashion (Hinton et al., 2006; Hinton and Salakhutdinov, 2006). For example, one can treat the visible layer v and the first hidden layer h(1) as a RBM, and then we can treat hidden layer h(1) as a visible layer and form a RBM with the hidden layer h(2). Following the stack-wise learning of RBMs weight parameters and instantiation of hidden variables in the top layer, learning the generative weights across all layers can be achieved by a backpropagation algorithm as in training standard neural networks. The pseudo-code for training a 4-layered DBN is as follows:
Input: Binary data matrix
Output: recognition and generative weights
Randomly initialize parameters
Train RBM for layer 1
Train RBM for layer 2
Train RBM for layer 3
Train RBM for layer 4
Backpropagation
2.4 Bimodal DBN (bDBN)
A traditional DBN assumes that data are from one common distribution, and the task is to use distributed hidden layers to capture the structure of this distribution. However, our task of transferring the knowledge learned from rat cells to human cells deviates from the traditional assumption in that humans and rats may use different pathways and signaling molecules to encode the response to a common stimulus. Thus our task is to learn a common encoding system that governs two distributions, which may each have its own mode, hence a bimodal problem. Inspired by the bimodal deep Boltzmann machine model and multimodal deep learning (Liang, 2015; Ngiam, 2011; Srivastava and Salakhutdinov, 2012), which uses a multi-layered deep network to model the joint distribution of images and associated text, we designed a modified variant of bimodal DBN (bDBN) to capture the joint distribution of rat and human proteomic data. Our hypothesis is that rat and human cells share a common encoding system that respond to a common stimulus, but utilize different proteins to carry out the response to the stimulus. Thus, we can use the hidden layers to represent the common encoding system, which regulates distinct human protein phosphorylation and rat phosphorylation responses.
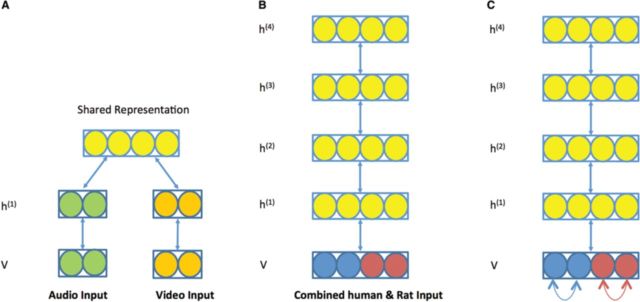
2.4.1 Training
Traditional bimodal models dealing with significantly different input modalities such as audio and video (Fig. 3A) (Ngiam, 2011; Srivastava and Salakhutdinov, 2012) usually require one or more separate hidden layers to first capture the statistical structure of each type of data and then model their joint distribution with common high level hidden layers. However, in our setting, although rat and human proteomic data have their own modalities, they are not drastically different. Therefore, instead of using two separate hidden layers, we devised a modified bimodal DBN, in which a rat training case and a human training case treated with a common stimulus are merged into a joint input vector for the bDBN and connected to a common hidden layer h(1) (Fig. 3B). In this model, the training procedure is the same as training a conventional DBN using the algorithm described in Section 2.3, but the prediction is carried out in a bimodal manner. Under this setting, the hidden layers are forced to encode the information that can be used to generate both rat and human data, i.e. the hidden layers behave as a common encoder.
Fig. 3.
Training DBN models. (A) A diagram of a conventional bimodal DBN. The green and orange nodes represent different input modalities, e.g. audio and video inputs, and each type is first modeled with a separate hidden layer, and the joint distribution is modeled with a common higher layer hidden nodes. (B) A 4-layered bimodal DBN for modeling rat and human proteomic data. The blue and red nodes represent human and rat phosphoproteins respectively. The bottom layer consists of observed variables. Upward arrows represent recognition weights and downward arrows represent generative weights. C) A sbDBN. Additional edges between proteins from the same species are added
2.4.2 Prediction
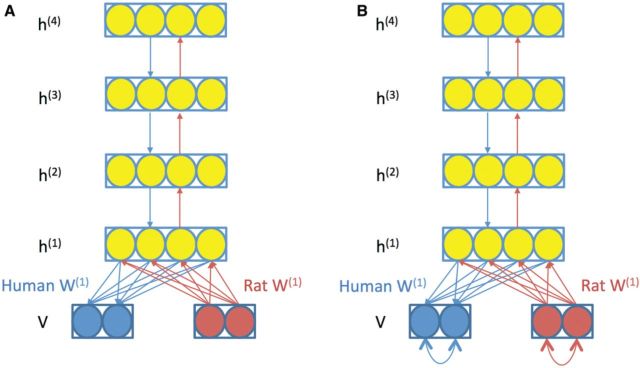
When using a trained bDBN to predict human cell response to a specific stimulus based on the observed rat cell response to the same stimulus, we only used the rat data to update the states of nodes in the first hidden layer, , with doubled edge weights (2 × W(1)Rat) from rat variables to hidden variables (red edges in Fig. 4). Then the upper hidden layers were updated using the same method as in a conventional DBN using the recognition weights. When the top hidden layer h(4) was updated using rat data, the bDBN propagated the information derived from rat data downwards to h(1) using generative weights as in a feed forward neural network to predict the human data (Fig. 4A). We finally predicted the human cell response with weights only from hidden variables in h(1) to human visible variables.
Fig. 4.
Prediction with bDBN and sbDBN models. (A) Prediction with bDBN. (B) Prediction with sbDBN. When predicting human phosphoprotein states, information derived from rat phosphoprotein states is propagated upward using weights represented by red arrows and then propagated downwards using the weights represented by blue arrows to predict human phosphoprotein states
2.5 Semi-restricted bimodal deep belief network (sbDBN)
Since signaling proteins in a phosphorylation cascade have regulatory relationships among themselves, we further modified the bottom Boltzmann machine, consisting of h(1) and v, into a semi-restricted Boltzmann (Taylor and Hinton, 2009), in which edges between proteins from a common species are allowed (Fig. 3C). In this model, the hidden variables in h(1) capture the statistical structure of the ‘activated regulatory edges’ between signaling proteins, instead of ‘activated protein nodes’. In this model, each human protein was connected to other human proteins, and the same rule was applied to each rat protein. However, we didn’t allow interactions between human proteins and rat proteins. The interaction between proteins, which is represented as , was added into the negative phase shown below:
| (13) |
| (14) |
where is the influence of the phosphorylation states of other proteins on that of the ith protein.
| (15) |
2.6 Performance evaluation
We adopted the evaluation metrics that were used to evaluate and compare the performance of submitted models in the SBV IMPROVER challenge, which include AUROC (area under receiver operator characteristic; Bradley, 1997), AUPRC (area under the precision-recall curve; Davis and Goadrich, 2006; Goadrich et al., 2004), Jaccard Similarity (Dombek et al., 2000), Matthews correlation coefficient (Petersen et al., 2011), Spearman correlation (Brott et al., 1989) and Pearson correlation (Adler and Parmryd, 2010), to measure the accuracy of the prediction. In all metrics except for Jaccard Similarity, the higher the score, the more accurate the model is. We performed a series of cross-validation experiments, in which we held out the three repeated experiments corresponding to one stimulus of both rat and human cells, performed model training, and test the performance using the held-out samples. All results discussed in the paper were derived from these cross-validation experiments.
2.7 Model selection
When training a deep hierarchical model, often the first task is to determine the structure of the model, i.e. the number of layers and the number of hidden nodes per layer. However, currently there is no well-established method for model selection when training deep learning models. Therefore, we performed a series of cross-validation experiments to search for an ‘optimal’ structure for bimodal and semi-restricted bimodal DBNs. We set the initial structure of both bDBN and sbDBN to the following ranges: h(1): 30–50; h(2): 25–40; h(3): 20–30; and h(4): 20–25. We iteratively modified the structure of the model by changing the number of hidden nodes within a layer using a step size of 5 and explored all combinations in the range stated above. In this case, the total number of models tested is 120 (5*4*3*2) for both bDBN and sbDBN. Under each particular setting, we performed a leave-one-out experiment to assess the performance of a model. In such an experiment, we held out both human and rat data treated by a common stimulus as the test case, trained models with data treated by the rest of stimuli, and then we predicted the states of human phosphoproteins using the held-out rat data as illustrated in Figure 4. By doing this, we predicted human data treated by all stimuli, and we evaluated and compared the performance using the AUROC of different models and retained the model structure that led to the best performance. Note, during leave-one-out training of a model with a given structure, the parameters associated with each model can be different, and therefore the results reflect the fitness of the model with a particular structure after averaging out the impact of individual parameters, an approach closely related to Bayesian model selection (Bishop, 2006).
2.8 Baseline predictive models
As a comparison to bDBN and sbDBN, we formulated the task of predicting human cell response based on rat cell response to a common stimulus as a classification problem, and we employed two current state-of-the-art classification models, a support vector machine (SVM) (Bishop, 2006) with a Gaussian kernel (Karatzoglou et al., 2004) and an elastic-net regularized generalized linear model (GLMNET) (Friedman et al., 2010) to predict human cell responses. In this setting, we trained a classification model (SVM or GLMNET) for one human protein using a vector of rat proteomic data collected under a specific condition as input features (independent variables) and the human protein response under the same condition as a binary class variable (dependent variables). We trained one such classifier for each human protein class. We performed leave-one-out cross-validation using SVM and GLMNET models respectively. The results predicted by SVM and GLMNET were then compared with the results predicted by DBN and sbDBN using the metrics discussed in Section 2.6.
3 Results
3.1 The data
The protein phosphorylation response data in this study was provided by SBV IMPROVER (SBV IMPROVER, 2013). The data contains the phosphorylation status of 16 proteins collected after exposing rat and human cells to 26 different stimuli (Table 1). Each stimulus was repeated 3 times. The SBV IMPROVER organizers preprocessed the proteomic data into binary values to represent if a protein was phosphorylated under a specific condition. We directly utilized the binary input for our DBN models.
Table 1.
Proteins and stimuli involved in this study
| Stimuli | 5AZA, AMPHIREGULIN, BETAHISTINE, BISACODYL, CHOLESTEROL, CLENBUTEROL, EGF, EGF8, FLAST, FORSKOLIN, HIGHGLU, IFNG, IGFII, IL4, MEPYRAMINE, NORETHINDRONE, ODN2006, PDGFB, PMA, PROKINECITIN2, PROMETHAZINE, SEROTONIN, SHH, TGFA, TNFA, WISP3, DME |
| Proteins | AKT1, CREB1, FAK1, GSK3B, HSPB1, IKBA, KS6A1, KS6B1, MK03, MK09, MK14K11, MP2K1, MP2K6, PTN11, TF65, WNK1 |
3.2 Model selection results
In order to identify the ‘optimal’ model structure that perform well, we examined the performance of each model with a specific structure configuration stated in Section 2.7. For a given model, we performed a leave-one-out cross validation experiment and calculated the AUROC for the model. The average of the AUROCs for 120 bDBN models was 0.80, and the highest one is 0.86. The bDBN structure yielding the best AUROC consisted of four hidden layers with the following numbers of nodes 35, 30, 30 and 20, from h(1) to h(4) respectively. For sbDBN, the mean of the AUROCs for 120 candidate models is 0.86 and the highest one was 0.93. The number of nodes for the four layers for the best sbDBN model was 30, 30, 30 and 20, from h(1) to h(4) respectively. A tentative explanation for the different numbers in h(1) between bDBN and sbDBN is that the edges between the visible variables in the sbDBN partially captured the statistical structures of the visible variables, which reduced the need for additional nodes in the layer h(1). In the following sections, we report the results derived from bDBN and sbDBN with these two specific structures with the highest AUROCs.
3.2.1 Hyper parameters used for model training
The weights were updated using a learning rate of 0.1, momentum of 0.9 and a weight decay of 0.0002. The weights were initialized with random values sampled from a standard normal distribution multiplied by 0.1. Contrastive divergence learning was started with n = 1 and increased in small steps during training.
3.3 Comparison among different models
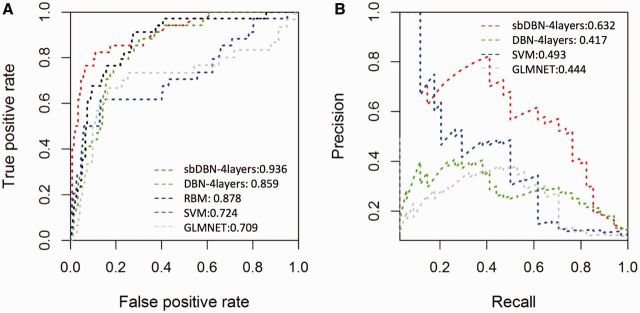
Table 2 shows the comparisons between different predictive models in terms of 6 evaluation metrics. We highlighted the best value for each metric using bold face letters. When comparing bDBN with SVN and GLMNET, the results show that bDBN performs better in terms of AUROC and Spearman’s correlation, but underperformed in terms of AUPRC, Jaccard similarity, and Pearson correlation. This is potentially due to the fact that we performed model selection mainly using AUROC as the criteria. Strikingly, with the addition of protein-protein edges in the visible layer, the 4-layered sbDBN performs much better than all other models measured in all metrics.
Table 2.
Leave-one-out accuracy scores of models
| AUPRC | AUROC | Jaccard. Similarity | Matthews. Correlation. Coefficient | Speaman. Correlation | Pearson. Correlation | |
|---|---|---|---|---|---|---|
| 4-layered bDBN | 0.417 | 0.859 | 0.750 | 0.373 | 0.323 | 0.235 |
| 4-layered sbDBN | 0.632 | 0.936 | 0.531 | 0.616 | 0.391 | 0.460 |
| SVM | 0.493 | 0.724 | 0.692 | 0.411 | 0.231 | 0.392 |
| GLMNET | 0.444 | 0.709 | 0.717 | 0.374 | 0.194 | 0.282 |
Based on the AUROC value, the performance of the 4-layered sbDBN > 4-layered bDBN > SVM > GLMNET. However, ranking varies depending on the scoring method. It is known that models pursuing optimal area under the ROC curve is not guaranteed to optimize the area under the Precision-Recall curve (Davis and Goadrich, 2006). Indeed, we noted that the AUROC for the 4-layered DBN is better than the one for GLMNET. However, the AUPRC for the 4-layered DBN is worse than the one for GLMNET (Table 2; Fig. 5).
Fig. 5.
ROC and RPC curves of different models. (A) Performance results of four models in terms of AUROC. (B) Performance results of four models in terms of AUPRC
3.4 Biological interpretation of learned edges between proteins in sbDBN
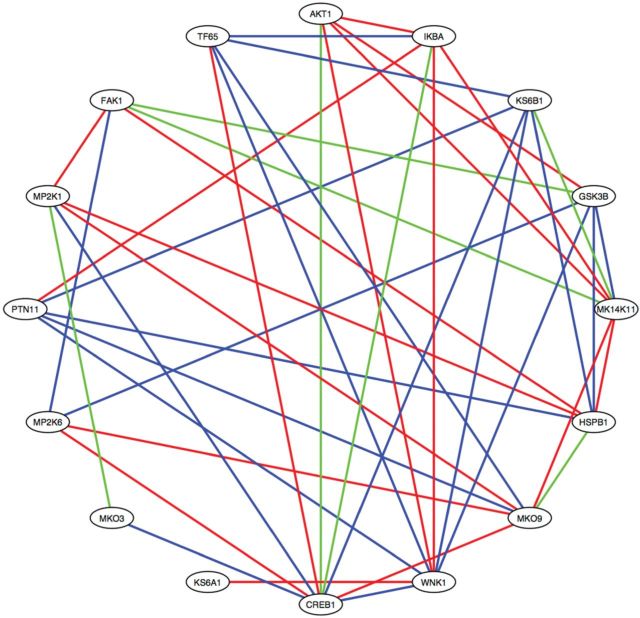
The best predictive power of the sbDBN reflects the importance of capturing the correlation between signaling proteins. We then investigated whether the learned correlations between signaling proteins are biologically sensible, although it should be noted that Boltzmann machine models cannot infer causal relationships. For each protein, we picked the top 3 strongest interaction edges for rat and human respectively, and we organized the results as shown in Figure 6. In this figure, if the interaction between a pair of proteins exists in both rat and human data, the edge is colored green. If the interaction is rat only, there is a blue line between the two proteins. If the interaction is human only, there is a red line between the two proteins. The results indicate that, while some common correlations are shared between rat and human cells, different covariance structure exists in different proteomic data.
Fig. 6.
Protein correlation network learned from the 4-layered sbDBN. Ovals represent the proteins. A green line represents a common edge shared between human proteins and rat proteins; a red line represents an edge between human proteins; a blue line represents an edge between rat proteins
Due to the fact that signal transduction in live cells are dynamic events, it is difficult to thoroughly evaluate the accuracy of inferred interactions even through further experimentations. Conventional evaluation metrics such as sensitivity and specificity are difficult to assess in this study. Since it is possible that the signal transduction between a pair of proteins known to have a regulatory relationship may not be present under the experimental conditions of this study, accurately assessing sensitivity is challenging; similarly, since there are seldom reports or databases stating that signal transduction never occurred between a pair of proteins, it is challenging to assess if the lack of an edge between a pair of proteins in our model really represents a true negative outcome. As such, conventional metrics such as AUROC cannot be applied in our evaluation. However, we noted that we were able to assess with reasonable confidence the positive predictive value (PPV) of the model, i.e. the percentage of the predicted signal transduction interactions that is known in literature. We performed a comprehensive literature review and cited the references supporting the predicted regulatory relationship and known protein-protein interactions in Supplementary Tables. The results indicate that most of the predicted regulatory relationships are supported by the literature or have evidence of physical interactions between the proteins. Thus, the results support the notion that the sbDBN correctly captured the correlation (thereby signal transduction or cross talks) between phosphoproteins.
4 Discussion
In this study, we investigated the utility of novel deep hierarchical models in a trans-species learning setting. To our knowledge, this is the first report using deep hierarchical models to address this type of problem. Our results indicate that, by learning to represent a common encoding system for both rat and human cells, the deep learning models outperform contemporary state-of-the-art classifiers in this trans-species learning task.
The empirical success of deep hierarchical models may be attributed to the following advantages. First, the DBN is capable of learning novel representations of the data that are salient to the task at hand. The DBN models are more compatible to the biological systems that generate the observed data. The hidden variables at the different layers of the DBN models can capture information with different degrees of abstraction, thus allowing the models to capture a more complex covariance structure of the observed variables. It is possible that hidden nodes at lower layers, e.g. h(1), directly capture the covariance of the observed protein phosphorylation states, whereas the higher layers can capture the crosstalk between signaling pathways that only occur in response to specific stimuli. Thus, shallow models that only concentrate on the covariance at the level of observed variables, such as SVM and elastic network, would have difficulties capturing such a high-level covariance structure of the data. It is now well appreciated that feature-learning methods, such as DBN, tend to outperform feature selection methods in complex domains, such as image classification and speech recognition (Bengio et al., 2012; Hinton et al., 2006; Hinton and Salakhutdinov, 2006). Second, DBN strives to learn the common encoding system for both human and rat data, and it naturally performs multi-label classification by taking into account the covariance of the class variables. However, a conventional classifier, such as a SVM, can only predict one human protein as the class variable in an independent manner, thus failing to capture the covariance of class variables and yielding inferior performance.
The sbDBN model developed in this study provides a novel approach capable of simultaneously learning interactions and predicting the state of phosphoproteins. Interestingly, the model assigns differential weights to the edges between phosphoproteins when comparing those from rat and human cells, which potentially indicates that different parts of signaling pathways are preferentially utilized in a species-specific manner. However, this hypothesis still needs to be experimentally tested in a relatively larger dataset.
Deep hierarchical models are particularly suited for modeling cellular signaling systems, because signaling molecules in cells are organized as a hierarchical network and information in the system is compositionally encoded. Our results indicate that DBNs were capable of capturing the complex information embedded in proteomic data. Interestingly, in contrast to the training of deep learning models in a machine learning setting such as object recognition in image analysis where usually a large number of training cases is required, our results show that the DBN models performed very well given a moderate size of training cases. This indicates that biological data tend to have strong signals that can be captured by DBNs with relative ease. Our study demonstrates the feasibility of using deep hierarchical models to simulate cellular signaling systems in general, and we foresee that deep hierarchical models will be widely used in systems biology. For example, one can use deep hierarchical models to study how cells encode the signals regulating gene expression, to detect which signaling pathway is perturbed in a specific pathological condition, e.g. cancer. Finally, models like our bDBN and sbDBN provide a novel approach to simultaneously model multiple types of ‘omics’ data in an ‘integromics’ fashion.
Funding
This research was supported by the National Library Of Medicine of the National Institutes of Health under Award Number R01LM 010144, R01LM012011 and U54HG008540.
Conflict of Interest: none declared.
Supplementary Material
References
- Adler J., Parmryd I. (2010) Quantifying colocalization by correlation: the Pearson correlation coefficient is superior to the Mander's overlap coefficient. Cytom Part A, 77A, 733–742. [DOI] [PubMed] [Google Scholar]
- Alberts B., et al. (2008) Molecular Biology of the Cell. New York, NY: Garland Science, Taylor & Francis Group, LLC. [Google Scholar]
- Bengio Y., et al. (2012) Representation learning: a review and new perspectives. arXiv.org. [DOI] [PubMed] [Google Scholar]
- Bishop C.M. (2006) Pattern Recognition and Machine Learning. Springer, New York. [Google Scholar]
- Bradley A.P. (1997) The use of the area under the roc curve in the evaluation of machine learning algorithms. Pattern Recogn., 30, 1145–1159. [Google Scholar]
- Brott T., et al. (1989) Measurements of acute cerebral infarction—a clinical examination scale. Stroke, 20, 864–870. [DOI] [PubMed] [Google Scholar]
- Brown S.D. (2011) Disease model discovery and translation. Introduction. Mammalian Genome Off. J. Int. Mammalian Genome Soc., 22, 361. [DOI] [PubMed] [Google Scholar]
- Carreira-Perpinan M.A., Hinton G.E. (2005) On Contrastive Divergence Learning, In: Artificial Intelligence and Statistics, pp. 33–40. [Google Scholar]
- Davis J., Goadrich M. (2006) The relationship between Precision-Recall and ROC curves Proceedings of the 23rd International Conference on Machine Learning, pp. 233–240. [Google Scholar]
- Dombek P.E., et al. (2000) Use of repetitive DNA sequences and the PCR to differentiate Escherichia coli isolates from human and animal sources. Appl. Environ. Microb., 66, 2572–2577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J., et al. (2010) Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw., 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Goadrich M., et al. (2004) Learning ensembles of first-order clauses for recall-precision curves: a case study in biomedical information extraction. Lect. Notes Artif. Int., 3194, 98–115. [Google Scholar]
- Hinton G.E., et al. (2006) A fast learning algorithm for deep belief nets. Neural Comput., 18, 1527–1554. [DOI] [PubMed] [Google Scholar]
- Hinton G.E., Salakhutdinov R.R. (2006) Reducing the dimensionality of data with neural networks. Science, 313, 504–507. [DOI] [PubMed] [Google Scholar]
- Jin B., et al. (2008) Multi-label literature classification based on the Gene Ontology graph. BMC Bioinformatics, 9, 525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karatzoglou A., et al. (2004) kernlab—an S4 package for kernel methods in R. J. Stat. Softw., 11, 1. [Google Scholar]
- Liang M., et al. (2015) Integrative data analysis of multi-platform cancer data with a multimodal deep learning approach. IEEE Trans. Comput. Biol. Bioinf, 99, 1. [DOI] [PubMed] [Google Scholar]
- McGonigle P., Ruggeri B. (2014) Animal models of human disease: challenges in enabling translation. Biochem. Pharmacol., 87, 162–171. [DOI] [PubMed] [Google Scholar]
- Ngiam J., et al. (2011) Multimodal deep learning Proceedings of the 28th International Conference on Machine Learning (ICML-11). [Google Scholar]
- Omar B.A., et al. (2013) Enhanced beta cell function and anti-inflammatory effect after chronic treatment with the dipeptidyl peptidase-4 inhibitor vildagliptin in an advanced-aged diet-induced obesity mouse model. Diabetologia, 56, 1752–1760. [DOI] [PubMed] [Google Scholar]
- Petersen T.N., et al. (2011) SignalP 4.0: discriminating signal peptides from transmembrane regions. Nat. Methods, 8, 785–786. [DOI] [PubMed] [Google Scholar]
- Poussin C., et al. (2014) The species translation challenge—a systems biology perspective on human and rat bronchial epithelial cells. Scientific Data, 1, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhrissorrakrai K., et al. (2015) Understanding the limits of animal models as predictors of human biology: lessons learned from the sbv IMPROVER Species Translation Challenge. Bioinformatics, 31, 471–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salakhutdinov R., et al. (2007) Restricted Boltzmann Machines for Collaborative Filtering Proceedings of the 24th International Conference on Machine Learning, pp. 791–798. [Google Scholar]
- SBV IMPROVER. (2013) SBV IMPROVER: Species Translation Challenge Overview. [Google Scholar]
- Srivastava N., Salakhutdinov R. (2012) Multimodal learning with deep Boltzmann machines. In: NIPS, pp. 2231–2239. [Google Scholar]
- Taylor G.W., Hinton G.E. (2009) Factored conditional restricted Boltzmann Machines for modeling motion style In: Proceedings of the 26th Annual International Conference on Machine Learning, pp. 1025–1032. [Google Scholar]
- Tsoumakas G., Katakis I. (2007) Multi-label classification: an overview. Data Warehousing Mining, 3, 1–13. [Google Scholar]
- Welling M., Hinton G.E. (2002) A new learning algorithm for Mean Field Boltzmann Machines. Lect. Notes Comput. Sci., 2415, 351–357. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.