Prediction of hydrogen and carbon chemical shifts from RNA using database mining and support vector regression

Abstract

The Biological Magnetic Resonance Data Bank (BMRB) contains NMR chemical shift depositions for over 200 RNAs and RNA-containing complexes. We have analyzed the ¹H NMR and ¹³C chemical shifts reported for non-exchangeable protons of 187 of these RNAs. Software was developed that downloads BMRB datasets and corresponding PDB structure files, and then generates residue-specific attributes based on the calculated secondary structure. Attributes represent properties present in each sequential stretch of five adjacent residues and include variables such as nucleotide type, base-pair presence and type, and tetraloop types. Attributes and ¹H and ¹³C NMR chemical shifts of the central nucleotide are then used as input to train a predictive model using support vector regression. These models can then be used to predict shifts for new sequences. The new software tools, available as stand-alone scripts or integrated into the NMR visualization and analysis program NMRViewJ, should facilitate NMR assignment and/or validation of RNA ¹H and ¹³C chemical shifts. In addition, our findings enabled the recalibration a ring-current shift model using published NMR chemical shifts and high-resolution X-ray structural data as guides.

Introduction

RNAs participate in a large and growing number of known biological functions including catalysis, transcriptional regulation, maintenance of sub-cellular structure, intracellular trafficking, antiviral restriction, and of course, storage and transmission of genetic information (Bartel 2004; Bessonov et al. 2008; Boisvert et al. 2007; Brodersen and Voinnet 2006; Doudna and Rath 2002; Edwards et al. 2007; Hassouna et al. 1984; Kim 2005; Korostelev and Noller 2007; Steitz 2008; Wakeman et al. 2007). A significant portion of the Eukaryotic genome is transcribed into non-coding RNAs, and many of these have unknown functions (Ponting et al. 2009). Secondary structures of non-coding RNAs with known functions appear to be evolutionarily conserved (Hamada 2015), and it is now generally accepted that, like proteins, RNA function is tightly correlated with structure. Compared to proteins, understanding of RNA structure–function relationships is limited, due in part to a paucity of structural information: There are presently about 2700 RNA-containing structure depositions in the Nucleic Acid Database (NDB; http://ndbserver.rutgers.edu), whereas more than 99,000 protein-containing structures have been deposited in the Protein Databank (PDB; http://www.rcsb.org/pdb/home/home.do).

The development of tools to facilitate NMR signal assignment and/or assignment validation could be of significant assistance in expanding the RNA structure pipeline. Assignment of chemical shifts to individual atoms is generally a prerequisite to the determination of angular and distance restraints used to calculate 3D RNA structures (Wüthrich 1995). In addition, because chemical shifts are dependent on 3D structure, they have potential intrinsic value as restraints for structure calculations. A variety of approaches have been used to predict chemical shifts in nucleic acids, including an empirical database approach we employed that is based on a central nucleotide and its neighbors (Barton et al. 2013). A similar approach was originally developed to analyze proton shifts in DNA (Altona et al. 2000; Kwok and Lam 2013; Lam 2007; Lam et al. 2007; Ng and Lam 2015). Trends in shift patterns for ¹³C have also been determined by the examination of database depositions (Fares et al. 2007). Where 3D structural information is available chemical shifts can be predicted using physical parameters such as ring current shifts (Cromsigt et al. 2001; Dejaegere et al. 1999; Sahakyan and Vendruscolo 2013), data mining approaches with multiple structure based attributes (Frank et al. 2013), distance-based approaches (Frank et al. 2014), or ab initio quantum mechanical calculations (Fonville et al. 2012). A primary motivation for developing an RNA chemical shift prediction algorithm was to be able to predict shifts in the absence of 3D structures, so that they could be used as an aid to the NMR assignment process. We have therefore focused on developing approaches that use attributes from the primary and secondary structure as input, and that are trained with shift values available in database depositions.

Our previous work focused on predicting ¹H NMR chemical shifts of non-exchangeable protons for residues in A-form helical regions of RNAs (Barton et al. 2013). That protocol, which employed a linear regression based method to estimate the contribution of different chemical environments derived from the nucleotide sequence and base-pairing, was able to predict shifts with a high degree of accuracy (cross validated rms deviation of 0.06 ppm). However, the approach required labor-intensive examination of various data types to generate the attribute descriptors used in training the prediction model, and was only used to model ¹H NMR chemical shifts for base-paired residues (G-C, A-U, or G*U) that were both preceded and followed by additional base paired residues.

Unlike DNA, RNA is often found in a variety of non-helical conformations, and these non-helical residues often play central functional roles. Restricting predictions to helical regions therefore meant that assignments for residues in interesting structural regions were not predictable. The ability to predict ¹³C NMR chemical shifts could also be useful, both for facilitating assignment of heteronuclear ¹H-¹³C NMR spectra and as potential restraints for structure determination. We therefore expanded our prediction model to include both hydrogen and carbon shifts, and also to include residues in non-A-form RNA conformations (i.e. the complete RNAs under investigation). We also automated the data mining and secondary structure assessment protocols, enabling convenient refinement of the prediction models as new data are added to the databanks, and have incorporated these new tools into both stand-alone and existing software packages.

Methods

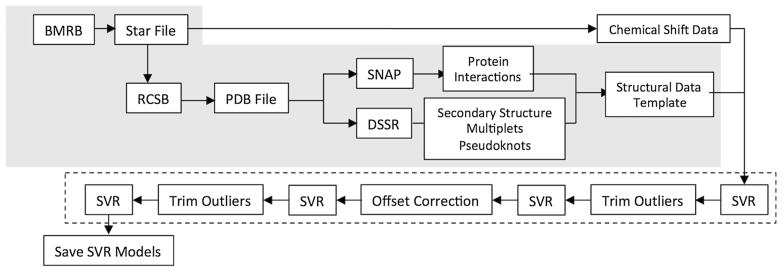
The NMR chemical shift data were analyzed using a set of computer programs that are a major rewrite and extension of the RNAShifts program described in our earlier publication (Barton et al. 2013). The software was rewritten in the Python programming language and several major enhancements were made. First, the retrieval of data files was automated. The program begins by using an input file with a list of entry numbers corresponding to depositions at the Biological Magnetic Resonance Data Bank (BMRB). This input list was generated using the BMRB web site to search for entries containing RNA and RNA-protein shifts. RNAShifts2 automatically fetches the corresponding version 3.1 BMRB STAR file for each entry, and then using the BMRBLIB software extracts the PDB ID within the star file, and fetches the PDB structure file from the PDB website (Fig. 1).

Fig. 1.

Flow chart for the automated data retrieval and analysis process. Steps enclosed in the shaded box represent the automated protocol used for fetching data and attribute generation. Steps within the dashed box are involved in modeling the data. The SVR boxes encompass using the SVR algorithm to train a model, predict shifts and calculate rms errors. Output at the last step includes saving the results of the tenfold cross validation

Our original data analysis relied on the tedious manual analysis of PDB files, literature references and the BMRB entries to generate our set of predictive attributes. The second major advance was to largely automate this process (Fig. 1). Attribute generation involves the use of our own Python scripts and invocations of the external programs Defining the Secondary Structures of RNA (DSSR) and Structures of Nucleic Acid-Protein Structures (SNAP), components of the 3DNA suite of software programs (Lu and Olson 2008; Lu et al. 2010). Using the structural information from the PDB file, DSSR identifies secondary structural information including base pairing, multiples, pseudoknots, multiple chains, and other attributes. SNAP also uses the PDB file to identify any protein interactions within the RNA structure. The output files of these two external programs are parsed and the relevant information is synthesized into an output template file that contains all the derived attributes for each BMRB entry in a format used for RNAShifts2 as illustrated in Fig. S1 of the Supplementary Material. There were cases where RNAShifts2 could not properly generate a template for certain BMRB entries, where no PDB file was available, or where we had locally derived data that hadn’t yet been deposited in the BMRB database. To handle these situations we allow the software to check for and use manually generated template entries. Intermediate files (including BMRB entry files and PDB files) are cached so when the software is run multiple times the files are only fetched or generated if they are not already present.

The RNA chemical shift prediction analysis focuses on the central nucleotide in a stretch of five nucleotides: [5′-n_i−2–n_i−1–N–n_i+1–n_i+2-3′] (N = nucleotide for which the NMR shifts are being evaluated; n = neighboring nucleotides). The list of attributes generated using the automated protocol described above thereby describes the chemical environment surrounding the central nucleotide. Each nucleus is currently described by a set of 10 attributes. The first five represent the nucleotide and its base paired nucleotide (if any) for each of the five sequential positions. Watson–Crick base pairing, loops, mismatches and similar attributes are all implicitly represented in the base pair entry at each position. The first (n_i−2) and last (n_i+2) positions are represented in a simplified format where the nucleotide and its base pair are only presented as being either a purine or pyrimidine (rather than the four specific nucleotides used at the other three positions). Empty values for the first one or two, and last one or two positions, are used at the 5′ and 3′ termini. The remaining five attributes represent any additional attributes for each of the five positions. These include values such as the position in a tetraloop, multiplets, stacking, and pseudoknots. Figure S1 of the Supplementary Material illustrates a simple RNA sequence, the text file description of the template, and an example set of attributes that are used as input to the support vector regression software.

Available chemical shift values were extracted from the BMRB files for non-exchangeable (H₈, H₂, H₆, H₅, H₁′, H₂′, and H₃′) protons and the corresponding carbon nuclei. Inclusion of data for carbon nuclei is another significant advance from our previous work. Adding additional atoms or elements (N or P) requires the trivial addition of the element and atom names to an input file. At present we’ve restricted the program to the carbon and hydrogen elements and the above atoms, as they are the ones with the most comprehensive set of currently available data.

In our original work we used a linear analysis with PACE regression (Wang and Witten 2002) to model the contributions of each attribute to the observed chemical shift. This allowed a simple calculation of the modeled chemical shift, and an understanding of the relative contributions of different attributes. The linear contribution model however limits the ability to model different environments without using an excessively large number of attributes. In the current work we’ve allowed for more complex attribute contributions by using support vector regression (SVR) with non-linearity provided by a Radial Basis Function Kernel. There is a wide range of data mining algorithms that could potentially be used for predicting chemical shift values from a set of attributes including decision trees, neural networks, and linear regression (Witten et al. 2011). The SVR technique was chosen both for its ability to produce a sparse solution at the global minimum (Bishop 2006), but also because efficient code was available to readily include the prediction model as an integrated component in NMRViewJ. Alternative methods such as neural networks were investigated, but require complex decisions about network topology and the code libraries did not lend themselves to simple embedding of the prediction code. SVR calculations were performed using the Java library, libsvm (Chang and Lin 2011) which could be used both in a standalone mode for training, but also used as an integrated library in NMRViewJ. As with our previous work we assessed the quality of the predictions using a tenfold stratified cross-validation during our analysis. This method trains the model on 90 % of the data and uses this to predict the remaining 10 %. This process is repeated ten times using a different set of data each time and derives rms deviations based on the whole process. Cross-validation was done as implemented in the libsvm library.

The quality of predictions depends in part on factors that are not included in the training model and on the quality of the input data. We did not explicitly include sample conditions (pH, temperature, ionic strength, etc.). These can have both an overall effect on the average shifts, and an influence on the shifts of particularly sensitive nuclei. Factors that influence the overall quality of the data include errors in referencing and specific miss-assignments. We minimize the impact of these factors on the performance of the predictive models in two ways: automatic reference adjustment and outlier removal. We skipped any BMRB files where we could detect that the molecular structure had unusual attributes such as DNA-RNA hybrids or extensive use of non-standard nucleotides or nucleotide linkers as these were unlikely to be represented in sufficient numbers for accurate modeling.

Reference adjustment was performed by a two-step procedure. First we used a protocol for adjusting the carbon chemical shifts based on the expected shifts of GC–GC pairs commonly found at the termini of synthesized RNA (Aeschbacher et al. 2012). Certain carbon shifts in these terminal nuclei have characteristic shifts. Deviation of measured shifts from the expected value is particularly good for detecting a common error of approximately 2.7 ppm made when calibrating the carbon shifts. Next we used the consensus-based procedure described in our earlier publication. In this protocol the predictive model is trained once and the average error for the proton and carbon shifts from each BMRB entry is calculated. The average error in the prediction is then subtracted from each shift and the model is then retrained with the now corrected shift data. This is a useful addition to the reference protocol because not all sequences have the GC–GC terminal pairs or some necessary shifts may be missing. Additionally, we noted that different referencing errors could be observed for different carbon types. For example, the reference error for carbon atoms in the ribose ring could be different from the error for base carbons, suggesting that users made different reference errors in different NMR experiments. Because of this we calculated the reference error separately for ribose and base atoms. If the error was similar for both categories a single average correction was used.

The compensation for assignment errors and other non-modeled effects on specific chemical shifts was done by manually and automatically trimming outliers. Obvious errors in shifts that were observed in plots were manually removed by entering an atom identifier into a text file. Atoms with entries in this error file were ignored during subsequent analysis steps. The automated trimming was performed by running two passes of the prediction analysis. The rms deviation between the experimental and predicted values were calculated using all the data for each atom of each of the four bases, and any data values that were beyond three times the measured rms deviation value were marked as being outliers. The second pass was then performed on the database excluding the outliers.

Output of the above analysis includes the cross-validated rms for each atom, an overall rms for carbon and protons, and prediction models in libsvm format. Additionally, average prediction errors for each BMRB file and various atom specific reports can be generated.

The good results of the prediction analysis (see “Results and discussion” section) suggested the possibility of using our model to calibrate parameters used in deriving chemical shifts with a ring current shift model. We used the prediction model to predict the chemical shifts of the sequence of the 19-residue A-form helical RNA of chains C and D of PDB entry 1QC0 (1.55 Å resolution). The sequence and helix secondary structure were provided to our prediction software and predicted proton shifts determined.

Ring current effects can be described (Case 1995) as the product of three terms, G(r), a geometric factor that depends on the position (r) of the target atom relative to the aromatic ring, B a constant representing contributions of a benzene ring (here set to 5.455 × 10⁻⁶ Å ), and i an intensity factor that scales the contribution of a specific ring type to that of benzene:

$${\mathrm{\sigma }}_{\text{rc}}=\text{iBG}(\mathbf{r})$$ (1)

The PDB model was loaded into NMRViewJ and for each proton with a predicted chemical shift we calculated the geometric contribution (G) of each aromatic ring to the proton (Haigh and Mallion 1980) multiplied by the i and B values given by Case (1995). A matrix equation was then established as follows:

$$\mathbf{Ax}=\mathbf{b}$$ (2)

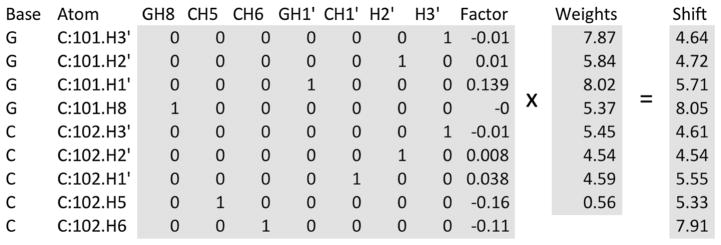
Each row of the matrix A and vector b represents one of the predicted protons. The first 13 columns of matrix A are binary values with only one of the columns set to 1. That column represents the type of the proton. Proton types were AH2, AH8, GH8, CH5, UH5, CH6, UH6, AH1′, GH1′, CH1′, UH1′, H2′, H3′. Preliminary analysis showed little difference in shifts for H2′ and H3′ so we minimized the number of total attribute columns by grouping of H2′ and H3′ into single types for the four different bases. The final column of matrix A contains the sum of all the ring current contributions of all nearby rings in the structure. Figure 2 illustrates the matrix equation. The matrix equation was then solved for the vector x using a Singular Value Decomposition (SVD). The first 13 elements of the solution vector represent the shift of each of the 13 proton types in the absence of any aromatic ring current shift (other than the effect of a given aromatic ring on its own protons). The final element of the solution vector represents a scaling factor that multiplies the ring current contribution calculated using the Haigh-Maillion theory and the intensity factors calculated by Case (1995).

Fig. 2.

A representation of the math matrices used for calibrating ring-current shift parameters. The first and last shaded regions represent the matrix A and vector b that are input into the Singular Value Decomposition (SVD) algorithm to solve the equation Ax = b for the vector x (representing the contribution of each term). The actual matrix A used has additional rows for the remaining atoms in the structure, and additional columns for additional atom types (for the A and U residues), and the vector b has additional rows (for the additional atoms). The final column, labeled Factor, represents the sum of product of the geometric factors and ring current intensity parameter (Case 1995) calculated for all aromatic rings near the corresponding atom. All the other columns of the matrix are set to 0, except the column that represents the atom type for that row

The utility of the new reference shifts and the scaled intensity factor in doing ring-current shift calculations of new structures was established by calculating the chemical shifts of protons in a set of PDB structures with assigned chemical shifts. For this test we used a set of PDB models used previously (Frank et al. 2013). For each PDB model, the rms deviation of the calculated shift with the assigned values from the corresponding BMRB file was determined. We used the structures as obtained directly from the PDB, without any additional refinement. Calculated shifts were done in four ways: using the average value for the proton from the BMRB database, using ring-current shifts as described in Case (1995) [but using our own software implementation, not the original Shifts program (Xu and Case 2001)], using the ring-current shifts with the above calibration, and using our SVR prediction.

Results and discussion

Referencing

Generation of useful shift prediction models from database-derived shifts requires properly referenced and assigned data. Deposited shifts from both protein and nucleic acids are however subject to errors of referencing and errors in assignment. A variety of methods for checking protein chemical shift assignments have been developed, including LACS (Wang et al. 2005), RefDB (Zhang et al. 2003) and PANAV (Wang et al. 2010). In our previous work on RNA shift prediction we used similar procedures to that used in RefDB and that work by performing two cycles of prediction. The average error for each BMRB entry after the first cycle is used as a correction before starting the second prediction cycle. An alternative protocol for correcting referencing errors in RNA spectra based on the expected shifts of five specific atoms has also been described (Aeschbacher et al. 2012). In the current study we used a combination of the two methods. As the two-cycle prediction-correction technique basically works by forming a consensus reference and then correcting datasets relative to that it’s useful to ensure that obvious errors are minimized before the first cycle. So on datasets that are amenable to the procedure we used the procedure of (Aeschbacher et al. 2012) prior to the first prediction cycle. Because not every data set has necessary atoms for 5-atom correction procedure, it is important to also do the two-cycle correction.

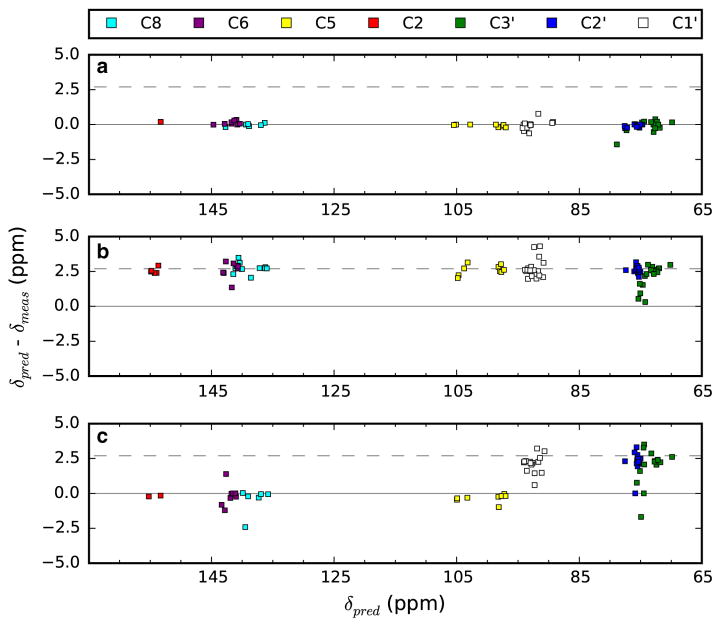
Figure 3 shows an example of three different BMRB entries with different referencing situations. The plots are the deviation between predicted and measured shifts and are done without any reference correction. BMRB entry 5705 can be seen to have an average error near 0.0 demonstrating that the data set is well referenced and that shifts can be well predicted with our protocol. BMRB entry 18,975 has an average error near 2.7 ppm, a value consistent with a common error of referencing where the reference is set to tetramethylsilane (TMS) rather than 2,2-dimethylsilapentane-5-sulfonic acid (DSS) (Aeschbacher et al. 2012). BMRB entry 5932 has the property that the chemical shifts for the carbons of the aromatic bases are correctly referenced, but the sugar carbons are offset by an amount suggesting that the datasets used to acquire them were incorrectly referenced to tetramethylsilane (TMS). Errors such as that found in entry 5932 led us to calculate the reference correction for aromatic base carbons and sugar carbons separately. If the two corrections were similar they were averaged, otherwise the two sets of carbon shifts were corrected separately.

Fig. 3.

Plots of the deviation between measured and predicted values (δ_pred – δ_meas) for three different BMRB entries. The plots are from calculations done without using our offset correction and trimming protocols, so represent fits to the raw chemical shift data. Data is taken from prediction runs using all BMRB entries, not just those illustrated. a BMRB entry 5705, b BMRB entry 18,975, c BMRB entry 5932. The dashed line corresponds to the common error of 2.7 ppm (Aeschbacher et al. 2012)

Outlier analysis

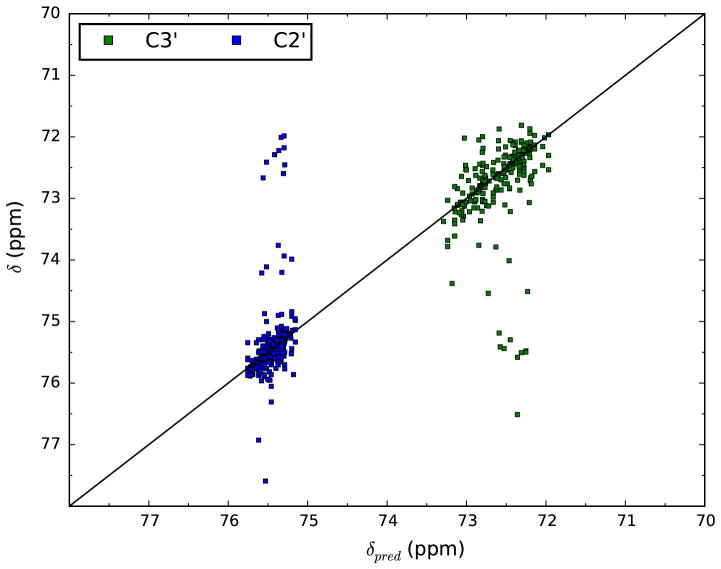
Analysis of the data shows that outliers, values where the error in prediction is significantly larger than was typical, were present. These outliers could be due to unusual chemical environments where our prediction model doesn’t work well, or could be due simple errors and mis-assignments in the original datasets. Some errors were quite obvious and were manually eliminated. For example, BMRB entry 19,018 has a variety of shifts set to precisely 0.0. We assumed that these were errors and eliminated them. Other errors show particular patterns. For example, Fig. 4 shows a plot of the predicted versus measured values for the C2′ and C3′ atoms from reference corrected, but untrimmed analyses. The plot shows groups of shifts for C2′ atoms that are at the expected values for the C3′ atoms, and shifts for C3′ atoms at the expected values of C2′ atoms. This pattern of shifts located symmetrically across the diagonal are consistent with, but not definitive proof of, what would happen if the assignments for these two atoms were interchanged. We did not attempt to correct for possible interchange of the C2′ and C3′ shifts, but the effect of this would be minimized by our overall protocol of automatically trimming out shifts that were more the 3 times the average rms error for each atom type.

Fig. 4.

Plots of predicted versus measured values for the C3′ and C2′ atoms. Data is taken from the output of a prediction run done with the offset correction protocol, but without any trimming of outliers

The protocol used for removing outliers undoubtedly removes some data values that are correct and thereby minimizes the range of chemical shift environments that are successfully predicted by the algorithm. However, the limited number of available chemical shift datasets for RNA available from the BMRB means that some attribute combinations are represented by a very small number of examples. Indeed for many attribute combinations only zero or one data value is available. Given this fact it is almost impossible to automatically and correctly distinguish between outliers that are due to poorly predicted valid data rather than invalid data values. We included the trimming protocol as we expect that retaining errant values could corrupt the prediction model that results from the training process. The total number of shifts removed in our protocol is, however, relatively small. Approximately 2 % of shifts were removed in our analysis. By comparison, the “reduced” dataset used in (Cromsigt et al. 2001) removed 25 % of the shifts. We expect that as additional datasets are deposited more examples of unusual attribute environments will be available and the number of valid data values eliminated as outliers will be reduced. We provide a full list of trimmed data values in Table S1 of the supplementary information.

Data retrieval and template generation

Our previous work relied on manual download and analysis of data files. This required an amount of time and effort that are a barrier to regular updates of the training database. However, the relatively small number of RNA entries in the BMRB makes it important to keep adding new entries to our training database to ensure broad coverage of possible RNA sequences and secondary structures. Automation of the data retrieval and template generation has allowed us to develop a routine protocol (Fig. 1) for regularly updating the database. In the first update since our previous work we’ve significantly increased the number of BMRB entries. The current automated protocol relies on having available PDB files and so not all entries could be analyzed automatically with the current protocol. We should note that while PDB files are used for determining features such as the secondary structure, we are not making direct use of 3D coordinates in the prediction model.

Of the 254 BMRB entries automatically downloaded, twenty-one were missing PDB IDs, eleven were not compatible with the DSSR program, and two had invalid PDB entries. Additional entries were automatically dropped from the analysis, when, for example, the software couldn’t make an exact match of the sequence in the BMRB entry with that in the PDB file. The final analysis used a total of 187 files, a significant increase from the 126 used in our original analysis. The list of BMRB entries that were considered and the status of each is shown in Supplementary Table S2. Replacing the analysis done by an experienced person with the automated routines could result in errors in the analysis. Before proceeding with the use of the full database, we compared the analysis done with the automatically generated template with that resulting from the original manual analysis. To do this, we performed the chemical shift modeling calculations on the original manual template versus the automatically generated template for only the original 126 BMRB entries. In this way, any differences in the calculations would only be based on the differences of the analysis and template creation and not on any extra BMRB entries.

Training the prediction model using our new scripts and the new SVR regression fitting, but with the manual attribute template from our previous publication (Barton et al. 2013) yields similar results to that obtained previously. We previously reported the analysis of 3758 hydrogen shifts in A-form helical regions with an overall rms deviation of 0.056 ppm. Our new procedure, but with the same template, used 4066 shifts and resulted in an overall rms deviation of 0.052 ppm. The new protocol uses a somewhat greater number of shifts in part because of new attribute categorization code and the details of the computerized identification of attributes.

Table 1 compares the manual and automated analysis for both hydrogen and carbon nuclei in more detail. The analysis with the manual template used a total of 11,953 hydrogen nuclei and 5559 carbon nuclei, while the automated template used 12,354 and 5559 respectively. In calculating the overall rms predictions we did the calculation separately for atoms in canonical and non-canonical helical regions, other regions, and for all atoms together (see Table 1 footnotes for definitions of the categories). The training and validation protocol was run using the manual and automated templates. The cross validated rms (xrms) was calculated during the prediction analysis and done without dividing into the three categories. The error in prediction as measured by the rms deviation between measured and calculated shifts was essentially the same when using the automatically generated template in comparison to that using the completely manual template. For the hydrogen nuclei analyzed with the manual template, the rms for the canonical, non-canonical, other and all atoms were 0.05, 0.06, 0.09, and 0.08 ppm, respectively. Using the automated template for hydrogen nuclei resulted in the same values (within 0.01 ppm) indicating that our automated template generation generates comparable results to the manual analysis. Comparison of the carbon nuclei also showed good agreement between manual and automated templates. Using the manual template the rms values for the canonical, non-canonical, other and all-atoms were 0.41, 0.42, 0.79 and 0.68, respectively. Analysis with the automated template agreed within 0.02 ppm. The cross-validated rms for the analysis of hydrogen nuclei was 0.12 ppm with either the manual or automated template. The cross-validated rms for carbon is of course higher than that for hydrogen, but the manual and automated templates were both 0.80 ppm. The above results confirm that our largely automated attribute analysis procedure is producing results similar to that obtained by tedious manual analysis.

Table 1.

Prediction results for different attribute categories^a

Category	Manualb		Automatedc		Automated-Plusd
	rms	n	rms	n	rms	sdev	n
Hydrogen
Cross-validated	0.12	12,131	0.12	11,953	0.13	1.33	18,774
Canonicale	0.05	2007	0.05	2061	0.06	1.28	3020
Non-canonicalf	0.05	2059	0.06	1966	0.07	1.29	2903
Otherg	0.09	8065	0.10	7926	0.11	1.35	12,851
All	0.08	12,131	0.08	11,953	0.10	1.33	18,774
Carbon
Cross-validated	0.80	5554	0.80	5559	0.83	28.44	9642
Canonicale	0.41	1040	0.41	1072	0.46	28.04	1630
Non-canonicalf	0.42	949	0.42	916	0.47	28.34	1526
Otherg	0.79	3565	0.81	3571	0.85	28.57	6486
All	0.68	5554	0.69	5559	0.75	28.44	9642

^aOutput from the support vector regression analysis. The SVR is done separately on each atom type. This table presents the values aggregated across all the hydrogen and carbon atoms used. The columns labeled rms represent the square root of the mean of squared deviations between predicted and experimental values for all the data in the corresponding category. The rms values in the cross-validated rows are the output from the SVR program when performing a tenfold stratified cross-validation and are based on the data values in all categories. Other rms values are calculated on the indicated subset of data values. The columns labeled n represent the number of data values used in the specified category. The column labeled sdev is the standard deviation of all the experimental hydrogen or carbon shifts in the corresponding categories and is included only for the automated-plus section as this measure of dispersion is very similar for all three groups

^bManual refers to analysis done using the attribute templates created by manual analysis and the shift datasets used in our previous analysis (Barton et al. 2013)

^cAutomated refers to analysis done using the mostly-automated attribute generation described in this paper using the same set of datasets as in our previous analysis

^dAutomated-Plus refers to analysis done using the automated analysis described here and the new larger number of datasets

^eCanonical bases are the central base in a 5 base stretch in which all 5 base pairs have GC or AU base pairing and no other attributes such as being in a triplet, kissing interaction or pseudoknots are present

^fNon-canonical bases are the same as canonical, but the first and/or fifth bases may be GU wobble base pairs, mismatched, unpaired (e.g. loops) or not-present (e.g. the 5′ or 3′ termini)

^gOther bases are all bases that are in neither the canonical nor non-canonical categories

Increase in shifts and attributes

Using the automated analysis and the expanded list of BMRB entries greatly increased the total number of shifts in the database (Table 1). The new automated downloading and analysis protocol results in a database with 58 % more hydrogen nuclei and 74 % more carbon nuclei. Increasing the size of the database was accomplished without significant increase in prediction error. The cross-validated rms for all hydrogen shifts was increased by only 0.01 ppm to a value of 0.13 ppm, and carbon prediction rms was increased by only 0.03 ppm to 0.83 ppm.

The SVR models resulting from training on the chemical shift database yields prediction values even if the exact set of attributes is not present in the training database, but it is of course expected that prediction quality will be better if there are examples in the database. Accordingly it is relevant to determine the increase of unique attributes relative to our previous publication. The numbers of unique attributes for the manual, automated, and automated-plus were 1750, 1671, and 2389, respectively. We expect that fewer attribute combinations are available in the automated process in comparison to the manual analysis, on the original list of BMRB entries, because the automated analysis does not yet take into account some attributes that can be identified with careful manual analysis. Increasing the database size, however, significantly increased the number of unique attributes because of the greater variety of RNA molecules included. And the good results described above indicate that we have an appropriate set of attributes.

Nucleotide base environments

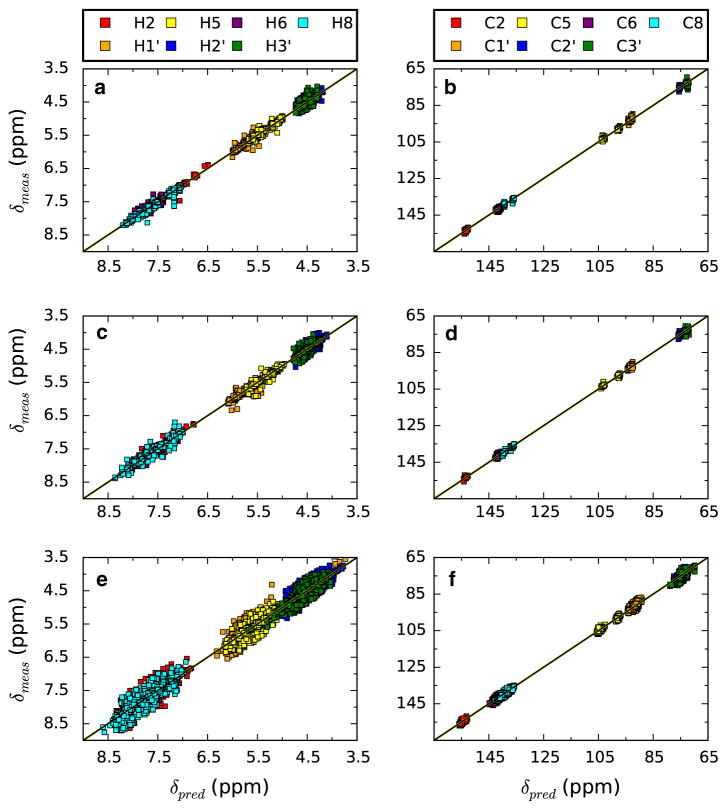
In our previous publication we restricted the analysis to only residues that were within A-form helical regions. This was done, in part, because we expected that the linear analysis of chemical shifts used was less able to model more varied conformations, and because of the difficulty in manually analyzing all regions. In the current study we expanded this to include all regions of RNA secondary structure as defined using dot-bracket notation. As indicated in Table 1 this dramatically increases the total number of shifts that can be used for training and prediction. Approximately two-thirds of the hydrogen (12,851 of 18,774) and carbon (6486 of 9642) shifts are in regions labeled other. Predictions in these regions are not as good, as measured by the rms prediction error, as those in unperturbed helical regions, but are still in a range (0.11 ppm for hydrogen and 0.88 ppm for carbon) that should be very useful for aiding in the assignment of RNA spectra. Plots of the predicted versus measured values for hydrogen and carbon for the full dataset list are shown in Fig. 5. This figure shows the data for the canonical, non-canonical and other shifts (see Table 1 for category descriptions) plotted separately. Some shifts in the canonical hydrogen plot (Fig. 5a) appear to be outliers that might be expected to have been trimmed in the outlier procedure. That procedure trims shifts whose prediction errors are 3 times the rmsd. Since the rmsd is calculated from the analysis of all shifts some shifts that might otherwise be trimmed are retained. Further refinements of our code could be done to calculate the rmsd for trimming for individual categories.

Fig. 5.

Plots of predicted versus measured values for the complete set of atoms obtained with the automated procedure described here. a, c and e are hydrogen shifts, and b, d and f are carbon shifts. a and b are canonical shifts in helices, c and d are non-canonical shifts in helices, and e and f are other shifts (see Table 1)

The actual SVR regressions are done on each atom type separately and the number of shifts and cross-validated RMS are shown for each atom in Table 2. Most hydrogen atoms are predicted with an rms error near the mean value of 0.13. The largest prediction error (0.20 ppm) was found for the H2 proton of adenine. Prediction errors for most carbon atoms were similar to the mean value of 0.83, but the values for the C3′ carbons appeared noticeably higher with an average value of 1.29 ppm (Table 3).

Table 2.

Prediction results for different atom types^a

Hydrogen	n	trim	xrms	sdev	Carbon	n	trim	xrms	sdev
AH2	911	24	0.20	0.41	AC2	569	6	0.61	1.02
AH8	903	23	0.16	0.25	AC8	557	7	0.68	1.09
GH8	1317	45	0.14	0.34	GC8	767	18	0.69	1.61
CH5	1148	22	0.11	0.26	CC5	597	21	0.54	0.68
UH5	854	19	0.14	0.28	UC5	461	13	0.74	1.04
CH6	1154	22	0.10	0.19	CC6	649	15	0.59	0.95
UH6	863	18	0.11	0.17	UC6	490	10	0.81	1.19
AH1′	905	20	0.14	0.19	AC1′	527	10	1.03	1.29
GH1′	1321	26	0.12	0.30	GC1′	694	10	0.93	1.31
CH1′	1143	14	0.12	0.18	CC1′	605	17	0.63	1.07
UH1′	845	20	0.14	0.19	UC1′	471	13	0.92	1.42
AH2′	834	15	0.15	0.19	AC2′	352	11	0.72	0.80
GH2′	1215	32	0.12	0.21	GC2′	508	18	0.67	0.76
CH2′	1034	29	0.10	0.19	CC2′	467	12	0.48	0.87
UH2′	779	15	0.13	0.21	UC2′	361	10	0.45	0.56
AH3′	767	18	0.14	0.19	AC3′	334	8	1.37	1.71
GH3′	1125	31	0.13	0.23	GC3′	468	14	1.16	1.65
CH3′	959	23	0.11	0.15	CC3′	434	11	1.07	2.02
UH3′	697	6	0.11	0.15	UC3′	331	1	1.56	2.16
Total	18,774	422	0.13	1.33	Total	9642	225	0.83	28.44

^aOutput from the support vector regression analysis. The columns labeled n represent the number of shifts of each atom type used in the SVR regression analysis. The columns labeled trim represent the number of shifts that were trimmed out between the first and second SVR steps. The columns labeled xrms represent the square root of the mean of squared deviation between predicted and measured chemical shifts as calculated in the tenfold cross-validation. The column labeled sdev is the standard deviation of all the experimental hydrogen or carbon shifts for the corresponding atom type

Table 3.

Ring current shift parameters^a

AH2	AH8	GH8	CH5	UH5	CH6	UH6
7.93	8.33	7.87	5.84	5.76	8.02	8.01
AH1′	GH1′	CH1′	UH1′	H2′	H3′	Ratio
5.38	5.37	5.45	5.50	4.54	4.59	0.559

^aOutput from the ring current shift calibration protocol. Entries for specified atoms are the reference shifts to which the ring current correction is added. Ratio is the value by which the intensity factor, i, of Eq. (1) was scaled

Ring current shift calibration

Chemical shifts are ultimately determined not by the somewhat abstract set of attributes we use in this analysis, but by specific physicochemical interactions. In RNA the apparent currents induced in aromatic rings largely dominate these effects. Empirical calibration of the magnitudes of the ring-current shifts and other contributions to RNA chemical shifts has been hampered by the lack of high quality structural data. Calibration of similar mechanisms in protein chemical shifts has generally been done by using NMR derived chemical shifts combined with structural information calculated not from the NMR structures, but rather from structures derived from X-ray crystallography. The great difficulty of obtaining appropriate crystals of RNA has meant that there is not a large set of X-ray structures with NMR chemical shifts available for performing the calibration.

One method of calibrating the ring-current shifts has relied on quantum-mechanical calculations of the effect of aromatic rings on a proton positioned in various orientations relative to the ring. These calculations form the basis of the Shifts program (Xu and Case 2001). One of the possible issues in translating these calibrations from the idealized simulation environment to predicting shifts in actual RNA molecules is the fact that RNA molecules can be highly dynamic (Bothe et al. 2011). Ring current effects are then likely to be averaged over a variety of conformations.

As an alternate approach to calibration we’ve used a high-resolution X-ray structure of RNA as the source of structural information, and chemical shifts predicted using the methodology of this paper. By doing this we can take advantage of the multiple available assigned shift sets that are used in training our model. The chemical shift was calculated as an intrinsic chemical shift plus a contribution from the nearby aromatic rings. The ring-current contribution was modeled as a value calculated using the individual ring current factors for each ring type as calculated by Case (1995), but with the contribution scaled by an adjustable factor. The output of the linear least squares analysis of the data is a new set of intrinsic shifts for each proton, and a single overall scaling parameter. The best fit was obtained with a scaling factor of 0.53. This analysis is strictly empirical, but the scaling factor less than 1.0 suggests that the magnitude of the ring current effect is overestimated in the quantum mechanical calculations of model systems relative to that observed in dynamical RNA structures in solution. Our analysis was set up to also allow the contribution of individual ring types to be calculated. The rms deviation of predicted from measured shifts for the analysis done using a single adjustable scale factor with the target factors from Case (1995), and that using adjustable values for each ring type were both 0.10 ppm. The lack of an improvement in fit indicates that there is no statistical justification in using the additional parameters and so we only use the scaled Case parameters. Obtaining calibrations for individual ring factors would likely require using additional structural models.

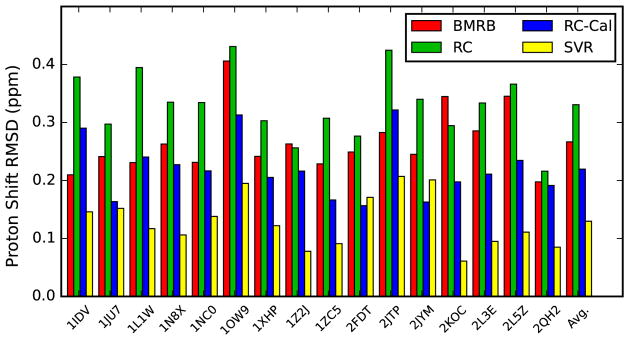
Evaluation of chemical shift predictions ought to be done relative to an appropriate baseline, which we consider to be simple prediction based on the average chemical shift for a given atom and nucleotide type. Predictive models that are based on secondary or tertiary structures should result in a significant improvement. We’ve compared various models by predicting the shifts of a set of BMRB entries with corresponding PDB models that were previously used (Frank et al. 2013).

Figure 6 shows predictions on these 16 different PDB models. Predictions were done using the simple average shift from the BMRB data, the ring current shift model as implemented in NMRViewJ using both the original parameters from Case and our re-calibrated intrinsic shifts and scaling factor, and the values predicted using the secondary structure based SVR model. The average RMS for each prediction type is also indicated. Simple prediction with BMRB averages gives an overall RMS of 0.27 ppm. With this set of structures, and our implementation of the ring-current shift model, no improvement in prediction quality is obtained with the original Case parameters. The rms we determined (0.33 ppm) is similar to that (0.35 ppm) reported by (Frank et al. 2013) using the SHIFTS (Dejaegere et al. 1999) program itself suggesting that our implementation of the model is valid. We obtain a significant improvement in the prediction quality using our ring-current calculation code, but with the empirical recalibration of the parameters (rms = 0.22 ppm). A somewhat surprising result is that the secondary structure based prediction using our current SVR gives a significant improvement in prediction quality (rms = 0.13 ppm) relative to the 3D structure based ring current calculation. This is likely in part due to the fact that NMR 3D structures of RNA are not always of high quality in part because their calculation depends significantly on force field parameters (Tolbert et al. 2010) and there is a virtually complete lack of X-ray structures with corresponding NMR chemical shift sets. Additionally dynamics are not included in the 3D shift predictions and may significantly affect the average shifts.

Fig. 6.

Plot of the root mean squared (rms) prediction error for proton chemical shifts for 16 different RNA molecules. Structures were taken from the indicated PDB entries. Four different methods were used to calculate predicted values. The values for bars labeled BMRB are from setting the prediction value to the mean shift of the corresponding atom type as taken from data at the BMRB (Ulrich et al. 2008). RC are from a ring current shift calculation within NMRViewJ (Johnson and Blevins 1994) using parameters from (Case 1995), RC-Cal are also a ring current calculation within NMRViewJ, but with the calibrated ring-current parameters described here, and SVR prediction are from the output of the SVR calculation described here

Recently, two new algorithms for 3D shift prediction were described. The first is a “black box” approach based on a large number of descriptors used in a random forest training algorithm (Frank et al. 2013). The second algorithm is based on simple calculation based on inter-atomic distances in a 3D structure and is therefore easier to implement within molecular dynamics simulations to aid in structure refinement (Frank et al. 2014). Prediction quality was described in this paper (Frank et al. 2014) in terms of the mean absolute error (mae), rather than the rms deviation and was shown to be better, as analyzed on all bases in a set of PDB files not used in the training, than that using either the SHIFTS (Dejaegere et al. 1999) or NUCHEMICS (Cromsigt et al. 2001) programs that are based on ring current shifts. The lack of a squared term in the mae (as compared to rms) gives less weight to values with large deviations. Using the mae minimizes the effect of outliers caused by errors, but may deemphasize prediction quality in non-helical regions where prediction may be more difficult. Our recalibrated ring-current model, on the set of PDB structures reported here, gives a similar prediction error (mae = 0.17) compared to that previously reported (Frank et al. 2014) (mae = 0.15) indicating that even without using 3D structural information we can obtain good prediction quality.

Conclusions

The present study shows that high quality predictions can be made for both proton and carbon chemical shifts in RNA molecules using information that is primarily derived from the nucleotide sequence and secondary structure. In particular, we did not train our predictive models based on coordinates from 3D models, in part because RNA structure determination relies heavily on force field parameters used during refinement, and many of the deposited RNA structures have helical properties that deviate significantly from expected values (Tolbert et al. 2010). Prediction models calibrated in this way can be used early in the NMR analysis process to aid in the assignment of new sequences. We’ve implemented the prediction tool within NMRViewJ (Johnson and Blevins 1994) where it can be used both to aid in the manual assignment of RNA molecules and to validate assignments. High quality predictions will also be useful in automated tools that are under development in our own and other labs (Aeschbacher et al. 2013; Krahenbuhl et al. 2014; Sripakdeevong et al. 2014; van der Werf et al. 2013).

The relatively small number of chemical shift depositions for RNA molecules makes it important to continue training the prediction model as new data becomes available. The implementation of the automated procedure described here makes the protocol very simple and should facilitate this ongoing process. Comparison with our previous manual procedure indicates that the automated protocol gives excellent results. Expansion of the training dataset has significantly increased the number of training attributes in the database and should thereby improve the prediction quality on novel sequences. We expect that further improvements in our analysis scripts will allow a higher percentage of available BMRB NMR-STAR files to be used automatically.

Observation of outliers and referencing errors, even in relatively recent depositions indicate that more attention can be paid to ensuring the quality of deposited data. Incorporation of the prediction tool within NMRViewJ should facilitate the validation of chemical shift assignments.

The prediction model here is based on qualitative descriptions of the nucleotide sequence and base pairing, and yet quantitative physicochemical effects such as ring-current shifts that depend on 3D structure and dynamics ultimately determine chemical shifts. A fundamental problem in using structure based shift models is the need to calibrate the models using very high quality 3D structures. Calibration of structure-based chemical shift models for proteins is commonly done with shifts derived from NMR analysis, but with the structures derived from X-ray crystallography (Shen and Bax 2010). Unfortunately there are very few X-ray structures of RNA with corresponding chemical shift sets so this approach is not yet feasible. Our recalibration of ring-current shifts using an X-ray structure combined with our secondary-structure based model shifts shows that 3D based predictions can be improved. Even with this improvement our secondary structure based models predict the shifts with higher accuracy. This suggests that the quality of 3D based RNA structure predictions could be significantly improved with an increased availability of better structural models.