The structure and timescales of heat perception in larval zebrafish

SUMMARY

Avoiding temperatures outside the physiological range is critical for animal survival, but how temperature dynamics are transformed into behavioral output is largely not understood. Here, we used an infrared laser to challenge freely swimming larval zebrafish with “white-noise” heat stimuli and built quantitative models relating external sensory information and internal state to behavioral output. These models revealed that larval zebrafish integrate temperature information over a time-window of 400 ms preceding a swimbout and that swimming is suppressed right after the end of a bout. Our results suggest that larval zebrafish compute both an integral and a derivative across heat in time to guide their next movement. Our models put important constraints on the type of computations that occur in the nervous system and reveal principles of how somatosensory temperature information is processed to guide behavioral decisions such as sensitivity to both absolute levels and changes in stimulation.

Graphical Abstract

Introduction

While temperatures in the environment constantly change, animals need to keep their internal temperature within a tight physiological range. Zebrafish are endemic to shallow waters, which are subject to large temperature fluctuations caused by differences in sunlight-intensity (Engeszer et al., 2007). They detect changes in temperature and modify their behavior to maintain appropriate body-temperature. From three days post fertilization (dpf) larval zebrafish robustly avoid both hot and cold temperature (Gau et al., 2013) and increase their swim intensity in response to changes in water temperature (Prober et al., 2008). Like other vertebrates they mainly detect ambient temperature via neurons in the trigeminal and dorsal root ganglia (Patapoutian et al., 2003; Sagasti et al., 2005), in particular neurons expressing the transient receptor potential channel TrpV1 (Gau et al., 2013).

In spite of growing cellular- and molecular-level understanding of temperature sensation, little is known about how perception of temperature is transformed into behavioral output in larval zebrafish and other vertebrates in general. However, knowing these sensorimotor transformations is crucial to understand the computations performed by the nervous system to guide behavioral decisions in response to temperature changes (Clark et al., 2013). We therefore set out to characterize the “temporal receptive field of heat perception” in larval zebrafish. Specifically, we defined the timescales over which they integrate temperature information and their sensitivity to absolute levels and changes in this somatosensory input. To probe the temporal dynamics of heat sensation, we developed a setup that allows us to quickly and precisely heat freely swimming larval zebrafish by means of an infrared laser while extracting behavioral parameters with high temporal precision. Larval zebrafish initiate discrete swim bouts with variable speeds and turn angles (Budick and O'Malley, 2000), which allowed us to build models relating sensory input to swimming in a similar way as otherwise used in neuroscience to relate sensory input to neuronal firing. In this context, we utilized a “whitenoise” heat stimulation paradigm to identify stimuli that preferentially trigger swimming behavior in 9–11 dpf larval zebrafish. By fitting generalized linear models that relate both temperature input and bout history to the probability of swim initiation we showed that larval zebrafish mainly integrate temperature information in a time-interval of 400 ms preceding a swim bout. Within this 400 ms window zebrafish compute a sum and a difference across temperature in time, making swim initiation sensitive to both absolute as well as changes in temperature. Fitting models to different swim types based on distance moved revealed differing temporal receptive fields. This indicates that larval zebrafish differentially weigh sensory input before committing to different swim trajectories.

Results

A setup to deliver precise heat stimuli to larval zebrafish

Probing dynamics of heat perception requires delivering stimuli to freely swimming larval zebrafish with high temporal precision, while the large thermal capacity of water makes it impractical to heat the whole behavioral arena. We therefore built a setup using a 980 nm infrared laser to directly heat pigmented larval zebrafish (Figure 1A). Since this approach only delivers energy to a small volume of water without heating the remainder of the chamber, passive cooling on stimulus offset is expected to be quick as well.

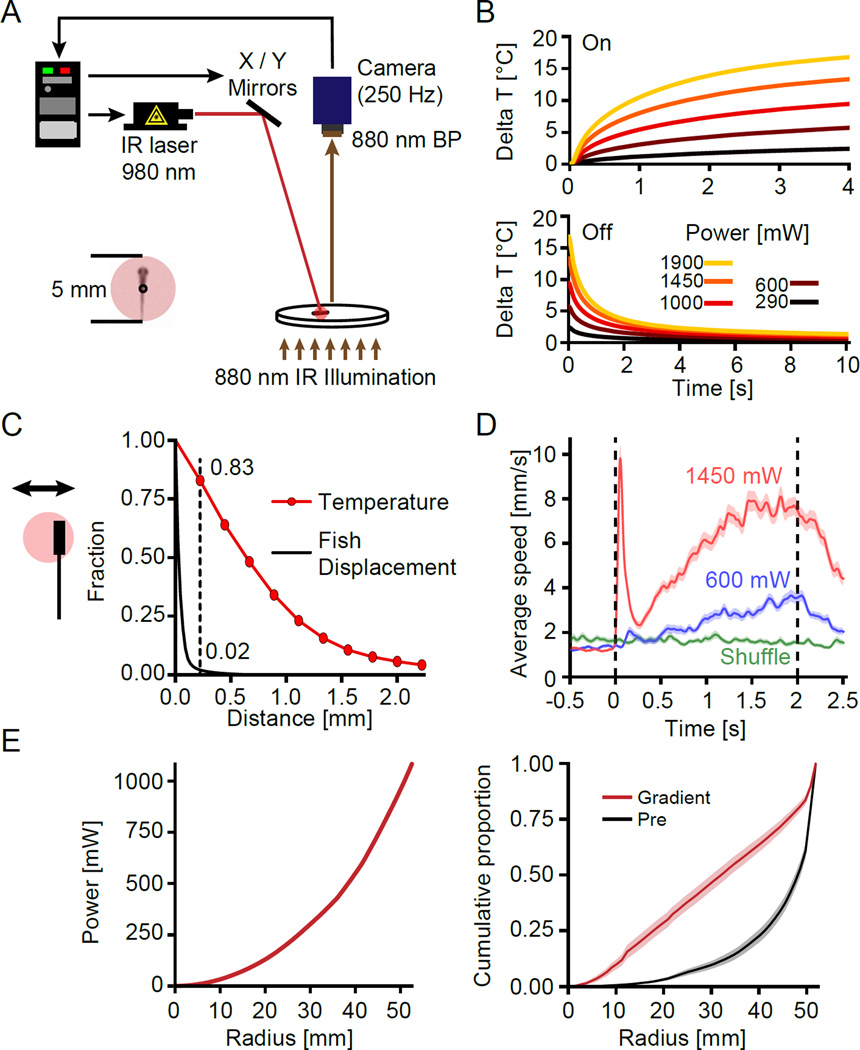
Figure 1. A setup for heating freely swimming larval zebrafish with high temporal and spatial precision.

(A) Schematic of the laser tracking setup. Note that the schematic is not to scale, mirrors were ~47 cm above the dish resulting in scan angles < 7 degrees at all times. Inset depicts a typical larval zebrafish (10 dpf) with the laser spot centered on the centroid (black circle) of the fish.

(B) Analysis of heating dynamics. The beam was parked directly on the center of a 4 mm by 840 µm thermistor submerged in the same chamber used for experiments. Top panel shows change in temperature during 4 s long heating steps. Bottom panel indicates the respective cool-down after the laser turned off. Line color indicates laser power at sample.

(C) Spatial heating extent at 1000 mW. The beam center was parked at the indicated distances from the thermistor and the temperature 4 s after heating onset was determined. The plot shows the fraction of maximum temperature reached at each distance (red line) and the fraction of fish that displace more than that distance within one camera frame during a movement (black line). Text at dashed line indicates that heating at 0.22 mm distance is 83 % of maximum and only 2 % of swim bouts resulted in a per-frame displacement larger than 0.22 mm.

(D) Behavioral response of larval zebrafish to 2 s long steps of the indicated laser power at sample. Traces indicate average swim speed across fish aligned to power onset (red and blue curve) or aligned to random time-points (green curve, control). Shaded regions indicate bootstrap standard error. Dashed black lines mark the on- and off-set of power respectively (N = 40 fish).

(E) Average radial distribution in power gradient experiment. Left panel shows the power at sample delivered to larval zebrafish based on their radial position. Right panel shows cumulative distribution of time spent during the experiment at each given radius averaged across fish. Black curve indicates cumulative distribution while the laser is off and red curve indicates cumulative distribution in response to power gradient depicted on the left. Shaded regions indicate bootstrap standard error (N = 25 fish).

See also Movie S1 and Figure S1.

We tracked larval zebrafish at 250 Hz using custom written software to extract their position and heading angle in real time. We used this information to control a pair of galvanometric mirrors that kept the laser beam centered on the fish and at the same time controlled the output power of the laser.

Because of their pigmentation we expected that larval zebrafish would be directly heated by our laser rather than indirectly via absorption by the surrounding water. To test this prediction we used a thermal imager comparing heating of agarose droplets that were either empty or contained an embedded larval zebrafish. The presence of larval zebrafish in the droplet increased magnitude and slope of the temperature rise in response to a laser pulse (Figure S1A) indicating that we indeed directly heat the fish. Embedding a 4 mm long, 840 µm diameter thermistor in droplets led to similar heating profiles as embedding a larval zebrafish. We therefore estimated the temperature changes caused by our laser by parking the beam on a thermistor submerged in the experimental chamber. By delivering steps of laser power we determined heating kinetics (Figure 1B) and estimated the steady-state temperature of the fish to be 8.8 °C above the baseline temperature of 22 °C per watt of laser power. The halftime of temperature rise and decay was on the order of 700 ms indicating that we have good temporal control over the fish temperature. The measured temperatures are overall in good agreement with observed behavioral effects. Namely, power levels above 1400 mW for extended time were noxious to larval zebrafish, as evidenced by long strings of escape movements followed by a reduction in baseline movement for prolonged time periods. These noxious effects are expected at temperatures above 34 °C (Gau et al., 2013).

Comparing temperature falloff within the 5 mm diameter laser spot with per-frame distances traveled by larval zebrafish during bouts suggests that the fish only has minimal control over experienced temperature (Figure 1C) especially since fish are heated directly by the laser rather than via the surrounding water. Furthermore, heat delivered to the periphery of the spot is minimal and hence baseline water temperature did not change over the course of our experiments.

With these baseline parameters established, we turned to behavioral experiments. Fish reacted to step increases in laser power (Figure S1B–D and Movie S1). Aligning swim speed based on laser onset across 40 fish (Figure 1D) shows that larval zebrafish reacted quickly to laser onset, especially for higher laser powers. In response to 1450 mW power steps, fish often performed an initial escape maneuver of large magnitude within 50 ms after laser onset evidenced by a peak of activity followed by a short period of quiescence before a general increase in swim activity (Figure 1D, S1D). On average, fish responded 830 ms after stimulus onset for 1450 mW and after 980 ms for 600 mW steps in power. This increase in swim-vigor declined with similar kinetics as cooling after laser offset. These results demonstrate that laser heating can induce behavioral changes with high temporal precision.

Larval zebrafish avoid hot temperatures and we wanted to know whether we could replicate this in our setup. We therefore exposed larval zebrafish to a radial gradient of laser power from 0 mW in the center to 1084 mW power at sample at the edge of a 11 cm diameter dish, corresponding to a virtual temperature gradient from 22 °C to 32 °C (Figure 1E, left panel). In the absence of laser stimulation, larval zebrafish performed thigmotaxis, that is they tracked the wall of the chamber. Preference changed under gradient conditions and fish spent significantly more time closer to the center of the chamber as evidenced by a leftward shift in the cumulative distribution of time spent at each radial position (Figure 1E, right panel; p = 0, k = 0.41, 2 sample KS test). When fish were subjected to gradient conditions, bout frequency and displacement increased in a graded manner with increasing radius and hence laser power (Figure S1E–F). This modulation of behavior likely forms part of a heat avoidance strategy as fish did not actively direct swims towards the center (Figure S1H). The observed effects argue that our setup delivers aversive heat stimuli to larval zebrafish that are interpreted similarly to heated water conditions (Gau et al., 2013).

In summary the laser setup delivers temporally precise heat stimuli enabling us to implement a variety of experimental protocols, including both open-loop experiments, such as random laser stimulation, as well as closed-loop experiments, such as laser avoidance.

A protocol to probe temporal properties of heat processing

Having demonstrated that our setup can present larval zebrafish with salient heat stimuli, we wanted to probe the temporal structure of heat processing using a random temperature stimulation protocol. Such protocols are well suited to identify the structure of ideal stimuli triggering a response, in our case swimming of larval zebrafish.

We presented 100 fish with randomly fluctuating laser power levels and recorded their behavior at the same time (Figure 2A) extracting 241,513 swim bouts during stimulation periods. Each stimulation lasted for one minute followed by a one-minute rest period as this length minimized habituation to the stimulus (Figure S2A). We changed the laser power on average every 200 ms, drawing new power levels from a Gaussian distribution. This resulted in temperatures on average 7 °C above baseline (Figure 2B, μ = 29 °C, σ = 1 °C) and a stimulus autocorrelation time of 960 ms (Figure 2C, S2B).

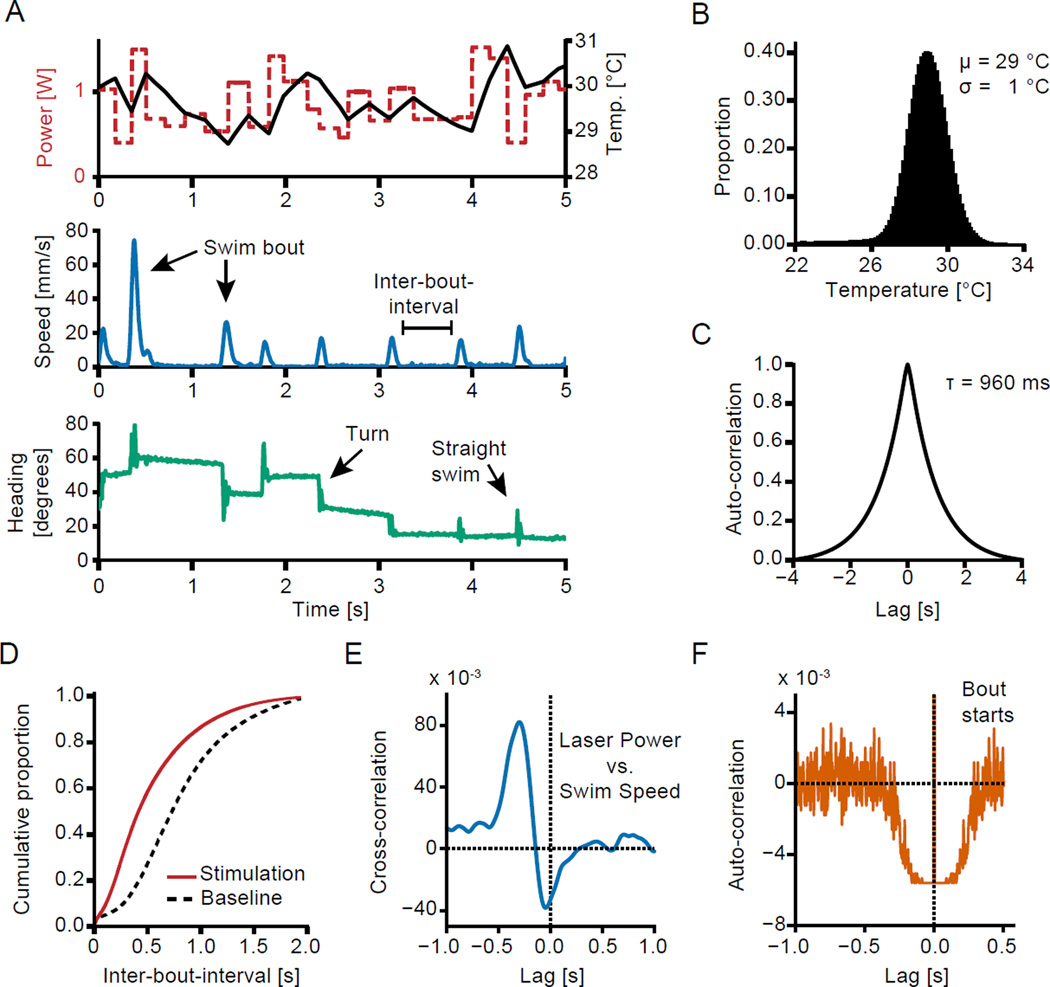
Figure 2. White noise heating paradigm.

(A) Example traces illustrating laser input and extracted behavioral parameters. A 5 s long example from the middle of one trial of one experiment is shown. Top panel shows the at-sample laser power (dashed red line) and the temperature calculated based on the heating model (solid black line). Middle panel shows instant speed profile of the larval zebrafish and bottom panel reveals changes in heading direction due to turns. Arrows indicate example swim parameters.

(B) Histogram of temperature values in each 40 ms timebin across all experiments.

(C) Autocorrelation of the temperature stimulus. Autocorrelation time is 960 ms.

(D) Cumulative distribution of interbout intervals across all experiments. The dashed black line is the cumulative distribution of inter-bout-intervals during resting, the solid red line depicts the cumulative distribution during laser stimulation. The rightward shift of the curve indicates a shortening of inter-bout-intervals during stimulation and hence an increase in bout frequency. (N = 88,349 bouts during resting and N = 241,433 bouts during stimulation phases).

(E) Cross correlation of power at sample and instantaneous speed at different indicated lags.

(F) Autocorrelation of bout starts (y-axis clipped at 4×10⁻³). The autocorrelation trace is flat for ~ 80 ms around timepoint 0 because of a hard threshold in allowed minimal bout duration.

(E–F) Dotted black lines indicate 0 lag and 0 correlation respectively. Both correlations are derived from all stimulus trials of the same example fish as depicted in panel A.

See also Figure S2.

Swim bout intervals decreased during stimulation compared to resting, evidenced by a rightward shift in the cumulative distribution of interbout intervals (Figure 2D). This is in line with previous reports that swim activity increases with increasing temperature (Prober et al., 2008). The median interbout interval decreased from 804 ms during resting to 432 ms during laser stimulation (distribution shift: p = 0, k = 0.33, 2 sample KS test). Other swim parameters such as bout displacement and turn angle changed as well but to a lesser extent (Figure S2C–D). In particular almost all bouts during stimulation were regular swims rather than fast escapes (Figure S2E) since we kept power levels below 1400 mW at sample for more than 95% of experimental time. Keeping power levels below the noxious range kept fish healthy allowing us to collect many swims per fish. However, this approach comes with the caveat that our study did not characterize responses to noxious heat stimuli.

We cross-correlated the delivered laser power and the fish’s swim speed to reveal timescales over which laser power dynamics influence swimming. Figure 2E shows that increases in swim-speed are correlated with both increases in laser power as well as a rapid decline in power just before the onset of a swim. This suggests that transient increases in laser power in a 500 ms window can drive swimming. At the same time auto-correlation of bout starts (Figure 2F) revealed that swim initiation is reduced for about 300 ms after the start of a previous bout. This auto-correlation indicates that bout initiation is a history dependent process with a refractory period which is also present during resting phases (Figure S2G).

Swim initiation is sensitive to heat level and changes in temperature

Cross-correlations indicate that both temperature sensation and bout history influence swim initiation. We therefore sought a way of integrating these phenomena into a model to describe sensorimotor transformations from heat perception to behavioral output. We fit generalized linear models to our data that relate temperature and the timing of the last bout to swim initiation. These models are akin to models relating sensory input and spike history to neuronal firing ((Paninski, 2004), see Figure 3A and Materials and Methods for details).

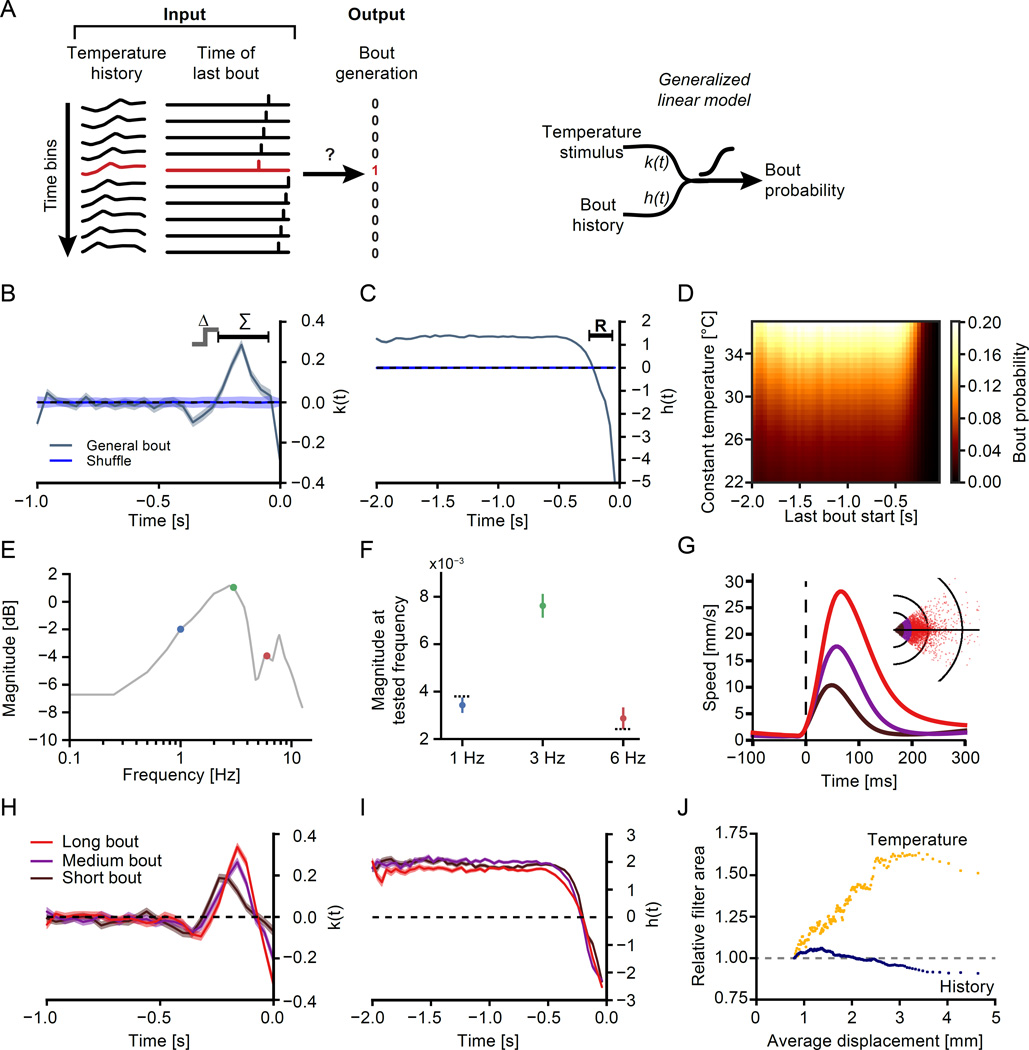
Figure 3. Generalized linear models of bout initiation in response to heat.

(A) Schematic of the derivation of the generalized linear model (left panel) and its makeup (right panel). Left: All traces are discretized into 40 ms time-bins. The input to the model consists of the stimulus history over the last second as well as the timing of the previous bout within the past 2 seconds. The bout timing is used as the output in order to derive model coefficients by logistic regression. Time at which a bout occurred is labeled in red. Data shown is a 250 ms slice of one experiment. The panel on the right illustrates how the sensory filter k(t) and the history filter h(t) create a response which is transformed into a bout probability via a logistic nonlinearity.

(B) Coefficients of the temperature responsive part k(t) of the generalized linear model (GLM, grey) versus time before a bout. The blue trace indicates coefficients obtained from a control consisting of rotations of the temperature trace relative to the bout start times. Δ indicates filter part sensitive to increases in temperature in time while Σ indicates the 300 ms long main integrative part of the filter.

(C) Coefficients of the bout history responsive part h(t) of the GLM (grey) as well as shuffled control (blue) versus time before a bout. R indicates 240 ms refractory period after previous bout initiation. Shaded area in (B) and (C) indicates the bootstrap standard error. (N = 241,513 bouts)

(D) Heat map indicating the predicted probability of bout initiation based on the given constant temperature and time since the last bout.

(E) Plot of the Fourier transform of the sensory filter depicted in (B). Grey line indicates magnitude in dB of the filter at each frequency (log-log plot). Colored circles indicate frequencies tested behaviorally.

(F) Response magnitude across 50 fish that were stimulated with amplitude matched temperature fluctuations at 1 Hz, 3 Hz and 6 Hz. Error bars indicate bootstrap standard error, N = 450 trials each. Dashed black lines indicate predicted response magnitude given the response at 3 Hz based on the filter magnitudes at 1 Hz and 6 Hz respectively. (Average magnitudes: 3.4 × 10⁻³ at 1 Hz, 7.6 × 10⁻³ at 3 Hz, 2.9 × 10⁻³ at 6 Hz. Comparison of value predicted by frequency response to 1Hz, n.s., p = 0.13, comparison of value predicted by frequency response to 6Hz, n.s., p = 0.16, bootstrap hypothesis test).

(G)–(I) GLMs for bouts of different displacement (N=27543 bouts in each group).

(G) Average speed profiles during “Short”, “Medium” and “Long” bouts. Inset depicts endpoints of different bout categories if the fish were facing left (black circles delineate 2,4 and 8mm of displacement for orientation).

(H) Coefficients of the temperature responsive part k(t) of displacement category GLMs versus time before a bout.

(I) Coefficients of the bout history responsive part h(t) of displacement category GLMs versus time before a bout. Shaded areas in (H) and (I) indicate bootstrap standard errors.

(J) Absolute area of Temperature (yellow) and bout-history (blue) filter for groups of 25,000 bouts with the indicated average displacement relative to the area of filters with the lowest displacement (indicated by dashed grey line).

See also Figure S3.

By design, our models consist of two filters (Figure 3A), one for the transformation of sensory input (Figure 3B) and one revealing the influence of the time of the previous bout on the probability of swim initiation (Figure 3C). The sensory filter reflects the fact that larval zebrafish mostly consider temperature information in a 400 ms time window to guide swim initiation, which is revealed by comparison with a model derived from randomly shuffled data (Figure 3B). The sum of all filter coefficients is positive, which means that the fish increases its response with increasing temperature. Notably, we observe a trough of negative coefficients just before the large peak in the filter at 300 ms, suggesting that the filter effectively computes a positive derivative across heat in time around 350 ms before the start of the bout (Figure 3B). Swim initiation is therefore sensitive to both absolute temperature levels as well as increases in temperature.

The model’s bout history component indicates that bout generation is gated by a refractory period of 240ms after a previous bout was initiated (Figure 3C). A consequence of the individual components of the model is that bout probability is predicted to increase with increasing temperature and that this increase is suppressed by the refractory period (Figure 3D).

To test how well our model would generalize to new data we used a cross-validation approach. We randomly split our data into training sets of 80 experiments and test sets consisting of the remaining 20. We fit the model on each training set using it to predict response probabilities in the test set. Binning by probability we correlated predicted and observed bout counts, resulting in a correlation with r = 0.997 ± 0.002 while the slope of a linear fit between observed and predicted bout occurrences was 1.01 ± 0.07 indicating that the model generalizes very well to new data. Additionally, we used the cross-validation sets to assess the model’s performance as a classifier by receiver-operator-curve analysis. This analysis revealed that the model will rank a randomly chosen timepoint in which a bout occurred more highly than a randomly chosen timepoint between bouts in 71 ± 1% of cases, demonstrating that the model can classify bouts versus inter-bouts effectively.

The structure of the sensory filter suggests that the sensory system shows reduced sensitivity to fast fluctuations and adaptation to slow fluctuations in the heat stimulus. Specifically, the Fourier transform of the filter (Figure 3E) indicates that fish are especially sensitive to heat fluctuations around 3Hz. Since our “white-noise” stimulus did not probe all frequencies equally (Figure S2B) we tested this prediction by exposing an additional set of 50 fish to small, amplitude matched, laser fluctuations at 1, 3 as well as 6 Hz (Figure S3A–B). The 3 Hz stimulus indeed resulted in significantly greater modulation of response probabilities than the 1 or 6 Hz stimuli, while the average bout frequency was around 1.3 Hz in all cases (Figure 3F and Figure S3C–D; 3 vs. 1Hz, p = 8×10⁻⁴; 3 vs. 6 Hz, p = 6×10⁻⁶; bootstrap hypothesis test). The observed changes in response magnitude are different from the predictions based on filter structure (dashed black lines versus responses at 1 and 6Hz in Figure 3F) but this difference is not unexpected given the non-linearity of the system and the effect of bout history on swim initiation. In summary, our models show that fish integrate heat information over a limited timeframe of 400 ms and that movement initiation is both sensitive to absolute heat levels and changes in temperature.

Sensory information is differentially weighted to guide motor output

Larval zebrafish execute swim-bouts of different speeds and with different turn magnitudes (see traces in Figure 2A for examples) and these differences are controlled by different motor centers (Huang et al., 2013; Severi et al., 2014). We therefore wondered whether we could detect differences in sensory processing depending on swim speed or turn angle. To this end we fitted models relating temperature sensation and bout history to the initiation of bouts with differing swim kinematics.

To test whether distance moved within swim bouts effected the fish’s receptive field, we divided bouts into three bins according to their displacement (27,543 bouts each bin; Short bout = 0.9 mm, Medium bout d̄ = 1.7 mm, Long bout d̄ = 3.7 mm; inset in Figure 3G); these bins contain bouts in which fish achieve increasing instantaneous speeds during swims (Figure 3G). Fitting generalized linear models to these three categories revealed a continuous modulation of the temporal receptive field (Figure 3H). In particular, we observed a sharpening of the peak in the filter increasing the weighting of sensory information close to the bout start, as evidenced by an increase in the filter maximum together with the zero-crossing of the filter moving closer to the bout start (Figure 3H). Furthermore, we observed modulation of a negative filter component just before the bout start where coefficients become more negative for longer bouts. This indicates that drops in temperature proximal to a bout start bias larval zebrafish towards fast, extended swims.

Apart from the temperature filter there is also a slight modulation of the bout history component of the model, namely a stronger suppression of longer bouts after short bout intervals (Figure 3I). Since longer bouts are the result of faster swims (Figure 3G) and likely require a larger energy investment, we wondered whether there is a global difference in how larval zebrafish weight sensory information depending on a future choice of bout speed. To this end we fitted models on groups of bouts with increasing average displacements (N=25,000 bouts in each group) and calculated the respective areas of the temperature and history filter. A larger area causes the filter to be more sensitive to departures from the ideal stimulus and we therefore used the filter areas as measures of “importance” of the respective information in bout selection. The area of the temperature filter is correlated to bout displacement (r = 0.93) while the area of the bout-history filter shows a strong anti-correlation (r = −0.93). Overall, there is a more than 1.5 fold increase in the temperature filter area with increasing bout displacement and a slight decrease of the bout-history filter area (Figure 3J).

A similar analysis subdividing swims based on their turn magnitude revealed no consistent modulation of the temperature filter preceding different turns (Figure S3E–G). However, we note that turning seems to be insensitive to temperature drops before the start of a bout (Figure S3F). The strongest observable effect was that large turns are suppressed for intermediate inter-bout intervals (Figure S3G). Turn modulation also does not show a shift in weighting sensory versus history information as the areas of both model components show a decline with increasing turn magnitudes (Figure S3H; r = −0.77 for temperature filter and r = −0.98 for history filter). Cross validations, performed in the same manner as for the general bout model, indicate a similarly good generalization for all category models (Table S1). In summary we have shown that receptive fields differ for different bout types, especially for the modulation of displacement of individual swims. These differences argue that larval zebrafish weigh sensory information in order to select movement types.

The models accurately predict bout initiation and intervals

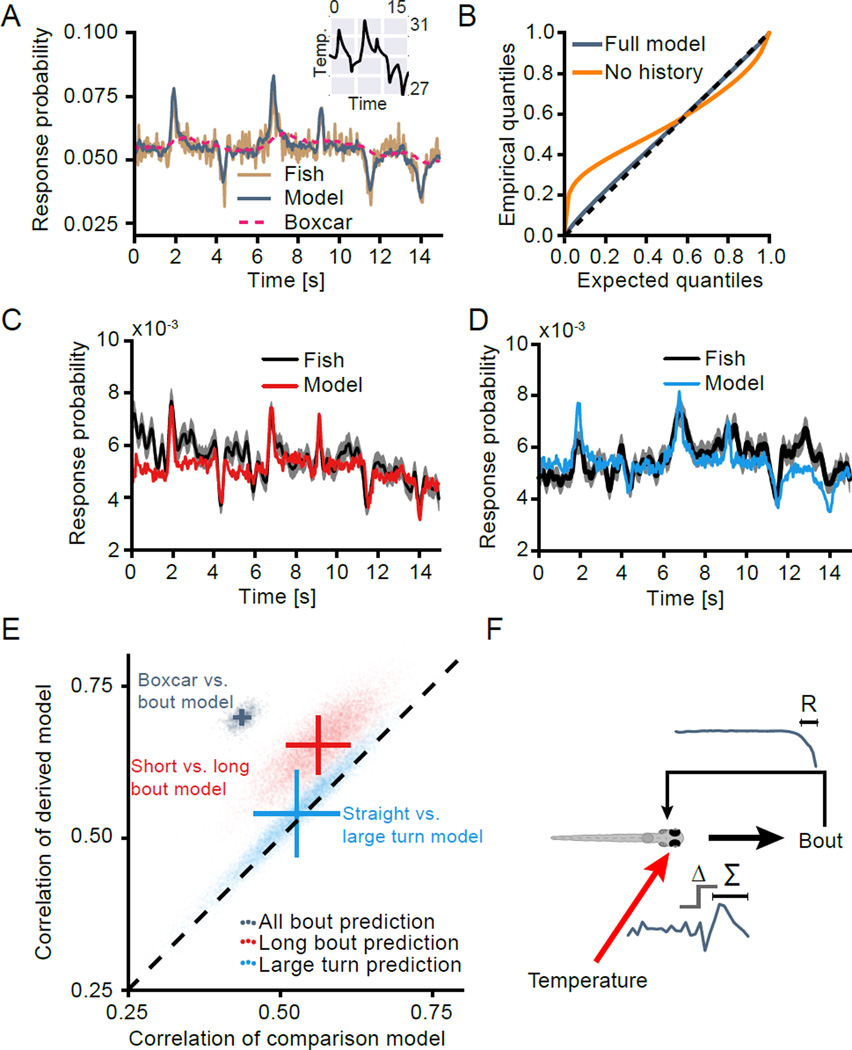
To determine the power of our models in predicting bout initiation outside the context of “whitenoise” presentation, we ran a second set of stimulations. These consisted of repetitive presentations of a 15 s long temperature stimulus. This stimulus was derived by concatenating 6 scaled, two-second-long, bout triggered stimulus averages interleaved with gaps at mean stimulus intensity (Figure 4A inset). The repetitive presentation allowed us to construct a peristimulus time-histogram (PSTH) of bout initiation probabilities and compare it to model instantiations in response to the same stimulus. Comparing model predictions and the PSTH across 50 fish (grey and brown lines in Figure 4A) reveals that the bout initiation model is good at capturing response dynamics induced by the varying temperature stimulus. We wanted to test whether this prediction accuracy relies on the filter structure. To this end we constructed a second, artificial model in which we replaced the sensory filter with a flat line integrating to the same value as the true model while fully preserving the history filter of the original model. We termed this model “boxcar model”. This model will report the same steady state bout probabilities as depicted in Figure 3D. However, the boxcar model fails at capturing the response dynamics, demonstrating that the structure of the temperature kernel is crucial for accurate prediction of behavior (dashed pink line in Figure 4A). Overall, across multiple bootstrap variates, the true model always has a higher correlation to the observed behavior than the boxcar model (r̄_model = 0.70, r̄_boxcar = 0.44).

Figure 4. Generalized linear models accurately predict swimming behavior.

(A) Comparison of predicted and actual bout probabilities in playback periods. Grey line indicates the response predicted by the generalized linear model given the temperature fluctuations during the playback phase. Brown line indicates actual response probabilities across 50 zebrafish during playback (peri-stimulus-time-histogram). Dashed pink line indicates response predictions for an alternate model with a flat temperature filter but the same history filter as the true model. This “Boxcar” model is constructed such that its response to steady state temperatures is the same as that of the general bout GLM. Inset depicts the temperature stimulus during playback trials.

(B) Comparison of expected and empirical quantiles of interbout interval distributions after application of the time rescaling theorem. Rescaling based on the prediction of the full model is shown in grey, a model that is heat responsive but lacks a history component is shown in orange. Dashed line marks the identity, which is the expected fit of a model that perfectly captures observed inter-bout-intervals.

(C, D) Comparison of predicted and actual bout probabilities in playback periods. Red and blue lines indicate the response predicted by the long bout and large turn generalized linear models respectively. Black lines indicate actual response probabilities across 50 zebrafish during playback for the respective bout category, filtered with a window size of 125 ms. Shaded area indicates bootstrap standard error.

(E) Comparison of correlation of predictions during playback periods versus true response probabilities between the model derived from the given bout-type (y-axis) and a comparison model (x-axis) for 10000 bootstrap samples each. Grey cloud compares the performance of a boxcar model with the general bout model in predicting general bouts. Red cloud compares the performance of the “Long-bout” model and the “Short-bout” model in predicting long bouts. Blue cloud compares the performance of the “Large-turn” model and the “Straight-bout” model in predicting large turns. Crosses indicate the mean correlation with bars depicting bootstrap standard errors.

(F) Schematic depiction of how temperature history and self-generated behavior influence bout decisions in larval zebrafish.

See also Figure S4.

Next we sought a way of determining whether our model captures the statistics of bout initiation well, in other words, whether it can explain interbout intervals observed during the experiment. For this analysis we made use of the time-rescaling theorem, which allows us to re-map observed swim intervals using the response probabilities predicted by the model for each individual timepoint. If our model reflects the true bout initiation process, the remapped latencies should be uniformly distributed on the interval [0, 1). Comparison of expected and observed quantiles of this distribution is shown in Figure 4B (grey line). The juxtaposition to the identity line revealed that the model is indeed nearly complete in capturing the bout initiation process. This performance, however, crucially relies on the bout history component of the model as a comparison model refit without this component fails to reproduce the observed bout latencies (Figure 4B, orange line). In particular, a model that assumes purely sensory driven bout-initiation overestimates short latencies, due to a lack of a refractory period.

The displacement and turn category models also had good power in predicting bouts of the same category during playback (Figure 4C–D). However, predictive power was lower than for the model predicting initiation of all bouts, which is expected since the category models are each derived from a much smaller number of bouts (on the order of 12 %). In addition, we could use the playback period to test whether the observed differences in the model filters carry meaning. If they do, we would expect bouts in a given category to be better predicted by their own model type than by a different category model. For displacement modulation, long bouts during playback are indeed significantly better predicted by the long bout model than the short bout category model (99.8% of bootstrap variates; Figure 4E), while large turns on the other hand are not significantly better predicted by the large turn model than the straight bout model (better in only 80.3% of bootstrap variates; Figure 4E). Similar results are obtained when the intermediate models (medium bout model and small turn model) are used to predict bouts from the more extreme categories (data not shown).

Apart from predicting average fish data we wondered how model predictions of single fish data would compare with fish-to-fish variability of responses. Behavior during playback periods was variable with an average correlation of r̄ = 0.32 between fish considering all bouts. Model predictions of individual fish behavior had an average correlation of d̄ = 0.33 to single fish data indicating that our model has the same predictive power over single fish behavior as knowing the response of another fish. Correlations for bout category models were overall lower, as expected, and fish-to-fish correlations were often lower than correlations between the model and individual fish (Figure S4). This indicates that our model does not fully capture fish variability but rather predicts an average behavior.

In summary our model of heat-driven swim initiation is accurate in predicting behavioral responses outside the “white-noise” stimulation context. Furthermore, it encompasses most information that is necessary to describe the observed behavioral parameters. Playback validation also revealed that differences in bout category models are meaningful as prediction accuracy improves if a model from the same category as the predicted bout is used.

Discussion

A major goal in neuroscience is to understand how nervous systems generate appropriate motor outputs in response to sensory information. Recent advances in imaging and recording techniques allow observing large parts of the nervous system in behaving animals, making it possible to relate sensory stimuli and motor output to neural activity (Ahrens et al., 2013; Giocomo, 2014; Portugues et al., 2014). However, to understand these large datasets, it is important to know how sensory information is transformed into behavioral output and which sensory features are relevant for guiding motor actions. Models of input-output transformations have led to important insights into processes as diverse as contrast adaptation in the retina (Baccus and Meister, 2002) and bacterial chemotaxis (Block et al., 1982). During thermotaxis, E. coli, C. elegans and Drosophila larvae respond to temperature changes by changing the bias between turns and straight runs and studies of these sensorimotor transformations suggest that this modulation depends on both absolute levels as well as changes in temperature (Clark et al., 2007; Klein et al., 2015; Paster and Ryu, 2008; Ryu and Samuel, 2002).

In the present study we investigated the transformation of thermosensory information to swim initiation in freely swimming larval zebrafish. Random white noise stimuli have been used to map receptive fields of diverse neuronal types such as visual receptive fields in the retina (Sakai et al., 1988) or spectro-temporal as well as spatial receptive fields in auditory neurons (Hermes et al., 1981; Jenison et al., 2001). Here we use a similar stimulus set to relate thermosensory input to behavioral output, effectively mapping the temporal receptive field of heat perception in larval zebrafish. By fitting generalized linear models relating thermosensory input to swim bout initiation we could demonstrate that larval zebrafish integrate temperature information mostly over short timescales of 400 ms to decide on bout initiation (Figure 3B). These timescales do not seem to vary with interbout interval and are considerably shorter than recently reported for Drosophila larvae, which seem to integrate temperature over multiple seconds to decide on changes in their run mode (Klein et al., 2015). However, with inter-bout-intervals on the order of 1 s in unstimulated fish, the observed integration time seems well matched to behavioral output (Figure 2D). Also humans will report temperature changes within 700 ms after reaching perception threshold (Yarnitsky and Ochoa, 1991), a timeframe that may reflect integration times similar to larval zebrafish. The temperature filter of our model indicates sensitivity to both absolute heat levels and changes in temperature effectively leading to fast responses after a step-change in temperature followed by adaption. Fast timescale adaptation is common in sensory systems and has been observed in bacterial chemotaxis (Block et al., 1982), mammalian thermosensory fibers (Duclaux and Kenshalo, 1980; Schepers and Ringkamp, 2010) and recently also in thermosensory projection neurons in adult Drosophila (Frank et al., 2015; Liu et al., 2015). This computational makeup endows larval zebrafish with the ability to react to temperature changes over a wide range of absolute temperatures and may help explain why very small temperature changes on the order of 0.1 °C can be used as conditioned stimuli in fish (Bull, 1936).

By subdividing swim-bouts according to covered distance or associated turn angle we could show that temporal receptive fields differ depending on swim types (Figure 3G–J and Figure S3E–H). This indicates that different bout types are preferentially triggered by different stimuli. We observed incremental changes in the temporal receptive field when considering bouts of different displacement. Notably, there is a clear increase in a second negative lobe proximal to the bout start for swims of larger displacement while the area of this lobe is smaller for large turns compared to straight swims. This might indicate that if fish performed a reorienting maneuver that led to improved, cooler conditions, they subsequently perform a long straight swim, a strategy that potentially aids in heat avoidance. Globally we observed a shift in model sensitivity towards sensory information over bout history with increasing bout displacement, which suggests that fish undertake more energy intensive maneuvers only after appropriate sensory input. This is not the case for increasing turn magnitude, however. Turn angle changes only require modulation of the first tail undulation (Huang et al., 2013) contrary to modulations in swim speed (Severi et al., 2014), hence the increase in energy investment is likely smaller for increasing turn magnitude than for increasing displacement. Overall the observed changes in receptive fields are small and likely only reflect changing biases in sensory processing rather than causing changes in bout displacement such as those observed in our gradient experiment (Figure S1F).

Larval zebrafish avoid cold as well as hot temperatures (Gau et al., 2013) and in theory our receptive fields may reflect these two opposing phenomena. However, given the average temperature of our stimulus (29 °C) with a lower limit of 22 °C it is unlikely that we probed any cryophobic responses. It is important to note that the derived filters likely reflect the synthesis of multiple parallel computations with potentially differing “ideal stimuli”. This effect may for example be reflected in the changes observed in the negative lobe proximal to bout start upon changes in bout displacement. These changes may reflect changing dominance between circuits preferentially responding to heating versus circuits preferentially responding to cooling. An example for such parallel processing lines was recently uncovered in the Drosophila nervous system where thermosensory projection neurons preferentially signal ON and OFF responses independently (Frank et al., 2015). Parallel channels like these may underlie the complex filters we observe that relate sensory input to motor output on a whole-organism level.

In summary, our study reveals how thermosensory information is transformed into behavioral actions in larval zebrafish (Figure 4F). We identified the temporal receptive fields of heat perception and derived models that accurately capture behavioral responses to dynamic temperature stimuli. In total, we showed that larval zebrafish integrate temperature information over fast timescales, making them react quickly to temperature changes. Our models also suggest that zebrafish increase weighting of sensory information over internal state when selecting more energy-intensive maneuvers. These models put important constraints on the computations that are carried out by the nervous system and will assist in designing functional imaging experiments that can further delineate the neuronal circuits underlying these sensorimotor transformations.

Materials and Methods

All experiments were conducted on 9–11 dpf zebrafish larvae of an outcross between TL and AB wild types, fed powder food from day 5 onwards. All experiments followed the guidelines of the National Institutes of Health and were approved by the Standing Committee on the Use of Animals in Research of Harvard University.

Behavioral apparatus

While larval zebrafish were freely exploring their arena in the dark we acquired images at 250 Hz extracting their position and heading angle in realtime using custom written software. This position information was used to set the angles of a set of two scan-mirrors such that the beam of a 980nm laser was centered on the center of mass of the fish object at all times. The power of the infrared diode laser was controlled according to the behavioral paradigm. A similar setup was recently used to exogenously activate neurons in freely walking Drosophila adults (Bath et al., 2014).

A fish-sized thermistor was used to derive a simple model relating laser power to temperature in order to fit models relating temperature rather than laser power to behavior. See Supplemental Materials for a detailed description of the setup and temperature calibration.

Behavior

Experiments were conducted in the dark in a circular arena made of clear acrylic with a diameter of 11 cm and a water depth of 4 mm.

WHITE NOISE

After a 10 minute long habituation phase fish were stimulated for 1 minute followed by a 1 minute long rest period. These cycles were repeated 44 times per fish.

In pure white-noise experiments (N = 50 fish) the stimulus consisted of laser power values drawn randomly from a Gaussian distribution (μ = 1200 mW, σ = 450 mW). Power levels switched on average every 200 ms with switching times drawn from a Gaussian distribution as well (σ = 48 ms).

Another experimental set (N = 50 fish) included playback periods. For these fish every 1 minute stimulation period was divided into four 15 s long stretches. The first and third stretch consisted of white noise stimulation as above while the second and fourth consisted of a fixed sequence of laser powers to assess model performance.

For analysis purposes our temperature model was used to convert laser power traces to fish temperature traces. All models were fit on temperatures rather than laser powers. The autocorrelation time of the temperature stimulus was defined as the time where the autocorrelation decays to 1/e and was estimated according to (Thompson, 2010).

See supplemental materials and methods for a description of the other behavioral protocols.

DATA ANALYSIS

Fish that completed all trials were included in the analysis. Occasionally fish would stop moving during the assay or would not move at normal frequency during an experiment’s habituation phase. Such experiments were stopped and not used for analysis.

Extracted fish positions and heading angles were used to identify periods of swimming (bouts) and intermittent rest phases (inter-bouts) and to assign overall displacement and turn angles to all bouts (see Supplemental Methods for details). Only white-noise stimulation phases of experiments were considered for model fitting. To describe the behavior both in relation to temperature input and previous bout time, generalized linear models were fitted to the data, assuming a binomial distribution for the output (bout vs. no bout) and using a logistic function as the link.

Our models predict the probability of a bout to occur in a time bin (40 ms) given the heat stimulus experienced by the fish in the past second u⃗(t) and given the timing of the fish’s last bout in the past two seconds n⃗(t). Bout history was limited to 2 s since less than one percent of bouts during stimulation phases occurred more than 2 s after a previous bout start. The models are composed of two filter kernels as per equation (1), the temporal receptive field of heat perception k⃗ as well as the history term h⃗, which encompasses refractive periods or bursting in bout generation.

$$r(t)=b_0+{\overrightarrow{k}}^T\overrightarrow{u}(t)+{\sum }_{i=1}^{50}{h}_i{n}_{t-i}|n_{t-i}=\{\begin{array}{cc}1\hfill & \mathit{\text{if}}(t-i)\mathit{\text{is time of last bout}}\hfill \\ 0\hfill & \mathit{\text{otherwise}}\hfill \end{array}$$ (1)

Given the response r(t) to sensory heat perception and internal bout state, the bout probability is then given by a simple logistic transformation of the response:

$$p(\mathit{\text{bout}}|r(t))=\frac{e^{r(t)}}{1+e^{r(t)}}$$ (2)

See Supplemental Materials for further details and fitting of bout category models and Table S2 for the constant terms.

MODEL VALIDATION

For model cross-validations the data was split randomly into a training set containing 80% of our experiments and a test set consisting of the remaining experiments. Models were fitted on the training set and two metrics were computed on the test set to assess model performance. First, the models were used to predict probability of bout occurrence for each time point in the test set. Binning time points by predicted probability the number of expected bouts in each probability bin was determined and the correlation as well as the slope of the fit between these predicted numbers and the real number of bouts per bin in the test set were computed. Second, the classifier performance of our model was estimated by computing the area under the ROC curve for classifying bout versus inter-bout frames in the test set.

The time rescaling theorem was employed (Brown et al., 2002) to test how accurately our general bout model can predict bout latencies, see Supplemental Materials for details. The playback periods were used to test how well our models predict responses to changes in temperature. Specifically, the models were used to predict the probability of bout initiation according to (1, 2) and then bouts were instantiated according to these probabilities. Since the history part of our models depends on general bout occurrence rather than specific categories, when instantiating bout categories, the model predicting all bouts was used to instantiate bouts as well. The average of 100,000 instantiations was then compared to the PSTH derived from experimental data. Fish were found to be overall more active during playback than white-noise stimulation periods even though the average temperature is the same (1.1 fold increase in bout frequency). Since models are derived from the white-noise periods, predicted probabilities were corrected by this factor.